Numerical Simulation of the Hot Rolling Process of Steel Beams
Abstract
:1. Introduction
2. Materials and Methods
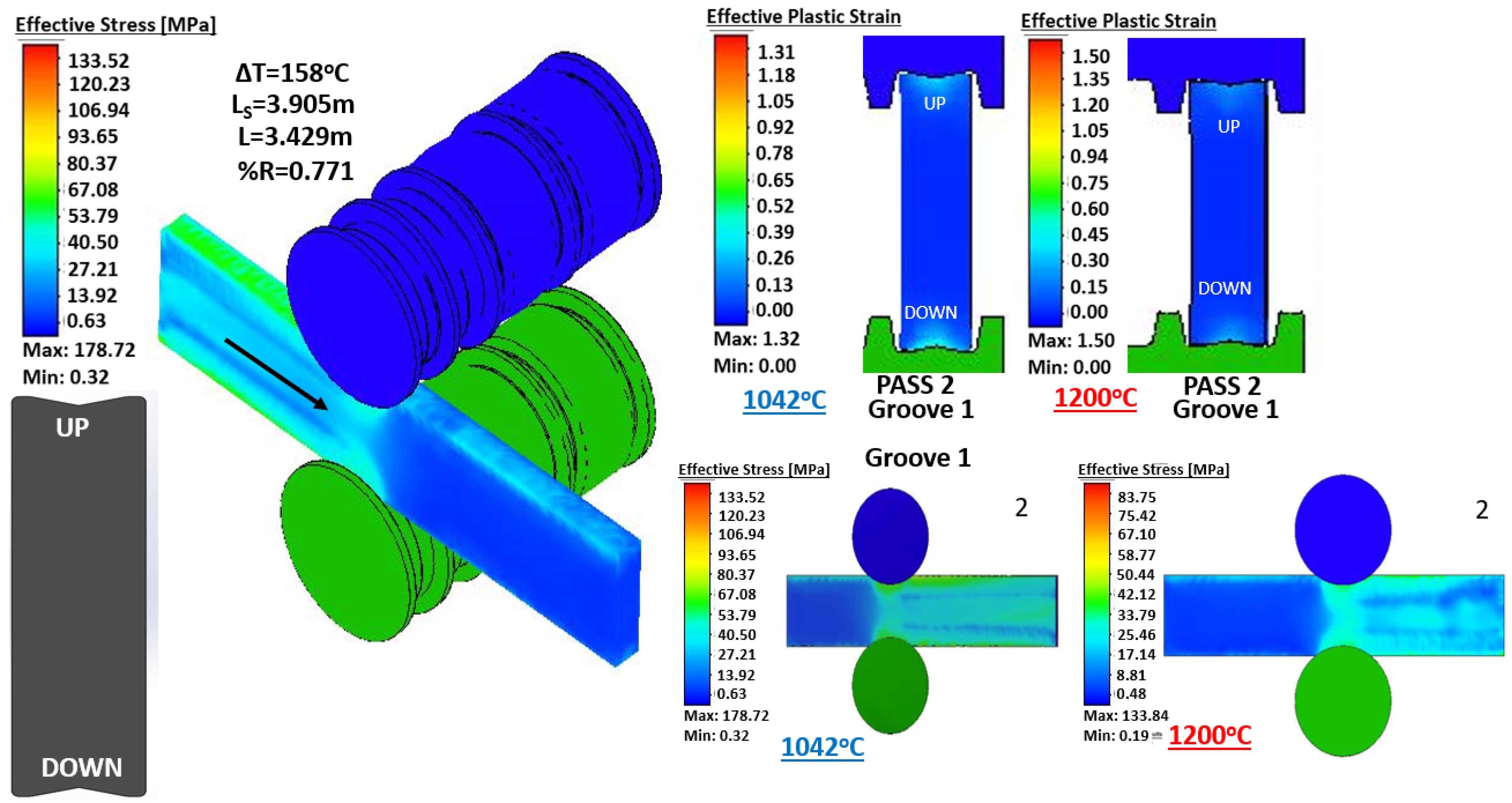
3. Results and Discussion
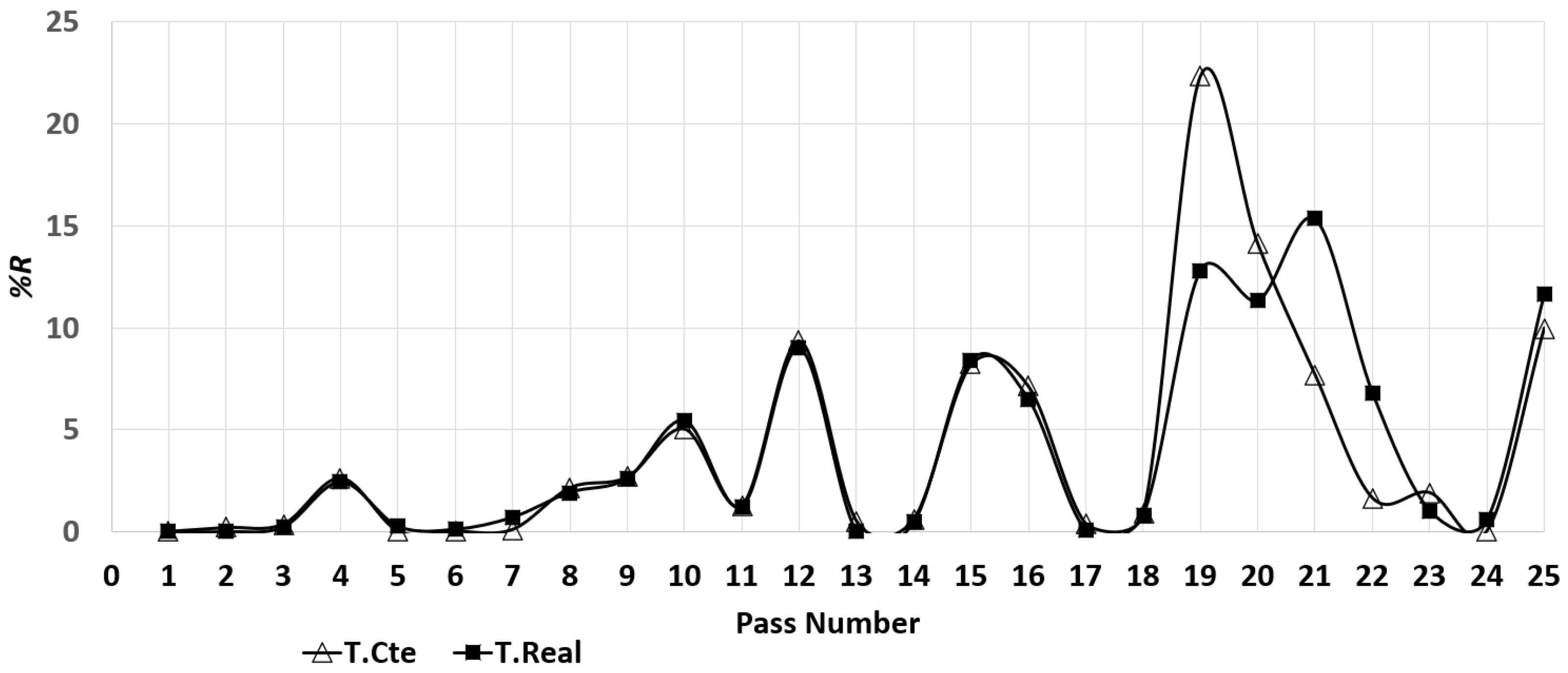
Comparison between Hot Rolling Process at Constant Temperature and Real Temperature
4. Conclusions
- The use of a FEM sofware to simulate 25 consecutive passes of hot rolling allowed to determine the distribution of effective stress, effective plastic strain, rolling moment, rolling power, final length and area of cross-section of the beam at each rolling pass. The results were in good agreement with those obtained from in-plant measurements.
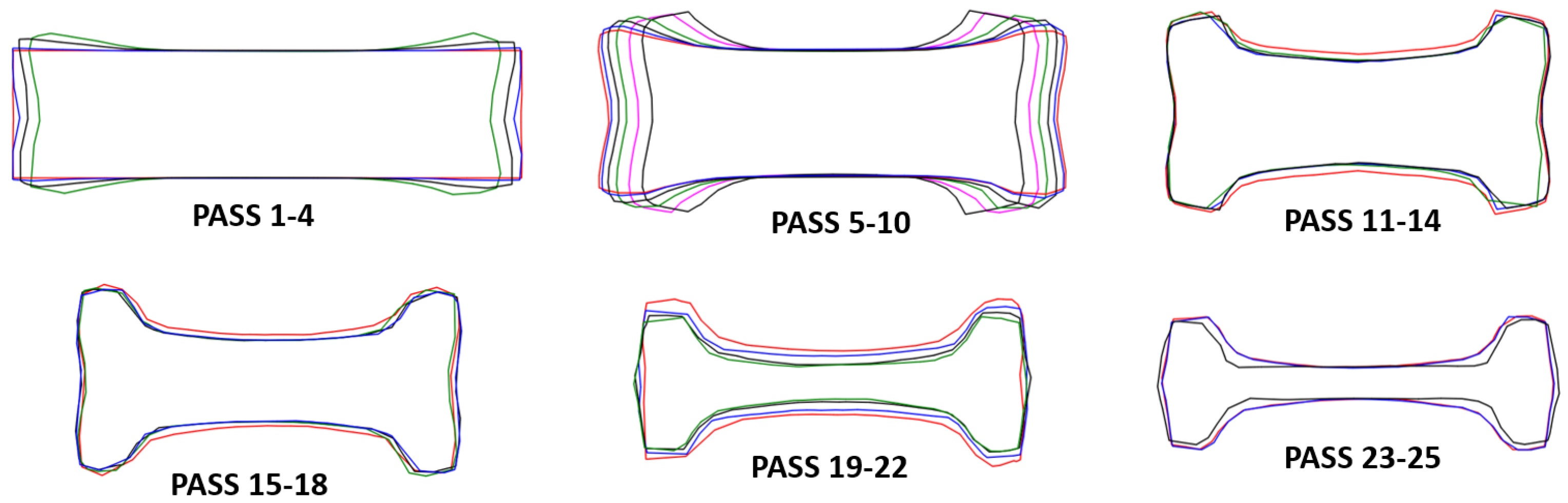
- The numerical simulation was validated comparing the geometry of the cross-section with in-plant measurements after the 25 passes, reporting a very similar shape and deviation of only 2.37% in area.
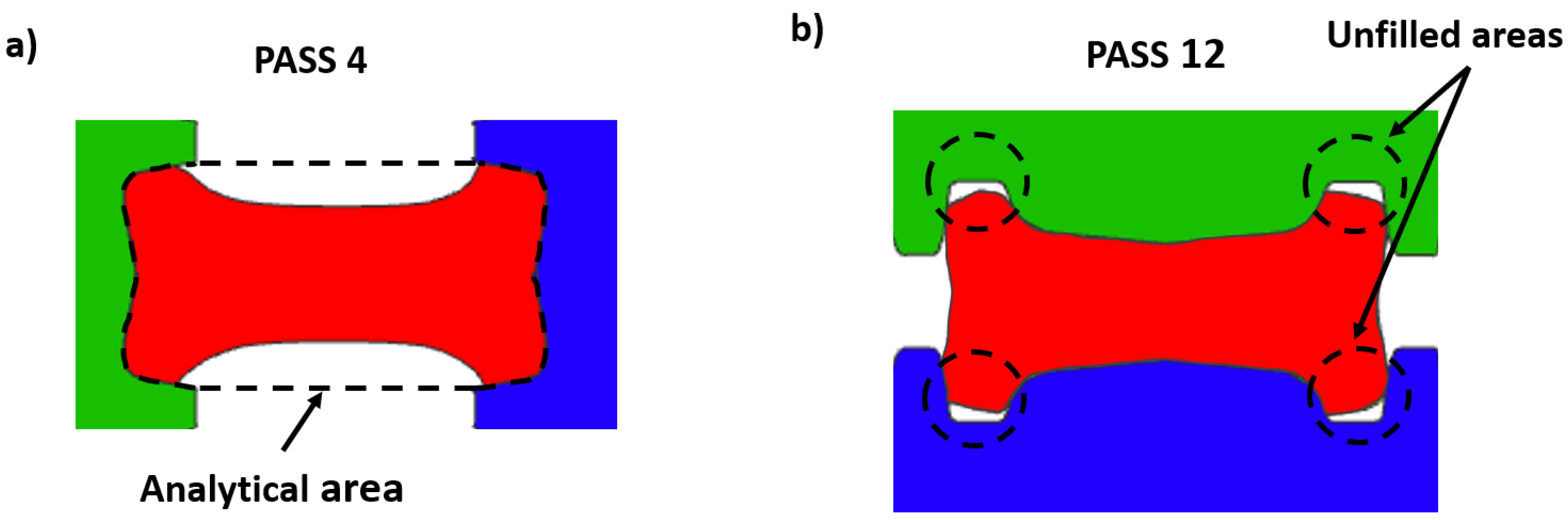
- In the simulations, the reduction of cross-sectional area predicted unfilled areas between the work rolls, a common observation in the real process. This topic is very extensive and interesting to dedicate a future complete article in order to study the methodology of correct groove-roll design.
- The incorrect metal heating before the rolling process might result in substantial quality defects and possible damage in the mill due to the excessive demand of power to roll the cold material. Proper deformation and metal flow depends, among others, on the uniform heating of the beam prior to the beginning of the rolling.
- This study demonstrates the usefulness of the mathematical simulation to observe and quantify details essentially imposible to obtain in the production plant, which can be the key to obtain high quality products and minimize economic losses due to rejections and defects in production.
- Using the present research methodology, it is possible to save time, money and have a better control of the process, generating the possibility of innovating in the production of profiles with more complex geometries and new materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kurt, G.; Yaşar, N. Comparison of Experimental, Analytical and Simulation Results for Hot Rolling of S275JR quality Steel. J. Mater. Res. Technol. 2020, 9, 5204–5215. [Google Scholar] [CrossRef]
- Kwon, H.C.; Im, Y.T. Interactive Computer-Aided-Design System For Roll Pass and Profile Design in Bar Rolling. J. Mater. Process. Technol. 2002, 123, 399–405. [Google Scholar] [CrossRef]
- Mori, K.; Osakada, K.; Oda, T. Simulation of Plane-Strain Rolling by the Rigid-Plastic Finite Element Method. Int. J. Mech. Sci. 1982, 24, 519–527. [Google Scholar] [CrossRef]
- Nalawade, R.S.; Marje, V.R.; Balachandran, G.; Balasubramanian, V. Effect of Pass Shedule and Groove Design on the Metal Deformation of 38Mn VS6 in the Initial Passes of Hot Rolling. Sadhana 2016, 41, 111–124. [Google Scholar] [CrossRef] [Green Version]
- Ståhalberg, U.; Göransson, A. Heavy Reductions by Means of ’Non-Bite’ Rolling, Including some Observations on Workpiece Shape. J. Mech. Work. Technol. 1986, 12, 373–384. [Google Scholar] [CrossRef]
- Lee, Y.; Choi, S.; Kim, H.; Choo, W.Y. An experimental study of the mean effective strain in rod (or bar) rolling process. Met. Mater. Int. 2000, 6, 525–531. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, S.I.; Choi, S.; Jang, B.L.; Choo, W.Y. Mathematical model to simulate thermo-mechanical controlled processing in rod (or bar) rolling. Met. Mater. Int. 2001, 7, 519–530. [Google Scholar] [CrossRef]
- Mróz, S.; Jagiela, K.; Dyja, H. Determination of the energy and power parameters during groove-rolling. J. Achiev. Mater. Manuf. Eng. 2007, 22, 59–62. [Google Scholar]
- Shahani, A.; Nodamaie, S.; Salehinia, I. Parametric Study of Hot Rolling Process by the Finite Element Method. Sci. Iran. 2009, 16, 130–139. [Google Scholar]
- Licheng, Y.; Jinchen, J.; Jinxiang, H.; Liwei, N. Prediction of Process Parameters on Stress and Strain Field in Hot Rolling Process Using Finite Element Method. J. Inf. Technol. 2011, 10, 2406–2412. [Google Scholar]
- Nalawade, R.S.; Puranik, A.J.; Balachandran, G.; Mahadik, K.N.; Balasubramanian, V. Simulation of Hot Rolling Deformation at Intermediate Passes and its Industrial Validity. Int. J. Mech. Sci. 2013, 77, 8–16. [Google Scholar] [CrossRef]
- Braga, F.V.; Escobar, E.P.; Ávila, T.J.R.; de Oliveira, N.J.L.; Andrade, M.S. Recrystallization of Niobium Stabilized Ferritic Stainless Steel During Hot Rolling Simulation by Torsion Tests. J. Mater. Res. Technol. 2016, 5, 92–99. [Google Scholar] [CrossRef] [Green Version]
- Rout, M.; Pal, S.K.; Singh, S.B. Prediction of edge profile of plate during hot cross rolling. J. Manuf. Process. 2018, 31, 301–309. [Google Scholar] [CrossRef]
- Hanoglu, U.; Šarler, B. Rolling Simulation System for Non-Symmetric Groove Types. Procedia Manuf. 2018, 15, 121–128. [Google Scholar] [CrossRef]
- Rappaz, M.; Bellet, M.; Deville, M.O.; Snyder, R. Numerical Modeling in Materials Science and Engineering; Springer: Berlin, Germany, 2003; pp. 309–310. [Google Scholar]
- Duan, X.; Sheppard, T. Prediction of Temperature Evolution by FEM During Multi-Pass Hot Flat Rolling of Aluminum Alloys. Model. Simul. Mater. Sci. Eng. 2001, 9, 525–538. [Google Scholar] [CrossRef]
- Byon, S.M.; Kim, S.I.; Lee, Y. Predictions of roll force under heavy-reduction hot rolling using a large-deformation constitutive model. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 483–494. [Google Scholar] [CrossRef]
- Shah, S.M.; Nélias, D.; Coret, M. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel. Finite Elem. Anal. Des. 2012, 61, 1–11. [Google Scholar] [CrossRef] [Green Version]
- MSC Corporation. Marc, Feature Pack 1, Volume A: Theory and User Information; MSC Software Corporation: Newport Beach, CA, USA, 2019; pp. 1–1039. [Google Scholar]
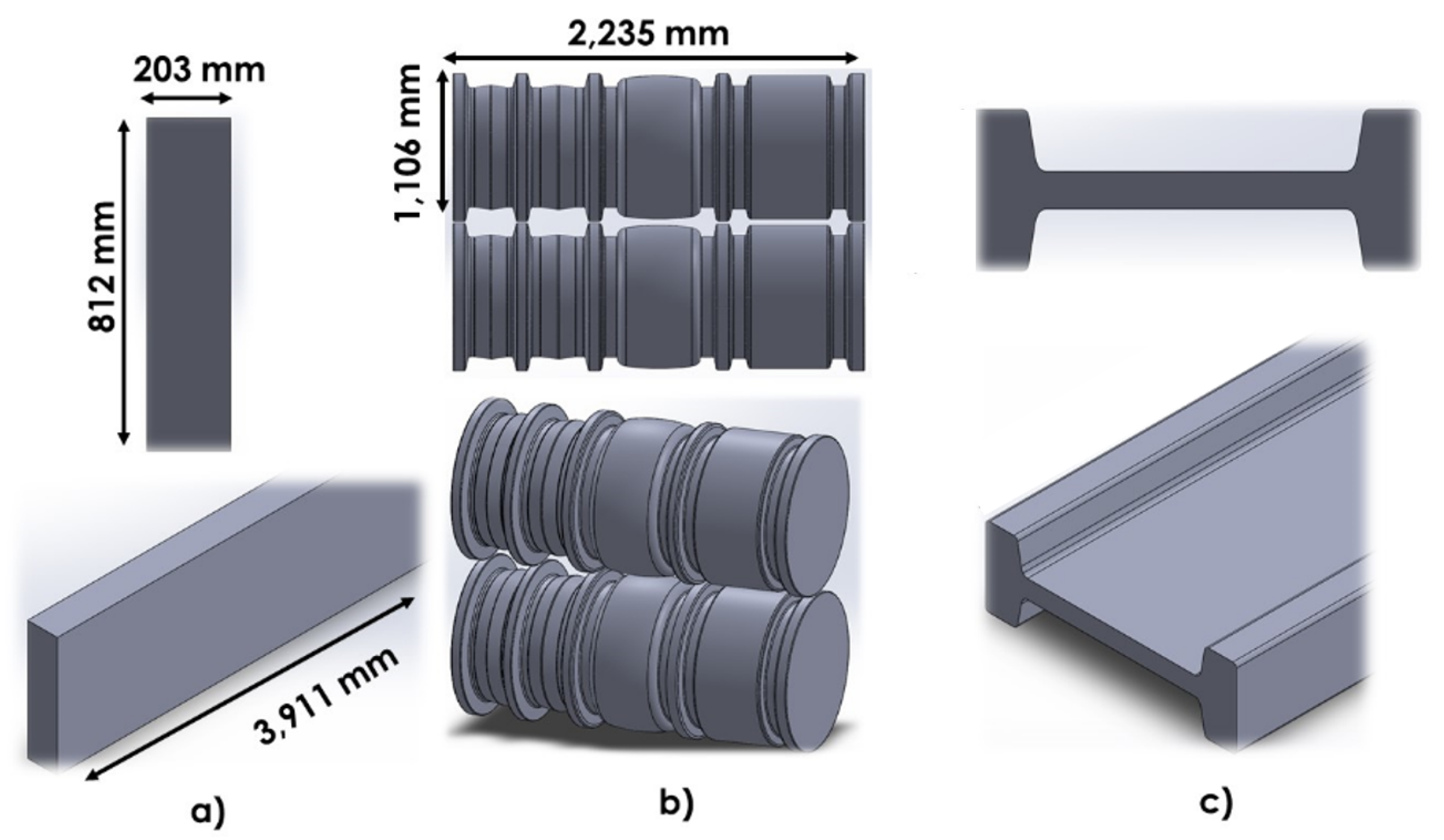







| Model Parameter | Value |
|---|---|
| Billet cross section | 812 × 203 |
| Billet length | 3911 |
| Input billet temperature | 1200 |
| Initial temperature of rolls | 65 |
| Work roll diameter | 1104.90 |
| Work roll barrel length | 2184.40 |
| Heat transfer coefficient | 50 |
| Coefficient of friction | 0.3–0.4 in function of temperature |
| Thermal conductivity | 26–29 in function of temperature |
| Thermal expansion | |
| Billet us specific heat capacity | 640–660 in function of temperature |
| Billet us density | 7850 |
| Poisson’s ratio of billet | 0.3 |
| Young’s modulus of billet | 90–130 GPa in function of temperature |
| Revolutions per minute RPM | 60–65 depending on pass |
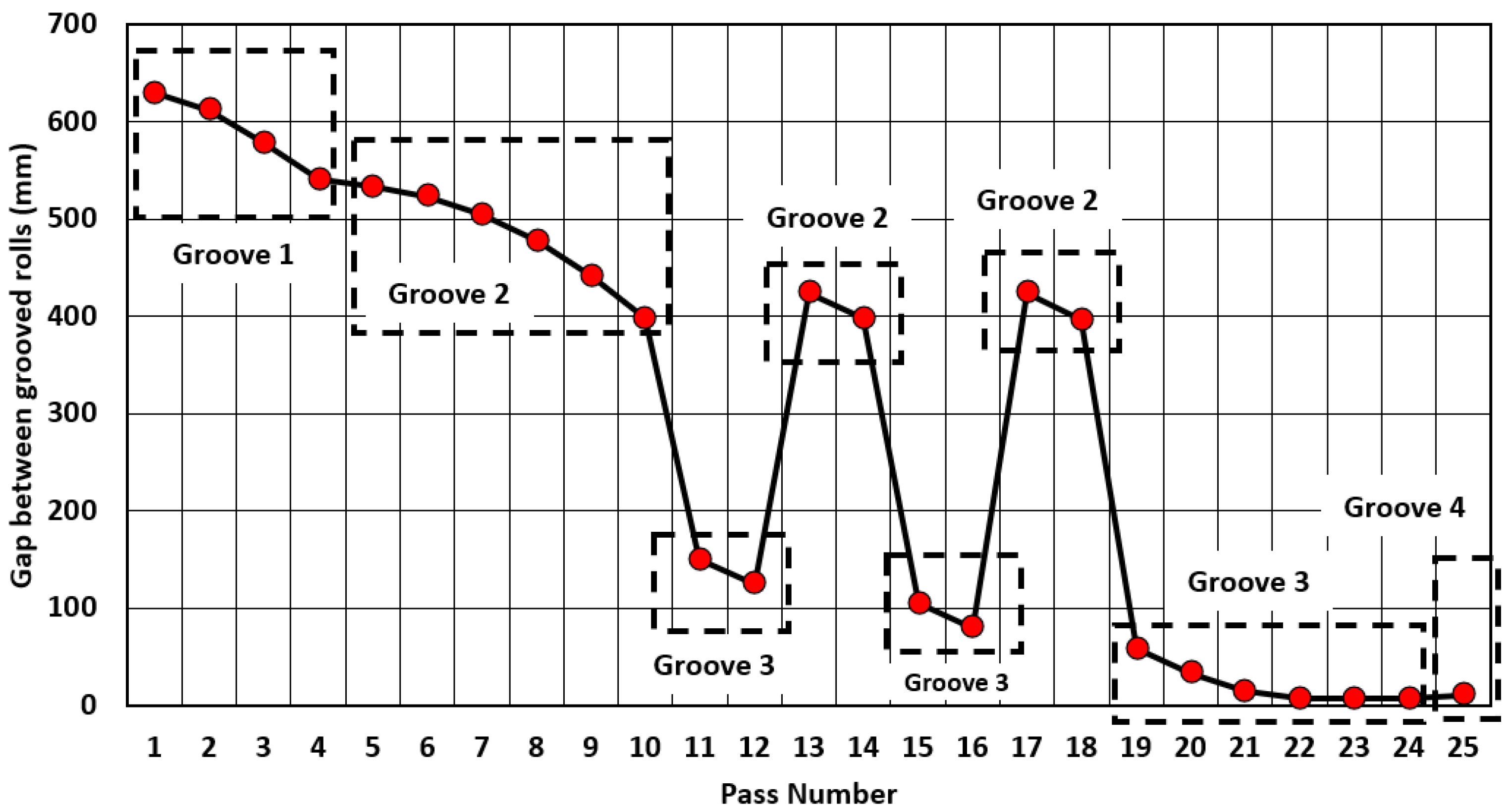
| Pass | Gap | Hot Mill Direction | Groove | RPM | Beam Orientation |
|---|---|---|---|---|---|
| 1 | 630 | Forward | 1 | 65 | Initial orientation |
| 2 | 612 | Backward | 1 | 65 | |
| 3 | 579 | Forward | 1 | 65 | |
| 4 | 541 | Backward | 1 | 65 | |
| 5 | 533 | Forward | 2 | 65 | |
| 6 | 523 | Backward | 2 | 65 | |
| 7 | 505 | Forward | 2 | 65 | |
| 8 | 477 | Backward | 2 | 65 | |
| 9 | 441 | Forward | 2 | 65 | |
| 10 | 398 | Backward | 2 | 65 | clockwise rotation |
| 11 | 149 | Forward | 3 | 60 | clockwise rotation |
| 12 | 124 | Backward | 3 | 60 | |
| 13 | 424 | Forward | 2 | 65 | clockwise rotation |
| 14 | 399 | Backward | 2 | 65 | |
| 15 | 105 | Forward | 3 | 65 | clockwise rotation |
| 16 | 80 | Backward | 3 | 65 | |
| 17 | 424 | Forward | 2 | 65 | clockwise rotation |
| 18 | 396 | Backward | 2 | 65 | |
| 19 | 58 | Forward | 3 | 65 | clockwise rotation |
| 20 | 33 | Backward | 3 | 65 | |
| 21 | 15 | Forward | 3 | 65 | clockwise rotation |
| 22 | 6 | Backward | 3 | 65 | |
| 23 | 6 | Forward | 3 | 65 | clockwise rotation |
| 24 | 6 | Backward | 3 | 65 | |
| 25 | 10 | Forward | 4 | 65 |
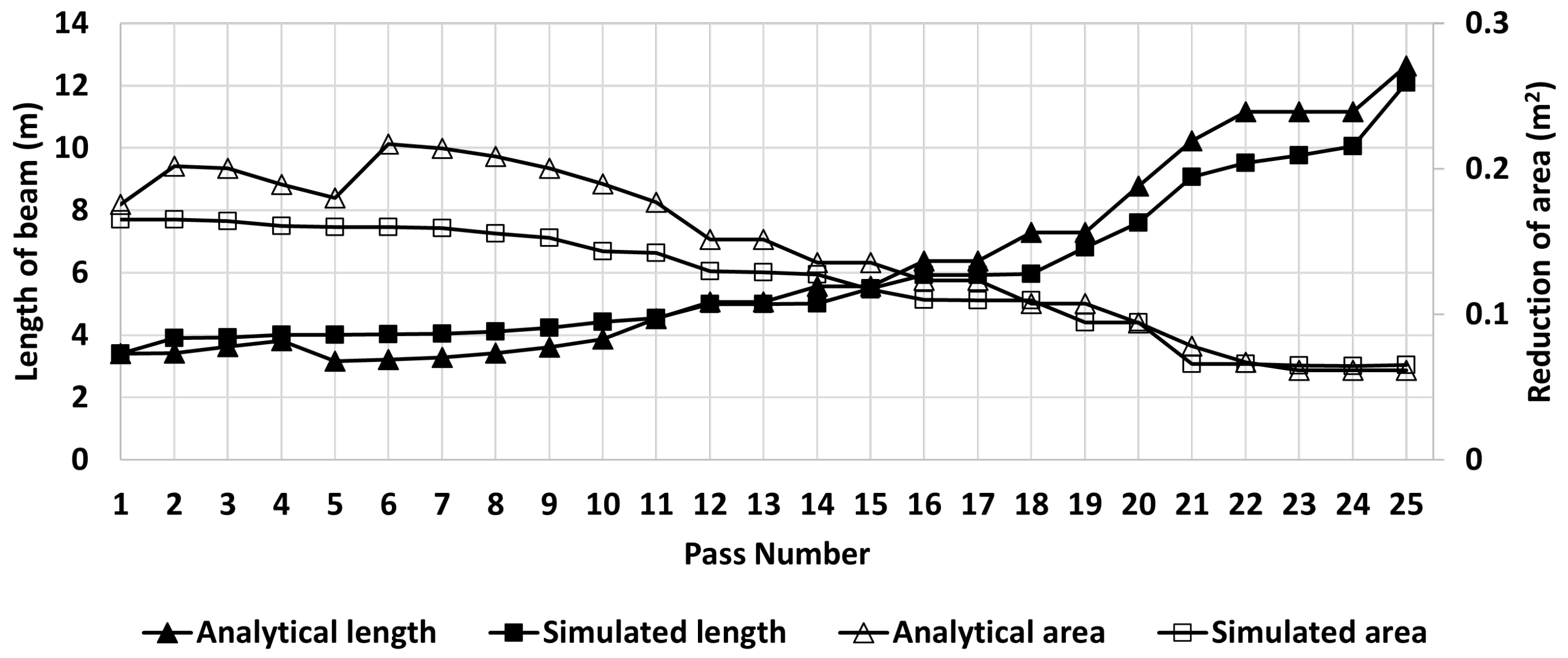
| Pass | %R | L (mm) | Pass | %R | L (mm) |
|---|---|---|---|---|---|
| 1 | 14.97 | 3402.26 | 14 | 8.39 | 5559.95 |
| 2 | 0.77 | 3428.68 | 15 | 8.93 | 5668.32 |
| 3 | 5.42 | 3625.43 | 16 | 12.9 | 6383.60 |
| 4 | 4.91 | 3812.91 | 17 | 13.1 | 6895.20 |
| 5 | 20.5 | 3164.17 | 18 | 12.45 | 7291.50 |
| 6 | 1.39 | 3208.84 | 19 | 12.45 | 7301.23 |
| 7 | 2.46 | 3290.00 | 20 | 16.92 | 8777.06 |
| 8 | 3.97 | 3426.25 | 21 | 14.26 | 10,237.22 |
| 9 | 5.27 | 3616.92 | 22 | 8.31 | 11,165.44 |
| 10 | 6.75 | 3878.94 | 23 | 0 | 11,165.44 |
| 11 | 14.38 | 4530.74 | 24 | 0 | 11,165.44 |
| 12 | 10.51 | 5063.07 | 25 | 11.62 | 12,653.51 |
| 13 | 10.51 | 5063.07 |
| Pass Number | Temperature (C) | Pass Number | Temperature (C) |
|---|---|---|---|
| 1 | 1049 | 14 | 904 |
| 2 | 1042 | 15 | 900 |
| 3 | 1035 | 16 | 916 |
| 4 | 1019 | 17 | 932 |
| 5 | 1003 | 18 | 917 |
| 6 | 948 | 19 | 902 |
| 7 | 892 | 20 | 882 |
| 8 | 934 | 21 | 863 |
| 9 | 975 | 22 | 869 |
| 10 | 947 | 23 | 875 |
| 11 | 919 | 24 | 872 |
| 12 | 913 | 25 | 869 |
| 13 | 907 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Alvarado, A.; Arreola-Villa, S.A.; Calderón-Ramos, I.; Servín Castañeda, R.; Mendoza de la Rosa, L.A.; Chattopadhyay, K.; Morales, R. Numerical Simulation of the Hot Rolling Process of Steel Beams. Materials 2021, 14, 7038. https://doi.org/10.3390/ma14227038
Pérez-Alvarado A, Arreola-Villa SA, Calderón-Ramos I, Servín Castañeda R, Mendoza de la Rosa LA, Chattopadhyay K, Morales R. Numerical Simulation of the Hot Rolling Process of Steel Beams. Materials. 2021; 14(22):7038. https://doi.org/10.3390/ma14227038
Chicago/Turabian StylePérez-Alvarado, Alejandro, Sixtos Antonio Arreola-Villa, Ismael Calderón-Ramos, Rumualdo Servín Castañeda, Luis Alberto Mendoza de la Rosa, Kinnor Chattopadhyay, and Rodolfo Morales. 2021. "Numerical Simulation of the Hot Rolling Process of Steel Beams" Materials 14, no. 22: 7038. https://doi.org/10.3390/ma14227038
APA StylePérez-Alvarado, A., Arreola-Villa, S. A., Calderón-Ramos, I., Servín Castañeda, R., Mendoza de la Rosa, L. A., Chattopadhyay, K., & Morales, R. (2021). Numerical Simulation of the Hot Rolling Process of Steel Beams. Materials, 14(22), 7038. https://doi.org/10.3390/ma14227038









