Prediction of System Parameters of Carbon-Based Composite Structure for Different Carbon Fiber Orientations with Mode Information at Reference Angle Only
Abstract
:1. Introduction
2. Theoretical Background for System Parameter Prediction
3. Identification of Modal Parameters of CBC Specimens
4. Prediction of Modal Parameters
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hegde, S.; Shenoy, B.S.; Chethan, K.N. Review on carbon fiber reinforced polymer (CBC) and their mechanical performance. Mater. Proc. 2019, 19, 658–662. [Google Scholar] [CrossRef]
- Keyte, J.; Pancholi, K.; Njuguna, J. Recent development in graphene oxide/epoxy carbon fiber-reinforced composites. Front. Mater. 2019, 6, 224. [Google Scholar] [CrossRef]
- Lui, Y.; Zwingmann, B.; Schlaich, M. Carbon fiber reinforced polymer for cable structures-a review. Polymers 2015, 7, 2078–2099. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Masmoudi, R. Axial response of concrete-filled FRP tube (CFFT) columns with internal bars. J. Compos. Sci. 2018, 2, 57. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-F.; Tsai, T.-H.; Yang, T.-H. A novel strengthening method for damaged pipeline under high temperature using inorganic insulation material and carbon fiber reinforced plastic composite material. Materials 2019, 12, 3484. [Google Scholar] [CrossRef] [Green Version]
- Mahboob, A.; Gil, L.; Bernat-Maso, E.; Eskenati, A.R. Experimental and numerical study of shear interface response of hybrid thin CBC-concrete slabs. Materials 2021, 14, 5184. [Google Scholar] [CrossRef]
- Chen, J.; Xu, Y.; Gao, Y. Topology optimization of metal and carbon fiber reinforced plastic (CBC) laminated battery-hanging structure. Polymers 2020, 12, 2495. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.-H.; Lee, J.-W.; Kim, J.-H.; Ahn, T.-M.; Ko, D.-C. Design of center pillar with composite reinforcements using hybrid molding method. Materials 2021, 14, 2047. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, M.; Wang, J.; Jang, D.; Nam, I.; Huang, B. A comparative study on the electrical and piezoresistive sensing characteristics of GFRP and CBC composites with hybridized incorporation of carbon nanotubes, graphenes, carbon nanofibers, and graphite nanoplatelets. Sensors 2021, 21, 7291. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; An, Q.; Cai, X.; Chen, M.; Ming, W. Influence of fiber orientation on single-point cutting fracture behavior of carbon-fiber/epoxy prepreg sheets. Materials 2015, 8, 6738–6751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashrafi, S.A.; Miller, P.W.; Wandro, K.M.; Kim, D. Characterization and effects of fiber pull-outs in hole quality of carbon fiber reinforced plastics composite. Materials 2016, 9, 828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, P.-C.; Fang, J.-C.; Lin, J.-W.; Tran, X.V.; Ching, Y.-C. Preheated (heat-assisted) clinching process for Al/CBC cross-tension specimens. Materials 2020, 13, 4170. [Google Scholar] [CrossRef]
- Kim, J.W.; Nam, J.; Jeon, J.; Lee, S.W. A study on machining performance of micro-drilling of multi-directional carbon fiber reinforced plastic (MD-CBC) based on nano-solid dry lubrication using graphene nano platelets. Materials 2021, 14, 685. [Google Scholar] [CrossRef] [PubMed]
- Hosoi, A.; Kawada, H. Fatigue life prediction for transverse crack initiation of CBC cross-fly and quasi-isotropic laminates. Materials 2018, 11, 1182. [Google Scholar] [CrossRef] [Green Version]
- Rescalvo, F.J.; Abarkane, C.; Suarez, E.; Valverde-Palacios, I.; Gallego, A. Pine beams retrofitted with FRP and popular planks: Mechanical behavior. Materials 2019, 12, 3081. [Google Scholar] [CrossRef] [Green Version]
- Barile, C.; Casavola, C.; Moramarco, V.; Pappalettere, C.; Vimalathithan, P.K. Bonding characteristics of single- and joggled-lap CBC specimens: Mechanical and acoustic investigations. Appl. Sci. 2020, 10, 1782. [Google Scholar] [CrossRef] [Green Version]
- Sim, K.-B.; Baek, D.; Shin, J.-H.; Shim, G.-S.; Jang, S.-W.; Kim, H.-J.; Hwang, J.-W.; Roh, J.U. Enhanced surface properties of carbon fiber reinforced plastic by epoxy modified primer with plasma for automotive applications. Polymers 2020, 12, 556. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-U.; Seo, H.-S.; Jang, H.-Y. Study on mechanical bearing strength and failure modes of composite materials for marine structures. J. Mar. Sci. Eng. 2021, 9, 726. [Google Scholar] [CrossRef]
- Go, S.-H.; Lee, M.-S.; Hong, C.-G.; Kwac, L.-K.; Kim, H.-G. Correlation between drop impact energy and residual compressive strength according to the lamination of CBC with EVA sheets. Polymers 2020, 12, 224. [Google Scholar] [CrossRef] [Green Version]
- Ewins, D.J. Modal Testing, 3rd ed.; Research Studies Press Ltd.: Hertfordshire, UK, 2000. [Google Scholar]
- Inman, D.J. Engineering Vibration, 4th ed.; Pearson: Singapore, 2013. [Google Scholar]
- Surgeon, M.; Wevers, M. Modal analysis of acoustic emission signals from CBC laminates. NDTE Int. 1999, 32, 311–322. [Google Scholar] [CrossRef]
- Ding, G.; Xie, C.; Zhang, G.; Song, G.; Zhou, Z. Modal analysis based on finite element method and experimental validation on carbon fiber composite drive shaft considering steel joints. Mater. Res. Innov. 2015, 19, S5748–S5753. [Google Scholar] [CrossRef]
- Garcia, C.; Wilson, J.; Trendafilova, I.; Yang, L. Vibratory behavior of glass fibre reinforced polymer (GFRP) interleaved with nylon nanofibers. Compos. Struct. 2017, 176, 923–932. [Google Scholar] [CrossRef] [Green Version]
- Jinguang, Z.; Hairu, Y.; Guozhi, C.; Zeng, Z. Structural and modal analysis of carbon fiber reinforced polymer raft frame. J. Low Freq. Noise Vib. Act. Control 2018, 37, 577–589. [Google Scholar] [CrossRef]
- Kim, C.J. Sensitivity analysis of the frequency response function of carbon-fiber-reinforced plastic specimens for different direction of carbon fiber as well as spectral loading pattern. Materials 2019, 12, 2983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, H.Y.; Kim, C.J.; Lee, J. Modal damping coefficient estimation of carbon-fiber reinforced plastic material considering temperature condition. Materials 2020, 13, 2872. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.J. Temperature-dependent dynamic characteristics of carbon-fiber-reinforced plastic for different spectral loading patterns. Materials 2020, 13, 5238. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.J. Comparison of mode shapes of carbon-fiber-reinforced plastic material considering carbon fiber direction. Crystals 2021, 11, 311. [Google Scholar] [CrossRef]
- Kim, C.J. Modal parameter tracking in a carbon fiber-reinforced structure over different carbon fiber orientations. J. Mar. Sci. Eng. 2021, 9, 1214. [Google Scholar] [CrossRef]
- Kim, C.J. Relationship between structural stiffness and viscous damping coefficient in reinforced carbon structure under varying carbon fiber orientations. Crystals 2021, 11, 1252. [Google Scholar] [CrossRef]
- Muhan Composite Materials Co., Ltd. Home Page. Available online: http://www.mhcomposite.com/EN/sub/sub2_1_2.php (accessed on 2 January 2021).


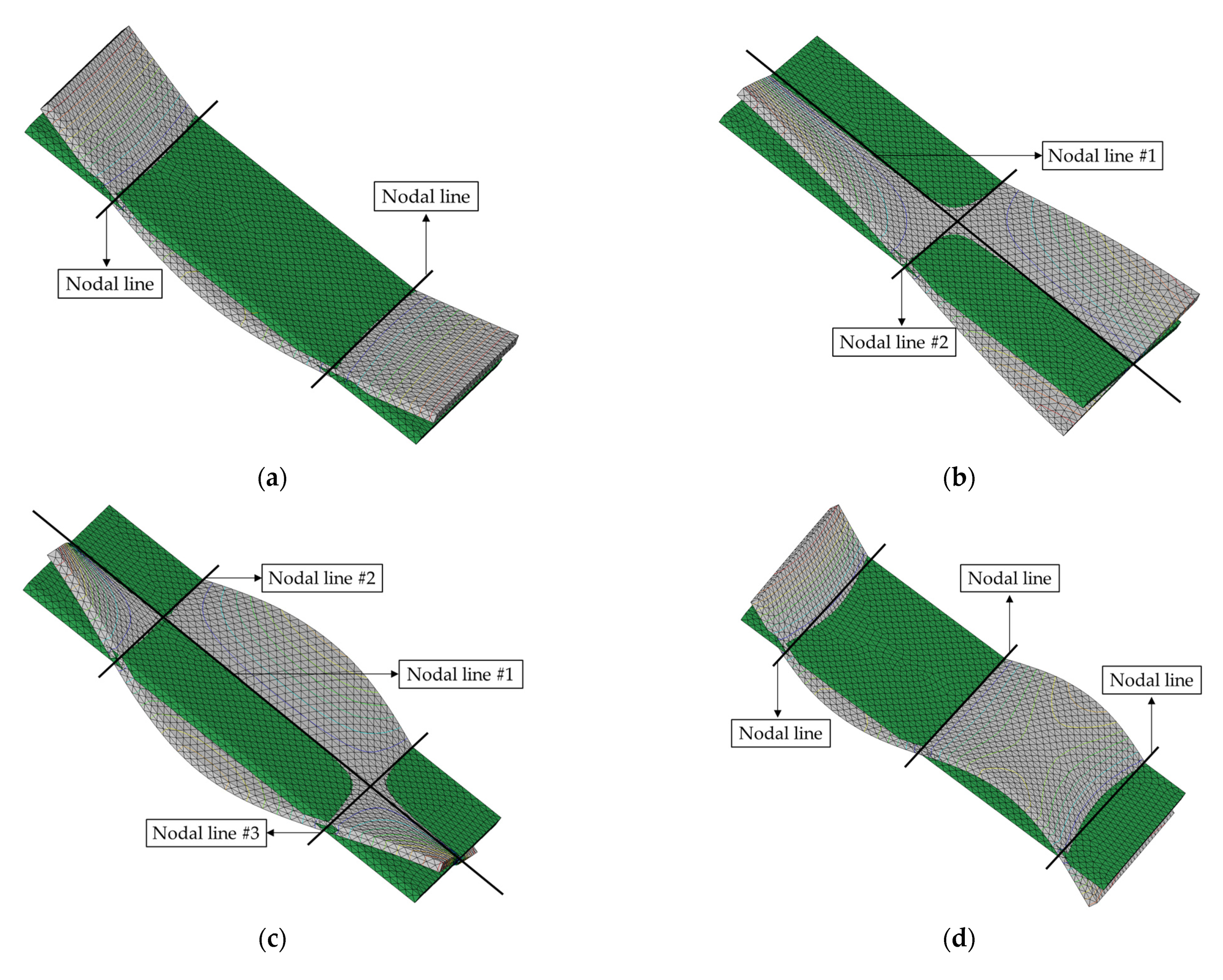
 : first bending mode;
: first bending mode;  : second bending mode;
: second bending mode;  : third bending mode; (b) torsional modes,
: third bending mode; (b) torsional modes,  : first torsional mode;
: first torsional mode;  : second torsional mode [30,31].
: second torsional mode [30,31].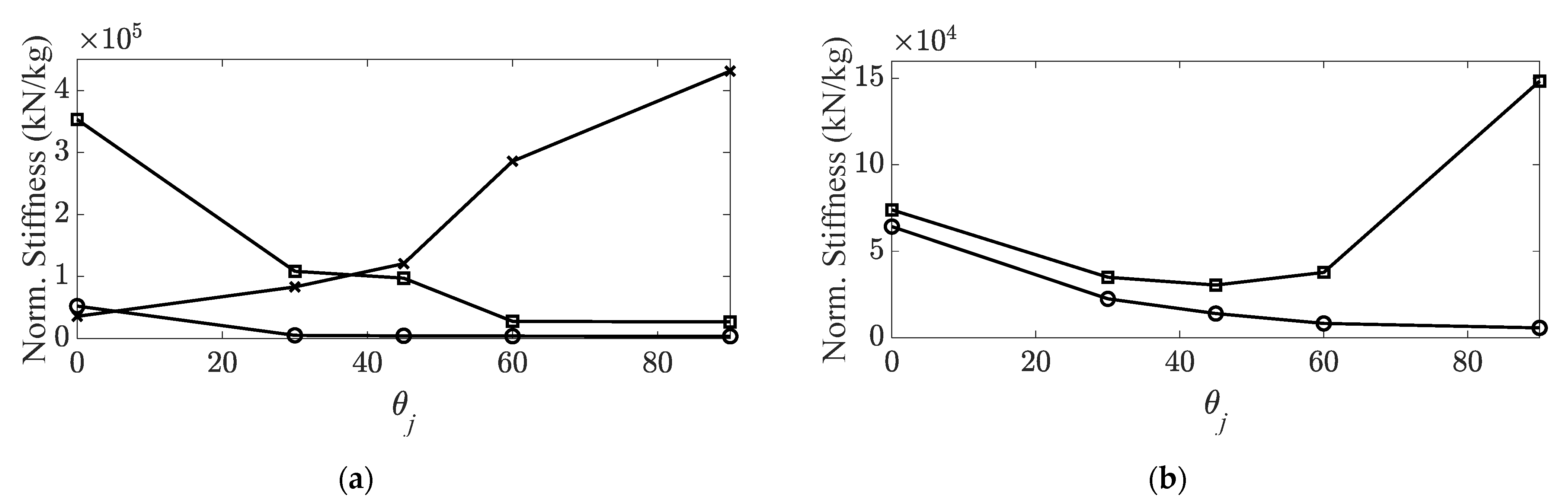
 : first bending mode;
: first bending mode;  : second bending mode;
: second bending mode;  : third mode.; (b) torsional modes,
: third mode.; (b) torsional modes,  : first torsional mode;
: first torsional mode;  : second torsional mode [30,31].
: second torsional mode [30,31].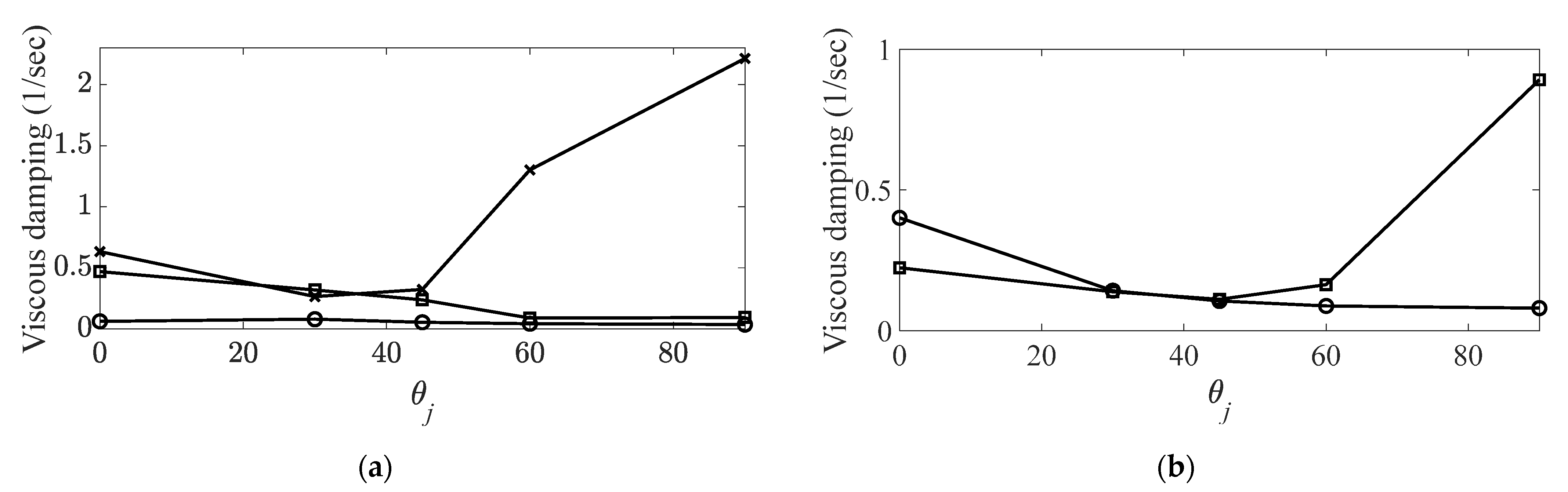

 : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode;
: third bending mode;  : second torsional mode; (b) damping coefficient ratios,
: second torsional mode; (b) damping coefficient ratios,  : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode,
: third bending mode,  : second torsional mode.
: second torsional mode.
 : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode;
: third bending mode;  : second torsional mode; (b) damping coefficient ratios,
: second torsional mode; (b) damping coefficient ratios,  : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode,
: third bending mode,  : second torsional mode.
: second torsional mode.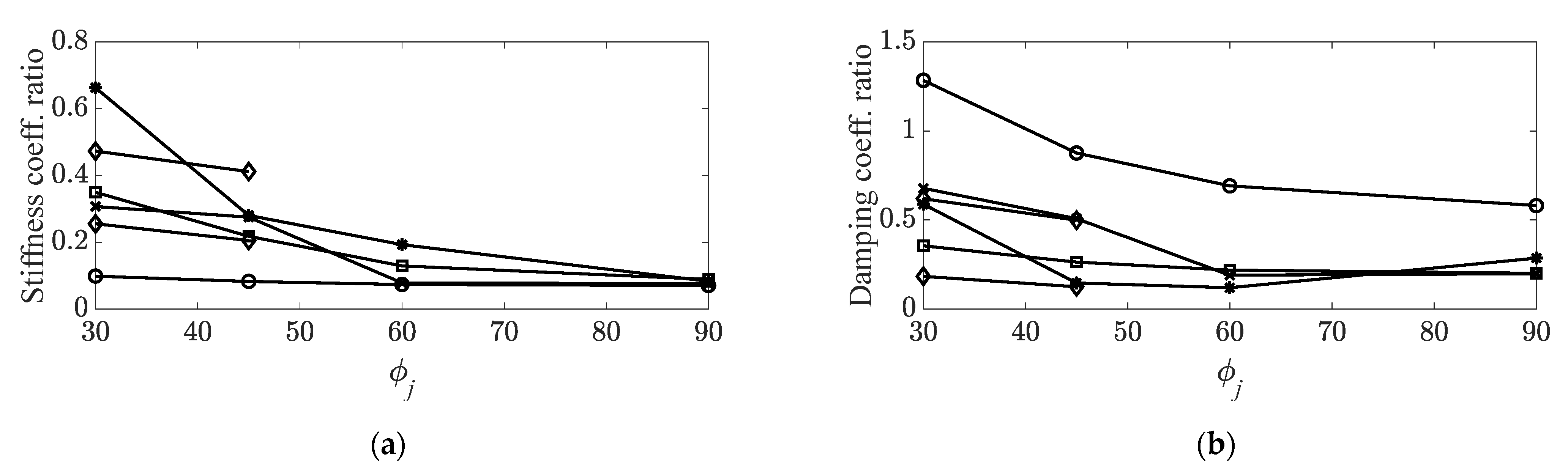
 : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode;
: third bending mode;  : averaged curve; (b) damping coefficient ratios,
: averaged curve; (b) damping coefficient ratios,  : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode;
: third bending mode;  : averaged curve.
: averaged curve.
 : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode;
: third bending mode;  : averaged curve; (b) damping coefficient ratios,
: averaged curve; (b) damping coefficient ratios,  : first bending mode;
: first bending mode;  : first torsional mode;
: first torsional mode;  : second bending mode;
: second bending mode;  : third bending mode;
: third bending mode;  : averaged curve.
: averaged curve.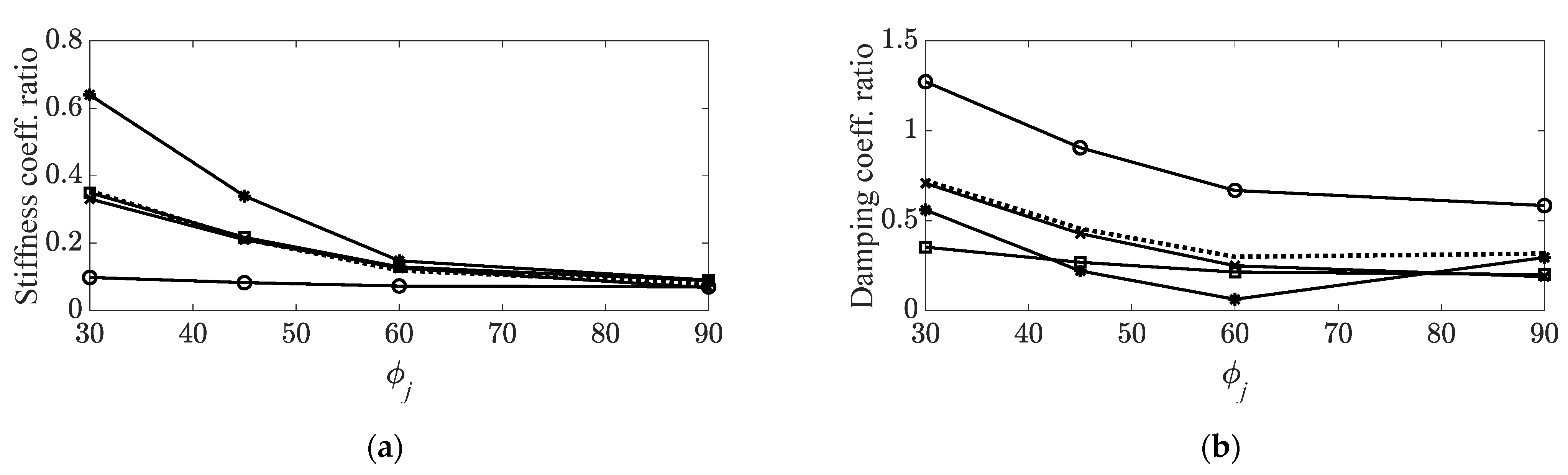
 : measured parameter;
: measured parameter;  : predicted parameter with direct fitting curve function;
: predicted parameter with direct fitting curve function;  : predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).
: predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).
 : measured parameter;
: measured parameter;  : predicted parameter with direct fitting curve function;
: predicted parameter with direct fitting curve function;  : predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).
: predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).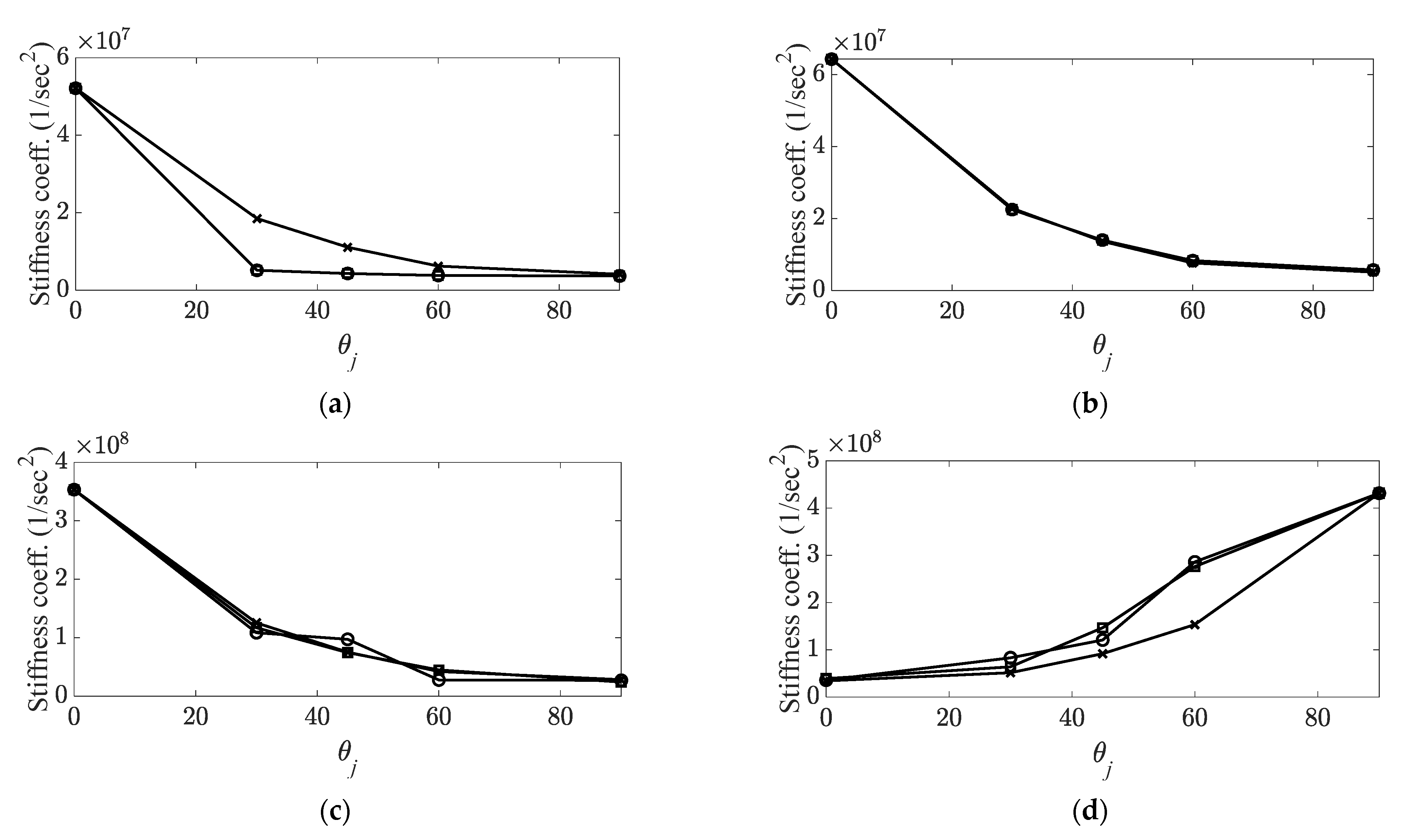
 : measured parameter;
: measured parameter;  : predicted parameter with direct fitting curve function;
: predicted parameter with direct fitting curve function;  : predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).
: predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).
 : measured parameter;
: measured parameter;  : predicted parameter with direct fitting curve function;
: predicted parameter with direct fitting curve function;  : predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).
: predicted parameter with representative fitting-curve function. (a) First mode (first bending); (b) second mode (first torsional); (c) fourth mode (second bending); (d) fifth mode (third bending).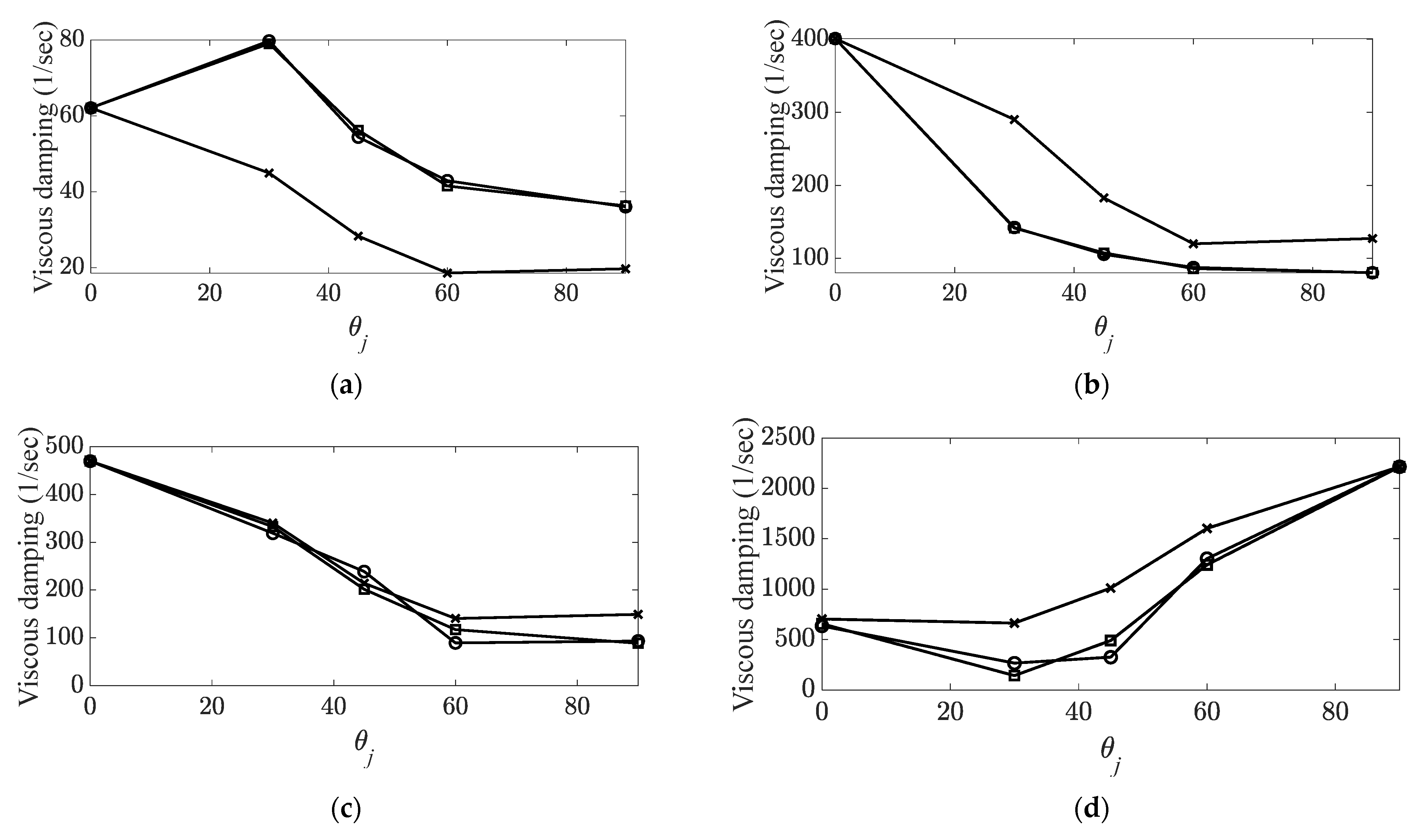
| Specimen | Resonance Frequency (Hz) | Modal Damping Ratio (%) | Mode Shape |
|---|---|---|---|
| CBC specimen #1 | 1149.1 | 0.4 | Bending (first) |
| 1276.1 | 2.5 | Torsional (first) | |
| 1368.7 | 1.3 | Torsional (second) | |
| 2990.9 | 1.3 | Bending (second) | |
| 951.0 | 5.3 | Bending (third) | |
| CBC specimen #2 | 360.6 | 0.39 | Bending (first) |
| 754.5 | 0.21 | Torsional (first) | |
| 941.1 | 0.82 | Torsional (second) | |
| 1657.6 | 0.01 | Bending (second) | |
| 1450.4 | 0.55 | Bending (third) | |
| CBC specimen #3 | 330.4 | 1.3 | Bending (first) |
| 595.6 | 1.4 | Torsional (first) | |
| 878.0 | 1.0 | Torsional (second) | |
| 1568.9 | 1.2 | Bending (second) | |
| 1749.2 | 1.5 | Bending (third) | |
| CBC specimen #4 | 310.6 | 1.1 | Bending (first) |
| 458.5 | 1.5 | Torsional (first) | |
| 979.0 | 1.3 | Torsional (second) | |
| 835.0 | 0.9 | Bending (second) | |
| 2690.4 | 3.9 | Bending (third) | |
| CBC specimen #5 | 305.1 | 0.9 | Bending (first) |
| 380.0 | 1.7 | Torsional (first) | |
| 1938.5 | 3.7 | Torsional (second) | |
| 824.1 | 0.9 | Bending (second) | |
| 3305.1 | 5.3 | Bending (third) |
| Mode | Maximum Parameter Case | Rearranged Angle Sequence | Corresponding Angle Increase |
|---|---|---|---|
| First bending | |||
| First torsional | |||
| Second torsional | |||
| Second bending | |||
| Third bending |
| System Parameter | Representative Curve-Fitting Polynomial Function |
|---|---|
| Viscous damping coefficient | |
| Stiffness coefficient |
| System Parameter | Mode | Relative Error (%) | |
|---|---|---|---|
| Direct Function | Indirect Function | ||
| Viscous damping coefficient | First bending | 0.078 | 98.64 |
| First torsional | 0.15 | 4.44 | |
| Second bending | 20.83 | 19.14 | |
| Third bending | 11.38 | 22.57 | |
| Average | 8.11 | 36.20 | |
| Stiffness coefficient | First bending | 1.65 | 38.75 |
| First torsional | 0.89 | 54.51 | |
| Second bending | 11.22 | 26.85 | |
| Third bending | 21.21 | 79.35 | |
| Average | 8.74 | 49.87 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.-J. Prediction of System Parameters of Carbon-Based Composite Structure for Different Carbon Fiber Orientations with Mode Information at Reference Angle Only. Materials 2021, 14, 7626. https://doi.org/10.3390/ma14247626
Kim C-J. Prediction of System Parameters of Carbon-Based Composite Structure for Different Carbon Fiber Orientations with Mode Information at Reference Angle Only. Materials. 2021; 14(24):7626. https://doi.org/10.3390/ma14247626
Chicago/Turabian StyleKim, Chan-Jung. 2021. "Prediction of System Parameters of Carbon-Based Composite Structure for Different Carbon Fiber Orientations with Mode Information at Reference Angle Only" Materials 14, no. 24: 7626. https://doi.org/10.3390/ma14247626
APA StyleKim, C.-J. (2021). Prediction of System Parameters of Carbon-Based Composite Structure for Different Carbon Fiber Orientations with Mode Information at Reference Angle Only. Materials, 14(24), 7626. https://doi.org/10.3390/ma14247626






