Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties
Abstract
:1. Introduction
2. Models
- l—specifies the length of the side of the core of the structure,
- t—specifies the number of rows of the core discs on the side of the core of the structure,
- s—specifies the separation of neighbouring cores of the structure.
3. Method
Simulation Details
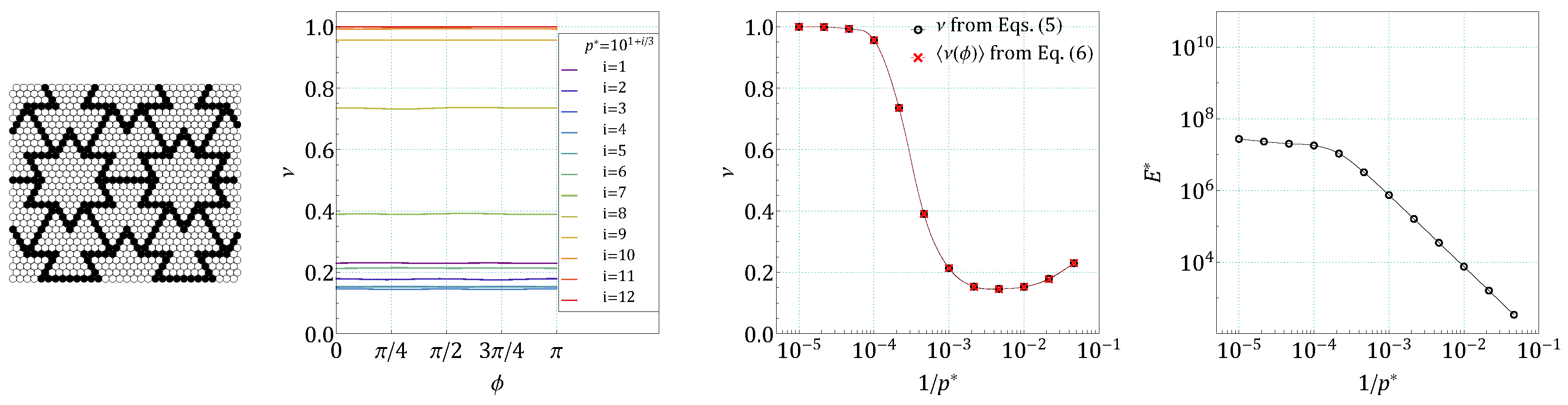
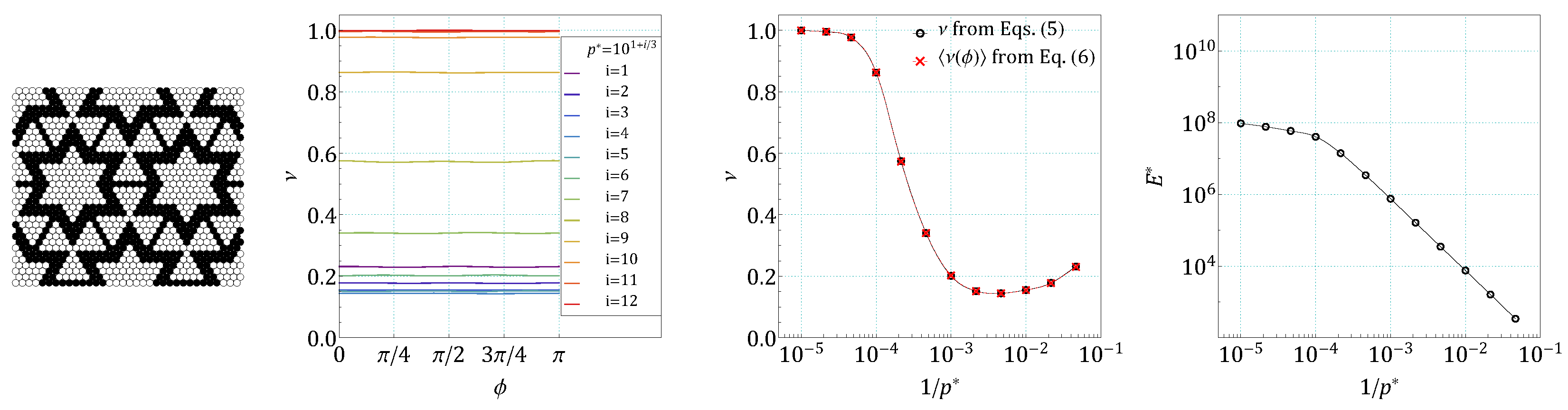
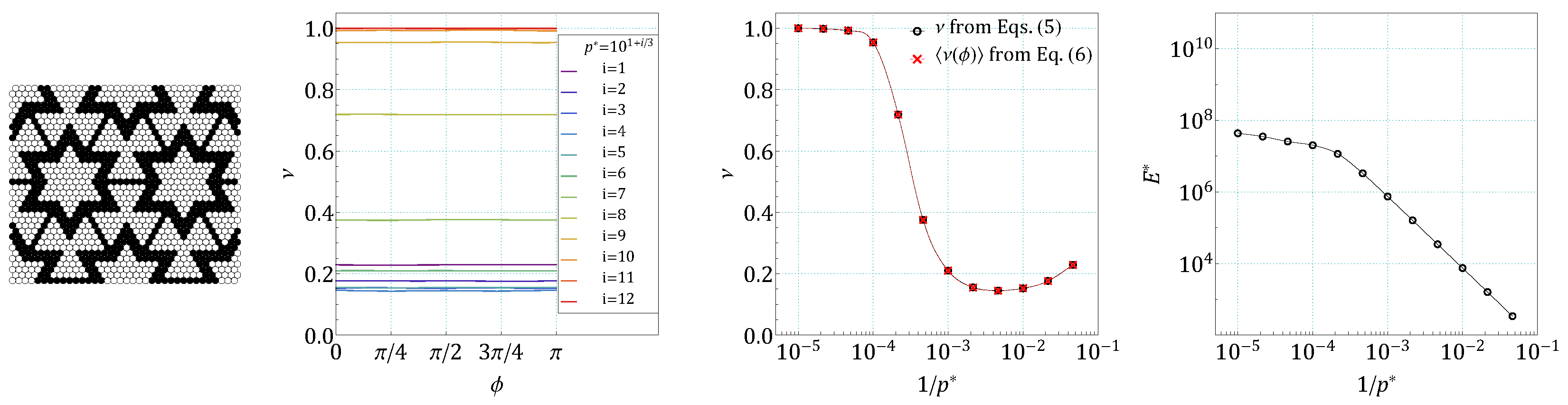
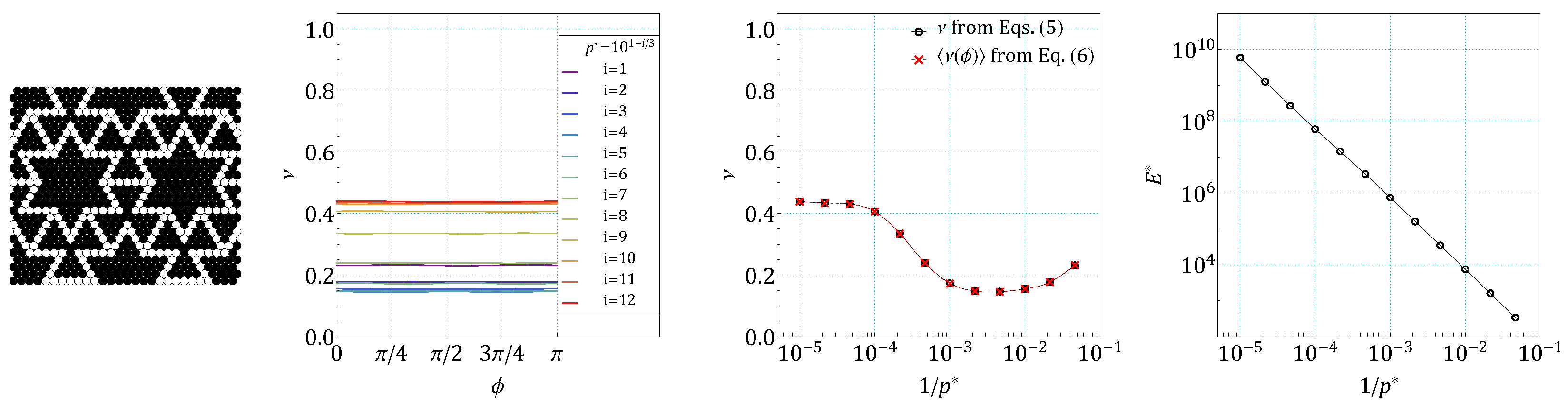
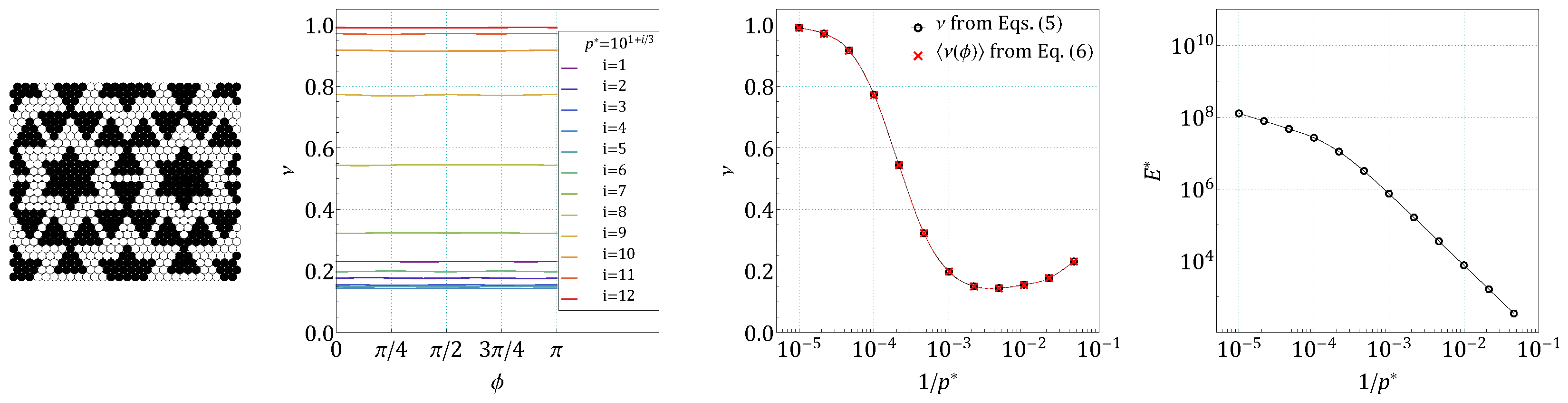
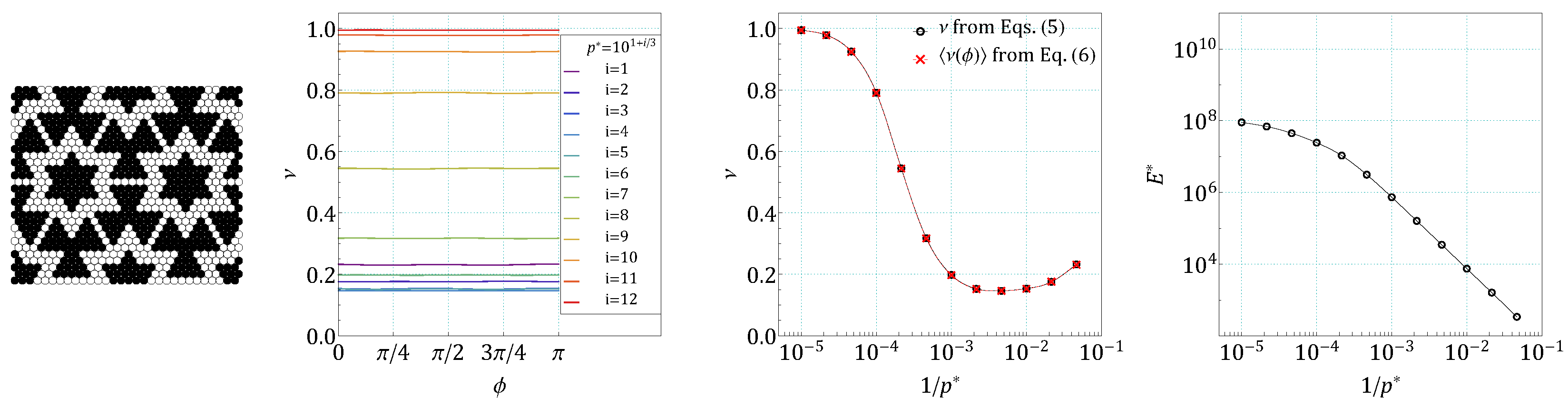
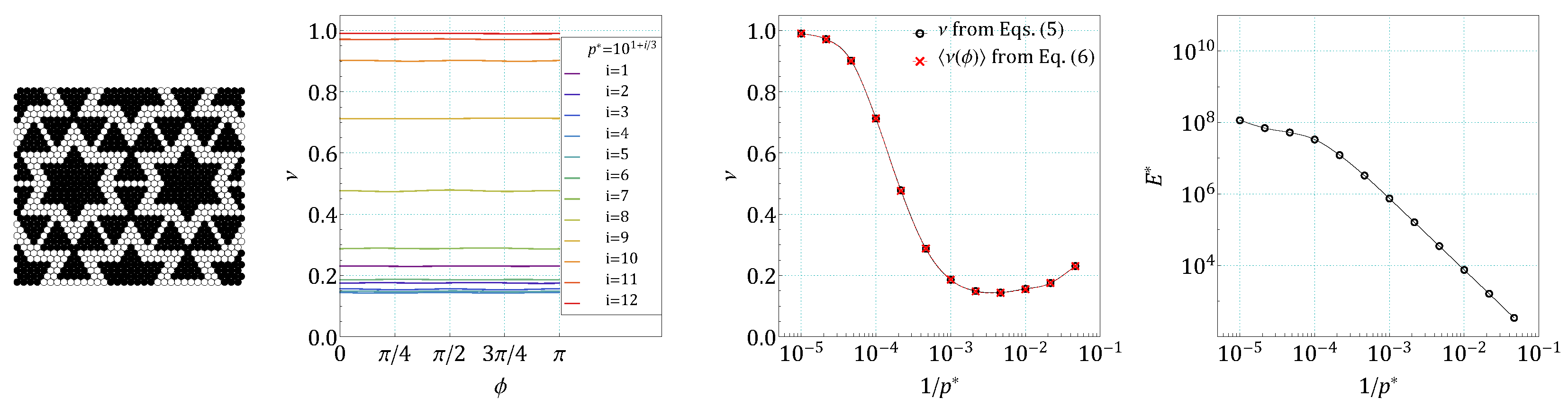
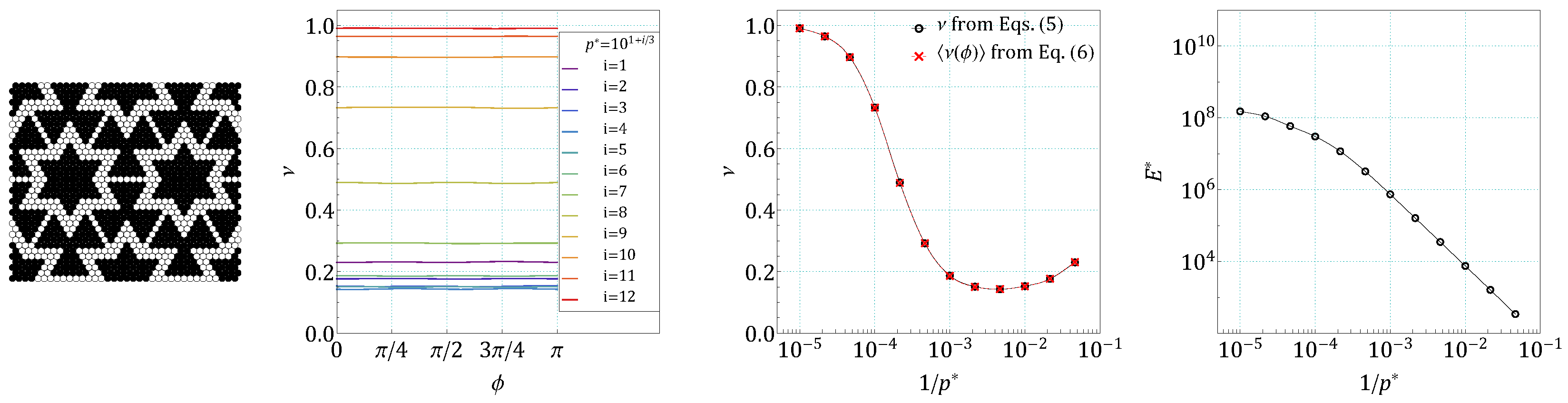
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PR | Poisson’s ratio |
| 2D | two-dimensional |
| HD | hard disc |
| MC | Monte Carlo |
| isobaric-isothermal ensemble |
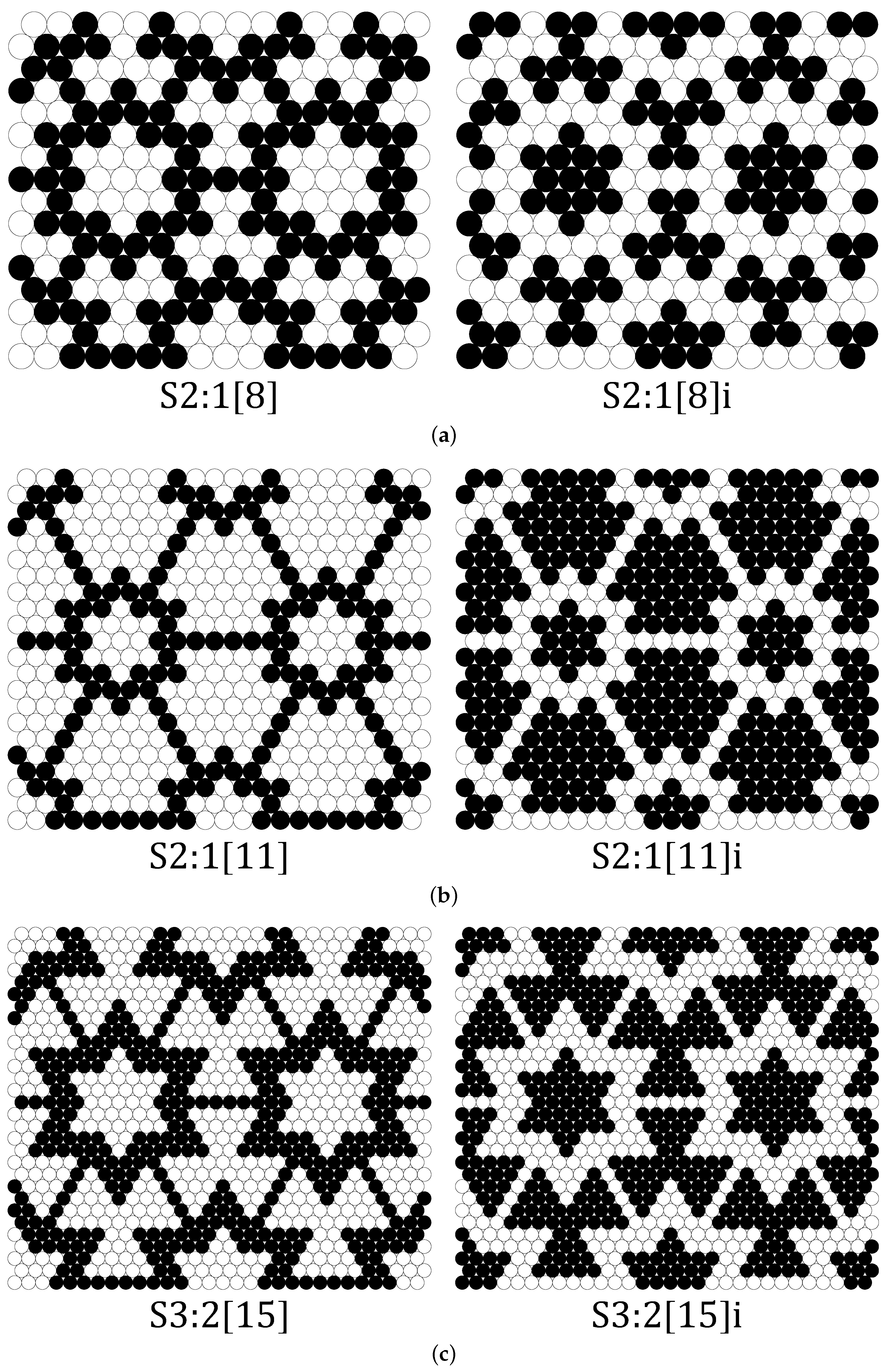
Appendix A

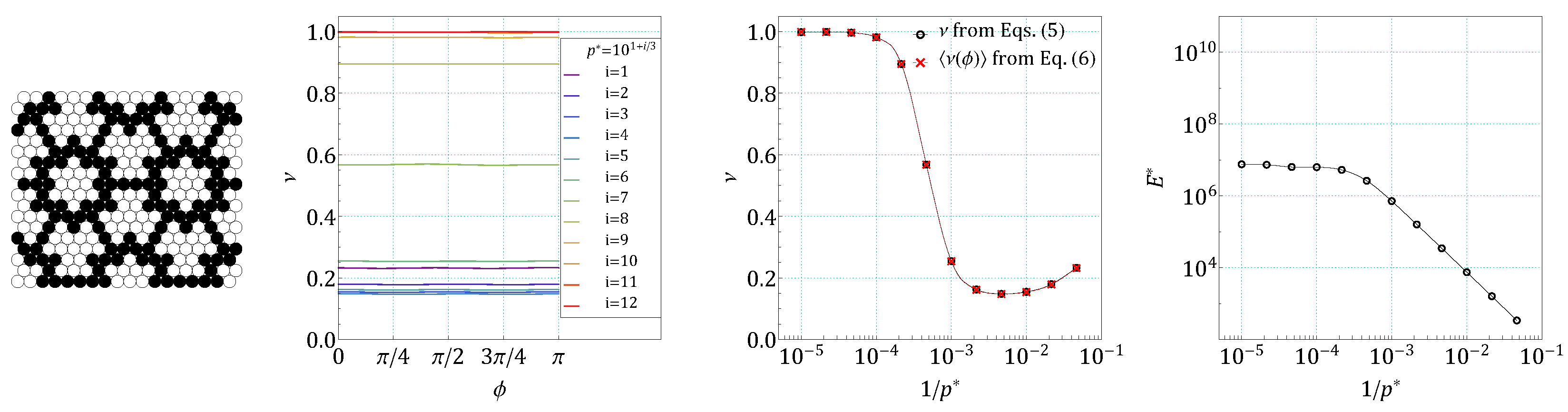
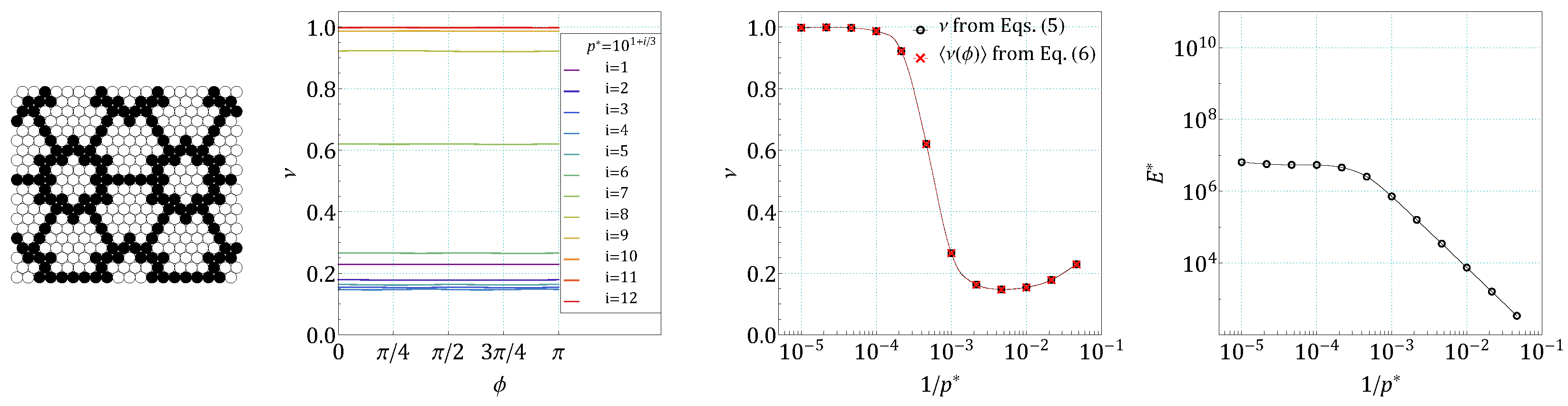
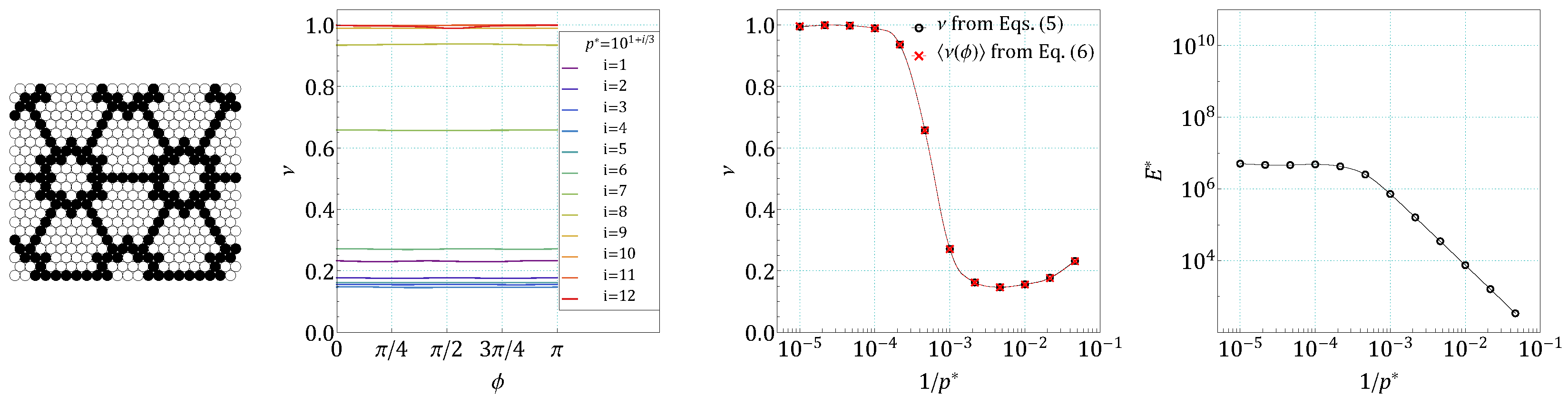
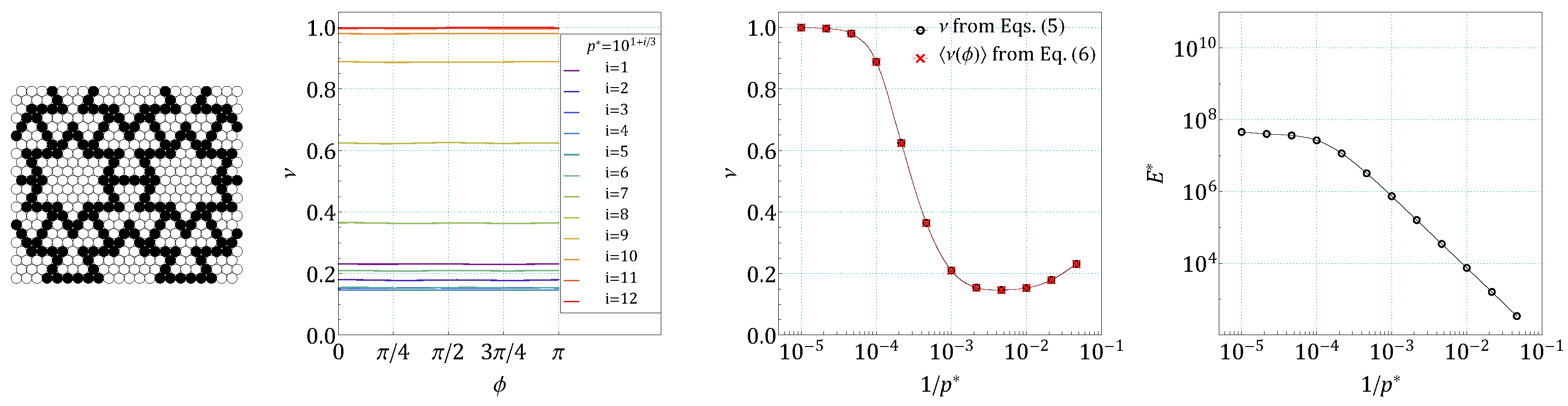
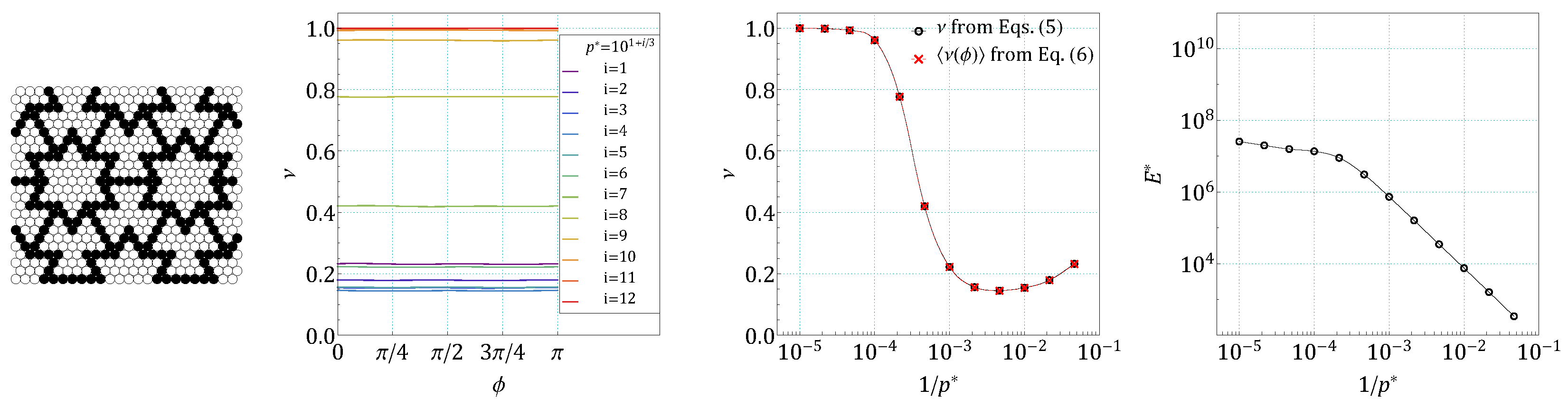

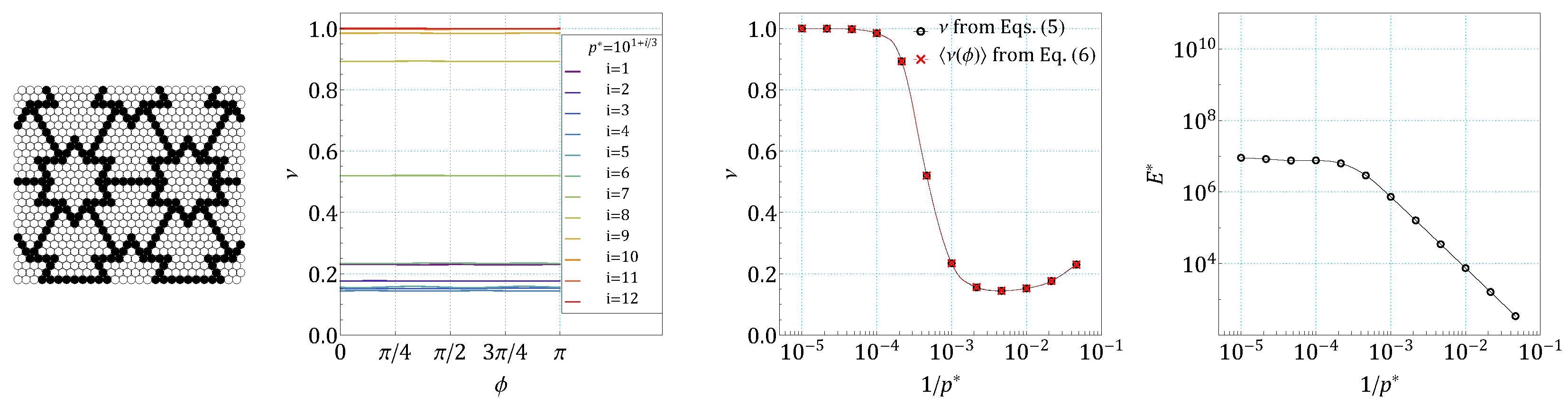
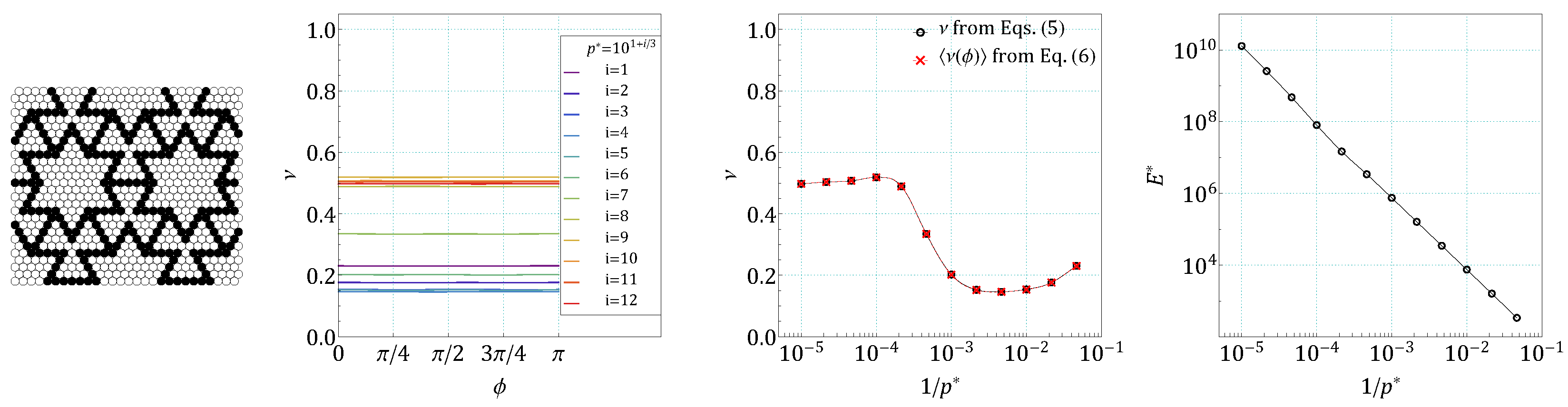
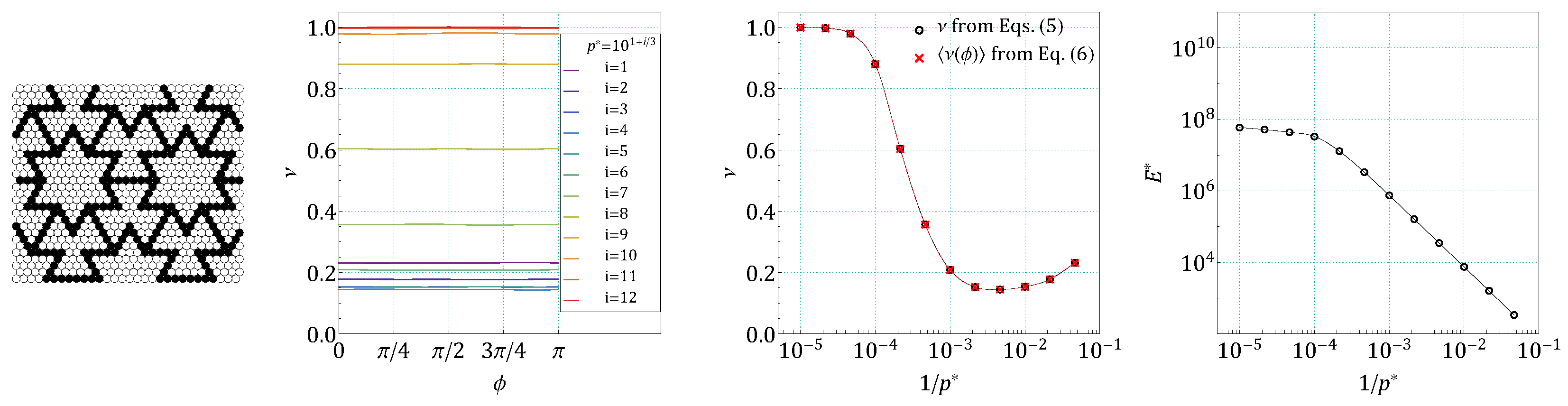

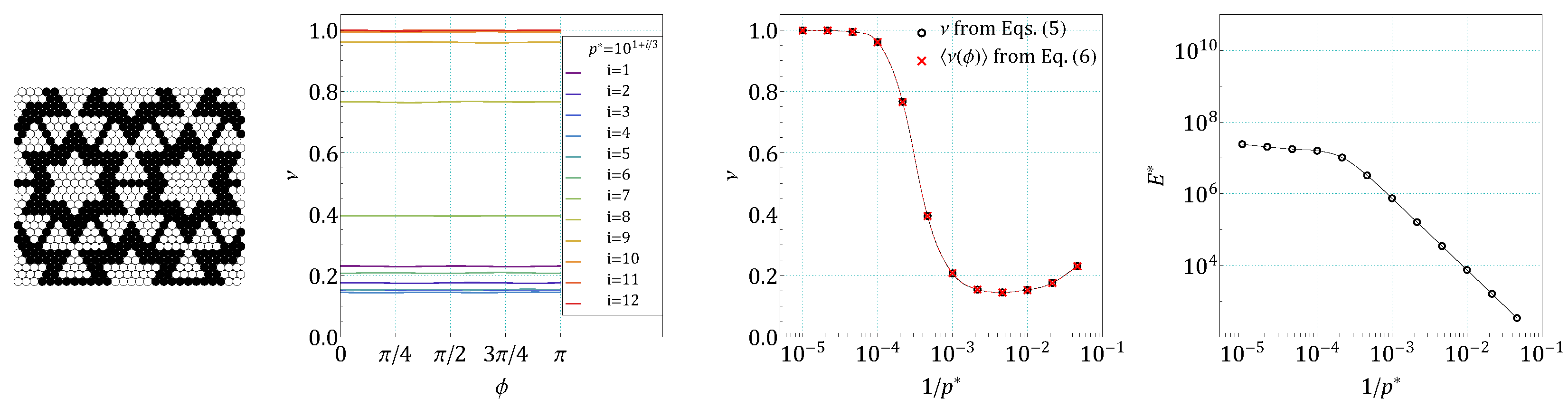

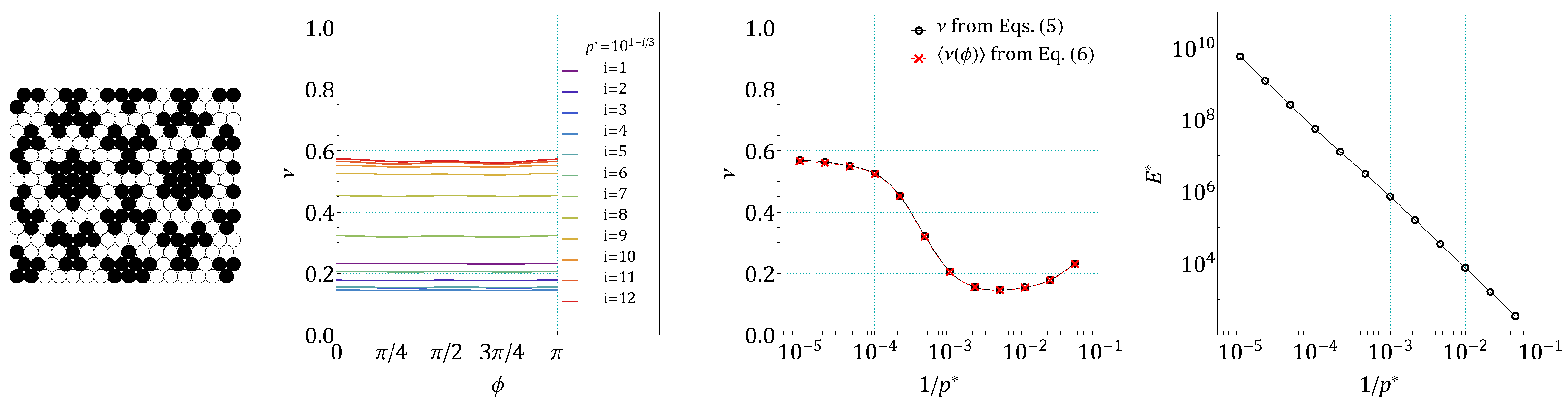
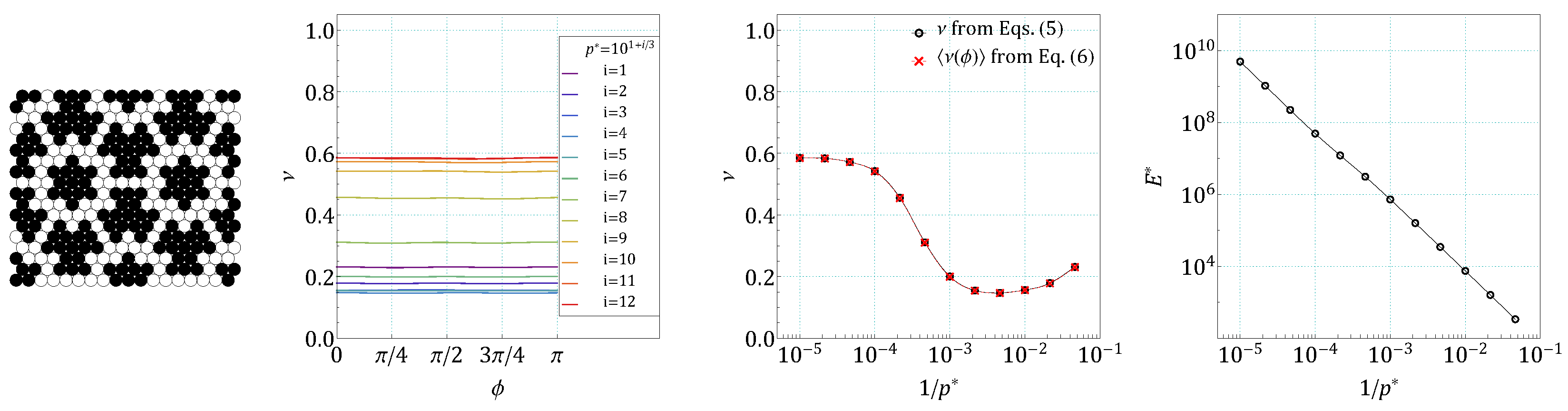
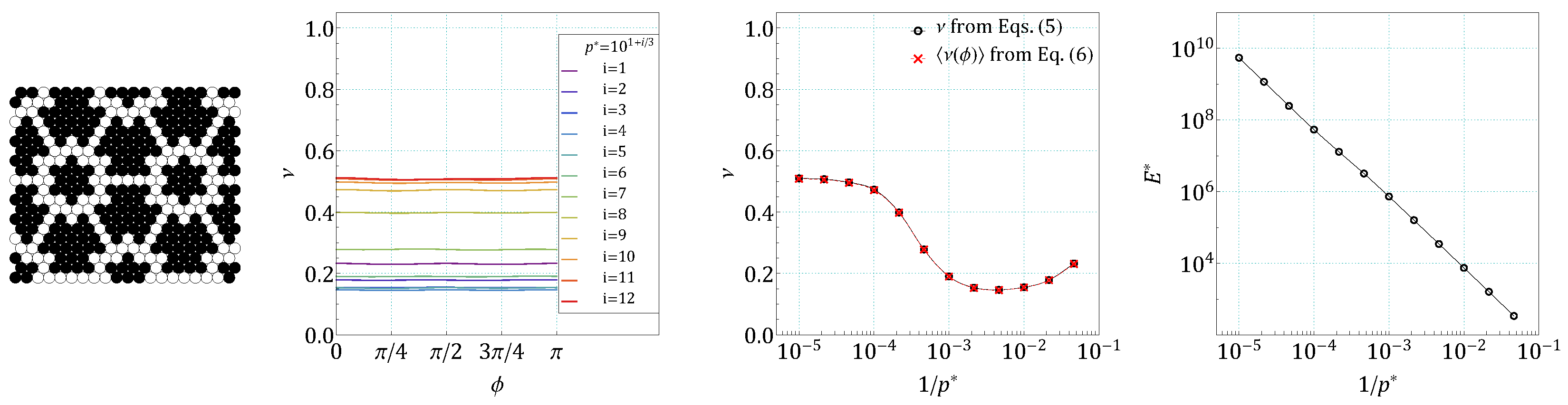
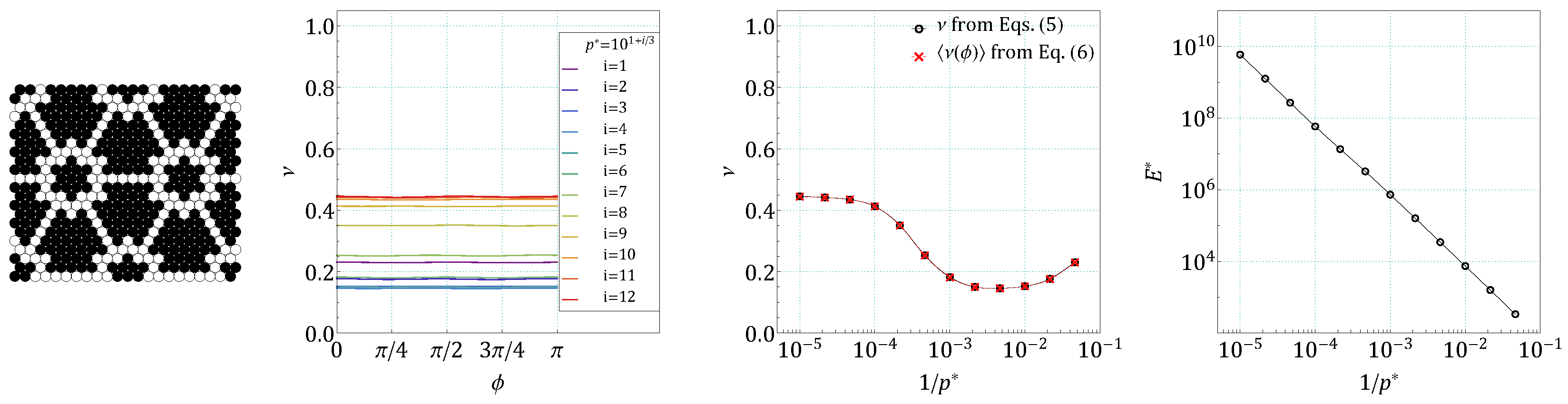
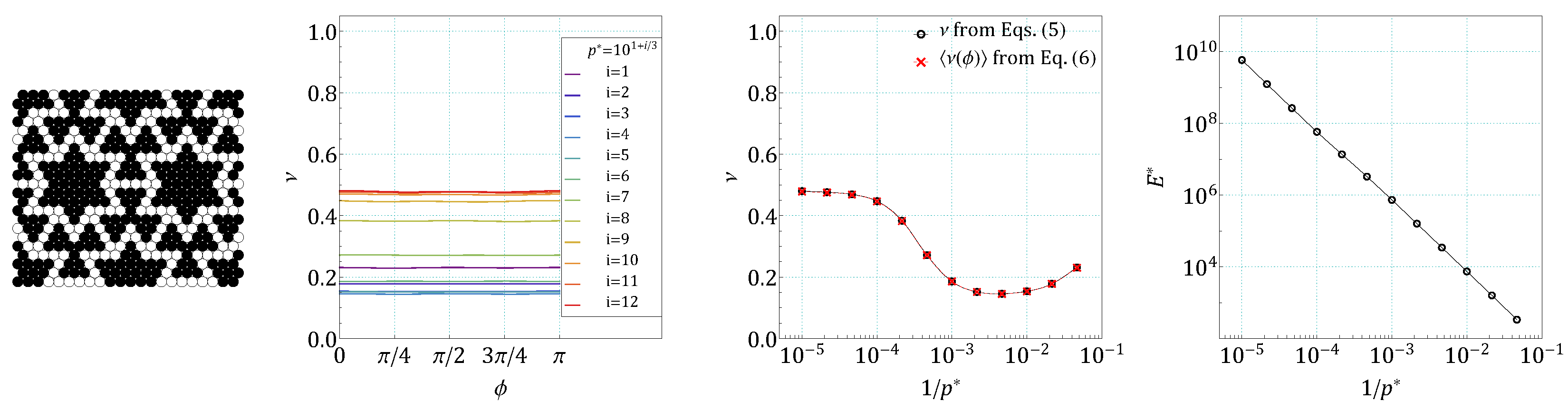
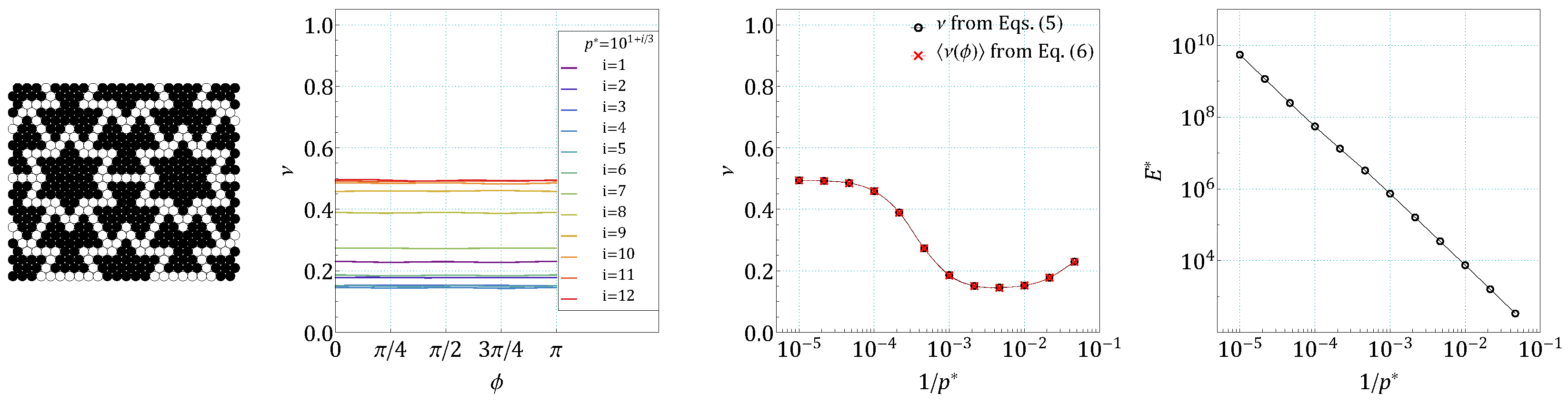
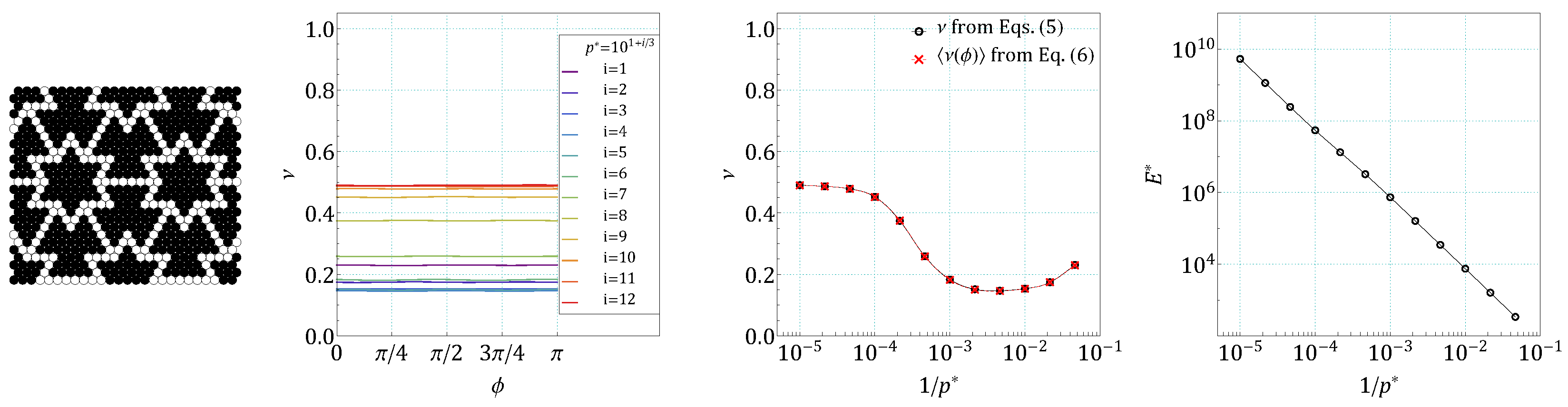
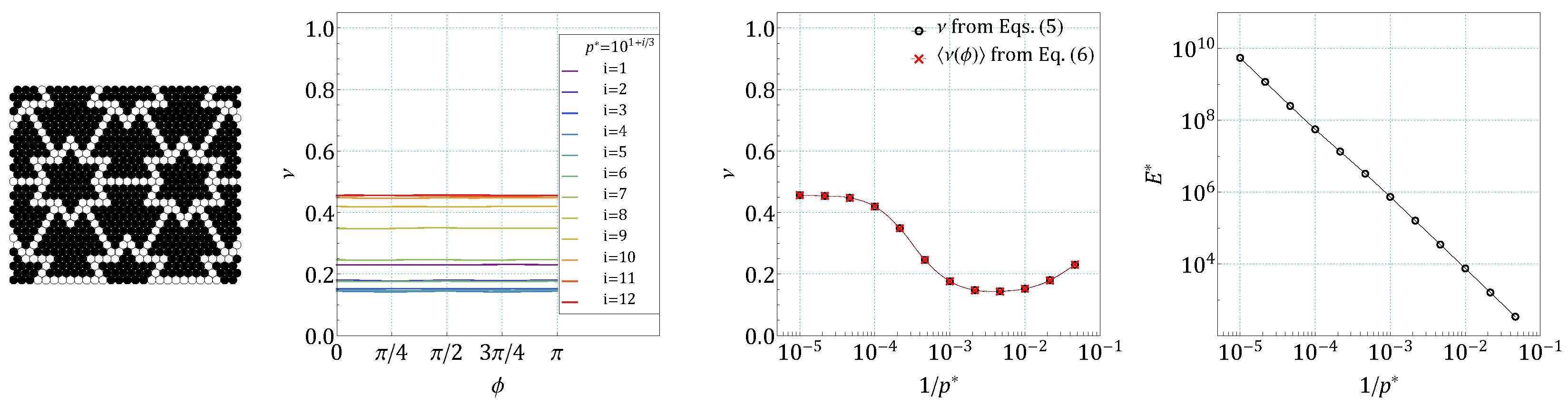


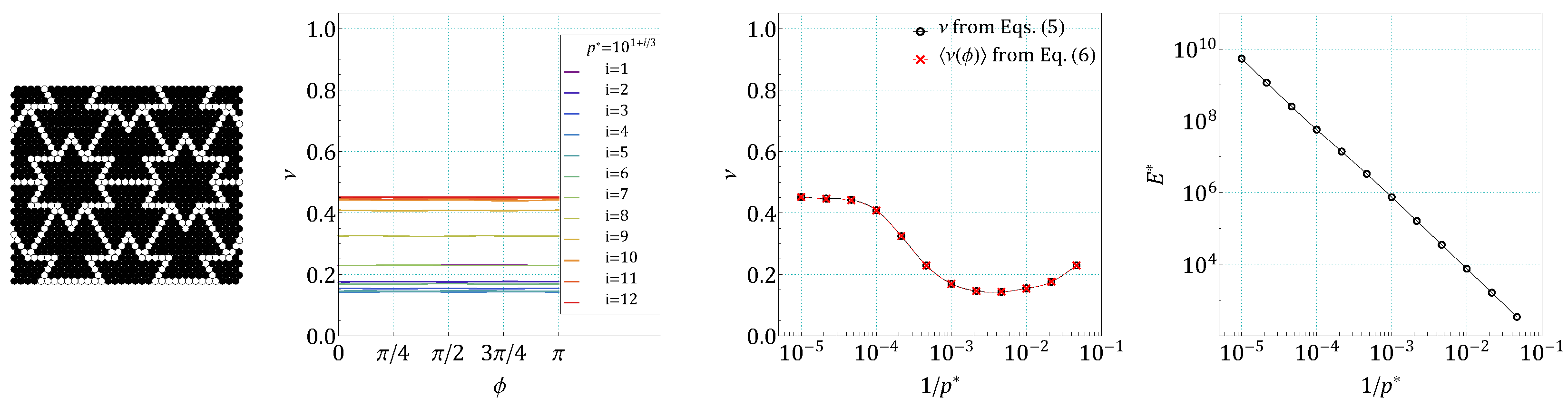
References
- Landau, L.; Lifshits, E. Theory of Elasticity, 3rd ed.; Pergamon Press: Oxford, UK, 1993. [Google Scholar]
- Lakes, R.S. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 25–42. [Google Scholar]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio =-1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Kolpakov, A.G. On the determination of the averaged moduli of elastic gridworks. Prikl. Matem. Mekham. 1985, 49, 969–977. [Google Scholar]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Rothenburg, L. Note on a random isotropic granular material with negative Poisson’s ratio. Int. J. Eng. Sci. 1988, 26, 373–383. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional Isotropic System with a Negative Poisson Ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simulat. 2005, 31, 925–935. [Google Scholar] [CrossRef] [Green Version]
- Ai, L.; Gao, X.L. An analytical model for star-shaped re-entrant lattice structures with the orthotropic symmetry and negative Poisson’s ratios. Int. J. Mech. Sci. 2018, 145, 158–170. [Google Scholar] [CrossRef]
- Rad, M.S.; Hatami, H.; Ahmad, Z.; Yasuri, A.K. Analytical solution and finite element approach to the dense re-entrant unit cells of auxetic structures. Acta Mech. 2019, 230, 2171–2185. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C.Q. Analyses on the in-plane impact resistance of auxetic double arrowhead honeycombs. J. App. Mech. Trans. ASME 2015, 82, 1–9. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, L.; Zhou, Z.; Ma, Z.D.; Wang, C.; Wang, Y. Theoretical, numerical and experimental analysis of three-dimensional double-V honeycomb. Mater. Des. 2018, 139, 380–391. [Google Scholar] [CrossRef]
- Yang, H.; Wang, B.; Ma, L. Mechanical properties of 3D double-U auxetic structures. Int. J. Solid Struct. 2019, 180, 13–29. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Sun, R.; Scarpa, F.; Wang, J. In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers 2019, 11, 1132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Lu, Z.; Yang, Z.; Yang, C. Directions dependence of the elastic properties of a 3D augmented re-entrant cellular structure. Mater. Des. 2017, 134, 151–162. [Google Scholar] [CrossRef]
- Li, X.; Lu, Z.; Yang, Z.; Wang, Q.; Zhang, Y. Yield surfaces of periodic honeycombs with tunable Poisson’s ratio. Int. J. Mech. Sci. 2018, 141, 290–302. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Yang, Z.; Lu, Z. Novel auxetic structures with enhanced mechanical properties. Extreme Mech. Lett. 2019, 27, 59–65. [Google Scholar] [CrossRef]
- Strek, T.; Kedziora, P.; Maruszewski, B.; Pozniak, A.; Tretiakov, K.V.; Wojciechowski, K.W. Finite element analysis of auxetic obstacle deformation and fluid flow in a channel. J. Non. Cryst. Solids 2009, 355, 1387–1392. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Grima, J.N.; Attard, D. A Novel Mechanical Metamaterial Exhibiting Auxetic Behavior and Negative Compressibility. Materials 2020, 13, 79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strek, T.; Matuszewska, A.; Jopek, H. Finite element analysis of the influence of the covering auxetic layer of plate on the contact pressure. Phys. Status Solidi B 2017, 254, 1700103. [Google Scholar] [CrossRef]
- Morozow, D.; Barlak, M.; Werner, Z.; Pisarek, M.; Konarski, P.; Zagórski, J.; Rucki, M.; Chałko, L.; Łagodziński, M.; Narojczyk, J.; et al. Wear resistance improvement of cemented tungsten carbide deep-hole drills after ion implantation. Materials 2021, 14, 239. [Google Scholar] [CrossRef]
- Tarlochan, F. Sandwich Structures for Energy Absorption Applications: A Review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef] [PubMed]
- Pyskir, A.; Collet, M.; Dimitrijevic, Z.; Lamarque, C.-H. Enhanced Vibration Isolation with Prestressed Resonant Auxetic Metamaterial. Materials 2021, 14, 6743. [Google Scholar] [CrossRef] [PubMed]
- Strek, T.; Jopek, H.; Idczak, E.; Wojciechowski, K.W. Computational Modelling of Structures with Non-Intuitive Behaviour. Materials 2017, 10, 1386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bilski, M.; Pigłowski, P.M.; Wojciechowski, K.W. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Negative Poisson ratios at negative pressures. Mol. Phys. Rep. 1995, 10, 129–136. [Google Scholar]
- Wojciechowski, K.W. Remarks on “Poisson Ratio beyond the Limits of the Elasticity Theory”. J. Phys. Soc. Jpn. 2003, 72, 1819–1820. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Bilski, M.; Wojciechowski, K.W. Maximum Poisson’s Ratios in Planar Isotropic Crystals of Binary Hard Discs at High Pressures. Phys. Status Solidi B 2017, 254, 1700543. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Perturbation Theory of the Thermody-namic Properties of Simple Liquids. J. Chem. Phys. 1971, 55, 5422. [Google Scholar] [CrossRef]
- Allen, M.P.; Evans, G.T.; Frenkel, D.; Mulder, B.M. Hard Convex Body Fluids. Adv. Chem. Phys. 1993, 86, 1–166. [Google Scholar]
- Brańka, A.C.; Pierański, P.; Wojciechowski, K.W. Rotatory phase in a system of hard cyclic hexamers; an experimental modelling study. J. Phys. Chem. Solids 1982, 43, 817–818. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Monte Carlo simulations of highly anisotropic two-dimensional hard dumbbell-shaped molecules: Nonperiodic phase between fluid and dense solid. Phys. Rev. B 1992, 46, 26–39. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D. Order through entropy. Nat. Mater. 2015, 14, 9–12. [Google Scholar] [CrossRef]
- Aoki, K.M.; Ito, N. Effect of size polydispersity on granular materials. Phys. Rev. E 1996, 54, 1990–1996. [Google Scholar] [CrossRef]
- Both, J.A.; Hong, D.C. Variational Approach to Hard Sphere Segregation under Gravity. Phys. Rev. Lett. 2002, 88, 124301. [Google Scholar] [CrossRef] [Green Version]
- Gueorguiev, G.K.; Pacheco, J.M.; Stafström, S.; Hultman, L. Silicon–metal clusters: Nano-templates for cluster assembled materials. Thin Solid Films 2006, 515, 1192–1996. [Google Scholar] [CrossRef]
- Gueorguiev, G.K.; Goyenola, C.; Schmidt, S.; Hultman, L. CFx: A first-principles study of structural patterns arising during synthetic growth. Chem. Phys. Lett. 2011, 516, 62–67. [Google Scholar] [CrossRef] [Green Version]
- Kimizuka, H.; Ogata, S.; Shibutani, Y. High-Pressure Elasticity and Auxetic Property of α-Cristobalite. Mater. Trans. 2005, 46, 1161–1166. [Google Scholar] [CrossRef] [Green Version]
- Kimizuka, H.; Kaburaki, H. Molecular dynamics study of the high-temperature elasticity of SiO2 polymorphs: Structural phase transition and elastic anomaly. Phys. Status Solidi B 2005, 242, 607–620. [Google Scholar] [CrossRef]
- Harkati, E.; Daoudi, N.; Bezazi, A.; Haddad, A.; Scarpa, F. In-plane elasticity of a multi re-entrant auxetic honeycomb. Compos. Struct. 2017, 180, 130–139. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Strain fluctuations and elastic constants. J. Chem. Phys. 1982, 76, 2662–2666. [Google Scholar] [CrossRef]
- Ray, J.R.; Rahman, A. Statistical ensembles and molecular dynamics studies of anisotropic solids. J. Chem. Phys. 1984, 80, 4423–4426. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Tretiakov, K.V.; Kowalik, M. Elastic properties of dense solid phases of hard cyclic pentamers and heptamers in two dimensions. Phys. Rev. E 2003, 67, 036121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tokmakova, S.P. Stereographic projections of Poisson’s ratio in auxetic crystals. Phys. Status Solidi B 2005, 242, 721–729. [Google Scholar] [CrossRef]
- Bilski, M.; Wojciechowski, K.W. Tailoring Poisson’s ratio by introducing auxetic layers. Phys. Status Solidi B 2016, 253, 1318–1323. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bilski, M.; Wojciechowski, K.W.; Stręk, T.; Kędziora, P.; Grima-Cornish, J.N.; Dudek, M.R. Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties. Materials 2021, 14, 7837. https://doi.org/10.3390/ma14247837
Bilski M, Wojciechowski KW, Stręk T, Kędziora P, Grima-Cornish JN, Dudek MR. Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties. Materials. 2021; 14(24):7837. https://doi.org/10.3390/ma14247837
Chicago/Turabian StyleBilski, Mikołaj, Krzysztof W. Wojciechowski, Tomasz Stręk, Przemysław Kędziora, James N. Grima-Cornish, and Mirosław R. Dudek. 2021. "Extremely Non-Auxetic Behavior of a Typical Auxetic Microstructure Due to Its Material Properties" Materials 14, no. 24: 7837. https://doi.org/10.3390/ma14247837





