Pertechnetate/Perrhenate Surface Complexation on Bamboo Engineered Biochar
Abstract
1. Introduction
- -
- enrich and supplement the characterization of prepared materials’ structural properties;
- -
- batch sorption investigation influenced by pH, contact time, and equilibrium study;
- -
- potentiometric titration and dynamic sorption experiments;
- -
- theoretical models’ applications.
2. Materials and Methods
2.1. Materials Preparation
2.2. Materials Characterization
2.2.1. X-ray Fluorescence
2.2.2. Acid-Base Titrations
2.3. Batch and Dynamic Sorption Experiments
2.3.1. Speciation Analysis
2.3.2. Pertechnetate/Perrhenate Sorption by Batch Technique and Column Porosity Determination
2.3.3. Pertechnetate/Perrhenate Sorption by Dynamic Technique
3. Results and Discussion
3.1. Material Characterization
3.1.1. XRF
3.1.2. Acid-Base Titration
3.2. Batch Adsorption Experiments
3.2.1. Speciation Study
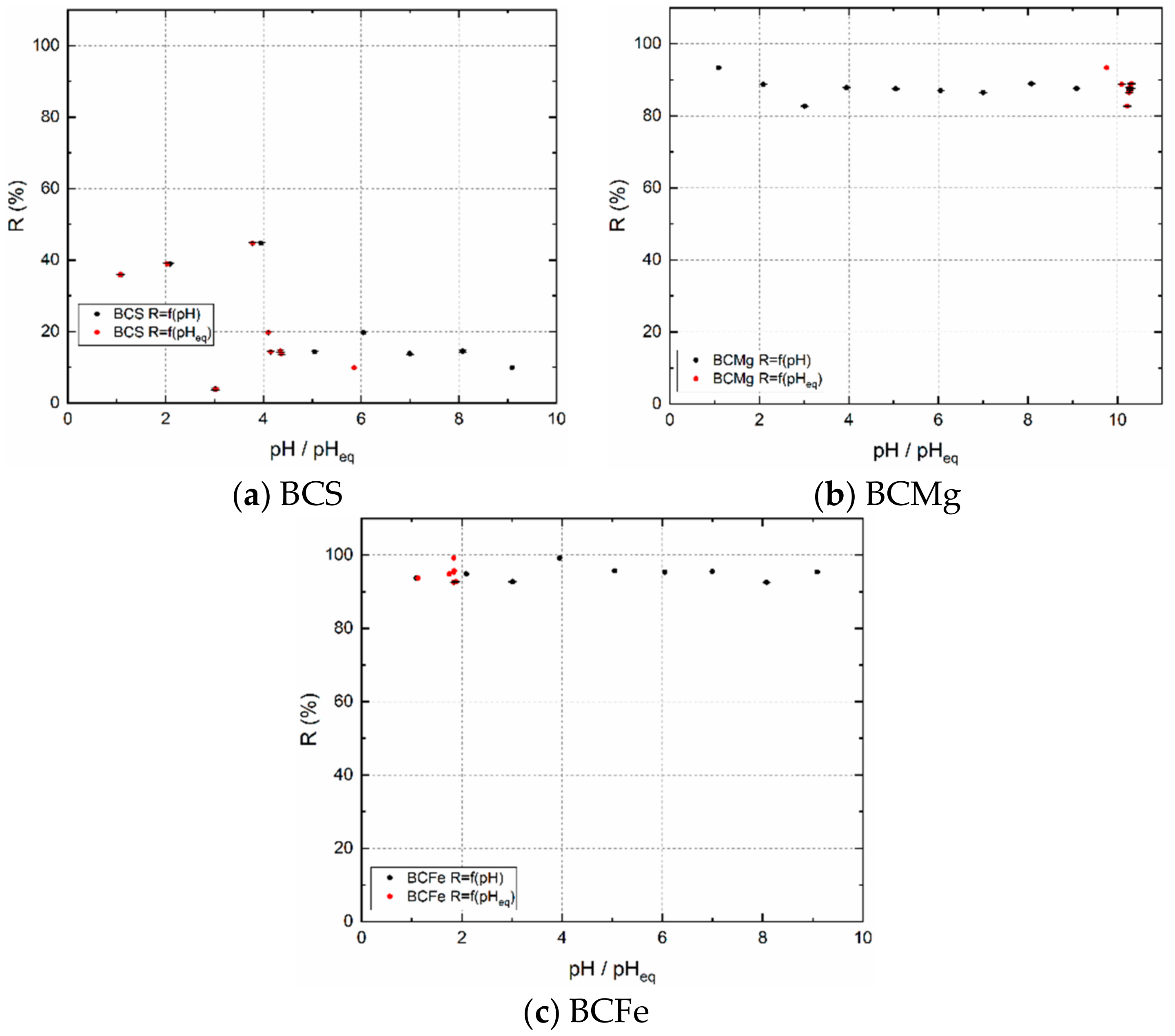
3.2.2. Dependence of Sorption Percentage R on pH
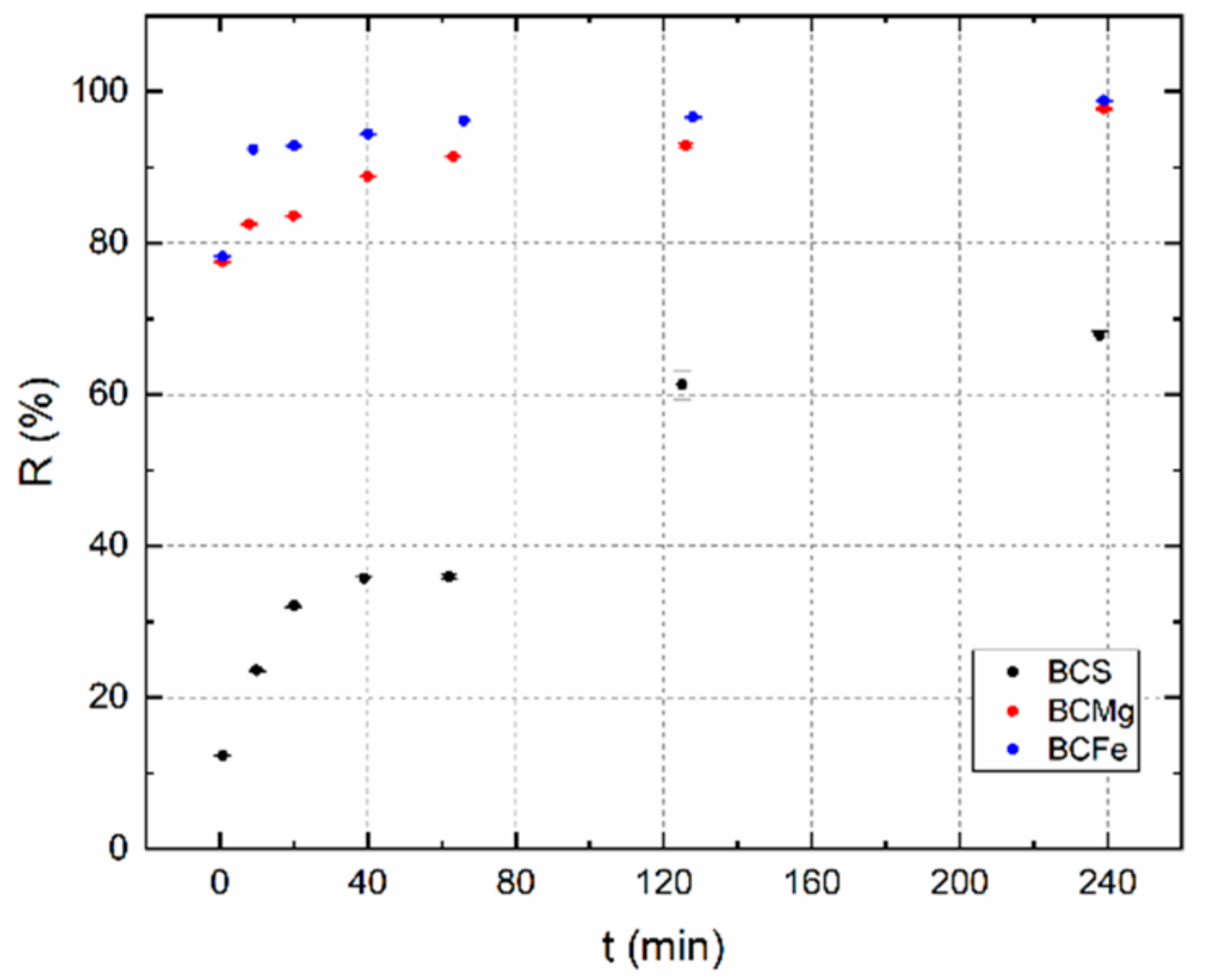
3.2.3. Determination of the Sorption Equilibrium Time
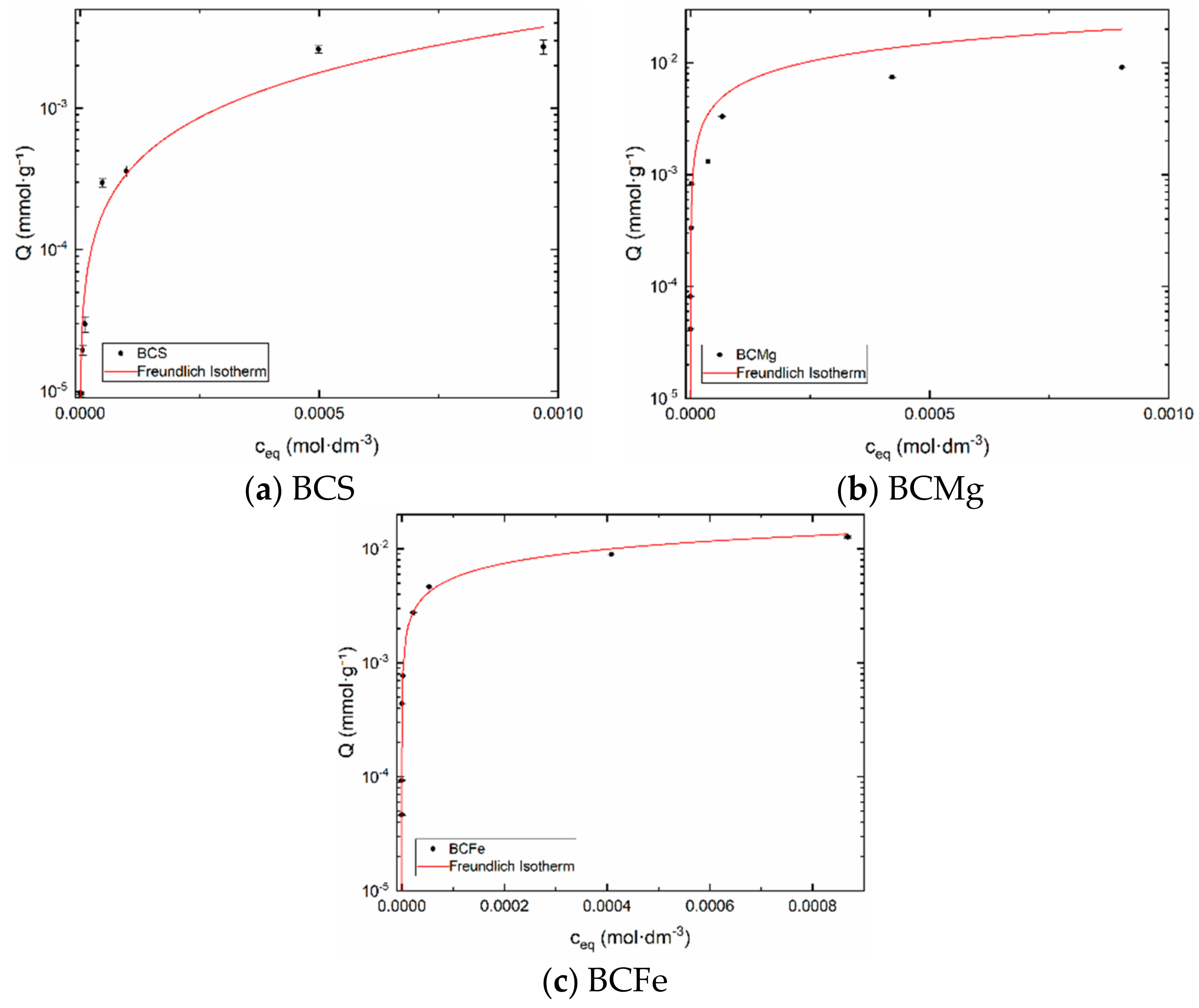
3.2.4. Freundlich Isotherm
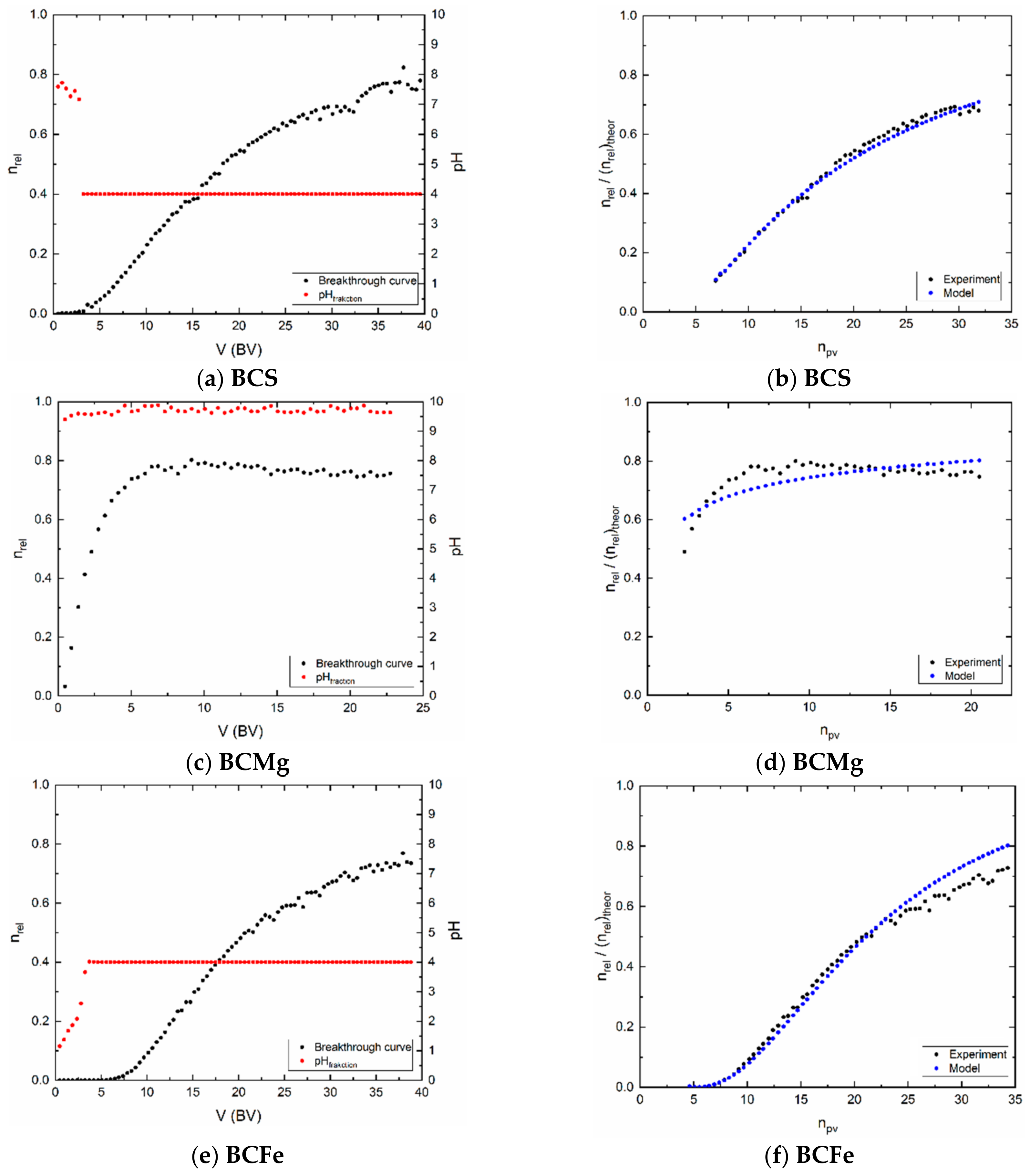
3.3. Dynamic Sorption Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, D.; Seaman, J.C.; Kaplan, D.I.; Heald, S.M.; Sun, C. Pertechnetate TcO4− sequestration from groundwater by cost-effective organoclays and granular activated carbon under oxic-environmental conditions. Chem. Eng. J. 2019, 360, 1–9. [Google Scholar] [CrossRef]
- Chen, L.; Yin, X.; Yu, Q.; Lu, S.; Meng, F.; Ning, S.; Wang, X.; Wei, Y. Rapid and selective capture of perrhenate anion from simulated groundwater by a mesoporous silica-supported anion exchanger. Micropor. Mesopor. Mater. 2019, 274, 155–162. [Google Scholar] [CrossRef]
- Isaacs, M.; Lange, S.; Deissmannn, G.; Bosbach, D.; Mildowski, A.E.; Read, D. Retention of Technetium-99 by grout and backfill cements: Implications for the safe disposal of radioactive waste. Appl. Geochem. 2020, 116, 104580. [Google Scholar] [CrossRef]
- Emerson, P.H.; Gebru, A.; Boglaienko, D.; Katsenovich, Y.P.; Kandel, S.; Levitskaia, T.G. Impact of zero valent iron aging on reductive removal of technetium-99. J. Environ. Chem. Eng. 2020, 8, 103767. [Google Scholar] [CrossRef]
- Hu, H.; Jiang, B.; Wu, H.; Zhang, J.; Chen, X.H. Bamboo (Acidosasa edulis) shoot shell biochar: Its potential isolation and mechanism to perrhenate as a chemical surrogate for pertechnetate. J. Environ. Radioact. 2016, 165, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Schwochau, K. Technetium Chemistry and Radiopharmaceutical Applications; Wiley-VCH: Weinheim, Germany, 2000; ISBN 3-527-29496-1. [Google Scholar]
- Serne, R.J.; Crum, J.V.; Riley, B.J.; Levitskaia, T.G. Options for the Separation and Immobilization of Technetium; (No. PNNL-25834; EMSP-RPT-029Rev0); Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2016. [Google Scholar]
- TrisKem International. Extraction Chromatography. Technical Documentation. Available online: https://www.triskem-international.com/scripts/files/5addcf96423962.97324869/technical_doc_all-products_web-0.pdf (accessed on 11 November 2020).
- Viglašová, E.; Daňo, M.; Galamboš, M.; Rosskopfová, O.; Rajec, P.; Novák, I. Column studies for the separation of 99mTc using activated carbon. J. Radioanal. Nucl. Chem. 2016, 307, 591–597. [Google Scholar] [CrossRef]
- Hu, H.; Sun, L.; Gao, Y.; Wang, T.; Huang, Y.; Lv, C.; Zhang, Y.F.; Huang, Q.; Chen, X.; Wu, H. Synthesis of ZnO nanoparticles-anchored biochar composites for selective removal of perrhenate, a surrogate for pertechnetate, from radioactive effluents. J. Hazard. Mat. 2020, 387, 121670. [Google Scholar] [CrossRef]
- Pandey, D.; Daverey, A.; Arunachalam, K. Biochar: Production, properties and emerging role as a support for enzyme immobilization. J. Clean. Prod. 2020, 255, 120267. [Google Scholar] [CrossRef]
- Khan, M.B.; Cui, X.; Jilan, G.; Lu, L.T.M.; Cao, X.; Sahito, Z.A.; Hamid, Y.; Hussain, B.; Yang, X.; He, Z. New insight into the impact of biochar during vermi-stabilization of divergent biowastes: Literature synthesis and research pursuits. Chemosphere 2020, 238, 124679. [Google Scholar] [CrossRef]
- Rajapaksha, A.U.; Chen, S.S.; Tsang, D.C.; Zhang, M.; Vithanage, M.; Mandal, S.; Gao, B.; Bolan, N.S.; Ok, Y.S. Review: Engineered/designer biochar for contaminant removal/immobilization from soil and water: Potential and implication of biochar modification. Chemosphere 2016, 148, 276–291. [Google Scholar] [CrossRef]
- O’Toole, A.; Andersson, D.; Gerlach, A.; Glaser, B.; Kammann, C.; Kern, J.; Kuoppamäki, K.; Mumme, J.; Schmidt, H.P.; Schulze, M. Current and future applications for biochar. In Biochar in European Soils and Agriculture—Science and Practice, 1st ed.; Taylor & Francis Group: Abingdon, UK, 2016; pp. 253–280. ISBN 9780367606046. [Google Scholar]
- Beesley, L.; Marmiroli, M. The immobilization and retention of soluble arsenic, cadmium and zinc by biochar. Environ. Pollut. 2011, 159, 474–480. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Zimmerman, A.R.; Harris, W. Surface chemistry variations among a series of laboratory-produced biochars. Geoderma 2011, 163, 247–255. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Z.; Lv, S. A novel magnetic biochar efficiently sorbs organic pollutants and phosphates. Bioresour. Technol. 2011, 102, 716–723. [Google Scholar] [CrossRef]
- Li, H.; Dong, X.; Da Silva, E.B.; De Oliviera, L.M.; Chen, Y.; Ma, L.Q. Mechanisms of metal sorption by biochars: Biochar characteristics and modifications. Chemosphere 2017, 178, 466–478. [Google Scholar] [CrossRef] [PubMed]
- Thinnes, K.R.; Abdullah, E.C.; Mubarak, N.M.; Ruthiraan, M. Synthesis of magnetic biochar from agricultural waste biomass to enhancing route for waste-water polymer application: A review. Renew. Sust. Energ. Rev. 2017, 67, 257–276. [Google Scholar] [CrossRef]
- El-Naggar, A.; Lee, S.S.; Rinklebe, J.; Farooq, M.; Song, H.; Sarmah, A.K.; Zimmerman, A.R.; Ahmad, M.; Shaheen, S.M.; Ok, Y.S. Biochar application to low fertility soils: A review of current status, and future prospects. Geoderma 2019, 337, 536–554. [Google Scholar] [CrossRef]
- Lu, H.P.; Li, Z.A.; Gascó, G.; Méndez, A.; Shen, Y.; Paz-Ferreiro, J. Use of magnetic biochars for the immobilization of heavy metals in a multi-contaminated soil. Sci. Total. Environ. 2018, 622–623, 892–899. [Google Scholar] [CrossRef]
- Mazarji, M.; Aminzadeh, B.; Baghdadi, M.; Bhantnagar, A. Removal of nitrate from aqueous solution using modified granular activated carbon. J. Mol. Liq. 2017, 233, 139–148. [Google Scholar] [CrossRef]
- Viglašová, E.; Galamboš, M.; Diviš, D.; Danková, Z.; Daňo, M.; Krivosudský, L.; Lengauer, C.L.; Matik, M.; Briančin, J.; Soja, G. Engineer biochar as a tool for nitrogen pollutants removal: Preparation, characterization and sorption study. Desalin. Wat. Treat. 2020, 191, 318–331. [Google Scholar] [CrossRef]
- Daňo, M.; Viglašová, E.; Galamboš, M.; Štamberg, K.; Kujan, J. Surface Complexation Models of Pertechnetate on Biochar/Montmorillonite Composite—Batch and Dynamic Sorption Study. Materials 2020, 13, 3108. [Google Scholar] [CrossRef]
- Viglašová, E.; Galamboš, M.; Danková, Z.; Krivosudský, L.; Lengauer, C.L.; Hood-Nowotny, R.; Soja, G.; Rompel, A.; Matík, M.; Briančin, J. Production, characterization and adsorption studies of bamboo-based biochar/montmorillonite composite for nitrate removal. Waste Manag. 2018, 79, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Filipská, H.; Štamberg, K. Mathematical modeling of a Cs(I)-Sr(II)-bentonite-magnetite sorption system, simulating the processes taking place in a deep geological repository. Acta Polytech. 2005, 45, 11–18. [Google Scholar] [CrossRef]
- Lutzenkirchen, J. Surface Complexation Modelling, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 11, ISBN 9780123725721. [Google Scholar]
- Dvořák, L.; Ledvinka, M.; Sobotka, M. Famulus 3.5. Software; Charles University: Prague, Czech Republic, 1993. [Google Scholar]
- Steven, J.W. Calibration Method Using a Stable and Safe Redox Standard Solution. U.S. Patent 6,350,367 B1, 26 February 2002. [Google Scholar]
- Rahmani, A.; Mousavi, H.Z.; Fazli, M. Effect of nanostructure alumina on adsorption of heavy metals. Desalination 2010, 253, 94–100. [Google Scholar] [CrossRef]
- Rachinskii, V.V. The General Theory of Sorption Dynamics and Chromatography; Springer Verlag US: Boston, MA, USA, 1965; ISBN 978-1-4757-0063-3. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications, Inc.: New York, NY, USA, 1972; ISBN 9780444001146. [Google Scholar]
- Štamberg, K.; Palagyi, Š. Effect of grain size on the sorption and desorption of 137Cs in crushed granite columns and ground water system under dynamic conditions. J. Radioanal. Nucl. Chem. 2012, 293, 127–134. [Google Scholar] [CrossRef]
- Luyckx, M.; Hausman, J.-F.; Lutts, S.; Guerriero, G. Silicon and Plants: Current Knowledge and Technological Perspectives. Front. Plant. Sci. 2017, 8, 411. [Google Scholar] [CrossRef]
- Ang, K.L.; Li, D.; Nikoloski, A.N. The effectiveness of ion exchange resins in separating uranium and thorium from rare earth elements in acidic aqueous sulfate media. Part 1. Anionic and cationic resins. Hydrometallurgy 2017, 174, 147–155. [Google Scholar] [CrossRef]
- Takeno, N. Atlas of Eh-pH Diagrams. Intercomparison of Thermodynamic Databases; Open File Report No. 419; Geological Survey of Japan: Tokyo, Japan, 2005. [Google Scholar]
- Huinink, H.P.; Zahn, D. Elucidating water dynamics in MgCl2 hydrates from moleculardynamics simulation. Solid State Sci. 2017, 69, 64–70. [Google Scholar] [CrossRef]
- Hellman, H.; Laitinen, R.S.; Kaila, L.; Jalonen, J.; Hietapelto, V.; Jokela, J.; Sarpola, J.; Sarpola, A.; Rämö, J. Identification of hydrolysis products of FeCl3·6 H2O by ESI-MS. J. Mass. Spectrom. 2006, 41, 1421–1429. [Google Scholar] [CrossRef]

| Column | Sorption Solution | ||
|---|---|---|---|
| Sample | m (g) | pH | c(NH4ReO4) (mol·dm−3) |
| BCS | 0.3437 | 4 | 1 × 10−3 |
| BCMg | 0.4358 | 1 | 5 × 10−⁴ |
| BCFe | 0.5769 | 4 | 1 × 10−3 |
| Sample | Element | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BCS | Si | P | Cl | Fe | Ni | Ag | |||||||||
| BCMg | Mg | Si | S | P | Cl | K | Ca | Cr | Fe | Ni | Zn | Rb | Rb | Ag | |
| BCFe | Al | Cl | K | Ca | Cr | Fe | Ni | Zn | Rb | Rb | Ag | ||||
| Sample | Elements | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| BCS | C | O | Mg | Al | P | Cl | K | Ca | |
| BCMg | C | O | Mg | Al | Cl | ||||
| BCFe | C | O | Mg | Al | P | Cl | K | Fe | |
| K1 | K2 | Kex | [SOH]tot (mol·kg−1) |
|---|---|---|---|
| (1.54 ± 24.9) × 1015 | (1.53 ± 0.16) × 1011 | (8.71 ± 13.8) × 10−1 | (6.07 ± 0.03) × 10−2 |
| WSOS/DF | χ2 | σi | [S]tot (mol·kg−1) |
| 10.3 | 1.34 × 102 | 0.1 | (8.94 ± 0.05) × 10−2 |
| ΣTc (mol·dm−3) | ΣRe (=KReO4) (mol·dm−3) | pH0 | pHend | F1 [ReO4−] | F2 [HReO4] | F3 [KReO4] |
|---|---|---|---|---|---|---|
| 10−10 | 10−2 | 0 | 3.6 | 0.34 | 9.80 × 10−11–3.90 × 10−7 | 0.66 |
| 10−10 | 10−3 | 0 | 3.6 | 0.84 | 2.40 × 10−10–0.96 × 10−7 | 0.16 |
| 10−10 | 10−4 | 0 | 3.6 | 0.98 | 2.28 × 10−10–1.13 × 10−6 | 0.02 |
| 10−10 | 10−5 | 0 | 3.6 | 0.99 | 2.88 × 10−10–1.15 × 10−6 | 0.002 |
| 10−10 | 10−4 | 0 | 10 | 0.98 | 7.11 × 10−17–1.13 × 10−6 | 0.02 |
| 10−12 | 10−3 | 0 | 3.6 | 0.84 | 2.41 × 10−10–9.60 × 10−7 | 0.16 |
| 10−12 | 10−4 | 0 | 3.6 | 0.98 | 2.83 × 10−10–1.43 × 10−6 | 0.02 |
| c(NH4ReO4) (mol·dm−3) | Eh(mV) | pH |
|---|---|---|
| 5 × 10−5 | 270.8 | 2 |
| 5 × 10−4 | 321.0 | 1 |
| 5 × 10−4 | 269.5 | 2 |
| 5 × 10−4 | 265.4 | 2 |
| 1 × 10−4 | 269.3 | 2 |
| 1 × 10−4 | 269.9 | 2 |
| 1 × 10−3 | 270.7 | 2 |
| 1 × 10−2 | 270.5 | 2 |
| Zobell’s solution 1 | −98.9 | 8.4 |
| Zobell’s solution 2 | −99.7 | 8.4 |
| Sample | pH | Rmax (%) | Dg (cm3·g−1) | Dg,min (cm3·g−1) | Dg,max (cm3·g−1) |
|---|---|---|---|---|---|
| BCS | 4 | 44.7 ± 0.2 | 80 ± 1 | 58 | 51,502 |
| BCMg | 1 | 93.3 ± 0.1 | 1383 ± 8 | 57 | 76,680 |
| BCFe | 4 | 99.2 ± 0.1 | 12,268 ± 284 | 58 | 52,015 |
| Scheme | kF | nF | R2 |
|---|---|---|---|
| BCS | (1.95 ± 0.17) × 101 | (8.71 ± 0.14) × 10−1 | 0.85487 |
| BCMg | (6.24 ± 2.08) × 1028 | (965 ± 3.31) × 10−2 | 0.86398 |
| BCFe | (215 ± 1.16) × 10−1 | (946 ± 0.67) × 10−3 | 0.98994 |
| WSOS/DF | χ2 | σi | Pe | |
|---|---|---|---|---|
| BCS | 0.301 | 16 | 0.1 | (1.93 ± 0.06) × 100 |
| BCMg | 0.627 | 23.8 | 0.1 | (19.5 ± 1.72) × 10-2 |
| BCFe | 1.16 | 72.9 | 0.1 | (544 ± 4.68) × 10-2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daňo, M.; Viglašová, E.; Štamberg, K.; Galamboš, M.; Galanda, D. Pertechnetate/Perrhenate Surface Complexation on Bamboo Engineered Biochar. Materials 2021, 14, 486. https://doi.org/10.3390/ma14030486
Daňo M, Viglašová E, Štamberg K, Galamboš M, Galanda D. Pertechnetate/Perrhenate Surface Complexation on Bamboo Engineered Biochar. Materials. 2021; 14(3):486. https://doi.org/10.3390/ma14030486
Chicago/Turabian StyleDaňo, Martin, Eva Viglašová, Karel Štamberg, Michal Galamboš, and Dušan Galanda. 2021. "Pertechnetate/Perrhenate Surface Complexation on Bamboo Engineered Biochar" Materials 14, no. 3: 486. https://doi.org/10.3390/ma14030486
APA StyleDaňo, M., Viglašová, E., Štamberg, K., Galamboš, M., & Galanda, D. (2021). Pertechnetate/Perrhenate Surface Complexation on Bamboo Engineered Biochar. Materials, 14(3), 486. https://doi.org/10.3390/ma14030486









