The Bond-Slip Relationship at FRP-to-Brick Interfaces under Dynamic Loading
Abstract
:1. Introduction
2. Single-Lap Shear Tests
2.1. Materials and Specimen Preparation
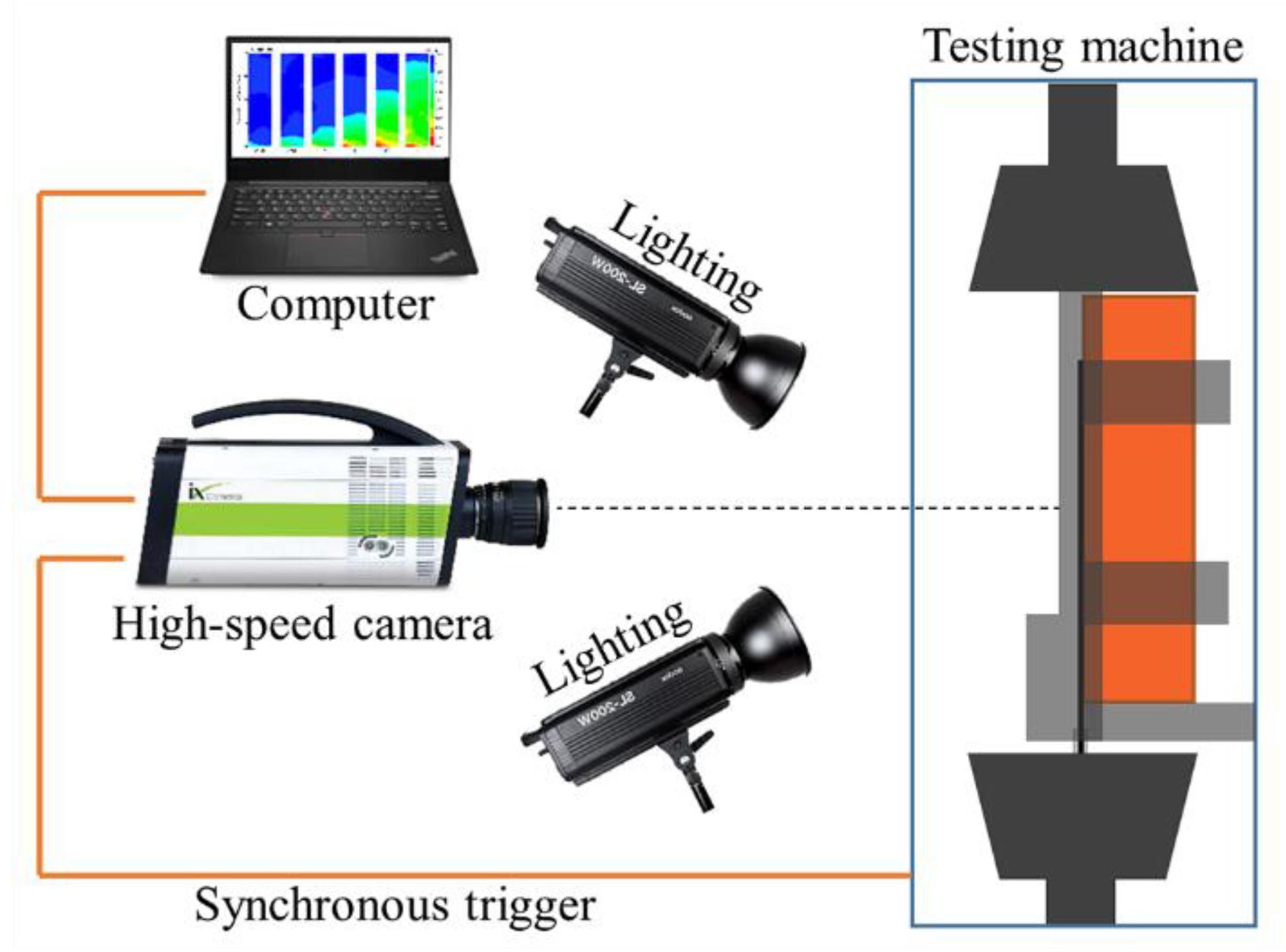
2.2. Instruments and Test Procedures
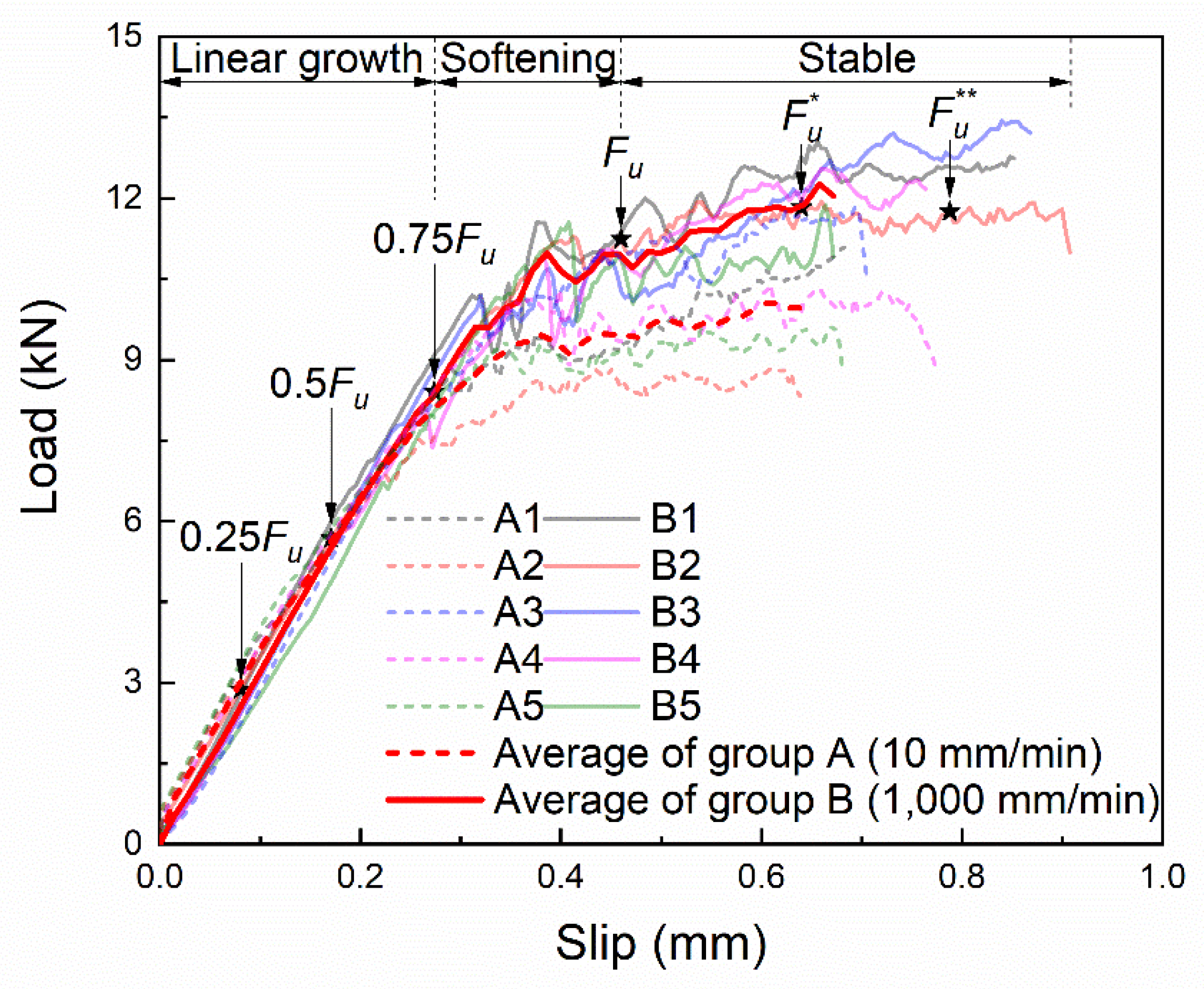
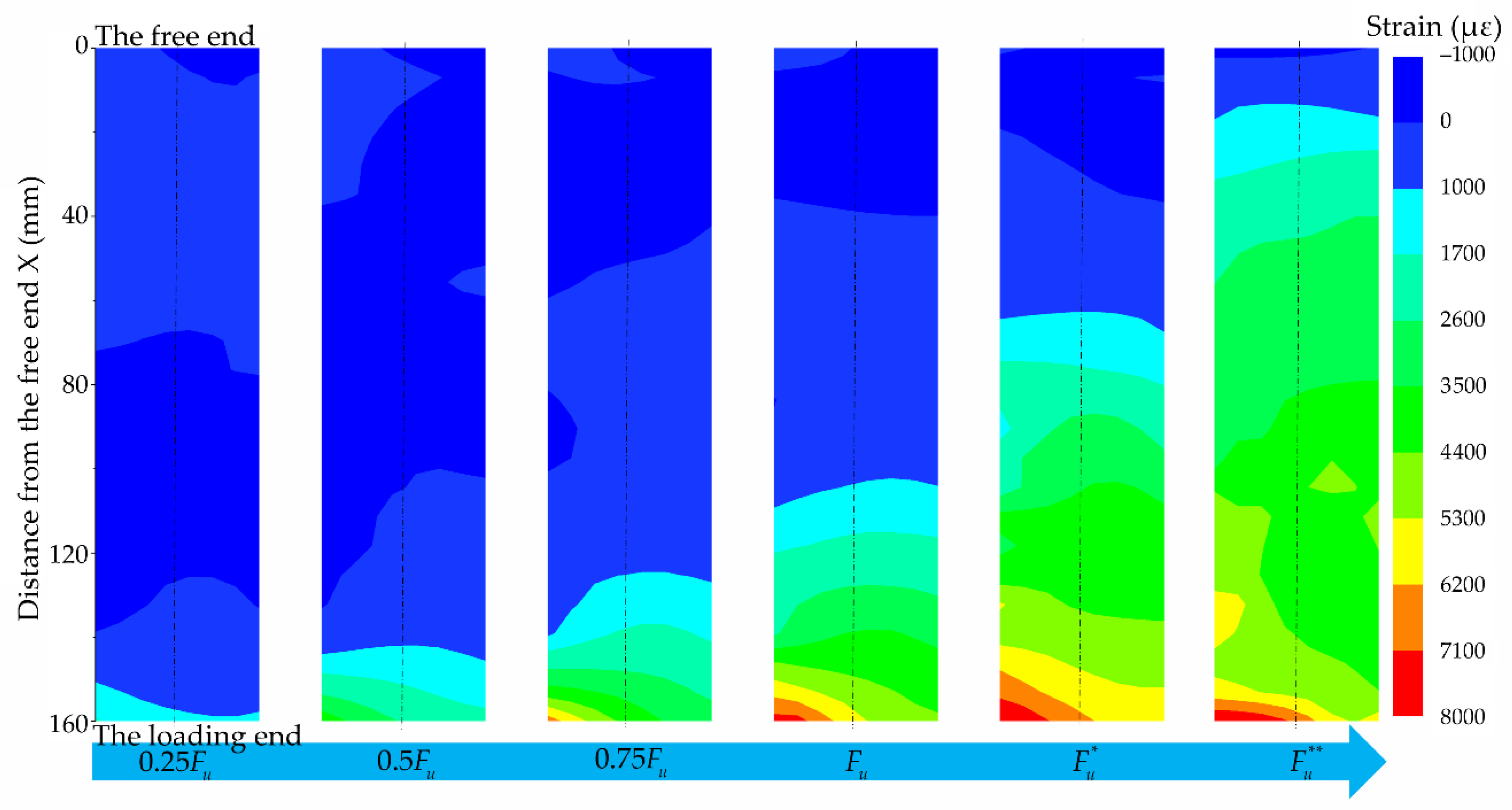
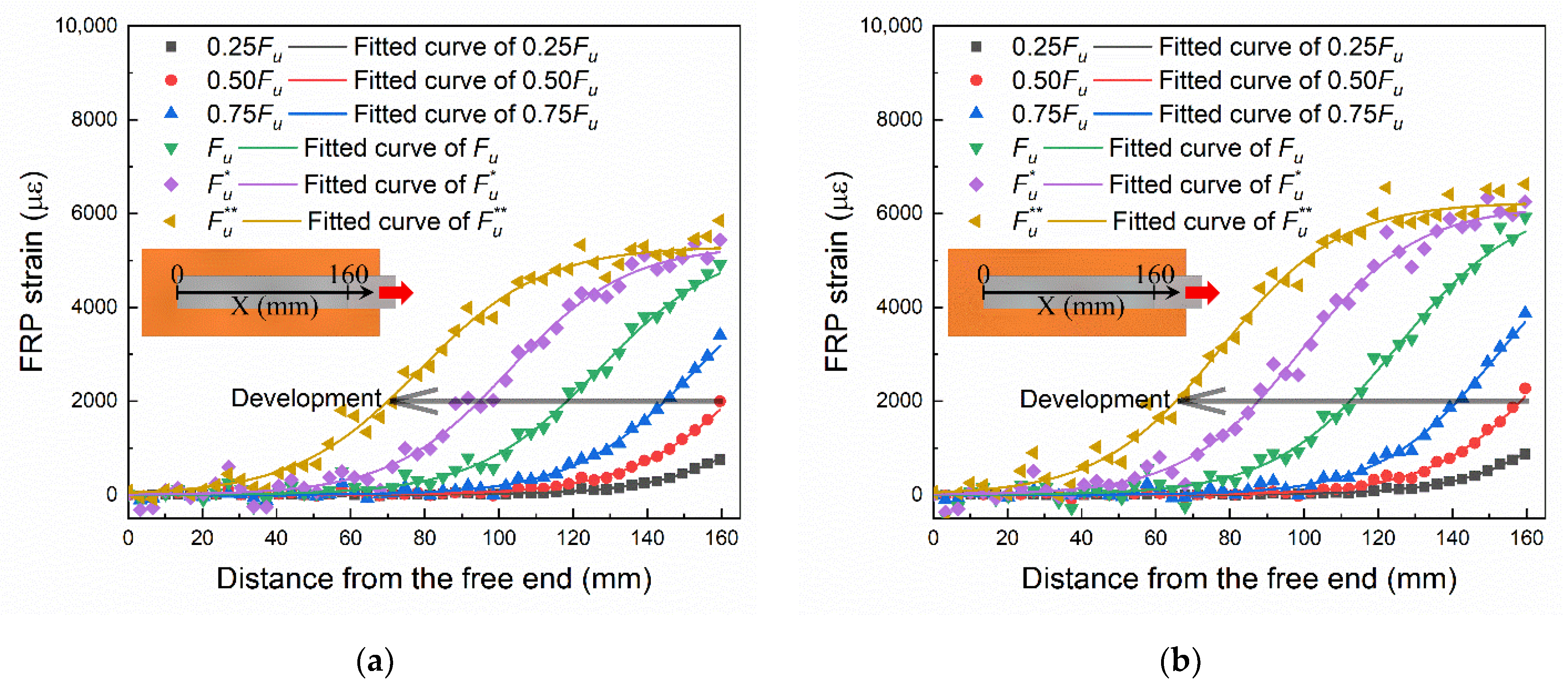
2.3. Test Results and Analysis
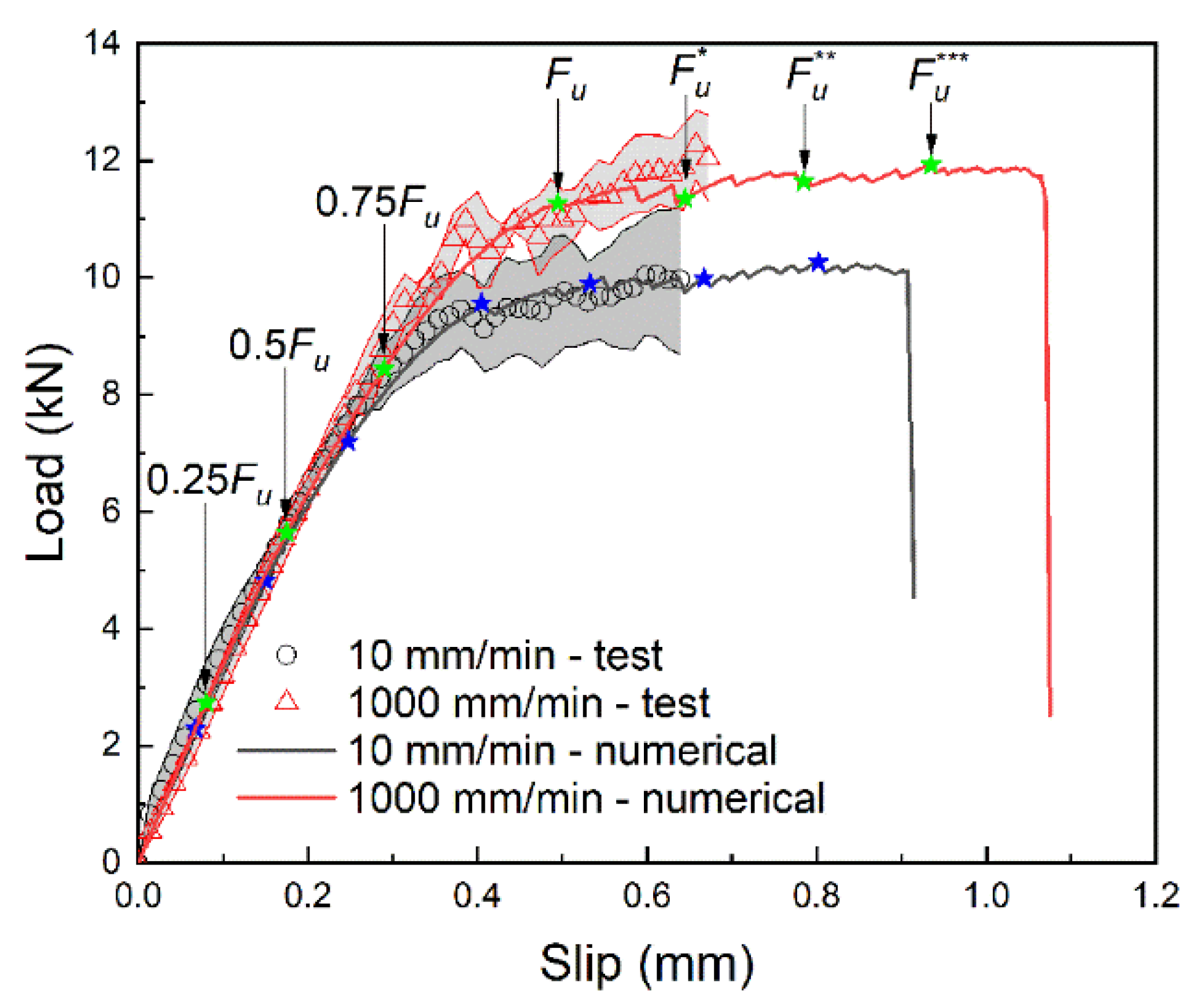
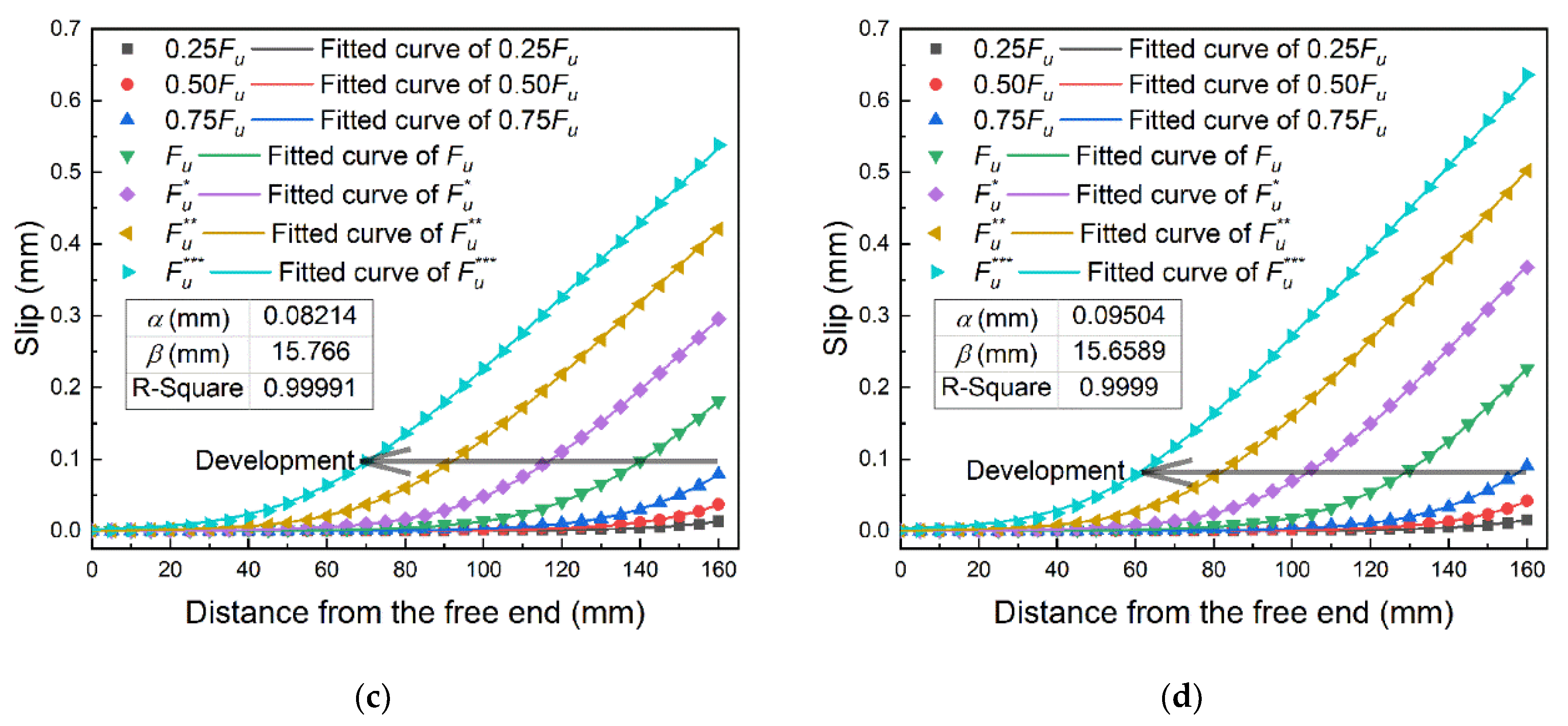
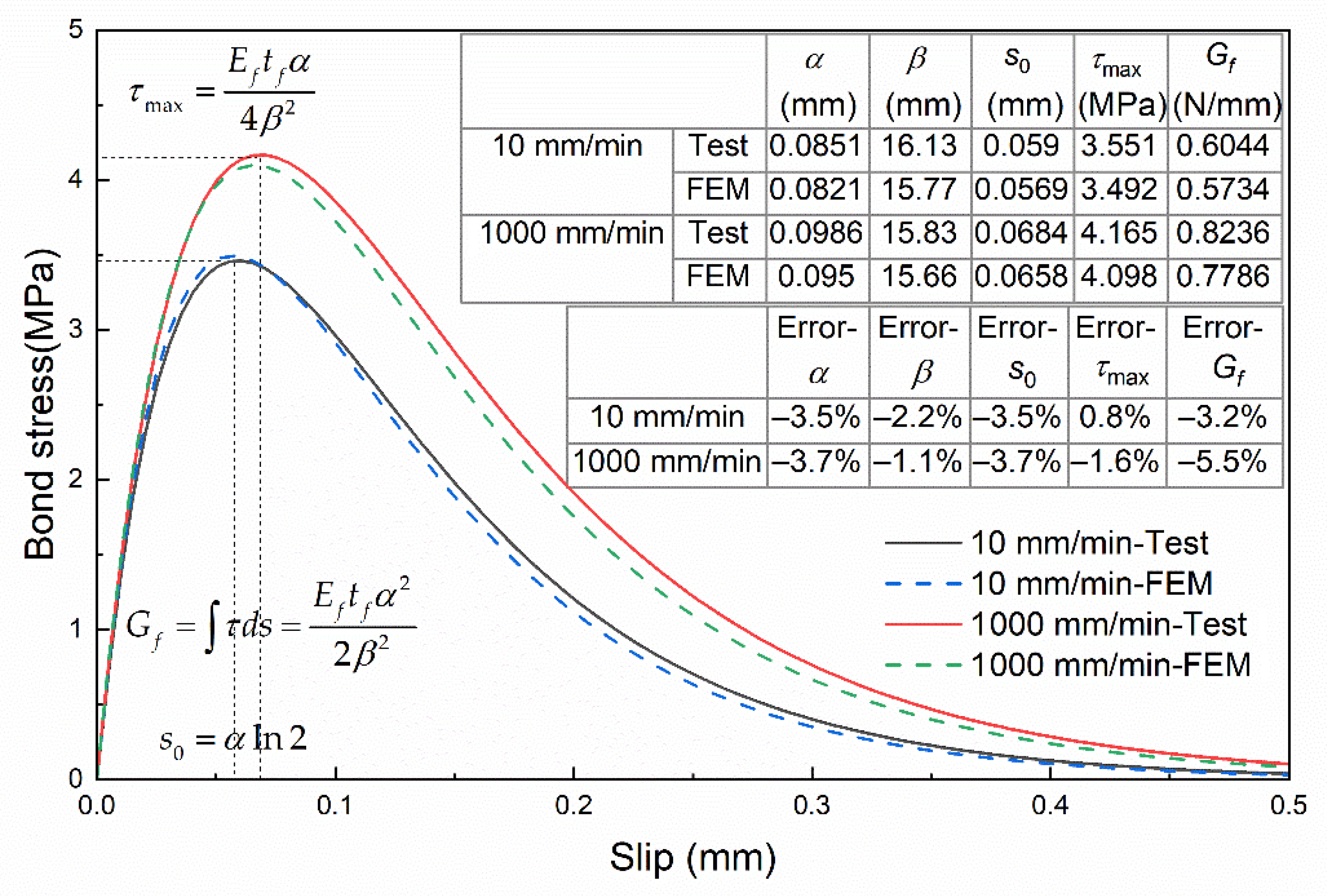
2.4. Bond–Slip Relationship
3. Numerical Analysis and Validation
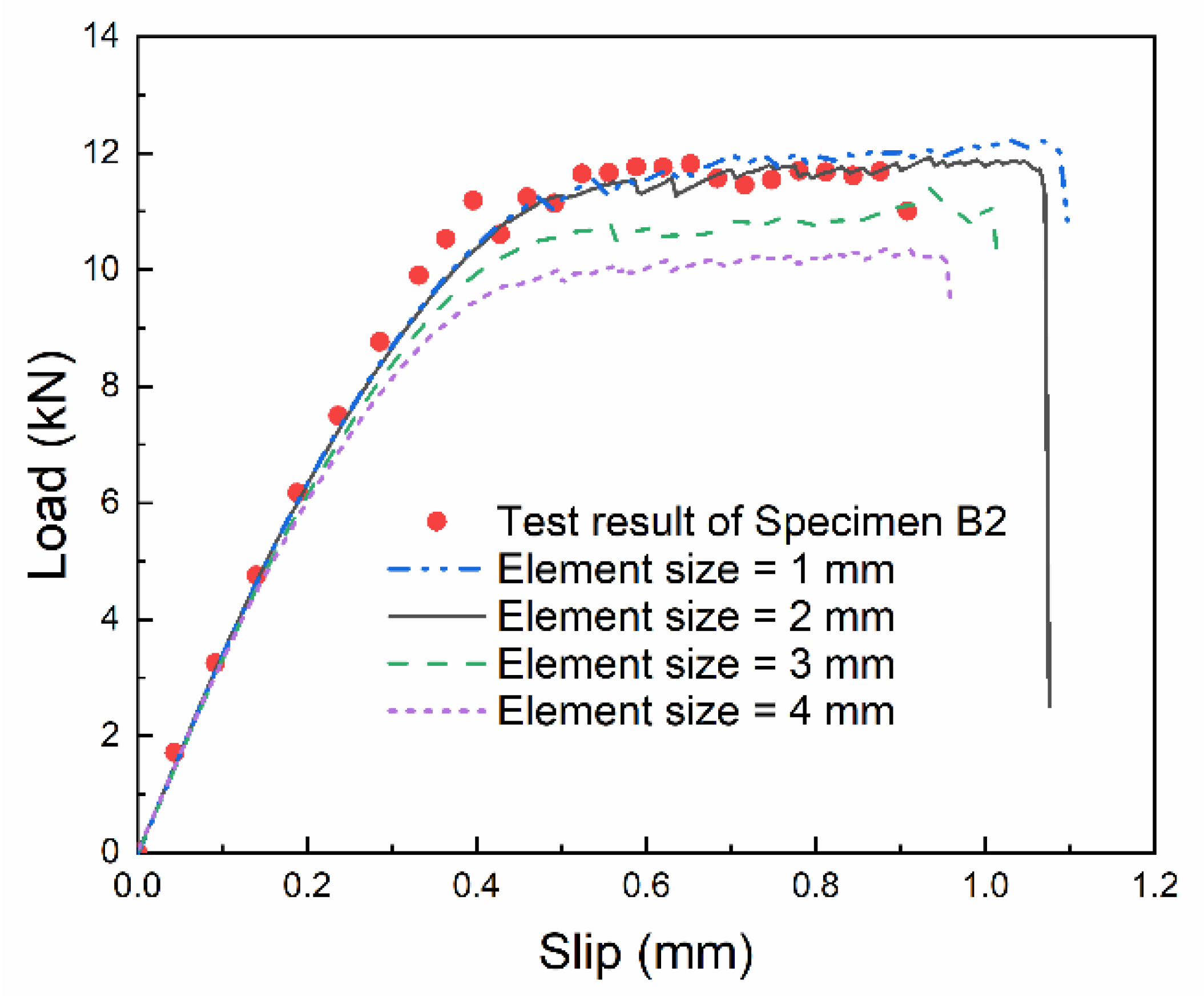
3.1. Numerical Modeling
3.2. Plastic-Damage Model
3.3. Strain Rate Effects on Materials
3.4. Results Validation and Analysis
3.4.1. Validation with Test Results
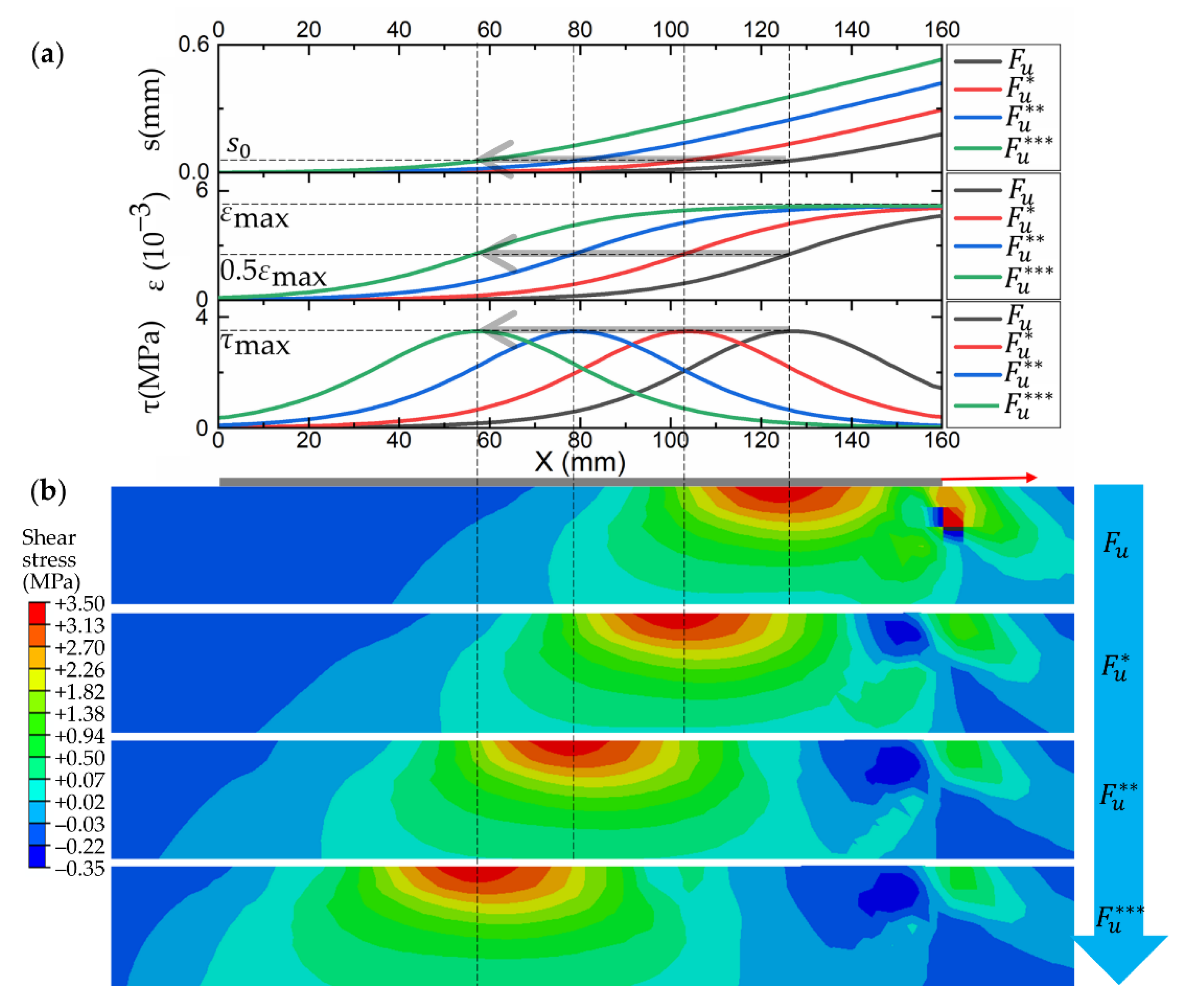
3.4.2. Debonding Analysis
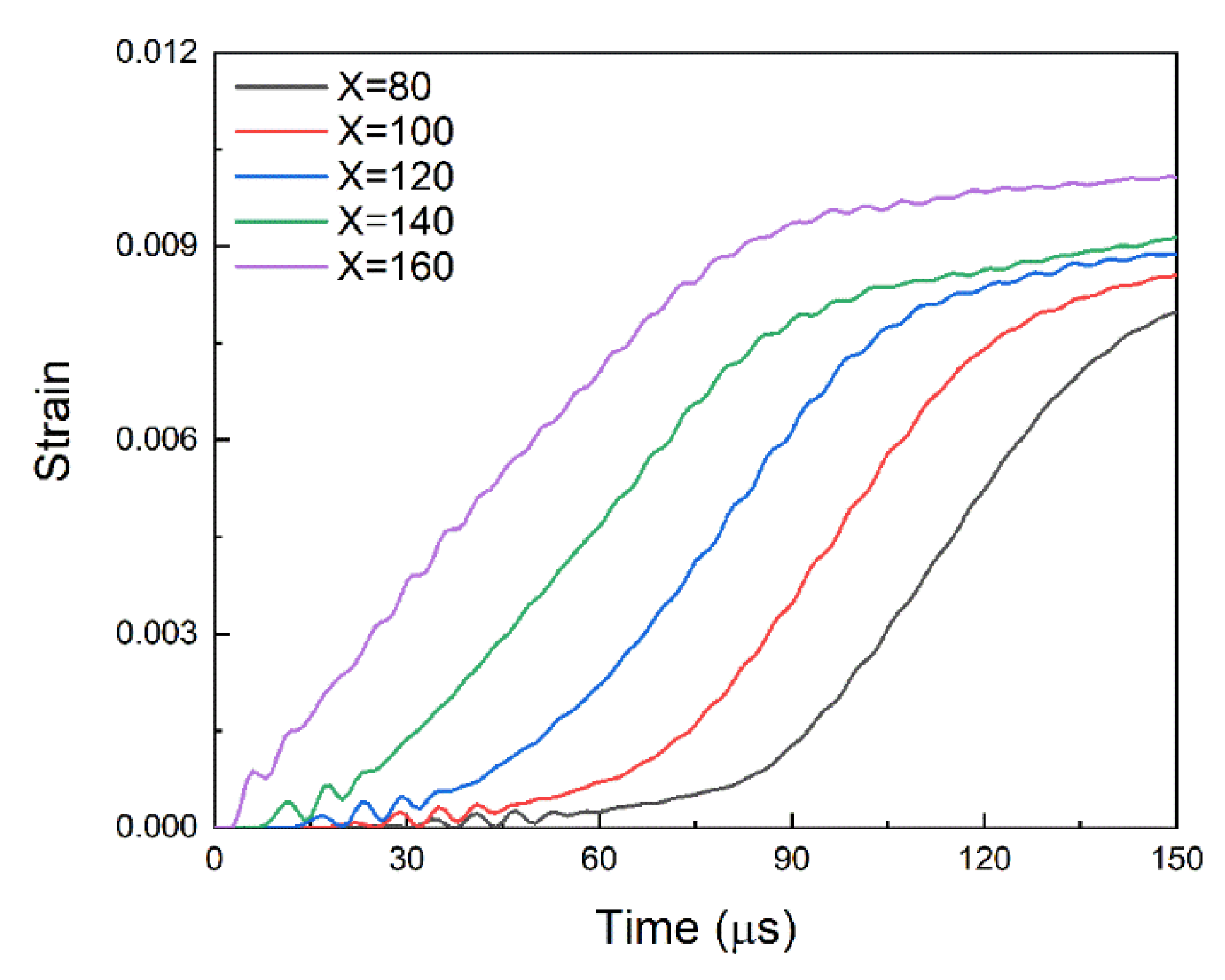
4. Parameter Study on Dynamic Behavior
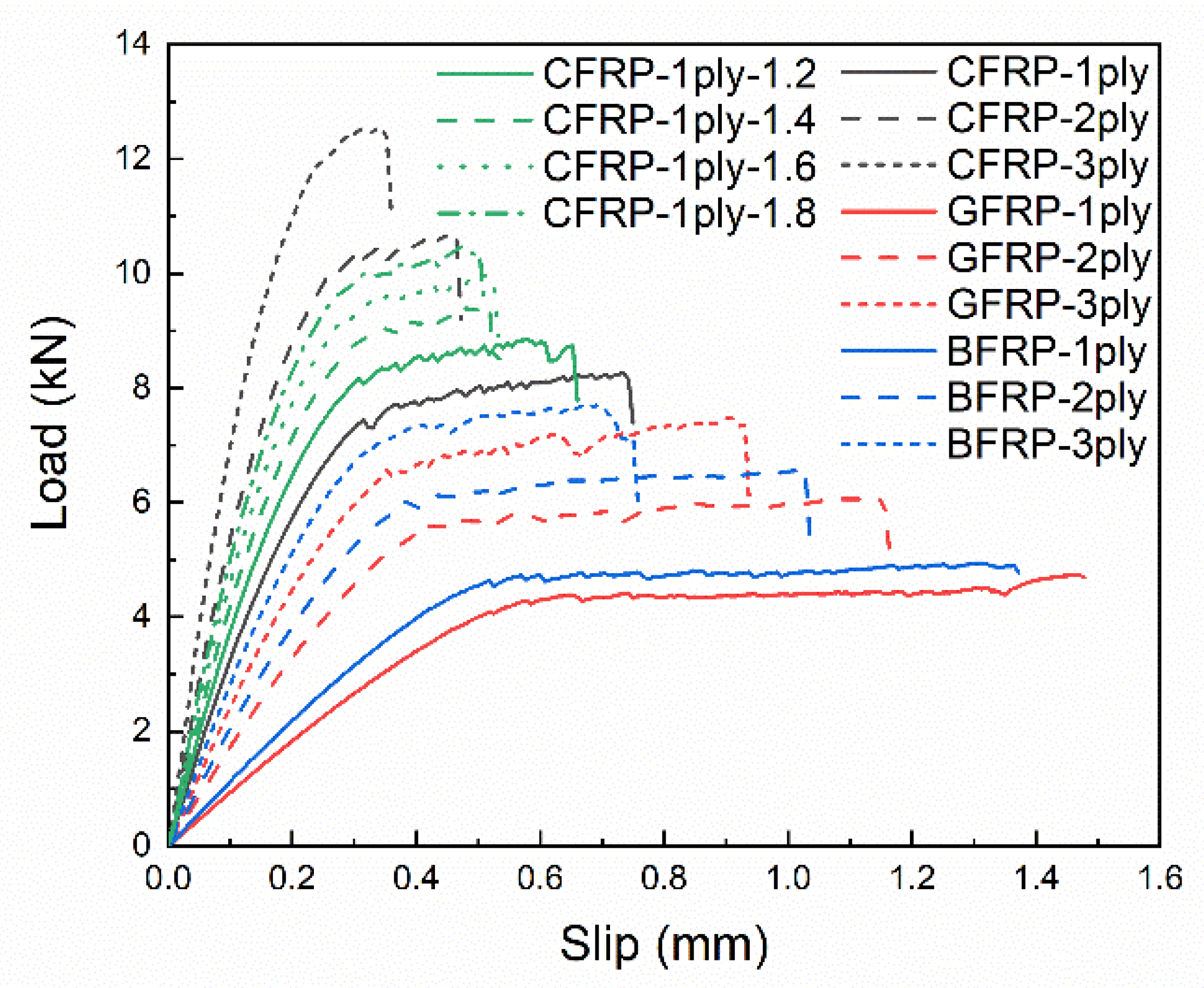
4.1. Effect of FRP Stiffness
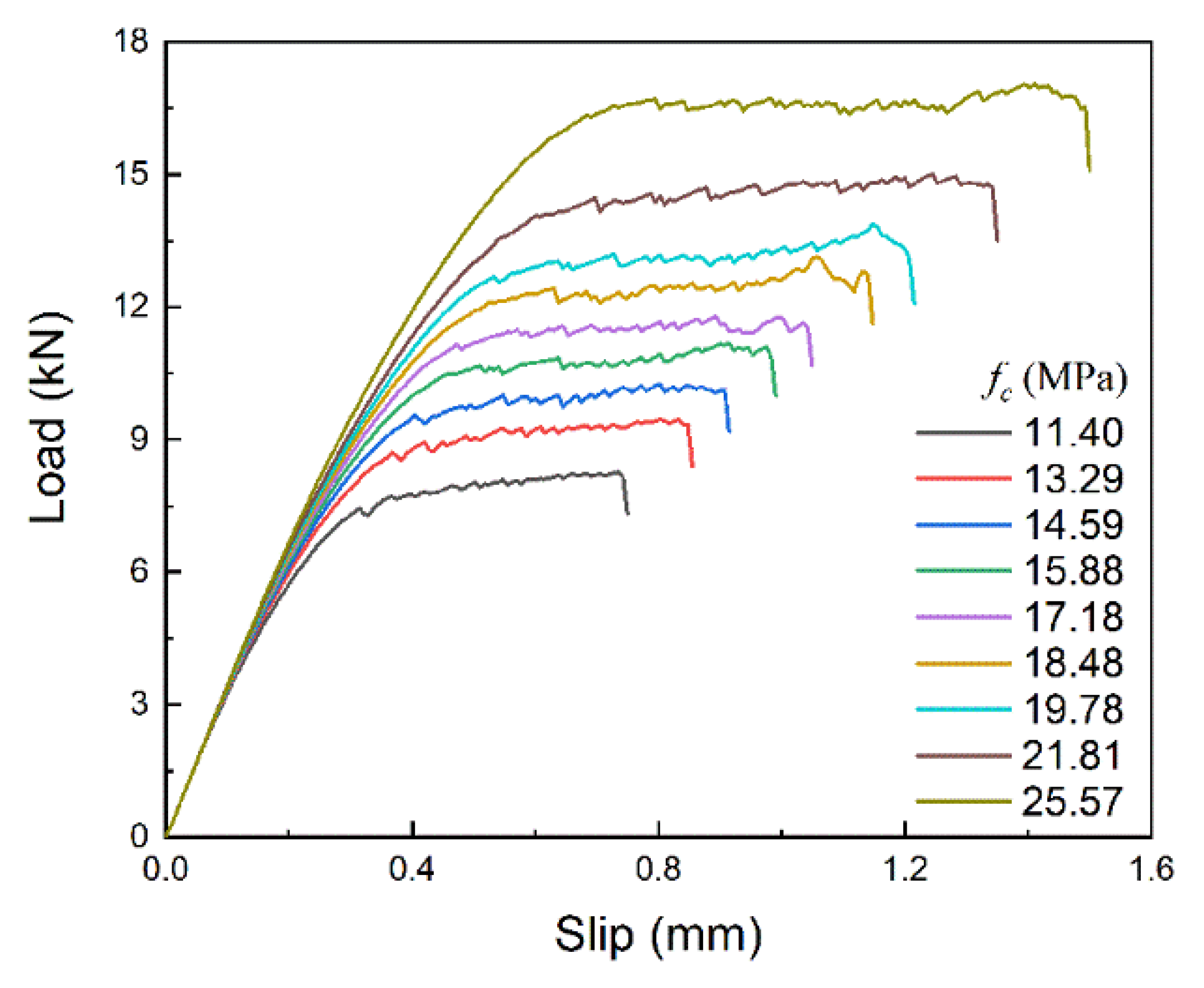
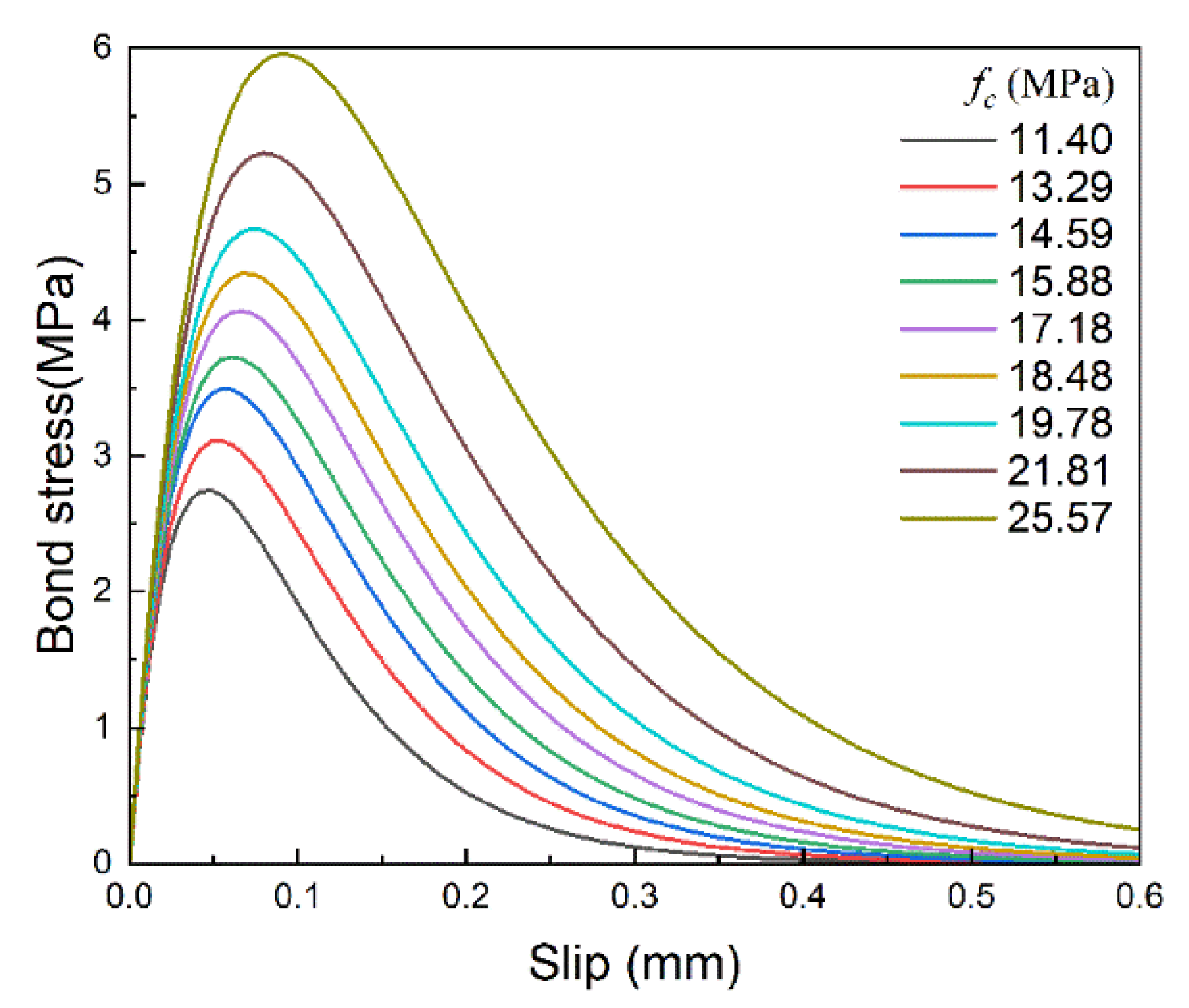
4.2. Effect of Brick Strength
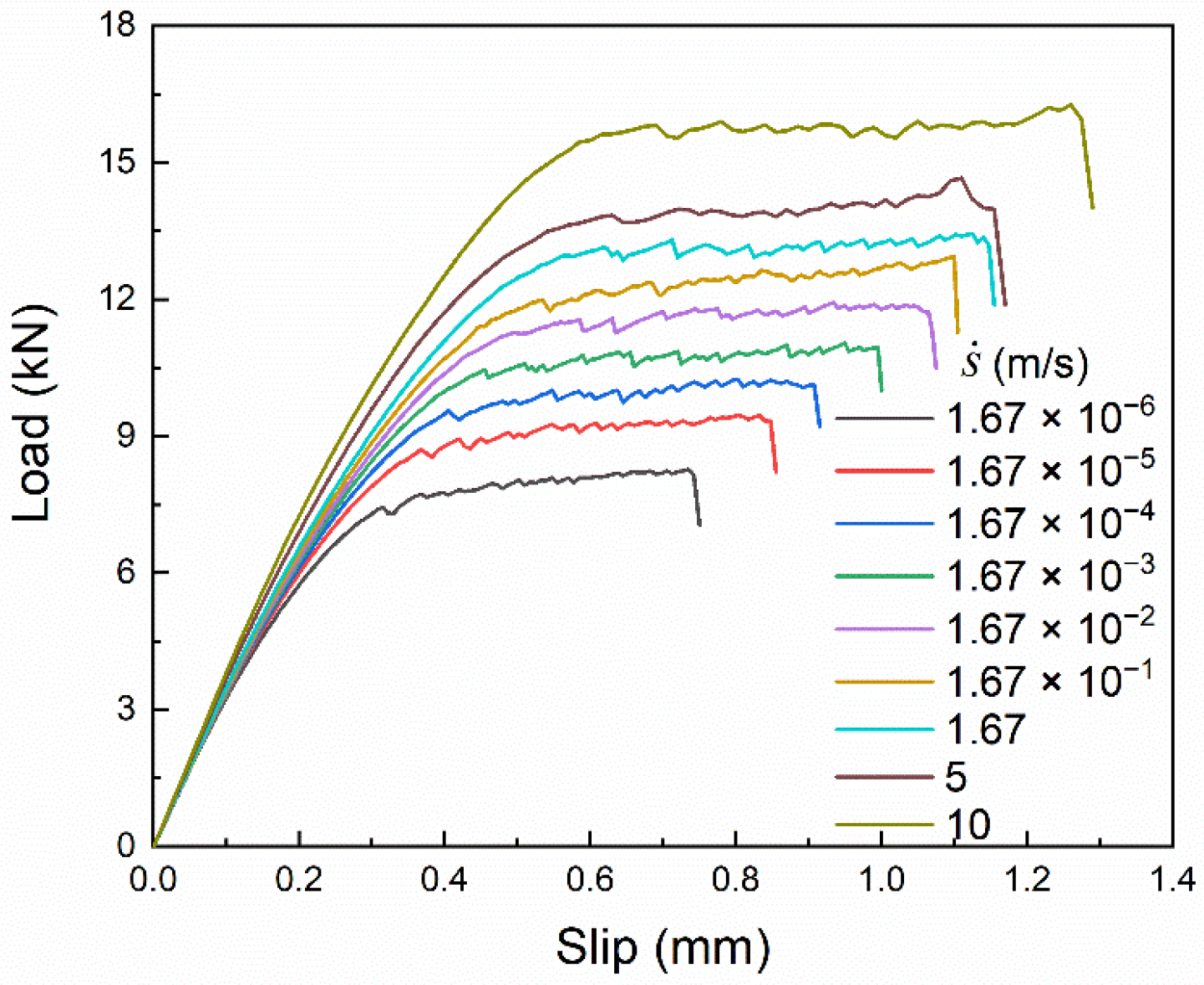
4.3. Effect of Slip Rate
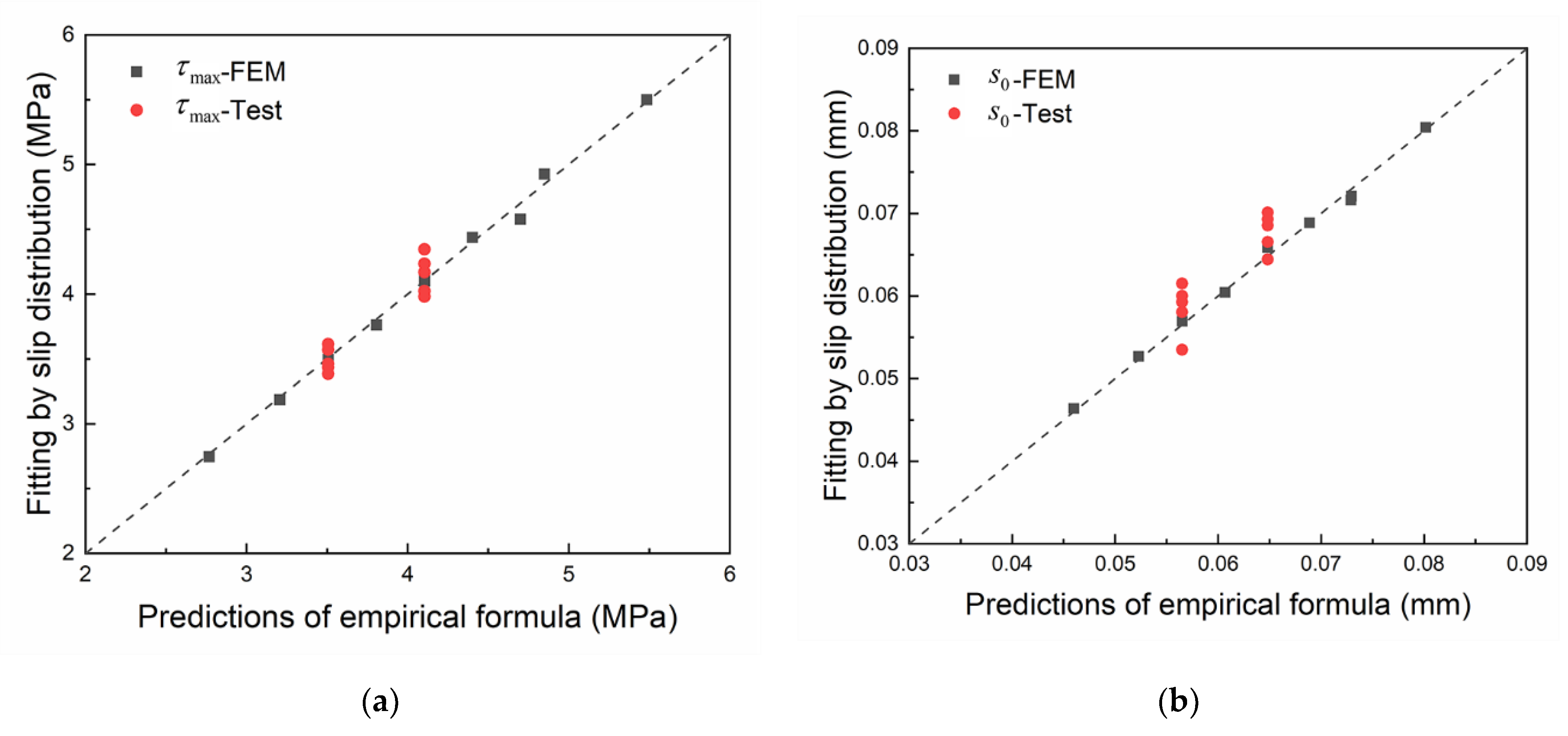
4.3.1. Empirical Formulas and Validation
4.3.2. Analysis and Discussion
5. Conclusions
- The numerical model based on the plastic-damage constitutive and the strain rate effects on material performance can simulate the FRP-to-brick interface behavior under different loading rates, and the numerical results of the bond–slip relationship are in good agreement with the test results.
- FRP stiffness mainly influences the shape of the bond–slip curve. As the maximum bond stress increases with increasing FRP stiffness, the corresponding slip at the maximum bond stress decreases and the interfacial fracture energy remains constant.
- Brick strength mainly influences the amplitude of the bond–slip curve. Both the maximum bond stress and the corresponding slip increase as the brick strength increases, and the shape of the bond–slip curve remains almost unchanged; thus, the interfacial fracture energy increases significantly.
- The variations of the bond–slip relationship under dynamic loading are mainly a consequence of the dynamic enhancement of brick strength, so the magnitude of the bond–slip curve changes significantly. However, the dynamic bond–slip relationship is also influenced by FRP stiffness especially within a specific slip rate range, where the strain rate sensitivity of FRP stiffness is stronger than that of brick strength.
- The empirical formulas considering dynamic FRP stiffness and dynamic brick strength can be used to predict the bond–slip relationship at the FRP-to-brick interface under dynamic loading, and its prediction results are in good agreement with the test and numerical results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buchan, P.; Chen, J. Blast resistance of FRP composites and polymer strengthened concrete and masonry structures—A state-of-the-art review. Compos. Part B Eng. 2007, 38, 509–522. [Google Scholar] [CrossRef]
- Tan, K.H.; Patoary, M.K.H. Blast Resistance of FRP-Strengthened Masonry Walls. I: Approximate Analysis and Field Explosion Tests. J. Compos. Constr. 2009, 13, 422–430. [Google Scholar] [CrossRef]
- Urgessa, G.S.; Maji, A.K. Dynamic Response of Retrofitted Masonry Walls for Blast Loading. J. Eng. Mech. 2010, 136, 858–864. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A.; Castori, G.; Coventry, K.A. Experimental Analysis of Dynamic Effects of FRP Reinforced Masonry Vaults. Materials 2015, 8, 8059–8071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borri, A.; Castori, G.; Corradi, M. Masonry Columns Confined by Steel Fiber Composite Wraps. Materials 2011, 4, 311–326. [Google Scholar] [CrossRef]
- Liang, H.; Li, S.; Lu, Y.; Yang, T. Reliability Analysis of Bond Behaviour of CFRP–Concrete Interface under Wet–Dry Cycles. Materials 2018, 11, 741. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, H.J.; Saleem, M.U. Flexural and Shear Strain Characteristics of Carbon Fiber Reinforced Polymer Composite Adhered to a Concrete Surface. Materials 2018, 11, 2596. [Google Scholar] [CrossRef] [Green Version]
- Min, X.; Zhang, J.; Wang, C.; Song, S.; Yang, D. Experimental Investigation of Fatigue Debonding Growth in FRP–Concrete Interface. Materials 2020, 13, 1459. [Google Scholar] [CrossRef] [Green Version]
- Gómez, J.; Llinàs, L.T.; Peña, C.B. Characterization and Simulation of the Bond Response of NSM FRP Reinforcement in Concrete. Materials 2020, 13, 1770. [Google Scholar] [CrossRef] [Green Version]
- Khalighi, Y.; Banthia, N. A Study of FRP–Concrete Bond under Impact. Appl. Mech. Mater. 2011, 82, 630–635. [Google Scholar] [CrossRef]
- Huo, J.; Liu, J.; Lu, Y.; Yang, J.; Xiao, Y. Experimental study on dynamic behavior of GFRP-to-concrete interface. Eng. Struct. 2016, 118, 371–382. [Google Scholar] [CrossRef]
- Pereira, J.M.; Lourenço, P.B. Experimental bond behaviour of GFRP and masonry bricks under impulsive loading. Mater. Struct. 2016, 49, 4799–4811. [Google Scholar] [CrossRef] [Green Version]
- Salimian, M.S.; Mostofinejad, D. Experimental Evaluation of CFRP-Concrete Bond Behavior under High Loading Rates Using Particle Image Velocimetry Method. J. Compos. Constr. 2019, 23, 04019010. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.-F.; Lu, Y.; Yang, Z.-J. Modelling Static and Dynamic FRP-Concrete Bond Behaviour Using a Local Concrete Damage Model. Adv. Struct. Eng. 2015, 18, 45–58. [Google Scholar] [CrossRef] [Green Version]
- Caggiano, A.; Martinelli, E.; Schicchi, D.; Etse, G. A modified Duvaut-Lions zero-thickness interface model for simulating the rate-dependent bond behavior of FRP-concrete joints. Compos. Part B Eng. 2018, 149, 260–267. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, W.; Pham, T.M.; Hao, H.; Cui, J.; Shi, Y. Strain rate effect on interfacial bond behaviour between BFRP sheets and steel fibre reinforced concrete. Compos. Part B Eng. 2019, 174, 107032. [Google Scholar] [CrossRef]
- Yuan, C.; Chen, W.; Pham, T.M.; Hao, H.; Cui, J.; Shi, Y. Influence of concrete strength on dynamic interfacial fracture behaviour between fibre reinforced polymer sheets and concrete. Eng. Fract. Mech. 2020, 229, 106934. [Google Scholar] [CrossRef]
- Li, Z.X.; Zhang, X.; Shi, Y. Experimental study on the dynamic bond behavior between CFRP and concrete under different slip rates. Eng. Struct. 2020, 216, 110788. [Google Scholar] [CrossRef]
- Yao, J.; Teng, J.; Chen, J. Experimental study on FRP-to-concrete bonded joints. Compos. Part B Eng. 2005, 36, 99–113. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Basilio, I.; Lourenço, P.B. Experimental Bond Behavior of FRP Sheets Glued on Brick Masonry. J. Compos. Constr. 2011, 15, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Fédération International du Béton (FIB). Externally Bonded FRP Reinforcement for RC Structures; Bulletin 14: Lausanne, Switzerland, 2001. [Google Scholar]
- Monti, G.; Renzelli, M.; Luciani, P. FRP adhesion in uncracked and cracked concrete zones. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete Structures, Singapore, 8–10 July 2003; World Scientific: Singapore, 2003; pp. 183–192. [Google Scholar]
- Comite Euro-International Du Beton. CEB-FIP Model Code 1990; Comite Euro-International Du Beton: Paris, France, 1991; pp. 87–109. [Google Scholar]
- Ghiassi, B.; Marcari, G.; Oliveira, D.V.; Lourenço, P.B. Numerical analysis of bond behavior between masonry bricks and composite materials. Eng. Struct. 2012, 43, 210–220. [Google Scholar] [CrossRef] [Green Version]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Nakaba, K.; Toshiyuki, K.; Tomoki, F.; Hiroyuki, Y. Bond Behavior between Fiber-Reinforced Polymer Laminates and Concrete. ACI Struct. J. 2001, 98, 359–367. [Google Scholar] [CrossRef]
- Savoia, M.; Ferracuti, B.; Mazzotti, C. Non Linear Bond-Slip Law for Frp-Concrete Interface. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete Structures, Singapore, 8–10 July 2003; World Scientific: Singapore, 2003; pp. 163–172. [Google Scholar]
- Ferracuti, B.; Savoia, M.; Mazzotti, C. Interface law for FRP-concrete delamination. Compos. Struct. 2007, 80, 523–531. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M.; Sacco, E. Bond behaviour of CFRP laminates glued on clay bricks: Experimental and numerical study. Compos. Part B Eng. 2011, 42, 330–340. [Google Scholar] [CrossRef]
- Mazzotti, C.; Ferracuti, B.; Bellini, A. Experimental bond tests on masonry panels strengthened by FRP. Compos. Part B Eng. 2015, 80, 223–237. [Google Scholar] [CrossRef]
- Mensah, C.; Wang, Z.; Bonsu, A.O.; Liang, W. Effect of Different Bond Parameters on the Mechanical Properties of FRP and Concrete Interface. Polymers 2020, 12, 2466. [Google Scholar] [CrossRef]
- Dai, J.G.; Ueda, T. Local Bond Stress Slip Relations for FRP Sheets-Concrete Interfaces. In Proceedings of the 6th International Symposium on FRP Reinforcement for Concrete Structuresth International Symposium on FRP Reinforcement for Concrete Structures, Singapore, 8–10 July 2003; World Scientific: Singapore, 2003; pp. 143–152. [Google Scholar]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond–slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Pan, J.; Wu, Y.-F. Analytical modeling of bond behavior between FRP plate and concrete. Compos. Part B Eng. 2014, 61, 17–25. [Google Scholar] [CrossRef]
- Dai, J.; Ueda, T.; Sato, Y. Unified Analytical Approaches for Determining Shear Bond Characteristics of FRP-Concrete Interfaces through Pullout Tests. J. Adv. Concr. Technol. 2006, 4, 133–145. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.W.; Wu, Y.F.; Yun, Y. Analytical modeling of the bond–slip relationship at FRP-concrete interfaces for adhesively-bonded joints. Compos. Part B Eng. 2010, 41, 423–433. [Google Scholar] [CrossRef]
- Ueda, T.; Dai, J.; Sato, Y. A nonlinear bond stress–slip relationship for FRP sheet–concrete interface. In Proceedings of the International Symposium on Latest Achievement of Technology and Research on Retrofitting Concrete Structures, Kyoto, Japan, 14–15 July 2003; pp. 113–120. [Google Scholar]
- Dai, J.; Ueda, T.; Sato, Y. Development of the Nonlinear Bond Stress–Slip Model of Fiber Reinforced Plastics Sheet–Concrete Interfaces with a Simple Method. J. Compos. Constr. 2005, 9, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.F.; Jiang, C. Quantification of Bond-Slip Relationship for Externally Bonded FRP-to-Concrete Joints. J. Compos. Constr. 2013, 17, 673–686. [Google Scholar] [CrossRef]
- Wu, Y.F.; He, L. Width effect of interfacial bond characteristics. Constr. Build. Mater. 2019, 220, 712–726. [Google Scholar] [CrossRef]
- Carrara, P.; Ferretti, D.; Freddi, F. Debonding behavior of ancient masonry elements strengthened with CFRP sheets. Compos. Part B Eng. 2013, 45, 800–810. [Google Scholar] [CrossRef]
- Mehrmashhadi, J.; Tang, Y.; Zhao, X.; Xu, Z.; Pan, J.J.; Van Le, Q.; Bobaru, F. The Effect of Solder Joint Microstructure on the Drop Test Failure—A Peridynamic Analysis. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 9, 58–71. [Google Scholar] [CrossRef]
- Mehrmashhadi, J.; Wang, L.; Bobaru, F. Uncovering the dynamic fracture behavior of PMMA with peridynamics: The importance of softening at the crack tip. Eng. Fract. Mech. 2019, 219, 106617. [Google Scholar] [CrossRef]
- Tao, Y.; Chen, J.F. Concrete Damage Plasticity Model for Modeling FRP-to-Concrete Bond Behavior. J. Compos. Constr. 2015, 19, 04014026. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- ABAQUS. Analysis User’s Manual, Version 6.11; Simulia: Maastricht, The Netherlands, 2011. [Google Scholar]
- China Academy of Building Research. Code for Design of Concrete Structures GB50010-2010; China Architecture & Building Press: Beijing, China, 2017. [Google Scholar]
- D’Altri, A.M.; D’Altri, A.M.; Carloni, C.; De Miranda, S. Numerical modeling of FRP strips bonded to a masonry substrate. Compos. Struct. 2018, 200, 420–433. [Google Scholar] [CrossRef]
- Jeon, B.; Stewart, R.J.; Ahmed, I.Z. Peridynamic simulations of brittle structures with thermal residual deformation: Strengthening and structural reactivity of glasses under impacts. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150231. [Google Scholar] [CrossRef] [Green Version]
- Bobaru, F.; Hu, W. The Meaning, Selection, and Use of the Peridynamic Horizon and its Relation to Crack Branching in Brittle Materials. Int. J. Fract. 2012, 176, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Shi, Y.; Li, Z.-X. Experimental study on the tensile behavior of unidirectional and plain weave CFRP laminates under different strain rates. Compos. Part B Eng. 2019, 164, 524–536. [Google Scholar] [CrossRef]
- Zhang, X.; Chiu, Y.-W.; Hao, H.; Hsieh, A.; Salter, N.; Cui, J. Dynamic compressive material properties of clay bricks at different strain rates. Constr. Build. Mater. 2018, 192, 754–767. [Google Scholar] [CrossRef]
- Ceroni, F.; De Felice, G.; Grande, E.; Malena, M.; Mazzotti, C.; Murgo, F.; Sacco, E.; Valluzzi, M.R. Analytical and numerical modeling of composite-to-brick bond. Mater. Struct. 2014, 47, 1987–2003. [Google Scholar] [CrossRef]












| Material | Type | Tensile/Compression Strength (MPa) | Young’s Modulus (GPa) | Failure Strain (%) | Nominal Thickness (mm) |
|---|---|---|---|---|---|
| Carbon fabric | UT70-30G | +4000/— | 253 | 1.7 | 0.167 |
| Epoxy adhesive | HM-180C3P | +38/— | 2.4 | 1.5 | — |
| Clay brick | MU15 | +2.85/−11.4 | 7.6 | — | — |
| Specimens | Loading Rate (mm/min) | α (mm) | β (mm) | (mm) | (MPa) | (N/mm) |
|---|---|---|---|---|---|---|
| A1 | 10 | 0.0851 | 15.92 | 0.0590 | 3.551 | 0.6044 |
| A2 | 10 | 0.0803 | 16.58 | 0.0557 | 3.090 | 0.4963 |
| A3 | 10 | 0.0949 | 16.06 | 0.0658 | 3.892 | 0.7387 |
| A4 | 10 | 0.0855 | 16.17 | 0.0593 | 3.461 | 0.5919 |
| A5 | 10 | 0.0796 | 15.90 | 0.0552 | 3.330 | 0.5302 |
| Average | 10 | 0.0851 | 16.13 | 0.0590 | 3.465 | 0.5923 |
| B1 | 1000 | 0.1058 | 15.63 | 0.0733 | 4.581 | 0.9693 |
| B2 | 1000 | 0.0989 | 15.84 | 0.0686 | 4.168 | 0.8245 |
| B3 | 1000 | 0.0971 | 15.76 | 0.0673 | 4.138 | 0.8036 |
| B4 | 1000 | 0.0992 | 16.02 | 0.0688 | 4.087 | 0.8108 |
| B5 | 1000 | 0.0921 | 15.90 | 0.0638 | 3.853 | 0.7097 |
| Average | 1000 | 0.0986 | 15.83 | 0.0684 | 4.165 | 0.8236 |
| (°) | ξ | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|
| 38 | 0.1 | 1.16 | 0.6667 | 1 × 10−5 |
| Specimens | (MPa) | (mm) | α (mm) | β (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CFRP-1ply | 253,388 | 0.167 | 0.0669 | 16.05 | 1.00 | 1.00 | 1.00 | 1.000 | 1.000 | 1.000 |
| CFRP-1ply-1.2 | 304,066 | 0.167 | 0.0650 | 16.84 | 1.20 | 0.97 | 1.05 | 1.059 | 0.972 | 1.029 |
| CFRP-1ply-1.4 | 354,743 | 0.167 | 0.0633 | 17.92 | 1.40 | 0.95 | 1.12 | 1.063 | 0.946 | 1.005 |
| CFRP-1ply-1.6 | 405,421 | 0.167 | 0.0617 | 18.56 | 1.60 | 0.92 | 1.16 | 1.105 | 0.923 | 1.019 |
| CFRP-1ply-1.8 | 456,098 | 0.167 | 0.0605 | 19.47 | 1.80 | 0.91 | 1.21 | 1.107 | 0.905 | 1.002 |
| CFRP-2ply | 253,388 | 0.334 | 0.0596 | 20.31 | 2.00 | 0.89 | 1.27 | 1.114 | 0.892 | 0.993 |
| CFRP-3ply | 253,388 | 0.501 | 0.0568 | 23.33 | 3.00 | 0.85 | 1.45 | 1.206 | 0.849 | 1.025 |
| GFRP-1ply | 84,251 | 0.120 | 0.0833 | 9.59 | 0.24 | 1.25 | 0.60 | 0.835 | 1.246 | 1.040 |
| GFRP-2ply | 84,251 | 0.240 | 0.0757 | 12.57 | 0.48 | 1.13 | 0.78 | 0.882 | 1.132 | 0.999 |
| GFRP-3ply | 84,251 | 0.360 | 0.0730 | 14.53 | 0.72 | 1.09 | 0.91 | 0.955 | 1.092 | 1.043 |
| BFRP-1ply | 88,397 | 0.140 | 0.0821 | 10.47 | 0.29 | 1.23 | 0.65 | 0.843 | 1.228 | 1.036 |
| BFRP-2ply | 88,397 | 0.280 | 0.0743 | 13.28 | 0.58 | 1.11 | 0.83 | 0.950 | 1.111 | 1.055 |
| BFRP-3ply | 88,397 | 0.420 | 0.0669 | 15.17 | 0.88 | 1.00 | 0.95 | 0.982 | 1.000 | 0.982 |
| (MPa) | α (mm) | β (mm) | ||||||
|---|---|---|---|---|---|---|---|---|
| 11.40 | 0.0669 | 16.05 | 1.00 | 1.00 | 1.00 | 1.000 | 1.000 | 1.000 |
| 13.29 | 0.0760 | 16.07 | 1.17 | 1.14 | 1.00 | 1.134 | 1.136 | 1.289 |
| 14.59 | 0.0821 | 15.77 | 1.28 | 1.23 | 0.98 | 1.273 | 1.228 | 1.563 |
| 15.88 | 0.0833 | 15.83 | 1.39 | 1.25 | 0.99 | 1.281 | 1.245 | 1.595 |
| 17.18 | 0.0947 | 15.70 | 1.51 | 1.42 | 0.98 | 1.480 | 1.415 | 2.096 |
| 18.48 | 0.1001 | 15.61 | 1.62 | 1.50 | 0.97 | 1.583 | 1.496 | 2.368 |
| 19.78 | 0.1068 | 15.55 | 1.74 | 1.60 | 0.97 | 1.701 | 1.597 | 2.716 |
| 21.81 | 0.1157 | 15.31 | 1.91 | 1.73 | 0.95 | 1.902 | 1.730 | 3.290 |
| 25.57 | 0.1317 | 15.25 | 2.24 | 1.97 | 0.95 | 2.182 | 1.969 | 4.295 |
| (m/s) | (1/s) | α (mm) | β (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1.67 × 10−6 | 1.96 × 10−5 | 1.000 | 1.000 | 0.0669 | 16.052 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| 1.67 × 10−5 | 2.00 × 10−4 | 1.009 | 1.165 | 0.0760 | 15.889 | 1.136 | 0.990 | 1.160 | 1.136 | 1.318 |
| 1.67 × 10−4 | 1.98 × 10−3 | 1.011 | 1.279 | 0.0821 | 15.766 | 1.228 | 0.982 | 1.273 | 1.228 | 1.563 |
| 1.67 × 10−3 | 2.00 × 10−2 | 1.016 | 1.393 | 0.0872 | 15.659 | 1.303 | 0.976 | 1.370 | 1.303 | 1.785 |
| 1.67 × 10−2 | 1.96 × 10−1 | 1.020 | 1.507 | 0.0950 | 15.659 | 1.421 | 0.976 | 1.493 | 1.421 | 2.121 |
| 1.67 × 10−1 | 1.98 | 1.024 | 1.621 | 0.0993 | 15.390 | 1.485 | 0.959 | 1.615 | 1.485 | 2.399 |
| 1.67 | 19.60 | 1.028 | 1.735 | 0.1033 | 15.452 | 1.544 | 0.963 | 1.666 | 1.544 | 2.574 |
| 5.00 | 56.34 | 1.093 | 1.766 | 0.1040 | 15.633 | 1.555 | 0.974 | 1.815 | 1.555 | 2.946 |
| 10.00 | 118.57 | 1.141 | 1.994 | 0.1160 | 15.959 | 1.735 | 0.994 | 2.002 | 1.735 | 3.473 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Yang, J.; Chi, L.Y. The Bond-Slip Relationship at FRP-to-Brick Interfaces under Dynamic Loading. Materials 2021, 14, 545. https://doi.org/10.3390/ma14030545
Zhang D, Yang J, Chi LY. The Bond-Slip Relationship at FRP-to-Brick Interfaces under Dynamic Loading. Materials. 2021; 14(3):545. https://doi.org/10.3390/ma14030545
Chicago/Turabian StyleZhang, Di, Jun Yang, and Li Yuan Chi. 2021. "The Bond-Slip Relationship at FRP-to-Brick Interfaces under Dynamic Loading" Materials 14, no. 3: 545. https://doi.org/10.3390/ma14030545
APA StyleZhang, D., Yang, J., & Chi, L. Y. (2021). The Bond-Slip Relationship at FRP-to-Brick Interfaces under Dynamic Loading. Materials, 14(3), 545. https://doi.org/10.3390/ma14030545






