An In Vitro–In Vivo Simulation Approach for the Prediction of Bioequivalence
Abstract
:1. Introduction
2. Materials and Methods
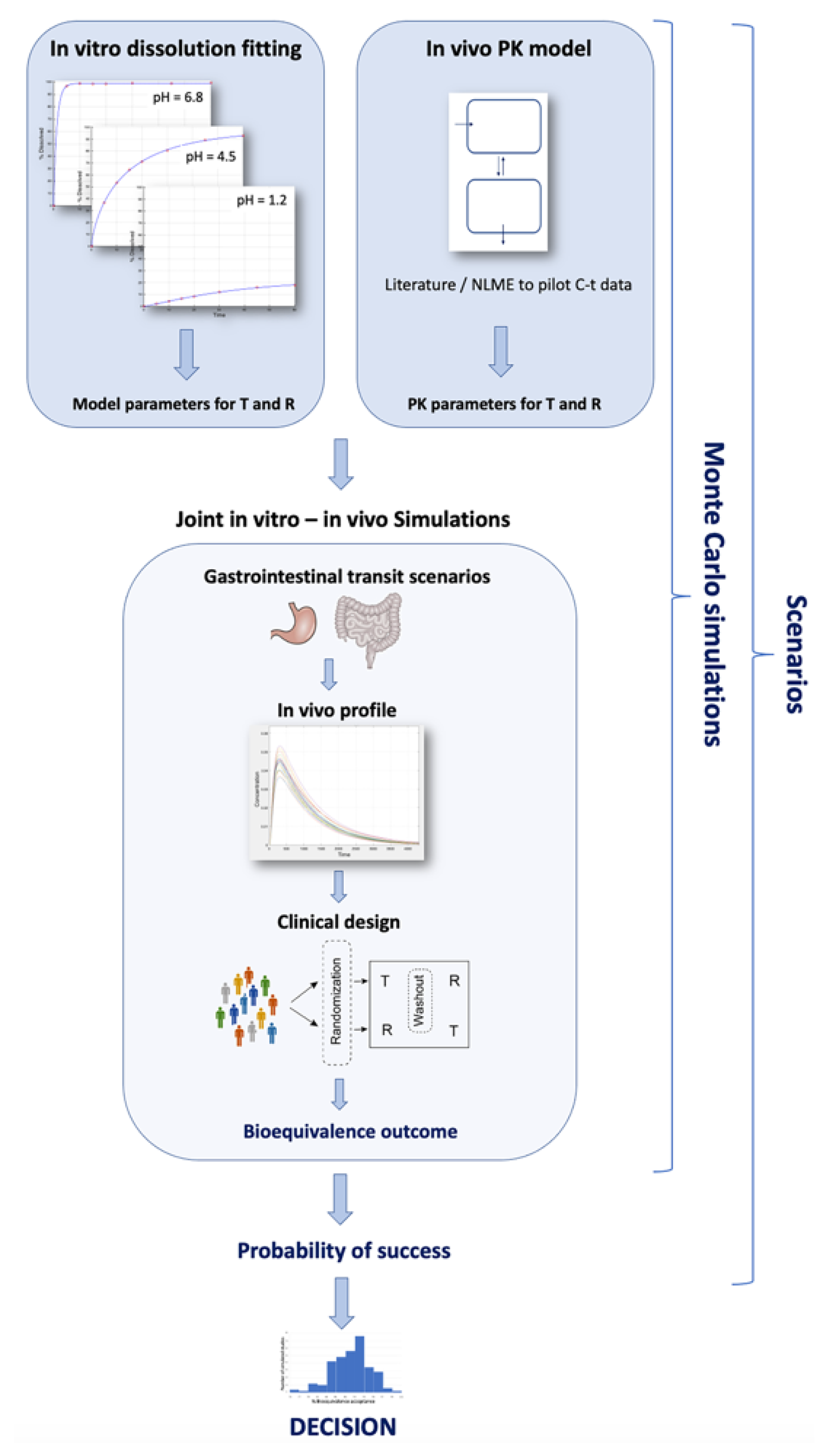
2.1. The IVIVS Methodology
2.1.1. Step 1: Mathematical Description of the In Vitro Dissolution Profiles
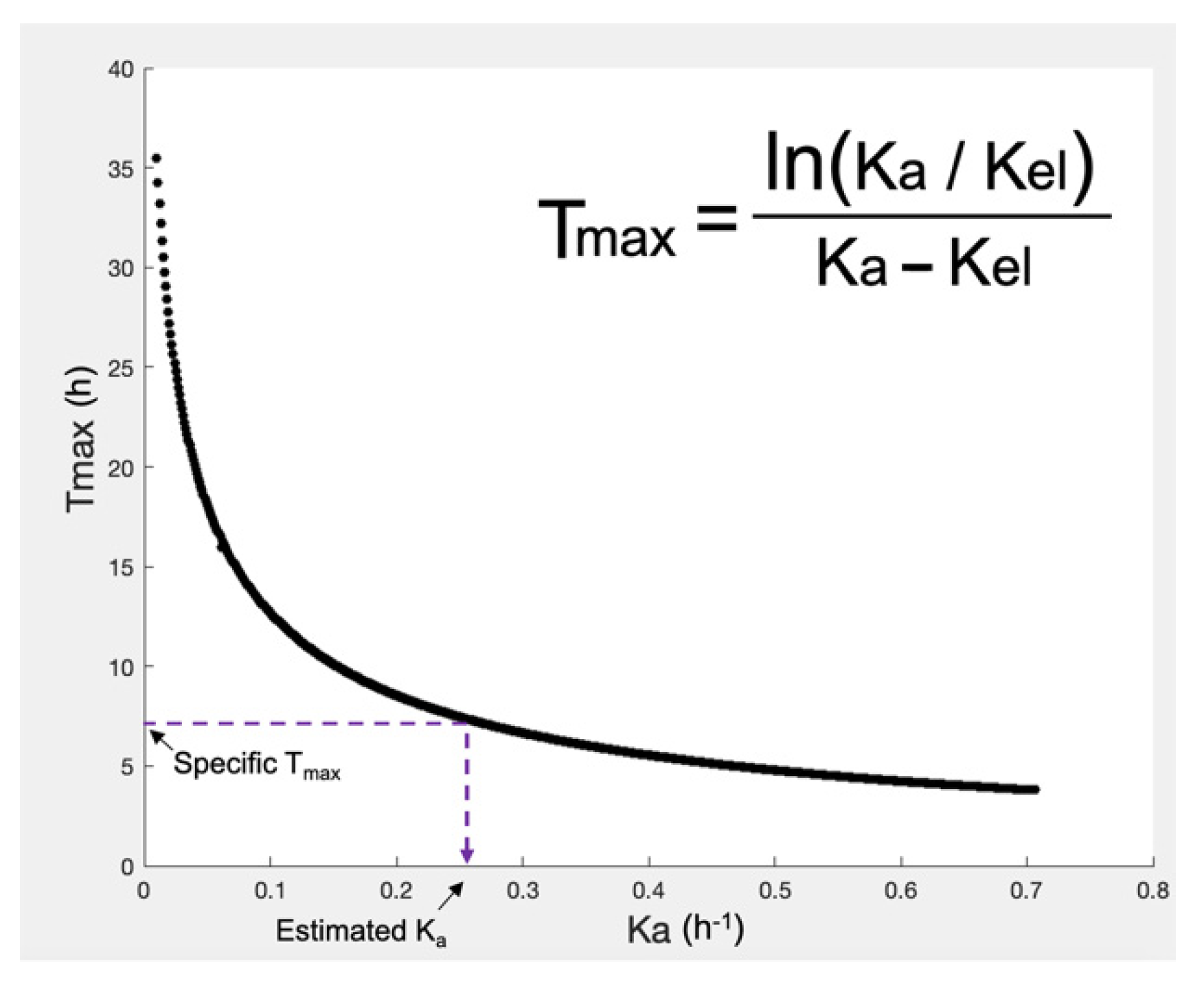
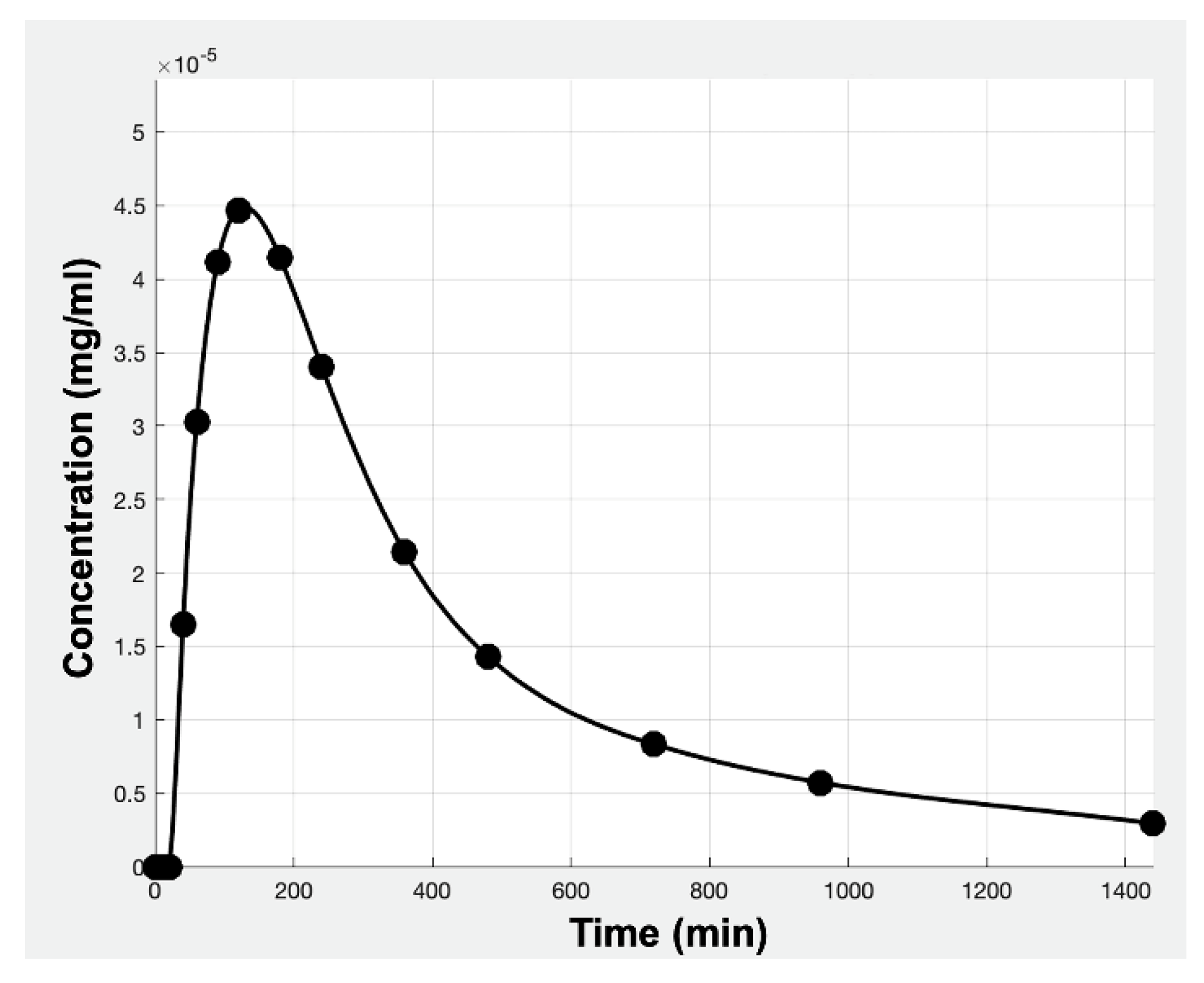
2.1.2. Step 2: Mathematical Description of In Vivo Pharmacokinetics
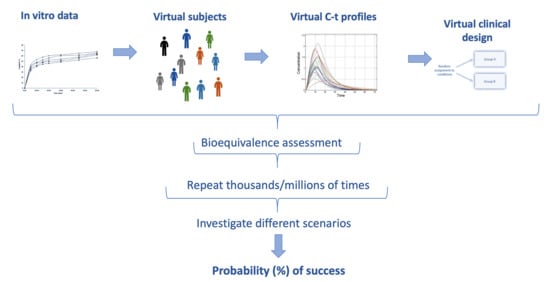
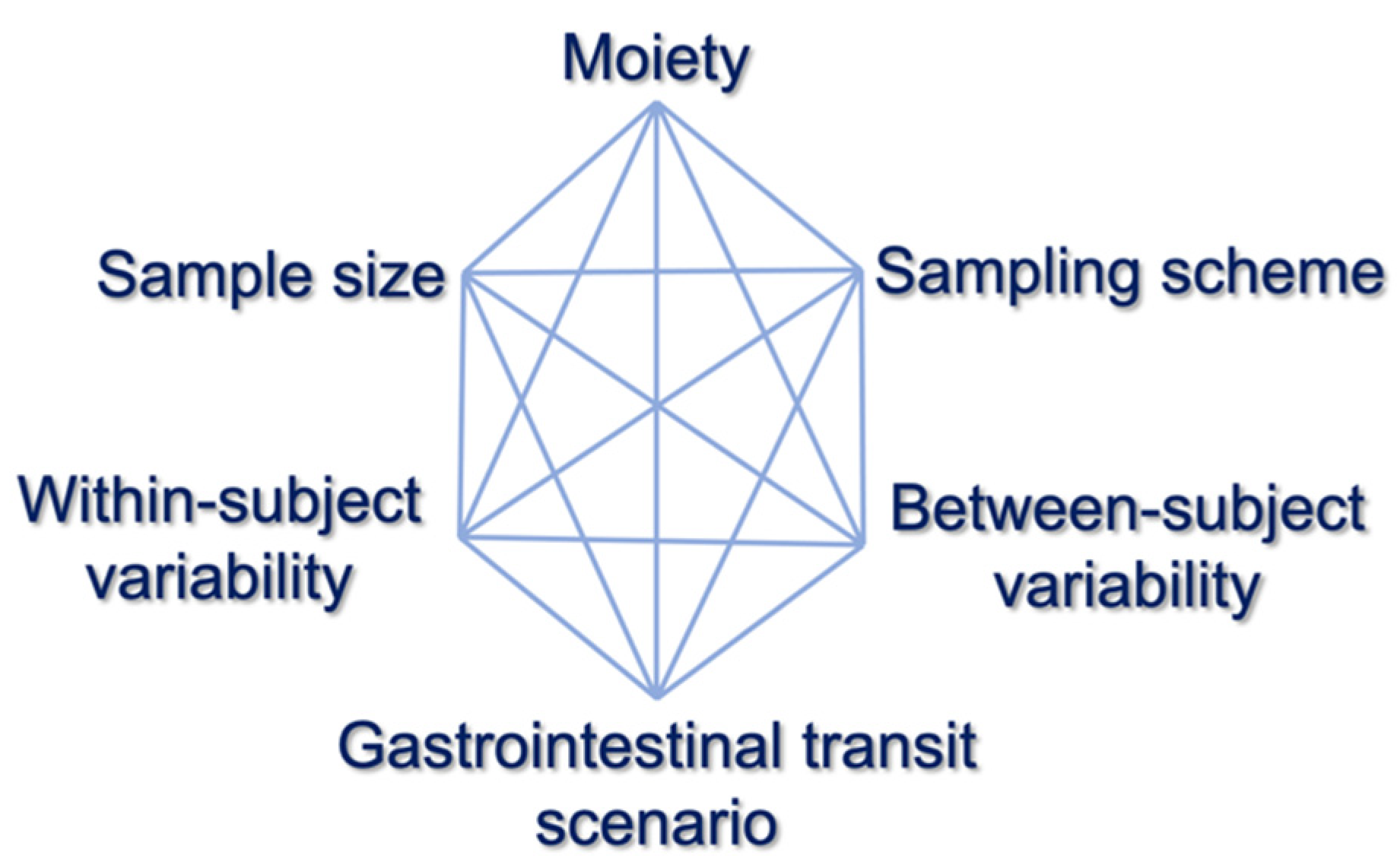
2.1.3. Step 3: In Vitro–In Vivo Simulations
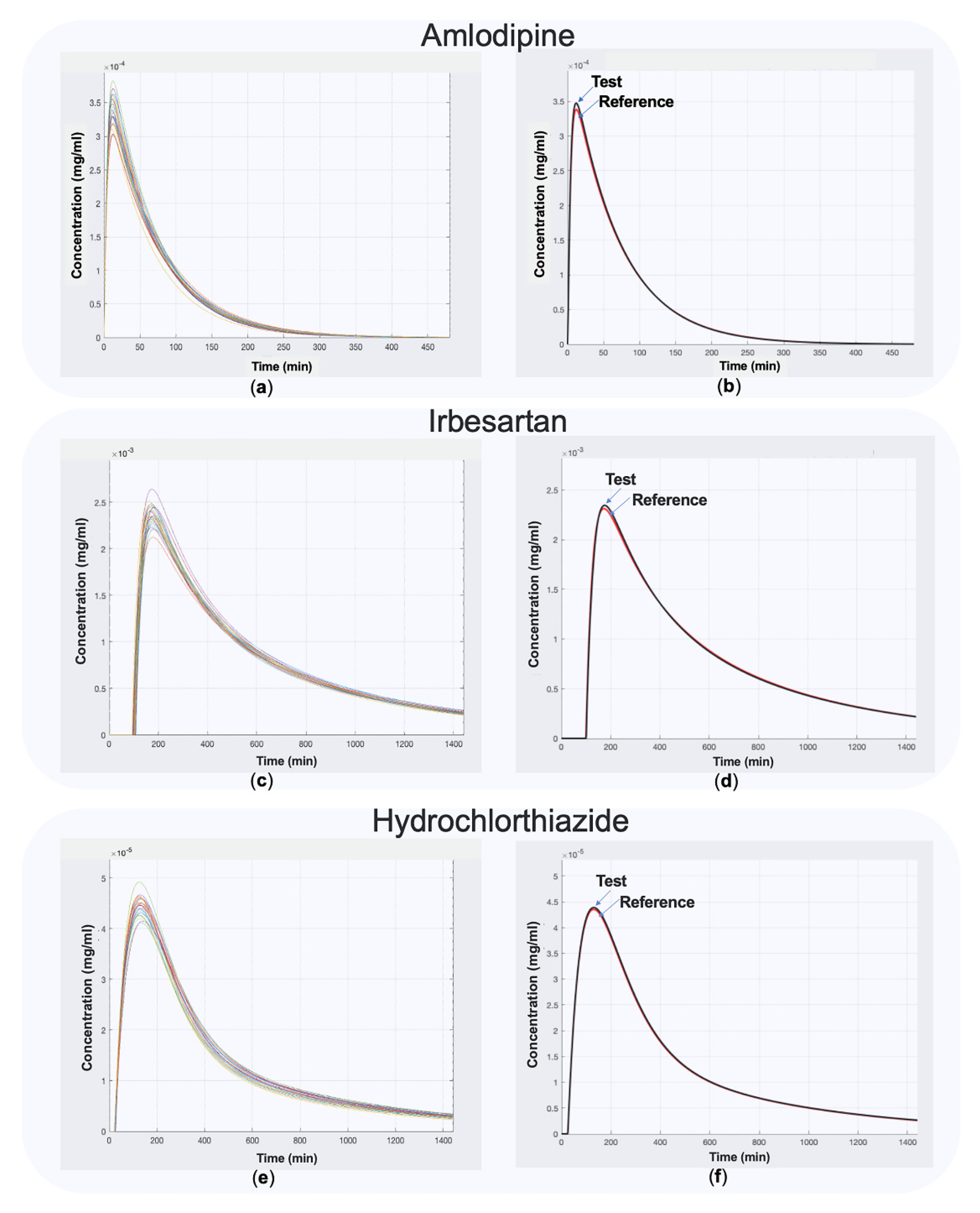
2.2. Application to Actual Data: The Cases of Amlodipine, Irbesartan, Hydrochlorthiazide
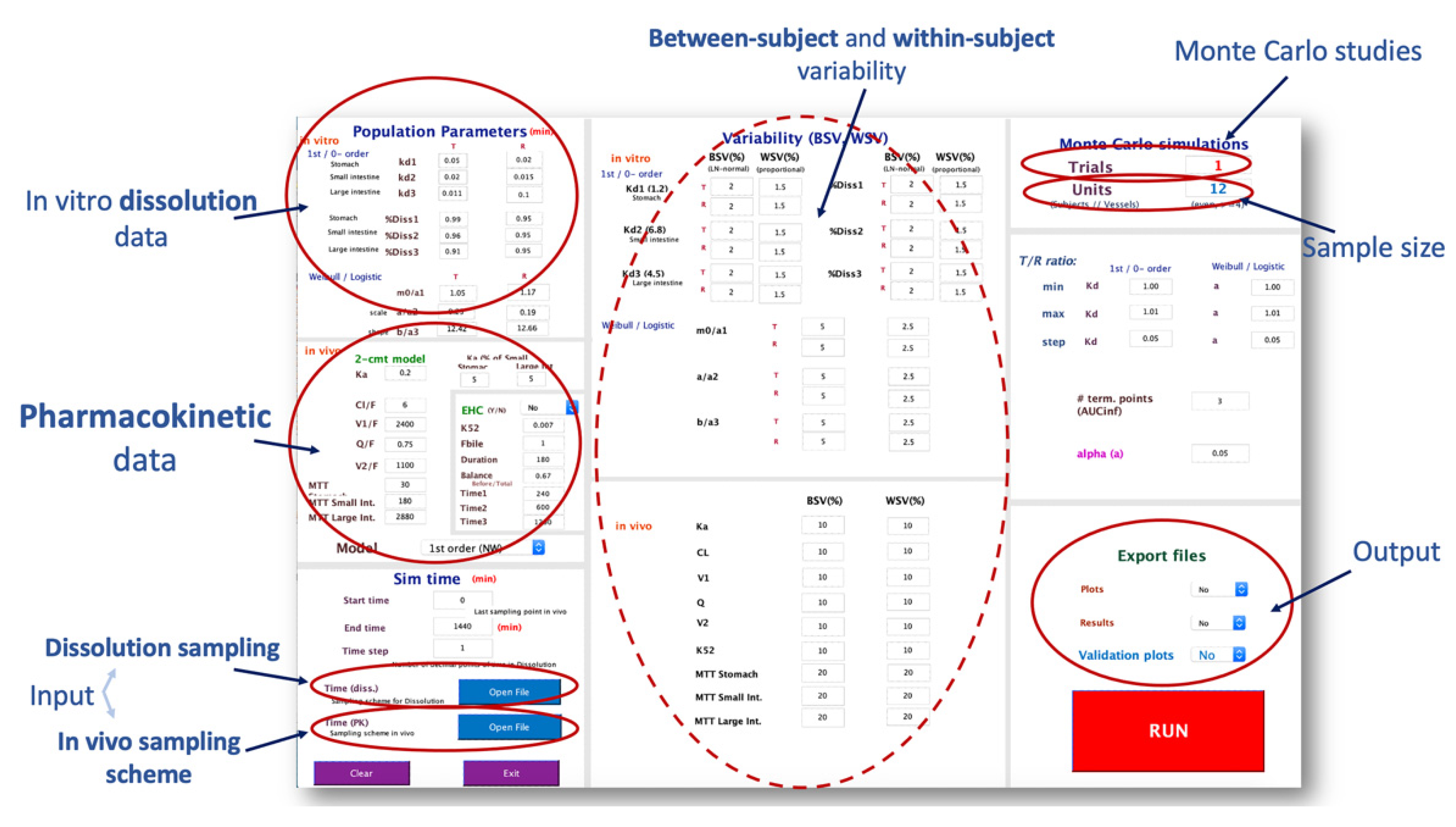
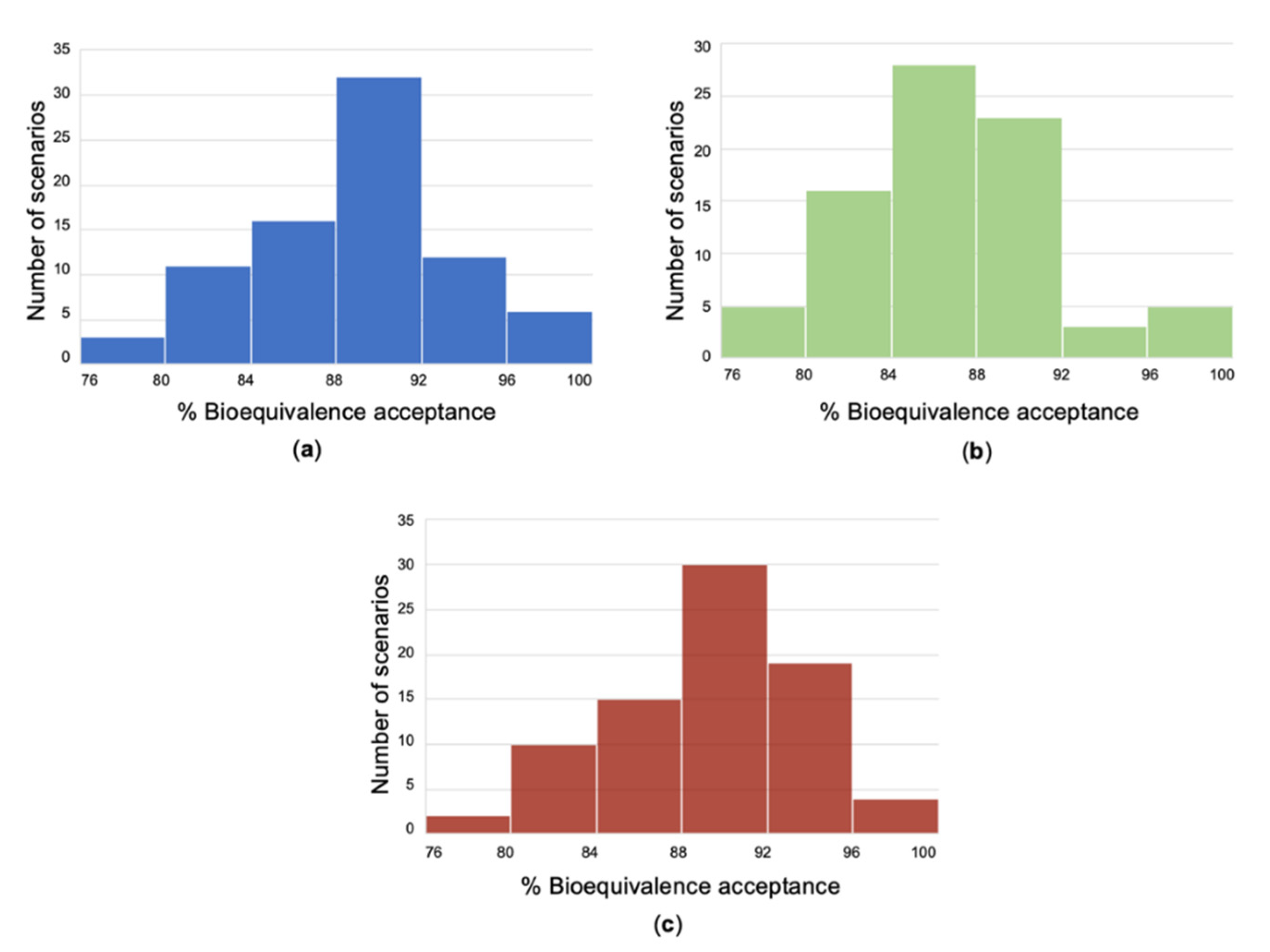
2.3. Validation
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Model 1 | Description 2 | Initial Conditions |
|---|---|---|
| dy1/dt = − Kd·y1 | Amount of drug undissolved | y1(0) = m0·Dose |
| dy2/dt = Kd·y1 − Ka·y2 | Amount of drug dissolved | y2(0) = 0 |
| dy3/dt = Ka·y2 − K34·y3 + K43⋅y4 − Kel·y3 | Amount of drug in the central compartment | y3(0) = 0 |
| dy4/dt = K34·y3 − K43·y4 | Amount of drug in the peripheral compartment | y4(0) = 0 |
| How the IVIVS is implemented | The IVIVS approach combines: (a) dissolution information (from the in vitro dissolution data), (b) statistics (e.g., starting from the simple typical estimation of bioequivalence according to the guidelines, to the use of probability distribution functions for the random generation of virtual subjects and the application of Monte Carlo simulations), (c) mathematics through the use of systems of differential equations to concomitantly describe the in vitro and in vivo kinetics, and (d) programming in a language to implement all these. |
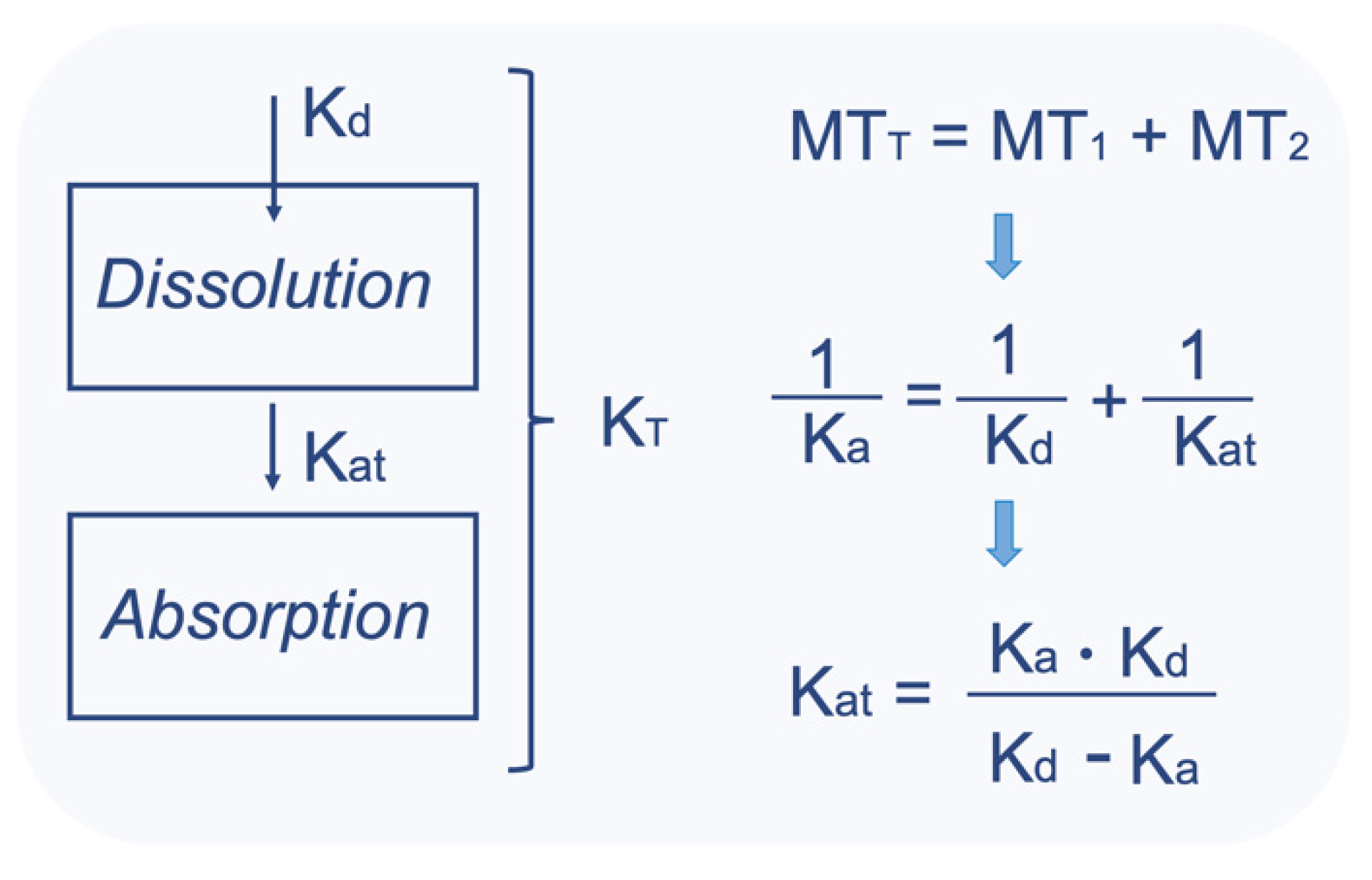
| The mathematical part of the simulations performed in the IVIVS | 1. Drug in the body can be in the following subsequent conditions (parts): (1a) solid drug in the GI (1b) drug dissolved in the GI (1c) drug in the central compartment, and (1d) drug in the peripheral compartment This arrangement derives from the conservation of mass (i.e., amount of drug). An additional compartment of the already eliminated drug could be added, but it would be useless to add one more differential equation to quantify something there is no need to describe it. 2. The GI parts “1a” and “1b” can refer either to fasted stomach with pH 1.2 (or fed stomach with pH 4.5), or small intestine (pH 6.8), or large intestine. 3. The entire situation (i.e., 1a, 1b, 1c, 1d) is described by systems of ordinary differential equations (ODEs). Thus, for our system, there is a need of four differential equations; one for each “part”. 4. In order to express the presence of drug in each different “segment” of the GI (namely, parts “1a” or “1b”), the concept of Mean Transit Time (MTT) is incorporated. 5. Using the MTT, we can define how much time the drug molecules spend within each segment of the GI, namely into segment “1a” or “1b” (since “1c” and “1d” refer to drug inside the body; plasma or tissues). 6. For each segment of the GI (stomach, small intestine, large intestine), different systems of ODEs and parameter values are used:
8. Since not all drug molecules enter or leave each GI part concomitantly, variability is added to the MTT. Thus, the residence (or in another view the “transit”) of drug inside the GI has a probabilistic nature according to the probability distribution utilized to add variability to the MTT. |
| Some consequences |
|
Appendix B
References
- European Medicines Agency 2010; Committee for Medicinal Products for Human Use (CHMP). Guideline on the Investigation of Bioequivalence. CPMP/EWP/QWP/1401/98 Rev. 1/ Corr **. London. 20 January 2010. Available online: https://www.ema.europa.eu/en/documents/scientific-guideline/guideline-investigation-bioequivalence-rev1_en.pdf (accessed on 23 December 2020).
- Food and Drug Administration (FDA) 2013. Guidance for Industry. Bioequivalence Studies with Pharmacokinetic Endpoints for Drugs Submitted under an ANDA. Draft Guidance. U.S. Department of Health and Human Services Food and Drug Administration Center for Drug Evaluation and Research (CDER). December 2013. Available online: https://www.fda.gov/files/drugs/published/Bioequivalence-Studies-With-Pharmacokinetic-Endpoints-for-Drugs-Submitted-Under-an-Abbreviated-New-Drug-Application.pdf (accessed on 23 December 2020).
- Emami, J. In vitro–In vivo correlation: From theory to applications. J. Pharm. Pharm. Sci. 2006, 9, 169–189. [Google Scholar]
- Njoku, J.O.; Silva, D.A.; Mukherjee, D.; Webster, G.K.; Löbenberg, R. In Silico Tools at Early Stage of Pharmaceutical Development: Data Needs and Software Capabilities. AAPS PharmSciTech 2019, 20, 243. [Google Scholar] [CrossRef]
- Cook, J.A. A technique to estimate in vivo dissolution profiles without data from a solution. AAPS J. 2012, 14, 433–436. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, S. In Vitro-In Vivo Correlation (IVIVC) and Determining Drug Concentrations in Blood from Dissolution Testing—A Simple and Practical Approach. Open Drug Deliv. J. 2010, 4, 38–47. [Google Scholar] [CrossRef]
- Cuesta-Gragera, A.; Navarro-Fontestad, C.; Mangas-Sanjuan, V.; González-Álvarez, I.; García-Arieta, A.; Trocóniz, I.F.; Casabó, V.G.; Bermejo, M. Semi-physiologic model validation and bioequivalence trials simulation to select the best analyte for acetylsalicylic acid. Eur. J. Pharm. Sci. 2015, 74, 86–94. [Google Scholar] [CrossRef] [PubMed]
- González-García, I.; García-Arieta, A.; Merino-Sanjuan, M.; Mangas-Sanjuan, V.; Bermejo, M. Defining level A IVIVC dissolution specifications based on individual in vitro dissolution profiles of a controlled release formulation. Eur. J. Pharm. Sci. 2018, 119, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Shah, D.K.; Loganzo, F.; Haddish-Berhane, N.; Musto, S.; Wald, H.S.; Barletta, F.; Lucas, J.; Clark, T.; Hansel, S.; Betts, A. Establishing in vitro-in vivo correlation for antibody drug conjugate efficacy: A PK/PD modeling approach. J. Pharmacokinet. Pharmacodyn. 2018, 45, 339–349. [Google Scholar] [CrossRef]
- Nguyen, M.A.; Flanagan, T.; Brewster, M.; Kesisoglou, F.; Beato, S.; Biewenga, J.; Crison, J.; Holm, R.; Li, R.; Mannaert, E.; et al. A survey on IVIVC/IVIVR development in the pharmaceutical industry—Past experience and current perspectives. Eur. J. Pharm. Sci. 2017, 102, 1–13. [Google Scholar] [CrossRef]
- Shrivas, M.; Khunt, D.; Shrivas, M.; Choudhari, M.; Rathod, R.; Misra, M. Advances in In Vivo Predictive Dissolution Testing of Solid Oral Formulations: How Closer to In Vivo Performance? J. Pharm. Innov. 2020, 15, 296–317. [Google Scholar] [CrossRef]
- Li, Z.; He, X.; Tian, S.; Feng, G.; Huang, C.; Xun, M.; Wu, Z.; Wang, Y. Simultaneous Evaluation of Dissolution and Permeation of Oral Drug Solid Formulations for Predicting Absorption Rate-Limiting Factors and In Vitro-In Vivo Correlations: Case Study Using a Poorly Soluble Weakly Basic Drug. AAPS PharmSciTech 2019, 20, 321. [Google Scholar] [CrossRef]
- Butler, J.; Hens, B.; Vertzoni, M.; Brouwers, J.; Berben, P.; Dressman, J.; Andreas, C.J.; Schaefer, K.J.; Mann, J.; McAllister, M.; et al. In vitro models for the prediction of in vivo performance of oral dosage forms: Recent progress from partnership through the IMI OrBiTo collaboration. Eur. J. Pharm. Biopharm. 2019, 136, 70–83. [Google Scholar] [CrossRef] [PubMed]
- Bermejo, M.; Meulman, J.; Davanço, M.G.; Carvalho, P.O.; Gonzalez-Alvarez, I.; Campos, D.R. In Vivo Predictive Dissolution (IPD) for Carbamazepine Formulations: Additional Evidence Regarding a Biopredictive Dissolution Medium. Pharmaceutics 2020, 12, 558. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef] [PubMed]
- Simcyp® Simulator. CERTARA. Available online: https://www.certara.com/app/uploads/Resources/Brochures/BR_SimcypSimulator-v3.pdf (accessed on 23 December 2020).
- GastroPlus®. Simulation Plus. Available online: https://www.simulations-plus.com/software/gastroplus/ (accessed on 23 December 2020).
- Certara Trial Simulator®. CERTARA. Available online: https://www.certara.com/app/uploads/2020/06/BR_TrialSimulator-1.pdf (accessed on 23 December 2020).
- PK-Sim® and MoBi®. OPEN SYSTEMS PHARMACOLOGY. Available online: http://www.open-systems-pharmacology.org (accessed on 23 December 2020).
- Bhagwat, S.; Schilling, U.; Chen, M.J.; Wei, X.; Delvadia, R.; Absar, M.; Saluja, B.; Hochhaus, G. Predicting Pulmonary Pharmacokinetics from In Vitro Properties of Dry Powder Inhalers. Pharm. Res. 2017, 34, 2541–2556. [Google Scholar] [CrossRef] [PubMed]
- Weber, B.; Hochhaus, G. A pharmacokinetic simulation tool for inhaled corticosteroids. AAPS J. 2013, 15, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Al-Tabakha, M.M.; Alomar, M.J. In Vitro Dissolution and In Silico Modeling Shortcuts in Bioequivalence Testing. Pharmaceutics 2020, 12, 45. [Google Scholar] [CrossRef] [Green Version]
- NONMEM®. ICON plc. Available online: https://iconplc.com/innovation/nonmem/ (accessed on 23 December 2020).
- MonolixTM. Lixoft. Simulation Plus. Available online: https://www.simulations-plus.com/software/monolix/ (accessed on 23 December 2020).
- WinNonlin®. CERTARA. Available online: https://www.certara.com/knowledge-base/what-is-winnonlin/ (accessed on 23 December 2020).
- Fernández-Teruel, C.; Molina, R.N.; González-Alvarez, I.; Navarro-Fontestad, C.; García-Arieta, A.; Casabó, V.G.; Bermejo, M. Computer simulations of bioequivalence trials: Selection of design and analyte in BCS drugs with first-pass hepatic metabolism: Linear kinetics (I). Eur. J. Pharm. Sci. 2009, 36, 137–146. [Google Scholar] [CrossRef]
- Fernández-Teruel, C.; Gonzalez-Alvarez, I.; Navarro-Fontestad, C.; García-Arieta, A.; Bermejo, M.; Casabó, V.G. Computer simulations of bioequivalence trials: Selection of design and analyte in BCS drugs with first-pass hepatic metabolism: Part II. Non-linear kinetics. Eur. J. Pharm. Sci. 2009, 36, 147–156. [Google Scholar] [CrossRef]
- Karalis, V.; Macheras, P. Examining the role of metabolites in bioequivalence assessment. J. Pharm. Pharm. Sci. 2010, 13, 198–217. [Google Scholar] [CrossRef] [Green Version]
- Karalis, V. The role of the upper sample size limit in two-stage bioequivalence designs. Int. J. Pharm. 2013, 456, 87–94. [Google Scholar] [CrossRef]
- Karalis, V.; Symillides, M.; Macheras, P. On the leveling-off properties of the new bioequivalence limits for highly variable drugs of the EMA guideline. Eur. J. Pharm. Sci. 2011, 44, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Karalis, V.; Macheras, P.; Van Peer, A.; Shah, V.P. Bioavailability and bioequivalence: Focus on physiological factors and variability. Pharm. Res. 2008, 25, 1956–1962. [Google Scholar] [CrossRef] [PubMed]
- Endrenyi, L.; Tothfalusi, L. Bioequivalence for highly variable drugs: Regulatory agreements, disagreements, and harmonization. J. Pharmacokinet. Pharmacodyn. 2019, 46, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Tothfalusi, L.; Endrenyi, L.; Midha, K.K. Scaling or wider bioequivalence limits for highly variable drugs and for the special case of C(max). Int. J. Clin. Pharmacol. Ther. 2003, 41, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Endrenyi, L.; Tothfalusi, L. Regulatory and study conditions for the determination of bioequivalence of highly variable drugs. J. Pharm. Pharm. Sci. 2009, 12, 138–149. [Google Scholar] [CrossRef] [PubMed]
- Endrenyi, L.; Tothfalusi, L. Determination of bioequivalence for drugs with narrow therapeutic index: Reduction of the regulatory burden. J. Pharm. Pharm. Sci. 2013, 16, 676–682. [Google Scholar] [CrossRef]
- Jacobi, A.; Shah, V.P.; Bashaw, E.D.; Benfeldt, E.; Davit, B.; Ganes, D.; Ghosh, T.; Kanfer, I.; Kasting, G.B.; Katz, L.; et al. Current challenges in bioequivalence, quality, and novel assessment technologies for topical products. Pharm. Res. 2014, 31, 837–846. [Google Scholar]
- Yang, Y.; Shah, R.B.; Yu, L.X.; Khan, M.A. In vitro bioequivalence approach for a locally acting gastrointestinal drug: Lanthanum carbonate. Mol. Pharm. 2013, 10, 544–550. [Google Scholar] [CrossRef]
- Chen, M.L.; Shah, V.; Patnaik, R.; Adams, W.; Hussain, A.; Conner, D.; Mehta, M.; Malinowski, H.; Lazor, J.; Huang, S.M.; et al. Bioavailability and bioequivalence: An FDA regulatory overview. Pharm. Res. 2001, 18, 1645–1650. [Google Scholar] [CrossRef]
- Van Peer, A. Variability and impact on design of bioequivalence studies. Basic Clin. Pharmacol. Toxicol. 2010, 106, 146–153. [Google Scholar] [CrossRef]
- González-García, I.; Mangas-Sanjuan, V.; Merino-Sanjuán, M.; García-Arieta, A.; Trocóniz, I.F.; Bermejo, M. Assessment of in vitro dissolution specifications based on an IVIVC and in vivo bioequivalence criteria. In Proceedings of the Twenty-fifth Meeting, Lisboa, Portugal, 7–10 June 2016; PAGE: Lisboa, Portugal, 2016. [Google Scholar]
- Duque, M.D.; Silva, D.A.; Issa, M.G.; Porta, V.; Löbenberg, R.; Ferraz, H.G. In Silico Prediction of Plasma Concentrations of Fluconazole Capsules with Different Dissolution Profiles and Bioequivalence Study Using Population Simulation. Pharmaceutics 2019, 11, 215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pepin, X.J.H.; Dressman, J.; Parrott, N.; Delvadia, P.; Mitra, A.; Zhang, X.; Babiskin, A.; Kolhatkar, V.; Seo, P.; Taylor, L.S.; et al. In Vitro Biopredictive Methods: A Workshop Summary Report. J. Pharm. Sci. 2020, 110, 567–583. [Google Scholar] [CrossRef] [PubMed]
- EMA Modelling and Simulation Working Party. Available online: https://www.ema.europa.eu/en/committees/working-parties-other-groups/chmp/modelling-simulation-working-party (accessed on 23 December 2020).
- US Food and Drug Administration. Population Pharmacokinetics Guidance for Industry Draft Guidance. U.S. Department of Health and Human Services Food and Drug Administration Center for Drug Evaluation and Research (CDER) Center for Biologics Evaluation and Research (CBER). July 2019. Available online: https://www.fda.gov/media/128793/download (accessed on 23 December 2020).
- US Food and Drug Administration. The Use of Physiologically Based Pharmacokinetic Analyses—Biopharmaceutics Applications for Oral Drug Product Development, Manufacturing Changes, and Controls Guidance for Industry. Draft Guidance. U.S. Department of Health and Human Services Food and Drug Administration Center for Drug Evaluation and Research (CDER). October 2020. Available online: https://www.fda.gov/media/142500/download (accessed on 23 December 2020).
- European Commission. Communication from the Commission to the European Parliament, The Council, The European Economic and Social Committee and the Committee of the Regions. Pharmaceutical Strategy for Europe. Brussels. 25 November 2020. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:52020DC0761&from=EN (accessed on 23 December 2020).
- Karatza, E.; Karalis, V. A Semi-Physiological Modeling & Simulation approach for guided decision making in R&D. In Proceedings of the AAPS Annual Meeting and Exposition, Washington, DC, USA, 4–7 November 2018; T1130-05-036. [Google Scholar]
- US Food and Drug Administration. Approval Package for: Application Number NDA 19-787/S30. Clinical Pharmacology and Biopharmaceutics Review, Norvasc®. Available online: https://www.accessdata.fda.gov/drugsatfda_docs/nda/2004/019787_S30_NORVASC_BIOPHARMR.pdf (accessed on 23 December 2020).
- Flynn, J.T.; Nahata, M.C.; Mahan, J.D.; Portman, R.J. PATH-2 Investigators. Population pharmacokinetics of amlodipine in hypertensive children and adolescents. J. Clin. Pharmacol. 2006, 46, 905–916. [Google Scholar] [CrossRef] [PubMed]
- Karatza, E.; Karalis, V. Delay differential equations for the description of Irbesartan pharmacokinetics: A population approach to model absorption complexities leading to dual peaks. Eur. J. Pharm. Sci. 2020, 153, 105498. [Google Scholar] [CrossRef]
- Van Wart, S.A.; Shoaf, S.E.; Mallikaarjun, S.; Mager, D.E. Population-based meta-analysis of hydrochlorothiazide pharmacokinetics. Biopharm. Drug Dispos. 2013, 34, 527–539. [Google Scholar] [CrossRef]
- Neves, R.; Almeida, S.; Filipe, A.; Spínola, A.C.; Abolfathi, Z.; Yritia, M.; Ortuño, J. Bioequivalence study of two different film-coated tablet formulations of losartan-hydrochlorothiazide in healthy volunteers. Arzneimittelforschung 2008, 58, 369–375. [Google Scholar]
- Hellmig, S.; Von Schöning, F.; Gadow, C.; Katsoulis, S.; Hedderich, J.; Fölsch, U.R.; Stüber, E. Gastric emptying time of fluids and solids in healthy subjects determined by 13C breath tests: Influence of age, sex and body mass index. J. Gastroenterol. Hepatol. 2006, 21, 1832–1838. [Google Scholar] [CrossRef]
- Karalis, V. Modeling and Simulation in Bioequivalence. In Modeling in Biopharmaceutics, Pharmacokinetics and Pharmacodynamics. Homogeneous and Heterogeneous Approaches, 2nd ed.; Iliadis, A., Macheras, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 227–255. [Google Scholar]
- Gray, V.A. Power of the Dissolution Test in Distinguishing a Change in Dosage form Critical Quality Attributes. AAPS PharmSciTech 2018, 19, 3328–3332. [Google Scholar] [CrossRef] [Green Version]
- Silva, D.A.; Al-Gousous, J.; Davies, N.M.; Chacra, N.B.; Webster, G.K.; Lipka, E.; Amidon, G.L.; Löbenberg, R. Biphasic Dissolution as an Exploratory Method during Early Drug Product Development. Pharmaceutics 2020, 12, 420. [Google Scholar] [CrossRef]
- Gao, Z. In vitro dissolution testing with flow-through method: A technical note. AAPS PharmSciTech 2009, 10, 1401–1405. [Google Scholar] [CrossRef]
- Dunne, A.; Devane, J.; O’Hara, T. The Relationship between In Vitro Drug Dissolution and In Vivo Absorption. J. R. Stat. Soc. 2001, 48, 125–133. [Google Scholar] [CrossRef]
- Costa, P.; Lobo, J.M.S. Modeling and comparison of dissolution profiles. Eur. J. Pharm. Sci. 2001, 13, 123–133. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug dissolution. Int. J. Pharm. 2013, 453, 12–24. [Google Scholar] [CrossRef] [PubMed]
- Higuchi, T. Rate of release of medicaments from ointment bases containing drugs in suspension. J. Pharm. Sci. 1961, 50, 874–875. [Google Scholar] [CrossRef] [PubMed]
- Korsmeyer, R.W.; Gurny, R.; Doelker, E.; Buri, P.; Peppas, N.A. Mechanisms of potassium chloride release from compressed, hydrophilic, polymeric matrices: Effect of entrapped air. J. Pharm. Sci. 1983, 72, 1189–1191. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A. Analysis of Fickian and non-Fickian drug release from polymers. Pharm. Acta Helv. 1985, 60, 110–111. [Google Scholar] [PubMed]
- Peppas, N.A.; Narasimhan, B. Mathematical models in drug delivery: How modeling has shaped the way we design new drug delivery systems. J. Control. Release 2014, 190, 75–81. [Google Scholar] [CrossRef]
- Riegelman, S.; Collier, P. The application of statistical moment theory to the evaluation of in vivo dissolution time and absorption time. J. Pharmacokinet. Biopharm. 1980, 8, 509–534. [Google Scholar] [CrossRef]
- Picazo, A.R.; Martinez-Martinez, M.T.; Colón-Useche, S.; Iriarte, R.; Sánchez-Dengra, B.; González-Álvarez, M.; García-Arieta, A.; González-Álvarez, I.; Bermejo, M. In Vitro Dissolution as a Tool for Formulation Selection: Telmisartan Two-Step IVIVC. Mol. Pharm. 2018, 15, 2307–2315. [Google Scholar] [CrossRef]
- Sánchez-Dengra, B.; González-García, I.; González-Álvarez, M.; González-Álvarez, I.; Bermejo, M. Two-step in vitro-in vivo correlations: Deconvolution and convolution methods, which one gives the best predictability? Comparison with one-step approach. Eur. J. Pharm. Biopharm. 2020, 158, 185–197. [Google Scholar] [CrossRef]
- Bermejo, M.; Hens, B.; Dickens, J.; Mudie, D.; Paixão, P.; Tsume, Y.; Shedden, K.; Amidon, G.L. A Mechanistic Physiologically-Based Biopharmaceutics Modeling (PBBM) Approach to Assess the In Vivo Performance of an Orally Administered Drug Product: From IVIVC to IVIVP. Pharmaceutics 2020, 12, 74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- National Center for Biotechnology Information. “PubChem Compound Summary for CID 2162, Amlodipine” PubChem. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Amlodipine (accessed on 14 January 2021).
- National Center for Biotechnology Information. “PubChem Compound Summary for CID 3749, Irbesartan” PubChem. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Irbesartan (accessed on 14 January 2021).
- National Center for Biotechnology Information. “PubChem Compound Summary for CID 3639, Hydrochlorothiazide” PubChem. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Hydrochlorothiazide (accessed on 14 January 2021).
- Maestrelli, F.; Cirri, M.; García-Villén, F.; Borrego-Sánchez, A.; Iborra, C.V.; Mura, P. Tablets of “Hydrochlorothiazide in Cyclodextrin in Nanoclay”: A New Nanohybrid System with Enhanced Dissolution Properties. Pharmaceutics 2020, 12, 104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanphui, P.; Devi, V.K.; Clara, D.; Malviya, N.; Ganguly, S.; Desiraju, G.R. Cocrystals of Hydrochlorothiazide: Solubility and Diffusion/Permeability Enhancements through Drug-Coformer Interactions. Mol. Pharm. 2015, 12, 1615–1622. [Google Scholar] [CrossRef] [PubMed]
- Sridhar, K.; Rahman, H.; Sosnik, A.; Mukherjee, U.; Natarajan, T.; Siram, K.; Krishnamoorthy, B. Production of Irbesartan Nanocrystals by High Shear Homogenisation and Ultra-Probe Sonication for Improved Dissolution Rate. Curr. Drug Deliv. 2016, 13, 688–697. [Google Scholar] [CrossRef]
- World Health Organization. Proposal to Waive In Vivo Bioequivalence Requirements for the WHO Model List of Essential Medicines Immediate Release, Solid Oral Dosage Forms. Working Document QAS/04.109/Rev.1. 2005. Available online: https://www.who.int/medicines/services/expertcommittees/pharmprep/QAS04_109Rev1_Waive_invivo_bioequiv.pdf (accessed on 23 December 2020).
- Lennernäs, H.; Lindahl, A.; Van Peer, A.; Ollier, C.; Flanagan, T.; Lionberger, R.; Nordmark, A.; Yamashita, S.; Yu, L.; Amidon, G.L.; et al. In Vivo Predictive Dissolution (IPD) and Biopharmaceutical Modeling and Simulation: Future Use of Modern Approaches and Methodologies in a Regulatory Context. Mol. Pharm. 2017, 14, 1307–1314. [Google Scholar] [CrossRef]
- Hens, B.; Sinko, P.D.; Job, N.; Dean, M.; Al-Gousous, J.; Salehi, N.; Ziff, R.M.; Tsume, Y.; Bermejo, M.; Paixão, P.; et al. Formulation predictive dissolution (fPD) testing to advance oral drug product development: An introduction to the US FDA funded ‘21st Century BA/BE’ project. Int. J. Pharm. 2018, 548, 120–127. [Google Scholar] [CrossRef]

| Location | Mean Transit Time (Minutes) | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Stomach | 10 | 20 | 30 | 45 | 60 |
| Small intestine | 180 | 200 | 215 | 240 | 265 |
| Large intestine | 1970 | 1940 | 1915 | 1875 | 1835 |
| Design | Sampling Times (in Minutes) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sparse | 0 | 10 | 40 | 60 | 90 | 160 | 240 | 480 | 720 | 1440 | |||||||
| Typical | 0 | 10 | 20 | 40 | 60 | 90 | 120 | 180 | 240 | 360 | 480 | 720 | 960 | 1440 | |||
| Dense | 0 | 10 | 20 | 40 | 60 | 80 | 100 | 120 | 150 | 180 | 240 | 360 | 480 | 600 | 720 | 960 | 1440 |
| Sample size | 12, 18, 24, 30, 36 |
| Sampling scheme 1 | Typical, Sparse, Dense |
| Gastrointestinal transit time 2 | Five scenarios |
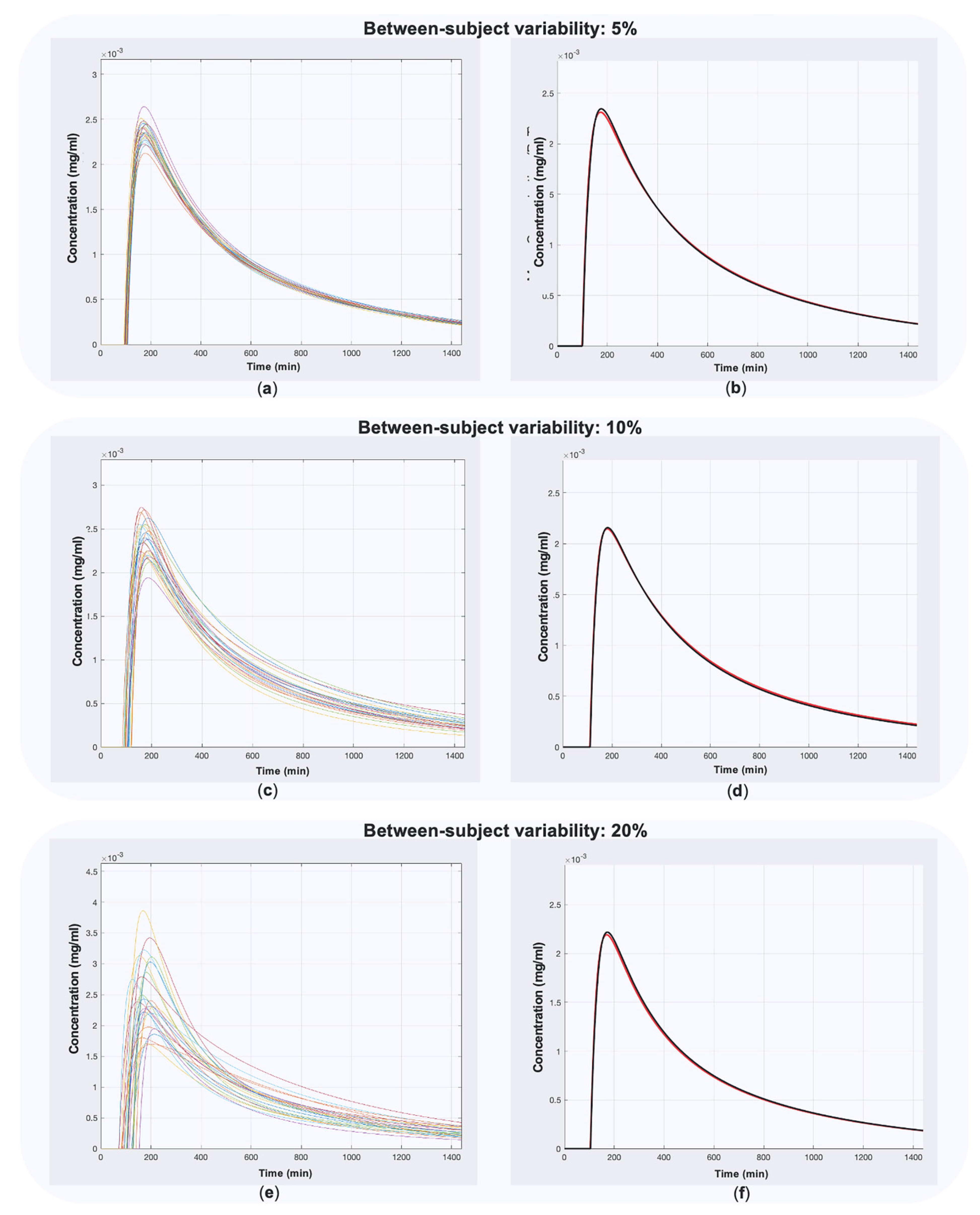
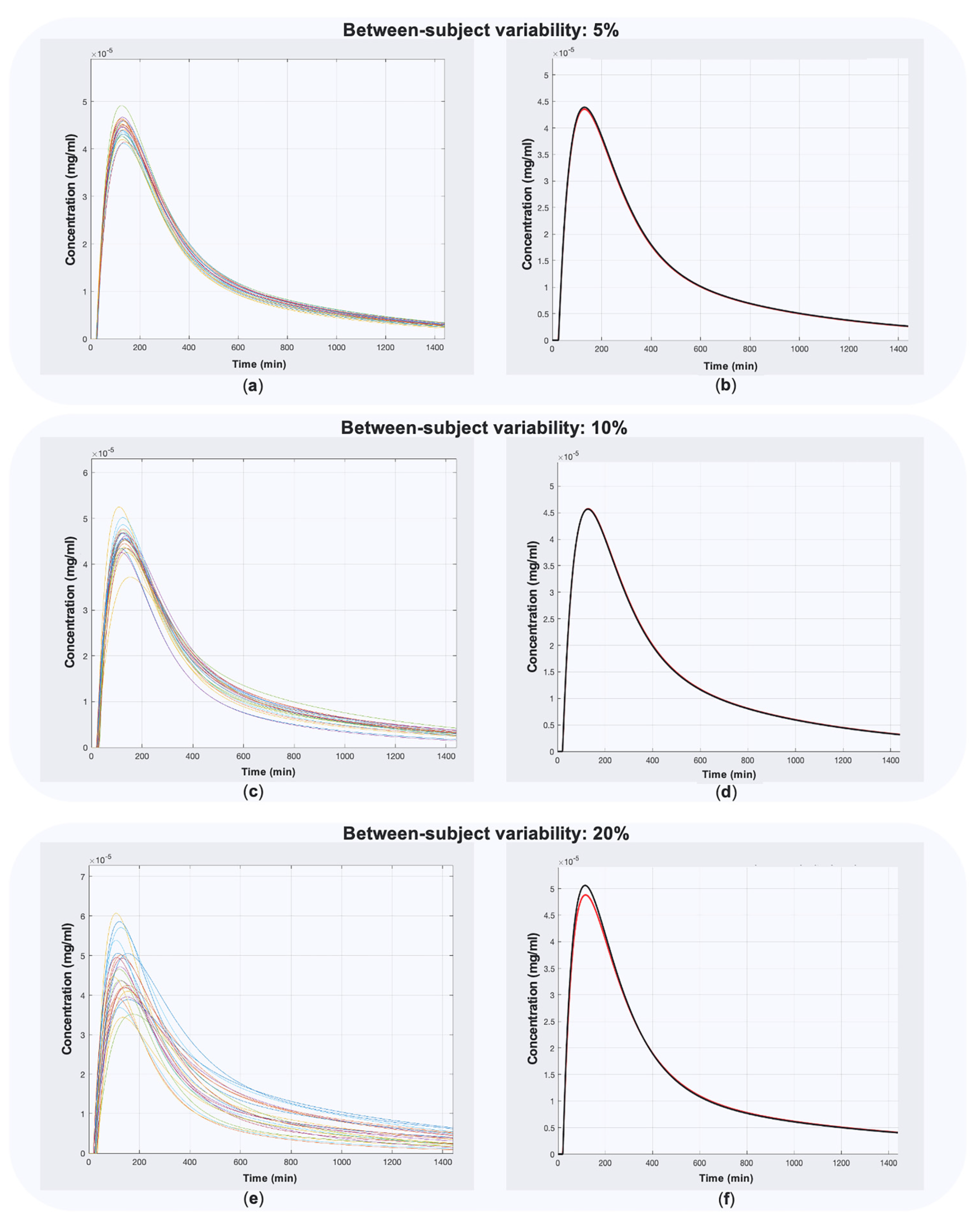
| Between-subject variability | 5%, 10%, 20% |
| Within-subject variability | 5%, 10%, 20% |
| Drug | Buffer | Parameter | Value | RSE% |
|---|---|---|---|---|
| Amlodipine | 1.2 | m0 | 0.9087 | 5.28 |
| Kd | 1.4954 | 10.2 | ||
| 4.5 | m0 | 0.856 | 13.28 | |
| Kd | 0.5734 | 7.68 | ||
| 6.8 | m0 | 0.898 | 3.18 | |
| Kd | 0.2886 | 2.93 | ||
| Irbesartan | 1.2 | m0 | 0.899 | 0.865 |
| Kd | 0.1726 | 6.98 | ||
| 4.5 | m0 | 0.0234 | 2.97 | |
| Kd | 0.1295 | 4.69 | ||
| 6.8 | m0 | 0.7076 | 3.76 | |
| Kd | 0.0811 | 1.26 | ||
| Hydrochlorthiazide | 1.2 | m0 | 0.9655 | 6.31 |
| Kd | 0.4534 | 22.78 | ||
| 4.5 | m0 | 0.9476 | 3.28 | |
| Kd | 0.2358 | 5.07 | ||
| 6.8 | m0 | 0.8874 | 4.66 | |
| Kd | 0.2934 | 3.62 |
| Source | Parameter 4 | Value | Used in Simulations |
|---|---|---|---|
| Amlodipine | |||
| Literature 1 | Ka (min−1) | 0.01417 | - |
| Cl/F (ml/min) | 370 | √ | |
| V1/F (ml) | 1300 | √ | |
| In vitro fittings | Kd_T (min−1) | 0.2886 | √ |
| Kd_R (min−1) | 0.2679 | √ | |
| Estimated “true” absorption rate constant | Kat_T (min−1) | 0.0149 | - |
| Kat_R (min−1) | 0.01496 | - | |
| Kat (min−1) | 0.01493 | √ | |
| Irbesartan | |||
| Literature 2 | Tlag (min) | 100.8 | √ |
| Ka (min−1) | 0.00507 | - | |
| Cl/F (ml/min) | 225 | √ | |
| Q/F (ml/min) | 295 | √ | |
| V1/F (ml) | 13,800 | √ | |
| V2/F (ml) | 85,800 | √ | |
| In vitro fittings | Kd_T (min−1) | 0.0811 | √ |
| Kd_R (min−1) | 0.0767 | √ | |
| Estimated “true” absorption rate constant | Kat_T (min−1) | 0.00541 | - |
| Kat_R (min−1) | 0.00544 | - | |
| Kat (min−1) | 0.00543 | √ | |
| Hydrochlorthiazide | |||
| Literature 3 | Tlag (min) | 24.24 | √ |
| Ka (min−1) | 0.01288 | - | |
| Cl/F (ml/min) | 575 | √ | |
| Q/F (ml/min) | 423.33 | √ | |
| V1/F (ml) | 137,000 | √ | |
| V2/F (ml) | 146,000 | √ | |
| In vitro fittings | Kd_T (min−1) | 0.2934 | √ |
| Kd_R (min−1) | 0.2776 | √ | |
| Estimated “true” absorption rate constant | Kat_T (min−1) | 0.01347 | - |
| Kat_R (min−1) | 0.01351 | - | |
| Kat (min−1) | 0.01349 | √ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vlachou, M.; Karalis, V. An In Vitro–In Vivo Simulation Approach for the Prediction of Bioequivalence. Materials 2021, 14, 555. https://doi.org/10.3390/ma14030555
Vlachou M, Karalis V. An In Vitro–In Vivo Simulation Approach for the Prediction of Bioequivalence. Materials. 2021; 14(3):555. https://doi.org/10.3390/ma14030555
Chicago/Turabian StyleVlachou, Marilena, and Vangelis Karalis. 2021. "An In Vitro–In Vivo Simulation Approach for the Prediction of Bioequivalence" Materials 14, no. 3: 555. https://doi.org/10.3390/ma14030555
APA StyleVlachou, M., & Karalis, V. (2021). An In Vitro–In Vivo Simulation Approach for the Prediction of Bioequivalence. Materials, 14(3), 555. https://doi.org/10.3390/ma14030555