Dynamic Disintegration of Explosively-Driven Metal Cylinder with Internal V-Grooves
Abstract
:1. Introduction
2. Theoretical Analysis
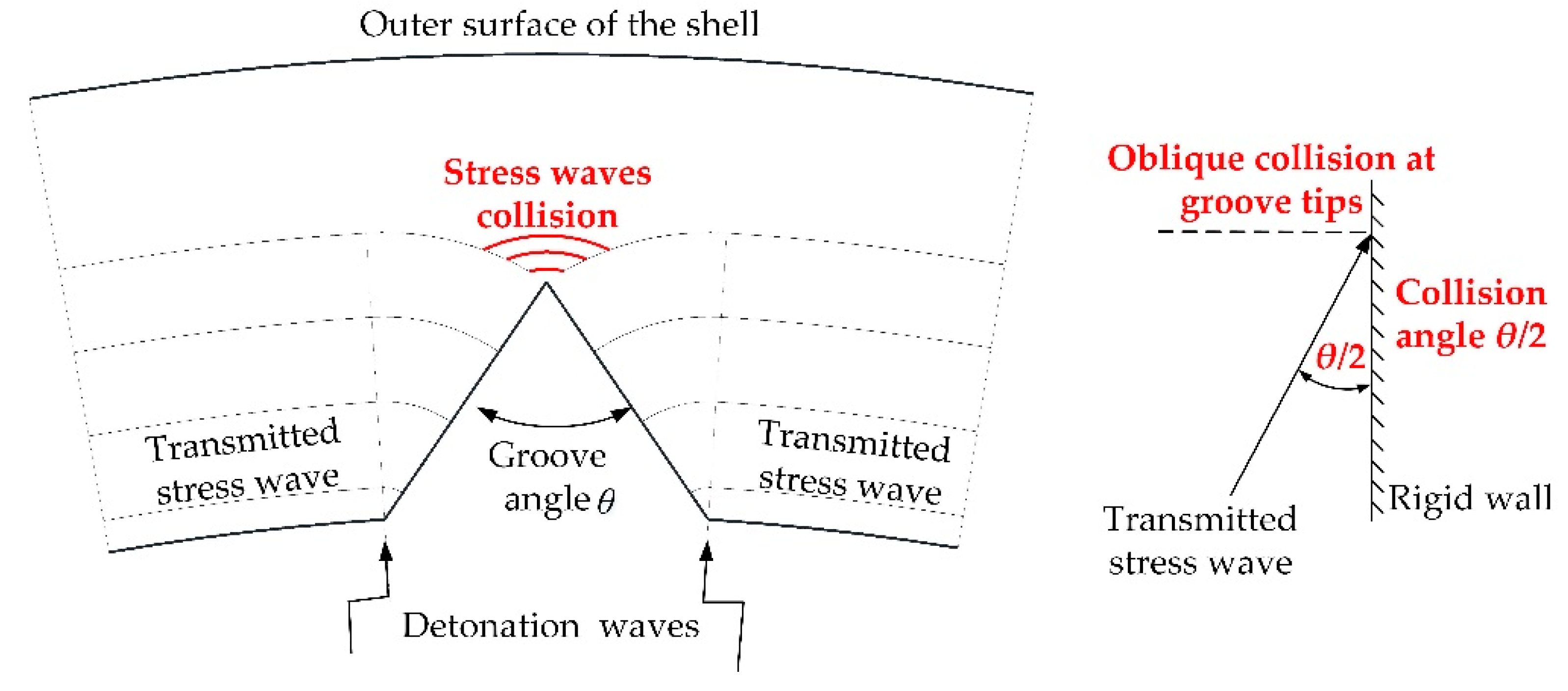
2.1. Stress Concentration Effect
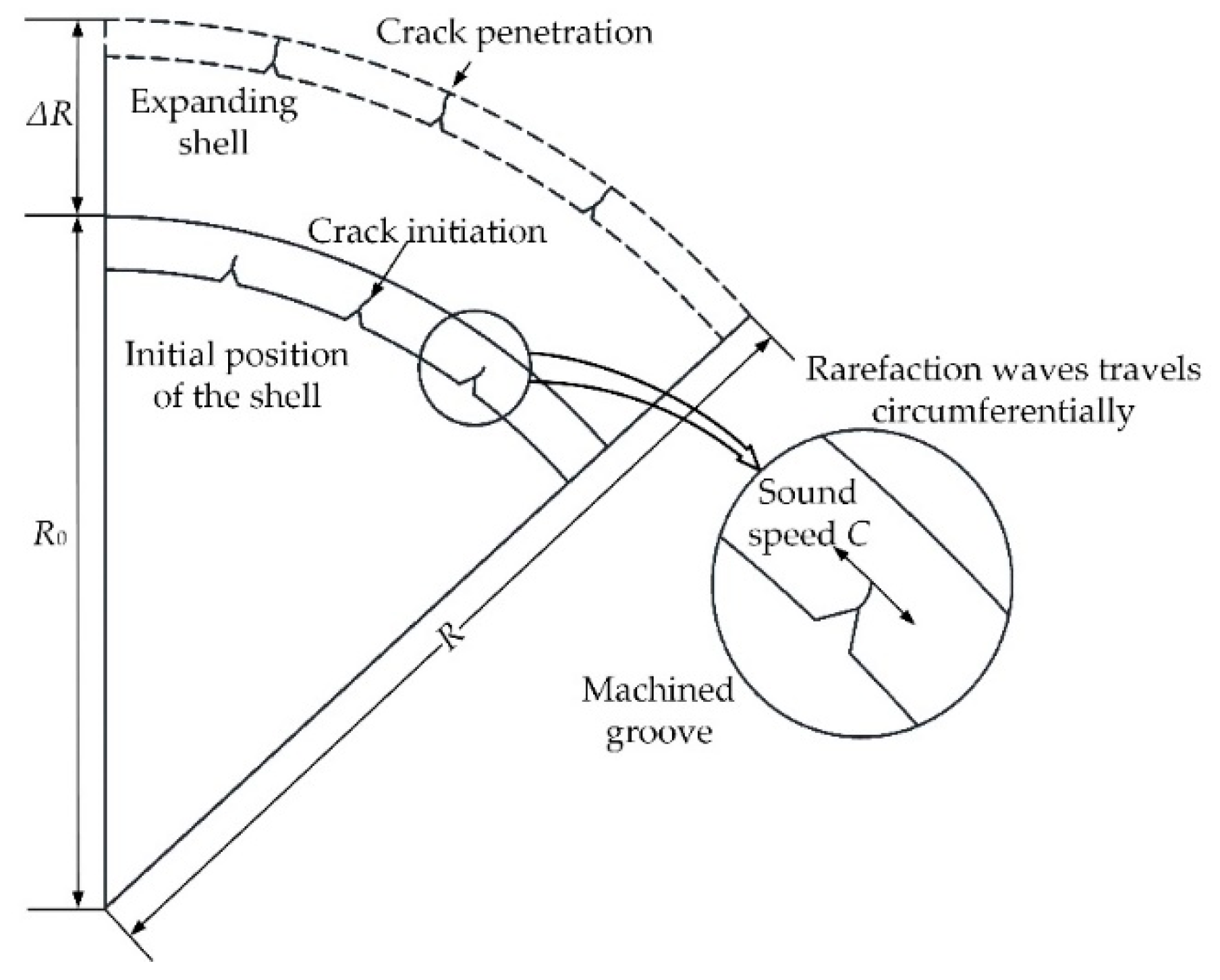
2.2. Dynamic Destruction of Grooved Shell
3. Numerical Simulation
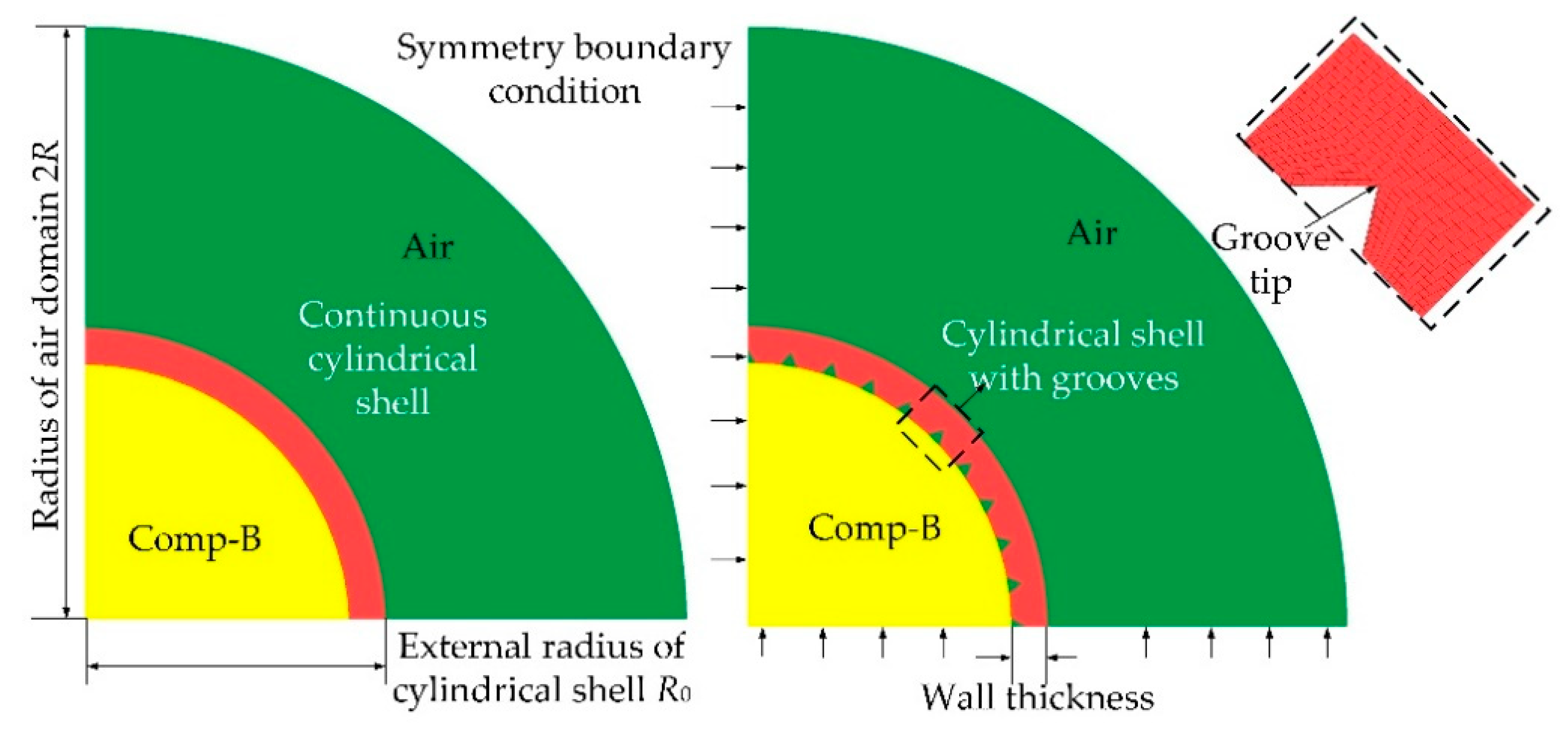
3.1. Numerical Simulation Models
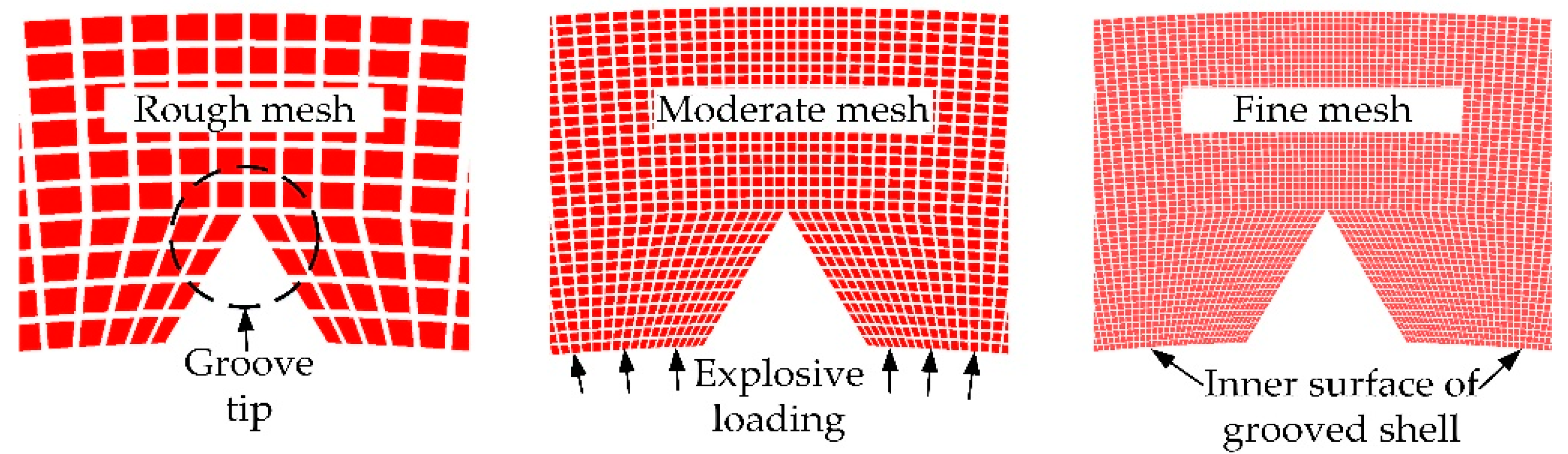
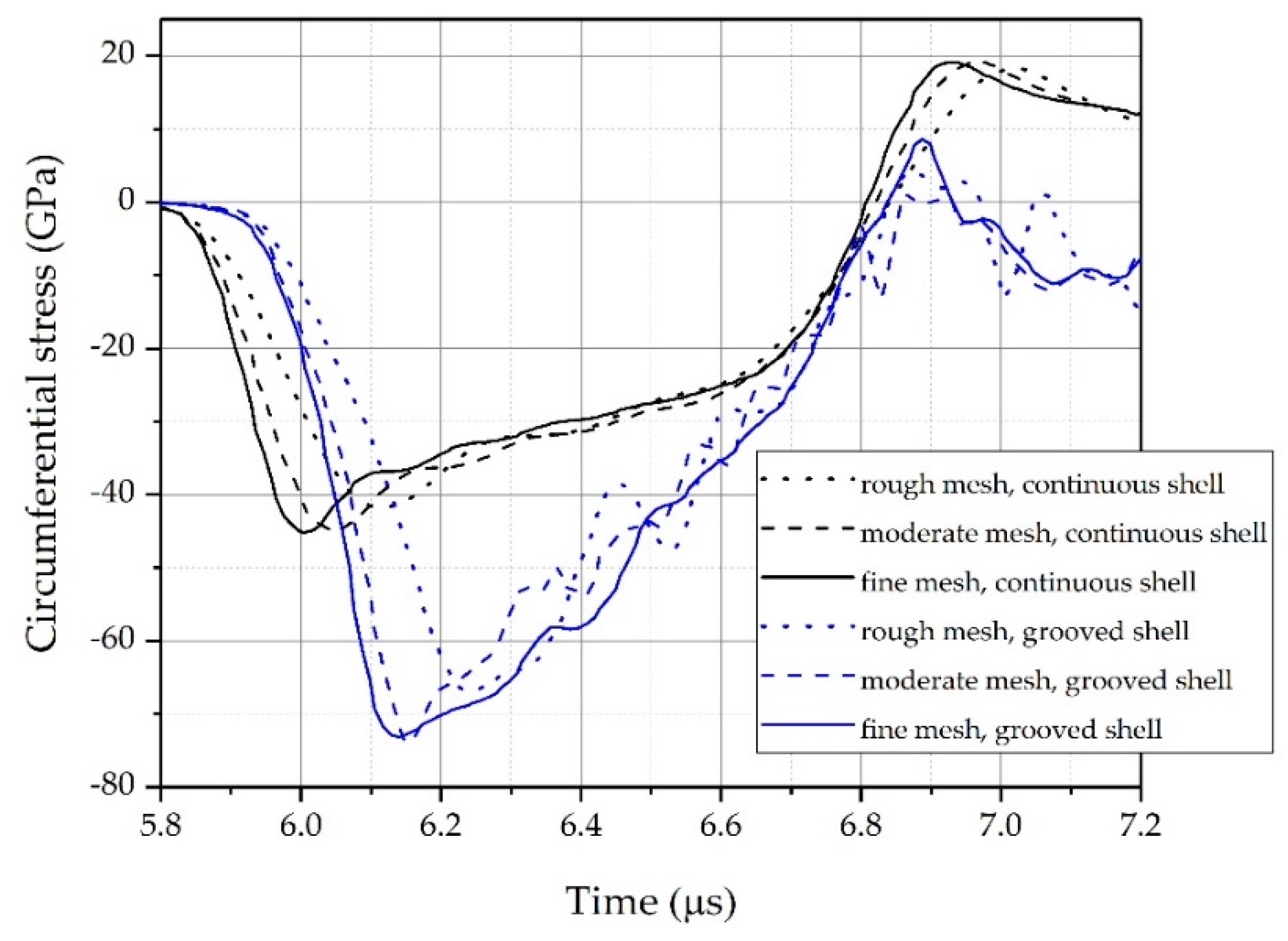
3.2. Mesh-Sensitivity Analysis
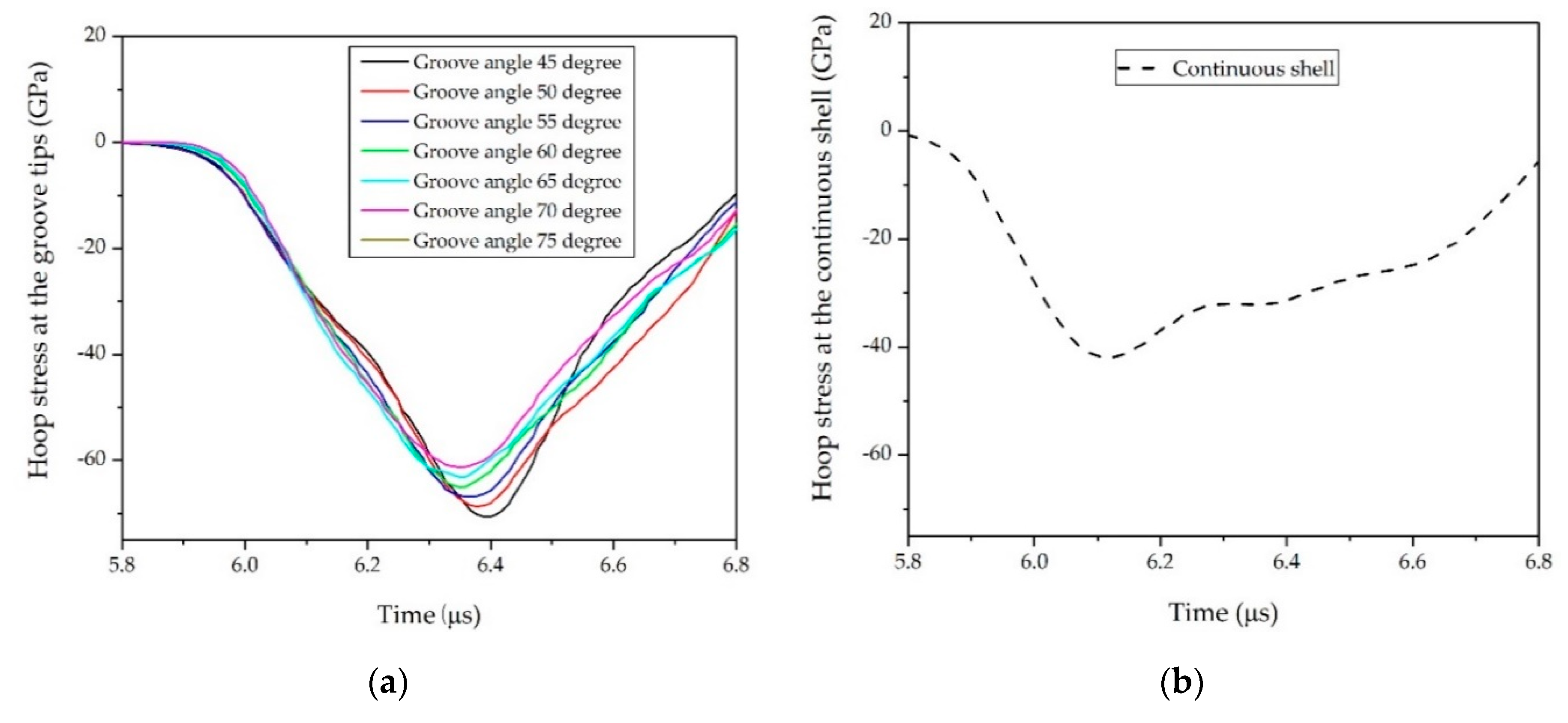
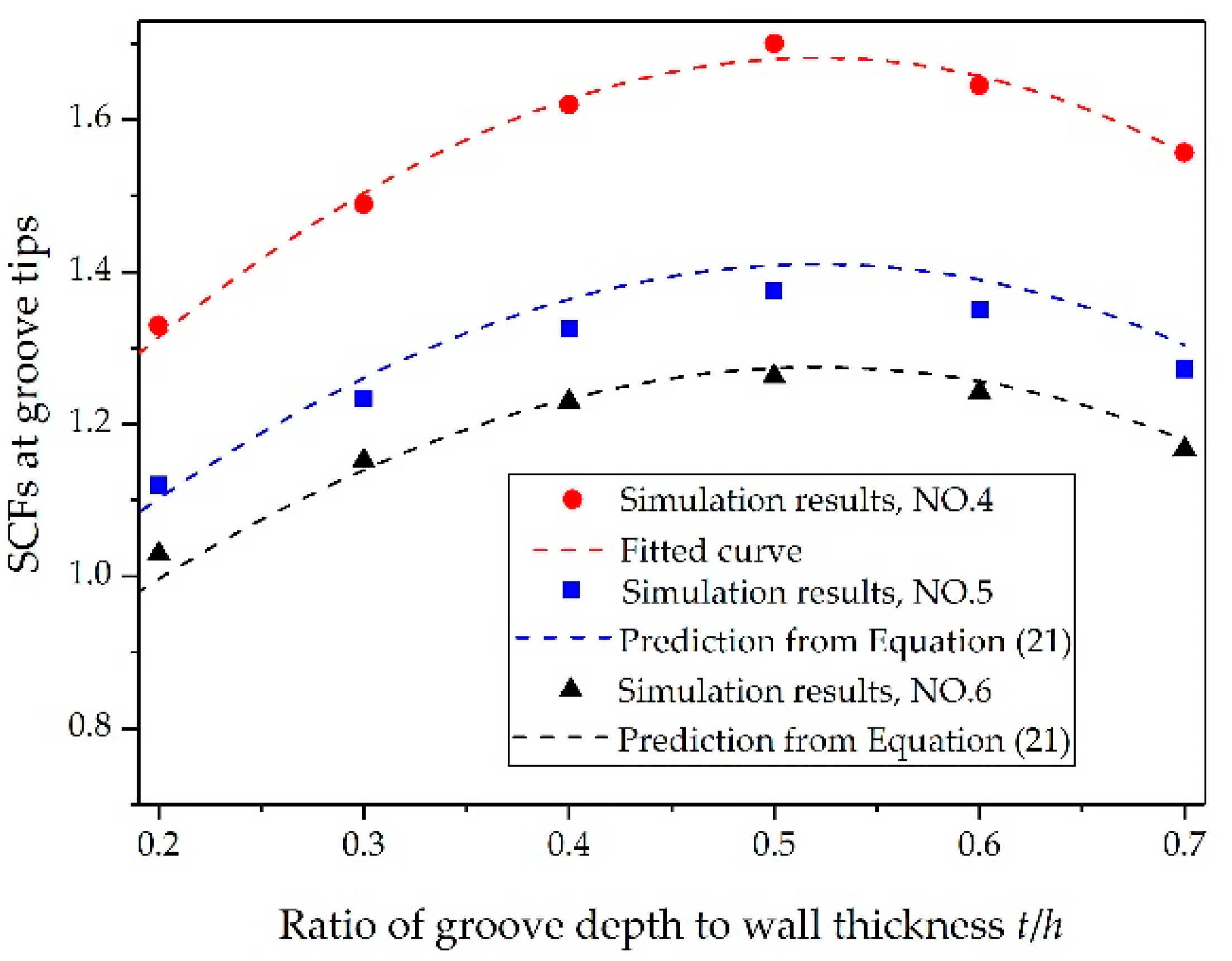
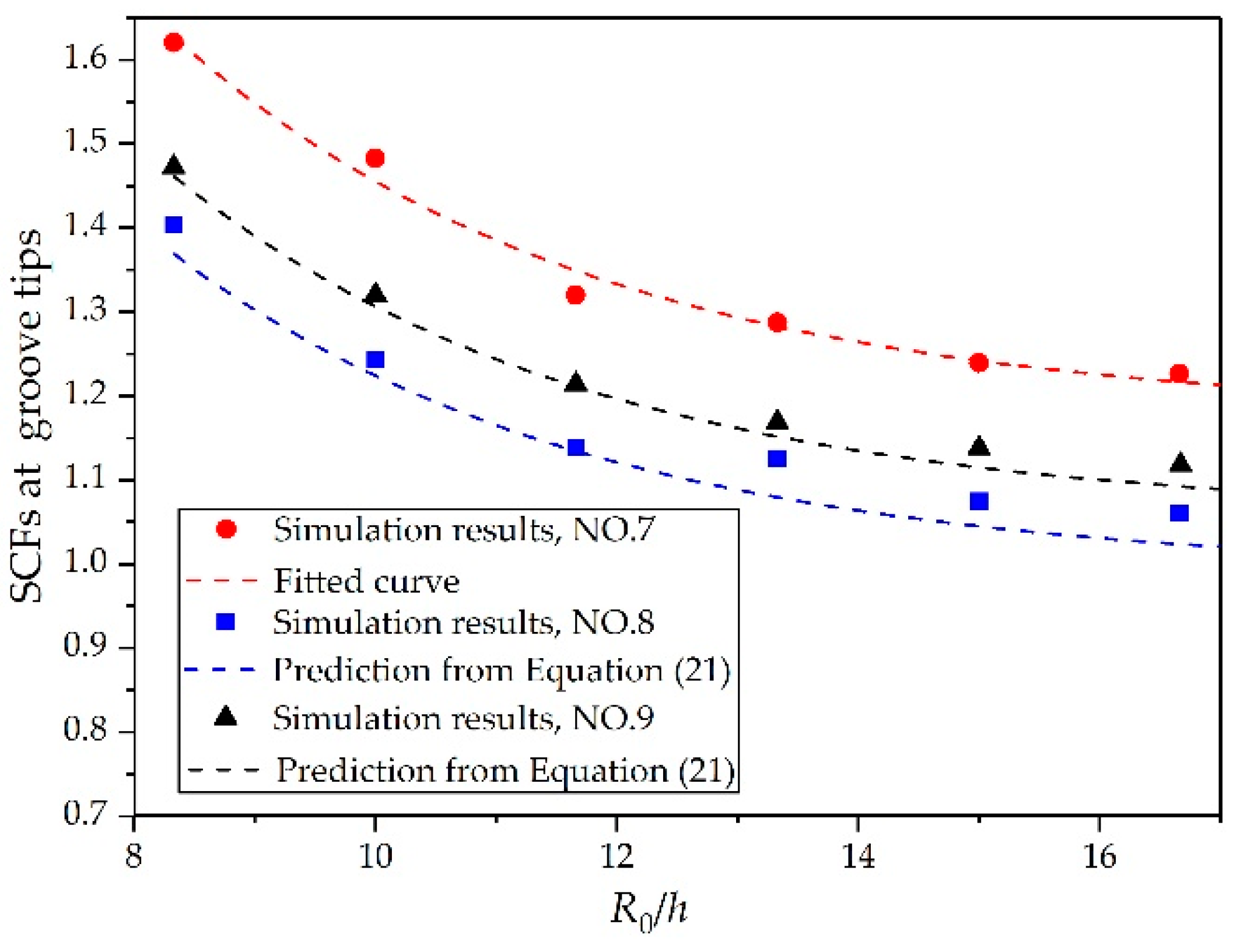
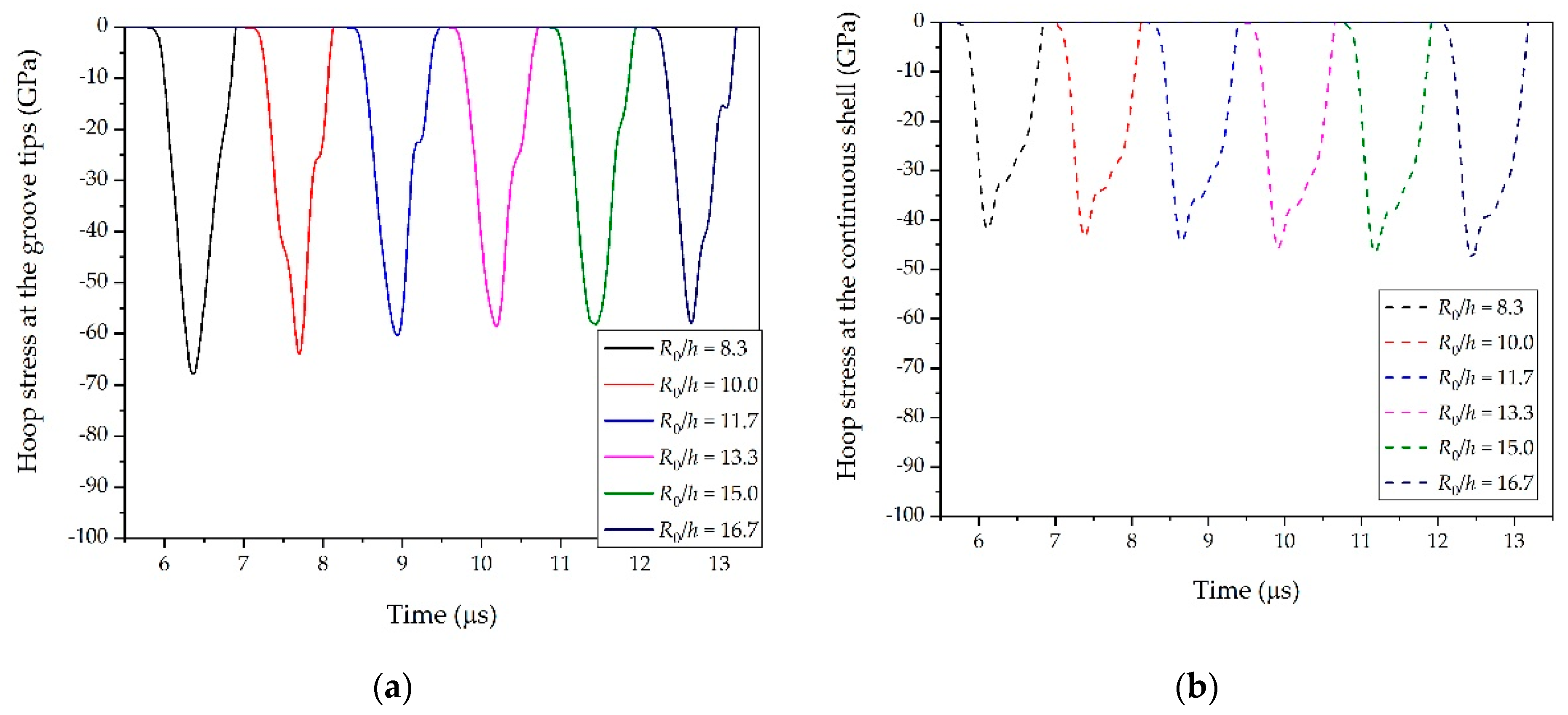
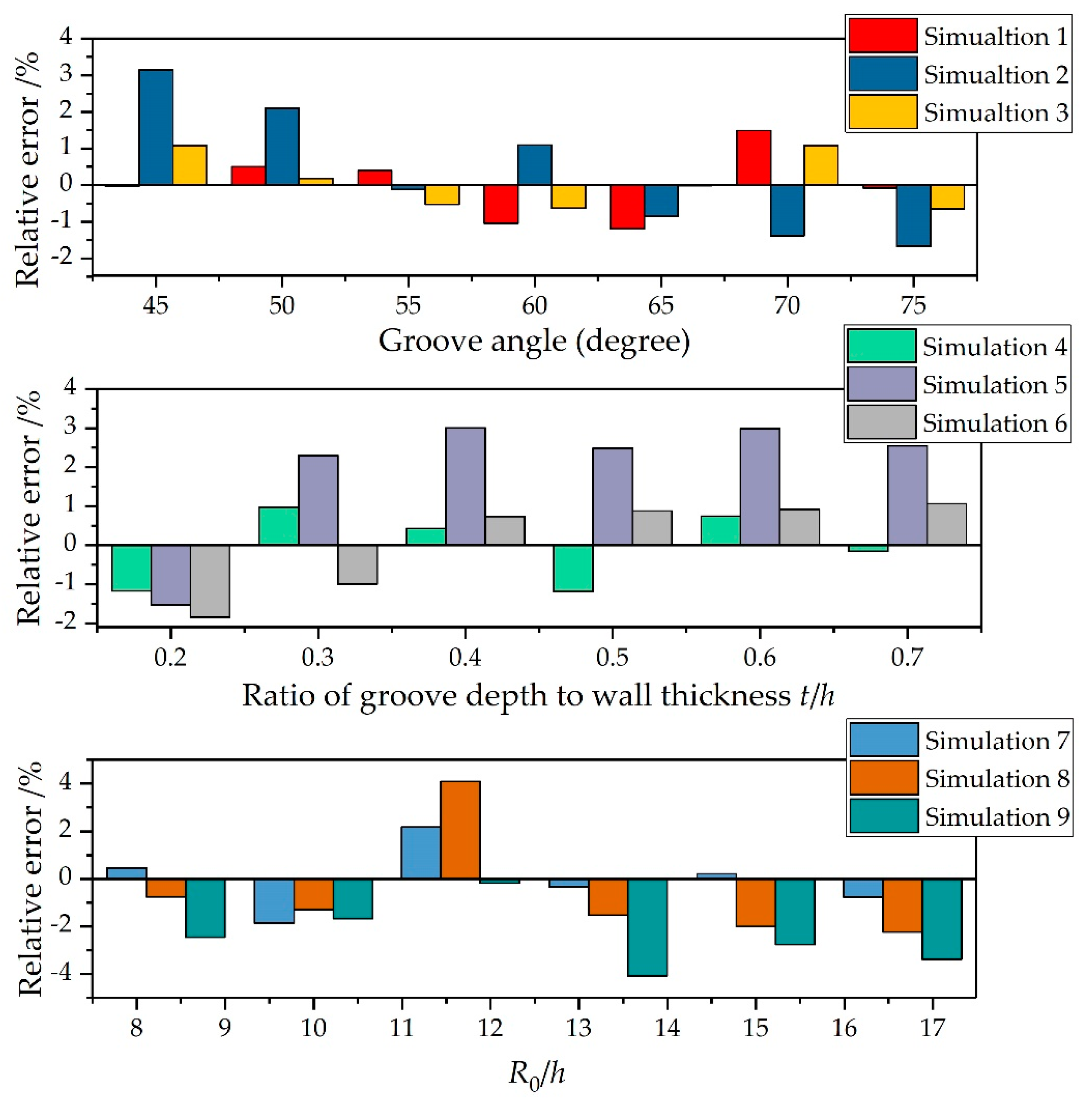
3.3. Determination of SCFs
4. Validation of the Proposed Model
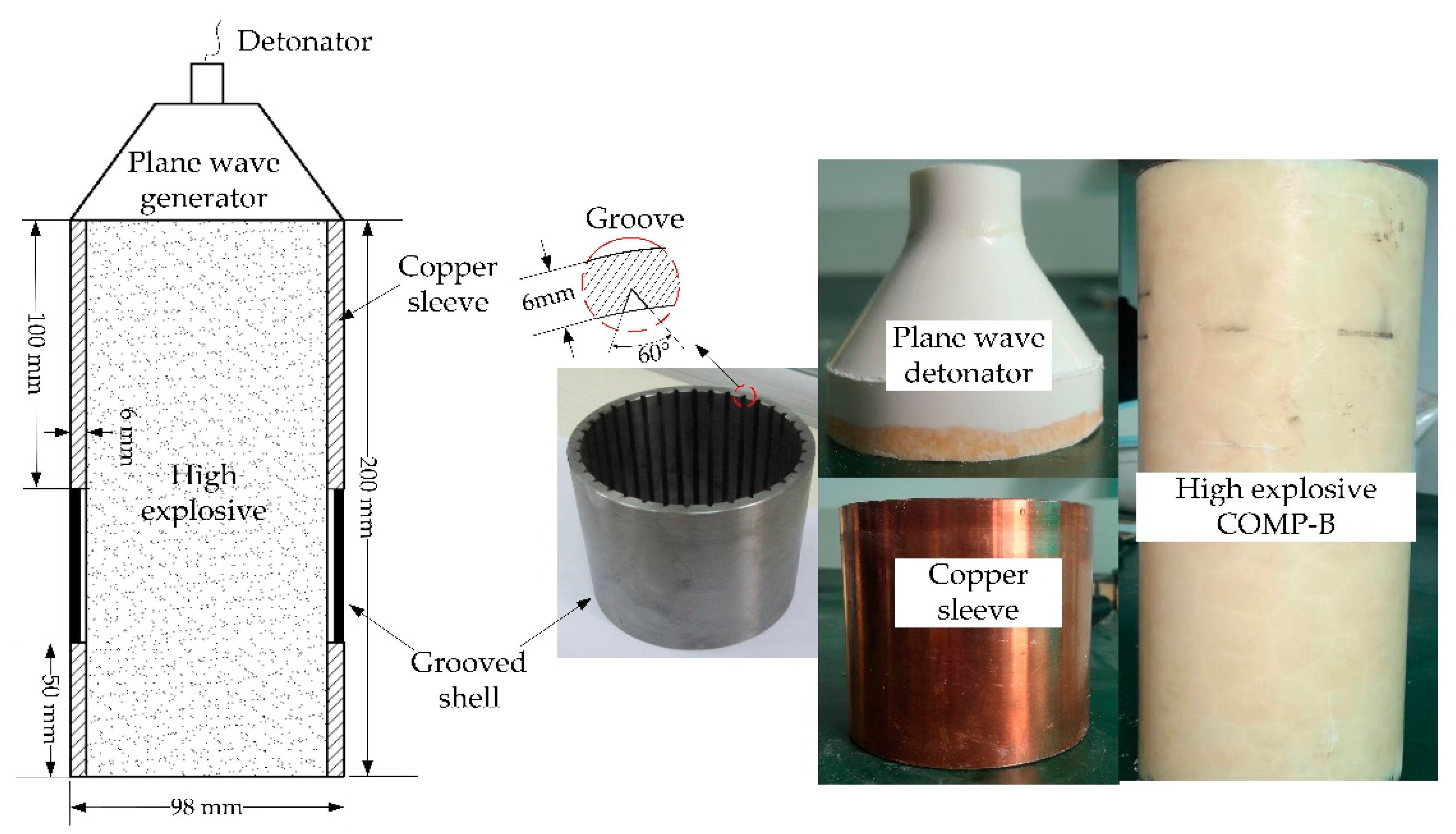
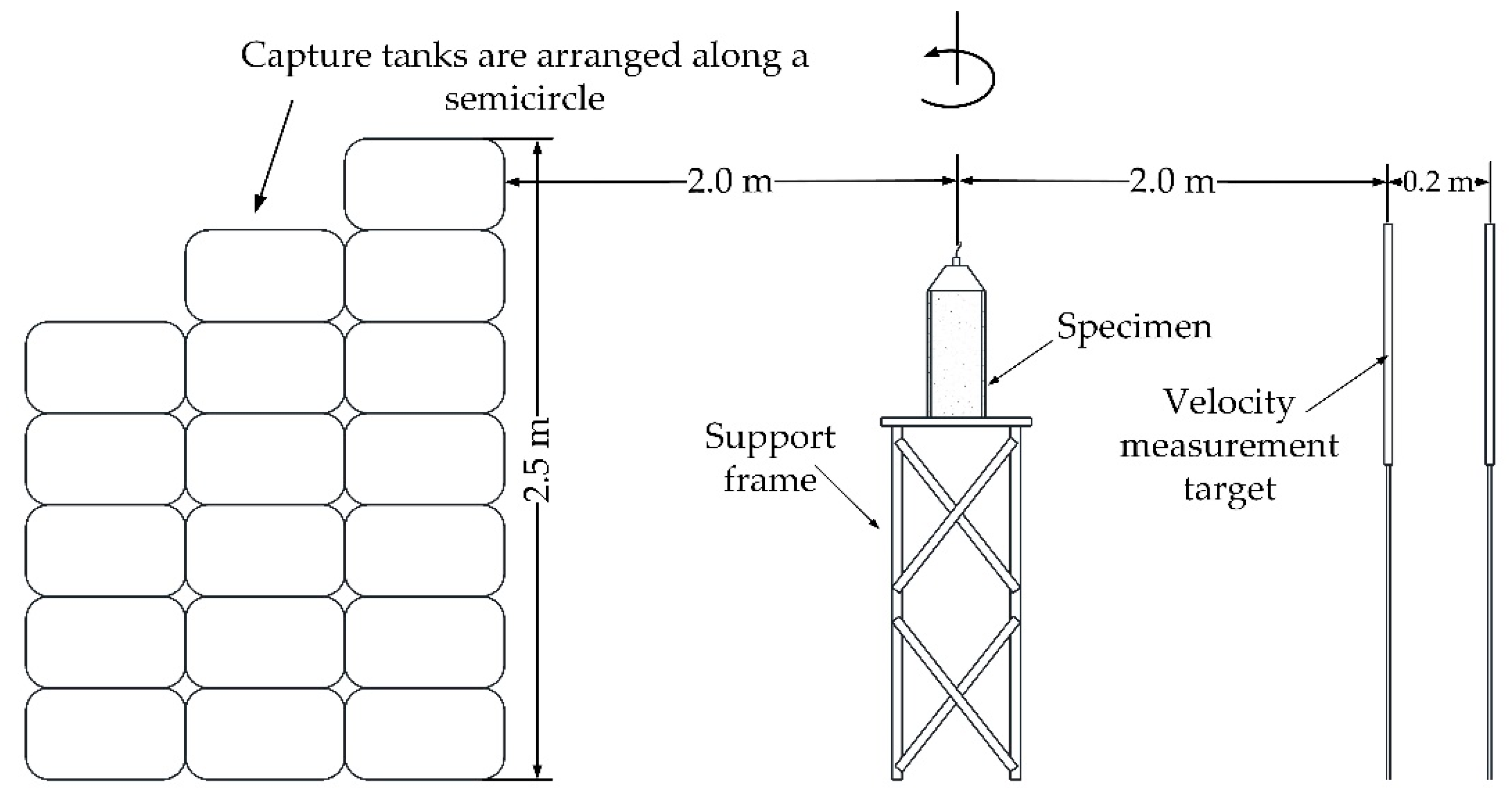
4.1. Description of Experiment
4.2. Experiment Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goto, D.M.; Becker, R.; Orzechowski, T.J.; Springer, H.K.; Sunwoo, A.J.; Synet, C.K. Investigation of the fracture and fragmentation of explosively driven rings and cylinders. Int. J. Impact Eng. 2008, 35, 1547–1556. [Google Scholar] [CrossRef]
- Ren, G.; Guo, Z.; Fan, C.; Tang, T.; Hu, H. Dynamic shear fracture of an explosively-driven metal cylindrical shell. Int. J. Impact Eng. 2016, 95, 35–39. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Ren, G.; Fan, C.; Tang, T.; Wang, X.; Hu, H. Experimental and numerical studies on the expanding fracture behavior of an explosively driven 1045 steel cylinder. Int. J. Impact Eng. 2017, 109, 240–252. [Google Scholar] [CrossRef]
- Taylor, G.I. The Fragmentation of Tubular Bombs; Scientific Papers of G. I. Taylor 3; Cambridge University Press: Cambridge, UK, 1963; p. 387. [Google Scholar]
- Hoggatt, C.R.; Recht, R.F. Fracture behavior of tubular bombs. J. Appl. Phys. 1968, 39, 1856–1862. [Google Scholar] [CrossRef]
- Feng, J.; Jing, F.; Zhang, G. Dynamic ductile fragmentation and the damage function model. J. Appl. Phys. 1997, 81, 2575–2578. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, S.S.; Ma, F. Experimental study on the expansion of metal cylinders by detonation. Int. J. Impact Eng. 2018, 114, 147–152. [Google Scholar] [CrossRef]
- An, X.Y.; Dong, Y.X.; Liu, J.Y.; Tian, C. General formula to calculate the fragment velocity of warheads with hollow core. Int. J. Impact Eng. 2018, 113, 1–8. [Google Scholar] [CrossRef]
- Zhu, J.J.; Li, W.B.; Wang, X.M.; Li, W.B. Effect of tempering temperature on expansion and fracture mechanism of 40CrMnSiB steel cylinder shell. Int. J. Impact Eng. 2017, 107, 38–46. [Google Scholar] [CrossRef]
- Singh, M.; Suneja, H.R.; Bola, M.S.; Prakash, S. Dynamic tensile deformation and fracture of metal cylinders at high strain rates. Int. J. Impact Eng. 2002, 27, 939–954. [Google Scholar] [CrossRef]
- Al-Hassani, S.T.S.; Johnson, W. The dynamics of the fragmentation process for spherical shells containing explosives. Int. J. Mech. Sci. 1969, 11, 811–823. [Google Scholar] [CrossRef]
- Ivanov, A.G. Explosive deformation and destruction of tubes. Strength Mater. 1976, 8, 1303–1306. [Google Scholar] [CrossRef]
- Hu, B.Y.; Dong, Q.D.; Han, C.S.; Wang, D.S.; Hu, H.B. Studies of expansion and fracture of explosive-filled steel cylinders. Explos. Shock Waves 1993, 13, 49–54. [Google Scholar]
- Feng, J.B.; Jing, F.Q.; Su, L.X.; Han, J.W. Studies of the explosion expanding-fracture process of a thin cylindrical shell. Chin. J. High Press. Phys. 1988, 2, 97–103. [Google Scholar]
- Liang, M.; Li, X.; Lu, F. Effects of U-notches on the dynamic fracture and fragmentation of explosively driven cylinders. Appl. Fract. Mech. 2015, 77, 50–58. [Google Scholar] [CrossRef]
- Pike, A.W.; Zuo, Q.H. Geometric design consideration for controlled fragmentation of metallic shells. Finite Elem. Anal. Des. 2014, 91, 59–67. [Google Scholar] [CrossRef]
- Villano, D.; Galliccia, F. Innovative technologies for controlled fragmentation warheads. J. Appl. Mech. 2013, 80, 1704. [Google Scholar] [CrossRef]
- Yang, Y.; Li, R.M.; Chen, R.W.; Zhang, R.M.; Jiang, R.; Zheng, R.G. Effects of pre-notches on the self-organization behaviors of shear bands in aluminum alloy. Mater. Sci. Eng. A 2010, 527, 5084–5091. [Google Scholar] [CrossRef]
- Kuroda, M.; Fok, S.L.; Marsden, B.J.; Oyadiji, S.O. Analyses of the multiple cracking behavior of brittle hollow cylinders under internal pressure. Int. J. Impact Eng. 2006, 32, 905–927. [Google Scholar] [CrossRef]
- Zhang, S.Z. Explosion and Impact Dynamics; Weapon Industry Press: Beijing, China, 1993; pp. 74–78. [Google Scholar]
- Lloyd, R.M. Conventional Warhead Systems Physics and Engineering Design; American Institute of Aeronautics: Reston, VA, USA, 1998; pp. 32–40. [Google Scholar]
- Arola, D.; Mccain, M.L. Surface texture and the stress concentration factor for FRP components with holes. J. Compos. Mater. 2003, 37, 1439–1460. [Google Scholar] [CrossRef]
- Troyani, N.; Hernández, S.I.; Villarroel, G.; Pollonais, Y.; Gomes, C. Theoretical stress concentration factors for short flat bars with opposite U-shaped notches subjected to in-plane bending. Int. J. Fatigue 2004, 26, 1303–1310. [Google Scholar] [CrossRef]
- Kosmatka, J.B.; Fries, R.H.; Reinholtz, C.F. Tension and bending stress concentration factors in ‘U’, ‘V’, and opposed ‘U’–‘V’ notches. J. Strain Anal. Eng. Des. 1990, 25, 233–240. [Google Scholar] [CrossRef]
- William, A.; Nader, Z.; Walter, N.; Bryan, A. Dynamic stress concentrations for an axially loaded strut at discontinuities due to an elliptical hole or double circular notches. Int. J. Impact Eng. 2004, 30, 255–274. [Google Scholar] [CrossRef]
- Mirzaei, M.; Najafi, M.; Niasari, H. Experimental and numerical analysis of dynamic rupture of steel pipes under internal high-speed moving pressures. Int. J. Impact Eng. 2015, 85, 27–36. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strain, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistic, The Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Gao, Y.; Feng, S.; Yan, X.; Zhang, B.; Zhou, T. Axial distribution of fragment velocities from cylindrical casing with air parts at two ends. Int. J. Impact Eng. 2020, 140, 103535. [Google Scholar] [CrossRef]
- Feng, H.; Bassim, M.N. Finite element modeling of the formation of adiabatic shear bands in AISI 4340 steel. Mater. Sci. Eng. A 1999, 266, 255–260. [Google Scholar] [CrossRef]
- Wright, T.W.; Walter, J.W. Stress collapse in adiabatic shear bands. J. Mech. Phys. Solids 1987, 35, 701–720. [Google Scholar] [CrossRef]
- Li, Y. Study on Theories and Technologies of Asymmetrically Initiated Warhead. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2016. [Google Scholar]
- Ma, L.; Xin, J.; Hu, Y.; Zheng, J. Ductile and brittle failure assessment of containment vessels subjected to internal blast loading. Int. J. Impact Eng. 2013, 52, 28–36. [Google Scholar] [CrossRef]
- Xu, H.Y.; Li, W.B.; Li, W.B.; Zhang, Q.; Yang, Y. Fracture mechanism of a cylindrical shell cut by circumferential detonation collision. Def. Technol. 2020, in press. [Google Scholar] [CrossRef]









| Component | NO. | Outside Radius of Shell (R0, mm) | Wall Thickness (h, mm) | Groove Depth (t, mm) | Groove Angle (θ, °) | R0/h | t/h |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 50 | 6 | 2.4 | 45, 50, 55, 60, 65, 70, 75 | 8.33 | 0.4 |
| 2 | 80 | 8 | 2.4 | 45, 50, 55, 60, 65, 70, 75 | 10 | 0.3 | |
| 3 | 75 | 5 | 3.0 | 45, 50, 55, 60, 65, 70, 75 | 15 | 0.6 | |
| 2 | 4 | 50 | 6 | 1.2, 1.8, 2.4, 3.0, 3.6, 4.2 | 60 | 8.33 | 0.2~0.7 |
| 5 | 80 | 8 | 1.6, 2.4, 3.2, 4.0, 4.8, 5.6 | 75 | 10 | 0.2~0.7 | |
| 6 | 75 | 5 | 1.6, 2.4, 3.2, 4.0, 4.8, 5.6 | 60 | 15 | 0.2~0.7 | |
| 3 | 7 | 100, 90, 80, 70, 60, 50 | 6 | 2.4 | 60 | 16.7, 15, 13.3, 11.7, 10, 8.33 | 0.4 |
| 8 | 133.3, 120, 106.7, 93.3, 80, 66.6 | 8 | 2.4 | 75 | 16.7, 15, 13.3, 11.7, 10, 8.33 | 0.3 | |
| 9 | 83.3, 75, 66.7, 58.3, 50, 41.7 | 5 | 3.0 | 70 | 16.7, 15, 13.3, 11.7, 10, 8.33 | 0.7 |
| Experiment Number. | Explosive Charge | Outer Diameter of Shells (mm) | Wall Thickness h (mm) | Groove Depth t (mm) | Groove Angle θ (degree) | t/h | Groove Root Radius (mm) |
|---|---|---|---|---|---|---|---|
| No. 1 | Comp-B | 98 | 6 | 1.2 | 60 | 0.2 | 0.3 |
| No. 2 | Comp-B | 98 | 6 | 2.4 | 60 | 0.4 | 0.3 |
| No. 3 | Comp-B | 98 | 6 | 3.0 | 60 | 0.5 | 0.3 |
| No. 4 | Comp-B | 98 | 6 | 4.2 | 60 | 0.7 | 0.3 |
| Experiment Numbers | t/h | v (m/s) | Theoretical Prediction of Fracture Strain ε | |||||
|---|---|---|---|---|---|---|---|---|
| AL-Hassani and Johnson [11] | Ivanov [12] | Theoretical Prediction | Experimental Result 1 | Error 2 | ||||
| No. 1 | 0.2 | 1472 | 2.46 | 0.462 | 0.398 | 0.194 | 0.208 | 6.7% |
| No. 2 | 0.4 | 1335 | 2.39 | 0.405 | 0.406 | 0.104 | 0.115 | 9.6% |
| No. 3 | 0.5 | 1228 | 2.25 | 0.365 | 0.410 | 0.086 | 0.096 | 10.4% |
| No. 4 | 0.7 | 1125 | 2.09 | 0.353 | 0.426 | 0.072 | 0.081 | 11.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Wu, C.; An, F.; Liao, S.; Xue, D.; Liu, J. Dynamic Disintegration of Explosively-Driven Metal Cylinder with Internal V-Grooves. Materials 2021, 14, 584. https://doi.org/10.3390/ma14030584
Zhou M, Wu C, An F, Liao S, Xue D, Liu J. Dynamic Disintegration of Explosively-Driven Metal Cylinder with Internal V-Grooves. Materials. 2021; 14(3):584. https://doi.org/10.3390/ma14030584
Chicago/Turabian StyleZhou, Mingxue, Cheng Wu, Fengjiang An, Shasha Liao, Dongyu Xue, and Jian Liu. 2021. "Dynamic Disintegration of Explosively-Driven Metal Cylinder with Internal V-Grooves" Materials 14, no. 3: 584. https://doi.org/10.3390/ma14030584






