Windblown Sand-Induced Degradation of Glass Panels in Curtain Walls
Abstract
:1. Introduction
2. Experimental Program
2.1. Materials
2.2. Specimens
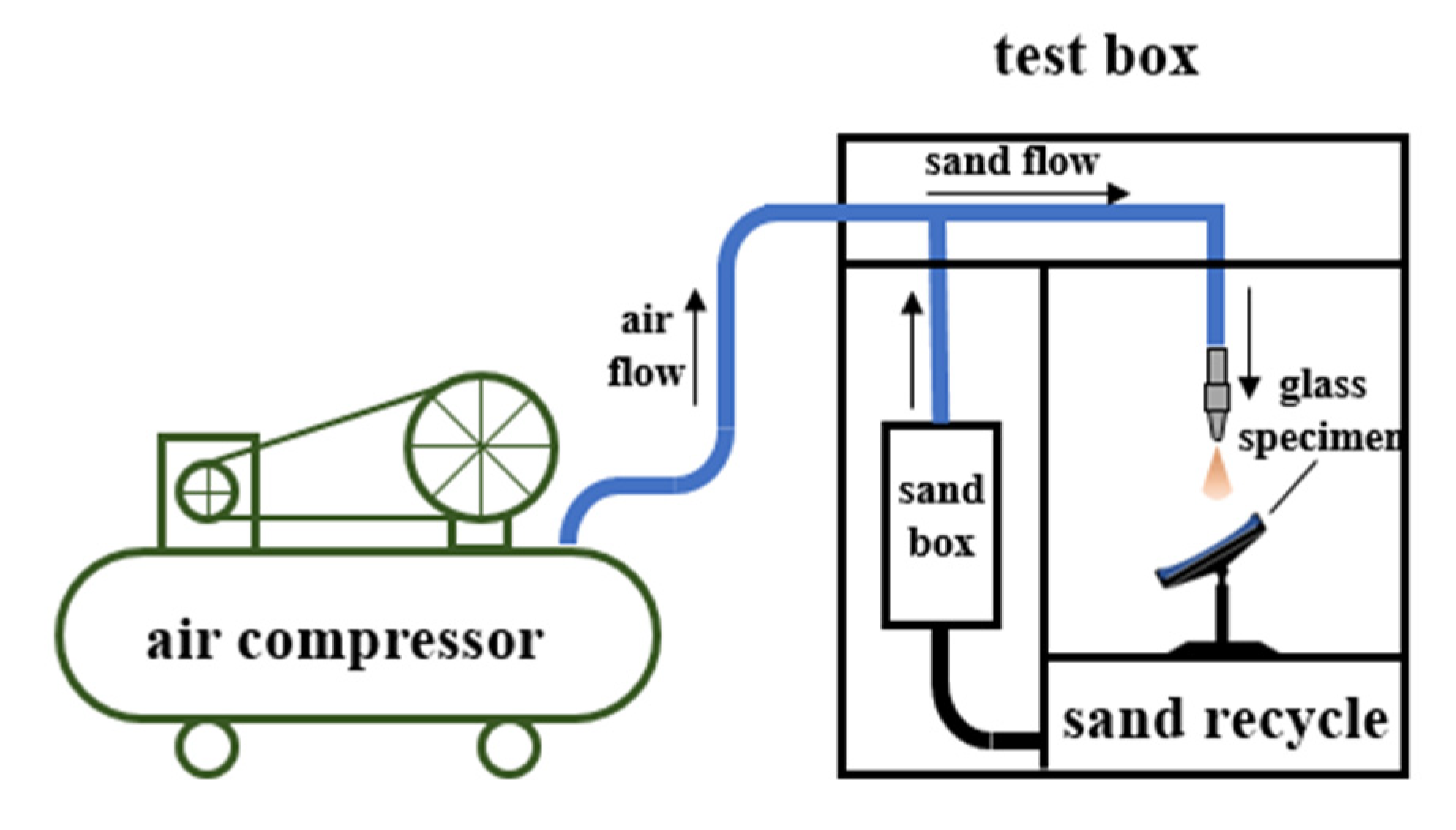
2.3. Experimental Equipment
2.4. Testing Methods
2.4.1. Mass Loss
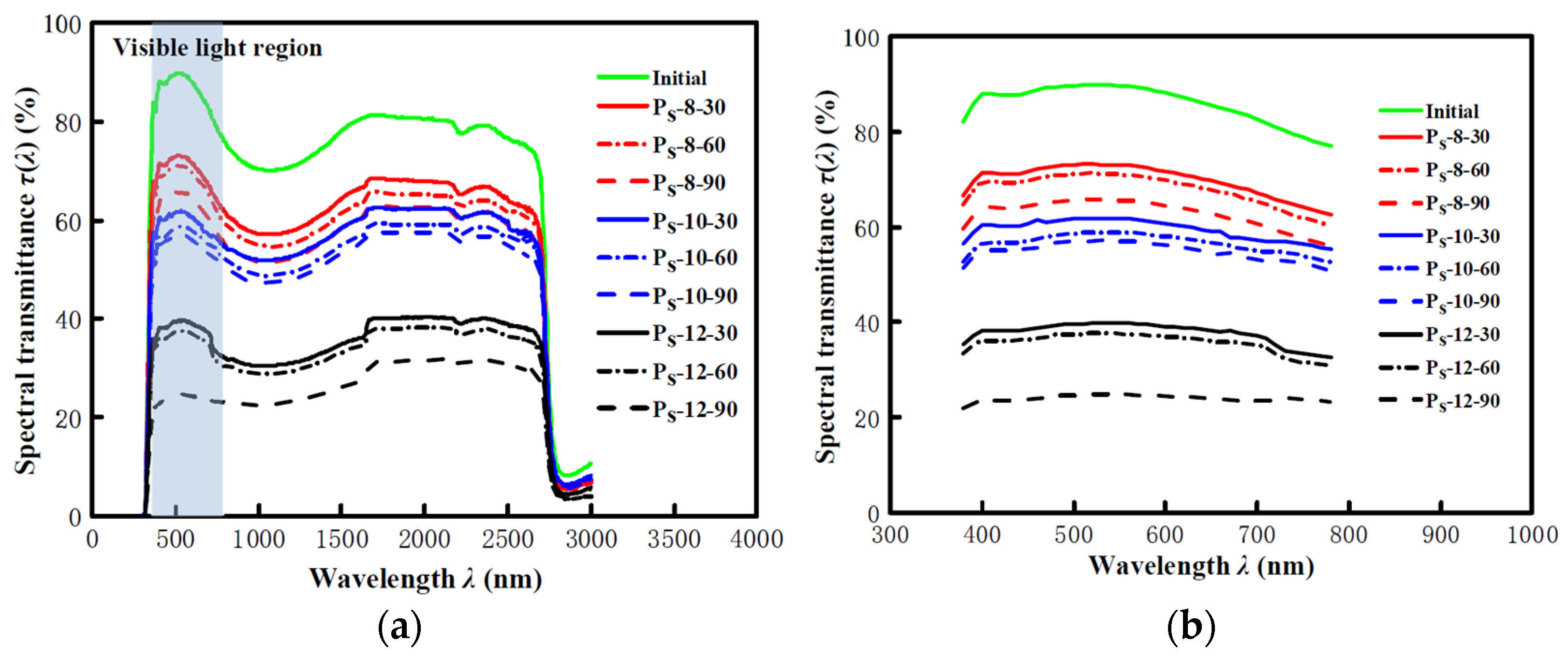
2.4.2. Visible Light Transmittance
2.4.3. Meso-Morphology
3. Results and Discussion
3.1. Damage Mode
3.2. Relative Mass Loss
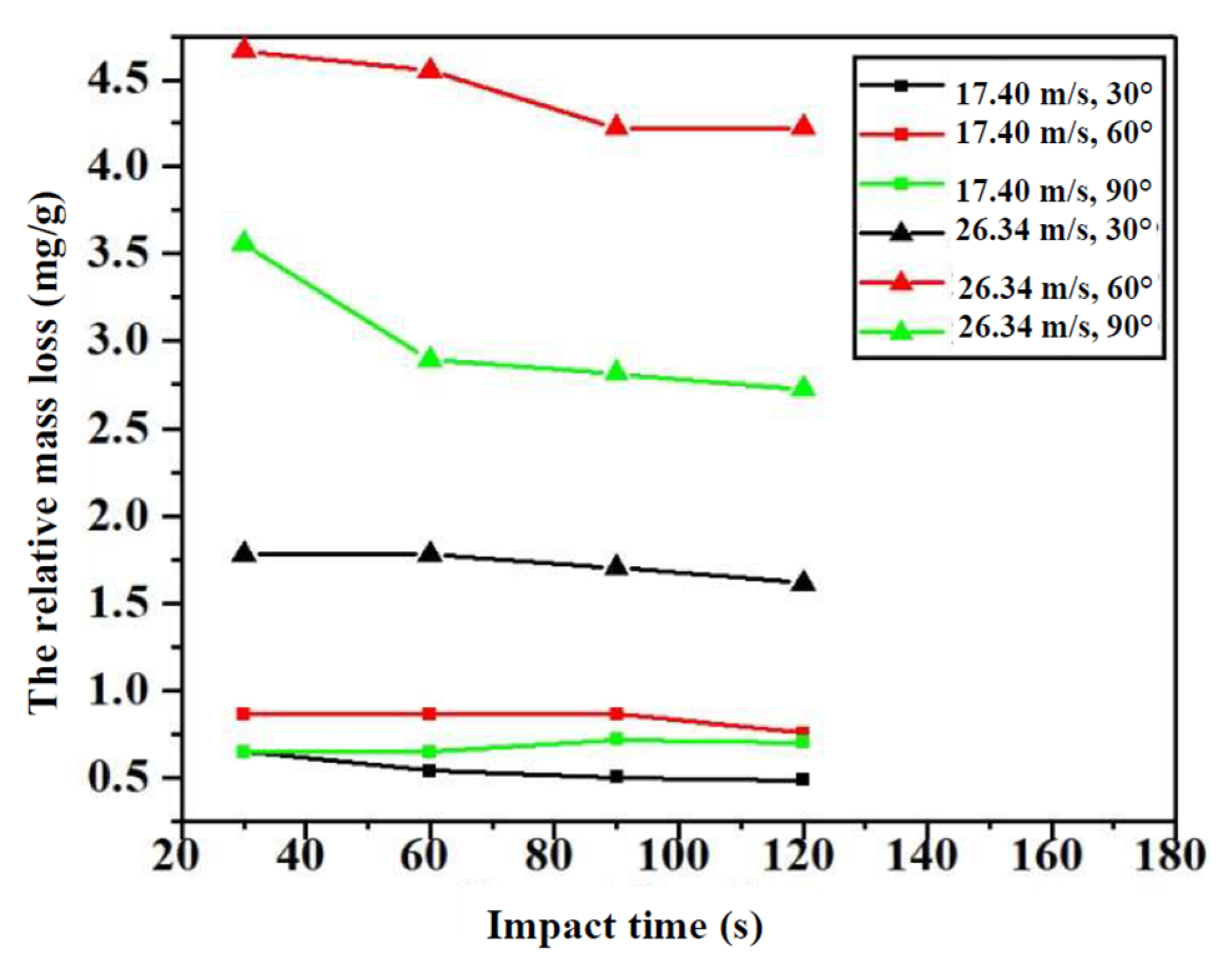
3.2.1. Effect of Impact Time on Relative Mass Loss of Glass Specimens
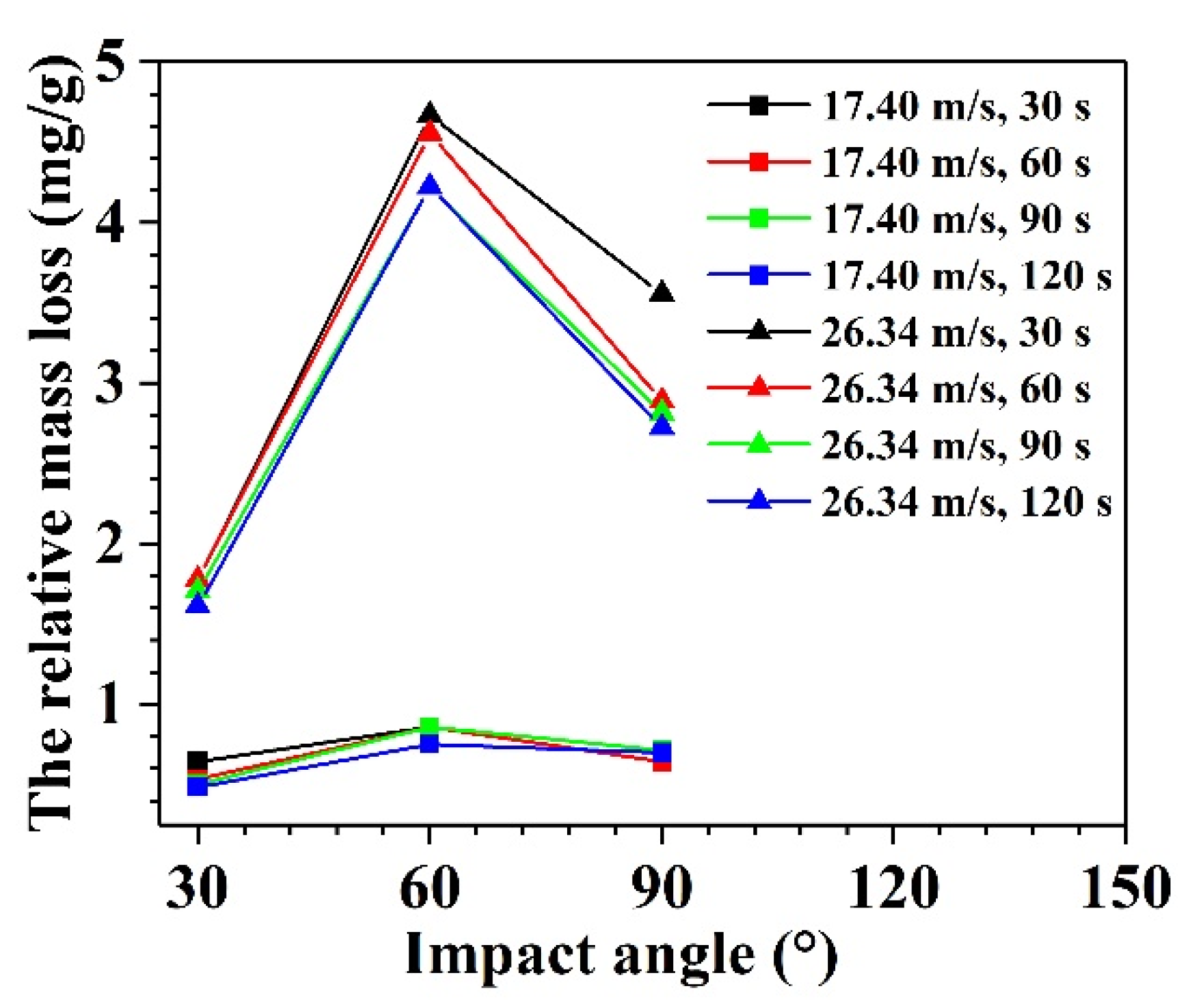
3.2.2. Effect of Impact Angles on Relative Mass Loss of Glass Specimens
3.3. Visible Light Transmittance
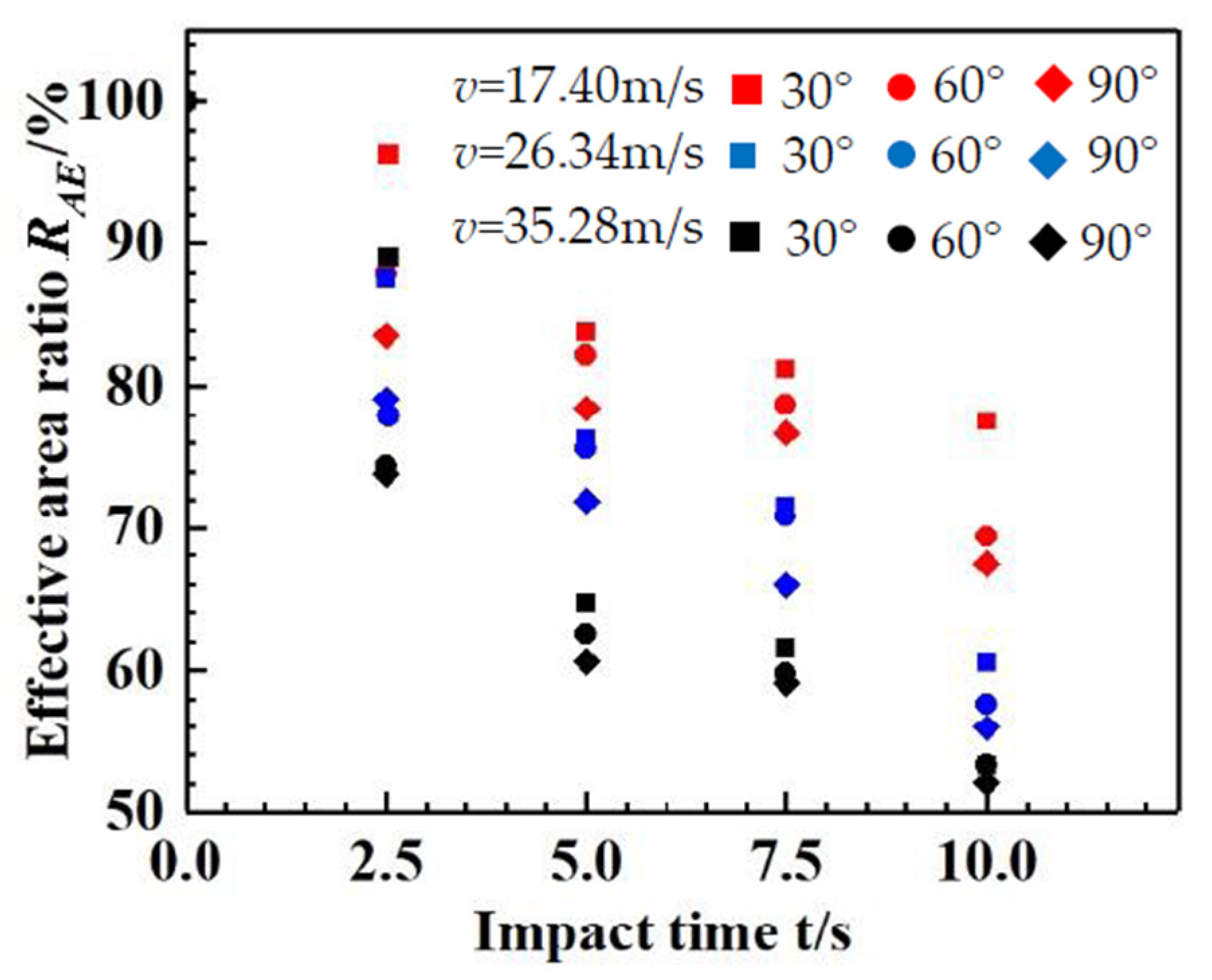
3.4. Effective Area Ratio
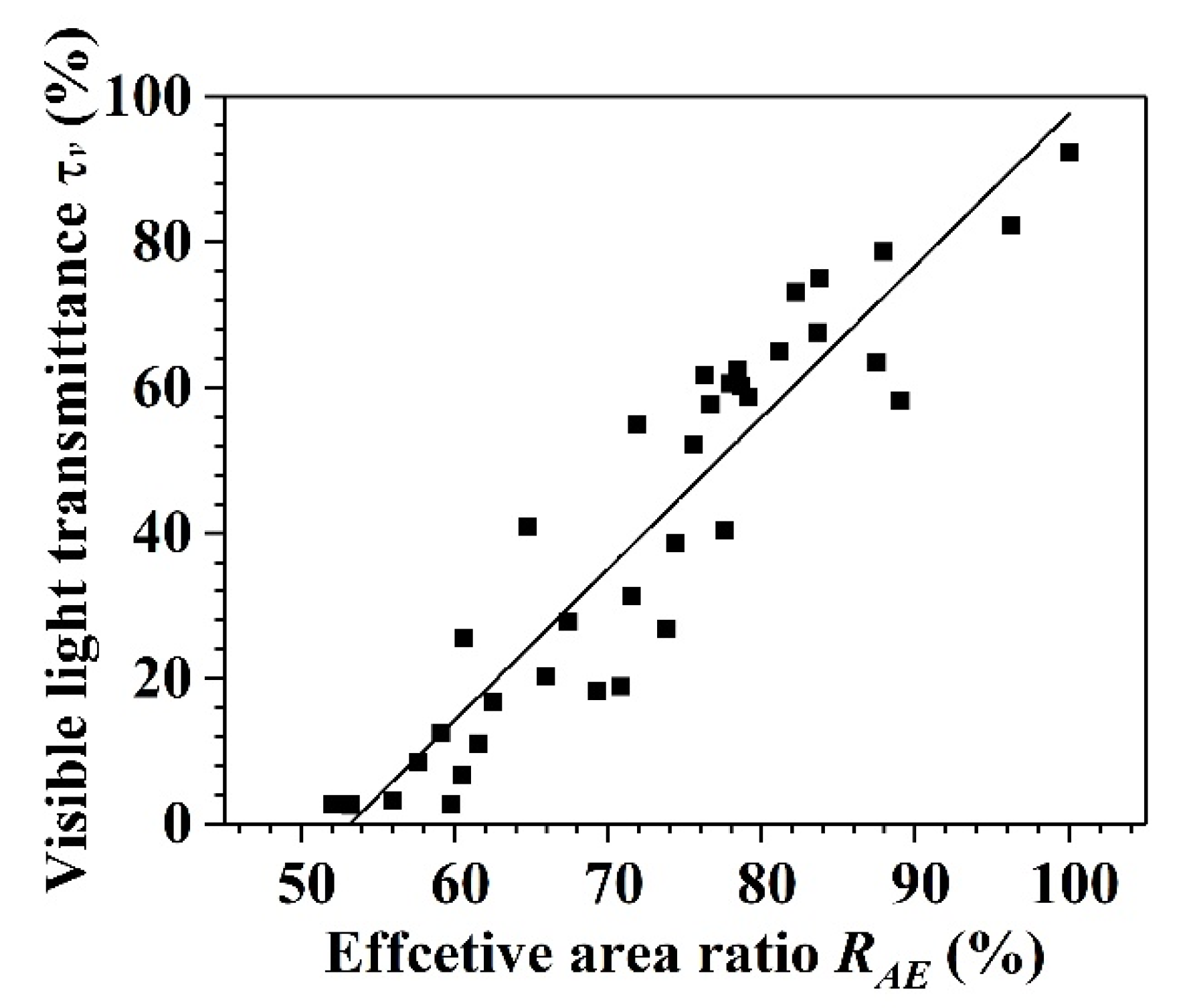
3.5. Relationship between Visible Transmittance and Effective Area Ratio
4. Conclusions
- (1)
- There are three damage modes in the glass panels subject to windblown sand: cutting, smashing, and plastic deformation. At low impact angles, the cutting mode predominates, whereas under high impact angles, the smashing and plastic deformation modes are dominant. In addition, with the growth of the wind force, the impact velocity of the particles increases and the plastic deformation develops better than the smashing mode (brittle damage), owing to the increase in strain rate at high-speed impact.
- (2)
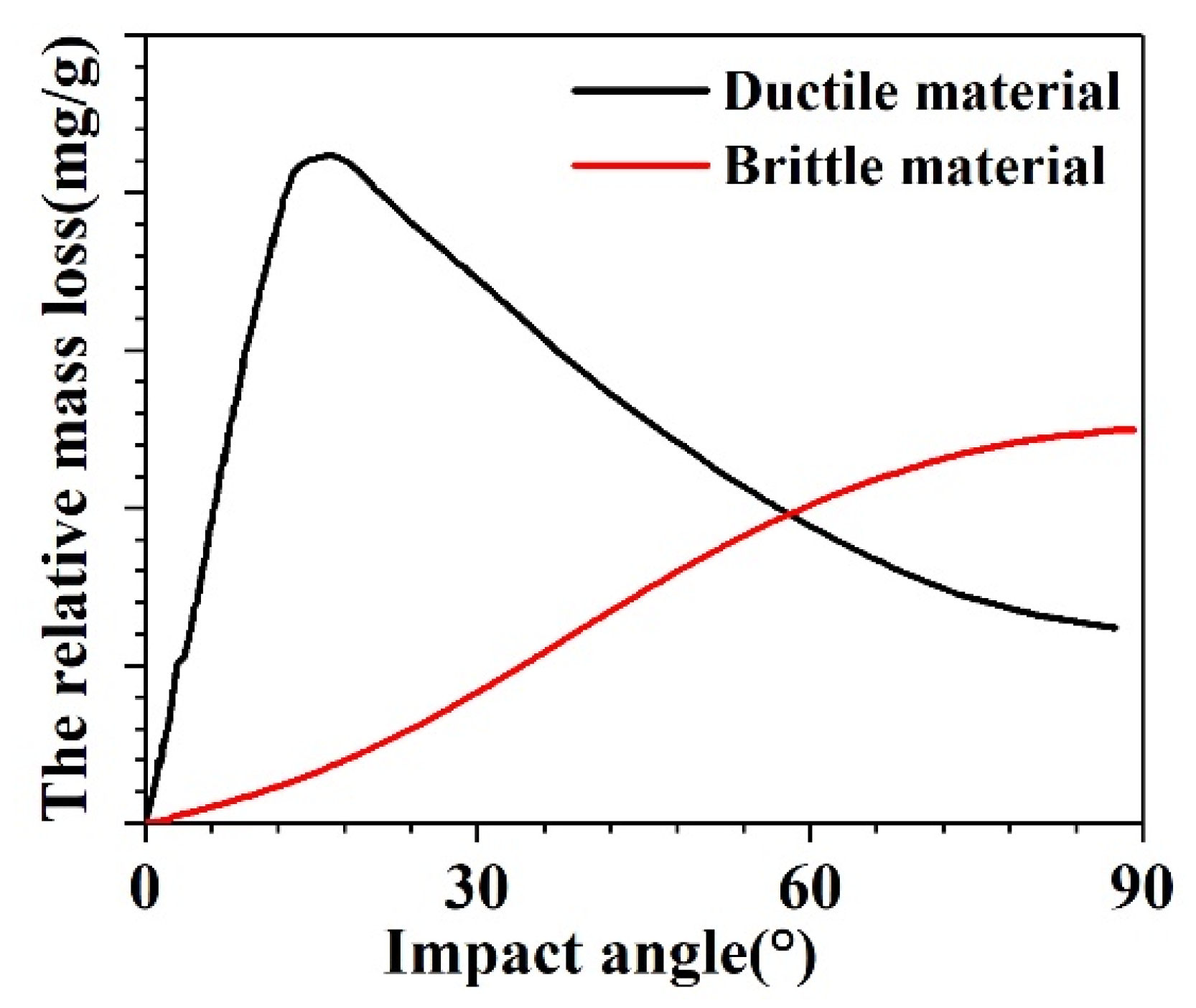
- With an increase in the impact time, the relative mass loss initially decreases and then remains steady. In contrast, with an increase in the impact angle, the relative mass loss initially increases and then decreases, which exhibits the properties of ductile materials.
- (3)
- With increases in the time or impact velocity, the visible light transmittance decreases gradually owing to damage accumulation, as expected.
- (4)
- The tendency of the variation in the effective area ratio under different situations is similar to that of the visible light transmittance. There exists an approximately positive linear relationship between the visible light transmittance and effective area ratio.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.J. Estimation method of sand abrasion in hydraulic structures. J. Hydraul. Eng. 1989, 7, 60–66. [Google Scholar] [CrossRef]
- Wang, Y.P.; Ju, C.C.; Wang, Q.C. Experimental Study on the Solid Particle Erosion of Concrete, Mortar and Cement Paste under Blown Sand Environment. China Railw. Sci. 2013, 34, 21–26. [Google Scholar] [CrossRef]
- Wang, Y.P. Experimental Study on Erosive Wear for Concrete and Protective Materials under Strong Wind-Sand Environment in Northwest. Master’s Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Ju, C.C. Study on the Erosion Wear of Concrete and Protective Material. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2014. [Google Scholar]
- Jiang, N. Experimental Study on Windblown Sand Erosion of Concrete under the Effect of Salt Soaking Erosion. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2016. [Google Scholar]
- Guo, J. Experimental Study on Sand Erosion of Cement Mortar Subjected to Multiple Factors of Freeze-Thaw and Dry-Wet Cycles in Compound Salt Solution. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2017. [Google Scholar]
- Zhang, Y.S. Erosion and Wear Protection Material for Concrete Structure in Strong Wind-Sand Environment. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2019. [Google Scholar]
- Hao, Y.H.; Fan, J.C.; Xing, Y.M.; Jiang, N.; Guo, J.; Liu, Y.C.; Feng, Y.J. Study of Concrete under Salt Freeze-Thaw Cycles and Wind-Blown Sand Erosion by Using Tiguchi Method. J. Build. Mater. 2017, 20, 124–129. [Google Scholar] [CrossRef]
- Hao, Y.H.; Xing, Y.M.; Yang, S.T. Erosion-wear Behavior of Steel Structure Coating Subject to Sandstorm. Tribology 2010, 30, 26–31. [Google Scholar] [CrossRef]
- Li, J. Study on Sand Erosion Resistance of Steel Structure Coatings under Multi-Factors Influence. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2019. [Google Scholar]
- Zhang, B.; Ji, G.J.; Liu, Q.S.; Shi, Z.M. Study on Erosion Behavior of TiO2 Nano Thin Films Coated on Glass by Sandstorm. J. Synth. Cryst. 2016, 45, 1670–1676. [Google Scholar] [CrossRef]
- Zhang, B. Study on the Sand Erosion Behavior of TiO2 Thin Films. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2017. [Google Scholar]
- Yang, S.C.; Li, K.; Duan, Y.X.; Yuan, C. Anti-Wind and Sand Erosion Properties of GF/Unsaturated Polyester Composite. Acta. Mater. Compos. Sin. 2011, 28, 77–82. [Google Scholar] [CrossRef]
- Jiang, J.W.; Shi, M.; Yin, M.Y.; Yu, X.G. Influencing Factors and Mechanism of Erosion Wear of WC-Co Cemented Carbide. China Tungsten Ind. 2020, 35, 48–55. [Google Scholar] [CrossRef]
- Ma, Z.; Li, J.; Yan, C.J.; Li, Z.C. Erosion Wear of Glass-ceramic Composite Coating from Fly Ash. Bull. Chin. Ceram. Soc. 2013, 32, 1684–1687. [Google Scholar] [CrossRef]
- Yuan, R.F. Experimental Study on Erosion Wear Behaviors of Fluoroplastic-Steel Composite Tubes. Master’s Thesis, Zhejiang University, Hangzhou, China, 2018. [Google Scholar]
- Wang, S. High-Speed Erosion Tests on Carbon Fiber Reinforced Polymer Plates. Sci. Technol. Innov. Her. 2020, 17, 106–110. [Google Scholar] [CrossRef]
- Liu, G. Study on the Erosion Wear Behaviors of the GFRP Impacted by Air Flow Containing Sands. Master’s Thesis, Hefei University of Technology, Hefei, China, 2013. [Google Scholar]
- Li, H. Experimental Study and Finite Element Simulation on Sand Erosion of Tempered Glass under Temperature and Humidity Fluctuations and Ultraviolet Rain. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2018. [Google Scholar]
- Fan, J.M.; Fan, C.M.; Wang, J. Erosion Mechanism of Brittle Glass by Micro-Abrasive Water Jet. Diam. Abras. Eng. 2010, 30, 1–5. [Google Scholar]
- Hao, Y.H.; Wu, R.G.; Zhao, C.G.; Guo, X.; Ya, R.H. Effect of Weathering on Erosion Resistance of Toughened Glass Based on Taguchi Method. Bull. Chin. Ceram. Soc. 2020, 39, 2980–2986. [Google Scholar] [CrossRef]
- Zhao, C.G. Experimental Study on the Damage Mechanism of Tempered Glass by Sand Erosio under the Combined Effect of Freeze-Thaw Cycle and Ultraviolet Radiation. Master’s Thesis, Inner Mongolia University of Technology, Hohhot, China, 2018. [Google Scholar]
- Hao, Y.H.; Guo, X.; Zhao, C.G.; Wu, R.G. Mechanics Mechanism of Wind-sand Erosion Damage on Tempered Glass Surface under Combined Freeze-thaw Cycles and Ultraviolet Irradiation. Surf. Technol. 2020, 49, 188–197. [Google Scholar] [CrossRef]
- Bouzid, S.; Azari, Z. Glass Damage by Impact. J. Ningbo Univ. Nat. Sci. Eng. Ed. 2003, 16, 354–362. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=NBDZ200304005&DbName=CJFQ2003 (accessed on 16 October 2020).
- Ismail, J.; Zaïri, F.; Naït-Abdelaziz, M.; Bouzid, S.; Azari, Z. Experimental and numerical investigations on erosion damage in glass by impact of small-sized particles. Wear 2011, 271, 817–826. [Google Scholar] [CrossRef]
- Hao, Y.H.; Li, H.; Ya, R.H.; Zhao, C.G. Erosion Performance and Damage Mechanism of Engineering Glass under the Action of Gas-solid Two-phase Flow. Bull. Chin. Ceram. Soc. 2017, 36. [Google Scholar] [CrossRef]
- Li, Z.P. Research on Simulation and Experiment of Grinding Optical Glass with Single Diamond Girt. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Sheldon, G.; Finnie, I. On the ductile behaviour of nominally brittle materials during erosive cutting. J. Eng. Ind. 1966, 88, 387–392. [Google Scholar] [CrossRef]
- Hao, Y.H.; Ya, R.H.; Liu, Y.L.; Li, H. Erosion damage mechanism analysis of tempered glass in a wind-blown sand environment. In Proceedings of the 2016 2nd International Conference on Energy Equipment Science and Engineering (Advances in Energy Science and Equipment Engineering), Guangzhou, China, 12 November 2016; Volume 2. [Google Scholar]
- GB/T 2680-1994. Determination of Light Transmittance, Solar Direct Transmittance, Total Solar Energy Transmittance and Ultraviolet Transmittance for Glass in Building and Related Glazing Factors; State Bureau of Technical Supervision: Beijing, China, 1994. [Google Scholar]




| Thickness T/mm | Gravity Density γg/(kN/m3) | Initial Visible Transmittance τv0/% | Design Strength fg/(N/mm2) | Modulus of Elasticity Eg/(N/mm2) | Poisson Ratio V |
|---|---|---|---|---|---|
| 6 | 25.6 | 92.34 | 28 | 0.72 × 105 | 0.20 |
| Specimen Type | Specimen Number | Abrasive Feed Rate m (g/s) | Impact Velocities v (m/s) | Impact Angles a (°) | Impact Time t (s) |
|---|---|---|---|---|---|
| Pa | Pa-1-30 | 15.5 | 17.40 | 30 | 0, 30, 60, 90, 120 |
| Pa-1-60 | 15.5 | 17.40 | 60 | ||
| Pa-1-90 | 15.5 | 17.40 | 90 | ||
| Pa-2-30 | 15.0 | 26.34 | 30 | ||
| Pa-2-60 | 15.0 | 26.34 | 60 | ||
| Pa-2-90 | 15.0 | 26.34 | 90 | ||
| Ps | Ps-1-30 | 15.5 | 17.40 | 30 | 0, 2.5, 5, 7.5, 10 |
| Ps-1-60 | 15.5 | 17.40 | 60 | ||
| Ps-1-90 | 15.5 | 17.40 | 90 | ||
| Ps-2-30 | 15.0 | 26.34 | 30 | ||
| Ps-2-60 | 15.0 | 26.34 | 60 | ||
| Ps-2-90 | 15.0 | 26.34 | 90 | ||
| Ps-3-30 | 14.8 | 35.28 | 30 | ||
| Ps-3-60 | 14.8 | 35.28 | 60 | ||
| Ps-3-90 | 14.8 | 35.28 | 90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Liu, R.; Yan, F.; Zhang, D.; Liu, J. Windblown Sand-Induced Degradation of Glass Panels in Curtain Walls. Materials 2021, 14, 607. https://doi.org/10.3390/ma14030607
Zhao Y, Liu R, Yan F, Zhang D, Liu J. Windblown Sand-Induced Degradation of Glass Panels in Curtain Walls. Materials. 2021; 14(3):607. https://doi.org/10.3390/ma14030607
Chicago/Turabian StyleZhao, Yuxi, Rongcheng Liu, Fan Yan, Dawei Zhang, and Junjin Liu. 2021. "Windblown Sand-Induced Degradation of Glass Panels in Curtain Walls" Materials 14, no. 3: 607. https://doi.org/10.3390/ma14030607
APA StyleZhao, Y., Liu, R., Yan, F., Zhang, D., & Liu, J. (2021). Windblown Sand-Induced Degradation of Glass Panels in Curtain Walls. Materials, 14(3), 607. https://doi.org/10.3390/ma14030607






