An 18-Month Analysis of Bond Strength of Hot-Dip Galvanized Reinforcing Steel B500SP and S235JR+AR to Chloride Contaminated Concrete
Abstract
1. Introduction
2. Materials
3. Methods
3.1. Strength Tests—Measuring the Force Pulling Out the Rebar from Concrete
3.2. Optical Tests—Measuring Displacements of Points with the Aramis Camera System
3.3. Electrochemical Testing of Corrosion of Concrete Reinforcement
3.4. 3D Scanning of Ribbed Rebars
4. Results
4.1. Effects of 3D Scanning of Ribbed Rebars
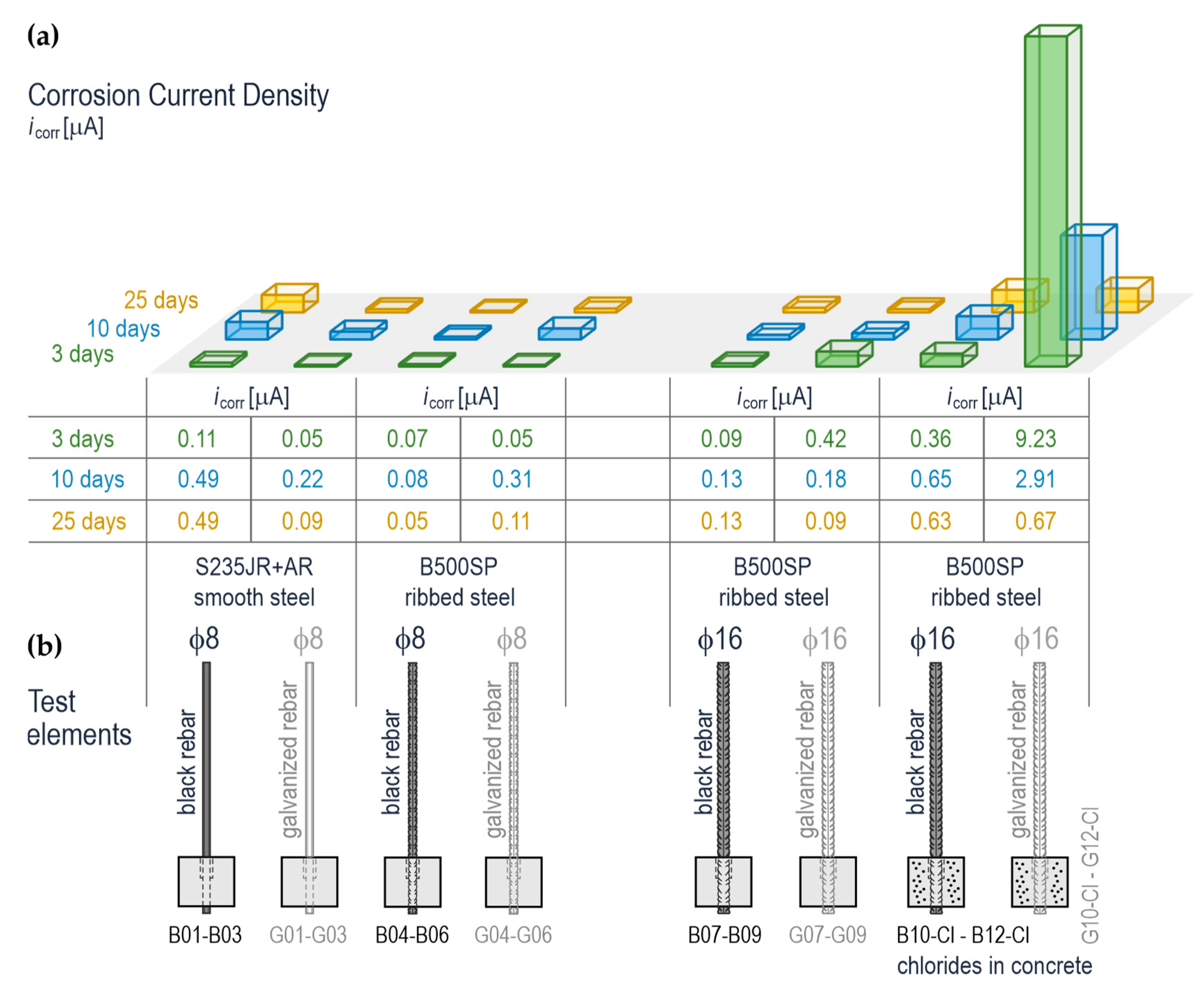
4.2. Test Results for Corrosion Potential of Rebars in Concrete
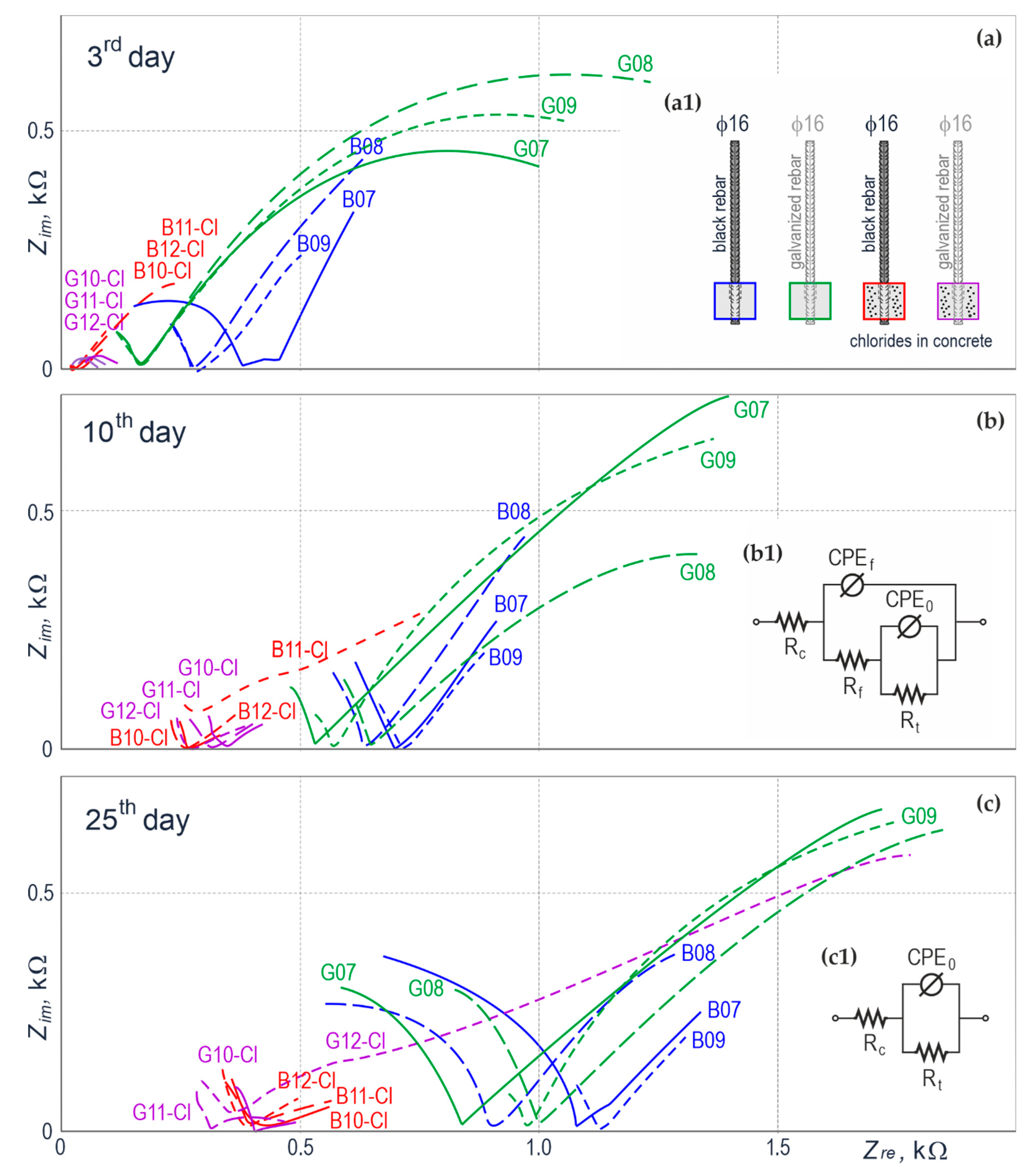
4.3. Impedance Results for Reinforcing Steel in Concrete
4.4. Potentiodynamic Results from Testing Polarization of Reinforcing Steel in Concrete
4.5. Results from Optical Measurements
4.6. Results from Measuring the Force Pulling Out Rebars from Concrete
5. Discussion
5.1. Causes of Failure of Test Elements
5.2. Effect of Selected Parameters on Maximum Bond Stresses
5.3. Evaluation of Anchorage Stiffness of Rebars in Concrete
6. Conclusions
- The failure of all elements with ribbed rebars ϕ8 mm (B500SP) was accompanied by yielding of the reinforcement regardless of the age of the test elements. The presence of zinc coating on the rebars was not significant for the failure.
- Yielding of the elements reinforced with smooth rebars ϕ8 mm (S235JR+AR) was noticed only in the second stage of the tests, that is, after 180 days from their preparation. This observation also refers to the anchorage of galvanized and black steel rebars.
- Yielding of the reinforcement was not found in the case of failure of any test element containing galvanized ribbed rebars ϕ16 mm (B500SP). This fact could not be attributed to the age of the test elements or traces of products from zinc corrosion found after the pull-out of the rebars. This means that the zinc coating on the reinforcement inhibited the full use of mechanical properties of the rebars ϕ16 mm made of steel grade B500SP.
- In the case of the elements with the anchored black steel ribbed rebars ϕ16 mm (B500SP), yielding was observed only for the elements at the age of 180 and 540 days.
- Generally, zinc coating reduced the stiffness of anchorage of ribbed rebars ϕ16 mm (B500SP) This stiffness was reduced even by 15% when the pull-out force was within the range of 0–60 kN.
- However, the chloride-induced corrosion clearly demonstrated its impact on the anchorage stiffness in the final phase of loading. For the same content of chlorides in concrete, the development of corrosion of black steel was considerably more intensive and was related to greater volume of corrosion products on the rebar surface. The products from the corrosion of iron and zinc deposited in concrete pores and filled voids, which caused an increase in the anchorage stiffness in that phase by as much as one order of magnitude.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Time (Day) | fci (MPa) | fcm (MPa) | Ecm (GPa) |
|---|---|---|---|
| 28 | 31.89 | ||
| 28 | 43.09 | ||
| 28 | 40.92 | ||
| 28 | 33.95 | 38.22 | 32.9 |
| 28 | 33.05 | ||
| 28 | 46.42 | ||
| 180 | 58.49 | ||
| 180 | 40.99 | ||
| 180 | 41.75 | ||
| 180 | 51.85 | 47.70 | 39.7 |
| 180 | 53.00 | ||
| 180 | 40.14 | ||
| 540 | 54.64 | ||
| 540 | 55.03 | ||
| 540 | 52.43 | ||
| 540 | 41.54 | 50.16 | 42.2 |
| 540 | 42.24 | ||
| 540 | 55.06 |
| Rebar Diameter (Steel Grade) | Type of Steel Rebar | Fy (kN) | Fy,mean (kN) | εu (%) | Ft (kN) | Ft/Fy |
|---|---|---|---|---|---|---|
| ϕ8 (S235JR+AR) | black smooth | 20.02 | 15 | 24.24 | 1.21 | |
| ϕ8 (S235JR+AR) | black smooth | 19.87 | 15 | 23.89 | 1.20 | |
| ϕ8 (S235JR+AR) | black smooth after pull-out | 20.22 | 14 | 24.45 | 1.21 | |
| ϕ8 (S235JR+AR) | galvanized smooth | 21.58 | 20.92 | 18 | 25.35 | 1.17 |
| ϕ8 (S235JR+AR) | galvanized smooth | 22.08 | 13 | 25.85 | 1.17 | |
| ϕ8 (S235JR+AR) | galvanized smooth after pull-out | 21.73 | 17 | 26.41 | 1.22 | |
| ϕ8 (B500SP) | black ribbed | 23.89 | 18 | 29.98 | 1.25 | |
| ϕ8 (B500SP) | black ribbed | 23.99 | 19 | 29.78 | 1.24 | |
| ϕ8 (B500SP) | black ribbed after pull-out | 25.70 | 8 | 31.29 | 1.22 | |
| ϕ8 (B500SP) | galvanized ribbed | 29.02 | 25.33 | 15 | 32.95 | 1.14 |
| ϕ8 (B500SP) | galvanized ribbed | 22.18 | 12 | 26.21 | 1.18 | |
| ϕ8 (B500SP) | galvanized ribbed after pull-out | 27.21 | 17 | 31.24 | 1.15 | |
| ϕ16 (B500SP) | black ribbed | 116.78 | 11 | 139.49 | 1.19 | |
| ϕ16 (B500SP) | black ribbed | 116.98 | 11 | 139.90 | 1.20 | |
| ϕ16 (B500SP) | black ribbed after pull-out | 115.17 | 10 | 138.29 | 1.20 | |
| ϕ16 (B500SP) | galvanized ribbed | 107.74 | 114.20 | 4 | 117.38 | 1.09 |
| ϕ16 (B500SP) | galvanized ribbed | 108.74 | 6 | 122.21 | 1.12 | |
| ϕ16 (B500SP) | galvanized ribbed after pull-out | 119.80 | 11 | 141.10 | 1.18 |
| Time (Day) | Specimen No. | Rebar Diameter (Steel Grade) (mm) | Fmax (kN) | Fmax,B Fmax,G (kN) | ||
|---|---|---|---|---|---|---|
| 28 | B01 | ϕ8 (S235JR+AR) | 8.47 | 0.43 | 0.38 | |
| 28 | B02 | ϕ8 (S235JR+AR) | 6.11 | 0.31 | 0.27 | 8.86 |
| 28 | B03 | ϕ8 (S235JR+AR) | 12.01 | 0.61 | 0.54 | |
| 28 | G01 | ϕ8 (S235JR+AR) | 7.67 | 0.39 | 0.34 | |
| 28 | G02 | ϕ8 (S235JR+AR) | 7.51 | 0.38 | 0.34 | 7.99 |
| 28 | G03 | ϕ8 (S235JR+AR) | 8.79 | 0.45 | 0.39 | |
| 28 | B04 | ϕ8 (B500SP) | 26.75 | 1.22 | 0.93 | |
| 28 | B05 | ϕ8 (B500SP) | 25.99 | 1.19 | 0.90 | 25.75 |
| 28 | B06 | ϕ8 (B500SP) | 24.51 | 1.12 | 0.85 | |
| 28 | G04 | ϕ8 (B500SP) | 22.61 | 1.03 | 0.79 | |
| 28 | G05 | ϕ8 (B500SP) | 21.56 | 0.98 | 0.75 | 22.48 |
| 28 | G06 | ϕ8 (B500SP) | 23.27 | 1.06 | 0.81 | |
| 28 | B07 | ϕ16 (B500SP) | 85.13 | 0.79 | 0.70 | |
| 28 | B08 | ϕ16 (B500SP) | 98.54 | 0.92 | 0.82 | 93.67 |
| 28 | B09 | ϕ16 (B500SP) | 97.39 | 0.91 | 0.81 | |
| 28 | G07 | ϕ16 (B500SP) | 87.44 | 0.81 | 0.72 | |
| 28 | G08 | ϕ16 (B500SP) | 90.88 | 0.85 | 0.75 | 88.94 |
| 28 | G09 | ϕ16 (B500SP) | 88.49 | 0.82 | 0.73 | |
| 28 | B10-Cl | ϕ16 (B500SP) | 67.33 | 0.63 | 0.56 | |
| 28 | B11-Cl | ϕ16 (B500SP) | 73.08 | 0.68 | 0.60 | 73.11 |
| 28 | B12-Cl | ϕ16 (B500SP) | 78.91 | 0.73 | 0.65 | |
| 28 | G10-Cl | ϕ16 (B500SP) | 73.27 | 0.68 | 0.61 | |
| 28 | G11-Cl | ϕ16 (B500SP) | 75.26 | 0.70 | 0.62 | 75.57 |
| 28 | G12-Cl | ϕ16 (B500SP) | 78.18 | 0.73 | 0.65 | |
| 180 | B13 | ϕ8 (S235JR+AR) | 20.25 | 1.04 | 0.91 | |
| 180 | B14 | ϕ8 (S235JR+AR) | 19.03 | 0.97 | 0.85 | 19.60 |
| 180 | B15 | ϕ8 (S235JR+AR) | 19.51 | 1.00 | 0.88 | |
| 180 | G13 | ϕ8 (S235JR+AR) | 18.81 | 0.96 | 0.84 | |
| 180 | G14 | ϕ8 (S235JR+AR) | 20.11 | 1.03 | 0.90 | 19.69 |
| 180 | G15 | ϕ8 (S235JR+AR) | 20.15 | 1.03 | 0.90 | |
| 180 | B16 | ϕ8 (B500SP) | 21.41 | 0.98 | 0.74 | |
| 180 | B17 | ϕ8 (B500SP) | 22.38 | 1.02 | 0.78 | 22.09 |
| 180 | B18 | ϕ8 (B500SP) | 22.48 | 1.03 | 0.78 | |
| 180 | G16 | ϕ8 (B500SP) | 20.39 | 0.93 | 0.71 | |
| 180 | G17 | ϕ8 (B500SP) | 19.74 | 0.90 | 0.69 | 20.39 |
| 180 | G18 | ϕ8 (B500SP) | 21.04 | 0.96 | 0.73 | |
| 180 | B19 | ϕ16 (B500SP) | 102.35 | 0.95 | 0.85 | |
| 180 | B20 | ϕ16 (B500SP) | 109.74 | 1.02 | 0.91 | 110.46 |
| 180 | B21 | ϕ16 (B500SP) | 119.29 | 1.11 | 0.99 | |
| 180 | G19 | ϕ16 (B500SP) | 90.61 | 0.84 | 0.75 | |
| 180 | G20 | ϕ16 (B500SP) | 92.97 | 0.86 | 0.77 | 92.83 |
| 180 | G21 | ϕ16 (B500SP) | 94.92 | 0.88 | 0.79 | |
| 540 | B22-Cl | ϕ16 (B500SP) | 109.87 | 1.02 | 0.91 | |
| 540 | B23-Cl | ϕ16 (B500SP) | 108.85 | 1.01 | 0.90 | 110.07 |
| 540 | B24-Cl | ϕ16 (B500SP) | 111.48 | 1.04 | 0.92 | |
| 540 | G22-Cl | ϕ16 (B500SP) | 99.80 | 0.93 | 0.83 | |
| 540 | G23-Cl | ϕ16 (B500SP) | 106.91 | 0.99 | 0.88 | 103.78 |
| 540 | G24-Cl | ϕ16 (B500SP) | 104.63 | 0.97 | 0.87 |
Appendix B
| Specimen No. | Δt (Day) | EAg|AgCl (V) | Rc (Ω) | Rf (Ω) | CPEf | Rt (Ω) | CPE0 | icorr | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Yf (Fsα− 1) | αf | Y0 (Fsα−1) | α0 | |||||||
| B07 | 3 | −0.097 | 444 | 2.50 × 104 | 1.18 × 10−2 | 0.715 | 0.01 | |||
| B08 | 3 | −0.173 | 276 | 1.07 × 104 | 4.05 × 10−3 | 0.587 | 0.02 | |||
| B09 | 3 | −0.175 | 290 | 8.68 × 104 | 6.54 × 10−3 | 0.524 | 0.00 | |||
| G07 | 3 | −0.333 | 171 | 1.75 × 103 | 1.70 × 10−3 | 0.655 | 0.24 | |||
| G08 | 3 | −0.292 | 170 | 2.32 × 103 | 1.35 × 10−3 | 0.672 | 0.21 | |||
| G09 | 3 | −0.302 | 174 | 2.01 × 103 | 1.46 × 10−3 | 0.664 | 0.23 | |||
| B10-Cl | 3 | −0.354 | 26 | 28 | 9.34 × 10−3 | 0.551 | 2.30 × 103 | 4.62 × 10−2 | 0.625 | 0.06 |
| B11-Cl | 3 | −0.378 | 24 | 1 | 7.86 × 10 | 0.029 | 1.13 × 103 | 6.86 × 10−3 | 0.588 | 0.24 |
| B12-Cl | 3 | −0.379 | 23 | 11 | 1.19 × 10−2 | 0.526 | 8.88 × 103 | 2.32 × 10−2 | 0.612 | 0.01 |
| G10-Cl | 3 | −0.857 | 27 | 3 | 5.28 × 10−1 | 0.099 | 3.41 × 101 | 2.23 × 10−2 | 0.461 | 9.95 |
| G11-Cl | 3 | −0.880 | 36 | 1 | 5.88 × 10−3 | 0.671 | 3.44 × 101 | 1.43 × 10−2 | 0.527 | 9.48 |
| G12-Cl | 3 | −0.872 | 29 | 33 | 1.48 × 10−2 | 0.619 | 3.28 × 101 | 1.78 × 10−2 | 0.521 | 9.90 |
| B07 | 10 | −0.166 | 701 | 9.71 × 103 | 6.63 × 10−3 | 0.572 | 0.02 | |||
| B08 | 10 | −0.238 | 646 | 6.42 × 103 | 3.70 × 10−3 | 0.634 | 0.03 | |||
| B09 | 10 | −0.207 | 596 | 9.32 × 103 | 3.70 × 10−3 | 0.598 | 0.02 | |||
| G07 | 10 | −0.629 | 538 | 5.06 × 103 | 1.69 × 10−3 | 0.566 | 0.06 | |||
| G08 | 10 | −0.752 | 663 | 1.68 × 103 | 1.80 × 10−3 | 0.602 | 0.23 | |||
| G09 | 10 | −0.713 | 648 | 4.45 × 103 | 1.89 × 10−3 | 0.614 | 0.09 | |||
| B10-Cl | 10 | −0.430 | 257 | 127 | 1.22 × 10−2 | 0.278 | 4.43 × 102 | 1.53 × 10−1 | 0.962 | 0.58 |
| B11-Cl | 10 | −0.853 | 229 | 4949 | 3.04 × 10−4 | 0.653 | 2.01 × 103 | 4.63 × 10−5 | 0.460 | 0.38 |
| B12-Cl | 10 | −0.427 | 130 | 151 | 1.01 × 10−3 | 0.049 | 1.06 × 103 | 1.80 × 10−2 | 0.406 | 0.24 |
| G10-Cl | 10 | −0.686 | 325 | 89 | 3.71 × 10−2 | 0.256 | 8.62 × 101 | 1.65 × 10−1 | 0.873 | 2.85 |
| G11-Cl | 10 | −0.778 | 21 | 2463 | 6.03 × 10−2 | 0.328 | 1.10 × 102 | 5.43 × 10−4 | 0.029 | 2.46 |
| G12-Cl | 10 | −0.830 | 269 | 14 | 1.60 × 10−1 | 0.744 | 5.91 × 101 | 1.45 × 10−2 | 0.504 | 3.29 |
| B07 | 25 | −0.215 | 1066 | 1.40 × 105 | 5.29 × 10−3 | 0.456 | 0.01 | |||
| B08 | 25 | −0.259 | 901 | 4.79 × 10+3 | 3.76 × 10−3 | 0.564 | 0.04 | |||
| B09 | 25 | −0.238 | 1237 | 1.81 × 104 | 5.81 × 10−3 | 0.496 | 0.01 | |||
| G07 | 25 | −0.684 | 838 | 3.88 × 103 | 1.58 × 10−3 | 0.541 | 0.06 | |||
| G08 | 25 | −0.723 | 1011 | 3.28 × 103 | 1.67 × 10−3 | 0.577 | 0.07 | |||
| G09 | 25 | −0.617 | 997 | 3.08 × 103 | 1.97 × 10−3 | 0.507 | 0.08 | |||
| B10-Cl | 25 | −0.388 | 400 | 6261 | 1.24 × 10−2 | 0.276 | 9.73 × 101 | 7.80 × 10−5 | 0.776 | 1.78 |
| B11-Cl | 25 | −0.421 | 372 | 323 | 5.34 × 10−3 | 0.325 | 9.50 × 101 | 4.15 × 10−5 | 1.000 | 1.87 |
| B12-Cl | 25 | −0.396 | 391 | 12 | 4.00 × 10−4 | 0.746 | 3.89 × 102 | 1.92 × 10−2 | 0.506 | 0.40 |
| G10-Cl | 25 | −0.644 | 402 | 94 | 4.73 × 10−3 | 0.402 | 1.79 × 102 | 3.20 × 10−3 | 0.000 | 1.38 |
| G11-Cl | 25 | −0.745 | 229 | 72750 | 6.30 × 10−3 | 0.064 | 1.88 × 102 | 1.19 × 10−4 | 0.833 | 1.23 |
| G12-Cl | 25 | −0.429 | 304 | 1065 | 2.05 × 10−4 | 0.397 | 5.13 × 102 | 6.29 × 10−4 | 0.563 | 0.52 |
References
- Yeih, W.; Huang, R.; Chang, J.J.; Yang, C.C. A pullout test for determining interface properties between rebar and concrete. Adv. Cem. Based Mater. 1997, 5, 57–65. [Google Scholar] [CrossRef]
- Gao, X.; Li, N.; Ren, X. Analytic solution for the bond stress-slip relationship between rebar and concrete. Constr. Build. Mater. 2019, 197, 385–397. [Google Scholar] [CrossRef]
- Desnerck, P.; Lees, J.M.; Morley, C.T. Bond behaviour of reinforcing bars in cracked concrete. Constr. Build. Mater. 2015, 94, 126–136. [Google Scholar] [CrossRef]
- Dybel, P.; Kucharska, M. Development of Bond Strength of Reinforcement Steel in New Generation Concretes. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 052058. [Google Scholar] [CrossRef]
- Ergün, A.; Kürklü, G.; Başpinar, M.S. The effects of material properties on bond strength between reinforcing bar and concrete exposed to high temperature. Constr. Build. Mater. 2016, 112, 691–698. [Google Scholar] [CrossRef]
- Pokorný, P.; Pernicová, R.; Tej, P.; Kolísko, J. Changes of bond strength properties of hot-dip galvanized plain bars with cement paste after 1 year of curing. Constr. Build. Mater. 2019, 226, 920–931. [Google Scholar] [CrossRef]
- Hamad, B.S.; Jumaa, G.K. Bond strength of hot-dip galvanized hooked bars in high strength concrete structures. Constr. Build. Mater. 2008, 22, 2042–2052. [Google Scholar] [CrossRef]
- Kayali, O.; Yeomans, S.R. Bond of ribbed galvanized reinforcing steel in concrete. Cem. Concr. Compos. 2000, 22, 459–467. [Google Scholar] [CrossRef]
- Mianowski, K. Metoda analizy przyczepności i rys w żelbecie. Arch. Inżynierii Lądowej 1990, 36, 81–102. [Google Scholar]
- Leibovich, O.; Yankelevsky, D.Z.; Dancygier, A.N. The effect of local rebar geometry on global strain measurements in pull out tests. Struct. Concr. 2020, 21, 413–427. [Google Scholar] [CrossRef]
- Edwards, A.; Yannopoulos, P.T. Local bond-stress to slip relationships for hot rolled deformed bars and mild steel palin rebars. J. ACI 1979, 67, 405–420. [Google Scholar]
- Stefanoni, M.; Angst, U.; Elsener, B. Corrosion rate of carbon steel in carbonated concrete—A critical review. Cem. Concr. Res. 2018, 103, 35–48. [Google Scholar] [CrossRef]
- Cao, C. 3D simulation of localized steel corrosion in chloride contaminated reinforced concrete. Constr. Build. Mater. 2014, 72, 434–443. [Google Scholar] [CrossRef]
- Stefanoni, M.; Angst, U.; Elsener, B. Local electrochemistry of reinforcement steel—Distribution of open circuit and pitting potentials on steels with different surface condition. Corros. Sci. 2015, 98, 610–618. [Google Scholar] [CrossRef]
- Ji, Y.S.; Zhao, W.; Zhou, M.; Ma, H.R.; Zeng, P. Corrosion current distribution of macrocell and microcell of steel bar in concrete exposed to chloride environments. Constr. Build. Mater. 2013, 47, 104–110. [Google Scholar] [CrossRef]
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction—A review. Cem. Concr. Compos. 2003, 25, 459–471. [Google Scholar] [CrossRef]
- Liu, X.; Niu, D.; Li, X.; Lv, Y.; Fu, Q. Pore solution pH for the corrosion initiation of rebars embedded in concrete under a long-term natural carbonation reaction. Appl. Sci. 2018, 8, 128. [Google Scholar] [CrossRef]
- Jaśniok, T.; Zybura, A. The course of the polarization process during elekctrochemical tests on reinforcement corrosion. Arch. Civ. Eng. 2007, 53, 109–129. [Google Scholar]
- Jaśniok, M.; Kołodziej, J. Testing with EIS technique to compare the effect of alkaline pH of concrete pore solution on rebars with or without zinc coating. Ochr. Przed Korozją 2016, 59, 170–174. [Google Scholar] [CrossRef]
- Jaśniok, M.; Kołodziej, J.; Dudek, M. Assessing effects of chloride-induced corrosion of galvanized reinforcing steel in cement mortar, using impedance spectroscopy and scanning microscopy. Ochr. przed Korozją 2018, 61, 176–181. [Google Scholar] [CrossRef]
- Dong, S.; Zhao, B.; Lin, C.; Du, R.; Hu, R.; Zhang, G.X. Corrosion behavior of epoxy/zinc duplex coated rebar embedded in concrete in ocean environment. Constr. Build. Mater. 2012, 28, 72–78. [Google Scholar] [CrossRef]
- Kołodziej, J.; Jaśniok, M. Polarization tests concerning chloride impact on protective zinc coatings applied on reinforcing steel in curing concrete. Ochr. Przed Korozją 2017, 60, 330–334. [Google Scholar] [CrossRef]
- Figueira, R.M.; Pereira, E.V.; Silva, C.J.R.; Salta, M.M. Corrosion protection of hot dip galvanized steel in mortar. Port. Electrochim. Acta 2013, 31, 277–287. [Google Scholar] [CrossRef]
- Bertola, F.; Canonico, F.; Irico, S. Innovative technology constituted of sulfoaluminate cement-based concrete and non corrosive reinforcement to produce durable and sustainable reinforced concretes. In Proceedings of the 15th International Congress on the Chemistry of Cement, Prague, Czech Republic, 16–20 September 2019. [Google Scholar]
- Dallin, G.; Gagné, M.; Goodwin, F.; Pole, S. Continuously Galvanized Reinforcing Steel; American Concrete Institute: Kansas City, MO, USA, 2015. [Google Scholar]
- Sistonen, E.; Cwirzen, A.; Puttonen, J. Corrosion mechanism of hot-dip galvanised reinforcement bar in cracked concrete. Corros. Sci. 2008, 50, 3416–3428. [Google Scholar] [CrossRef]
- Tittarelli, F.; Mobili, A.; Maria Vicerè, A.; Roventi, G.; Bellezze, T. Effect of the Type of Surface Treatment and Cement on the Chloride Induced Corrosion of Galvanized Reinforcements. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 022088. [Google Scholar] [CrossRef]
- FIB Bulletin 49 Corrosion Protection of Reinforcing Steels—Technical Report 2009; FIB: Lausanne, Switzerland, 2009.
- Yeomans, S.R. Galvanized Steel Reinforcement in Concrete: An Overview; Elsevier Science: New York, NY, USA, 2004. [Google Scholar]
- Pokorný, P.; Tej, P.; Kouřil, M. Evaluation of the impact of corrosion of hot-dip galvanized reinforcement on bond strength with concrete—A review. Constr. Build. Mater. 2017, 132, 271–298. [Google Scholar] [CrossRef]
- Tepfers, R. Cracking of concrete cover along anchored deformed reinforcing bars. Mag. Concr. Res. 1979, 31, 3–12. [Google Scholar] [CrossRef]
- Pereira, H.F.S.G.; Cunha, V.M.C.F.; Sena-Cruz, J. Numerical simulation of galvanized rebars pullout. Frat. Integrita Strutt. 2015, 31, 54–66. [Google Scholar] [CrossRef]
- Goto, Y. Cracks formed in concrete around deformed tension bars. ACI J. 1971, 68, 244–251. [Google Scholar]
- Lin, H.; Zhao, Y.; Feng, P.; Ye, H.; Ozbolt, J.; Jiang, C.; Yang, J.Q. State-of-the-art review on the bond properties of corroded reinforcing steel bar. Constr. Build. Mater. 2019, 213, 216–233. [Google Scholar] [CrossRef]
- Blomfors, M.; Zandi, K.; Lundgren, K.; Coronelli, D. Engineering bond model for corroded reinforcement. Eng. Struct. 2018, 156, 394–410. [Google Scholar] [CrossRef]
- Chinn, J.; Ferguson, P.M.; Thompson, J.N. Lapped splices in reinforced concrete beams. J. Am. Concr. Inst. 1955, 27, 201–214. [Google Scholar]
- Manfredi, G.; Pecce, M. Behaviour of bond between concrete and steel in a large post-yelding field. Mater. Struct. Matériaux Constr. 1996, 29, 506–513. [Google Scholar] [CrossRef]
- Jaśniok, M.; Sozańska, M.; Kołodziej, J.; Chmiela, B. A Two-Year Evaluation of Corrosion-Induced Damage to Hot Galvanized Reinforcing Steel B500SP in Chloride Contaminated Concrete. Materials 2020, 13, 3315. [Google Scholar] [CrossRef]
- Tepfers, R. Lapped tensile reinforcement splices. J. Struct. Div. Proc. Am. Soc. Civ. Eng. 1982, 108, 283–301. [Google Scholar]
- Law, D.W.; Molyneaux, T.C.K. Impact of corrosion on bond in uncracked concrete with confined and unconfined rebar. Constr. Build. Mater. 2017, 155, 550–559. [Google Scholar] [CrossRef]
- Li, F.; Yuan, Y. Effects of corrosion on bond behavior between steel strand and concrete. Constr. Build. Mater. 2013, 38, 413–422. [Google Scholar] [CrossRef]
- Coccia, S.; Imperatore, S.; Rinaldi, Z. Influence of corrosion on the bond strength of steel rebars in concrete. Mater. Struct. Constr. 2016, 49, 537–551. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y.; Yang, J.Q.; Feng, P.; Ozbolt, J.; Ye, H. Effects of the corrosion of main bar and stirrups on the bond behavior of reinforcing steel bar. Constr. Build. Mater. 2019, 225, 13–28. [Google Scholar] [CrossRef]
- Bilcik, J.; Holly, I. Effect of reinforcement corrosion on bond behaviour. Procedia Eng. 2013, 65, 248–253. [Google Scholar] [CrossRef]
- EN 1766 Eurocode: Products and Systems for the Protection and Repair of Concrete Structures—Test Methods—Reference Concretes for Testing; CEN-CENELEC: Brussels, Belgium, 2017.
- EN 1992-1-1. Eurocode 2: Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings; CEN-CENELEC: Brussels, Belgium, 2008.
- Ferguson, P.; Thompson, J. Development length of high strength reinforcing bars in bond. J. Am. Concr. Inst. 1962, 59, 887–992. [Google Scholar]
- Volk, W. Applied Statistics for Engineers; McGraw-Hill, Inc.: New York, NY, USA, 1969. [Google Scholar]






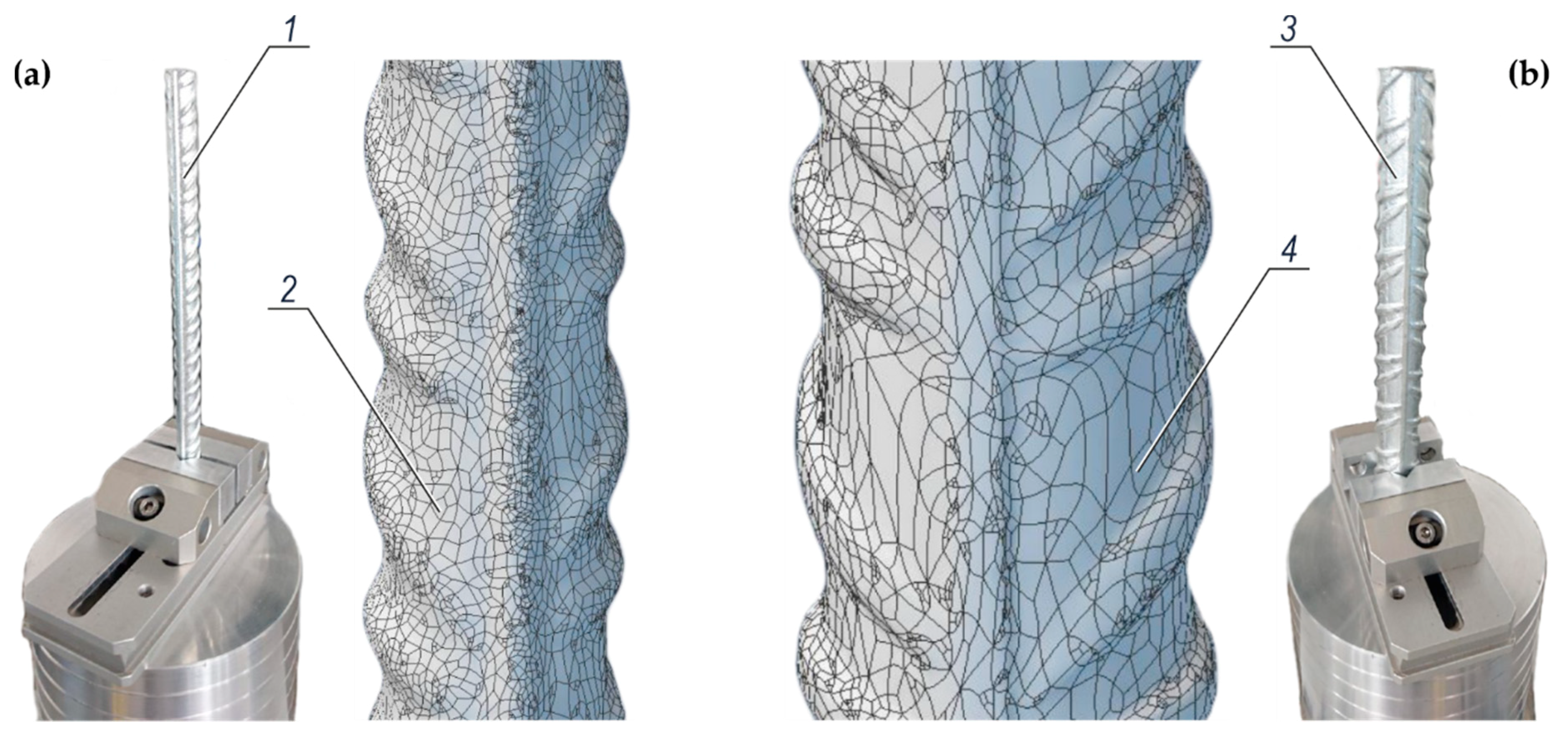








| Steel Grade | C | Mn | Si | P | S | Cu | N |
|---|---|---|---|---|---|---|---|
| B500SP | 0.24% | 1.65% | 0.60% | 0.06% | 0.06% | 0.85% | 0.01% |
| S235JR+AR | 0.17% | 1.40% | – | 0.045% | 0.045% | – | 0.009% |
| Rebar Diameter (Steel Grade) (mm) | (KN) | (KN) | (KN) | S (kN) |
|---|---|---|---|---|
| ϕ8 (S235JR+AR) | 20.92 | 19.56 | 22.26 | 0.98 |
| ϕ8 (B500SP) | 25.33 | 21.91 | 28.75 | 2.49 |
| ϕ16 (B500SP) | 114.20 | 107.52 | 120.52 | 4.86 |
| Time of Test (Day) | Fmax,B (kN) | Fmax,G (kN) | Fmax,B (kN) | Fmax,G (kN) | Fmax,B (kN) | Fmax,G (kN) | Fmax,B (kN) | Fmax,G (kN) |
|---|---|---|---|---|---|---|---|---|
| 28 | 8.86 | 7.99 | 25.75 (y) | 22.48 (y) | 93.67 | 88.94 | 73.11 | 75.57 |
| 180 | 19.60 (y) | 19.69 (y) | 22.09 (y) | 20.39 | 110.46 (y) | 92.83 | ||
| 540 | 110.17 (y) | 103.78 | ||||||
| Rebar (steel grade) | ϕ8 (S235JR+AR) smooth steel | ϕ8 (B500SP) ribbed steel | ϕ16 (B500SP) ribbed steel | ϕ16 (B500SP) ribbed steel + Cl | ||||
| Time of Test (Day) | fb,max,B (MPa) | fb,max,G (MPa) | fb,max,B (MPa) | fb,max,G (MPa) | fb,max,B (MPa) | fb,max,G (MPa) | fb,max,B (MPa) | fb,max,G (MPa) |
|---|---|---|---|---|---|---|---|---|
| 28 | 5.04 | 4.54 | 14.64 (y) | 12.78 (y) | 26.62 | 25.82 | 20.78 | 21.48 |
| 180 | 11.40 (y) | 19.69 (y) | 12.56 (y) | 11.59 | 31.39 (y) | 26.38 | ||
| 540 | 31.30 (y) | 29.49 | ||||||
| Rebar (steel grade) | ϕ8 (S235JR+AR) smooth steel | ϕ8 (B500SP) ribbed steel | ϕ16 (B500SP) ribbed steel | ϕ16 (B500SP) ribbed steel + Cl | ||||
| Rebar Diameter (Steel Grade) (mm) | fb,y,mean (MPa) | Minimum Value of Confidence Interval (MPa) | Maximum Value of Confidence Interval (MPa) |
|---|---|---|---|
| ϕ8 (S235JR+AR) | 11.89 | 11.12 | 12.65 |
| ϕ8 (B500SP) | 14.40 | 12.45 | 16.34 |
| ϕ16 (B500SP) | 32.46 | 30.56 | 34.25 |
| Specimens | 0.9 Fmax (kN) | Fmax (kN) | s (60 kN) (mm) | s (0.9 Fmax) (mm) | s (Fmax) (mm) | k (0–60 kN) (kN/mm) | k (0.9–1.0) Fmax (kN/mm) |
|---|---|---|---|---|---|---|---|
| B19 | 92.12 | 102.35 | 0.30 | 0.64 | 1.07 | 197.70 | 23.54 |
| B21 | 107.36 | 119.29 | 0.31 | 1.27 | 1.96 | 193.70 | 17.32 |
| G20 | 83.68 | 92.97 | 0.36 | 0.66 | 1.49 | 166.32 | 11.22 |
| G21 | 85.43 | 94.92 | 0.36 | 0.72 | 1.37 | 166.34 | 14.57 |
| B23-Cl | 97.97 | 108.86 | 0.31 | 0.59 | 0.69 | 194.72 | 104.23 |
| B24-Cl | 100.27 | 111.41 | 0.37 | 0.66 | 0.75 | 164.07 | 130.32 |
| G22-Cl | 89.82 | 99.8 | 0.30 | 0.57 | 0.67 | 200.00 | 96.04 |
| G24-Cl | 94.17 | 104.63 | 0.37 | 0.49 | 0.56 | 167.07 | 171.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaśniok, M.; Kołodziej, J.; Gromysz, K. An 18-Month Analysis of Bond Strength of Hot-Dip Galvanized Reinforcing Steel B500SP and S235JR+AR to Chloride Contaminated Concrete. Materials 2021, 14, 747. https://doi.org/10.3390/ma14040747
Jaśniok M, Kołodziej J, Gromysz K. An 18-Month Analysis of Bond Strength of Hot-Dip Galvanized Reinforcing Steel B500SP and S235JR+AR to Chloride Contaminated Concrete. Materials. 2021; 14(4):747. https://doi.org/10.3390/ma14040747
Chicago/Turabian StyleJaśniok, Mariusz, Jacek Kołodziej, and Krzysztof Gromysz. 2021. "An 18-Month Analysis of Bond Strength of Hot-Dip Galvanized Reinforcing Steel B500SP and S235JR+AR to Chloride Contaminated Concrete" Materials 14, no. 4: 747. https://doi.org/10.3390/ma14040747
APA StyleJaśniok, M., Kołodziej, J., & Gromysz, K. (2021). An 18-Month Analysis of Bond Strength of Hot-Dip Galvanized Reinforcing Steel B500SP and S235JR+AR to Chloride Contaminated Concrete. Materials, 14(4), 747. https://doi.org/10.3390/ma14040747







