Shock Absorbers Damping Characteristics by Lightweight Drop Hammer Test for Naval Machines
Abstract
1. Introduction
- evaluation of existing test data and procedures to confirm validation and verification of current and anticipated new M&S capabilities.
- UNDEX impulse response to water, i.e., a description of the propagation of the pressure impulse in water and its impact on the immersed area of the ship.
- Structural response of the ship’s hull to the UNDEX impulse.
- The reaction of the tested component in the form of anticipated vibrations and potential damage [5].
2. Materials and Methods
2.1. Shock Machine Stands
- Heavyweight shock machine. The heavyweight test is a test performed on a standard or large floating shock platform without restrictions on the maximum weight of the tested device.
- Medium weight shock machine. Weight of the tested equipment including all fixings necessary to attach it to the test machine should be less than 3356.5 kg.
- Lightweight shock machine. Weight of the tested item including all fixings necessary to attach it to the test machine should be less than 249.5 kg.
2.1.1. Construction of a Lightweight Shock Machine
2.1.2. Methodology of the Shock Tests
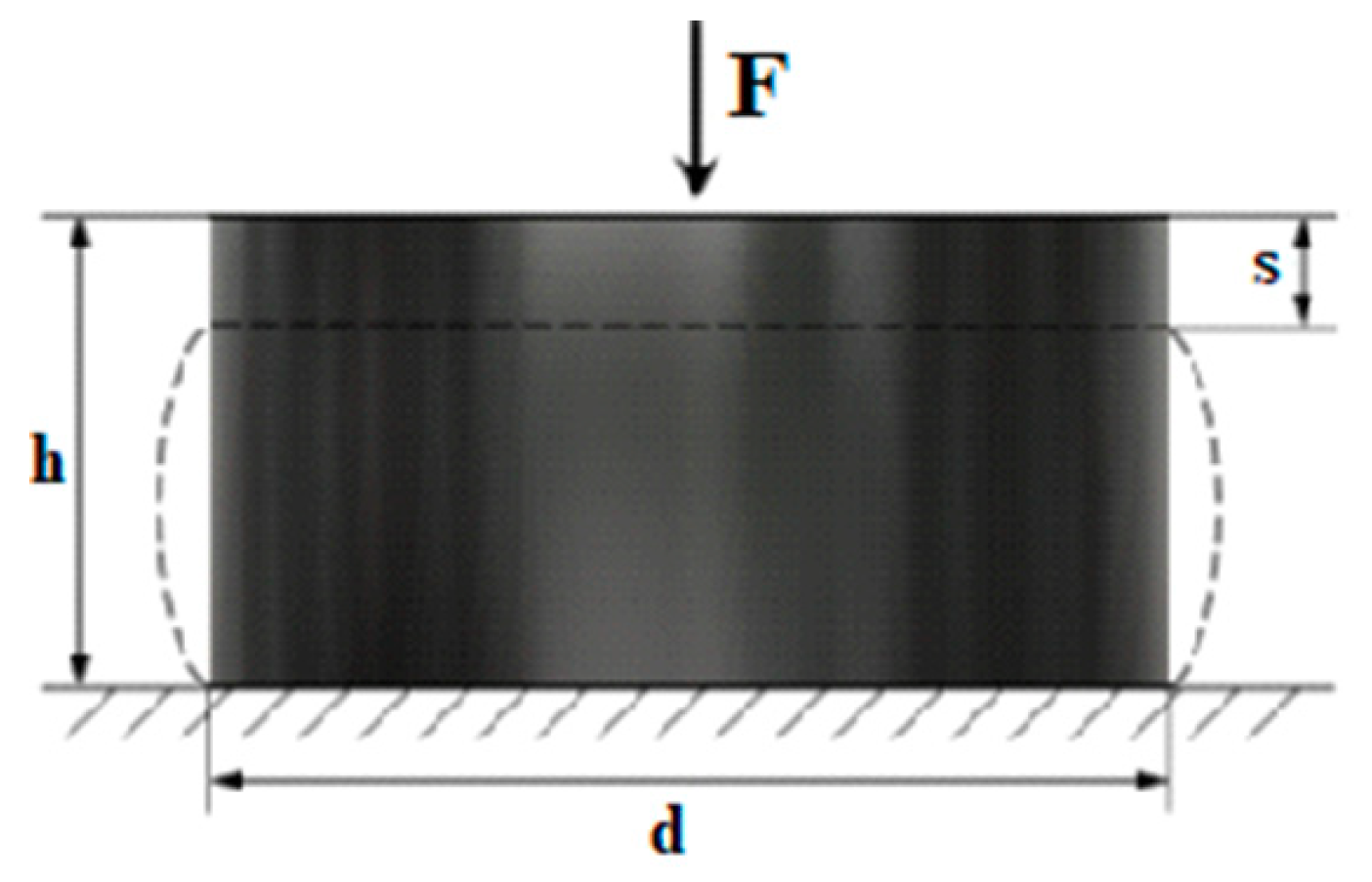
2.2. Tensile Testing of the Shock Absorbers
- CR—rubber based on chloroprene rubber,
- EPDM (ethylene propylene diene monomer)—rubber cross-linked in the process of sulfur vulcanization,
- NBR (nitrile rubber)—commonly known as oil-resistant rubber, i.e., a copolymer of butadiene and acrylonitrile,
- NR—natural rubber, also called rubber, is a flexible hydrocarbon polymer,
- PU—polyurethane is a polymer, which contains the urethane group NH-CO-O formed by combining hard (isocyanate) and elastic (polyol) parts.
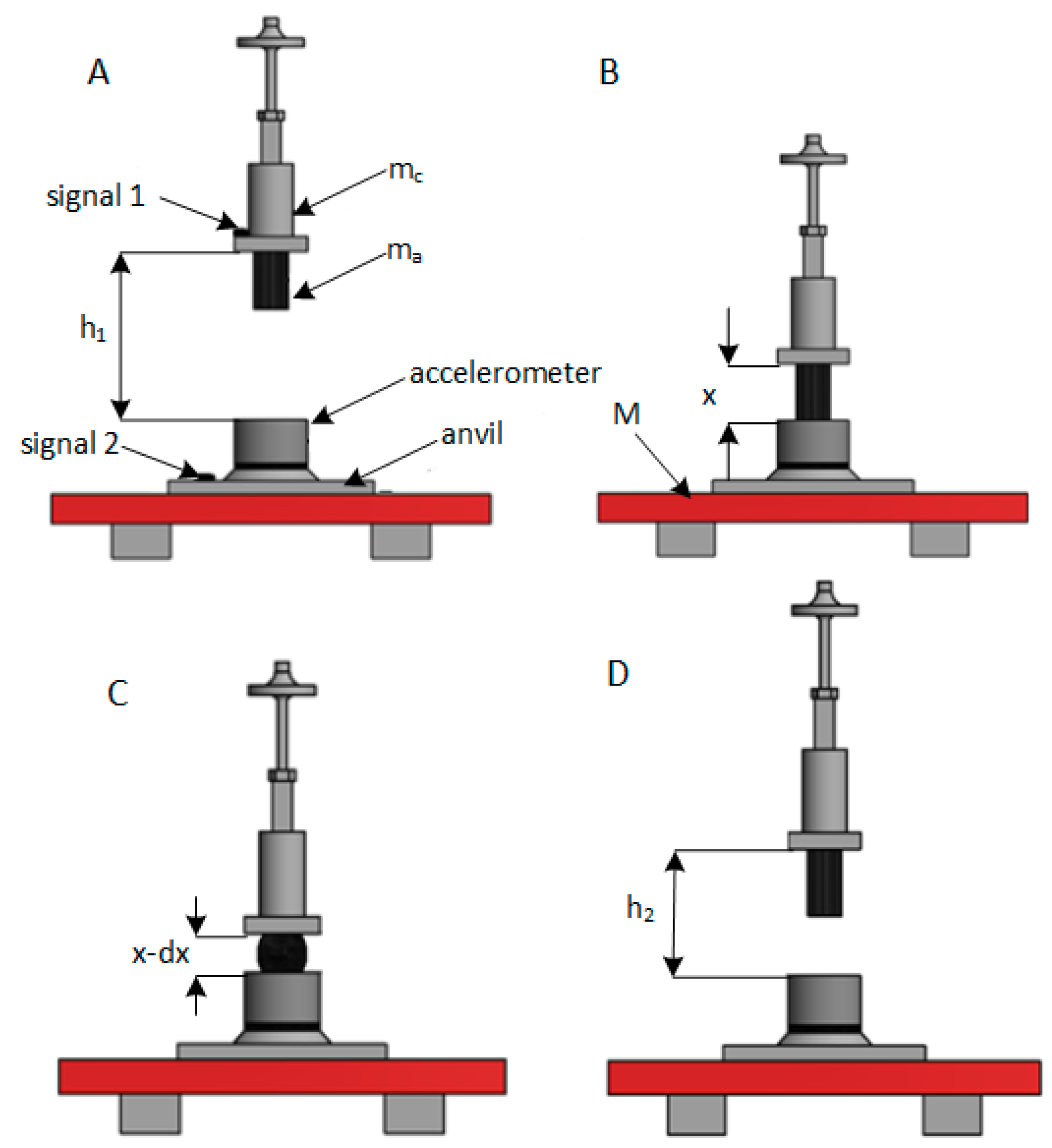
2.3. Hammer Testing of Shock Absorbers
- no air resistance,
- the shock absorber base is in parallel contact with the M foundation,
- the acceleration of the mass of the anvil is neglected due to its significantly greater mass
- anvil is completely rigid bod.
- k—the elasticity of the shock absorber is assumed to be linear (Hooke’s law for small drop height in which deflection of absorbers do not exceed 20% of their initial height)
- c—suppression as dissipation of all forms of energy.
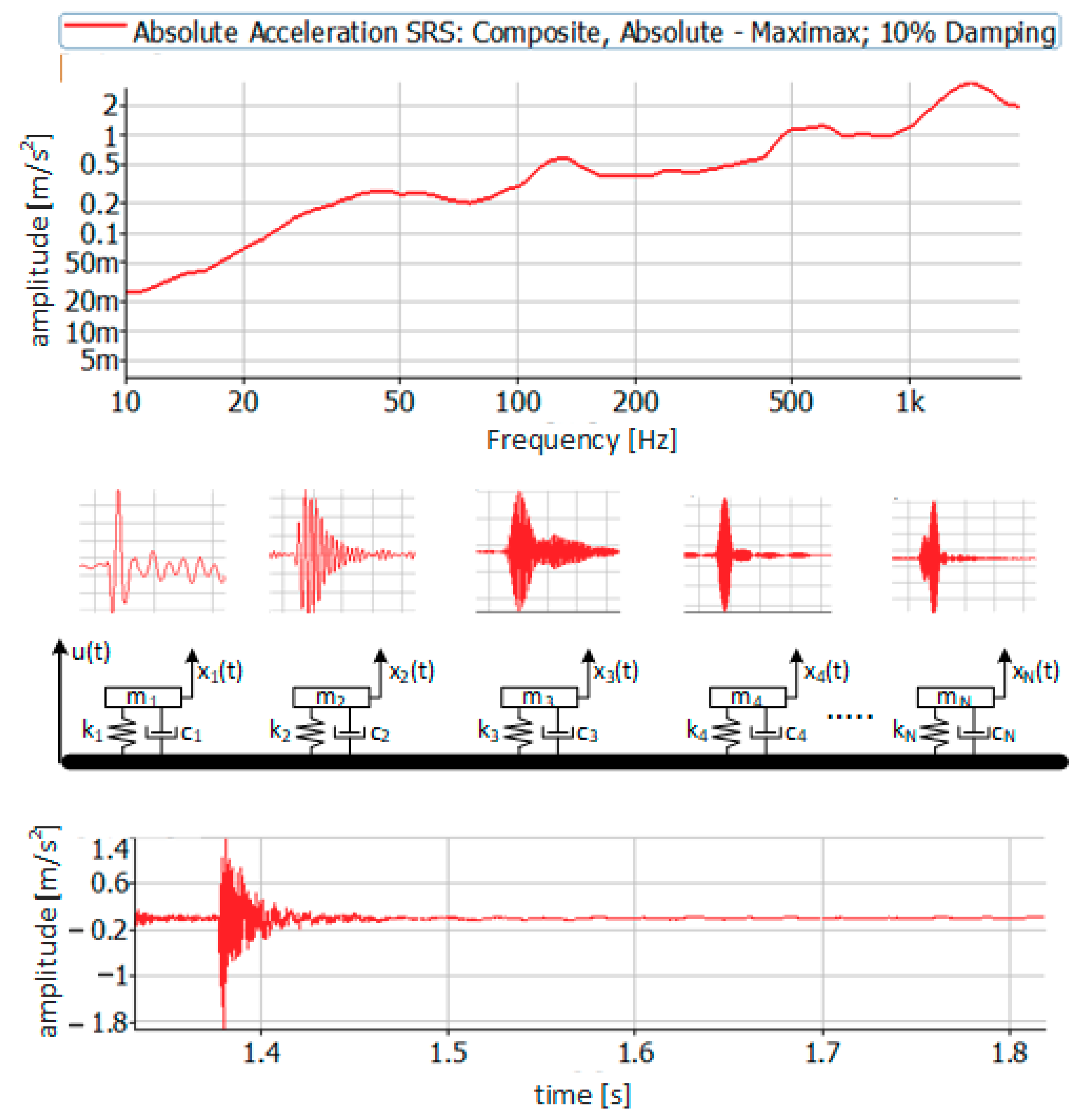
2.4. Shock Response Spectrum as a Tool of Damping Determination
3. Results
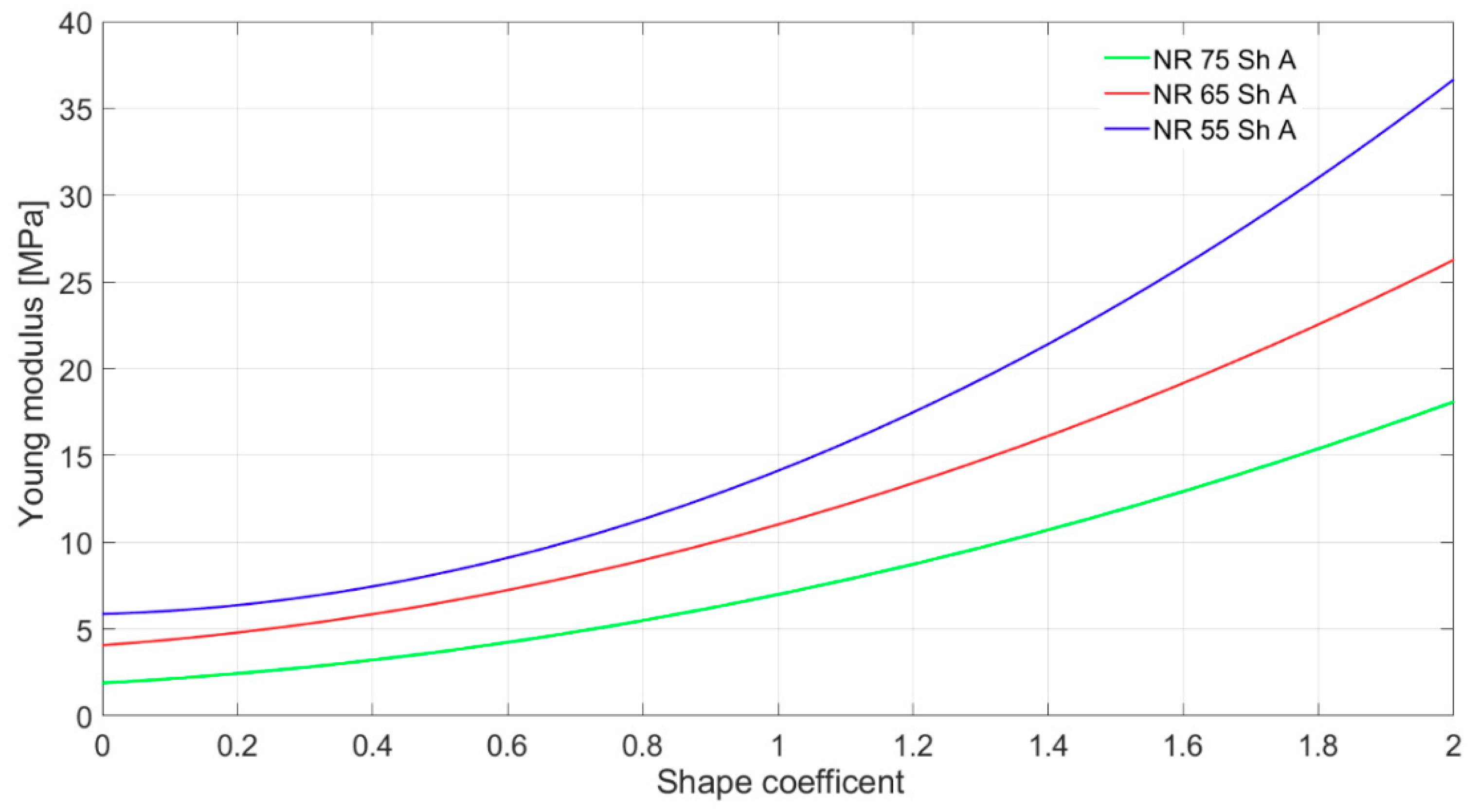
3.1. Tensile Testing of Shock Absorbers
3.2. Hammer Testing of Shock Absorbers
3.3. Shock Response Spectrum as a Tool of Damping Determination
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Michael, R.R.; Haupt, K.D.; Ganey, D.H.C.N.; Coats, D.T.W. Laboratory Test Requirements for Marine Shock Isolation Seats; Naval Surface Warfare Center Carderock Division: West Bethesda, MD, USA, 2018. [Google Scholar]
- Alexander, J.E. Shock Response Spectrum-A Primer. Sound Vib. 2009, 43, 6–15. [Google Scholar]
- Cao, L.; Fei, W.; Grosshans, H.; Cao, N. Simulation of Underwater Explosions Initiated by High-Pressure Gas Bubbles of Various Initial Shapes. Appl. Sci. 2017, 7, 880. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Wang, G.X.; Wang, Y. Numerical Modeling of Dual-Pulse Shock Test Machine for Simulating Underwater Explosion Shock Loads on Warship Equipments. J. Shanghai Jiaotong Univ. Sci. 2009. [Google Scholar] [CrossRef]
- Grzadziela, A.; Szturomski, B. Impact Modeling of Underwater Explosion. Solid State Phenom. 2013, 196, 51–61. [Google Scholar] [CrossRef]
- Szturomski, B.; Grzc Adziela, A.; Kiciński, R. Analysis of the Pressure Wave Parameters Caused by TNT Underwater Explosion Forced on the Hull of Minehunter. J. Vibroeng. 2014, 16, 4107–4125. [Google Scholar]
- Tappu, A.L.; Sen, A.K.; Lele, M.M. Design Sensitivity Analysis of Raft Foundation for Marine Engines and Machinery in Warships. Int. J. Eng. Res. Appl. 2013, 3, 1200–1206. [Google Scholar]
- Kumar, Y.P. On Shock Response of Marine Sandwich Structures Subjected to UNDEX Loading. Procedia Eng. 2017, 173, 1932–1942. [Google Scholar] [CrossRef]
- Reid, W. The Response of Surface Ships to Underwater Explosions; Defence Science and Technology Organization: Melbourne, Australia, 1996. [Google Scholar]
- Cordes, J.A.; Vo, P.; Lee, J.R.; Geissler, D.W.; Metz, J.D.; Troast, D.C.; Totten, A.L. Comparison of Shock Response Spectrum for Different Gun Tests. Shock Vib. 2013. [Google Scholar] [CrossRef]
- Grzadziela, A.; Szturomski, B.; Kluczyk, M. Diagnosis Design of Ship Hull Strength of Treated by Dynamic Load. Diagnostyka 2013, 14, 23–30. [Google Scholar]
- Shock Tests. High Impact Shipboard Machinery. Equipment and Systems Requirenmts For; MIL-S 901D (NAVY); US Information Systems Inc.: Pearl River, NY, USA, 1963. [Google Scholar]
- Grządziela, A. Model of impact underwater detonation. J. KONES Powertrain Transp. 2012, 19, 191–199. [Google Scholar] [CrossRef]
- Rubber, Vulcanized or Thermoplastic—Determination of Hardness—Part 4: Indentation Hardness by Durometer Method (Shore Hardness); ISO 48-4:2018; International Organization for Standardization: Geneva, Swiss, 2008.
- Irvine, T. An Introduction to the Shock Response Spectrum. Available online: file:///C:/Users/MDPI/AppData/Local/Temp/AN%20INTRODUCTION%20TO%20THE%20SHOCK%20RESPONSE%20SPECTRUM.pdf (accessed on 4 February 2021).
- Tuma, J.; Babiuch, M.; Koci, P. Calculation of a Shock Response Spectra. Acta Montan. Slovaca 2011, 16, 66–73. [Google Scholar]
- Alexander, J.E. A New Method To Synthesize a Shock Response Spectrum. In Partial Fulfillment of The Requirements for the Degree of Doctor of Philosophy; University Of Minnesota: Twin Cities, MN, USA, 2015. [Google Scholar]
- Zhang, M.; Drikakis, D.; Li, L.; Yan, X. Machine-Learning Prediction of Underwater Shock Loading on Structures. Computation 2019, 7, 58. [Google Scholar] [CrossRef]
- Yan, Y.; Li, Q.M. Low-Pass-Filter-Based Shock Response Spectrum and the Evaluation Method of Transmissibility between Equipment and Sensitive Components Interfaces. Mech. Syst. Signal Process. 2019. [Google Scholar] [CrossRef]
- Loo, M.S.; Le Cam, J.B.; Andriyana, A.; Robin, E. Inelastic Responses of Swollen Nitrile Rubber under Cyclic Loading. Rubber Chem. Technol. 2018. [Google Scholar] [CrossRef]
- Lasowicz, N.; Jankowski, R. Investigation of Behaviour of Metal Structures with Polymer Dampers under Dynamic Loads. Procedia Eng. 2017, 199, 2832–2837. [Google Scholar] [CrossRef]
- Merabia, S.; Sotta, P.; Long, D.R. Unique Plastic and Recovery Behavior of Nanofilled Elastomers and Thermoplastic Elastomers (Payne and Mullins Effects). J. Polym. Sci. Part B Polym. Phys. 2010, 48, 1495–1508. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Medvedev, G.A.; Caruthers, J.M. Time-Dependent Mechanical Behavior of Carbon Black Filled Elastomers. Rubber Chem. Technol. 2011. [Google Scholar] [CrossRef]
- Wei, W.; Yuan, Y.; Gao, X. Effects of Large Deformation and Velocity Impacts on the Mechanical Behavior of Filled Rubber: Microstructure-Based Constitutive Modeling and Mechanical Testing. Polymers 2020, 12, 2322. [Google Scholar] [CrossRef] [PubMed]


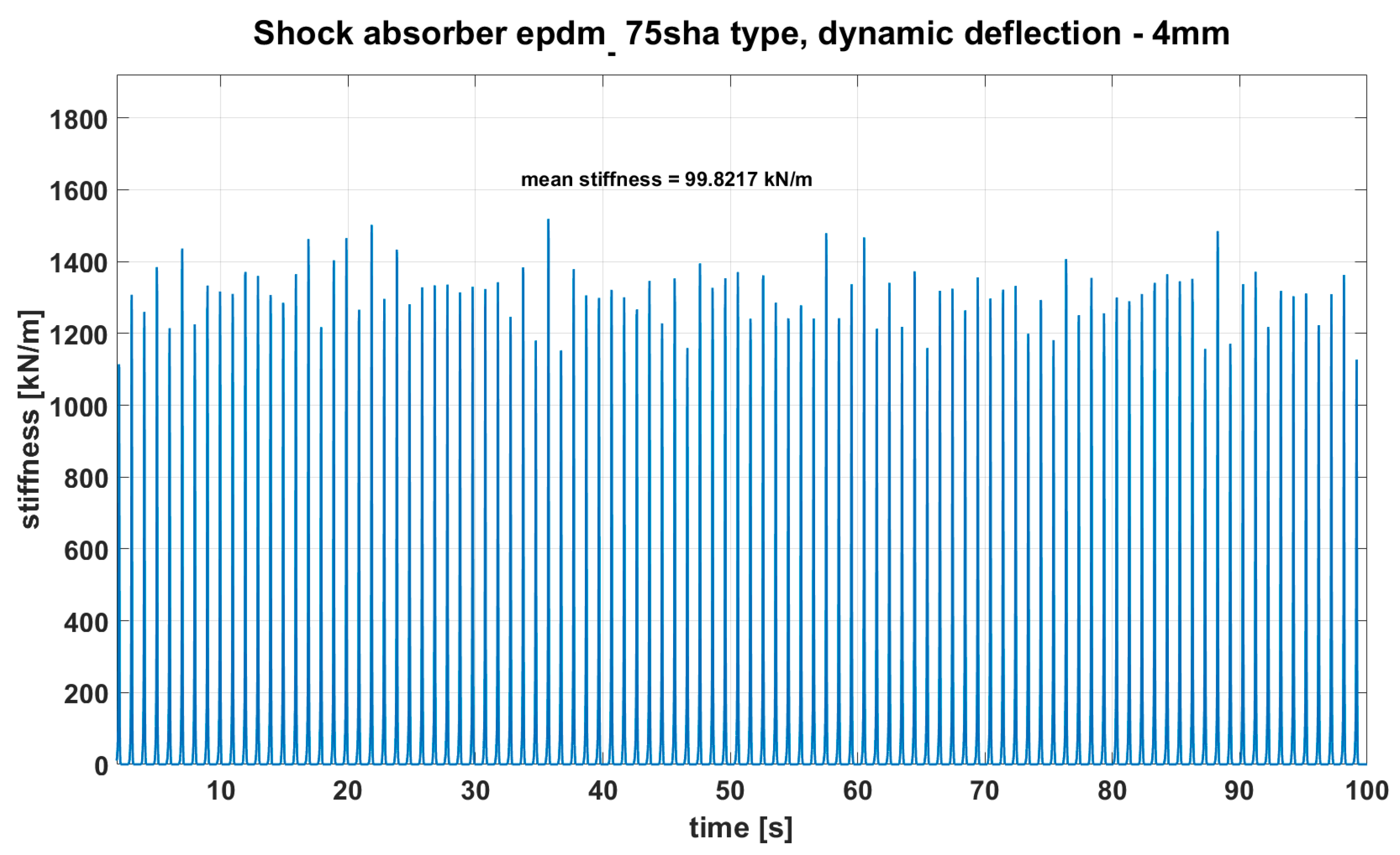
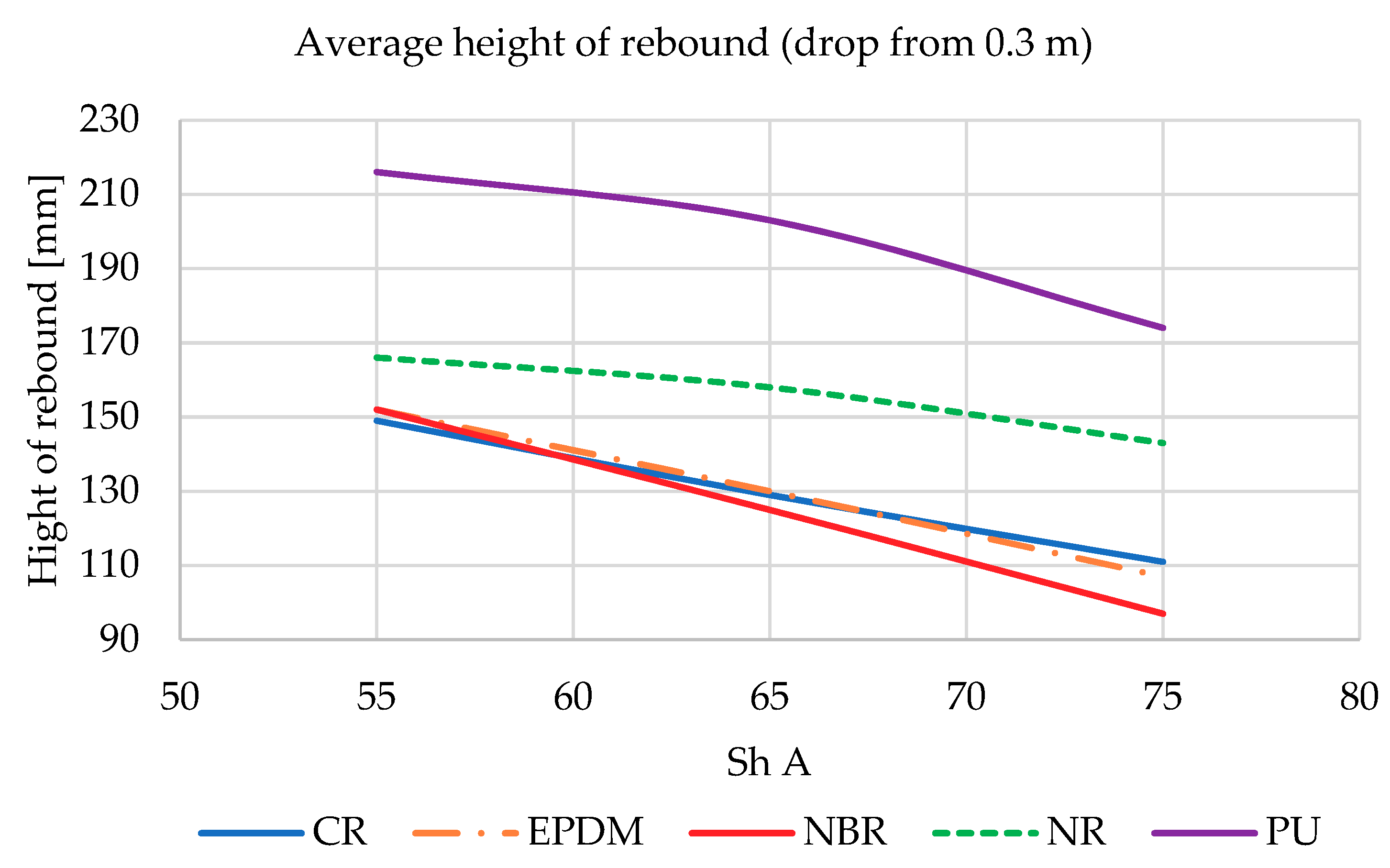
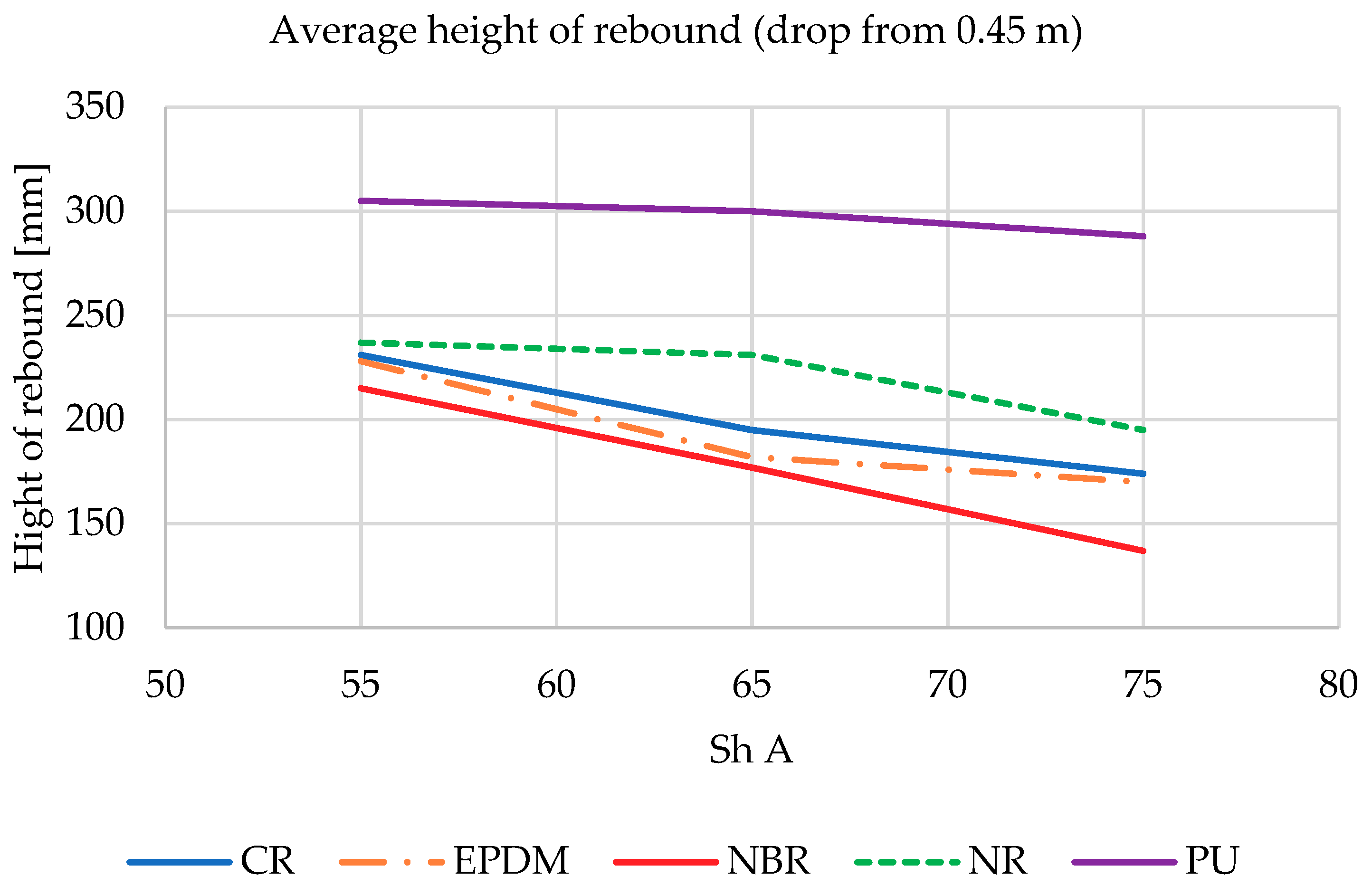
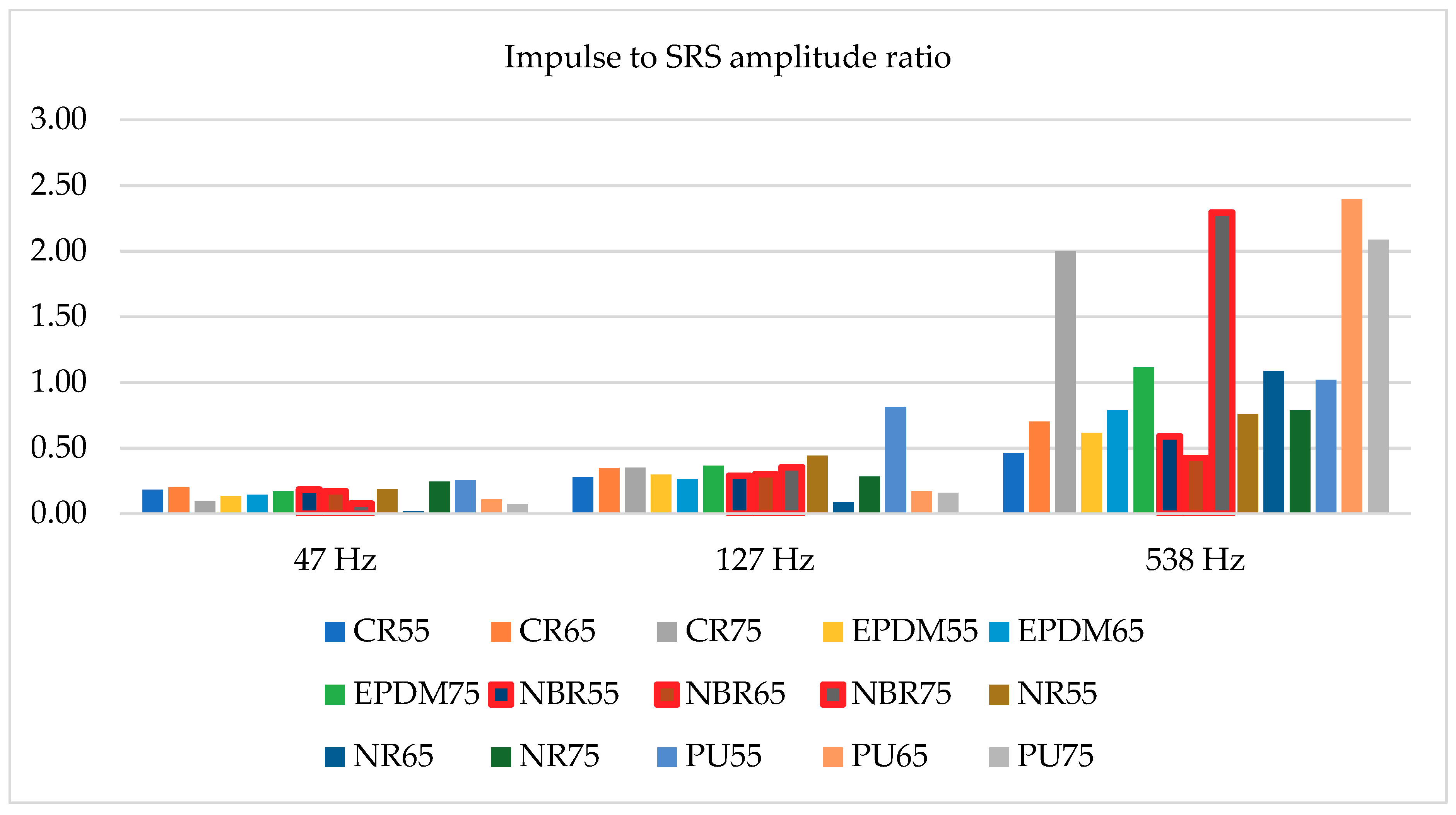

| Material and Its Stiffness Sh A | Deflection | Stiffness (kN/m) | High Speed Stiffness (kN/m) |
|---|---|---|---|
| CR55 | 4 mm | 41.7 | 59.2 |
| CR65 | 4 mm | 69.2 | 95.3 |
| CR75 | 4 mm | 121.8 | 159.8 |
| EPDM55 | 4 mm | 50.7 | 72.1 |
| EPDM65 | 4 mm | 54.3 | 79 |
| EPDM75 | 4 mm | 69.1 | 99.8 |
| NBR55 | 4 mm | 44.2 | 54.1 |
| NBR65 | 4 mm | 53.8 | 72.2 |
| NBR75 | 4 mm | 105.6 | 141.9 |
| NR55 | 4 mm | 53.4 | 76.4 |
| NR65 | 4 mm | 57.3 | 81.4 |
| NR75 | 4 mm | 94.5 | 127.2 |
| PU55 | 4 mm | 44.8 | 64.2 |
| PU65 | 4 mm | 68.4 | 89.1 |
| PU75 | 4 mm | 117.4 | 150.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grządziela, A.; Kluczyk, M. Shock Absorbers Damping Characteristics by Lightweight Drop Hammer Test for Naval Machines. Materials 2021, 14, 772. https://doi.org/10.3390/ma14040772
Grządziela A, Kluczyk M. Shock Absorbers Damping Characteristics by Lightweight Drop Hammer Test for Naval Machines. Materials. 2021; 14(4):772. https://doi.org/10.3390/ma14040772
Chicago/Turabian StyleGrządziela, Andrzej, and Marcin Kluczyk. 2021. "Shock Absorbers Damping Characteristics by Lightweight Drop Hammer Test for Naval Machines" Materials 14, no. 4: 772. https://doi.org/10.3390/ma14040772
APA StyleGrządziela, A., & Kluczyk, M. (2021). Shock Absorbers Damping Characteristics by Lightweight Drop Hammer Test for Naval Machines. Materials, 14(4), 772. https://doi.org/10.3390/ma14040772






