Multiphysics and Multiscale Modeling of Coupled Transport of Chloride Ions in Concrete
Abstract
1. Introduction
2. Methodology
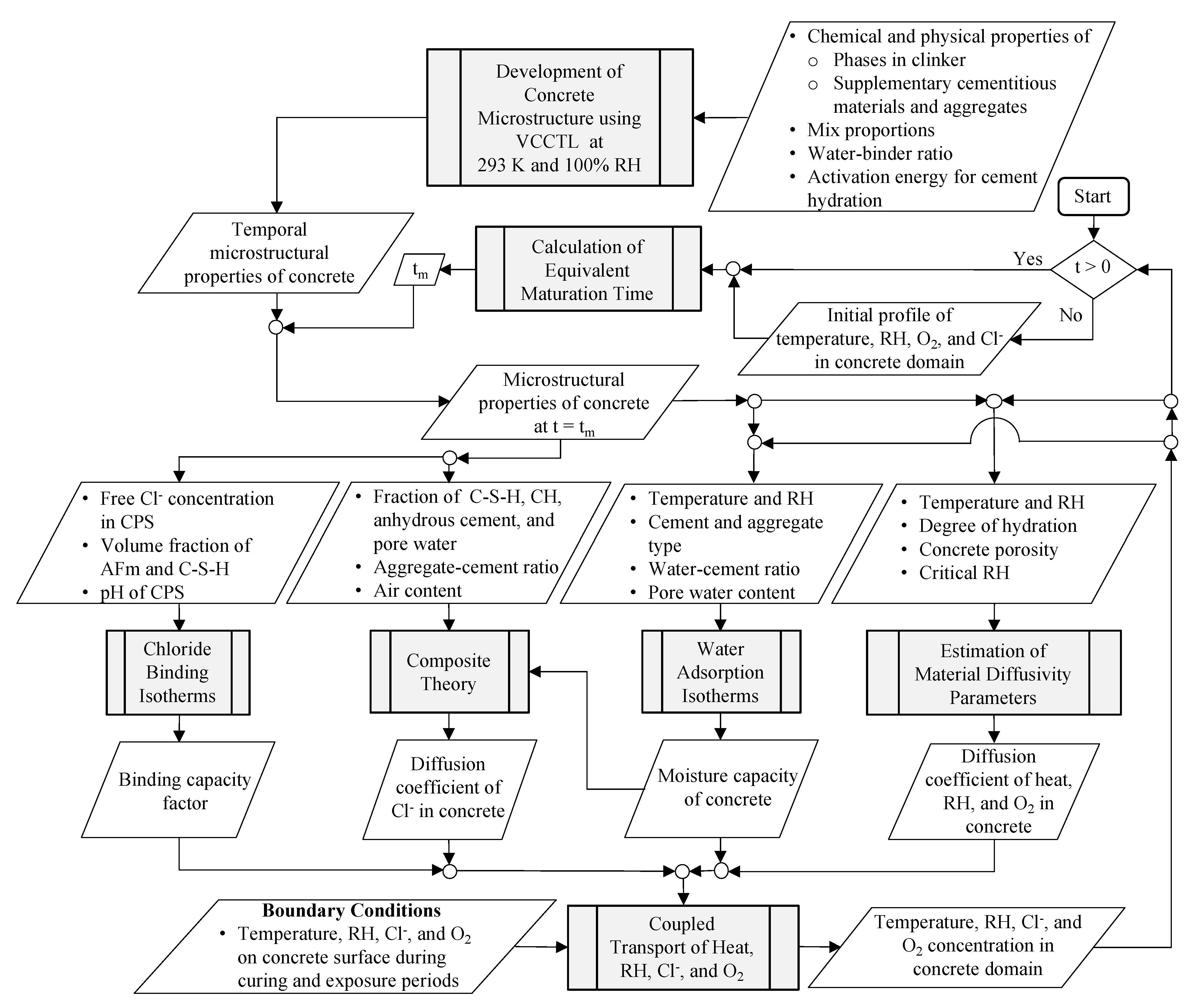
2.1. Overview
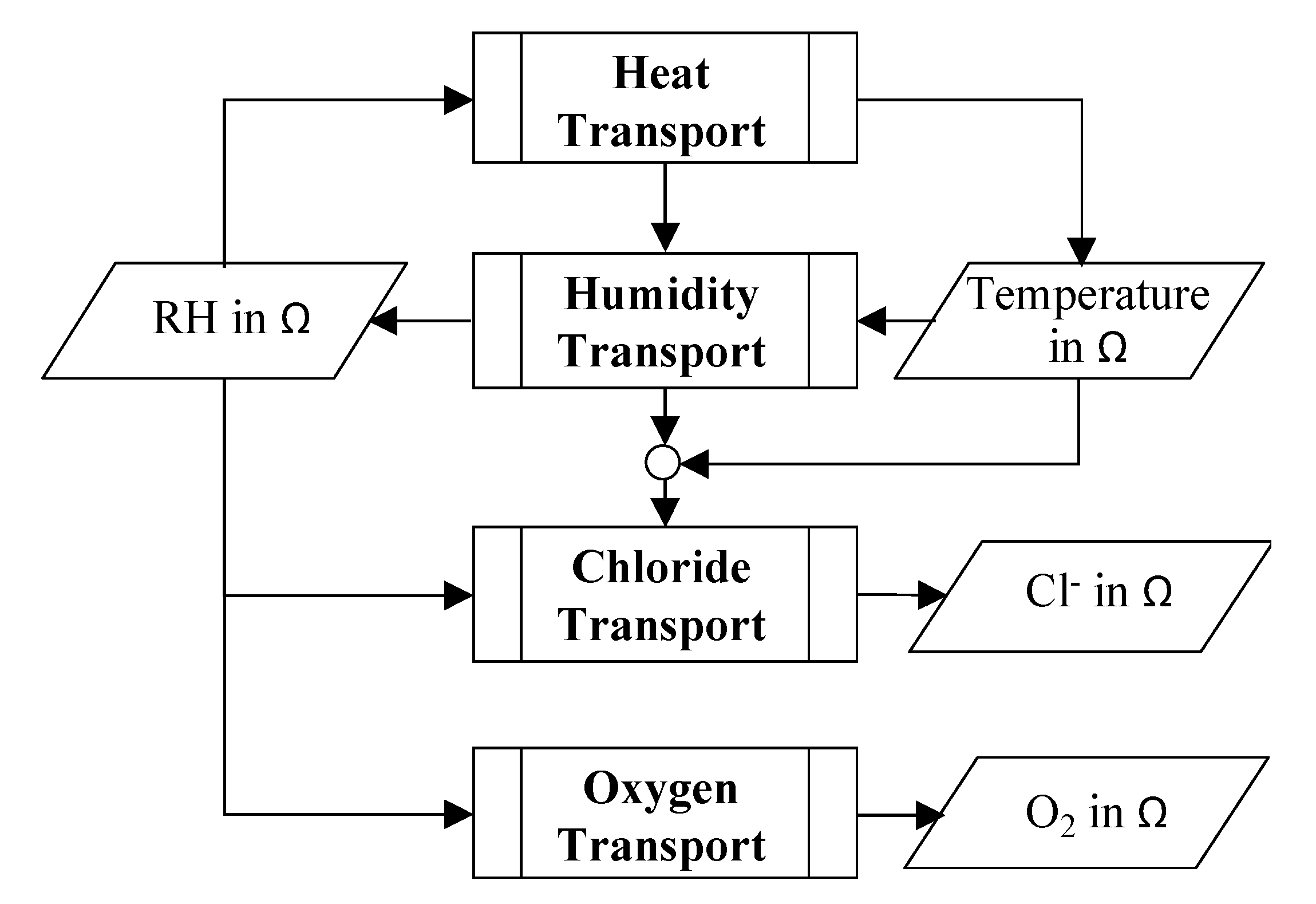
2.2. Governing Equations
2.3. Modeling of Concrete Microstructural Development
2.4. Water Adsorption and Chloride Binding Isotherms
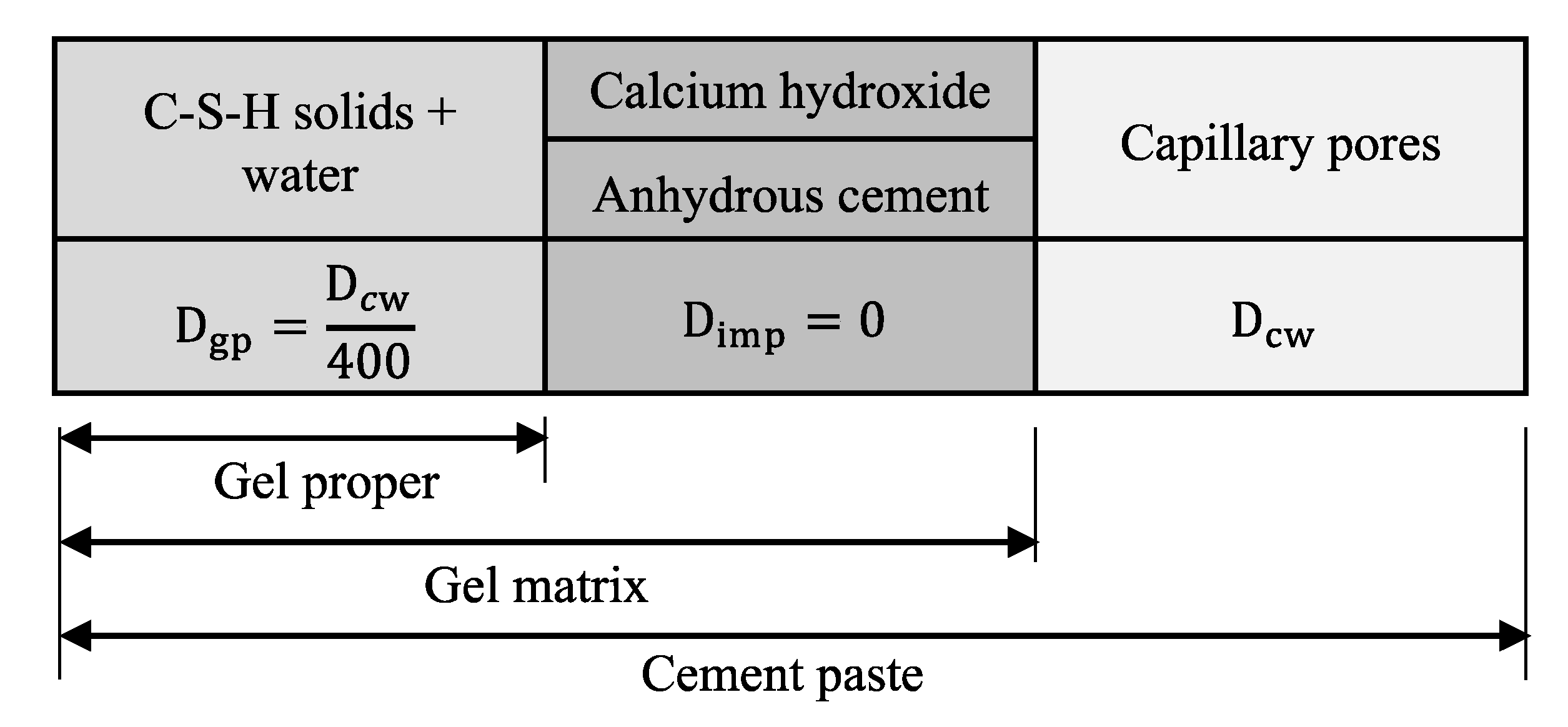
2.5. Composite Theory and Estimation of Material Diffusivity Parameters
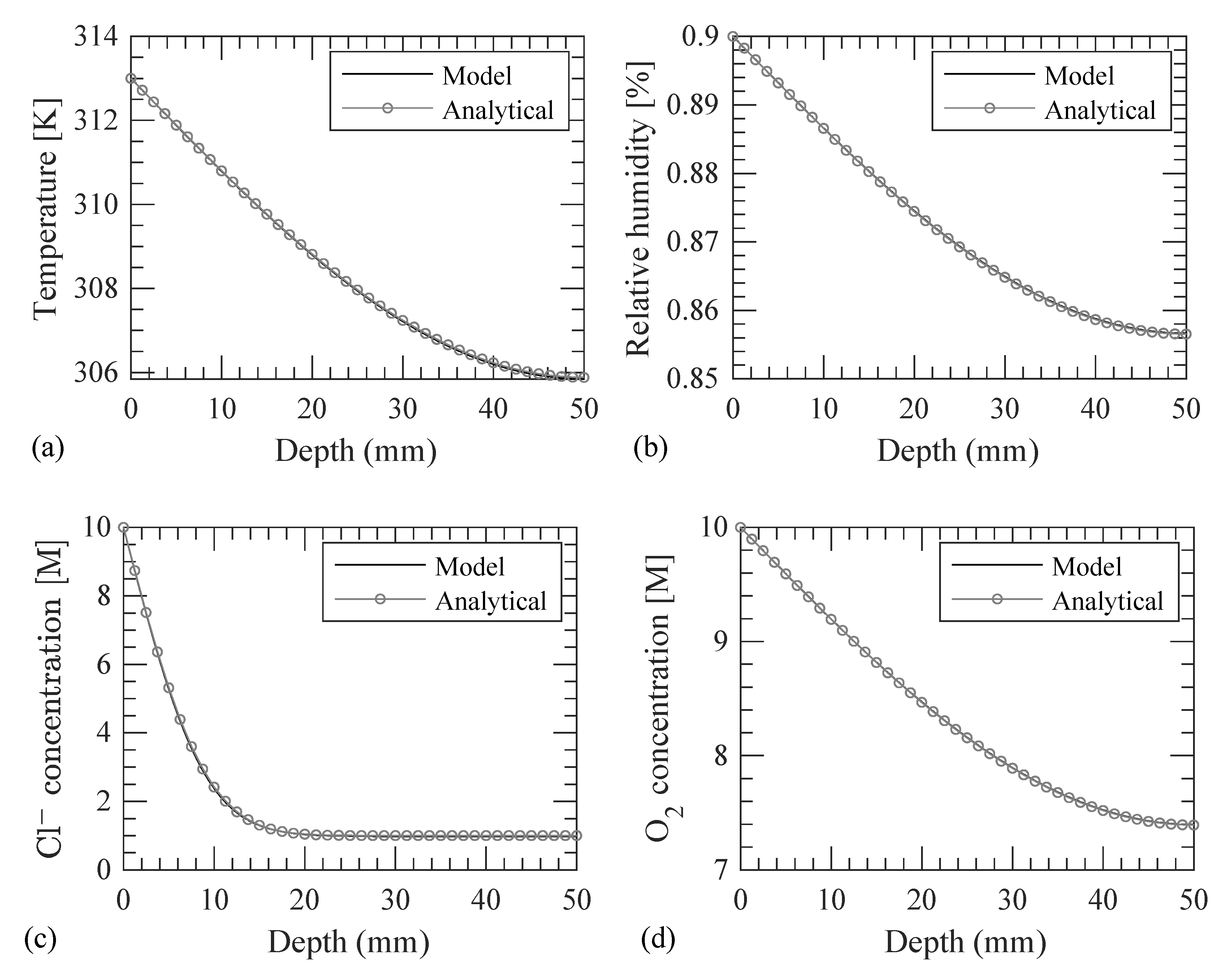
2.6. Implementation, Verification, and Sensitivity Studies
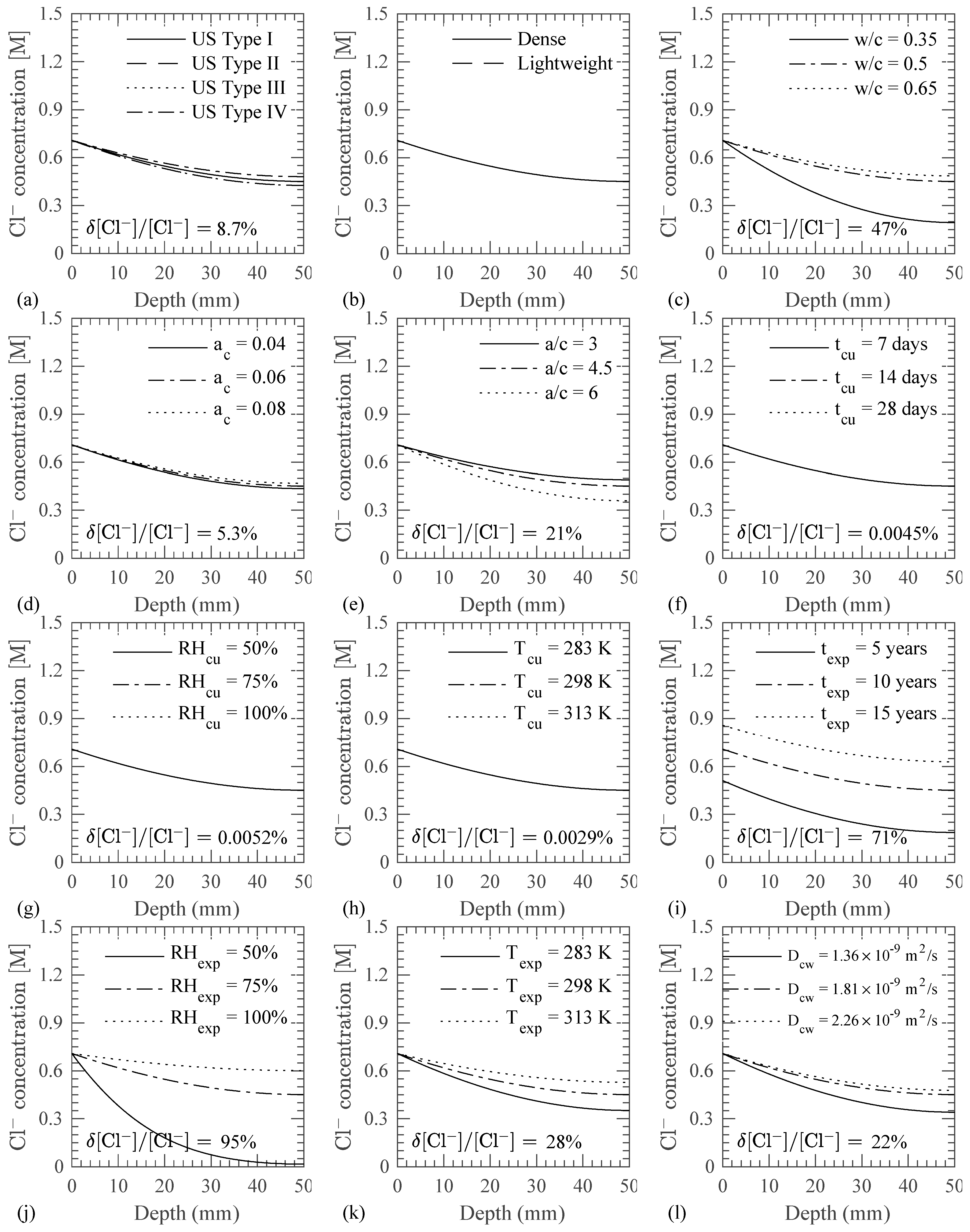
- As shown in Figure 7a,b, the cement and aggregate type affect the Cl− profile in the concrete through the water adsorption isotherms for cement paste and aggregate, as described in Section 2.4. The water adsorption isotherms for given aggregate and cement type affect the moisture capacity of cement paste and aggregate. However, the use of dense or lightweight aggregates did not have a significant impact on the Cl− transport profile for the test case.
- As shown in Figure 7c, the w/c ratio strongly influences the Cl− transport which is due to a change in the concrete porosity with changing w/c ratio. A highly porous concrete microstructure due to a higher w/c ratio increases the capillary pores and results in a faster diffusion of Cl− in the concrete as compared to the cases with a low w/c ratio.
- As seen in Figure 7d, the Cl− concentration in the concrete increases as the air content increases in the concrete. A higher air content increases the capillary porosity and hence the Cl− diffusion coefficient of the cement paste as per Equation (23).
- The effect of the aggregate content on Cl− diffusion is illustrated in Figure 7e. Since the aggregates are considered impermeable for Cl− transport, the Cl− diffusion coefficient reduces as the aggregate content increases.
- Curing duration and environment (temperature and RH) affect the development of the concrete microstructure, which results in different Cl− profiles in concrete. However, in this study, while taking into consideration the variation in the curing duration, the environmental conditions during curing and exposure periods are assumed to be the same, which resulted in insignificant differences in the Cl− concentration profiles in concrete as shown in Figure 7f.
- Similarly, the individual variation of temperature and RH during curing is found to have a little impact on the Cl− concentration profiles as seen in Figure 7g,h. This is due to the larger exposure period, i.e., 10 years, as compared to short curing period, i.e., 14 days.
- As shown in Figure 7i, the exposure duration affects the Cl− concentration in the concrete because more salt solution diffuses inside concrete as the exposure duration increases with constant environmental conditions and material parameters.
- As seen in Figure 7j, the variation in the RH during exposure period affects the Cl− transport in concrete. For 50% RH, which is less than the critical RH, i.e., 75%, negligible Cl− transport is observed as compared to 75% and 100% RH cases. This is due to a reduction in the RH diffusion coefficient as per Equations (27)–(29). Reduction in the RH diffusion coefficient results in a reduced rate of transport of RH. Since Cl− transport is coupled with RH transport (refer to Equations (10) and (21)), a reduced Cl− concentration is observed.
- As shown in Figure 7k, the Cl− transport is also affected from temperature during the exposure period. Since the variation in the temperature affects the RH transport (refer to Equations (27)–(29)), the degree of hydration (refer to Equation (13)), and the Cl− diffusion coefficient in the capillary water (refer to Equation (21)), a higher Cl− concentration is observed at the higher exposure temperature.
- As demonstrated in Figure 7l, the diffusion coefficient of Cl− in the capillary water significantly affects the Cl− transport in the concrete as per Equation (21). The higher diffusion coefficient in the capillary water results in a faster diffusion of Cl− in the concrete microstructure.
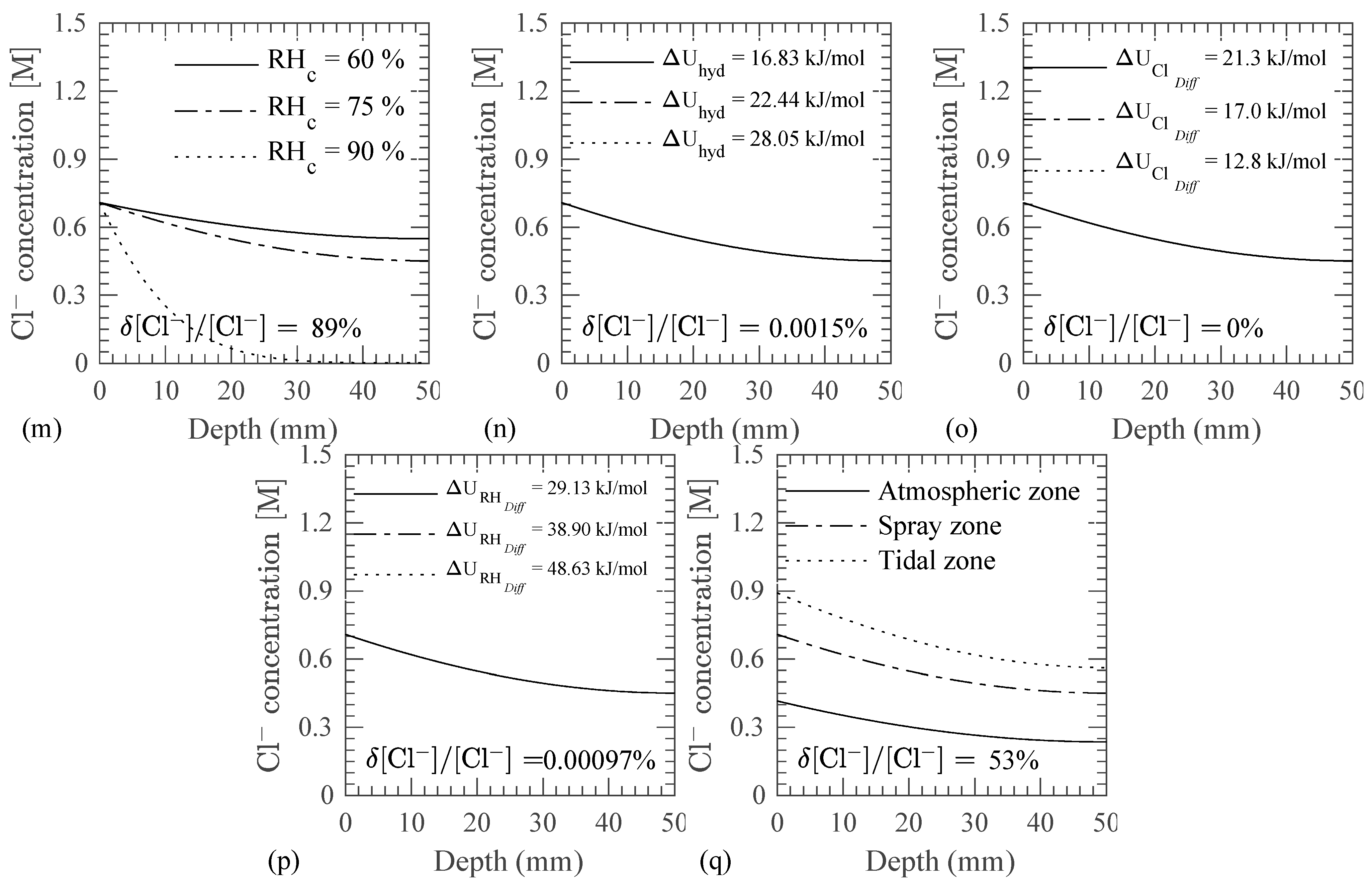
- As observed earlier in Figure 7j, a RH below the critical RH results in slower diffusion of Cl− in concrete, a similar trend is observed for the variation of the critical RH in the concrete microstructure as shown in Figure 7m. A higher critical RH causes more RH exposure below the critical RH, which results in a slower diffusion of RH as compared to cases with a lower critical RH. Thus, a lower Cl− concentration profile is observed for the cases with a higher critical RH as compared to the cases with a lower critical RH.
- The activation energy for hydration, Cl− diffusion, and RH diffusion are found to have a negligible impact on the Cl− concentration profile as shown in Figure 7n–p, respectively. Equal curing and exposure conditions result in the low sensitivity of the model to these parameters (as compared to other parameters) as per Equation (13), Equation (21), and Equation (29).
- The evolution of surface Cl− affects the Cl− concentration profile in the concrete as seen in Figure 7q. The evolution of the surface Cl− in an atmospheric zone is slower as compared to tidal and spray zones as indicated in Table 3. Therefore, a higher Cl− concentration in the concrete is observed in tidal and spray zones as compared to an atmospheric zone.
2.7. Validation
3. Case Study and Discussion
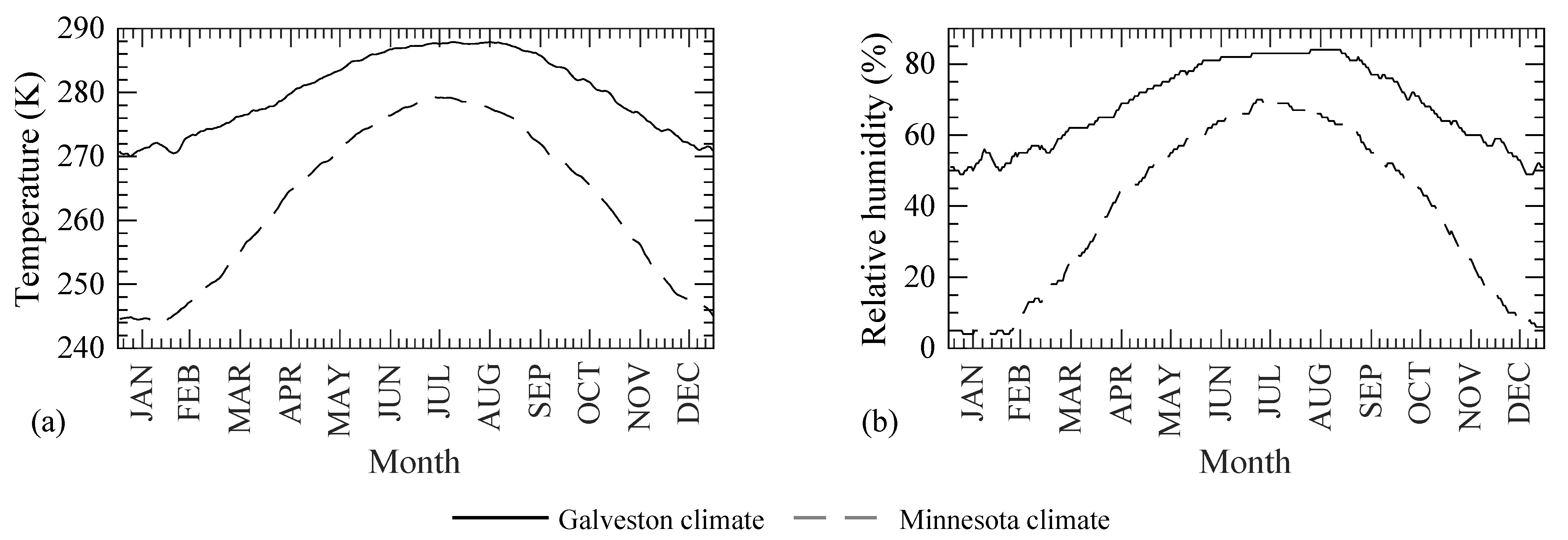
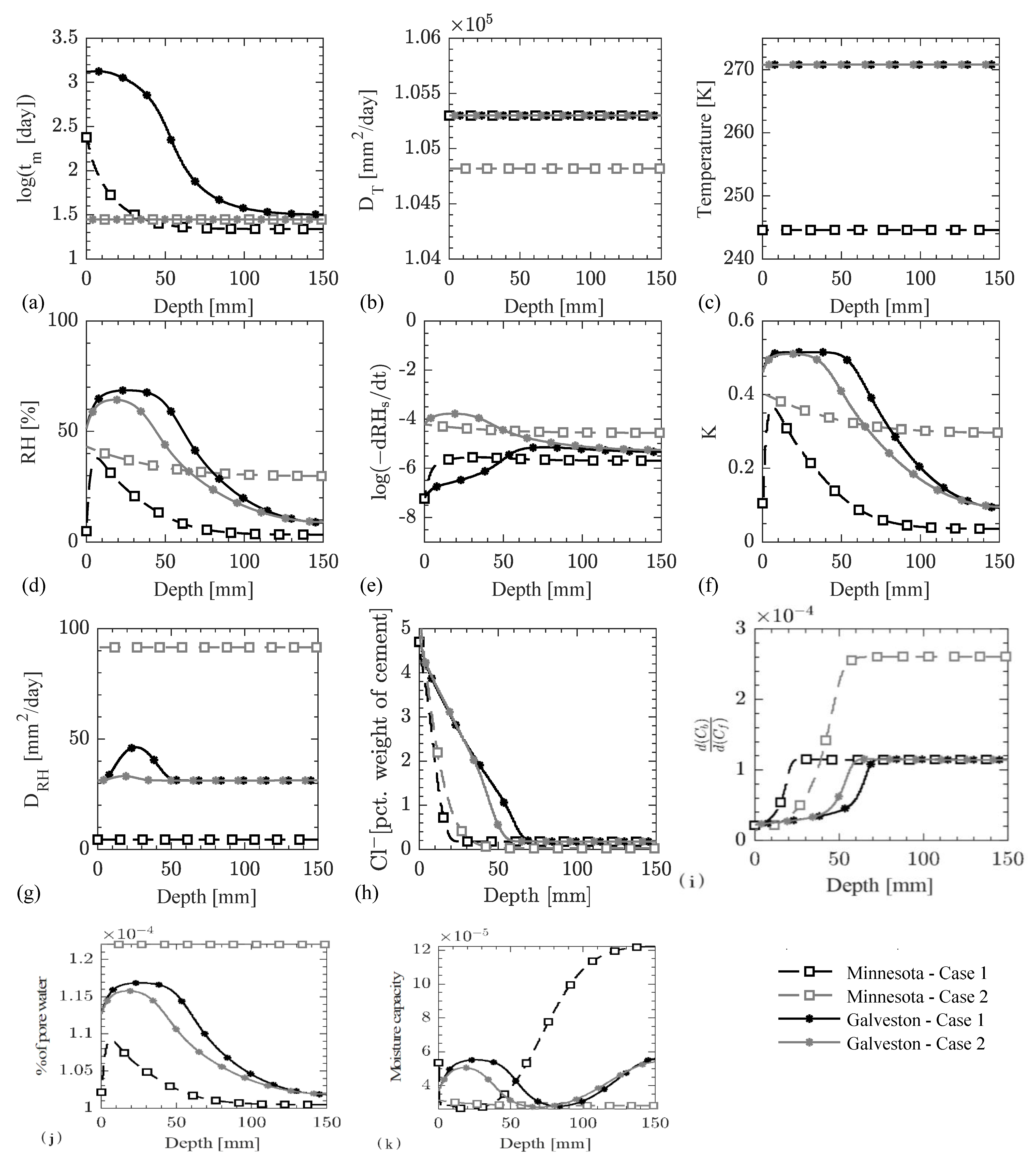
- It is clearly seen in Figure 13a that the concrete maturation time is enforced as 28 days for Case 2 in both climatic regions for the entire duration of the analysis. The equivalent maturation time for Case 1 is found to be larger in Galveston as compared to North Minnesota due to warm and humid environmental conditions in the former (refer to Figure 10). Since the equivalent maturation time is kept constant for Case 2, only the effects of temporal variation of temperature and RH on the modeling parameters are reflected. Case 1, on the other hand, accounts for both the time varying temperature and RH and the temporal changes in the microstructural properties.
- Figure 13b shows the variation of the thermal diffusivity along depth of the beam. Since the temperature diffusion coefficient depends on the degree of hydration as per Equation (26) (which is a function of the equivalent maturation time) and the equivalent maturation time is more than 21 days (as shown in Figure 13a), no significant change in the temperature diffusion coefficient is observed. The high thermal diffusivity and a time step of seven days used in the simulations resulted in an almost uniform temperature distribution in the concrete domain (see Figure 13c), which is approximately equal to the temperature on the concrete surface at the end of the year as shown in Figure 10.
- The variation in the RH profile in concrete is shown in Figure 13d. The RH value at the concrete surface depends on the RH value in two climatic zones in January (or at the beginning of a simulation year as shown in Figure 10). The RH value in the concrete domain depends on the history of RH values, rate of self-desiccation of RH, coupling term of RH diffusion with temperature, and the RH diffusion coefficient. Since the RH values at the concrete surface peaks in between June and August of each year, that peak travels in the concrete domain and appears at a certain depth in January. The peak diffuses more in Galveston as compared to North Minnesota due to colder and drier climate in the latter, which affects the rate of self-desiccation of RH (based on Equation (5)), coupling term with temperature diffusion (based on Equation (5)), and the diffusion coefficient for RH (based on Equation (27)).
- The instantaneous profile of rate of self-desiccation of RH in concrete domain at the end of 10 years, see Figure 13e, is governed by the temperature, RH, and the equivalent maturation time profiles in the concrete domain based on Equation (5). The rate of self-desiccation of RH is observed to be higher in Case 1 as compared to Case 2 in both climatic zones due to a higher equivalent maturation time. The instantaneous profiles for the coupling term and RH diffusion coefficient in the concrete domain at the end of 10 years (see respectively Figure 13f,g) depend on the RH profile (based on Equations (5) and (27)). Both achieve their peak values around the same depth with the peak of RH profile for both cases and climatic regions.
- As seen in Figure 13h, more Cl− diffused in Galveston as compared to North Minnesota due to a colder and drier climatic condition in the latter, which causes a lower temperature and RH profile in the concrete domain and a lower maturity and porosity in the concrete. Additionally, the drier climate in North Minnesota causes RH to be below the critical RH of 75%, which drastically reduces the Cl− diffusion as shown in the sensitivity study; see Figure 7m.
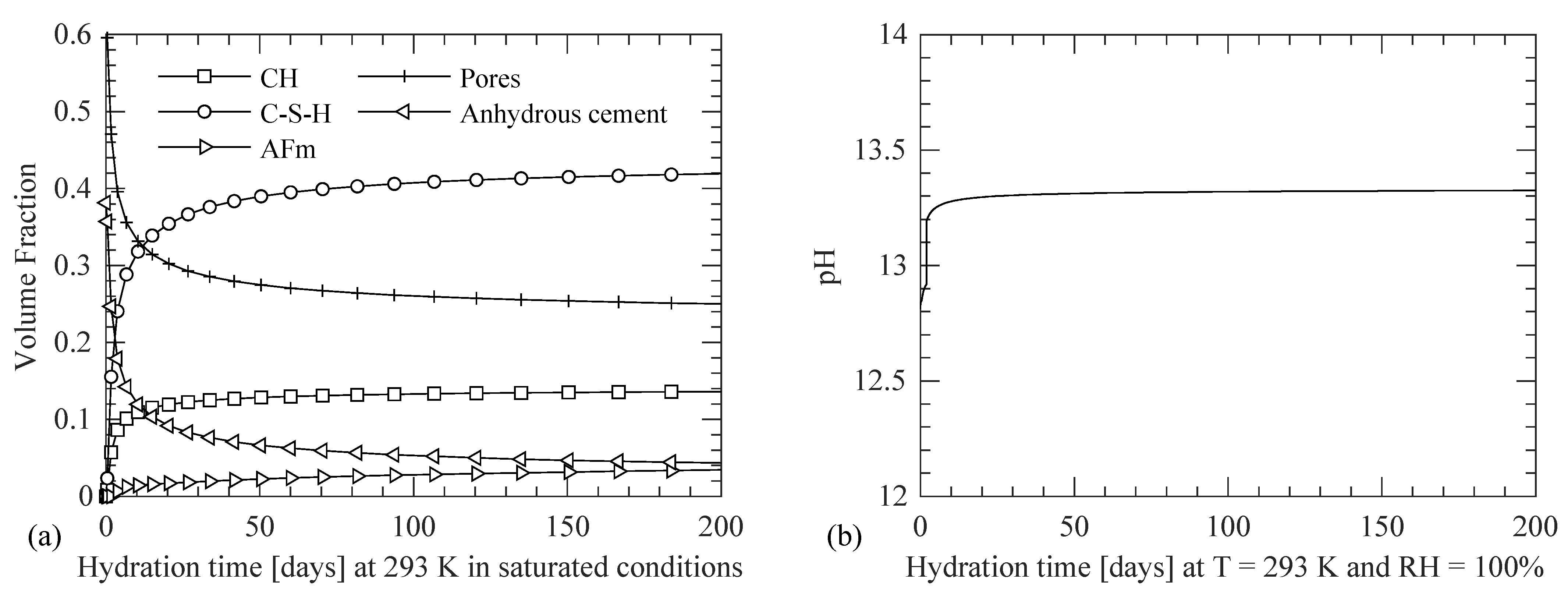
- The Cl− diffusion coefficient profile shown in Figure 13i follows the trend of the pore water content; see Figure 13k. As the concrete maturity decreases along the depth, as seen in Figure 13a, the weight fractions of C-S-H and AFm, and the pH of the CPS also decrease (see Figure 12a,b), which results in an increase in the binding capacity of the Cl− as shown in Figure 13j. Additionally, the decrease in the free Cl− concentration (see Figure 13h) contributes to the increase in the bound Cl− concentration, i.e., more Cl− per unit mole of free Cl− bound to the concrete surface at lower free Cl− concentrations as compared to higher free Cl− concentrations due to the presence of larger surface area of C-S-H and more binding sites on the AFm phases. The lower bound Cl− concentration in North Minnesota as compared to Galveston is due to the lower concrete maturity and the lower free Cl− concentration as per Figure 13a,h, respectively. The highest binding capacity is observed for Case 2 in North Minnesota climate, which is due to a combination of lower pH values (as a result of lower equivalent maturation time) and a lower free Cl− concentration as compared to the other three simulation cases.
- As discussed earlier, the concrete maturity decreases along the concrete depth which increases the concrete porosity based on Figure 12a. However, the RH decreases along the concrete depth as observed in Figure 13d, which determines the amount of water in these pores, and therefore, the pore water decreases along the concrete depth as seen in Figure 13k.
4. Conclusions
- The modeling framework is capable of accounting for the concrete material heterogeneity due to spatial and temporal distribution of temperature and RH conditions in the concrete domain to study the coupled transport problem. The temporal heterogenous concrete microstructure properties (volume fractions of C-S-H, CH, AFm, anhydrous cement, and pore water, and the pH of the CPS), temperature and RH profiles, water adsorption isotherms (dependent on temperature, RH, w/c ratio, type of cement and aggregates, fraction of cement and aggregates and pore water), Cl− binding isotherms (dependent on Cl− concentration, pH of the CPS, weight fractions of C-S-H and AFm), and composite theory (dependent on temperature, RH, a/c ratio, air content, and the fraction of pore water, C-S-H, CH, and anhydrous cement) are necessary to estimate the spatially and time varying material diffusivity parameters for heat, RH, Cl−, and O2 transport.
- From the sensitivity study, the w/c ratio, the exposure duration, the boundary conditions (temperature, RH, surface Cl− concentration, Cl− diffusion coefficient in the capillary water at 298 K, and the critical RH) are identified as key variables that affect the Cl− concentration in the concrete domain. The sensitivity of these parameters ranges from 22% (for Cl− diffusion coefficient in the capillary water at 298 K) to 95% (for RH during exposure period) for the analyzed case. It is important to obtain these parameters carefully to predict accurate Cl− concentration fields in the concrete domain.
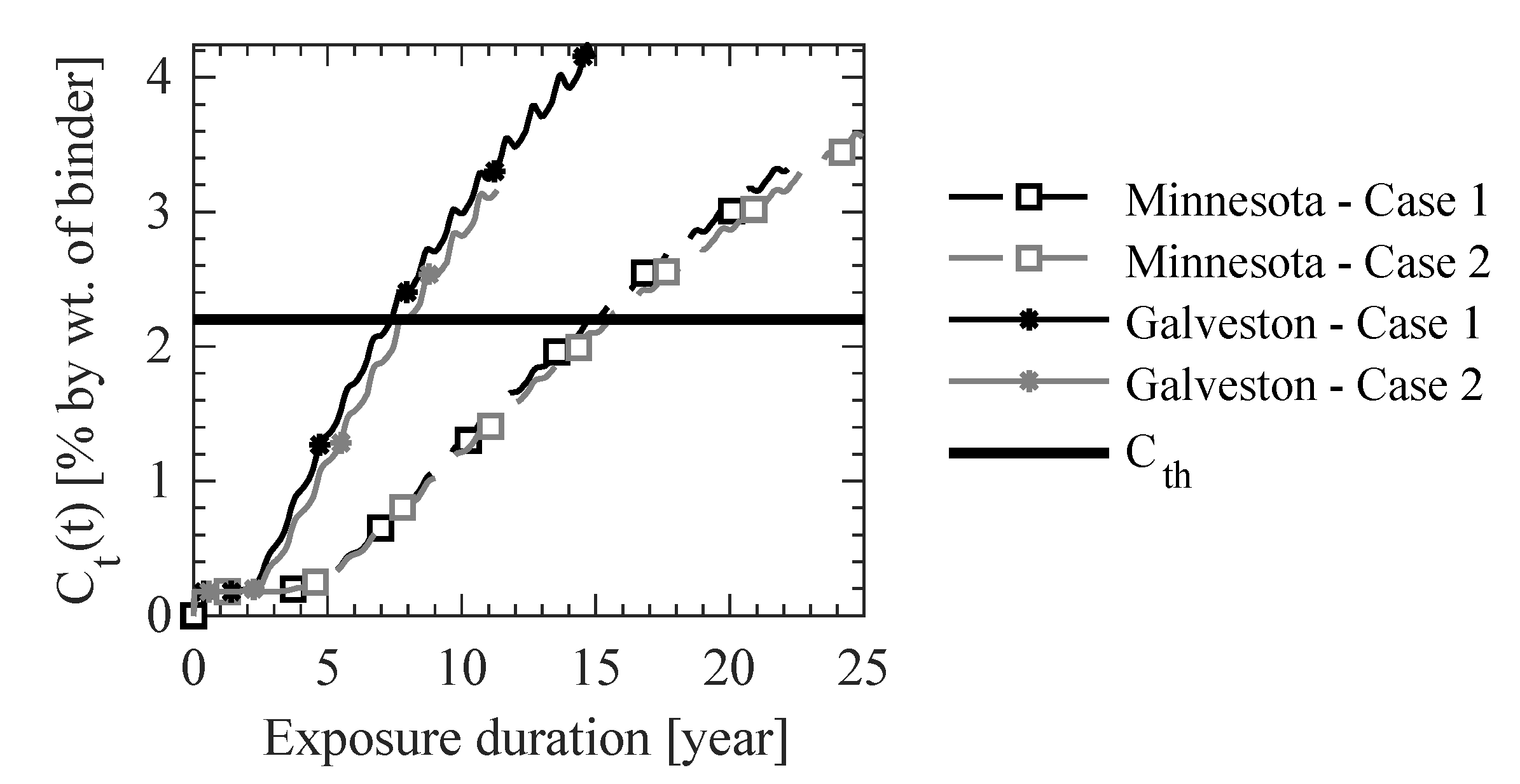
- The modeling framework was able to produce temporal and spatially varied concrete microstructure on a two-dimensional RC beam for given temperature and RH conditions. The obtained concrete microstructure was utilized to obtain the temperature, RH, and Cl− and in the concrete domain. The consideration of temporal concrete microstructure properties could result in a difference of as high as 480% after 10 years of exposure in Cl− concentration depending on the time and location of measurement along the depth of the concrete domain.
- The model could predict the temporal and spatial variation in the diffusion coefficients for RH, Cl−, and O2 in the concrete domain. Thus, the model can be utilized further to simulate the corrosion reactions of steel reinforcement that uses temporal variations in Cl− and O2 concentrations, temperature RH, and pH of the CPS. Furthermore, the degradation of RC structures due to Cl− induced corrosion of steel reinforcement can be studied by accounting for the temporal and spatial variations in the environmental conditions and microstructural properties of concrete.
- Further research is required to experimentally validate the microstructure development for concretes with SCMs. The proposed model can be further be improved to include the effect of SCMs on the transport of heat, RH, Cl−, and O2 in the concrete domain for concretes with SCMs, which are becoming more prevalent in the construction industry.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, Q.; Audenaert, K.; Shi, C.; De Schutter, G. Effect of temperature on transport of chloride ions in concrete. Concrete Repair 2008, 1, 159–160. [Google Scholar] [CrossRef]
- Saetta, A.V.; Scotta, R.V.; Vitaliani, R.V. Analysis of Chloride Diffusion into Partially Saturated Concrete. ACI Mater. J. 1993, 90, 441–451. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Najjar, L.J. Nonlinear water diffusion in nonsaturated concrete. Mater. Struct. 1972, 5, 3–20. [Google Scholar] [CrossRef]
- Costa, A.; Appleton, J. Chloride penetration into concrete in marine environment-Part II: Prediction of long term chloride penetration. Mater. Struct. 1999, 32, 354–359. [Google Scholar] [CrossRef]
- Song, H.-W.; Lee, C.-H.; Ann, K.Y. Factors influencing chloride transport in concrete structures exposed to marine environments. Cem. Concr. Compos. 2008, 30, 113–121. [Google Scholar] [CrossRef]
- Mustafa, M.; Yusof, K. Atmospheric chloride penetration into concrete in semitropical marine environment. Cem. Concr. Res. 1994, 24, 661–670. [Google Scholar] [CrossRef]
- Vu, K.A.T.; Stewart, M.G. Structural reliability of concrete bridges including improved chloride-induced corrosion models. Struct. Saf. 2000, 22, 313–333. [Google Scholar] [CrossRef]
- Zibara, H. Binding of External Chloride by Cement Pastes. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2001. [Google Scholar]
- Shi, X.; Xie, N.; Fortune, K.; Gong, J. Durability of steel reinforced concrete in chloride environments: An overview. Constr. Build. Mater. 2012, 30, 125–138. [Google Scholar] [CrossRef]
- Li, L.-Y.; Easterbrook, D.; Xia, J.; Jin, W.-L. Numerical simulation of chloride penetration in concrete in rapid chloride migration tests. Cem. Concr. Compos. 2015, 63, 113–121. [Google Scholar] [CrossRef]
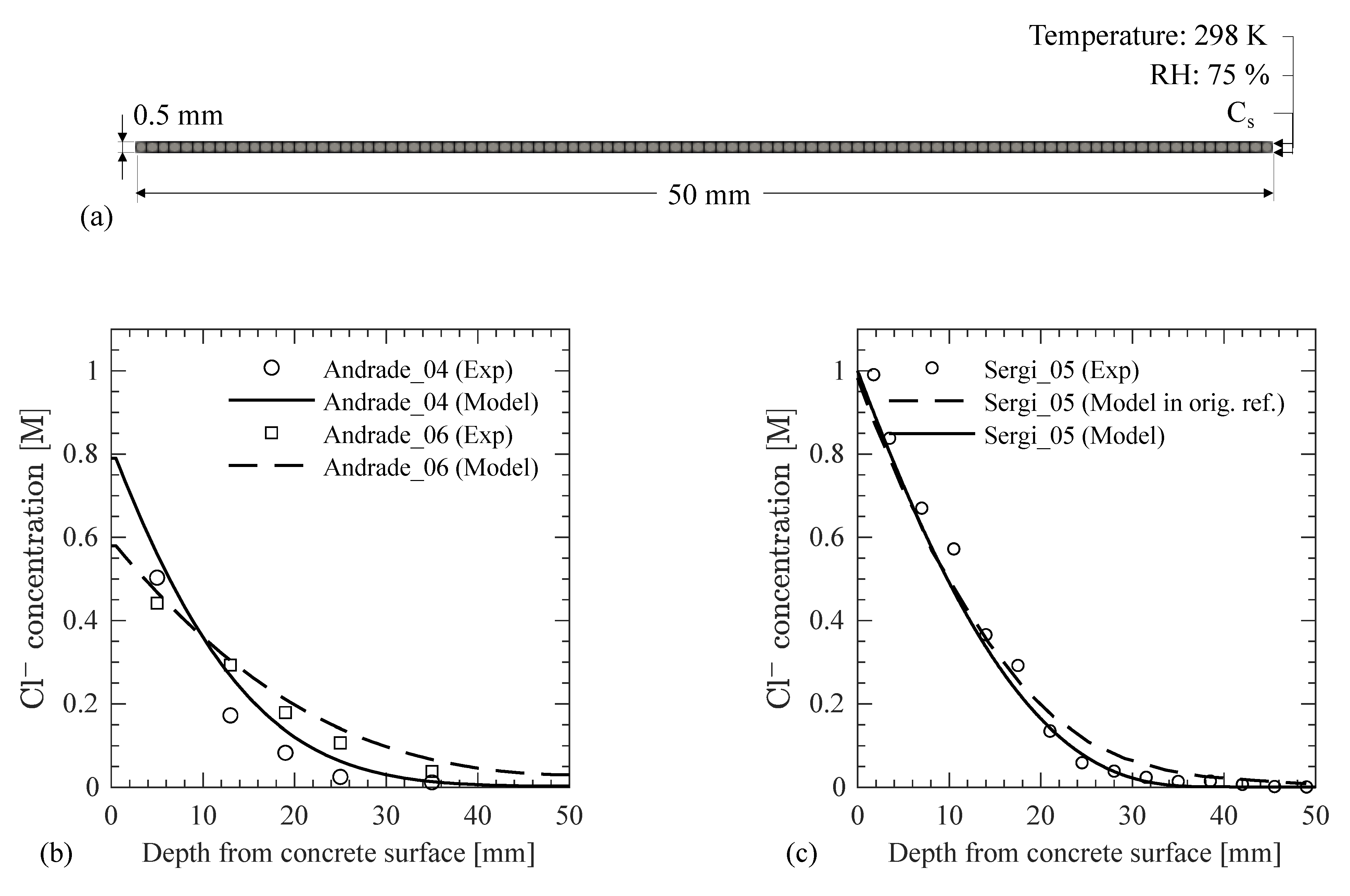
- Andrade, C.; Whiting, D. A comparison of chloride ion diffusion coefficients derived from concentration gradients and non-steady state accelerated ionic migration. Mater. Struct. 1996, 29, 476–484. [Google Scholar] [CrossRef]
- Mangat, P.S.; Molloy, B.T. Prediction of long term chloride concentration in concrete. Mater. Struct. 1994, 27, 338–346. [Google Scholar] [CrossRef]
- Page, C.L.; Lambert, P.; Vassie, P.R.W. Investigations of reinforcement corrosion. 1. The pore electrolyte phase in chloride-contaminated concrete. Mater. Struct. 1991, 24, 243–252. [Google Scholar] [CrossRef]
- Oh, B.H.; Jang, S.Y. Effects of material and environmental parameters on chloride penetration profiles in concrete structures. Cem. Concr. Res. 2007, 37, 47–53. [Google Scholar] [CrossRef]
- Xi, Y.; Bažant, Z.P. Modeling Chloride Penetration in Saturated Concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Nielsen, E.P.; Geiker, M.R. Chloride diffusion in partially saturated cementitious material. Cem. Concr. Res. 2003, 33, 133–138. [Google Scholar] [CrossRef]
- Kemper, M.; Timothy, J.; Kruschwitz, J.; Meschke, G. Modeling of Chloride and CO2 transport in intact and cracked concrete in the context of corrosion predictions of RC structures. Computational Modelling of Concrete Structures. 2010, pp. 503–512. Available online: papers2://publication/uuid/105F3D8A-F6CC-4D39-9976-474153C61A11 (accessed on 2 April 2016).
- Yang, Y.; Wang, M. Pore-scale modeling of chloride ion diffusion in cement microstructures. Cem. Concr. Compos. 2018, 85, 92–104. [Google Scholar] [CrossRef]
- Ann, K.Y.; Hong, S.I. Modeling Chloride Transport in Concrete at Pore and Chloride Binding. ACI Mater. J. 2018, 115, 595–604. [Google Scholar] [CrossRef]
- Powers, T.C.; Brownyard, T.L. Studies of the physical properties of hardened Portland cement paste. J. Proc. 1946, 43, 101–132. [Google Scholar]
- Bazant, Z.P. Constitutive equation for concrete creep and shrinkage based on thermodynamics of multiphase systems. Mater. Struct. 1970, 3, 3–36. [Google Scholar] [CrossRef]
- Bentz, D.P. Three-Dimensional Computer Simulation of Portland Cement Hydration and Microstructure Development. J. Am. Ceram. Soc. 1997, 80, 3–21. [Google Scholar] [CrossRef]
- Bentz, D.P. CEMHYD3D: A Three-Dimensional Cement Hydration and Microstructure Development Modeling Package Version 3.0; NISTIR 7232; U.S. Department of Commerce, Technology Administration, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005.
- Xi, Y.; Bažant, Z.P.; Jennings, H.M. Moisture diffusion in cementitious materials Adsorption isotherms. Adv. Cem. Based Mater. 1994, 1, 248–257. [Google Scholar] [CrossRef]
- Jain, A.; Gencturk, B.; Pirbazari, M.; Belarbi, A.; Kahraman, R.; Sohail, M.G. Influence of pH on Chloride Binding Isotherms for Cement Paste and Its Components. Cem. Concr. Res. 2021. [Google Scholar] [CrossRef]
- Gaston, D.; Newman, C.; Hansen, G.; Lebrun-Grandié, D. MOOSE: A parallel computational framework for coupled systems of nonlinear equations. Nucl. Eng. Des. 2009, 239, 1768–1778. [Google Scholar] [CrossRef]
- Na, O.; Cai, X.-C.; Xi, Y. Corrosion Prediction with Parallel Finite Element Modeling for Coupled Hygro-Chemo Transport into Concrete under Chloride-Rich Environment. Materials 2017, 10, 350. [Google Scholar] [CrossRef] [PubMed]
- van Breugel, K.; van Breugel, K. Simulation of Hydration and Formation of Structure in Hardening Cement-Based Materials. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1991. [Google Scholar]
- Bentz, D.P. A Three-Dimensional Cement Hydration and Microstructural Program. I. Hydration Rate, Heat of Hydration, and Chemical Shrinkage; Building and Fire Research Laboratory, National Institute of Technology: Gaithersburg, MD, USA, 1995. [Google Scholar]
- Xi, Y. A model for moisture capacities of composite materials Part II: Application to concrete. Comput. Mater. Sci. 1995, 4, 78–92. [Google Scholar] [CrossRef]
- Hirao, H.; Yamada, K.; Takahashi, H.; Zibara, H. Chloride Binding of Cement Estimated by Binding Isotherms of Hydrates. J. Adv. Concr. Technol. 2005, 3, 77–84. [Google Scholar] [CrossRef]
- Luping, T.; Nilsson, L.-O. Chloride binding capacity and binding isotherms of OPC pastes and mortars. Cem. Concr. Res. 1993, 23, 247–253. [Google Scholar] [CrossRef]
- Garboczi, E.J.; Bentz, D.P. Multi-Scale Picture of Concrete and Its Transport Properties: Introduction for Non-Cement Researchers; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 1996.
- Jensen, O.M. Chloride Ingress in Cement Paste and Mortar Measured by Electron Probe Micro Analysis; Technical University of Denmark: Lyngby, Denmark, 1999. [Google Scholar]
- De Schutter, G.; Taerwe, L. Specific heat and thermal diffusivity of hardening concrete. Mag. Concr. Res. 1995, 47, 203–208. [Google Scholar] [CrossRef]
- Baron, J. Properties of set concrete at early ages state-of-the-art-report. Mater. Struct. 1981, 14, 399–450. [Google Scholar] [CrossRef]
- Isgor, O.B.; Razaqpur, A.G. Modelling steel corrosion in concrete structures. Mater. Struct. 2006, 39, 291–302. [Google Scholar] [CrossRef]
- Bažant, Z.; Najjar, L. Drying of concrete as a nonlinear diffusion problem. Cem. Concr. Res. 1971, 1, 461–473. [Google Scholar] [CrossRef]
- Papadakis, V.; Vayenas, C.; Fardis, M. Physical and chemical characteristics affecting the durability of concrete. ACI Mater. J. 1991, 8, 186–196. [Google Scholar]
- Mackowski, D.W. Conduction heat transfer: Notes for MECH 7210. Mechanical Engineering Department Auburn University. 2011, pp. 1–242. Available online: http://www.eng.auburn.edu/users/mackodw/mech7210/condbook.pdf (accessed on 25 April 2020).
- Poon, C.S.; Lam, C.S. The effect of aggregate-to-cement ratio and types of aggregates on the properties of pre-cast concrete blocks. Cem. Concr. Compos. 2008, 30, 283–289. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Ye, G. Influence of moisture condition on chloride diffusion in partially saturated ordinary Portland cement mortar. Mater. Struct. 2018, 51, 36. [Google Scholar] [CrossRef]
- Sergi, G.; Yu, S.W.; Page, C.L. Diffusion of chloride and hydroxyl ions in cementitious materials exposed to a saline environment. Mag. Concr. Res. 1992, 44, 63–69. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO T 259-80: Standard Method of Test for Resistance of Concrete to Chloride Ion Penetration; AASHTO: Washington, DC, USA, 2002. [Google Scholar]
- Iowa Enviornmental Mesonet. Iowa State Univeristy. Available online: https://mesonet.agron.iastate.edu (accessed on 5 May 2020).
- Kim, C.-Y.; Kim, J.-K. Numerical analysis of localized steel corrosion in concrete. Constr. Build. Mater. 2008, 22, 1129–1136. [Google Scholar] [CrossRef]
- Sandberg, P. Chloride Initiated Reinforcement Corrosion in Marine Concrete; Report No. TVBM-1015; Lund University, Lund Institute of Technology, Division of Building Materials: Lund, Sweden, 1998. [Google Scholar]



| Parameters | Value |
|---|---|
| Cement type | ASTM Type I |
| Coarse aggregate type | Dense crushed limestone |
| Water-to-cement (w/c) ratio | 0.4 |
| Air content, ac [%] | 7.9 |
| Tri-calcium silicate (C3S) [%] | 59.8 |
| Di-calcium silicate (C2S) [%] | 20.7 |
| Tri-calcium aluminate (C3A) [%] | 8.1 |
| Tetra-calcium aluminoferrite (C4AF) [%] | 11.5 |
| Aggregate-to-cement (a/c) ratio | 1.9 |
| Curing duration, tcu [days] | 14 |
| RH during curing, RHcu [%] | 100 |
| Temperature during curing, Tcu [K] | 296 |
| Sample age at the start of experiment [days] | 104 |
| Exposure duration, texp [days] | 90 |
| RH during exposure, RHexp [%] | 100 |
| Temperature during exposure, Texp [K] | 296 |
| Cl− diffusion coefficient in capillary water at 298 K, Dcw [m2/s] | 2.03 × 10−9 |
| Modeling Assumptions | Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|---|
| Initial conditions | T (x, t = 0) [K] | 298 | 298 | 298 | 298 |
| RH (x, t = 0) [%] | 90 | 75 | 90 | 90 | |
| Cl− (x, t = 0) [M] | 1.0 | 1.0 | 1.0 | 1.0 | |
| O2 (x, t = 0) [M] | 1.0 | 1.0 | 1.0 | 1.0 | |
| Boundary conditions | T (x = 0, t) [K] | 313 | 298 | 298 | 298 |
| RH (x = 0, t) [%] | 90 | 90 | 90 | 90 | |
| Cl− (x = 0, t) [M] | 1.0 | 1.0 | 10.0 | 1.0 | |
| O2 (x = 0, t) [M] | 1.0 | 1.0 | 1.0 | 10.0 | |
| Parameters | DT [mm2/day] | 1 × 105 | * | * | * |
| DRH [mm2/day] | * | 30 | * | * | |
| Di [mm2/day] | * | * | 0.5 | * | |
| DO2 [mm2/day] | * | * | * | 300 | |
| d(RHs)/dt [1/day] | * | 0 | * | * | |
| Parameters | Base Value | Values for Sensitivity Analysis |
|---|---|---|
| Cement type | US Type I | US Type II, III, and IV |
| Aggregate type | Dense | Lightweight |
| Water-cement (w/c) ratio | 0.50 | 0.35 and 0.65 |
| Air content, ac [%] | 6 | 4 and 8 |
| Aggregate-to-cement (a/c) ratio | 4.5 | 3 and 6 |
| Curing duration, tcu [days] | 14 | 7 and 28 |
| RH during curing, RHcu [%] | 75 | 50 and 100 |
| Temperature during curing, Tcu [K] | 298 | 283 and 313 |
| Exposure duration, texp [years] | 10 | 5 and 15 |
| RH during exposure, RHexp [%] | 75 | 50 and 100 |
| Temperature during exposure, Texp [K] | 298 | 283 and 313 |
| Diffusion coefficient in capillary water at 298 K, Dcw [m2/s] | 2.03 × 10−9 | 2.26 × 10−9 and 1.36 × 10−9 |
| Critical RH, RHc [%] | 75 | 60 and 90 |
| Activation energy for hydration reactions, ΔUhyd [kJ/mol] | 22.44 | 16.83 and 28.05 |
| Activation energy for Cl− diffusion in capillary water, Δ [kJ/mol] | 17.0 | 21.25 and 12.75 |
| Activation energy for RH diffusion, Δ [kJ/mol] | 38.9 | 29.125 and 48.625 |
| Exposure zone for surface Cl− concentration, Cs (t) [%weight of concrete] | Spray zone | Tidal zone Atmospheric zone |
| Parameters | Andrade_04 | Andrade_06 | Sergi_05 |
|---|---|---|---|
| Cement type | Type I | Type I | Type I |
| Aggregate type | Dense crushed limestone | Dense crushed limestone | N.A. |
| Tri-calcium silicate (C3S) [%] | 59.8 * | 59.8 * | 41.3 |
| Di-calcium silicate (C2S) [%] | 20.7 * | 20.7 * | 27 |
| Tri-calcium aluminate (C3A) [%] | 8.1 * | 8.1 * | 14.2 |
| Tetra-calcium aluminoferrite (C4AF) [%] | 11.5 * | 11.5 * | 16.1 |
| Water-cement (w/c) ratio | 0.4 | 0.6 | 0.5 |
| Air content, ac [%] | 7.9 | 8 | 10 * |
| Aggregate-to-cement (a/c) ratio | 1.9 * | 1.9* | 0 |
| Curing duration, tcu [days], | 14 | 14 | 90 |
| RH during curing, RHcu [%] | 100 | 100 | 100 |
| Temperature during curing, Tcu [K] | 296 | 296 | 293 |
| Age of concrete at the start of the exposure [days] | 104 | 104 | 90 |
| Exposure duration, texp [days] | 90 | 90 | 100 |
| RH during exposure, RHexp [%] | 100 | 100 | 100 |
| Temperature during exposure, Texp [K] | 296 | 296 | 298 |
| Surface Cl− concentration at the end of the exposure period, Cs [M] | 0.75 | 0.552 | 1.00 |
| Temporal function of surface Cl− concentration, Cs (t) [M]* | Cs × log((10 × t/texp + 1)/1.1) | Cs × log((10 × t/texp + 1)/1.1) | Cs × log((10 × t/texp + 1)/1.1) |
| Cl− diffusion coefficient in capillary water at 298 K, Dcw [m2/s] * | 2.03 × 10−9 | 2.03 × 10−9 | 2.03 × 10−9 |
| Critical RH, RHc [%] * | 75 | 75 | 75 |
| Activation energy for hydration reactions, ΔUhyd [kJ/mol] * | 22.44 | 22.44 | 22.44 |
| Activation energy for Cl− diffusion in capillary water, Δ [kJ/mol] * | 17.0 | 17.0 | 17.0 |
| Activation energy for RH diffusion, Δ [kJ/mol] * | 38.9 | 38.9 | 38.9 |
| Parameters | Values |
|---|---|
| Cement type | Type I |
| Aggregate type | Dense crushed limestone |
| Tri-calcium silicate (C3S) [%] | 60.44 |
| Di-calcium silicate (C2S) [%] | 20.88 |
| Tri-calcium aluminate (C3A) [%] | 10.99 |
| Tetra-calcium aluminoferrite (C4AF) [%] | 7.69 |
| Water-cement (w/c) ratio | 0.50 |
| Air content, ac [%] | 6 |
| Aggregate-to-cement (a/c) ratio | 4.5 |
| Curing duration, tcu [days] | 14 |
| RH during curing, RHcu [%] | See Figure 10 |
| Temperature during curing, Tcu [K] | See Figure 10 |
| Age of concrete at the start of the exposure [days] | 14 |
| Exposure duration, texp [years] | 15 |
| RH during exposure, RHexp [%] | See Figure 10 |
| Temperature during exposure, Texp [K] | See Figure 10 |
| Temporal function of surface Cl− concentration, Cs (t) [M] | See Equation (32) |
| Temporal function of surface O2 concentration, O2 (t) [M] | 3 × 10−4 |
| Cl− diffusion coefficient in capillary water at 298 K, Dcw [m2/s] | 2.03 × 10−9 |
| Critical RH, RHc [%] | 75 |
| Activation energy for hydration reactions, ΔUhyd [kJ/mol] | 22.44 |
| Activation energy for Cl− diffusion in capillary water, Δ [kJ/mol] | 17.0 |
| Activation energy for RH diffusion, Δ [kJ/mol] | 38.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jain, A.; Gencturk, B. Multiphysics and Multiscale Modeling of Coupled Transport of Chloride Ions in Concrete. Materials 2021, 14, 885. https://doi.org/10.3390/ma14040885
Jain A, Gencturk B. Multiphysics and Multiscale Modeling of Coupled Transport of Chloride Ions in Concrete. Materials. 2021; 14(4):885. https://doi.org/10.3390/ma14040885
Chicago/Turabian StyleJain, Amit, and Bora Gencturk. 2021. "Multiphysics and Multiscale Modeling of Coupled Transport of Chloride Ions in Concrete" Materials 14, no. 4: 885. https://doi.org/10.3390/ma14040885
APA StyleJain, A., & Gencturk, B. (2021). Multiphysics and Multiscale Modeling of Coupled Transport of Chloride Ions in Concrete. Materials, 14(4), 885. https://doi.org/10.3390/ma14040885







