CFRP Origami Metamaterial with Tunable Buckling Loads: A Numerical Study
Abstract
:1. Introduction
2. Materials and Methods
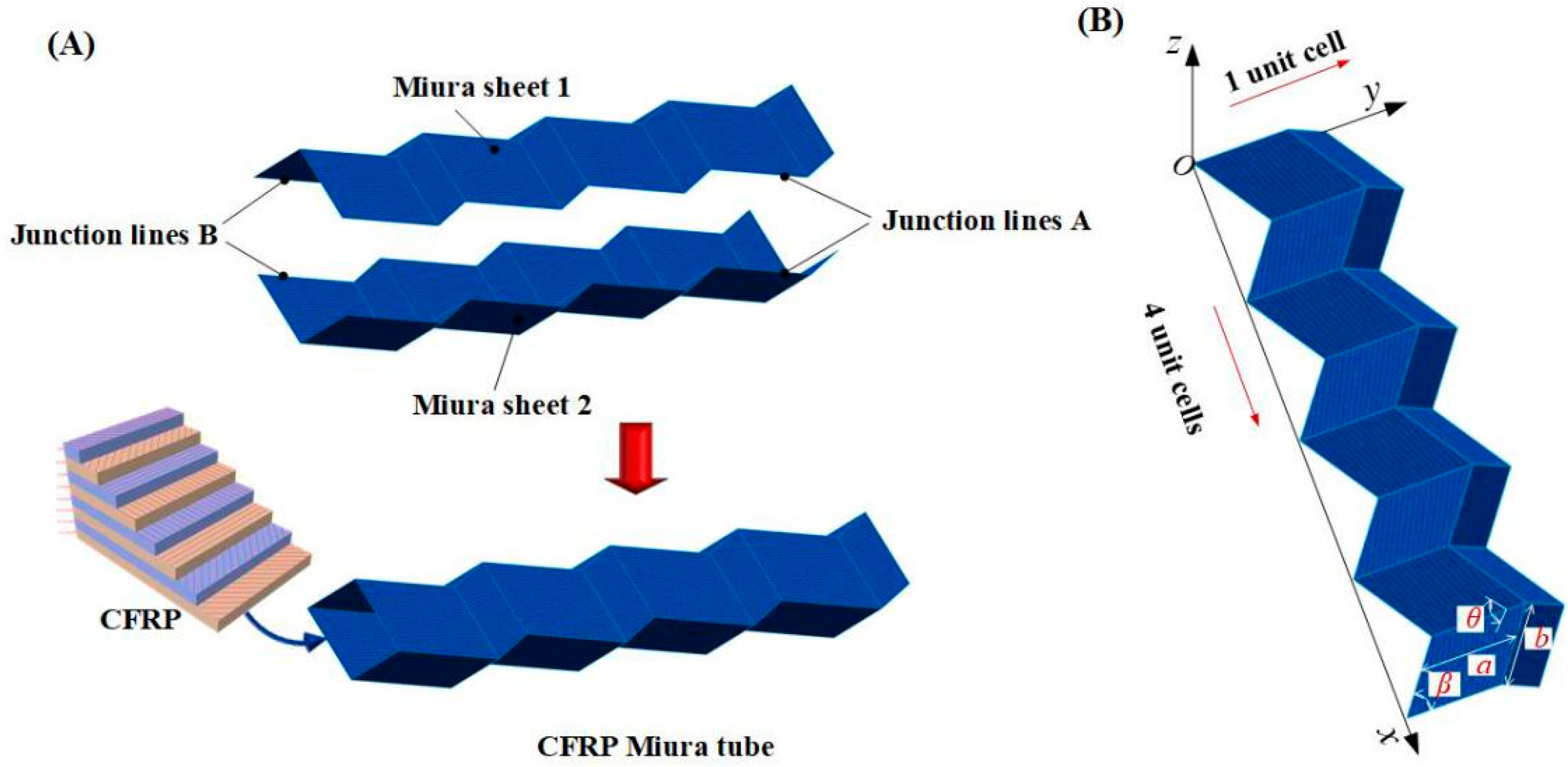
2.1. Modelling of the CFRP Origami Metamaterial
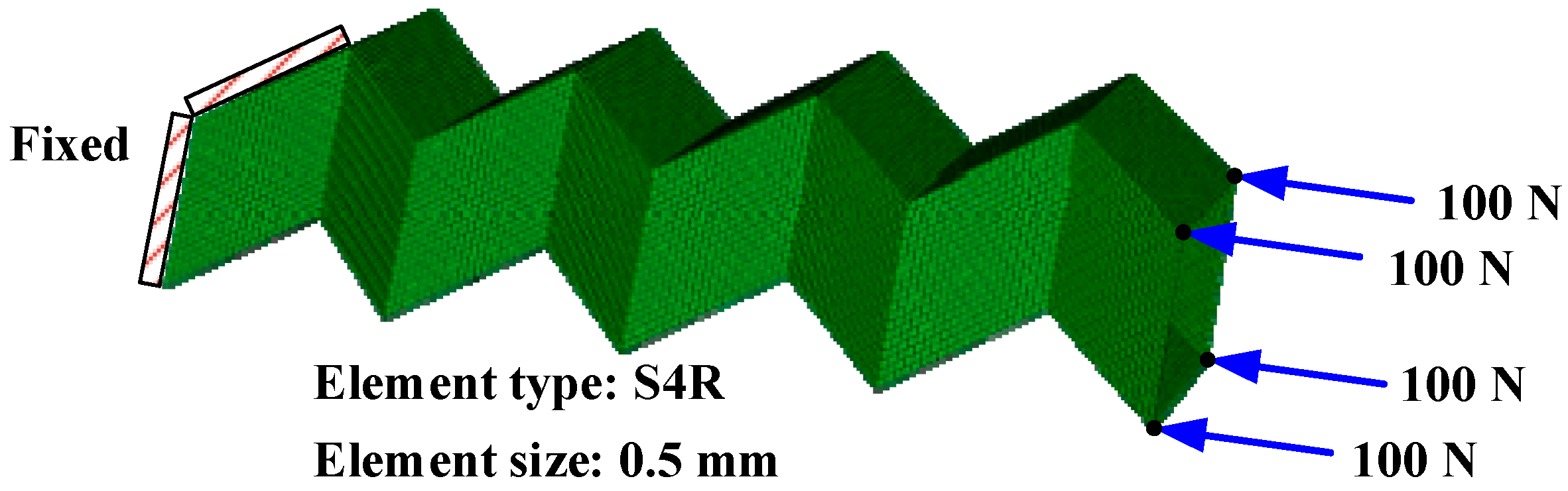
2.2. Numerical Simulations
2.3. Theoretical Prediction of the Axial Buckling Loads for a Classical CFRP Plate
3. Results
3.1. Validation of the FE Modelling Process for Calculating the Buckling Load
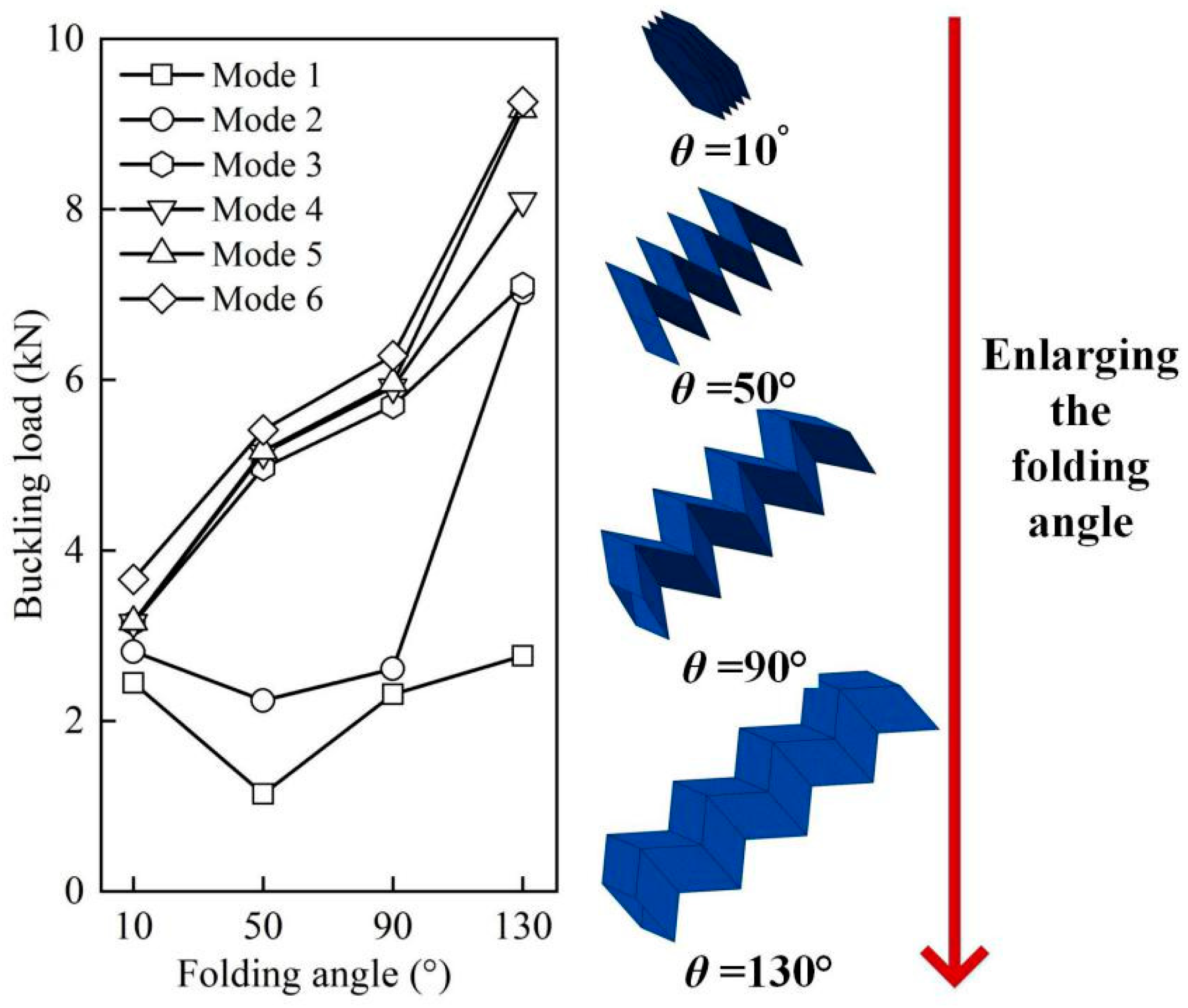
3.2. Influences of the Folding Angle
3.3. Influences of CFRP Properties
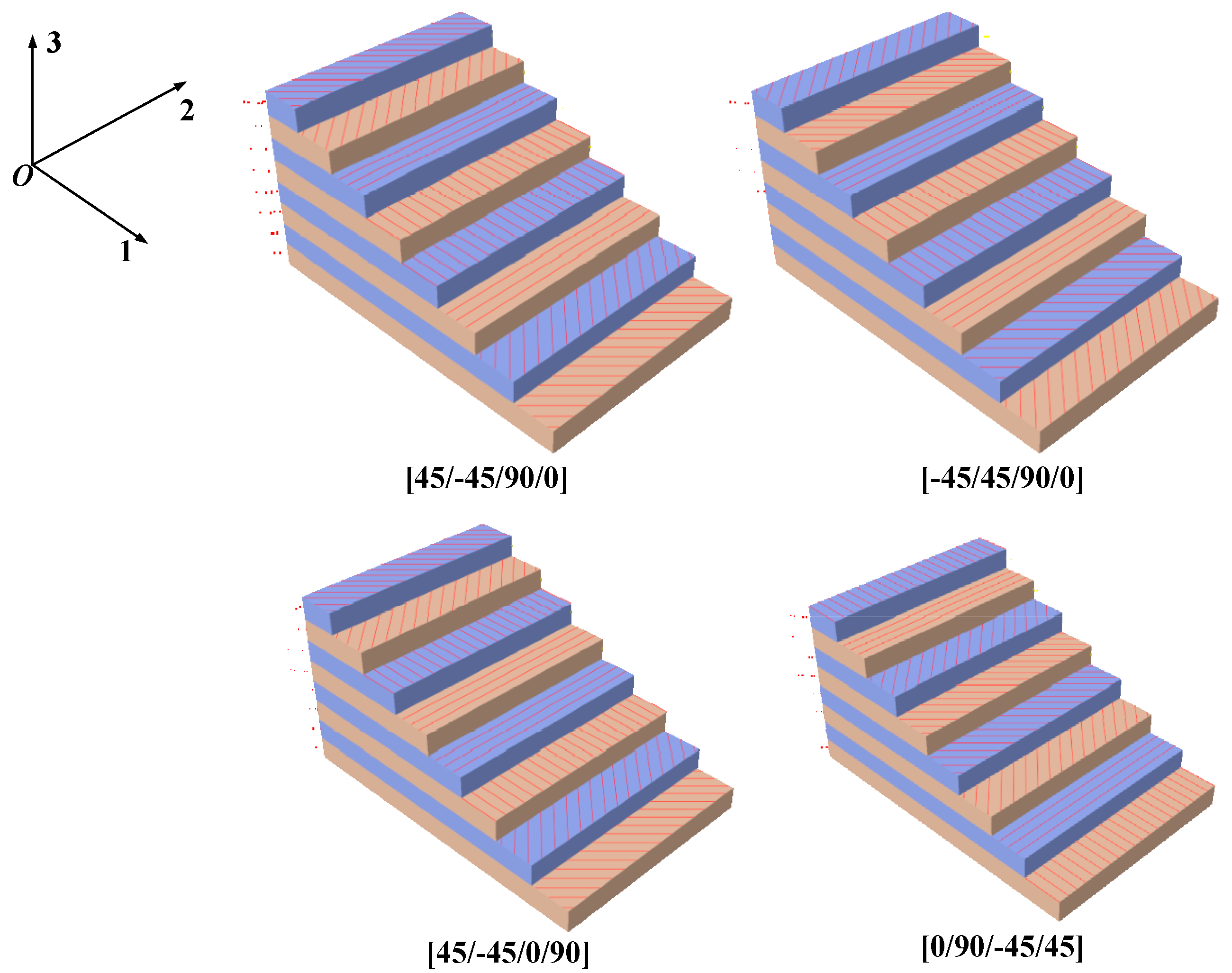
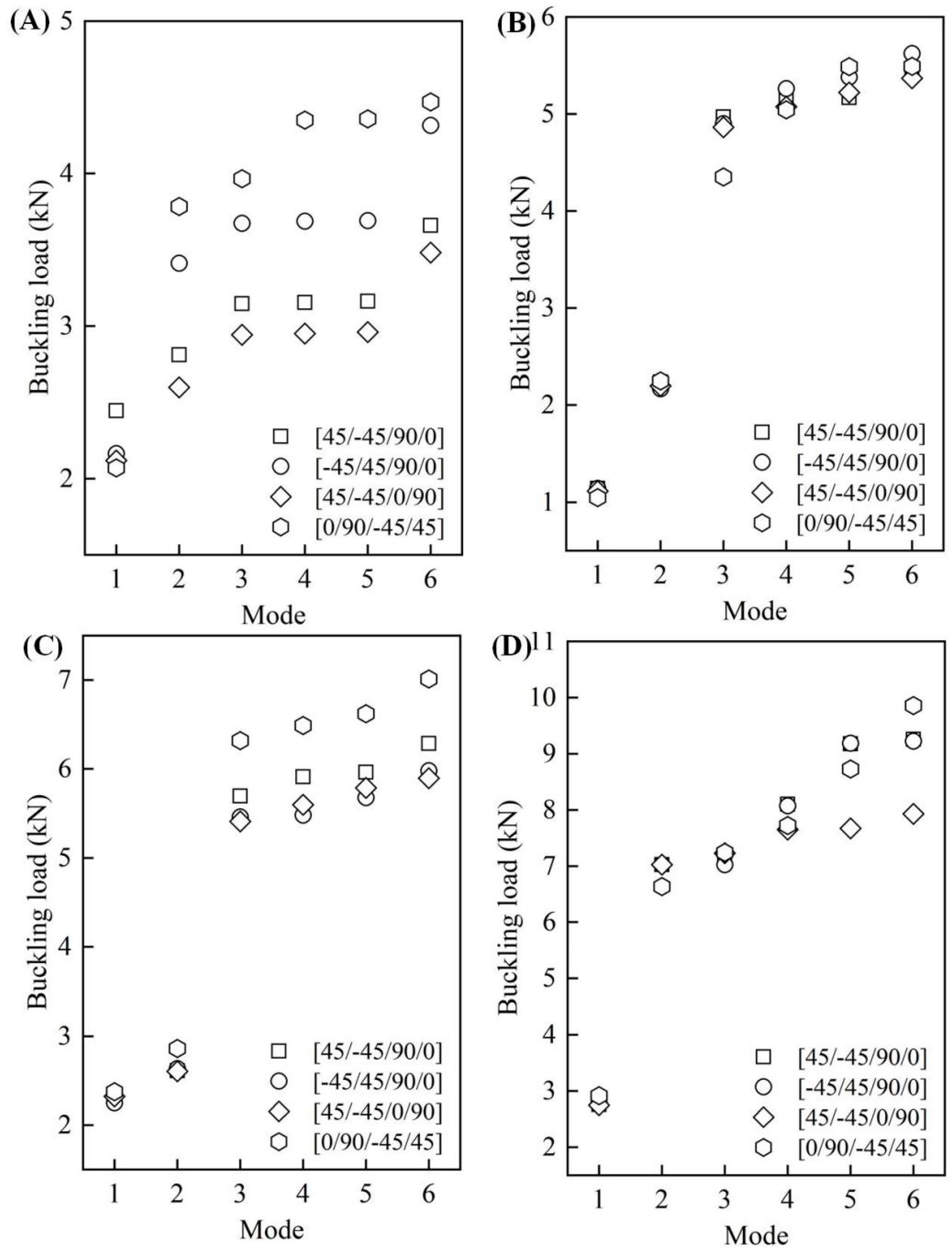
3.3.1. The Layer Order
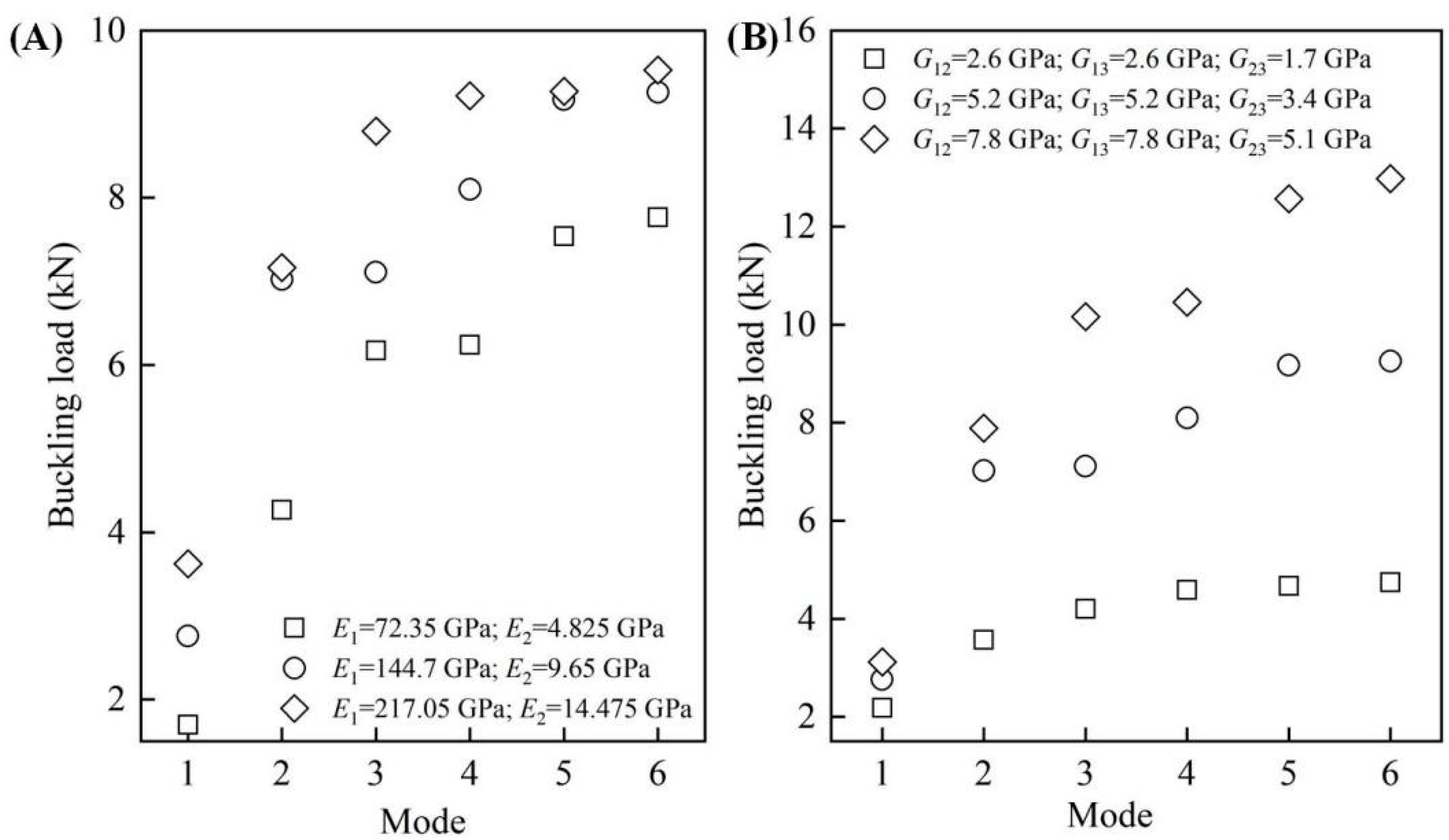
3.3.2. The Material Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, J.-H. Generalized variational principles for buckling analysis of circular cylinders. Acta Mech. 2020, 231, 899–906. [Google Scholar] [CrossRef]
- Tang, H.; Li, L.; Hu, Y. Buckling analysis of two-directionally porous beam. Aerosp. Sci. Technol. 2018, 78, 471–479. [Google Scholar] [CrossRef]
- Wagner, H.; Hühne, C.; Niemann, S. Robust knockdown factors for the design of spherical shells under external pressure: Development and validation. Int. J. Mech. Sci. 2018, 141, 58–77. [Google Scholar] [CrossRef]
- Hong, Z.; Liu, R. Three-dimensional explicit dynamic numerical method to simulate a deep-sea pipeline ex-hibiting lateral global buckling. Int. J. Steel Struct. 2019, 19, 1393–1407. [Google Scholar] [CrossRef]
- Tian, K.; Wang, B.; Hao, P.; Waas, A.M. A high-fidelity approximate model for determining lower-bound buckling loads for stiffened shells. Int. J. Solids Struct. 2018, 148, 14–23. [Google Scholar] [CrossRef]
- Wu, C.; Fang, J.; Li, Q. Multi-material topology optimization for thermal buckling criteria. Comput. Methods Appl. Mech. Eng. 2019, 346, 1136–1155. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, X.; Zhu, B. Design of buckling-induced mechanical metamaterials for energy absorption using topology optimization. Struct. Multidiscip. Optim. 2018, 58, 1395–1410. [Google Scholar] [CrossRef]
- Li, H.; Gao, L.; Li, H.; Tong, H. Spatial-varying multi-phase infill design using density-based topology optimi-zation. Comput. Methods Appl. Mech. Eng. 2020, 372, 113354. [Google Scholar] [CrossRef]
- Liu, J.; Wen, G.; Xie, Y.M. Layout optimization of continuum structures considering the probabilistic and fuzzy directional uncertainty of applied loads based on the cloud model. Struct. Multidiscip. Optim. 2016, 53, 81–100. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Li, T.; Cao, S.; Wang, L. Hoberman-sphere-inspired lattice metamaterials with tunable negative thermal expansion. Compos. Struct. 2018, 189, 586–597. [Google Scholar] [CrossRef]
- Wen, G.; Ou, H.; Liu, J. Ultra-wide band gap in a two-dimensional phononic crystal with hexagonal lattices. Mater. Today Commun. 2020, 24, 100977. [Google Scholar] [CrossRef]
- Silverberg, J.L.; Evans, A.A.; McLeod, L.; Hayward, R.C.; Hull, T.; Santangelo, C.D.; Cohen, I. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 2014, 345, 647–650. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Xu, S.; Wen, G.; Xie, Y.M. Mechanical behaviour of a creased thin strip. Mech. Sci. 2018, 9, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Lu, G.; Chen, Y.; Leong, Y.W. Deformation of the Miura-ori patterned sheet. Int. J. Mech. Sci. 2015, 99, 130–142. [Google Scholar] [CrossRef]
- Schenk, M.; Guest, S.D. Geometry of Miura-folded metamaterials. Proc. Natl. Acad. Sci. USA 2013, 110, 3276–3281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pydah, A.; Batra, R. Crush dynamics and transient deformations of elastic-plastic Miura-ori core sandwich plates. Thin-Walled Struct. 2017, 115, 311–322. [Google Scholar] [CrossRef]
- Cai, J.; Deng, X.; Zhou, Y.; Feng, J.; Tu, Y. Bistable behavior of the cylindrical origami structure with Kresling pattern. J. Mech. Des. 2015, 137, 061406. [Google Scholar]
- Fang, H.; Li, S.; Ji, H.; Wang, K.W. Dynamics of a bistable Miura-origami structure. Phys. Rev. E 2017, 95, 052211. [Google Scholar] [CrossRef] [Green Version]
- Fuchi, K.; Diaz, A.R.; Rothwell, E.J.; Ouedraogo, R.O.; Tang, J. An origami tunable metamaterial. J. Appl. Phys. 2012, 111, 084905. [Google Scholar] [CrossRef]
- Overvelde, J.T.; De Jong, T.A.; Shevchenko, Y.; Becerra, S.A.; Whitesides, G.M.; Weaver, J.; Hoberman, C.; Bertoldi, K. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of free-dom. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Q.; Fang, R.; Chen, W.; Hao, H. Origami metamaterial with two-stage programmable compressive strength under quasi-static loading. Int. J. Mech. Sci. 2021, 189, 105987. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Wen, G.; Qing, Q.; Wang, H.; Zhao, G. A Novel Design Framework for Structures/Materials with Enhanced Mechanical Performance. Materials 2018, 11, 576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Filipov, E.T.; Tachi, T.; Paulino, G.H. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 12321–12326. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.; Zhao, D.; Jin, Y.; Wang, M.; You, Z. Unified parametric modeling of origami-based tube. Thin-Walled Struct. 2018, 133, 226–234. [Google Scholar] [CrossRef]
- Yang, K.; Xu, S.; Shen, J.; Zhou, S.; Xie, Y.M. Energy absorption of thin-walled tubes with pre-folded origami patterns: Numerical simulation and experimental verification. Thin-Walled Struct. 2016, 103, 33–44. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, Y.; Wang, B. Crashworthiness design for trapezoid origami crash boxes. Thin-Walled Struct. 2017, 117, 257–267. [Google Scholar] [CrossRef]
- Yin, H.; Zheng, X.; Wen, G.; Zhang, C.; Wu, Z. Design optimization of a novel bio-inspired 3D porous structure for crashworthiness. Compos. Struct. 2021, 255, 112897. [Google Scholar] [CrossRef]
- Yang, K.; Xu, S.; Zhou, S.; Xie, Y.M. Multi-objective optimization of multi-cell tubes with origami patterns for energy absorption. Thin-Walled Struct. 2018, 123, 100–113. [Google Scholar] [CrossRef]
- Liu, J.; Ou, H.; Zeng, R.; Zhou, J.; Long, K.; Wen, G.; Xie, Y.M. Fabrication, dynamic properties and multi-objective optimization of a metal origami tube with Miura sheets. Thin-Walled Struct. 2019, 144, 106352. [Google Scholar] [CrossRef]
- Du, Y.; Song, C.; Xiong, J.; Wu, L. Fabrication and mechanical behaviors of carbon fiber reinforced composite foldcore based on curved-crease origami. Compos. Sci. Technol. 2019, 174, 94–105. [Google Scholar] [CrossRef]
- Deleo, A.A.; O’Neil, J.; Yasuda, H.; Salviato, M.; Yang, J. Origami-based deployable structures made of car-bon fiber reinforced polymer composites. Compos. Sci. Technol. 2020, 191, 108060. [Google Scholar] [CrossRef]
- Ciampaglia, A.; Fiumarella, D.; Niutta, C.B.; Ciardiello, R.; Belingardi, G. Impact response of an origa-mi-shaped composite crash box: Experimental analysis and numerical optimization. Compos. Struct. 2021, 256, 113093. [Google Scholar] [CrossRef]
- Ye, H.; Ma, J.; Zhou, X.; Wang, H.; You, Z. Energy absorption behaviors of pre-folded composite tubes with the full-diamond origami patterns. Compos. Struct. 2019, 221, 110904. [Google Scholar] [CrossRef]
- Gohari, S.; Sharifi, S.; Burvill, C.; Mouloodi, S.; Izadifar, M.; Thissen, P. Localized failure analysis of internally pressurized laminated ellipsoidal woven GFRP composite domes: Analytical, numerical, and experimental studies. Arch. Civ. Mech. Eng. 2019, 19, 1235–1250. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Wei, J.; Lin, B.; Xu, J.; Fang, S. Finite element analysis of grinding process of long fiber reinforced ceramic matrix woven composites: Modeling, experimental verification and material removal mechanism. Ceram. Int. 2019, 45, 15920–15927. [Google Scholar] [CrossRef]
- Wang, G.-D.; Melly, S.K. Three-dimensional finite element modeling of drilling CFRP composites using Abaqus/CAE: A review. Int. J. Adv. Manuf. Technol. 2017, 94, 599–614. [Google Scholar] [CrossRef]
- Gohari, S.; Sharifi, S.; Sharifishourabi, G.; Vrcelj, Z.; Abadi, R. Effect of temperature on crack initiation in gas formed structures. J. Mech. Sci. Technol. 2013, 27, 3745–3754. [Google Scholar] [CrossRef]
- ABAQUS User’s Manual, Version 6.14; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2014.
- Torabizadeh, M.A. Buckling of the Composite Laminates under Mechanical Loads with Different Layups using Different Plate Theories. Adv. Compos. Lett. 2015, 24, 096369351502400. [Google Scholar] [CrossRef]


| E1 | E2 | E3 | υ12 | υ13 | υ23 | G12 | G13 | G23 |
|---|---|---|---|---|---|---|---|---|
| 144.7 GPa | 9.65 GPa | 9.65 GPa | 0.30 | 0.30 | 0.45 | 5.2 GPa | 5.2 GPa | 3.4 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Chen, S.; Shen, T.; Wang, R.; Liu, J. CFRP Origami Metamaterial with Tunable Buckling Loads: A Numerical Study. Materials 2021, 14, 917. https://doi.org/10.3390/ma14040917
Zhu H, Chen S, Shen T, Wang R, Liu J. CFRP Origami Metamaterial with Tunable Buckling Loads: A Numerical Study. Materials. 2021; 14(4):917. https://doi.org/10.3390/ma14040917
Chicago/Turabian StyleZhu, Houyao, Shouyan Chen, Teng Shen, Ruikun Wang, and Jie Liu. 2021. "CFRP Origami Metamaterial with Tunable Buckling Loads: A Numerical Study" Materials 14, no. 4: 917. https://doi.org/10.3390/ma14040917
APA StyleZhu, H., Chen, S., Shen, T., Wang, R., & Liu, J. (2021). CFRP Origami Metamaterial with Tunable Buckling Loads: A Numerical Study. Materials, 14(4), 917. https://doi.org/10.3390/ma14040917







