Prediction Models Based on Regression and Artificial Neural Network for Moduli of Layers Constituted by Open-Graded Aggregates
Abstract
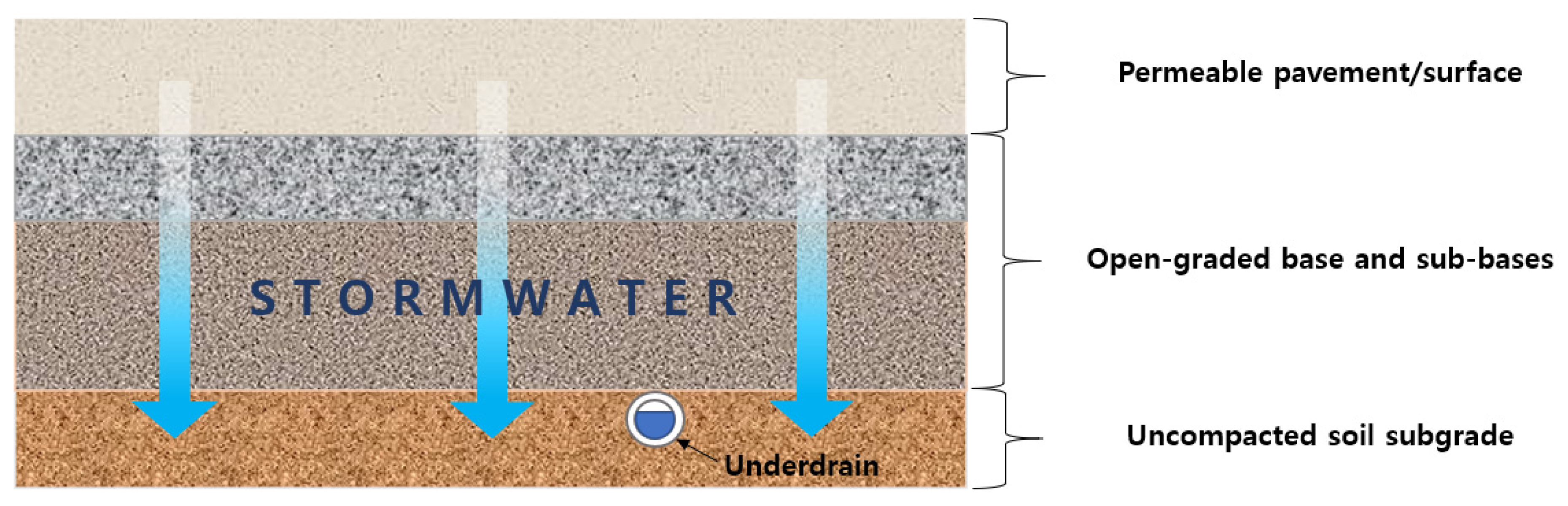
1. Introduction
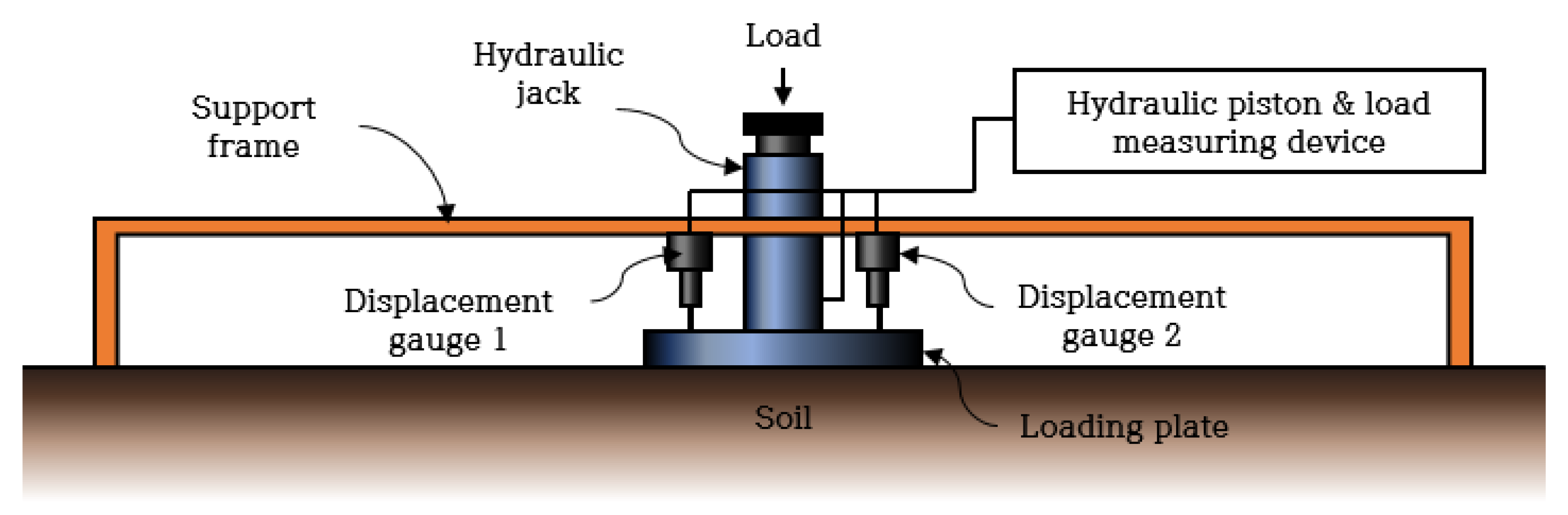
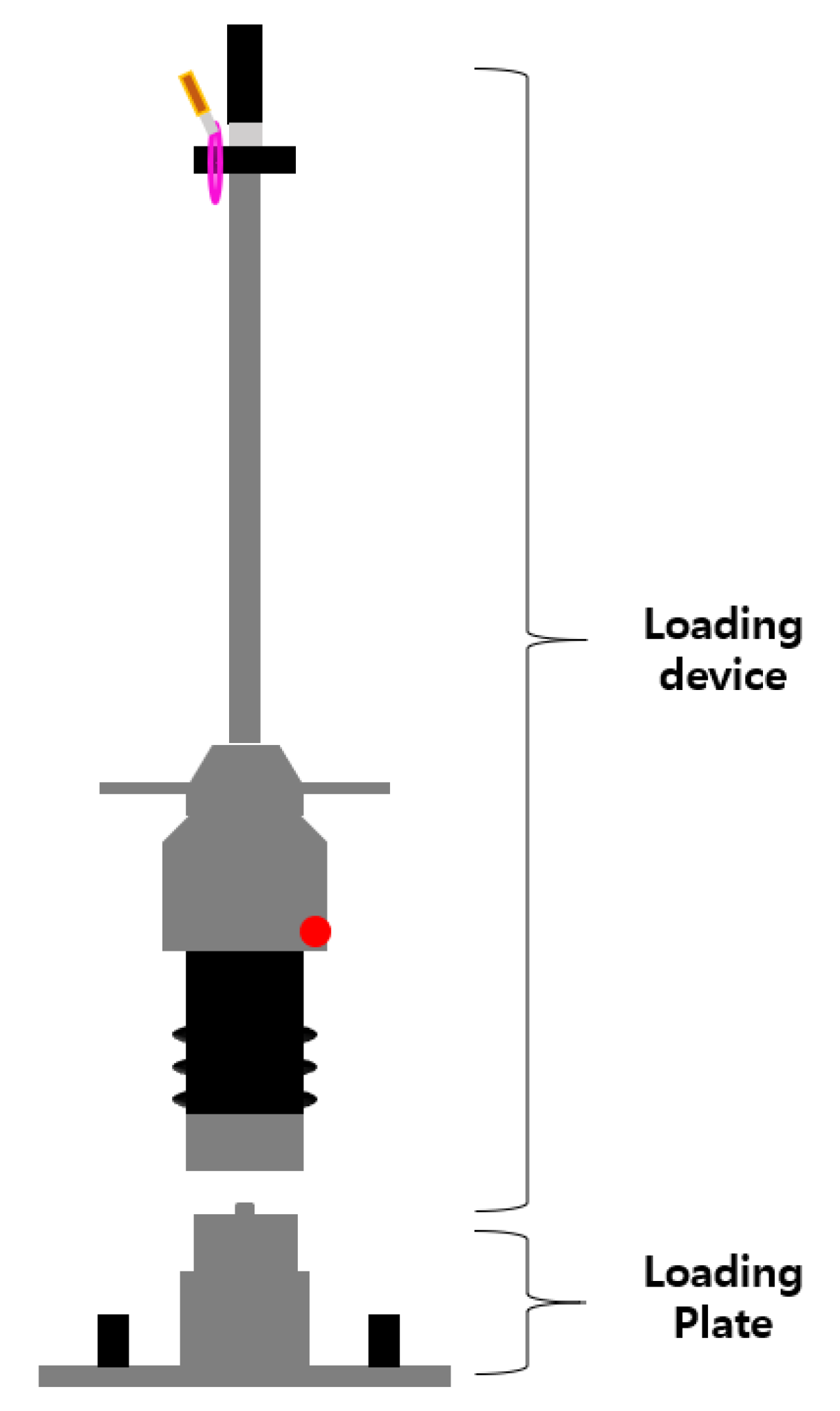
2. Field Modulus Evaluating Devices
3. Field Experiment
3.1. Test Materials
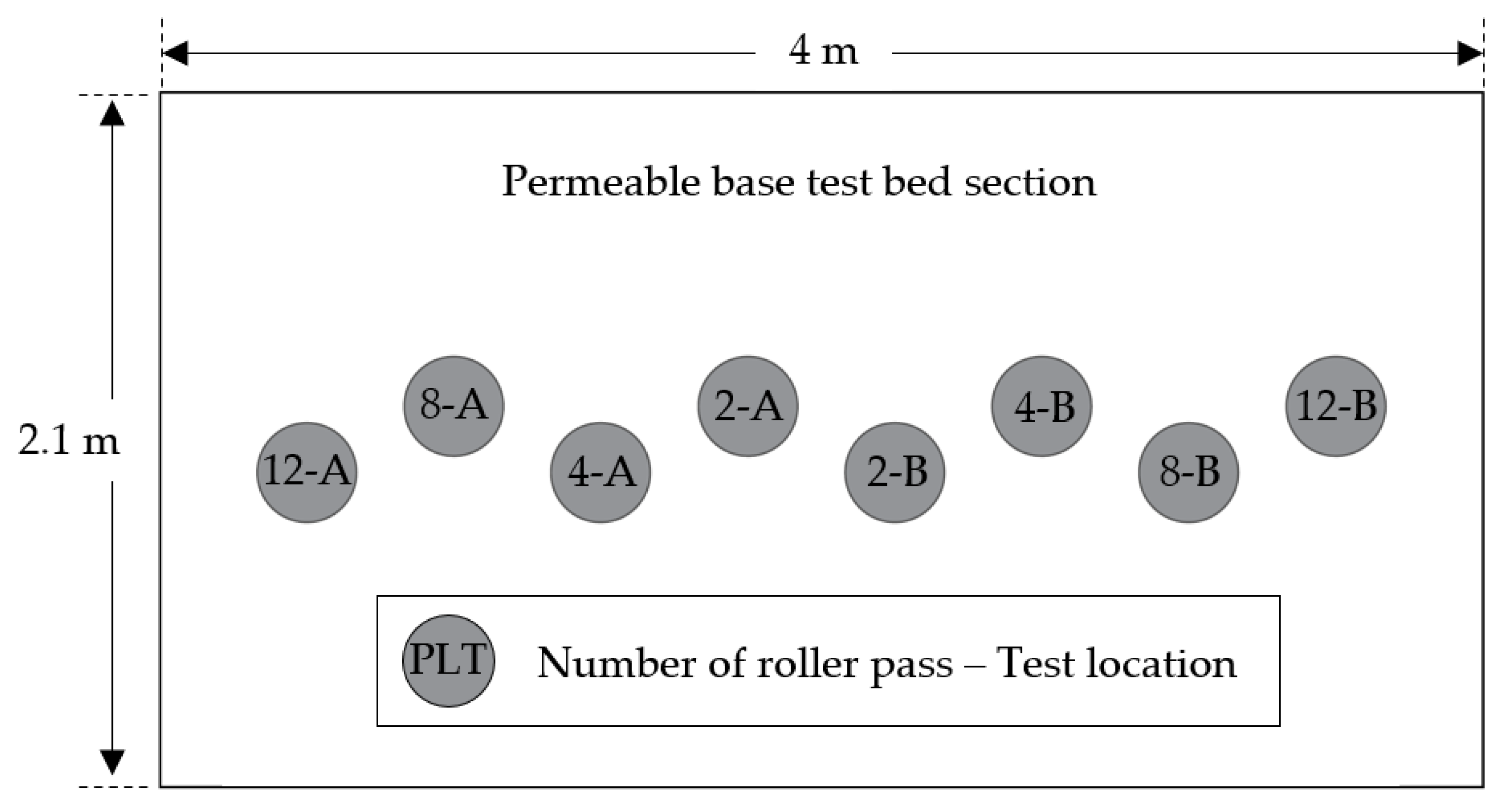
3.2. Test Program
4. Modulus of Open-Graded Aggregate
4.1. Field Test Results
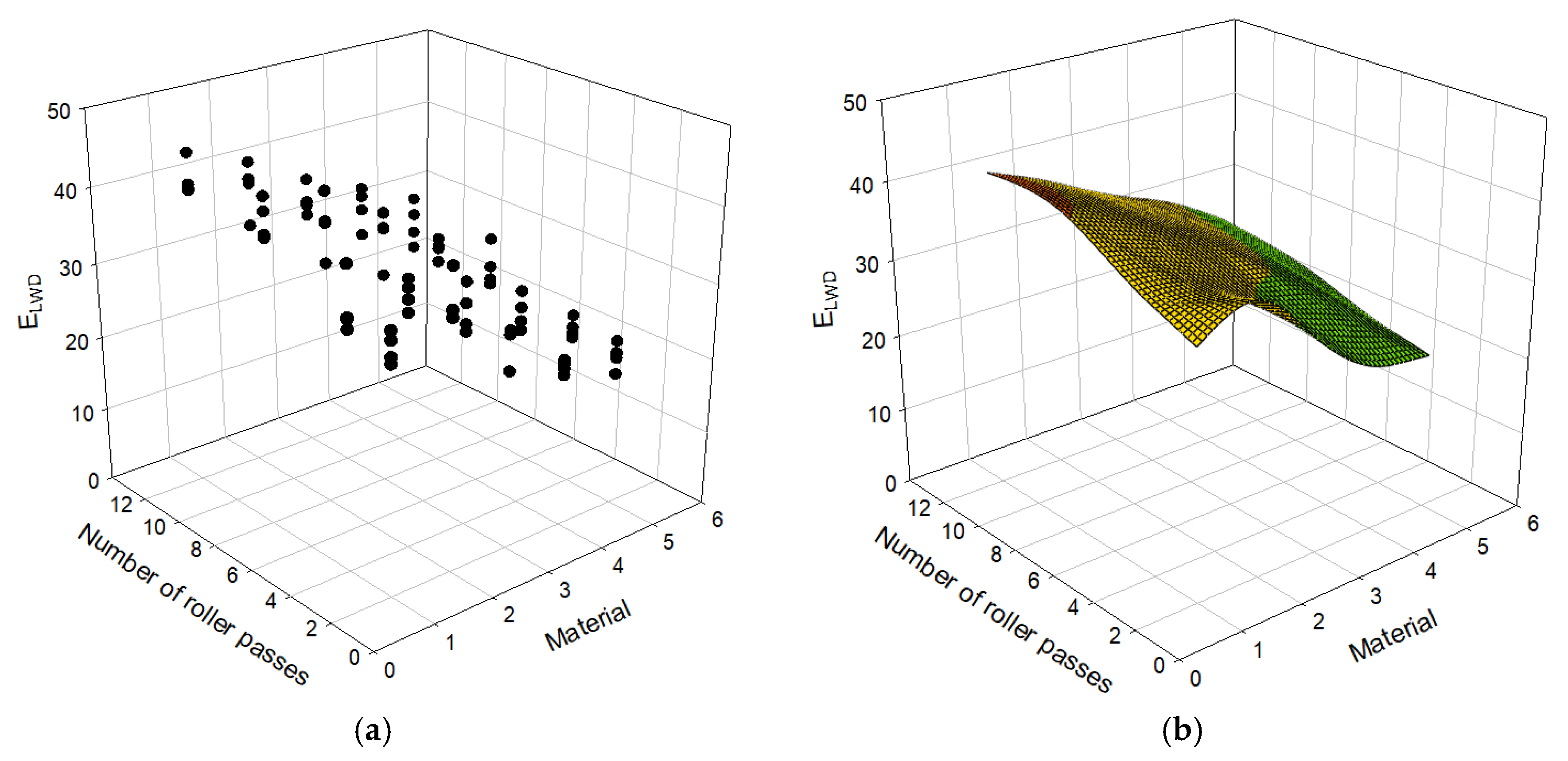
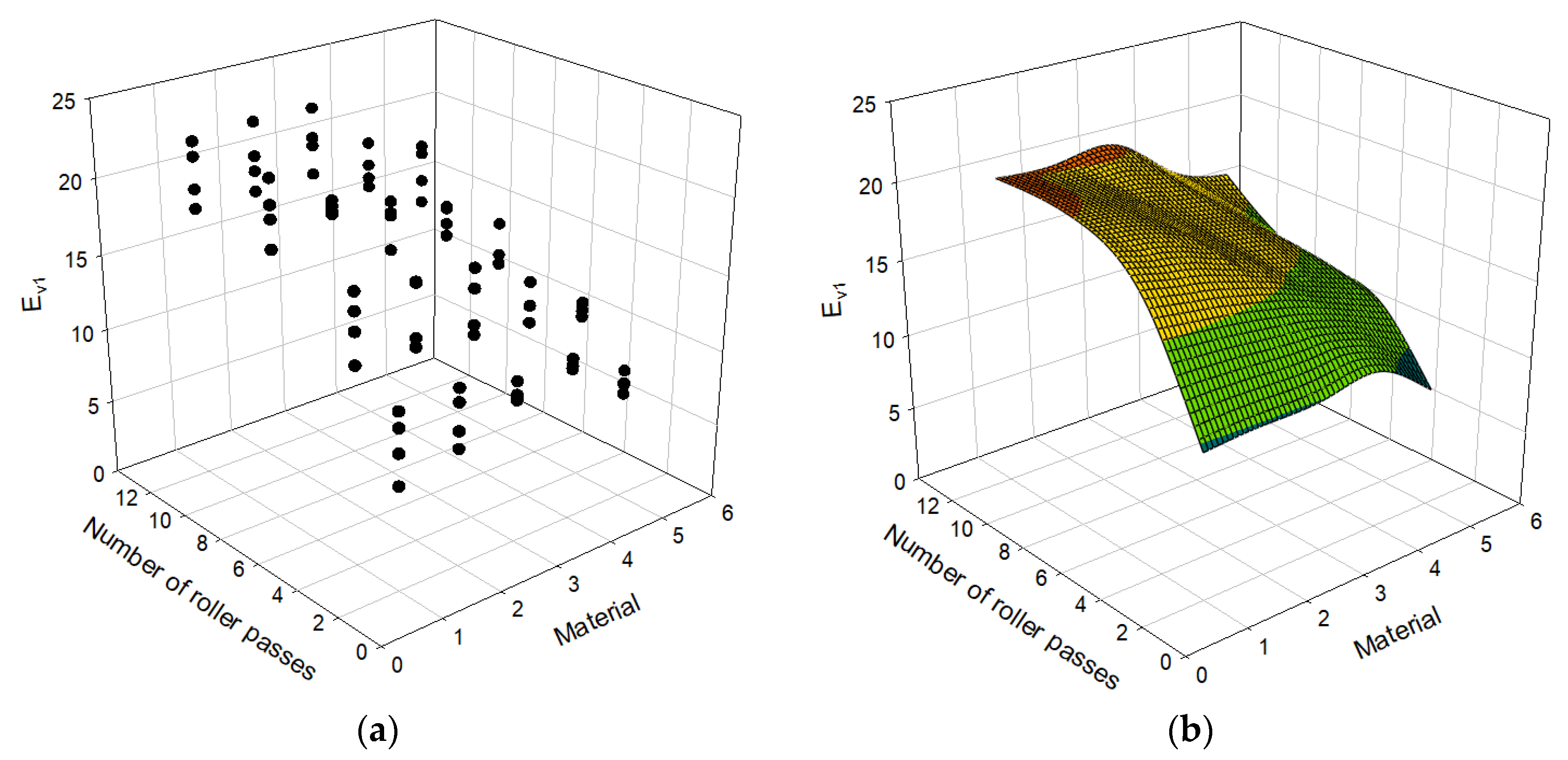
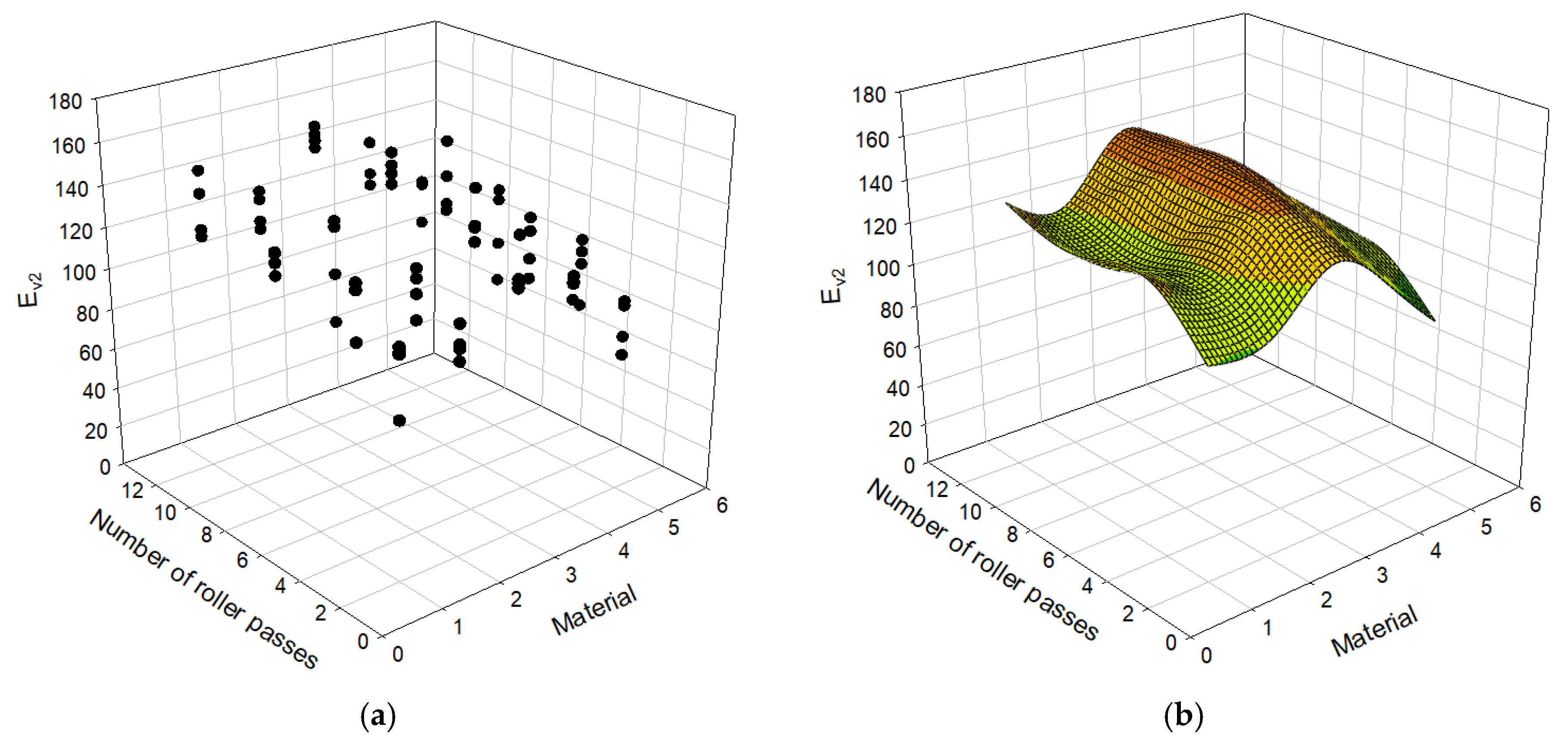
4.2. Modulus Results Depending on the Number of Roller Passes
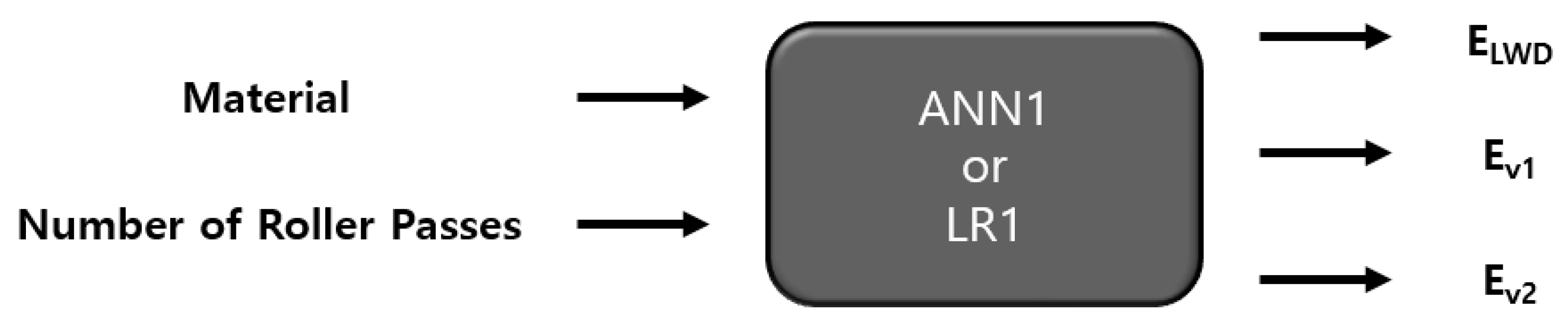
5. Artificial Neural Network and Linear Regression
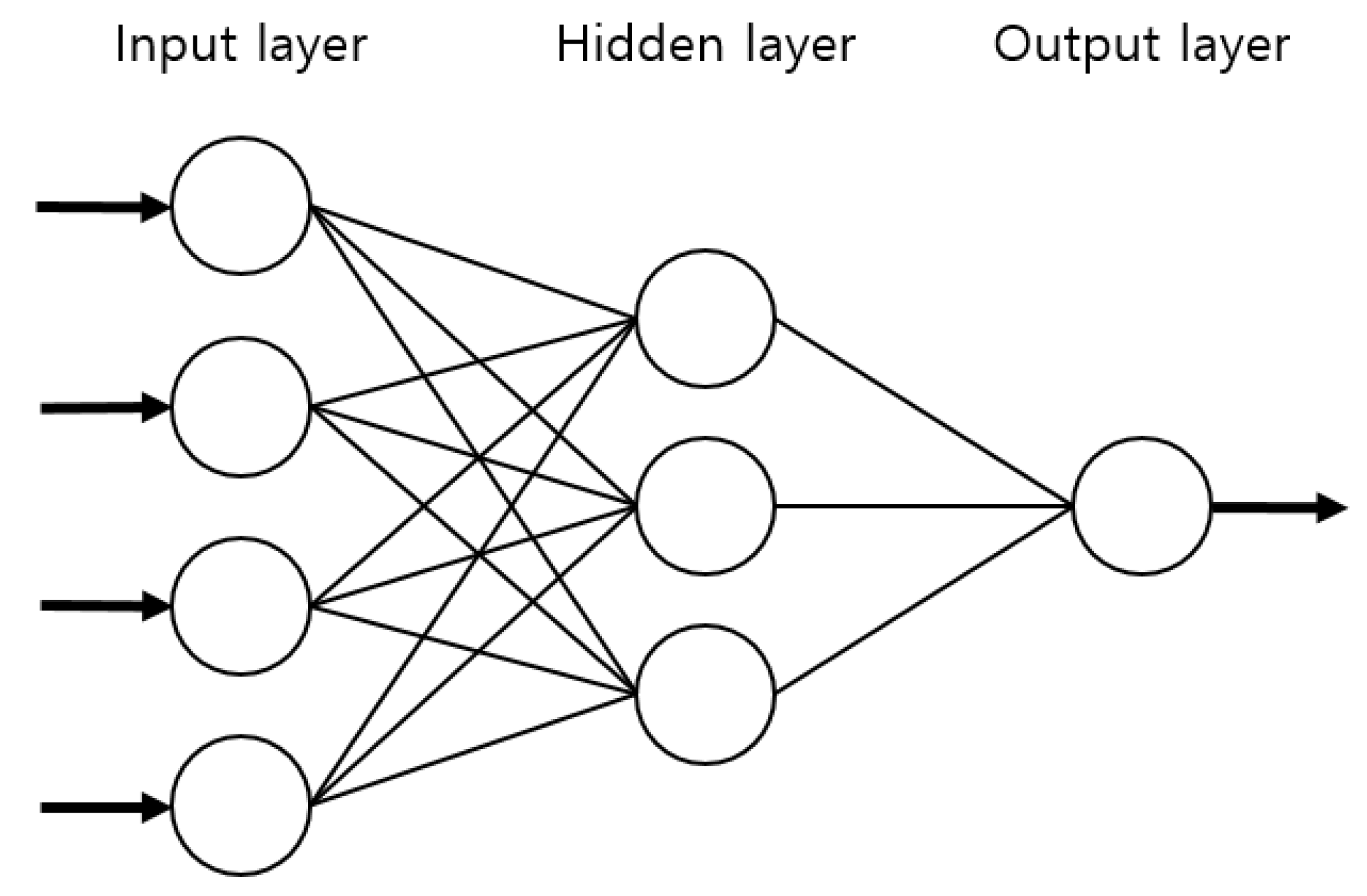
5.1. Artificial Neural Network Model
5.2. Linear Regression Model
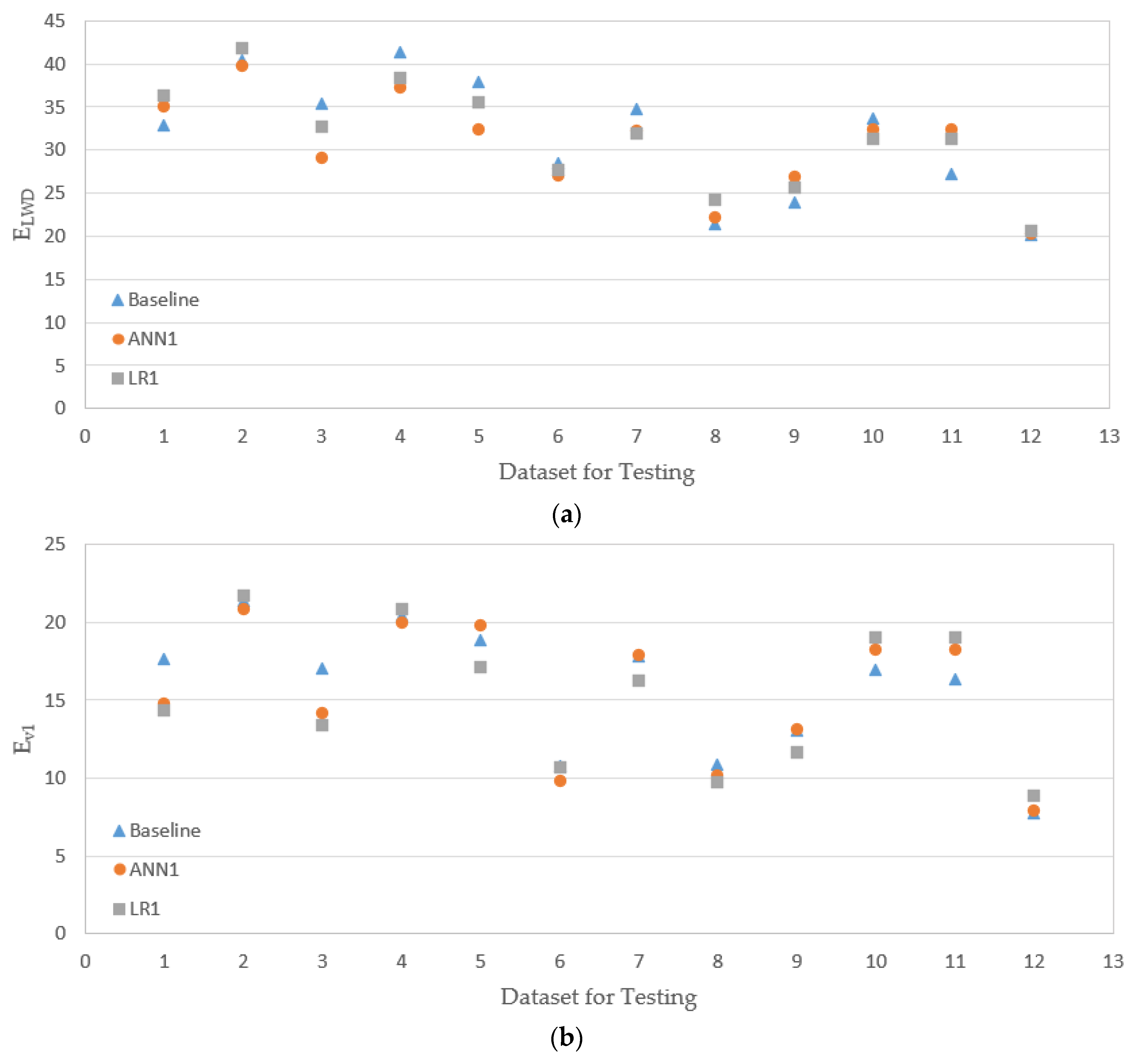
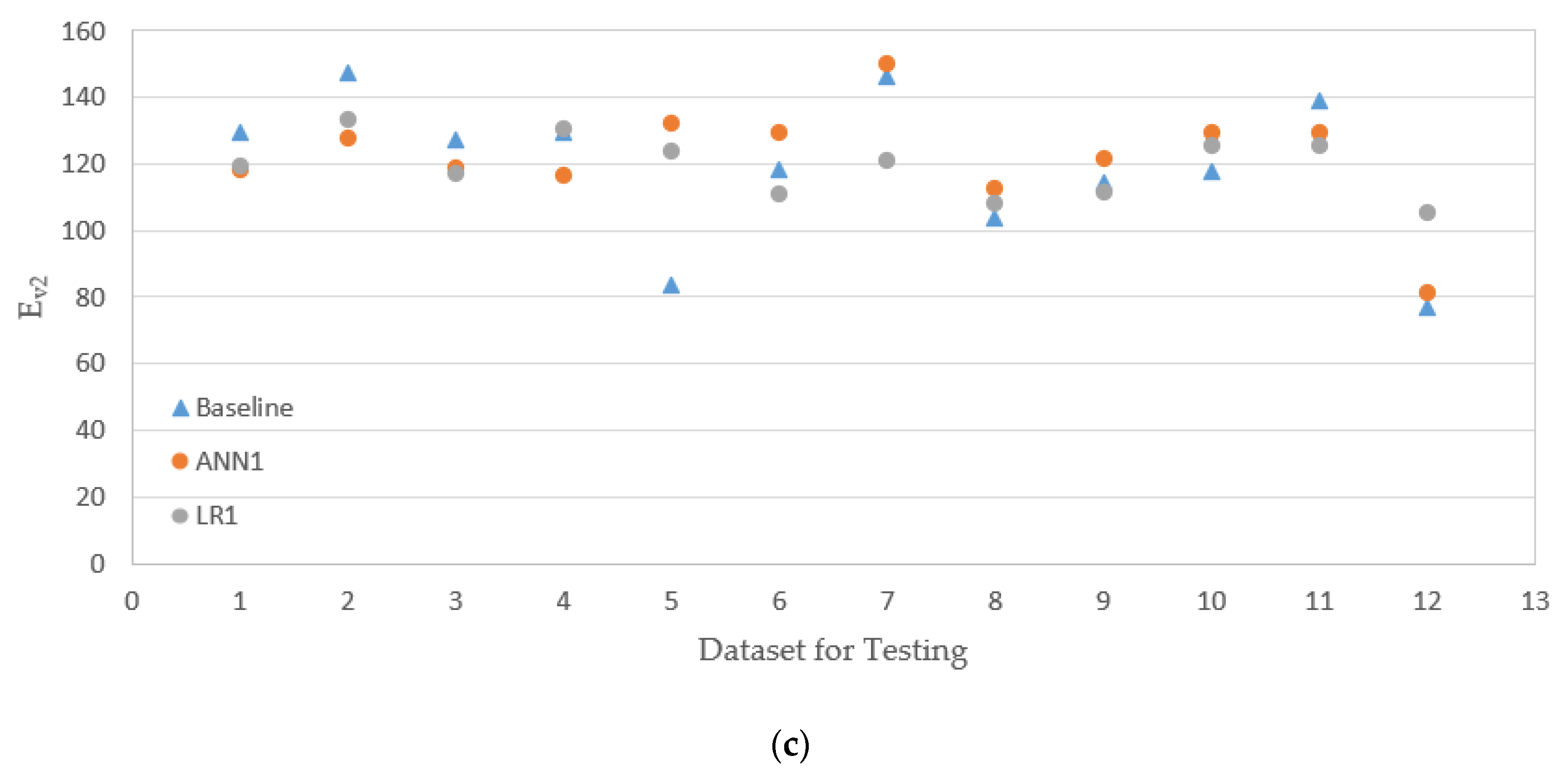
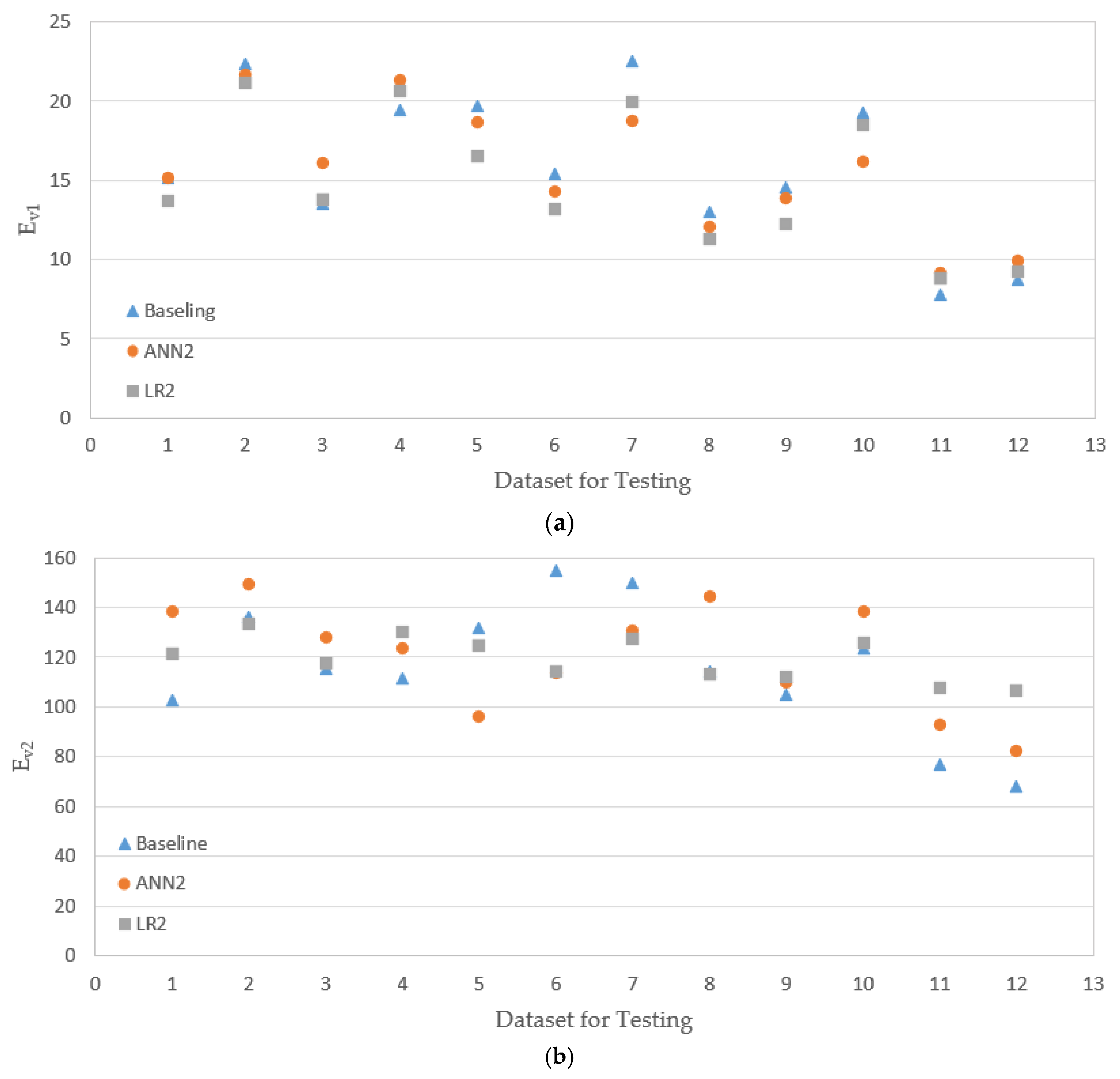
5.3. Evaluation Results and Comparison
6. Summary and Conclusions
- The modulus from the first loading curve of PLT was more sensitive to the number of roller passes than the moduli from the reloading curve of PLT and from LWD. It is due to the significant compressional and shear deformation that happens during the first loading of PLT, which does not appear during the reloading of PLT and dynamic loading of LWD.
- Overall, the moduli from PLT and LWD steeply increase until the number of roller passes reaches 4, and they gradually increase until the number of roller passes becomes 8. The number of roller passes 4, which is typically used in practice, may be an efficient number, but one may consider applying the number of roller passes 8 to achieve better stiffness for open-graded aggregates.
- The models that do have one less input (the modulus from LWD) actually performed a little better than the models with more inputs. When there is no good correlation between input and output (e.g., the moduli from PLT and LWD), adding more input variables does not necessarily help the prediction of the model.
- A set of simple linear equations were proposed to evaluate the moduli of open-graded aggregates from PLT and LWD based on the material type and the number of roller passes. The predictions based on ANN models did not necessarily provide a better match with the baseline compared to LR models.
- The stiffness results of LWD and PLT and regression equations presented in this study may be taken as references when CCC operations are made in open-graded aggregates. The characteristics of open-graded aggregates of different sizes, shapes, and minerals should be further studied for reliable application of open-graded aggregates to the base of permeable pavements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baek, S.-S.; Ligaray, M.; Pyo, J.; Park, J.-P.; Kang, J.-H.; Pachepsky, Y.; Chun, J.A.; Cho, K.H. A novel water quality module of the SWMM model for assessing low impact development (LID) in urban watersheds. J. Hydrol. 2020, 586, 124886. [Google Scholar] [CrossRef]
- Zahmatkesh, Z.; Burian, S.J.; Karamouz, M.; Tavakol-Davani, H.; Goharian, E. Low-Impact Development Practices to Mitigate Climate Change Effects on Urban Stormwater Runoff: Case Study of New York City. J. Irrig. Drain. Eng. 2015, 141, 04014043. [Google Scholar] [CrossRef]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of Low Impact Development Practices: Literature Review and Suggestions for Future Research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Dietz, M.E. Low Impact Development Practices: A Review of Current Research and Recommendations for Future Directions. Water Air Soil Pollut. 2007, 186, 351–363. [Google Scholar] [CrossRef]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and implementation of low impact development—A review. Sci. Total Environ. 2017, 607–608, 413–432. [Google Scholar] [CrossRef]
- Smith, D.R. Permeable Interlocking Concrete Pavements, 4th ed.; Interlocking Concrete Pavement Istitute: Herndon, VA, USA, 2011. [Google Scholar]
- Kumar, K.; Kozak, J.; Hundal, L.; Cox, A.; Zhang, H.; Granato, T. In-situ infiltration performance of different permeable pavements in a employee used parking lot—A four-year study. J. Environ. Manag. 2016, 167, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, B.E.; Lindow, K.C.; Smith, D.R. Permeable Pavements, 1st ed.; American Society of Civil Engineers: Reston, VA, USA, 2015. [Google Scholar]
- Brattebo, B.O.; Booth, D.B. Long-term stormwater quantity and quality performance of permeable pavement systems. Water Res. 2003, 37, 4369–4376. [Google Scholar] [CrossRef]
- Seoul Metropolitan City. Design, Construction and Maintenance Standards of Permeable Block Pavement; Seoul Metropolitan City: Seoul, Korea, 2013. [Google Scholar]
- Interpave. Understanding Permeable Paving and Suds, 6th ed.; Interpave: Leicester, UK, 2020. [Google Scholar]
- CMAA. Permeable Interlocking Concrete Pavements—Design and Construction Guide, PE01 November 2010 ed.; Concrete Masonry Association of Australia (CMAA): Artarmon, Australia, 2010. [Google Scholar]
- Abu-Farsakh, M.; Alshibli, K.A.; Nazzal, M.; Seyman, E. Assessment of In-Situ Test Technology for Construction Control of Base Courses and Embankments; FHWA/LA.041389; Louisiana Transportation Research Center: Boton Rouge, LA, USA, 2004. [Google Scholar]
- Alshibli, K.A.; Abu-Farsakh, M.; Seyman, E. Laboratory Evaluation of the Geogauge and Light Falling Weight Deflectometer as Construction Control Tools. J. Mater. Civ. Eng. 2005, 17, 560–569. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, D.X.; Wang, K.C.P.; Hall, K.D.; Qiu, Y. Mechanistic-empirical pavement design guide (MEPDG): A bird’s-eye view. J. Mod. Transp. 2011, 19, 114–133. [Google Scholar] [CrossRef]
- Board, T.R. Modulus-Based Construction Specification for Compaction of Earthwork and Unbound Aggregate; The National Academies Press: Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Nazzal, M. Non-Nuclear Methods for Compaction Control of Unbound Materials; National Cooperative Highway Research Program Synthesis 456; Transportation Research Board: Washington, DC, USA, 2014. [Google Scholar]
- DIN. Earthworks and Foundations—Soil Classification for Civil Engineering Purposes; DIN 18196; DIN Deutsches Institut für Normung e. V.: Berlin, Germany, 2011. [Google Scholar]
- ASTM International. Standard Test Method for Measuring Deflections Using a Portable Impulse Plate Load Test Device; ASTM E2835; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- ASTM International. Standard Test Method for Measuring Stiffness and Apparent Modulus of Soil and Soil-Aggregate in-Place by Electro-Mechanical Method; ASTM D6758; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- ASTM International. Standard Test Method for Use of the Dynamic Cone Penetrometer in Shallow Pavement Applications; ASTM D6951; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Fleming, P.; Frost, M.; Lambert, J. Review of Lightweight Deflectometer for Routine In Situ Assessment of Pavement Material Stiffness. Transp. Res. Rec. J. Transp. Res. Board 2007, 2004, 80–87. [Google Scholar] [CrossRef]
- Kim, D.; Park, S. Relationshop between the subgrade reaction modulus and the strain modulus obtained using a plate loading test. In Proceedings of the 9th World Congress on Railway Research, Lille, France, 22–26 May 2011. [Google Scholar]
- Lenke, L.R.; McKeen, G.R.; Grush, M.P. Laboratory Evaluation of GeoGauge for Compaction Control. Transp. Res. Rec. J. Transp. Res. Board 2003, 1849, 20–30. [Google Scholar] [CrossRef]
- Lin, D.F.; Liau, C.C.; Lin, J.D. Factors Affecting Portable Falling Weight Deflectometer Measurements. J. Geotech. Geoenviron. Eng. 2006, 132, 804–808. [Google Scholar] [CrossRef]
- Meehan, C.L.; Tehrani, F.S.; Vahedifard, F. A comparison of density-based and modulus-based in situ test measurements for compaction control. Geotech. Test. J. 2012, 35, 387–399. [Google Scholar] [CrossRef]
- Sulewska, M.J. The Control of Soil Compaction Degree by Means of LFWD. Balt J. Road Bridge E 2012, 7, 36–41. [Google Scholar] [CrossRef]
- Elhakim, A.F.; Elbaz, K.; Amer, M.I. The use of light weight deflectometer for in situ evaluation of sand degree of compaction. HBRC J. 2014, 10, 298–307. [Google Scholar] [CrossRef]
- Berney, E.S.; Mejais-Santiago, M.; Kyzar, J.D. Non-Nuclear Alternatives to Monitoring Moisture-Density Response in Soils; ERDC/GSL TR-13-6; U.S. Army Engineer Research and Development Center Geotechnical and Structures Laboratory: Vicksburg, MS, USA, 2013. [Google Scholar]
- Volovski, M.; Arman, M.; Labi, S. Developing Statistical Limits for Using the Light Weight Defl ectometer (LWD) in Construction Quality Assurance; FHWA/IN/JTRP-2014/10; Purdue University: West Lafayette, IN, USA, 2014. [Google Scholar]
- Research Society of Road and Traffic. Additional Technical Contractual Conditions and Guidelines for Earthwork in Road Construction and Technical Testing Instructions for Soil and Rock in Road Construction; Research Society of Road and Traffic: Koln, Germnay, 1994. [Google Scholar]
- Korean Agency for Technology and Standards. Standard Test Method for Plate Load Test on Soils for Road; KS F 2310; Korean Agency for Technology and Standards: Seoul, Korea, 2015.
- Choi, C. Stiffness Evaluation of Open-Graded Aggregate Base Corresponding to Compaction Level Based on Plate Load Tests; Pusan Natioanl University: Busan, Korea, 2019. [Google Scholar]
- Zorn, I. User Manual for the Light Weight Deflectometer (LWD) ZFG 3.0; Zorn: Stendal, Germany, 2011. [Google Scholar]
- Kim, D.-S.; Park, S.-Y.; Kim, S.-I. Evaluation of Correlation between Subgrade Reaction Modulus and Strain Modulus Using Plate Loading Test. J. Korean Geotech. Soc. 2008, 24, 57–67. [Google Scholar]
- Wiman, L.G. Accelerated Load Testing of Pavements: HVS-NORDIC Tests at VTI Sweden 2003–2004; VTI Rapport 544A; Swedish National Road and Transport Research Institute: Linköping, Sweden, 2006.
- Choi, Y.; Ahn, D.; Lee, Y.; Ahn, J. Compaction Quality Monitoring of Open-Graded Aggregates by Light Weight Deflectometer and Soil Stiffness Gauge. Sustainability 2020, 12, 2521. [Google Scholar] [CrossRef]
- Choi, Y.; Ahn, D.; Nguyen, T.H.; Ahn, J. Assessment of Field Compaction of Aggregate Base Materials for Permeable Pavements Based on Plate Load Tests. Sustainability 2018, 10, 3817. [Google Scholar] [CrossRef]
- AASHTO. AASHTO Guide for Design of Pavement Structures, 1993; AASHTO: Washington, DC, USA, 1993; Volume 1. [Google Scholar]
- ASTM International. Standard Test Method for Resistance to Degradation of Small-Size Coarse Aggregate by Abrasion and Impact in the Los Angeles Machine; ASTM C131/C131M-14; ASTM International: West Conshohocken, PA, USA, 2006. [Google Scholar]
- Agarwal, K.; Rana, M. Effect of ground water on settlement of footing in sand. Eur. Conf. Soil Mech. Found. Eng. 1987, 9, 751–754. [Google Scholar]
- Oh, W.; Vanapalli, S. Modelling the applied vertical stress and settlement relationship of shallow foundation in saturated and unsaturated sands. Can. Geotech. J. 2011, 48, 425–438. [Google Scholar] [CrossRef]
- Tompai, Z. Laboratory Evaluation of New B&C Light Falling Weight Deflectometer; IOS Press: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Nazzal, D. Field Evaluation of In-Situ Test Technology for QC/QA during Construction of Pavement Layers and Embankments; Louisiana State University: Baton Rouge, LA, USA, 2003. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 326. [Google Scholar]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Kim, B.-J.; Ho, J.-K.; Hwang, Y.-C. Prediction of Shear Wave Velocity on Sand Using Standard Penetration Test Results: Application of Artificial Neural Network Model. J. Korean Geotech. Soc. 2014, 30. [Google Scholar] [CrossRef]
- Moon, I.-J.; Kim, Y.-U. Correlation Analysis between Soil Shear Strength Parameters and Cone Index Using Artificial Neural Networks-1. J. Korea Acad.-Ind. Coop. Soc. 2015, 16. [Google Scholar] [CrossRef]
- MathWorks. What Is a Neural Network? Available online: https://kr.mathworks.com/discovery/neural-network.html (accessed on 14 October 2020).
- Microsoft. Perform a Regression Analysis. Available online: https://support.microsoft.com/en-us/office/perform-a-regression-analysis-54f5c00e-0f51-4274-a4a7-ae46b418a23e (accessed on 14 October 2020).
- Shahin, M.A. A review of artificial intelligence applications in shallow foundations. Int. J. Geotech. Eng. 2015, 9, 49–60. [Google Scholar] [CrossRef]
- Anderegg, R.; Kaufmann, K. Intelligent Compaction with Vibratory Rollers: Feedback Control Systems in Automatic Compaction and Compaction Control. Transp. Res. Rec. 2004, 1868, 124–134. [Google Scholar] [CrossRef]



| Test Material | Lithology | Material Composition by Volume | Cu 1 | Cc 2 | Specific Gravity | Abrasion Loss 3 (%) | ||
|---|---|---|---|---|---|---|---|---|
| D40 | D25 | D13 | ||||||
| D40 | Rhyolite | 100% | - | - | 2.88 | 1.19 | 2.67–2.75 | 12.8 |
| D40 + D25 | 50% | 50% | - | 2.99 | 1.08 | 9.8 | ||
| D25 | - | 100% | - | 2.48 | 1.02 | 10.3 | ||
| D25 + D13 | - | 50% | 50% | 2.84 | 1.16 | 11.2 | ||
| D13 | - | - | 100% | 2.79 | 1.16 | 12.3 | ||
| Material | Lift | Number of Roller Passes | Modulus Evaluation |
|---|---|---|---|
| D40 | First (30 cm) Second (30 cm) | 2 4 8 12 | PLT LWD |
| D40 + D25 | |||
| D25 | |||
| D25 + D13 | |||
| D13 |
| Dataset No. | Material | Number of Roller Passes | Location | ELWD (MPa) | Ev1 (MPa) | Ev2 (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| First Lift | Second Lift | Area A | Area B | ||||||
| 1 | 1 | 2 | O | O | 32.95 | 6.92 | 77.26 | ||
| 2 | O | O | 34.16 | 9.03 | 107.08 | ||||
| 3 | O | O | 30.07 | 10.62 | 107.81 | ||||
| 4 | O | O | 30.91 | 11.68 | 110.32 | ||||
| 5 | 4 | O | O | 32.94 | 17.66 | 129.37 | |||
| 6 | O | O | 31.67 | 15.19 | 102.47 | ||||
| 7 | O | O | 33.10 | 16.45 | 129.01 | ||||
| 8 | O | O | 39.64 | 13.09 | 125.98 | ||||
| 9 | 8 | O | O | 41.39 | 17.77 | 125.54 | |||
| 10 | O | O | 38.47 | 20.53 | 124.90 | ||||
| 11 | O | O | 43.27 | 22.18 | 114.55 | ||||
| 12 | O | O | 38.09 | 19.65 | 120.48 | ||||
| 13 | 12 | O | O | 44.52 | 18.07 | 115.87 | |||
| 14 | O | O | 39.73 | 19.32 | 119.19 | ||||
| 15 | O | O | 40.47 | 21.40 | 147.15 | ||||
| 16 | O | O | 39.88 | 22.35 | 136.34 | ||||
| 17 | 2 | 2 | O | O | 39.48 | 11.73 | 111.32 | ||
| 18 | O | O | 34.11 | 8.96 | 99.81 | ||||
| 19 | O | O | 33.21 | 10.82 | 101.90 | ||||
| 20 | O | O | 33.16 | 7.82 | 94.12 | ||||
| 21 | 4 | O | O | 32.87 | 16.97 | 122.44 | |||
| 22 | O | O | 31.20 | 12.91 | 103.39 | ||||
| 23 | O | O | 35.46 | 17.01 | 127.12 | ||||
| 24 | O | O | 34.31 | 13.49 | 115.38 | ||||
| 25 | 8 | O | O | 37.96 | 18.86 | 83.60 | |||
| 26 | O | O | 32.59 | 19.73 | 131.75 | ||||
| 27 | O | O | 41.82 | 19.38 | 128.94 | ||||
| 28 | O | O | 37.75 | 19.07 | 106.75 | ||||
| 29 | 12 | O | O | 41.33 | 20.42 | 129.75 | |||
| 30 | O | O | 39.10 | 19.45 | 111.28 | ||||
| 31 | O | O | 38.50 | 22.63 | 125.74 | ||||
| 32 | O | O | 32.94 | 18.13 | 115.32 | ||||
| 33 | 3 | 2 | O | O | 23.81 | 9.88 | 142.27 | ||
| 34 | O | O | 28.52 | 10.76 | 118.15 | ||||
| 35 | O | O | 29.05 | 9.70 | 120.44 | ||||
| 36 | O | O | 28.80 | 9.53 | 122.32 | ||||
| 37 | 4 | O | O | 27.26 | 13.05 | 137.16 | |||
| 38 | O | O | 26.24 | 12.39 | 137.85 | ||||
| 39 | O | O | 32.73 | 15.38 | 154.96 | ||||
| 40 | O | O | 29.93 | 16.69 | 130.55 | ||||
| 41 | 8 | O | O | 34.92 | 17.68 | 149.92 | |||
| 42 | O | O | 28.69 | 15.43 | 141.11 | ||||
| 43 | O | O | 36.87 | 18.59 | 155.86 | ||||
| 44 | O | O | 34.84 | 17.85 | 146.05 | ||||
| 45 | 12 | O | O | 36.97 | 22.57 | 149.79 | |||
| 46 | O | O | 33.49 | 20.64 | 143.28 | ||||
| 47 | O | O | 33.98 | 20.11 | 146.78 | ||||
| 48 | O | O | 32.18 | 18.24 | 153.81 | ||||
| 49 | 4 | 2 | O | O | 22.59 | 10.17 | 112.55 | ||
| 50 | O | O | 21.43 | 10.87 | 103.98 | ||||
| 51 | O | O | 20.57 | 10.39 | 115.08 | ||||
| 52 | O | O | 22.02 | 10.38 | 111.43 | ||||
| 53 | 4 | O | O | 25.12 | 13.03 | 133.66 | |||
| 54 | O | O | 26.91 | 11.91 | 127.44 | ||||
| 55 | O | O | 23.89 | 13.02 | 114.34 | ||||
| 56 | O | O | 29.07 | 14.58 | 105.12 | ||||
| 57 | 8 | O | O | 28.18 | 16.05 | 154.04 | |||
| 58 | O | O | 29.95 | 15.24 | 137.41 | ||||
| 59 | O | O | 30.21 | 17.17 | 124.13 | ||||
| 60 | O | O | 31.26 | 17.06 | 121.03 | ||||
| 61 | 12 | O | O | 33.66 | 16.94 | 117.71 | |||
| 62 | O | O | 30.72 | 19.30 | 123.29 | ||||
| 63 | O | O | 32.56 | 17.82 | 138.74 | ||||
| 64 | O | O | 27.24 | 16.35 | 138.90 | ||||
| 65 | 5 | 2 | O | O | 20.19 | 7.77 | 77.07 | ||
| 66 | O | O | 22.51 | 8.72 | 68.08 | ||||
| 67 | O | O | 18.03 | 7.13 | 94.38 | ||||
| 68 | O | O | 20.89 | 7.87 | 92.15 | ||||
| 69 | 4 | O | O | 20.28 | 11.92 | 115.13 | |||
| 70 | O | O | 20.92 | 12.00 | 109.36 | ||||
| 71 | O | O | 23.36 | 11.47 | 103.47 | ||||
| 72 | O | O | 21.74 | 11.03 | 83.25 | ||||
| 73 | 8 | O | O | 25.11 | 14.92 | 96.55 | |||
| 74 | O | O | 28.98 | 12.81 | 77.88 | ||||
| 75 | O | O | 22.71 | 12.20 | 123.13 | ||||
| 76 | O | O | 23.40 | 12.15 | 118.23 | ||||
| 77 | 12 | O | O | 27.90 | 15.70 | 90.83 | |||
| 78 | O | O | 23.23 | 18.10 | 90.66 | ||||
| 79 | O | O | 30.14 | 17.59 | 111.86 | ||||
| 80 | O | O | 25.37 | 14.22 | 110.25 | ||||
| Modulus | LR1 | ANN1 | ||
|---|---|---|---|---|
| Training | Testing | Training | Testing | |
| ELWD | 2.76 | 2.53 | 2.84 | 3.40 |
| Ev1 | 2.00 | 1.95 | 1.45 | 1.42 |
| Ev2 | 18.16 | 17.71 | 10.84 | 17.39 |
| Modulus | LR2 | ANN2 | ||
|---|---|---|---|---|
| Training | Testing | Training | Testing | |
| Ev1 | 1.96 | 1.77 | 1.49 | 1.86 |
| Ev2 | 17.55 | 21.23 | 9.33 | 23.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Choi, Y.; Ahn, D.; Ahn, J. Prediction Models Based on Regression and Artificial Neural Network for Moduli of Layers Constituted by Open-Graded Aggregates. Materials 2021, 14, 1199. https://doi.org/10.3390/ma14051199
Lee Y, Choi Y, Ahn D, Ahn J. Prediction Models Based on Regression and Artificial Neural Network for Moduli of Layers Constituted by Open-Graded Aggregates. Materials. 2021; 14(5):1199. https://doi.org/10.3390/ma14051199
Chicago/Turabian StyleLee, Yunje, Yongjin Choi, Donghyun Ahn, and Jaehun Ahn. 2021. "Prediction Models Based on Regression and Artificial Neural Network for Moduli of Layers Constituted by Open-Graded Aggregates" Materials 14, no. 5: 1199. https://doi.org/10.3390/ma14051199
APA StyleLee, Y., Choi, Y., Ahn, D., & Ahn, J. (2021). Prediction Models Based on Regression and Artificial Neural Network for Moduli of Layers Constituted by Open-Graded Aggregates. Materials, 14(5), 1199. https://doi.org/10.3390/ma14051199






