Effect of Peak Current Density on Tensile Properties of AZ31B Magnesium Alloy
Abstract
1. Introduction
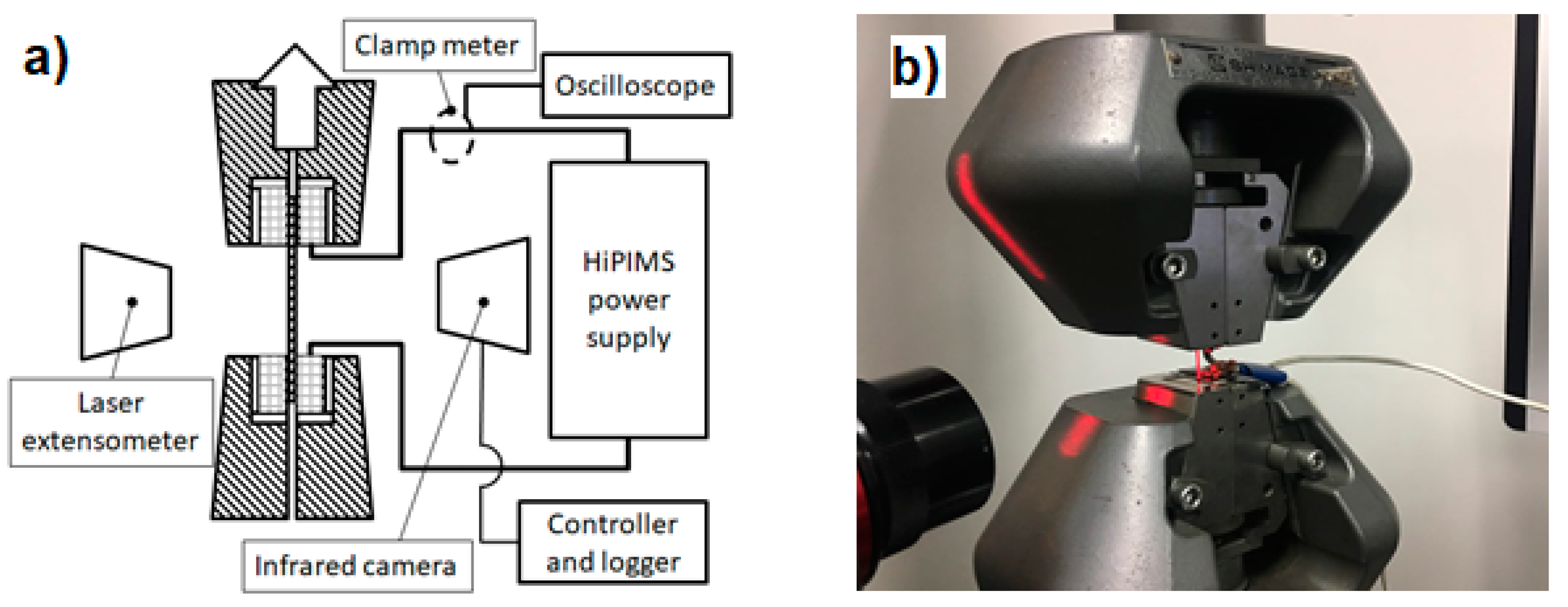
2. Experimental Methods
3. Results and Discussions
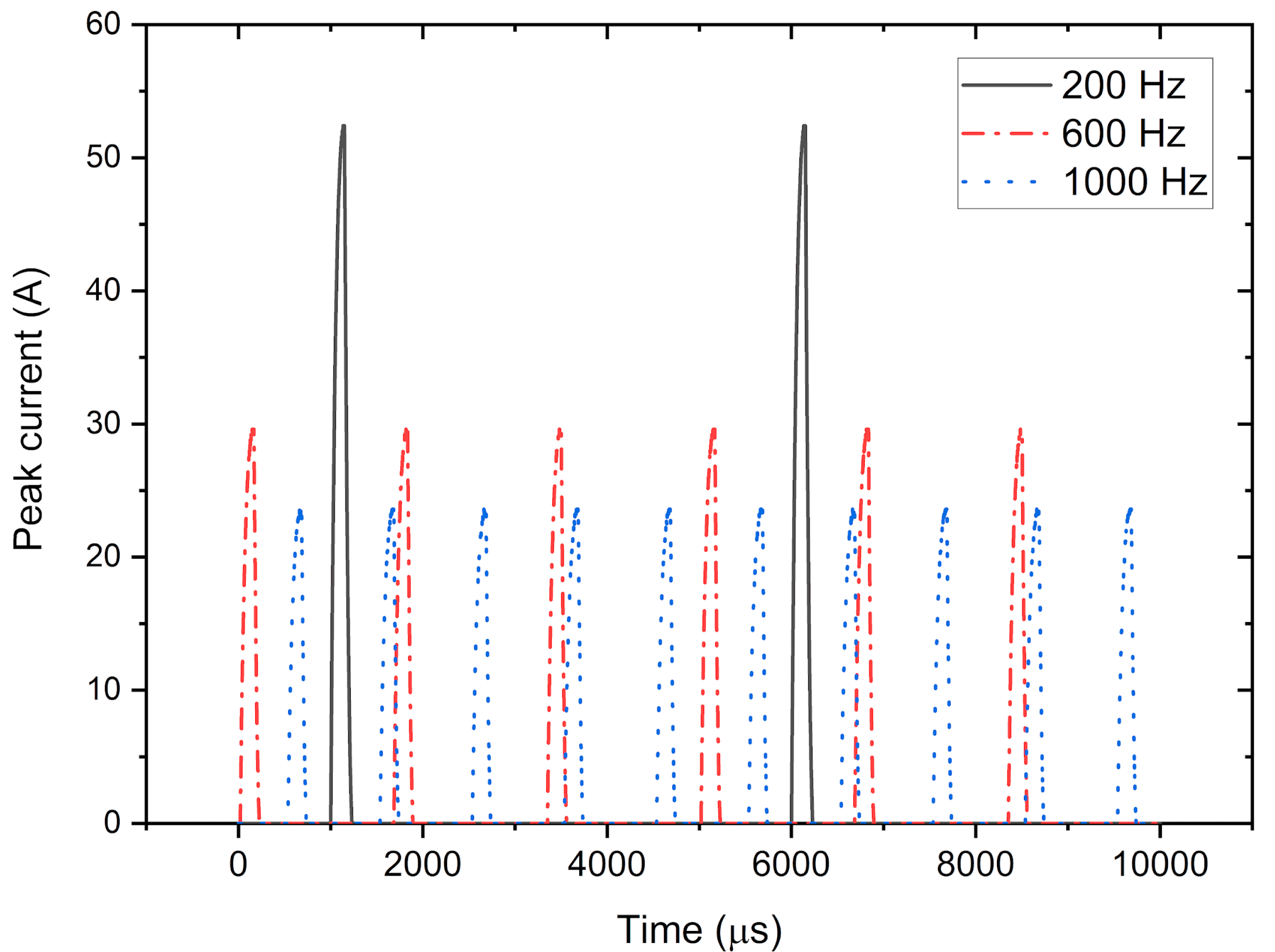
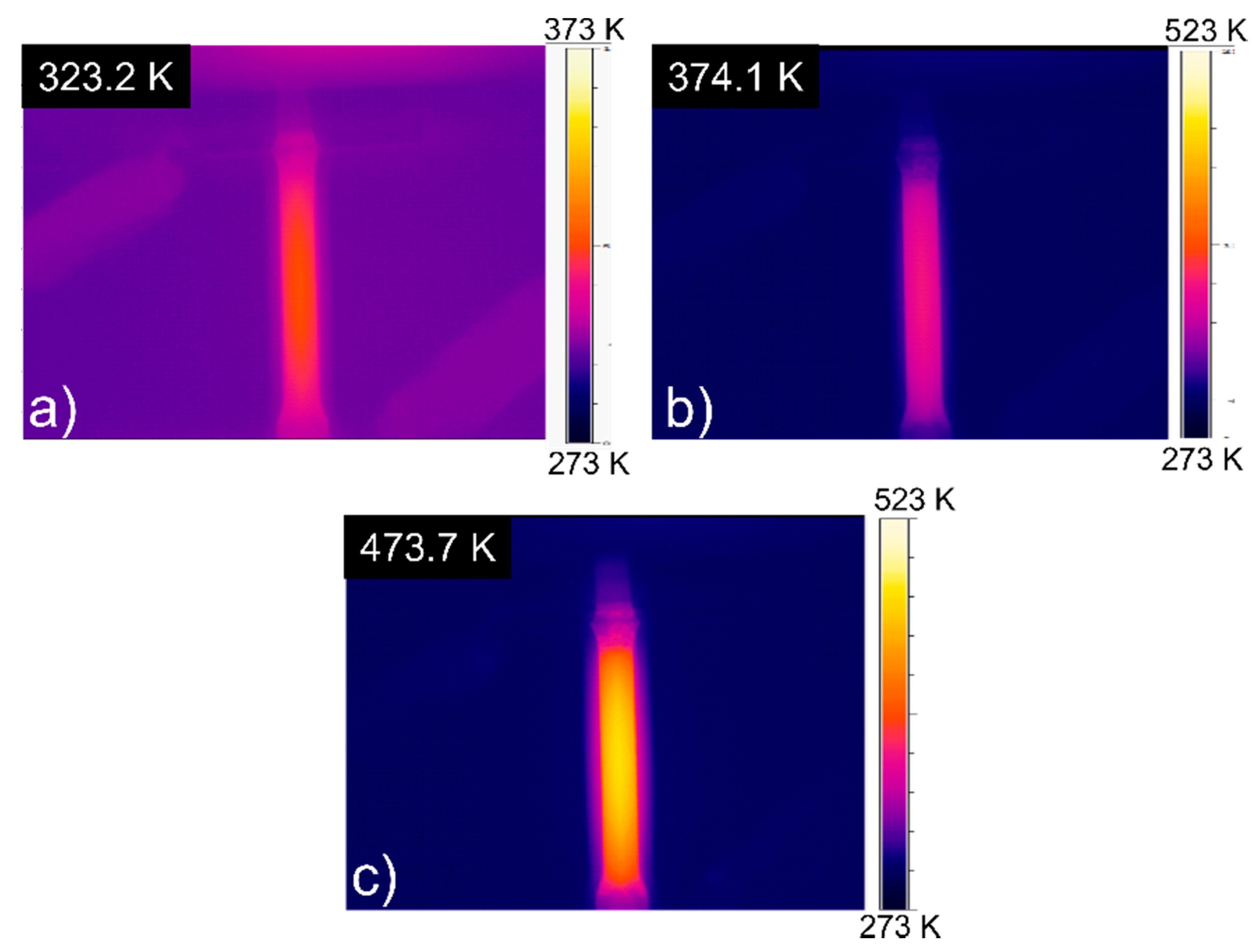
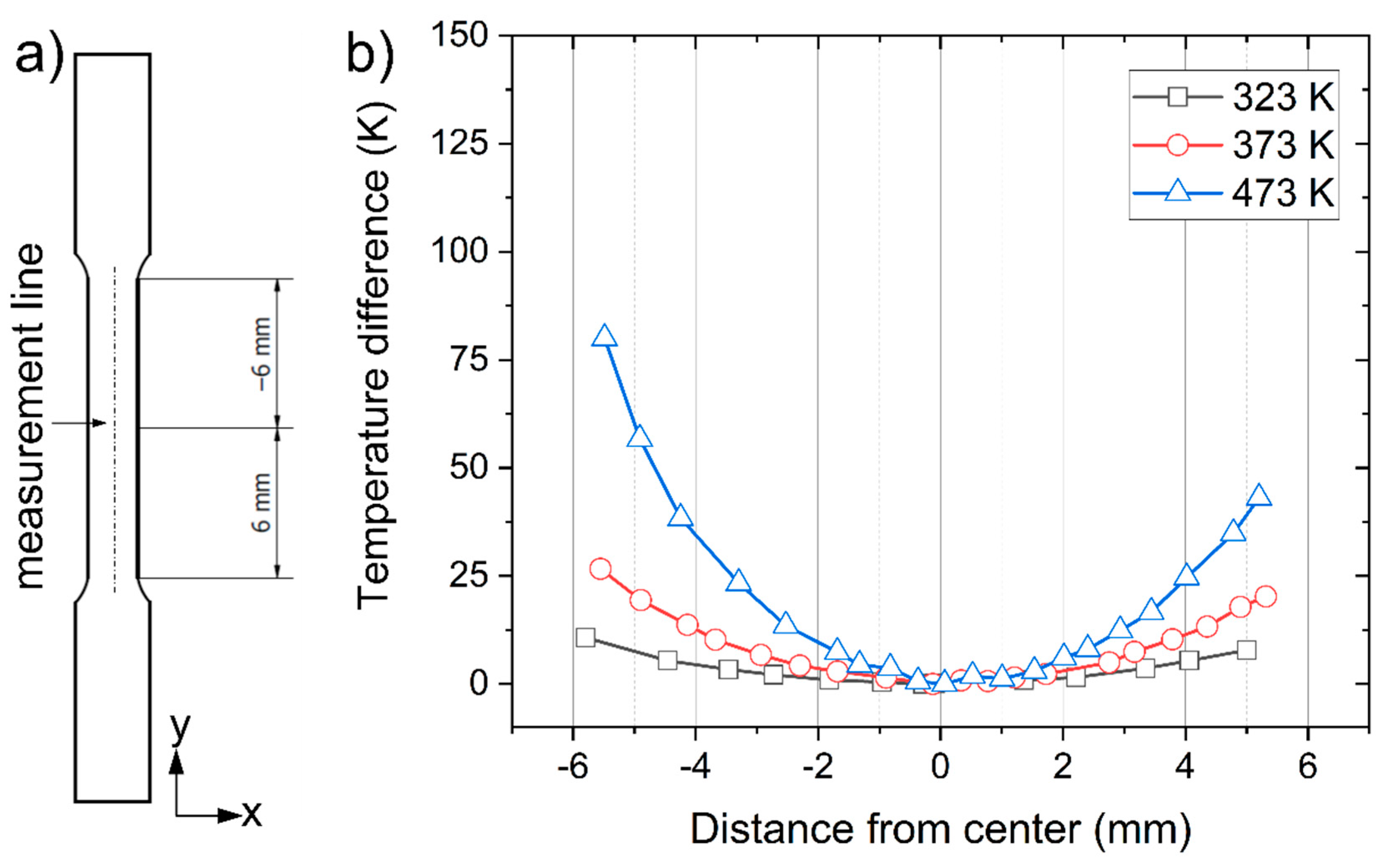
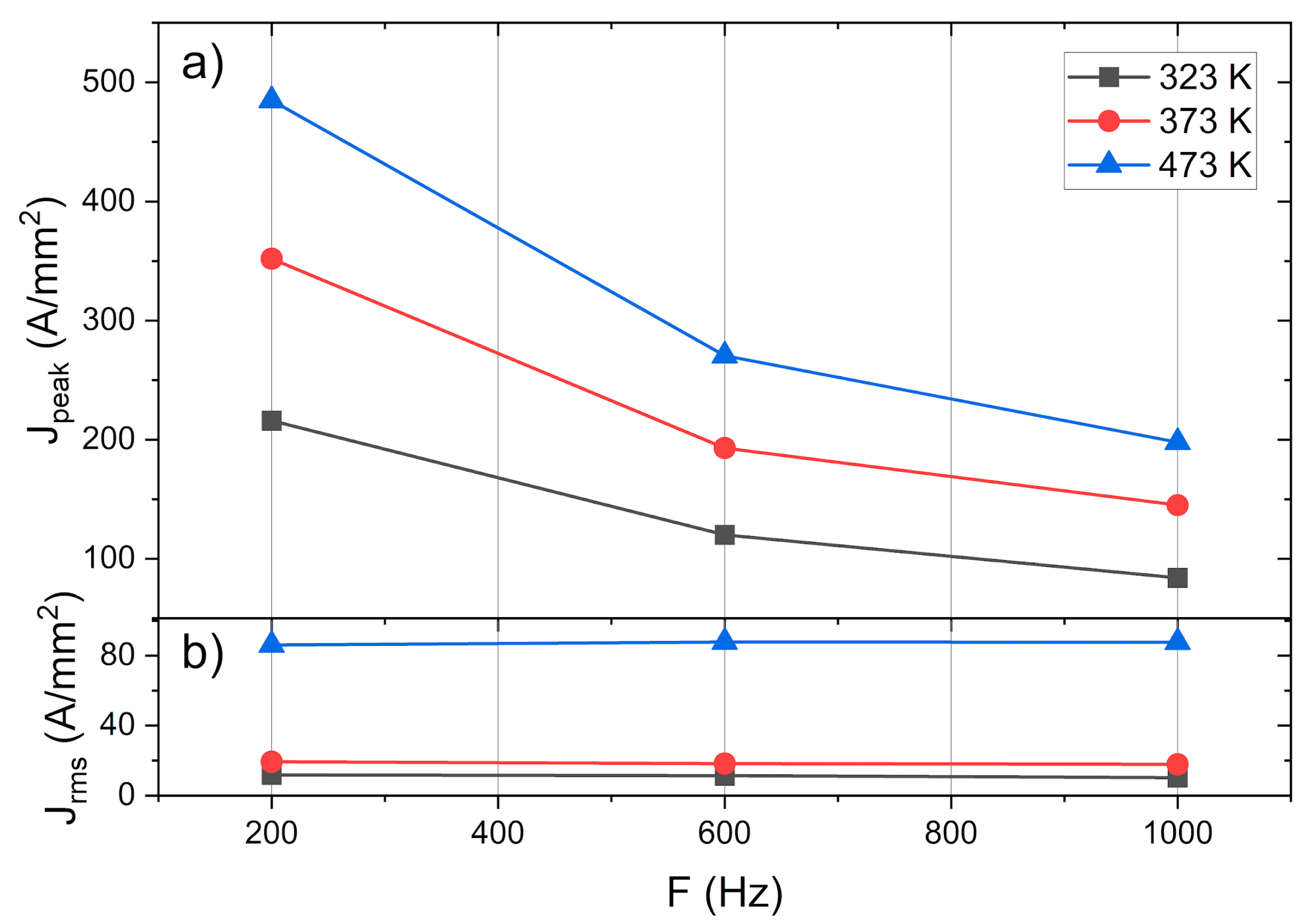
3.1. Thermal Behavior and Current Density
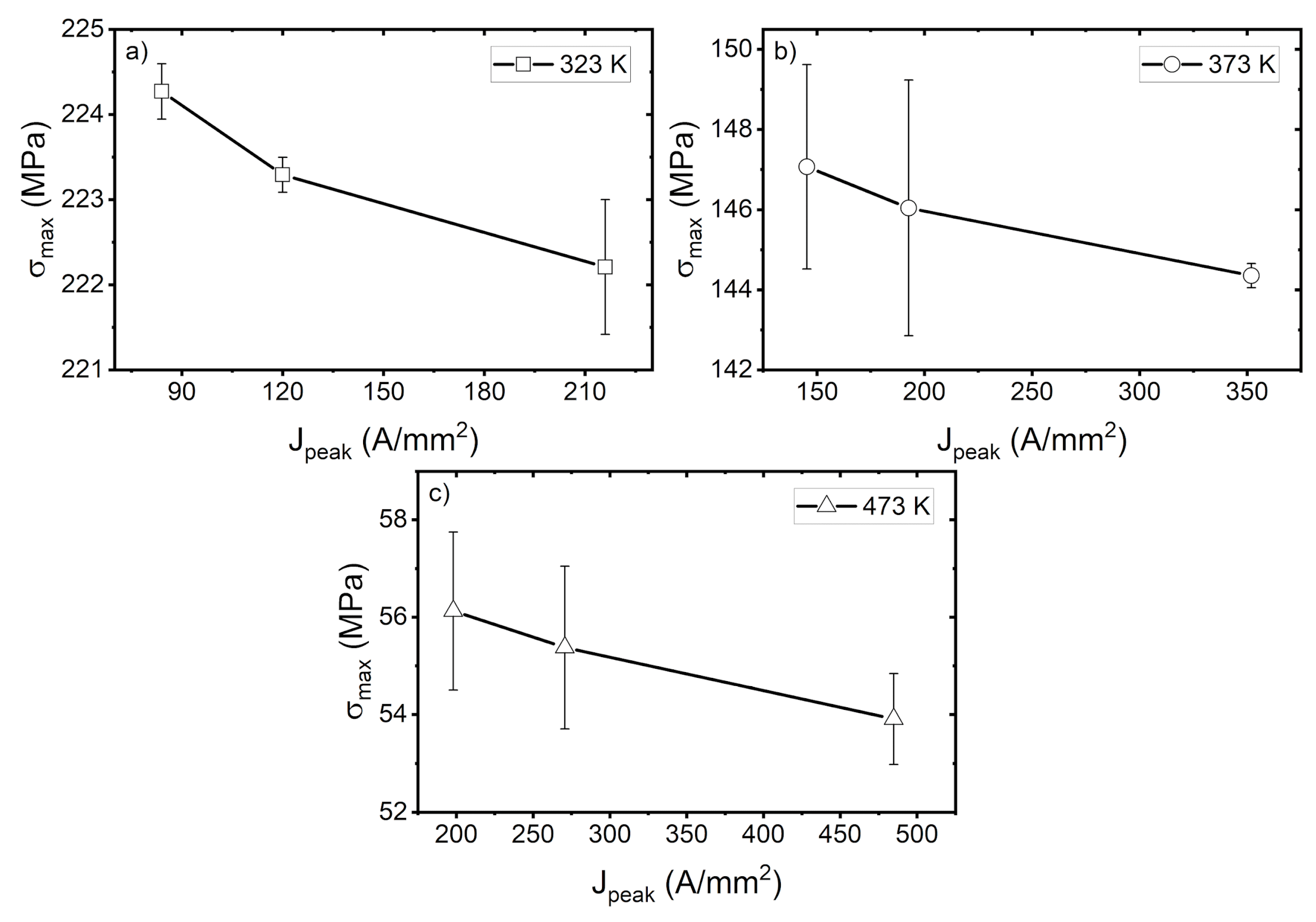
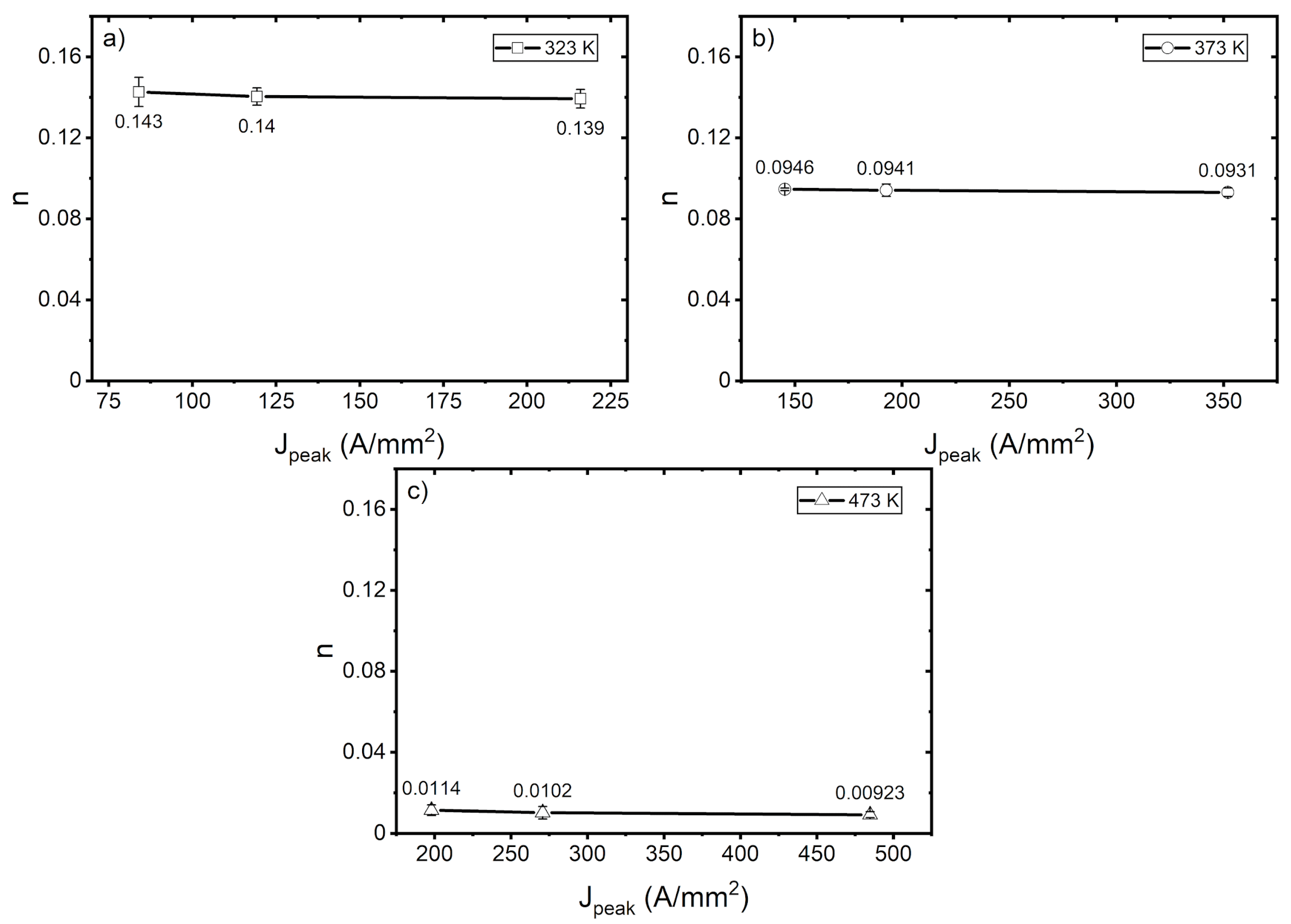
3.2. Tensile Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mueller, W.D.; Lucia Nascimento, M.; Lorenzo De Mele, M.F. Critical Discussion of the Results from Different Corrosion Studies of Mg and Mg Alloys for Biomaterial Applications. Acta Biomater. 2010, 6, 1749–1755. [Google Scholar] [CrossRef]
- Kravchenko, V.Y. Effect of Directed Electron Beam on Moving Dislocations. J. Exptl. Theor. Phys. 1967, 24, 1676–1688. [Google Scholar]
- Troitskii, O.A. Electromechanical Effect in Metals. ZhETF Pis. 1969, 10, 18–22. [Google Scholar]
- Conrad, H. Electroplasticity in Metals and Ceramics. Mater. Sci. Eng. 2000, A287, 276–287. [Google Scholar] [CrossRef]
- Perkins, T.A.; Kronenberger, T.J.; Roth, J.T. Metallic Forging Using Electrical Flow as an Alternative to Warm/Hot Working. J. Manuf. Sci. Eng. 2006, 129, 84–94. [Google Scholar] [CrossRef]
- Jones, J.J.; Mears, L.; Roth, J.T. Electrically-Assisted Forming of Magnesium AZ31: Effect of Current Magnitude and Deformation Rate on Forgeability. J. Manuf. Sci. Eng. 2012. [Google Scholar] [CrossRef]
- Song, J.; Jang, I.; Gwak, S.; Noh, W.; Lee, J.; Bae, G.; Kim, D. Effect of Pulsed Currents on the Springback Reduction of Ultra-High Strength Steels. Procedia Eng. 2017, 207, 359–364. [Google Scholar] [CrossRef]
- Aoyama, T.; Shimizu, T.; Zheng, Q.; Yang, M. Effect of Heating on Springback in Heat Assisted Microbending. Adv. Mater. Res. 2014, 939, 409–414. [Google Scholar] [CrossRef]
- Ao, D.; Chu, X.; Yang, Y.; Lin, S.; Gao, J. Effect of Electropulsing on Springback during V-Bending of Ti-6Al-4V Titanium Alloy Sheet. Int. J. Adv. Manuf. Technol. 2018, 96, 3197–3207. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Q.; Liu, K.; Peng, F.; Dong, X.; Wang, J. Investigation of Influence of Direct-Current Pulses on Springback during V-Bending of AZ31B Magnesium Alloy Sheet. J. Mater. Process. Technol. 2015. [Google Scholar] [CrossRef]
- Roh, J.H.; Seo, J.J.; Hong, S.T.; Kim, M.J.; Han, H.N.; Roth, J.T. The Mechanical Behavior of 5052-H32 Aluminum Alloys under a Pulsed Electric Current. Int. J. Plast. 2014. [Google Scholar] [CrossRef]
- Delobelle, V.; Chagnon, G.; Favier, D.; Alonso, T. Study of Electropulse Heat Treatment of Cold Worked NiTi Wire: From Uniform to Localised Tensile Behaviour. J. Mater. Process. Technol. 2016, 227, 244–250. [Google Scholar] [CrossRef]
- Zheng, Q.; Shimizu, T.; Shiratori, T.; Yang, M. Tensile Properties and Constitutive Model of Ultrathin Pure Titanium Foils at Elevated Temperatures in Microforming Assisted by Resistance Heating Method. Mater. Des. 2014, 63, 389–397. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Yan, S.; Zhang, N. Experimental Study and Analysis on the Electrically-Assisted Tensile Behaviors of Inconel 718 Alloy. Procedia Eng. 2017, 207, 365–370. [Google Scholar] [CrossRef]
- Fan, R.; Magargee, J.; Hu, P.; Cao, J. Materials Science & Engineering A Influence of Grain Size and Grain Boundaries on the Thermal and Mechanical Behavior of 70/30 Brass under Electrically-Assisted Deformation. Mater. Sci. Eng. A 2013, 574, 218–225. [Google Scholar] [CrossRef]
- Conrad, H.; Cao, W.D.; Sprecher, A.F. Constitutive Laws Pertaining to Electroplasticity in Metals; Springer: Berlin/Heidelberg, Germany, 1990; pp. 305–311. [Google Scholar]
- Molotskii, M.; Fleurov, V. Magnetic Effects in Electroplasticity of Metals. Phys. Rev. B 1995, 52, 15829–15834. [Google Scholar] [CrossRef]
- Lahiri, A.; Shanthraj, P.; Roters, F. Understanding the Mechanisms of Electroplasticity from a Crystal Plasticity Perspective. Model. Simul. Mater. Sci. Eng. 2019, 27, 085006. [Google Scholar] [CrossRef]
- Molotskii, M.I. Theoretical Basis for Electro- and Magnetoplasticity. Mater. Sci. Eng. A 2002, 287, 248–258. [Google Scholar] [CrossRef]
- Bao, W.; Chu, X.; Lin, S.; Gao, J. Electro-Plastic Effect on Tensile Deformation Behaviour and Microstructural Mechanism of AZ31B Alloy. Mater. Sci. Technol. 2016, 1–10. [Google Scholar] [CrossRef]
- Ghiotti, A.; Bruschi, S.; Simonetto, E.; Gennari, C.; Calliari, I.; Bariani, P. Electroplastic Effect on AA1050 Aluminium Alloy Formability. CIRP Ann. 2018, 4–7. [Google Scholar] [CrossRef]
- Van Hieu, N.; Salm, C. Effect of Current Crowding on Electromigration Lifetime Investigated by Simulation and Experiment. Comput. Mater. Sci. 2010, 49, S235–S238. [Google Scholar] [CrossRef]
- Kryvchenkova, O.; Cobley, R.J.; Kalna, K. The Current Crowding Effect in ZnO Nanowires with a Metal Contact. Mater. Today Proc. 2015, 2, 309–314. [Google Scholar] [CrossRef]



| Al | Zn | Mn | Si | Fe | Cu | Ni | Ca | Mg |
|---|---|---|---|---|---|---|---|---|
| 3.1 | 0.88 | 0.37 | 0.01 | 0.002 | <0.01 | <0.001 | 0.01 | Rem. |
| Target Temperature | Pulse Width | Strain Rate | Frequency |
|---|---|---|---|
| (K) | (µs) | (1/s) | (Hz) |
| 323 | 150 | 0.001 | 200 |
| 600 | |||
| 1000 | |||
| 373 | 200 | ||
| 600 | |||
| 1000 | |||
| 473 | 200 | ||
| 600 | |||
| 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Indhiarto, I.; Shimizu, T.; Yang, M. Effect of Peak Current Density on Tensile Properties of AZ31B Magnesium Alloy. Materials 2021, 14, 1457. https://doi.org/10.3390/ma14061457
Indhiarto I, Shimizu T, Yang M. Effect of Peak Current Density on Tensile Properties of AZ31B Magnesium Alloy. Materials. 2021; 14(6):1457. https://doi.org/10.3390/ma14061457
Chicago/Turabian StyleIndhiarto, Ichsan, Tetsuhide Shimizu, and Ming Yang. 2021. "Effect of Peak Current Density on Tensile Properties of AZ31B Magnesium Alloy" Materials 14, no. 6: 1457. https://doi.org/10.3390/ma14061457
APA StyleIndhiarto, I., Shimizu, T., & Yang, M. (2021). Effect of Peak Current Density on Tensile Properties of AZ31B Magnesium Alloy. Materials, 14(6), 1457. https://doi.org/10.3390/ma14061457






