Machine-Learning-Based Atomistic Model Analysis on High-Temperature Compressive Creep Properties of Amorphous Silicon Carbide
Abstract
1. Introduction
- In SiC fibers and matrices, the ratio of Si and C atoms is not necessarily stoichiometric but may be varied. For example, Hi-Nicalon, a typical SiC fiber, consists of Si and C of 39 at% and 60.4 at%, respectively [6]. Therefore, a constant-charge model, such as Vashishta et al. [11] and Kubo et al. [12], is not applicable any longer.
- Unlike a low-temperature condition, the local atomic structure can easily change at a high temperature via, e.g., creep and diffusion processes. In such situation, the bond-order type potential functions may cause qualitative and quantitative errors, because in general such potential functions tend to overestimate the bonding energy or critical force of bond breaking.
- It is also unclear what interactions are dominant on the mechanical properties of SiC at high temperature. In SiC, both ionic and covalent interactions are competitive and thus play an important role in deformation and fracture in SiC. That is true even in the case of a perfect crystal of SiC at 0 K, where cleavage, slip, and phase transition were observed with a slight difference in the loading condition in a first-principles (FP) analysis [14]. This complex feature of the interaction in SiC requires a highly flexible and versatile formulation in the potential model.
- The practical SiC materials include other types of atoms (e.g., B, O, N, Al, etc.) as impurities and/or dopants [15,16] (Relatedly, ceramic fibers consisting of Si, B, N, and C also have been produced [17]). Therefore, the potential function for the Si-C systems should be extendable to a many-species system for further investigation. The existence of such impurities and/or dopants also requires a flexible formulation of the potential model because the additional atoms can be metallic, covalent, or ionic.
2. Construction of Artificial Neural Network Potential Model
2.1. Formulation
2.2. Optimization Procedure and Reference Data
3. Validation of ANN Potential Function
3.1. Result of Optimization
3.2. Material Properties at Equilibrium States
3.3. Phase Stability of Crystalline SiC
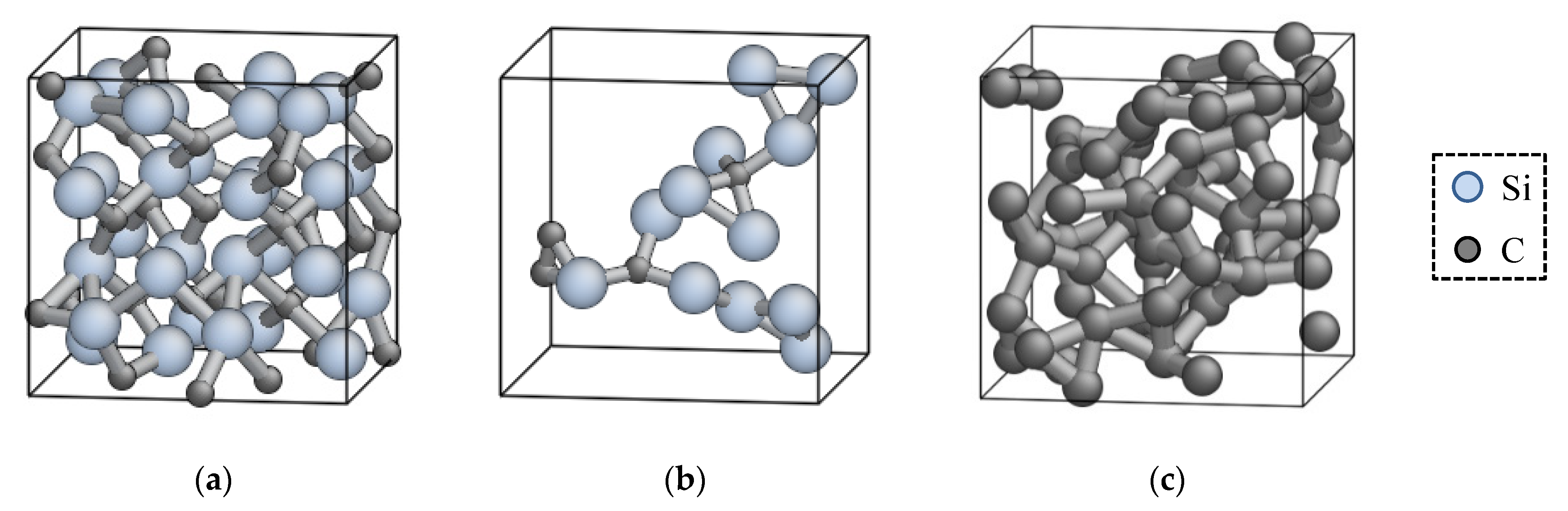
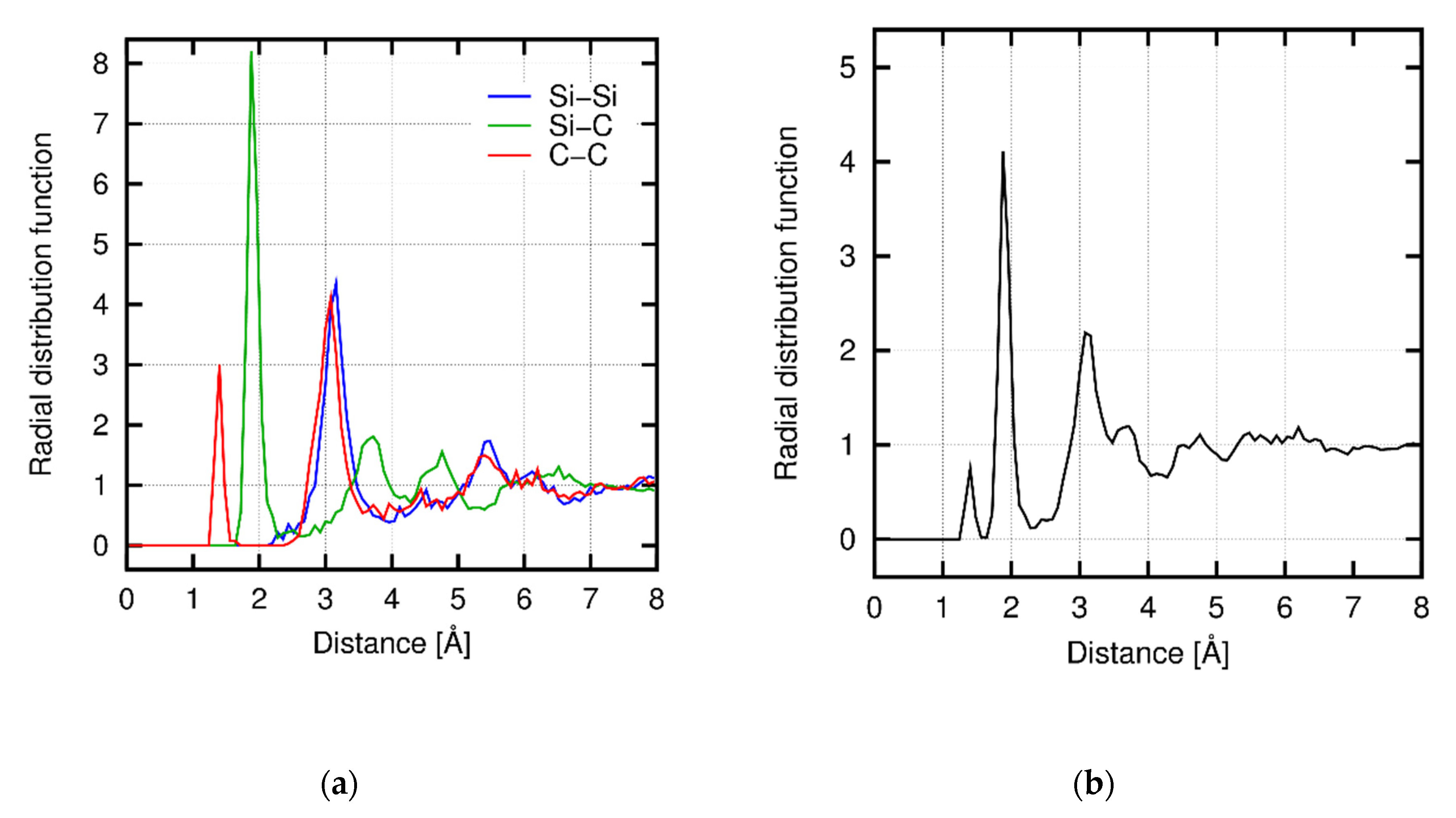
3.4. Structural Property of Amorphous SiC
4. Temperature-Dependence of Creep Properties of Amorphous SiC
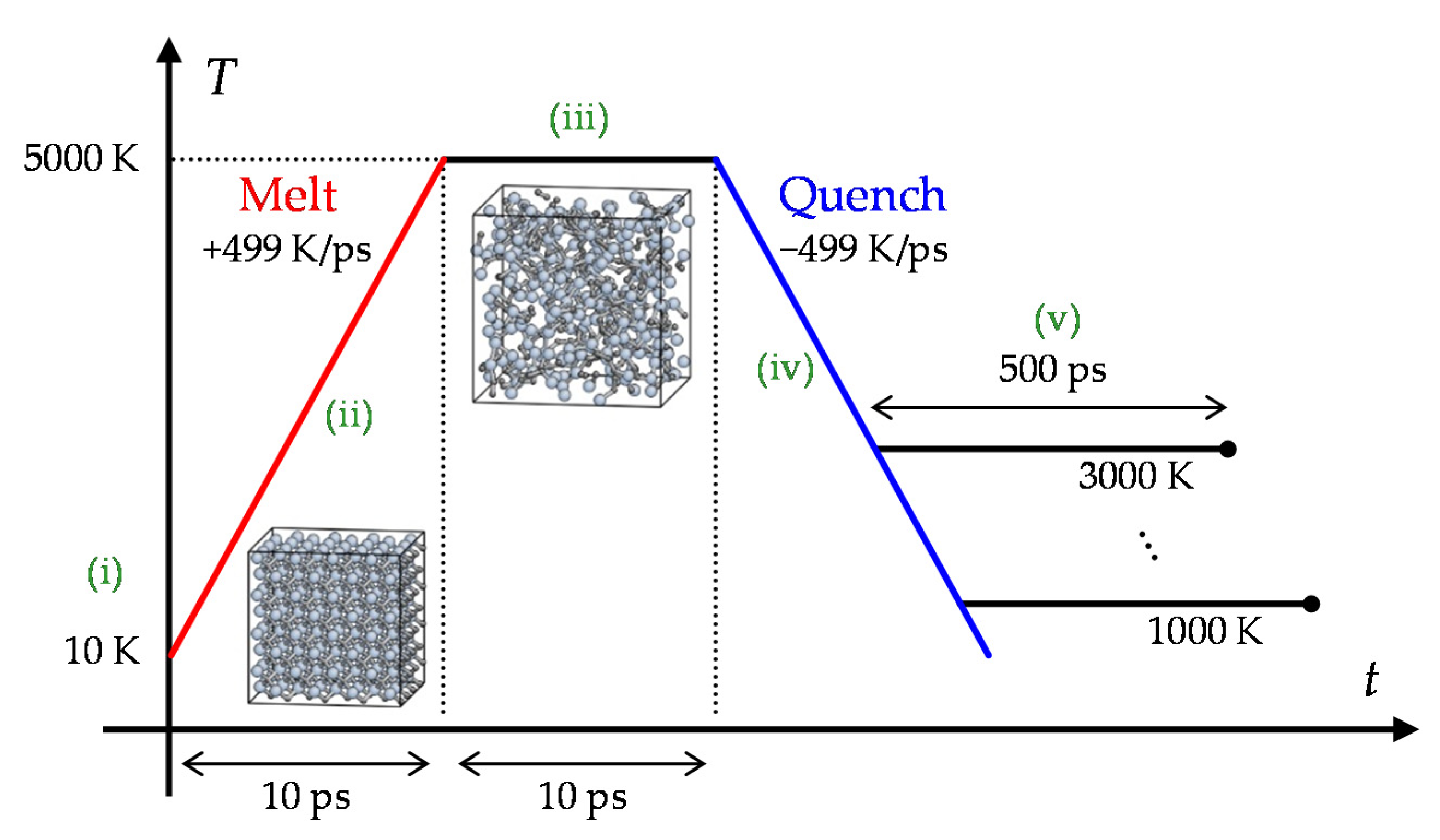
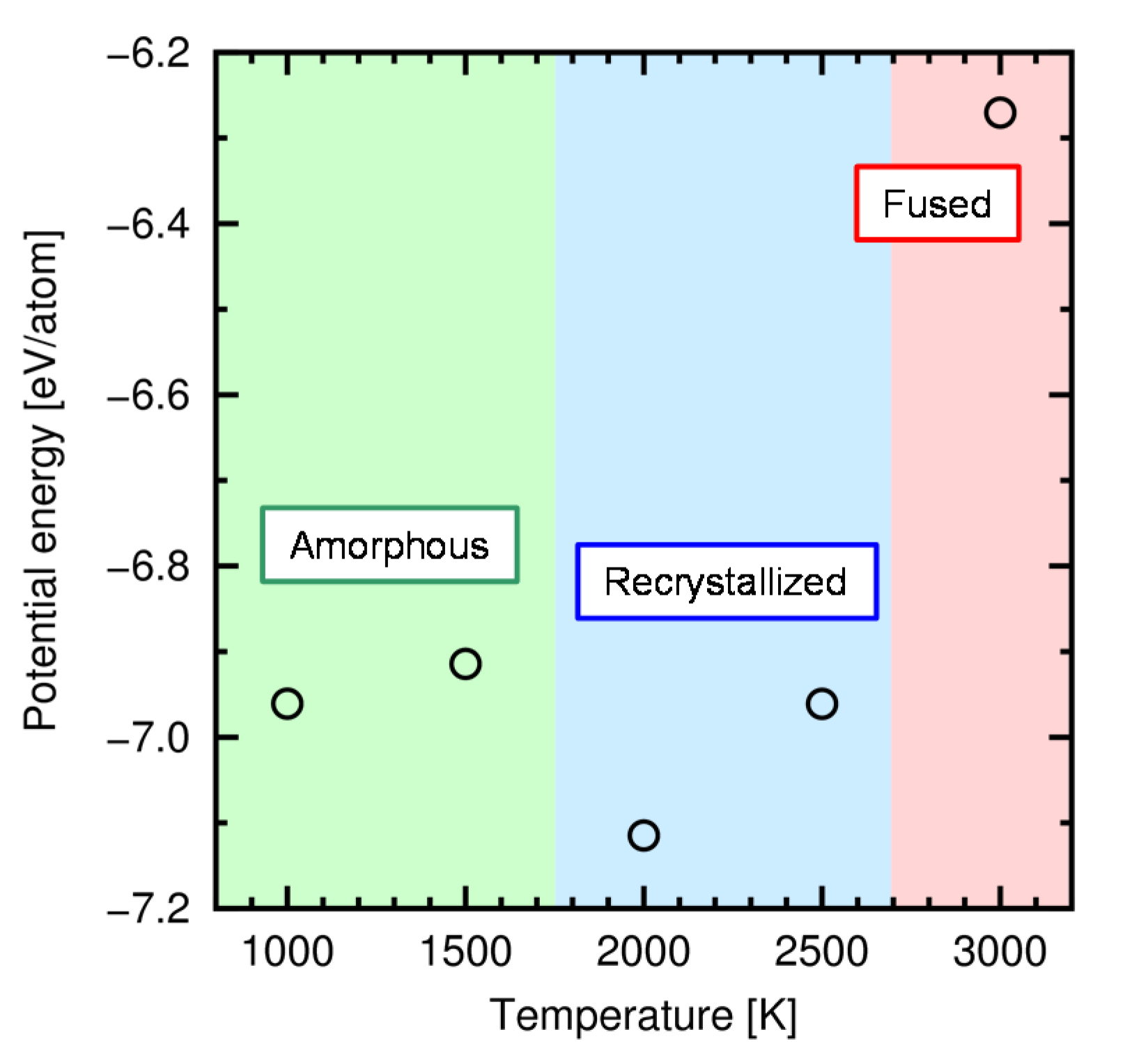
4.1. Preparation of Simulation Cells
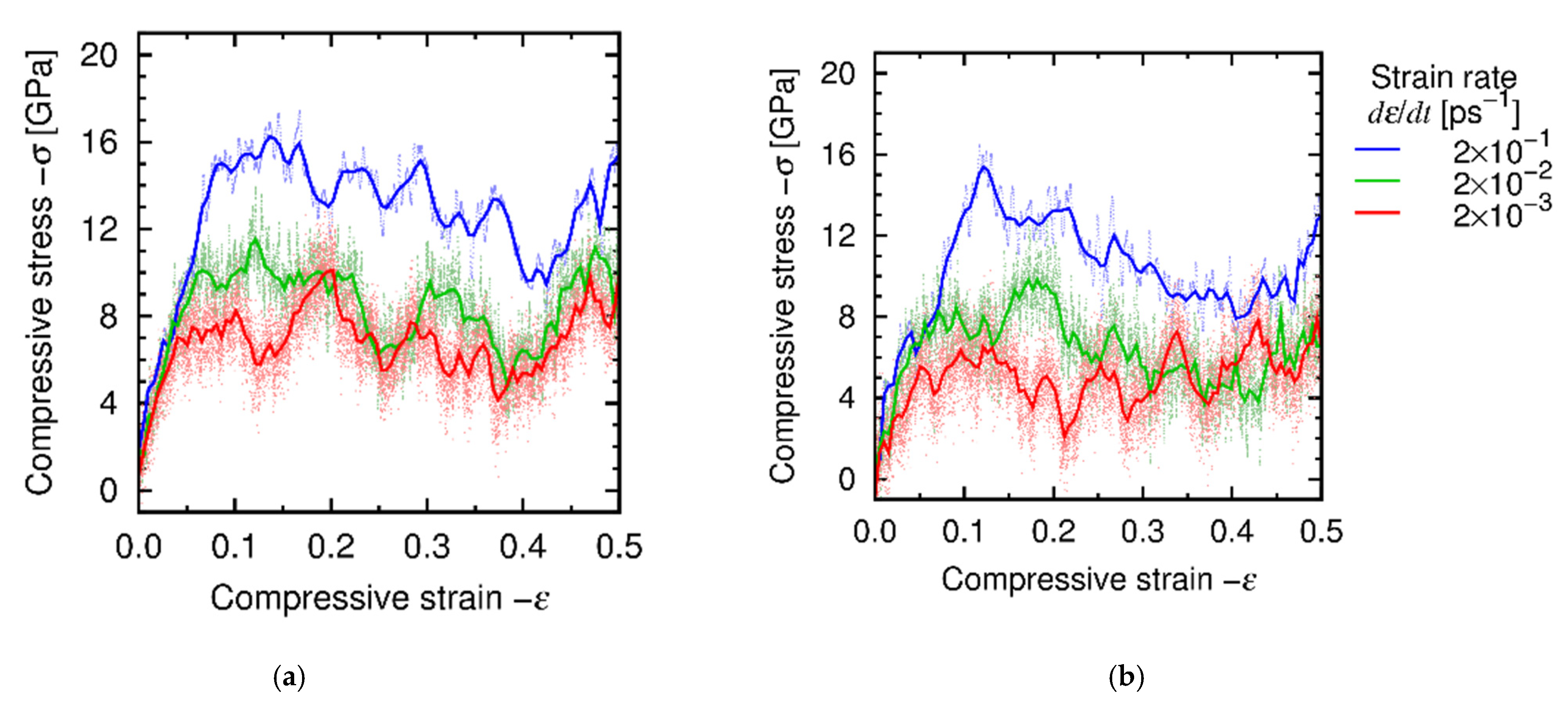
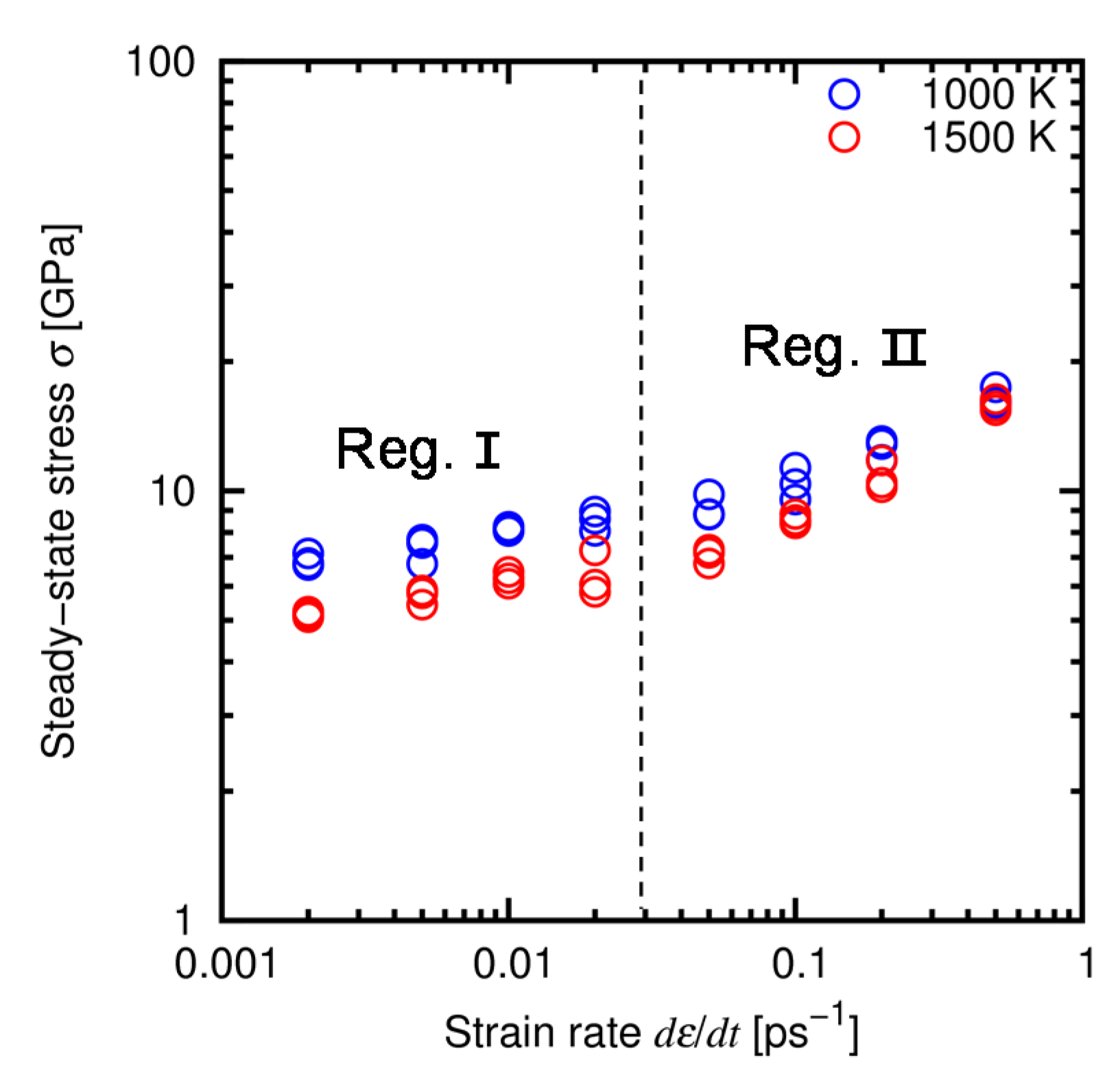
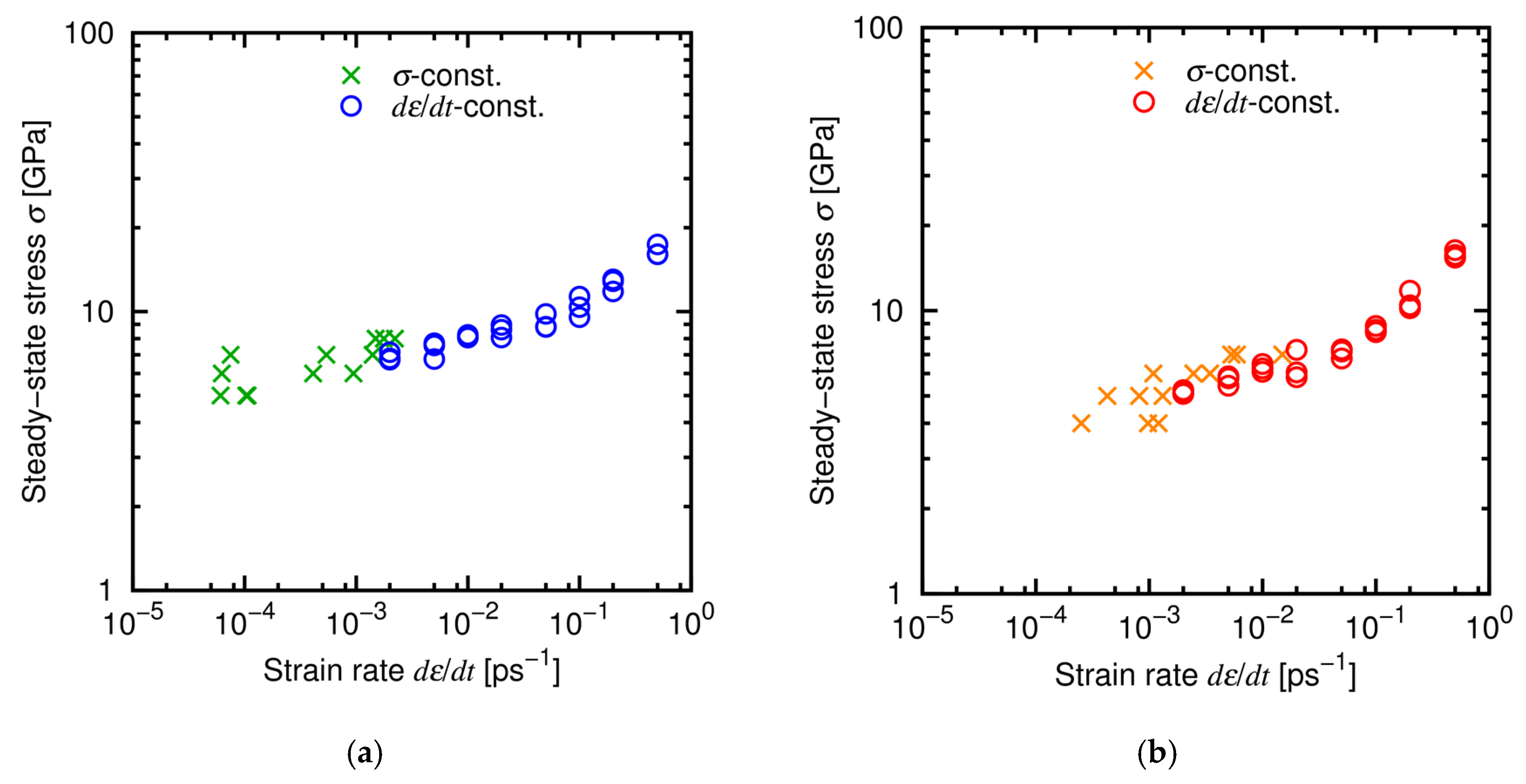
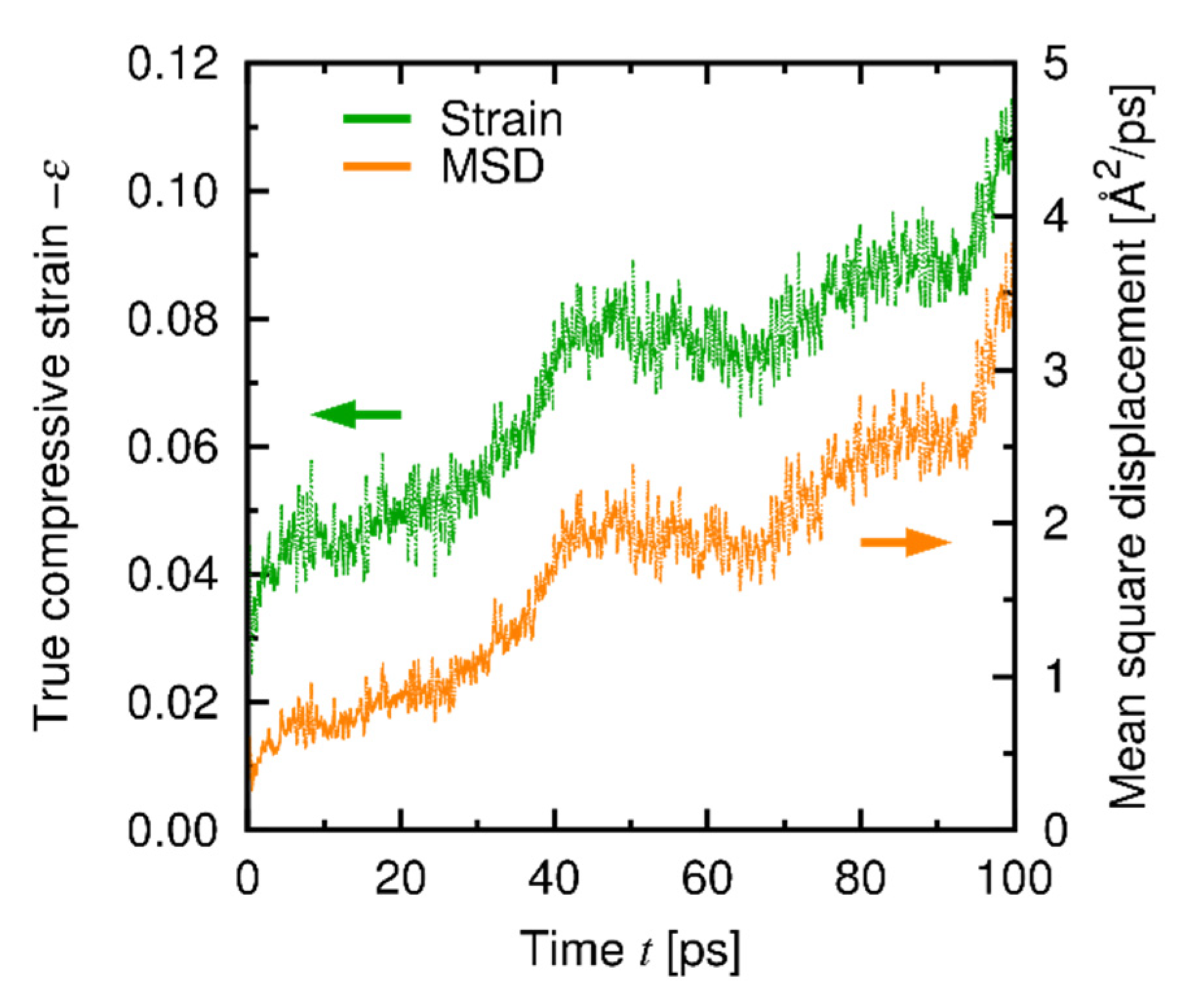
4.2. Deformation Condition
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
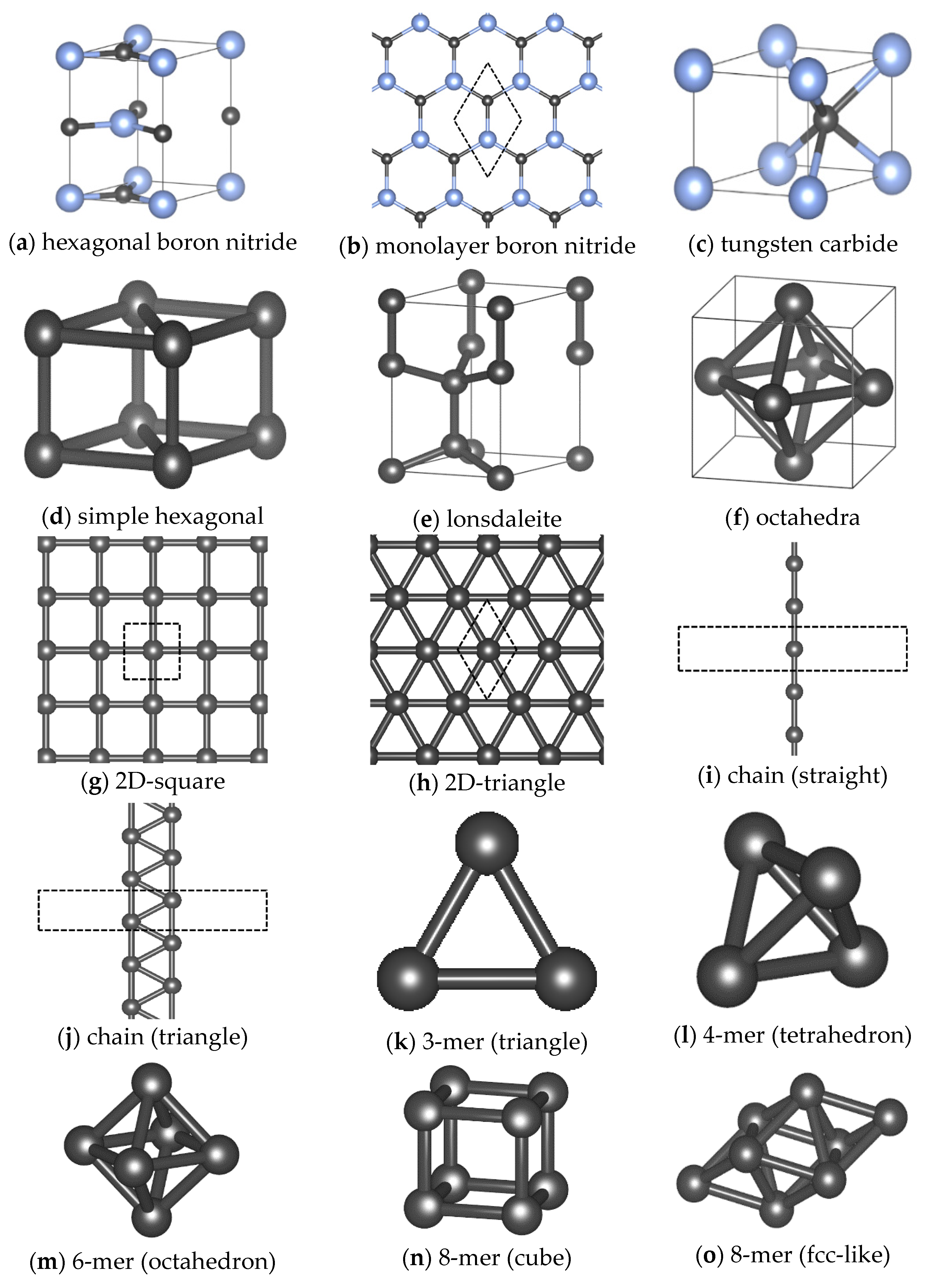
Appendix A. Typical Reference Crystal Structures
| System | Structure | Deformation Mode |
|---|---|---|
| SiC | zincblende (3C) | iso, xx, xx + yy, xx − yy, xy |
| wurtzite (2H) | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| rock salt | iso, xx, xx + yy, xx − yy, xy | |
| cesium chloride | iso, xx, xx + yy, xx − yy, xy | |
| hexagonal boron nitride * | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| monolayer boron nitride * | d = 0.80–3.00 Å | |
| fluorite (SiC2, CSi2) | iso, xx, xx + yy, xx − yy, xy | |
| tungsten carbide * | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| dimer | d = 0.80–4.00 Å | |
| Si | diamond | iso, xx, xx + yy, xx − yy, xy |
| graphene | d = 0.80–3.00 Å | |
| bcc | iso, xx, xx + yy, xx − yy, xy | |
| fcc | iso, xx, xx + yy, xx − yy, xy | |
| sc | iso, xx, xx + yy, xx − yy, xy | |
| simple hexagonal * | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| octahedra * | iso, xx, xx + yy, xx − yy, xy | |
| 2D-square * | d = 0.90–3.00 Å | |
| 2D-triangle * | d = 0.90–3.00 Å | |
| chain (straight) * | d = 0.90–4.00 Å | |
| dimer | d = 1.00–4.00 Å | |
| C | graphene | d = 0.80–3.00 Å |
| graphite (α, β) | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| diamond | iso, xx, xx + yy, xx − yy, xy | |
| lonsdaleite * | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| bcc | iso, xx, xx + yy, xx − yy, xy | |
| fcc | iso, xx, xx + yy, xx − yy, xy | |
| hcp | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| sc | iso, xx, xx + yy, xx − yy, xy | |
| simple hexagonal * | iso, xx, yy, zz, xx + yy, xx − yy, zx, zy | |
| octahedra * | iso, xx, xx + yy, xx − yy, xy | |
| 2D-square * | d = 0.80–3.00 Å | |
| 2D-triangle * | d = 0.80–3.00 Å | |
| chain (straight) * | d = 0.80–4.00 Å | |
| chain (triangle) * | d = 0.80–3.00 Å | |
| dimer | d = 0.80–4.00 Å | |
| 3-mer (triangle) * | d = 0.80–3.00 Å | |
| 4-mer (tetrahedron) * | d = 0.80–3.00 Å | |
| 6-mer (octahedron) * | d = 0.80–3.00 Å | |
| 8-mer (cube) * | d = 0.80–3.00 Å | |
| 8-mer (fcc-like) * | d = 0.80–3.00 Å |
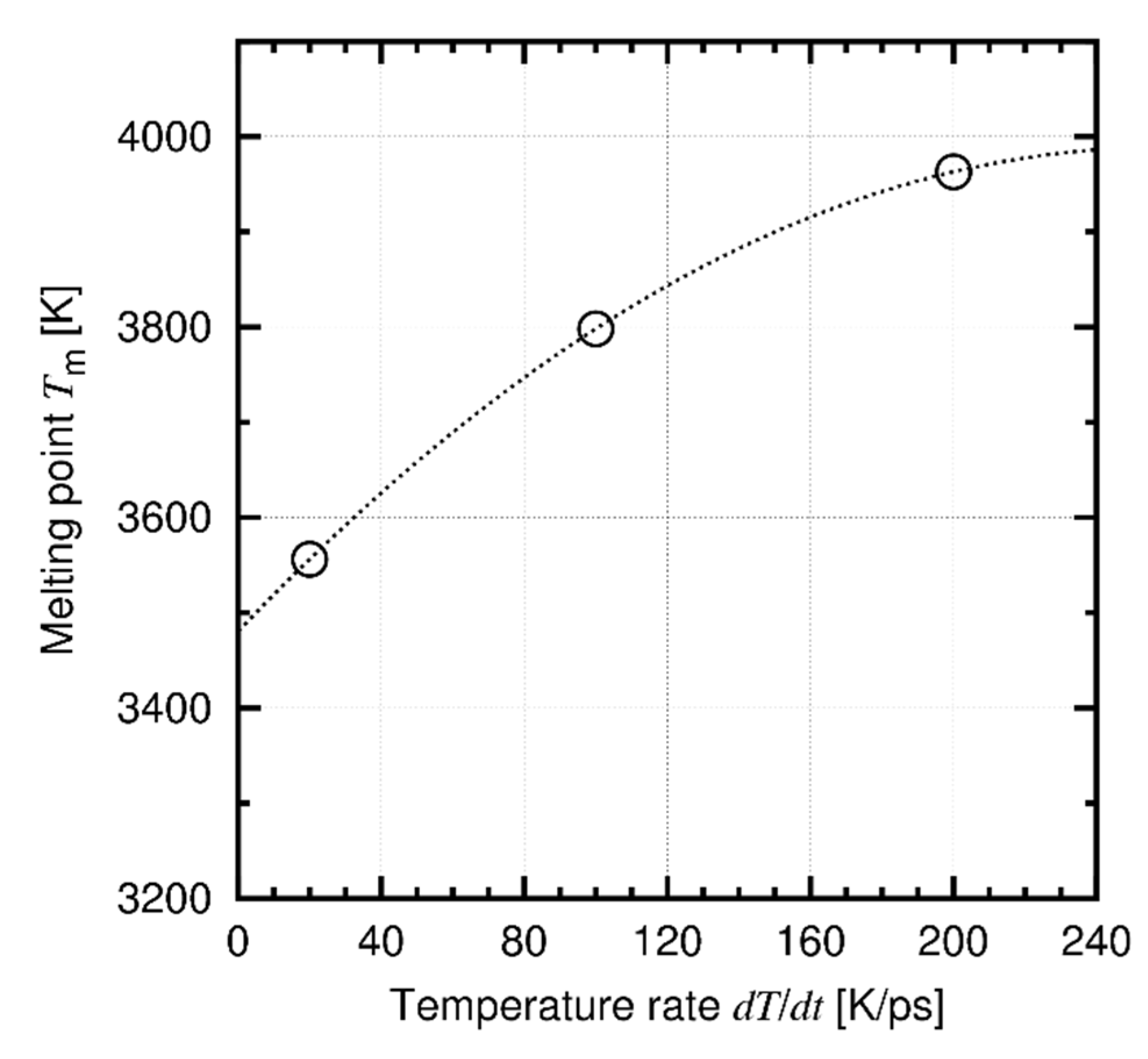
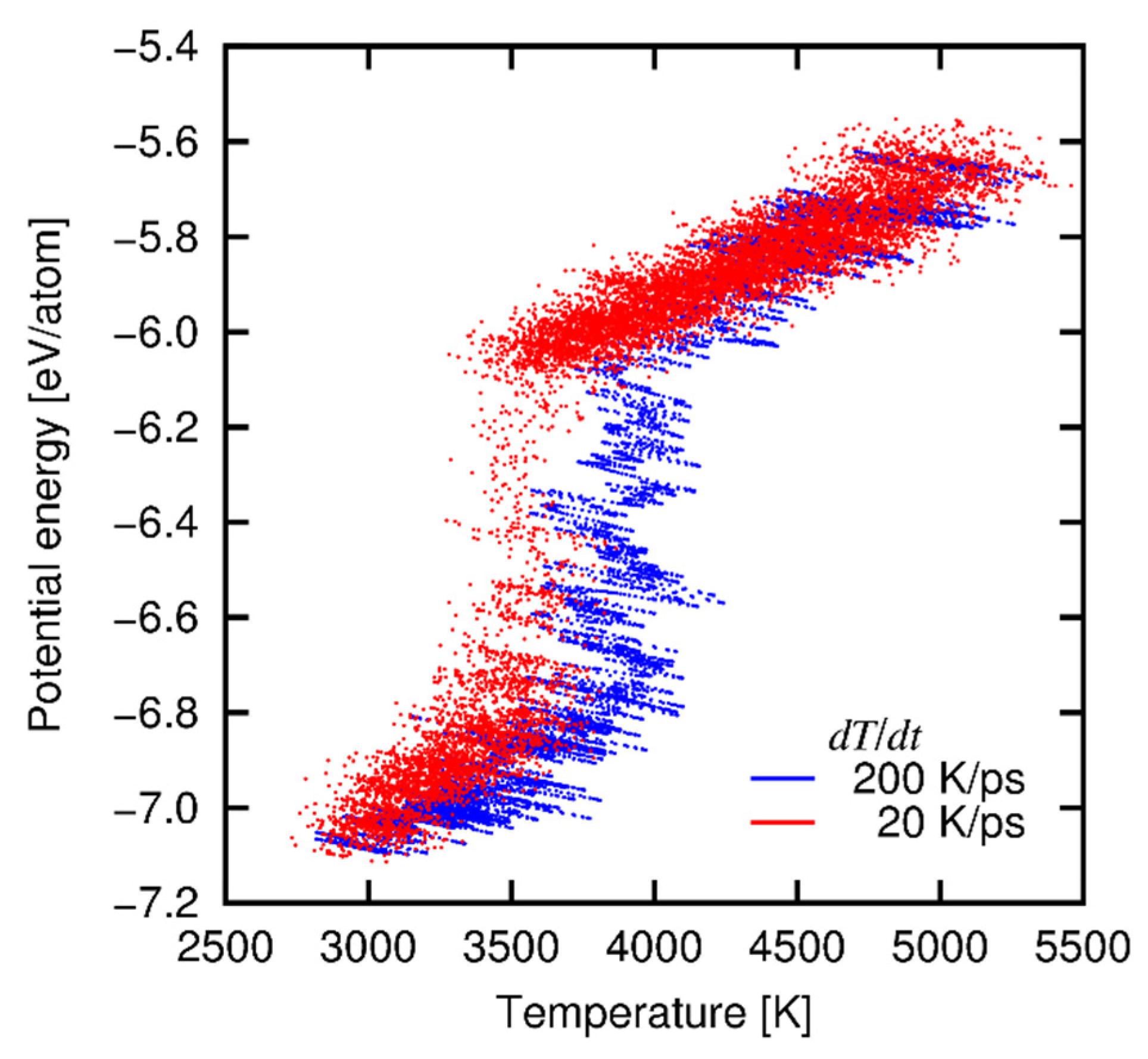
Appendix B. Approximation of Melting Point
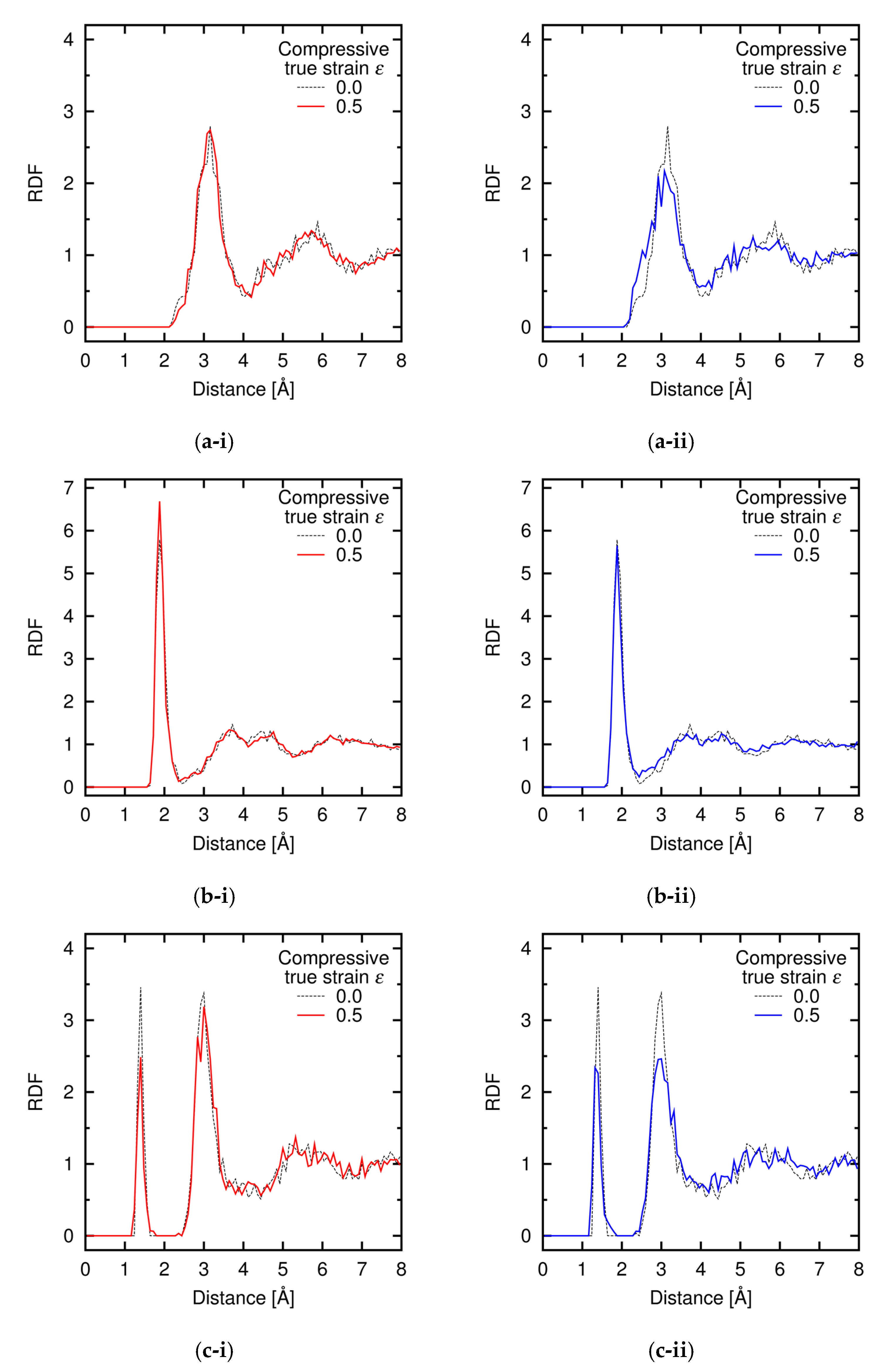
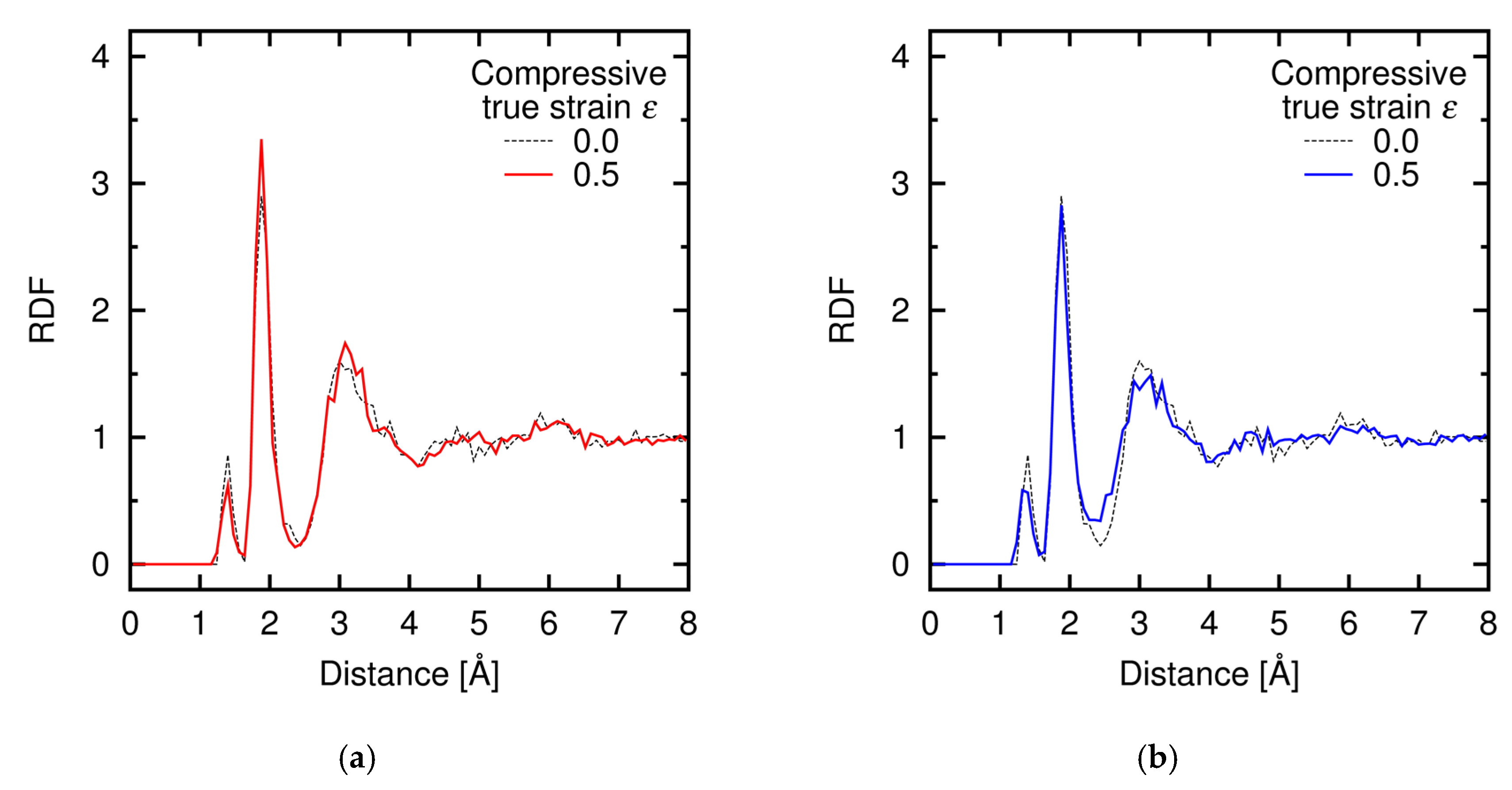
Appendix C. Radial Distribution Function during Deformation
References
- Droillard, C.; Lamon, J. Fracture toughness of 2-D woven SiC/SiC CVI-composites with multilayered interphases. J. Am. Ceram. Soc. 1996, 79, 849–858. [Google Scholar] [CrossRef]
- Xu, Y.; Cheng, L.; Zhang, L.; Yin, H.; Yin, X. High toughness, 3D textile, SiC/SiC composites by chemical vapor infiltration. Mater. Sci. Eng. A 2001, 318, 183–188. [Google Scholar] [CrossRef]
- Padture, N.P. Advanced structural ceramics in aerospace propulsion. Nat. Mater. 2016, 15, 804–809. [Google Scholar] [CrossRef] [PubMed]
- Perepezko, J.H. The hotter the engine, the better. Science 2009, 326, 1068–1069. [Google Scholar] [CrossRef]
- DiCarlo, J.A. Creep of chemically vapor deposited SiC fibres. J. Mater. Sci. 1986, 21, 217–224. [Google Scholar] [CrossRef]
- Bodet, R.; Bourrat, X.; Lamon, J.; Naslain, R. Tensile creep behaviour of a silicon carbide-based fibre with a low oxygen content. J. Mater. Sci. 1995, 30, 661–677. [Google Scholar] [CrossRef]
- Ruggles-Wrenn, M.B.; Lee, M.D. Fatigue behavior of an advanced SiC/SiC ceramic composite with a self-healing matrix at 1300 °C in air and in steam. Mater. Sci. Eng. A 2016, 677, 438–445. [Google Scholar] [CrossRef]
- Tersoff, J. Chemical order in amorphous silicon carbide. Phys. Rev. B 1994, 49, 16349–16352. [Google Scholar] [CrossRef] [PubMed]
- Erhart, P.; Albe, K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef]
- Huang, H.; Ghoniem, N.M.; Wong, J.K.; Baskes, M.I. Molecular dynamics determination of defect energetics in β-SiC using three representative empirical potentials. Modelling Simul. Mater. Sci. Eng. 1995, 3, 615–627. [Google Scholar] [CrossRef]
- Vashishta, P.; Kalia, R.K.; Nakano, A.; Rino, J.P. Interaction potential for silicon carbide: A molecular dynamics study of elastic constants and vibrational density of states for crystalline and amorphous silicon carbide. J. Appl. Phys. 2007, 101, 103515. [Google Scholar] [CrossRef]
- Kubo, A.; Nagao, S.; Umeno, Y. Molecular dynamics study of deformation and fracture in SiC with angular dependent potential model. Cumput. Mater. Sci. 2017, 139, 89–96. [Google Scholar] [CrossRef]
- Takamoto, S.; Yamasaki, T.; Nara, J.; Ohno, T.; Kaneta, C.; Hatano, A.; Izumi, S. Atomistic mechanism of graphene growth on a SiC substrate: Large-scale molecular dynamics simulations based on a new charge-transfer bond-order type potential. Phys. Rev. B 2018, 97, 125411. [Google Scholar] [CrossRef]
- Umeno, Y.; Kubo, A.; Nagao, S. Density functional theory calculation of ideal strength of SiC and GaN: Effect of multi-axial stress. Comput. Mater. Sci. 2015, 109, 105–110. [Google Scholar] [CrossRef]
- Lipowitz, J.; Barnard, T.; Bujalski, D.; Rabe, J.; Zank, G. Fine-diameter polycrystalline SiC fibers. Compos. Sci. Technol. 1994, 51, 167–171. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, X.-F.; Ritchie, R.O. Effects of grain boundary structure on the strength, toughness, and cyclic-fatigue properties of a monolithic silicon carbide. J. Am. Ceram. Soc. 2000, 83, 2079–2081. [Google Scholar] [CrossRef]
- Baldus, P.; Jansen, M.; Sporn, D. Ceramic fibers for matrix composites in high-temperature engine applications. Science 1999, 285, 699–703. [Google Scholar] [CrossRef] [PubMed]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef] [PubMed]
- Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef]
- Artrith, N.; Urban, A. An implementation of artificial neural-network potentials for atomistic materials simulations Performance for TiO2. Comput. Mech. Sci. 2016, 114, 135–150. [Google Scholar] [CrossRef]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics without electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef]
- Chmiela, S.; Tkatchenko, A.; Sauceda, H.E.; Poltavsky, I.; Schütt, K.T.; Müller, K.-R. Machine learning of accurate energy-conserving molecular force fields. Science Adv. 2017, 3, e1603015. [Google Scholar] [CrossRef] [PubMed]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef] [PubMed]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef]
- Mori, H.; Ozaki, H. Neural network atomic potential to investigate the dislocation dynamics in bcc iron. Phys. Rev. Mater. 2020, 4, 040601. [Google Scholar] [CrossRef]
- Eshet, H.; Khaliullin, R.Z.; Kühne, T.D.; Behler, J.; Parrinello, M. Ab initio quality neural network potential for sodium. Phys. Rev. B 2010, 81, 184107. [Google Scholar] [CrossRef]
- Artrith, N.; Hiller, B.; Behler, J. Neural network potentials for metals and oxides–First applications to copper clusters at zinc oxide. Phys. Status Solidi B 2013, 250, 1191–1203. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Eshet, H.; Kühne, T.D.; Behler, J.; Parrinello, M. Graphite-diamond phase coexistence study employing a neural-network mapping of the ab initio potential energy surface. Phys. Rev. B 2010, 81, 100103. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Eshet, H.; Kühne, T.D.; Behler, J.; Parrinello, M. Nucleation mechanism for the direct graphite-to-diamond phase transition. Nat. Mater. 2011, 10, 693–697. [Google Scholar] [CrossRef] [PubMed]
- Artrith, N.; Urban, A.; Ceder, G. Efficient and accurate machine-learning interpolation of atomic energies in compositions with many species. Phys. Rev. B 2017, 96, 014112. [Google Scholar] [CrossRef]
- Umeno, Y.; Kubo, A. Prediction of electronic structure in atomic model using artificial neural network. Comput. Mater. Sci. 2019, 168, 164–171. [Google Scholar] [CrossRef]
- Chandrasekaran, A.; Kamal, D.; Batra, R.; Kim, C.; Chen, L.; Ramprasad, R. Solving the electronic structure problem with machine learning. NPJ Comput. Mater. 2019, 5, 1–7. [Google Scholar] [CrossRef]
- Yeo, B.C.; Kim, D.; Kim, C.; Han, S.S. Pattern learning electronic density of states. Sci. Rep. 2019, 9, 5879. [Google Scholar] [CrossRef]
- Cannon, W.R.; Langdon, T.G. Creep of ceramics. J. Mater. Sci. 1983, 18, 1–50. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kubo, A.; Wang, J.; Umeno, Y. Development of interatomic potential for Nd-Fe-B permanent magnet and evaluation of magnetic anisotropy near the interface and grain boundary. Modelling Simul. Mater. Sci. Eng. 2014, 22, 065014. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- LAMMPS Web Page. Available online: https://lammps.sandia.gov (accessed on 24 March 2021).
- HidekiMori-CIT, Aenet-Lammps. Available online: https://github.com/HidekiMori-CIT/aenet-lammps (accessed on 24 March 2021).
- Lambrecht, W.R.L.; Segall, B.; Methfessel, M.; van Schilfgaarde, M. Calculated elastic constants and deformation potentials of cubic SiC. Phys. Rev. B 1991, 44, 3685–3694. [Google Scholar] [CrossRef] [PubMed]
- Merz, K.M.; Adamsky, R.F. Synthesis of the wurtzite form of silicon carbide. J. Am. Chem. Soc. 1959, 81, 201–251. [Google Scholar] [CrossRef]
- Lundqvist, D. On the crystal structure of silicon carbide and its content of impurities. Acta. Chem. Scand. 1948, 2, 177–191. [Google Scholar] [CrossRef][Green Version]
- Harris, G.L. Properties of Silicon, Emis Datareviews Series No. 4; INSPEC: London, UK, 1988. [Google Scholar]
- Every, A.G.; McCurdy, A.K. Numerical Data and Functional Relationships in Science and Technology; New Series, Group III; Ullmaier, H., Landolt-Börnstein, Eds.; Springer: Heidelberg, Germany, 1991; Volume 29, Pt. A. [Google Scholar]
- Halicioglu, T. Comparative study on energy-and structure-related properties for the (100) surface of β-SiC. Phys. Rev. B 1995, 51, 7217–7223. [Google Scholar] [CrossRef]
- Ercolessi, F.; Adams, J.B. Interatomic potentials from first-principles calculations: The force-matching method. Europhys. Lett. 1994, 26, 583–588. [Google Scholar] [CrossRef]
- Daviau, K.; Lee, K.K.M. Decomposition of silicon carbide at high pressures and temperatures. Phys. Rev. B 2017, 96, 174102. [Google Scholar] [CrossRef]
- Ishimaru, M.; Bae, I.-T.; Hirotsu, Y.; Matsumura, S.; Sickafus, K.E. Structural relaxation of amorphous silicon carbide. Phys. Rev. Lett. 2002, 89, 055502. [Google Scholar] [CrossRef] [PubMed]
- Ishimaru, M.; Hirata, A.; Naito, M.; Bae, I.-T.; Zhang, Y.; Weber, W.J. Direct observation of thermally induced structural changes in amorphous silicon carbide. J. Appl. Phys. 2008, 104, 033503. [Google Scholar] [CrossRef]





| 2-Body | 3-Body | |
|---|---|---|
| Combination type | X-Si, X-C | Si-X-Si, Si-X-C, C-X-C |
| Number of terms per combination | 16 | 4 |
| Cutoff radius rc [Å] | 8.0 | 6.5 |
| ANN | DFT | Exp. | MM T94 a/EA | |||
|---|---|---|---|---|---|---|
| SiC | 3C (zincblende) | a [Å] | 4.371 | 4.379 | 4.3596 b | 4.280/4.359 |
| E [eV/atom] | −7.540 | −7.532 | - | −6.434/−6.340 | ||
| C11 [GPa] | 425 | 384 | 390 b | 447/382 | ||
| C12 [GPa] | 189 | 127 | 142 b | 138/145 | ||
| C44 [GPa] | 190 | 233 | 256 b | 293/240 | ||
| 2H (wurtzite) | a [Å] | 3.082 | 3.091 | 3.076 c | - | |
| c [Å] | 5.103 | 5.073 | 5.048 c | - | ||
| E [eV/atom] | −7.539 | −7.530 | - | - | ||
| C11 [GPa] | 593 | 498 | - | - | ||
| C33 [GPa] | 592 | 537 | - | - | ||
| C12 [GPa] | 226 | 98 | - | - | ||
| C13 [GPa] | 94 | 49 | - | - | ||
| C44 [GPa] | 183 | 153 | - | - | ||
| 4H | a [Å] | 3.085 | - | 3.080 d | - | |
| c [Å] | 10.196 | - | 10.081 d | - | ||
| 6H | a [Å] | 3.088 | - | 3.080 d | - | |
| c [Å] | 15.294 | - | 15.098 d | - | ||
| Si | diamond | a [Å] | 5.486 | 5.469 | 5.429 e | 5.432/5.429 |
| E [eV/atom] | −5.418 | −5.424 | - | −4.63/−4.63 | ||
| C11 [GPa] | 137 | 154 | 168 e | 143/167 | ||
| C12 [GPa] | 66 | 57 | 65 e | 75/65 | ||
| C44 [GPa] | 135 | 74 | 80 e | 119/60 | ||
| C | diamond | a [Å] | 3.572 | 3.572 | 3.567 f | 3.556/3.566 |
| E [eV/atom] | −9.127 | −9.096 | - | −7.473/−7.373 | ||
| C11 [GPa] | 1336 | 1052 | 1081 f | 1010/1082 | ||
| C12 [GPa] | 663 | 126 | 125 f | 169/127 | ||
| C44 [GPa] | 785 | 551 | 579 f | 545/635 | ||
| graphene | d [Å] | 1.436 | 1.424 | 1.42 f | 1.555/1.475 | |
| E [eV/atom] | −9.261 | −9.230 | - | −5.314/−7.374 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubo, A.; Umeno, Y. Machine-Learning-Based Atomistic Model Analysis on High-Temperature Compressive Creep Properties of Amorphous Silicon Carbide. Materials 2021, 14, 1597. https://doi.org/10.3390/ma14071597
Kubo A, Umeno Y. Machine-Learning-Based Atomistic Model Analysis on High-Temperature Compressive Creep Properties of Amorphous Silicon Carbide. Materials. 2021; 14(7):1597. https://doi.org/10.3390/ma14071597
Chicago/Turabian StyleKubo, Atsushi, and Yoshitaka Umeno. 2021. "Machine-Learning-Based Atomistic Model Analysis on High-Temperature Compressive Creep Properties of Amorphous Silicon Carbide" Materials 14, no. 7: 1597. https://doi.org/10.3390/ma14071597
APA StyleKubo, A., & Umeno, Y. (2021). Machine-Learning-Based Atomistic Model Analysis on High-Temperature Compressive Creep Properties of Amorphous Silicon Carbide. Materials, 14(7), 1597. https://doi.org/10.3390/ma14071597






