Charge Carrier Processes and Optical Properties in TiO2 and TiO2-Based Heterojunction Photocatalysts: A Review
Abstract
:Table of Contents
- Introduction: why TiO2? ; page 2
- The role of TiO2 among photocatalysts. page 3
- Historical facts. page 7
- Electronic properties and fundamental charge carrier processes in TiO2. page 9
- 4.1.
- Charge trapping and electronic states. page 9
- 4.2.
- Electron trapping: trapping energies, nature of trap sites and time scales. page 10
- 4.3.
- Hole trapping: trapping energies, nature of trap sites and time scales. page 13
- Optical processes, charge recombination and photoluminescence in TiO2. page 13
- 5.1.
- Optical absorption. page 13
- 5.2.
- Electron-hole recombination and photoluminescence (PL) in TiO2. page 17
- 5.2.1.
- Relevance of photoluminescence analysis in TiO2. page 17
- 5.2.2.
- Basic properties of charge carrier recombination and PL in TiO2. page 18
- 5.2.3.
- Anatase photoluminescence. page 19
- 5.2.4.
- Rutile photoluminescence. page 22
- 5.3.
- Interplay between photogenerated charges and molecular O2 adsorption: the O2-dependent PL. page 23
- 5.3.1.
- O2-anatase interaction. page 23
- 5.3.2.
- O2-rutile interaction. page 25
- 5.3.3.
- Applications of O2-dependent PL of TiO2. page 26
- Intrinsic TiO2 as photocatalyst: mechanisms and limits. page 28
- 6.1.
- Basic photocatalytic processes and their characteristic times. page 28
- 6.2.
- Limitations of intrinsic TiO2 as photocatalyst. page 30
- Present and future trends for TiO2-based heterostructure photocatalysts and engineered TiO2. page 31
- 7.1.
- Engineered TiO2 nanocrystals. page 31
- 7.1.1.
- Black TiO2. page 31
- 7.1.2.
- Facet engineered TiO2. page 34
- 7.2.
- TiO2-based heterojunction photocatalysts. page 38
- 7.2.1.
- TiO2/metal heterostructures. page 39
- 7.2.2.
- TiO2/metal oxide semiconductors. page 41
- 7.2.3.
- TiO2/g-C3N4 heterostructures. page 42
- 7.2.4.
- Dye-sensitized TiO2. page 44
- Conclusions. page 46
1. Introduction: Why TiO2?
2. The Role of TiO2 among Photocatalysts
- (1)
- Large electron-hole recombination rates, as they would prevent the photogenerated charges from reaching the catalyst surface where the reaction between the adsorbed reactants shall occur.
- (2)
- Susceptibility to photocorrosion, which decreases their photocatalytic efficiency.
- (3)
- Scarce versatility of the material. By “versatility” here we mean the existence of reliable technological means to process/modify the material accordingly to the practical needs. For example: tuning of bandgap energy and/or modifying the optical spectrum of the material.
- (4)
- Other practical issues, such as poor chemical stability, scarce biocompatibility, scarce affordability of the material synthesis/processing, etc.

- (1)
- It is cost-effective, i.e., can be produced at reasonable costs also in view of large-scale uses;
- (2)
- It is photostable and resistant to corrosion;
- (3)
- It shows a satisfactorily photocatalytic efficiency (at least once UV illumination is used for undoped TiO2, as will be discussed in more detail next);
- (4)
- (5)
- Finally, in recent years the problem of scarce activation by visible sunlight (that will be discussed next) has been mitigated: novel strategies of doping development of novel composites—some of which will be discussed in the present work—is allowing to obtain interesting results also in the field of visible light-activated photocatalysis.
3. Historical Facts
4. Electronic Properties and Fundamental Charge Carrier Processes in TiO2
4.1. Charge Trapping and Electronic States
4.2. Electron Trapping: Trapping Energies, Nature of Trap Sites and Time Scales
4.3. Hole Trapping: Trapping Energies, Nature of Trap Sites and Time Scales
5. Optical Processes, Charge Recombination and Photoluminescence in TiO2
5.1. Optical Absorption
5.2. Electron-Hole Recombination and Photoluminescence (PL) in TiO2
5.2.1. Relevance of Photoluminescence Analysis in TiO2
5.2.2. Basic Properties of Charge Carrier Recombination and PL in TiO2
5.2.3. Anatase Photoluminescence
- (1)
- Non-equivalent recombination processes characterize anatase PL and lead to two spectrally separated contributions in the “green” and in the “red” part of the visible spectrum (i.e., centered at about 520 and 650 nm).
- (2)
- The overall anatase PL (i.e., both their spectral contribution) are subject to intensity quenching when the surface is exposed to O2. However, the “green” contribution is more sensitive than the “red”.
- (3)
- The excitation spectrum of anatase TiO2 follows the interband absorption curve. However, additional PL emission is still present at sub-bandgap excitation conditions [188], in particular when the titania has been subjected to reductive treatments [207]. This evidence indicates that the anatase PL is not exclusively caused by self-trapped exciton recombination, as stated in several earlier papers (this point has been mentioned at the beginning of the present subsection)
5.2.4. Rutile Photoluminescence
- (1)
- Rutile NIR-PL occurs at with a peak energy typically included in the wavelength interval 820–850 nm. While room temperature measurements typically display a single peak, some reports resolve different contributions (for example Reference [206])
- (2)
- The PLE analyses indicate that the rutile PL is clearly initiated by free carriers only, as no NIR-PL emission at sub-gap excitation is observed.
- (3)
- Exposing the rutile to O2 enhances its PL (contrary to the case of anatase).
5.3. Interplay between Photogenerated Charges and Molecular O2 Adsorption: The O2-Dependent PL
5.3.1. O2—Anatase Interaction
5.3.2. O2—Rutile Interaction
5.3.3. Applications of O2-Dependent PL of TiO2
6. Intrinsic TiO2 as Photocatalyst: Mechanisms and Limits
6.1. Basic Photocatalytic Processes and Their Characteristic Times
- (1)
- ions in water are oxidized by photogenerated holes (see Equation (6)).
- (2)
- Superoxide radicals react with protons () forming peroxidic radicals (), which, in turn form oxygen peroxide that further decomposes to hydroxyl radicals (see Equations (7)–(9)). Finally, photogenerated holes can also oxidize a pollutant molecule directly and trigger its degradation (see Equation (8) next). The corresponding reactions are:
6.2. Limitations of Intrinsic TiO2 as Photocatalyst
- (1)
- Strategies based on engineered TiO2 nanocrystals, that is centered on modifications and/or control of intrinsic properties of TiO2 nanocrystals, such as the stoichiometric composition or the surface termination (“facet engineering”),
- (2)
- Strategies based on the use of heterojunction photocatalysts, i.e., composites materials or in which TiO2 is electronically coupled with a different material acting as cocatalyst.
7. Present and Future Trends for TiO2-Based Heterostructure Photocatalysts and Engineered TiO2
7.1. Engineered TiO2 Nanocrystals
7.1.1. Black TiO2
7.1.2. Facet Engineered TiO2
7.2. TiO2-Based Heterojunction Photocatalysts
7.2.1. TiO2/Metal Heterostructures
7.2.2. TiO2/Metal Oxide Semiconductors
7.2.3. TiO2/g-C3N4 Heterostructures
7.2.4. Dye-Sensitized TiO2
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Habisreutinger, S.N.; Schmidt-Mende, L.; Stolarczyk, J.K. Photocatalytic Reduction of CO2 on TiO2 and Other Semiconductors. Angew. Chem. Int. Ed. 2013, 52, 7372–7408. [Google Scholar] [CrossRef] [PubMed]
- Low, J.; Cheng, B.; Yu, J. Surface Modification and Enhanced Photocatalytic CO2 Reduction Performance of TiO2: A Review. Appl. Surf. Sci. 2017, 392, 658–686. [Google Scholar] [CrossRef]
- Fujishima, A.; Zhang, X.; Tryk, D. TiO2 Photocatalysis and Related Surface Phenomena. Surf. Sci. Rep. 2008, 63, 515–582. [Google Scholar] [CrossRef]
- Kanan, S.; Moyet, M.A.; Arthur, R.B.; Patterson, H.H. Recent Advances on TiO2-Based Photocatalysts toward the Degradation of Pesticides and Major Organic Pollutants from Water Bodies. Catal. Rev. 2020, 62, 1–65. [Google Scholar] [CrossRef]
- Moniz, S.J.A.; Shevlin, S.A.; Martin, D.J.; Guo, Z.-X.; Tang, J. Visible-Light Driven Heterojunction Photocatalysts for Water Splitting—A Critical Review. Energy Environ. Sci. 2015, 8, 731–759. [Google Scholar] [CrossRef]
- Fajrina, N.; Tahir, M. A Critical Review in Strategies to Improve Photocatalytic Water Splitting towards Hydrogen Production. Int. J. Hydrog. Energy 2019, 44, 540–577. [Google Scholar] [CrossRef]
- Wang, Q.; Domen, K. Particulate Photocatalysts for Light-Driven Water Splitting: Mechanisms, Challenges, and Design Strategies. Chem. Rev. 2020, 67. [Google Scholar] [CrossRef]
- Clarizia, L.; Vitiello, G.; Pallotti, D.K.; Silvestri, B.; Nadagouda, M.; Lettieri, S.; Luciani, G.; Andreozzi, R.; Maddalena, P.; Marotta, R. Effect of Surface Properties of Copper-Modified Commercial Titanium Dioxide Photocatalysts on Hydrogen Production through Photoreforming of Alcohols. Int. J. Hydrog. Energy 2017, 42, 28349–28362. [Google Scholar] [CrossRef]
- Pellegrino, F.; Sordello, F.; Mino, L.; Minero, C.; Hodoroaba, V.-D.; Martra, G.; Maurino, V. Formic Acid Photoreforming for Hydrogen Production on Shape-Controlled Anatase TiO2 Nanoparticles: Assessment of the Role of Fluorides, {101}/{001} Surfaces Ratio, and Platinization. ACS Catal. 2019, 9, 6692–6697. [Google Scholar] [CrossRef]
- Qi, K.; Cheng, B.; Yu, J.; Ho, W. Review on the Improvement of the Photocatalytic and Antibacterial Activities of ZnO. J. Alloys Compd. 2017, 727, 792–820. [Google Scholar] [CrossRef]
- Prakash, J.; Sun, S.; Swart, H.C.; Gupta, R.K. Noble Metals-TiO2 Nanocomposites: From Fundamental Mechanisms to Photocatalysis, Surface Enhanced Raman Scattering and Antibacterial Applications. Appl. Mater. Today 2018, 11, 82–135. [Google Scholar] [CrossRef]
- Li, P.; Li, J.; Feng, X.; Li, J.; Hao, Y.; Zhang, J.; Wang, H.; Yin, A.; Zhou, J.; Ma, X.; et al. Metal-Organic Frameworks with Photocatalytic Bactericidal Activity for Integrated Air Cleaning. Nat. Commun. 2019, 10, 2177. [Google Scholar] [CrossRef] [PubMed]
- Fujishima, A.; Rao, T.N.; Tryk, D.A. Titanium Dioxide Photocatalysis. J. Photochem. Photobiol. C: Photochem. Rev. 2000, 1, 1–21. [Google Scholar] [CrossRef]
- Rajeshwar, K.; Chenthamarakshan, C.R.; Goeringer, S.; Djukic, M. Titania-Based Heterogeneous Photocatalysis. Materials, Mechanistic Issues, and Implications for Environmental Remediation. Pure Appl. Chem. 2001, 73, 1849–1860. [Google Scholar] [CrossRef]
- Diebold, U. The Surface Science of Titanium Dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Chen, X.; Mao, S.S. Titanium Dioxide Nanomaterials: Synthesis, Properties, Modifications, and Applications. Chem. Rev. 2007, 107, 2891–2959. [Google Scholar] [CrossRef]
- Henderson, M.A. A Surface Science Perspective on TiO2 Photocatalysis. Surf. Sci. Rep. 2011, 66, 185–297. [Google Scholar] [CrossRef]
- Dahl, M.; Liu, Y.; Yin, Y. Composite Titanium Dioxide Nanomaterials. Chem. Rev. 2014, 114, 9853–9889. [Google Scholar] [CrossRef]
- Etacheri, V.; Di Valentin, C.; Schneider, J.; Bahnemann, D.; Pillai, S.C. Visible-Light Activation of TiO2 Photocatalysts: Advances in Theory and Experiments. J. Photochem. Photobiol. Photochem. Rev. 2015, 25, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Al-Mamun, M.R.; Kader, S.; Islam, M.S.; Khan, M.Z.H. Photocatalytic Activity Improvement and Application of UV-TiO2 Photocatalysis in Textile Wastewater Treatment: A Review. J. Environ. Chem. Eng. 2019, 7, 103248. [Google Scholar] [CrossRef]
- Meng, A.; Zhang, L.; Cheng, B.; Yu, J. Dual Cocatalysts in TiO2 Photocatalysis. Adv. Mater. 2019, 1807660. [Google Scholar] [CrossRef]
- Naldoni, A.; Altomare, M.; Zoppellaro, G.; Liu, N.; Kment, Š.; Zbořil, R.; Schmuki, P. Photocatalysis with Reduced TiO2: From Black TiO2 to Cocatalyst-Free Hydrogen Production. ACS Catal. 2019, 9, 345–364. [Google Scholar] [CrossRef] [Green Version]
- Likodimos, V. Photonic Crystal-Assisted Visible Light Activated TiO2 Photocatalysis. Appl. Catal. Environ. 2018, 230, 269–303. [Google Scholar] [CrossRef]
- Xu, C.; Ravi Anusuyadevi, P.; Aymonier, C.; Luque, R.; Marre, S. Nanostructured Materials for Photocatalysis. Chem. Soc. Rev. 2019, 48, 3868–3902. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Chen, X.; Ong, W.-J.; Zhao, X.; Li, N. Surface and Heterointerface Engineering of 2D MXenes and Their Nanocomposites: Insights into Electro- and Photocatalysis. Chem 2019, 5, 18–50. [Google Scholar] [CrossRef] [Green Version]
- Dhakshinamoorthy, A.; Li, Z.; Garcia, H. Catalysis and Photocatalysis by Metal Organic Frameworks. Chem. Soc. Rev. 2018, 47, 8134–8172. [Google Scholar] [CrossRef] [PubMed]
- Kapilashrami, M.; Zhang, Y.; Liu, Y.-S.; Hagfeldt, A.; Guo, J. Probing the Optical Property and Electronic Structure of TiO2 Nanomaterials for Renewable Energy Applications. Chem. Rev. 2014, 114, 9662–9707. [Google Scholar] [CrossRef]
- Grätzel, M. Photoelectrochemical Cells. Nature 2001, 414, 7. [Google Scholar] [CrossRef] [PubMed]
- Carp, O. Photoinduced Reactivity of Titanium Dioxide. Prog. Solid State Chem. 2004, 32, 33–177. [Google Scholar] [CrossRef]
- Ghicov, A.; Schmuki, P. Self-Ordering Electrochemistry: A Review on Growth and Functionality of TiO2 nanotubes and Other Self-Aligned MOx Structures. Chem. Commun. 2009, 2791–2808. [Google Scholar] [CrossRef]
- Sanz, M.; Castillejo, M.; Amoruso, S.; Ausanio, G.; Bruzzese, R.; Wang, X. Ultra-Fast Laser Ablation and Deposition of TiO2. Appl. Phys. A 2010, 101, 639–644. [Google Scholar] [CrossRef] [Green Version]
- Paramasivam, I.; Jha, H.; Liu, N.; Schmuki, P. A Review of Photocatalysis Using Self-Organized TiO2 Nanotubes and Other Ordered Oxide Nanostructures. Small 2012, 8, 3073–3103. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Zhao, Z.; Kumar, A.; Boughton, R.I.; Liu, H. Recent Progress in Design, Synthesis, and Applications of One-Dimensional TiO2 Nanostructured Surface Heterostructures: A Review. Chem. Soc. Rev. 2014, 43, 6920–6937. [Google Scholar] [CrossRef]
- Pallotti, D.K.; Passoni, L.; Gesuele, F.; Maddalena, P.; Di Fonzo, F.; Lettieri, S. Giant O2-Induced Photoluminescence Modulation in Hierarchical Titanium Dioxide Nanostructures. ACS Sens. 2017, 2, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Kaur, N.; Singh, M.; Moumen, A.; Duina, G.; Comini, E. 1D Titanium Dioxide: Achievements in Chemical Sensing. Materials 2020, 13, 2974. [Google Scholar] [CrossRef]
- Sanz, M.; López-Arias, M.; Marco, J.F.; De Nalda, R.; Amoruso, S.; Ausanio, G.; Lettieri, S.; Bruzzese, R.; Wang, X.; Castillejo, M. Ultrafast Laser Ablation and Deposition of Wide Band Gap Semiconductors. J. Phys. Chem. C 2011, 115, 3203–3211. [Google Scholar] [CrossRef]
- Di Fonzo, F.; Casari, C.S.; Russo, V.; Brunella, M.F.; Li Bassi, A.; Bottani, C.E. Hierarchically Organized Nanostructured TiO2 for Photocatalysis Applications. Nanotechnology 2009, 20, 015604. [Google Scholar] [CrossRef] [Green Version]
- Kaempf, G.; Papenrot, W.; Holm, R. Degradation Processes in TiO2-Pigmented Paint Films on Exposure to Weathering. J. Paint Technol. 1974, 46, 56–63. [Google Scholar]
- Van Driel, B.A.; Van den Berg, K.J.; Smout, M.; Dekker, N.; Kooyman, P.J.; Dik, J. Investigating the Effect of Artists’ Paint Formulation on Degradation Rates of TiO2-Based Oil Paints. Herit. Sci. 2018, 6, 21. [Google Scholar] [CrossRef] [Green Version]
- Artesani, A.; Mosca, S.; Dozzi, M.V.; Valentini, G.; Comelli, D. Determination of Crystal Phases in Mixed TiO2 Paint Films by Non-Invasive Optical Spectroscopies. Microchem. J. 2020, 155, 104739. [Google Scholar] [CrossRef]
- Rompelberg, C.; Heringa, M.B.; Van Donkersgoed, G.; Drijvers, J.; Roos, A.; Westenbrink, S.; Peters, R.; Van Bemmel, G.; Brand, W.; Oomen, A.G. Oral Intake of Added Titanium Dioxide and Its Nanofraction from Food Products, Food Supplements and Toothpaste by the Dutch Population. Nanotoxicology 2016, 10, 1404–1414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popov, A.P.; Priezzhev, A.V.; Lademann, J.; Myllyla, R. TiO2 Nanoparticles as an Effective UV-B Radiation Skin-Protective Compound in Sunscreens. J. Phys. D-Appl. Phys. 2005, 38, 2564–2570. [Google Scholar] [CrossRef]
- Jaroenworaluck, A.; Sunsaneeyametha, W.; Kosachan, N.; Stevens, R. Characteristics of Silica-Coated TiO2 and Its UV Absorption for Sunscreen Cosmetic Applications. Surf. Interface Anal. 2006, 38, 473–477. [Google Scholar] [CrossRef]
- Velimirovic, M.; Wagner, S.; Monikh, F.A.; Uusimaeki, T.; Kaegi, R.; Hofmann, T.; Von der Kammer, F. Accurate Quantification of TiO2 Nanoparticles in Commercial Sunscreens Using Standard Materials and Orthogonal Particle Sizing Methods for verification. Talanta 2020, 215, 120921. [Google Scholar] [CrossRef]
- Fujishima, A.; Honda, K. Electrochemical Photolysis of Water at a Semiconductor Electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Renz, C. Lichtreaktionen Der Oxyde Des Titans, Cers Und Der Erdsäuren. Helv. Chim. Acta 1921, 4, 961–968. [Google Scholar] [CrossRef] [Green Version]
- Jacobsen, A.E. Titanium Dioxide Pigments: Correlation between Photochemical Reactivity and Chalking. Ind. Eng. Chem. 1949, 41, 523–526. [Google Scholar] [CrossRef]
- Baur, E.; Perret, A. Über Die Einwirkung von Licht Auf Gelöste Silbersalze in Gegenwart von Zinkoxyd. Helv. Chim. Acta 1924, 7, 910–915. [Google Scholar] [CrossRef]
- Baur, E.; Neuweiler, C. Über Photolytische Bildung von Hydroperoxyd. Helv. Chim. Acta 1927, 10, 901–907. [Google Scholar] [CrossRef]
- Renz, C. Über die Einwirkung von Oxyden auf Silbernitrat und Goldchlorid im Licht. Helv. Chim. Acta 1932, 15, 1077–1084. [Google Scholar] [CrossRef]
- Goodeve, C.F.; Kitchener, J.A. Photosensitisation by Titanium Dioxide. Trans. Faraday Soc. 1938, 34, 570–579. [Google Scholar] [CrossRef]
- Goodeve, C.F.; Kitchener, J.A. The Mechanism of Photosensitisation by Solids. Trans. Faraday Soc. 1938, 34, 902–908. [Google Scholar] [CrossRef]
- Rubin, T.R.; Calvert, J.G.; Rankin, G.T.; MacNevin, W. Photochemical Synthesis of Hydrogen Peroxide at Zinc Oxide Surfaces1. J. Am. Chem. Soc. 1953, 75, 2850–2853. [Google Scholar] [CrossRef]
- Markham, M.C.; Laidler, K.J. A Kinetic Study of Photo-Oxidations on the Surface of Zinc Oxide in Aqueous Suspensions. J. Phys. Chem. 1953, 57, 363–369. [Google Scholar] [CrossRef]
- Kennedy, D.R.; Ritchie, M.; Mackenzie, J. The Photosorption of Oxygen and Nitric Oxide on Titanium Dioxide. Trans. Faraday Soc. 1958, 54, 119–129. [Google Scholar] [CrossRef]
- Filimonov, V.N. Photocatalytic Oxidation of Gaseous Isopropanol on ZnO and TiO2. Dokl. Akad. Nauk SSSR 1964, 154, 922–925. [Google Scholar]
- McLintock, I.S.; Ritchie, M. Reactions on Titanium Dioxide; Photo-Adsorption and Oxidation of Ethylene and Propylene. Trans. Faraday Soc. 1965, 61, 1007–1016. [Google Scholar] [CrossRef]
- Fujishima, A.; Honda, K. Evidence of Photosensitized Electrolytic Oxidation on TiO2 Electrode from pH Change of Electrolyte Solution. J. Soc. Chem. Ind. Jpn. 1971, 74, 355–358. [Google Scholar] [CrossRef]
- Frank, S.N.; Bard, A.J. Heterogeneous Photocatalytic Oxidation of Cyanide and Sulfite in Aqueous Solutions at Semiconductor Powders. J. Phys. Chem. 1977, 81, 1484–1488. [Google Scholar] [CrossRef]
- Frank, S.N.; Bard, A.J. Heterogeneous Photocatalytic Oxidation of Cyanide Ion in Aqueous Solutions at Titanium Dioxide Powder. J. Am. Chem. Soc. 1977, 99, 303–304. [Google Scholar] [CrossRef]
- Frank, S.N.; Bard, A.J. Semiconductor Electrodes. 12. Photoassisted Oxidations and Photoelectrosynthesis at Polycrystalline Titanium Dioxide Electrodes. J. Am. Chem. Soc. 1977, 99, 4667–4675. [Google Scholar] [CrossRef]
- Singh, S.; Mahalingam, H.; Singh, P.K. Polymer-Supported Titanium Dioxide Photocatalysts for Environmental Remediation: A Review. Appl. Catal. Gen. 2013, 462–463, 178–195. [Google Scholar] [CrossRef]
- Di Paola, A.; García-López, E.; Marcì, G.; Palmisano, L. A Survey of Photocatalytic Materials for Environmental Remediation. J. Hazard. Mater. 2012, 211–212, 3–29. [Google Scholar] [CrossRef]
- Ayati, A.; Ahmadpour, A.; Bamoharram, F.F.; Tanhaei, B.; Mänttäri, M.; Sillanpää, M. A Review on Catalytic Applications of Au/TiO2 Nanoparticles in the Removal of Water Pollutant. Chemosphere 2014, 107, 163–174. [Google Scholar] [CrossRef] [PubMed]
- Varshney, G.; Kanel, S.R.; Kempisty, D.M.; Varshney, V.; Agrawal, A.; Sahle-Demessie, E.; Varma, R.S.; Nadagouda, M.N. Nanoscale TiO2 Films and Their Application in Remediation of Organic Pollutants. Coord. Chem. Rev. 2016, 306, 43–64. [Google Scholar] [CrossRef]
- Mamaghani, A.H.; Haghighat, F.; Lee, C.-S. Photocatalytic Oxidation Technology for Indoor Environment Air Purification: The State-of-the-Art. Appl. Catal. Environ. 2017, 203, 247–269. [Google Scholar] [CrossRef]
- Boyjoo, Y.; Sun, H.; Liu, J.; Pareek, V.K.; Wang, S. A Review on Photocatalysis for Air Treatment: From Catalyst Development to Reactor Design. Chem. Eng. J. 2017, 310, 537–559. [Google Scholar] [CrossRef]
- Tsang, C.H.A.; Li, K.; Zeng, Y.; Zhao, W.; Zhang, T.; Zhan, Y.; Xie, R.; Leung, D.Y.C.; Huang, H. Titanium Oxide Based Photocatalytic Materials Development and Their Role of in the Air Pollutants Degradation: Overview and Forecast. Environ. Int. 2019, 125, 200–228. [Google Scholar] [CrossRef]
- Laxma Reddy, P.V.; Kavitha, B.; Kumar Reddy, P.A.; Kim, K.-H. TiO2-Based Photocatalytic Disinfection of Microbes in Aqueous Media: A Review. Environ. Res. 2017, 154, 296–303. [Google Scholar] [CrossRef] [PubMed]
- Buchalska, M.; Kobielusz, M.; Matuszek, A.; Pacia, M.; Wojtyla, S.; Macyk, W. On Oxygen Activation at Rutile- and Anatase-TiO2. ACS Catal. 2015, 5, 7424–7431. [Google Scholar] [CrossRef]
- Di Paola, A.; Bellardita, M.; Palmisano, L. Brookite, the Least Known TiO2 Photocatalyst. Catalysts 2013, 3, 36–73. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhou, P.; Liu, J.; Yu, J. New Understanding of the Difference of Photocatalytic Activity among Anatase, Rutile and Brookite TiO2. Phys. Chem. Chem. Phys. 2014, 16, 20382–20386. [Google Scholar] [CrossRef]
- Mutuma, B.K.; Shao, G.N.; Kim, W.D.; Kim, H.T. Sol-Gel Synthesis of Mesoporous Anatase-Brookite and Anatase-Brookite-Rutile TiO2 Nanoparticles and Their Photocatalytic Properties. J. Colloid Interface Sci. 2015, 442, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kavan, L.; Grätzel, M.; Gilbert, S.E.; Klemenz, C.; Scheel, H.J. Electrochemical and Photoelectrochemical Investigation of Single-Crystal Anatase. J. Am. Chem. Soc. 1996, 118, 6716–6723. [Google Scholar] [CrossRef]
- Samsonov, G.V. The Oxide Handbook; IFI Data Base Library; Springer US: New York, NY, USA, 1973; ISBN 978-1-4615-9599-1. [Google Scholar]
- Leytner, S.; Hupp, J.T. Evaluation of the Energetics of Electron Trap States at the Nanocrystalline Titanium Dioxide/Aqueous Solution Interface via Time-Resolved Photoacoustic Spectroscopy. Chem. Phys. Lett. 2000, 330, 231–236. [Google Scholar] [CrossRef]
- Siripala, W.; Tomkiewicz, M. Interactions Between Photoinduced and Dark Charge Transfer across n–TiO2-Aqueous Electrolyte Interface. J. Electrochem. Soc. 1982, 129, 1240–1245. [Google Scholar] [CrossRef]
- Redmond, G.; Fitzmaurice, D.; Graetzel, M. Effect of Surface Chelation on the Energy of an Intraband Surface State of a Nanocrystalline Titania Film. J. Phys. Chem. 1993, 97, 6951–6954. [Google Scholar] [CrossRef]
- Boschloo, G.K.; Goossens, A. Electron Trapping in Porphyrin-Sensitized Porous Nanocrystalline TiO2 Electrodes. J. Phys. Chem. 1996, 100, 19489–19494. [Google Scholar] [CrossRef]
- Boschloo, G.; Fitzmaurice, D. Spectroelectrochemical Investigation of Surface States in Nanostructured TiO2 Electrodes. J. Phys. Chem. B 1999, 103, 2228–2231. [Google Scholar] [CrossRef]
- Ikeda, S.; Sugiyama, N.; Murakami, S.; Kominami, H.; Kera, Y.; Noguchi, H.; Uosaki, K.; Torimoto, T.; Ohtani, B. Quantitative Analysis of Defective Sites in Titanium (IV) Oxide Photocatalyst Powders. Phys. Chem. Chem. Phys. 2003, 5, 778–783. [Google Scholar] [CrossRef] [Green Version]
- Warren, D.S.; McQuillan, A.J. Influence of Adsorbed Water on Phonon and UV-Induced IR Absorptions of TiO2 Photocatalytic Particle Films. J. Phys. Chem. B 2004, 108, 19373–19379. [Google Scholar] [CrossRef]
- Rex, R.E.; Knorr, F.J.; McHale, J.L. Surface Traps of TiO2 Nanosheets and Nanoparticles as Illuminated by Spectroelectrochemical Photoluminescence. J. Phys. Chem. C 2014, 118, 16831–16841. [Google Scholar] [CrossRef]
- Hoffmann, M.R.; Martin, S.T.; Choi, W.; Bahnemann, D.W. Environmental Applications of Semiconductor Photocatalysis. Chem. Rev. 1995, 95, 69–96. [Google Scholar] [CrossRef]
- Knorr, F.J.; Mercado, C.C.; McHale, J.L. Trap-State Distributions and Carrier Transport in Pure and Mixed-Phase TiO2: Influence of Contacting Solvent and Interphasial Electron Transfer. J. Phys. Chem. C 2008, 112, 12786–12794. [Google Scholar] [CrossRef]
- Deskins, N.A.; Rousseau, R.; Dupuis, M. Distribution of Ti3+ Surface Sites in Reduced TiO2. J. Phys. Chem. C 2011, 115, 7562–7572. [Google Scholar] [CrossRef]
- Wallace, S.K.; Mckenna, K.P. Facet-Dependent Electron Trapping in TiO2 Nanocrystals. J. Phys. Chem. C 2015, 119, 1913–1920. [Google Scholar] [CrossRef]
- Selcuk, S.; Selloni, A. Facet-Dependent Trapping and Dynamics of Excess Electrons at Anatase TiO2 Surfaces and Aqueous Interfaces. Nat. Mater. 2016, 15, 1107–1112. [Google Scholar] [CrossRef]
- Asahi, T.; Furube, A.; Masuhara, H. Direct Measurement of Picosecond Interfacial Electron Transfer from Photoexcited TiO2 Powder to an Adsorbed Molecule in the Opaque Suspension. Chem. Phys. Lett. 1997, 275, 234–238. [Google Scholar] [CrossRef]
- Mercado, C.C.; Knorr, F.J.; McHale, J.L.; Usmani, S.M.; Ichimura, A.S.; Saraf, L.V. Location of Hole and Electron Traps on Nanocrystalline Anatase TiO2. J. Phys. Chem. C 2012, 116, 10796–10804. [Google Scholar] [CrossRef]
- Chiesa, M.; Paganini, M.C.; Livraghi, S.; Giamello, E. Charge Trapping in TiO2 Polymorphs as Seen by Electron Paramagnetic Resonance Spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 9435–9447. [Google Scholar] [CrossRef]
- Zawadzki, P. Absorption Spectra of Trapped Holes in Anatase TiO2. J. Phys. Chem. C 2013, 117, 8647–8651. [Google Scholar] [CrossRef]
- Setvin, M.; Hao, X.; Daniel, B.; Pavelec, J.; Novotny, Z.; Parkinson, G.S.; Schmid, M.; Kresse, G.; Franchini, C.; Diebold, U. Charge Trapping at the Step Edges of TiO2 Anatase (101). Angew. Chem.-Int. Edit. 2014, 53, 4714–4716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carey, J.J.; McKenna, K.P. Does Polaronic Self-Trapping Occur at Anatase TiO2 Surfaces? J. Phys. Chem. C 2018, 122, 27540–27553. [Google Scholar] [CrossRef] [Green Version]
- Szczepankiewicz, S.H.; Moss, J.A.; Hoffmann, M.R. Electron Traps and the Stark Effect on Hydroxylated Titania Photocatalysts. J. Phys. Chem. B 2002, 106, 7654–7658. [Google Scholar] [CrossRef]
- Henderson, M.A.; White, J.M.; Uetsuka, H.; Onishi, H. Photochemical Charge Transfer and Trapping at the Interface between an Organic Adlayer and an Oxide Semiconductor. J. Am. Chem. Soc. 2003, 125, 14974–14975. [Google Scholar] [CrossRef] [PubMed]
- Uetsuka, H.; Onishi, H.; Henderson, M.A.; White, J.M. Photoinduced Redox Reaction Coupled with Limited Electron Mobility at Metal Oxide Surface. J. Phys. Chem. B 2004, 108, 10621–10624. [Google Scholar] [CrossRef]
- Furube, A.; Asahi, T.; Masuhara, H.; Yamashita, H.; Anpo, M. Charge Carrier Dynamics of Standard TiO2 Catalysts Revealed by Femtosecond Diffuse Reflectance Spectroscopy. J. Phys. Chem. B 1999, 103, 3120–3127. [Google Scholar] [CrossRef]
- Jenkins, C.A.; Murphy, D.M. Thermal and Photoreactivity of TiO2 at the Gas−Solid Interface with Aliphatic and Aromatic Aldehydes. J. Phys. Chem. B 1999, 103, 1019–1026. [Google Scholar] [CrossRef]
- Chang, S.; Liu, W. Surface Doping Is More Beneficial than Bulk Doping to the Photocatalytic Activity of Vanadium-Doped TiO2. Appl. Catal. B-Environ. 2011, 101, 333–342. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Guan, Z.; Li, Q.; He, C.; Yang, J. Synergistic Effect of Surface and Bulk Single-Electron-Trapped Oxygen Vacancy of TiO2 in the Photocatalytic Reduction of CO2. Appl. Catal. B-Environ. 2017, 206, 300–307. [Google Scholar] [CrossRef]
- Hou, L.; Guan, Z.; Zhang, M.; He, C.; Li, Q.; Yang, J. Adjusting the Ratio of Bulk Single-Electron-Trapped Oxygen Vacancies/Surface Oxygen Vacancies in TiO2 for Efficient Photocatalytic Hydrogen Evolution. Catal. Sci. Technol. 2018, 8, 2809–2817. [Google Scholar] [CrossRef]
- Kamei, M.; Miyagi, T.; Ishigaki, T. Strain-Induced Charge Separation in the Photocatalytic Single Crystalline Anatase TiO2 Film. Chem. Phys. Lett. 2005, 407, 209–212. [Google Scholar] [CrossRef]
- Pacchioni, G. Oxygen Vacancy: The Invisible Agent on Oxide Surfaces. ChemPhysChem 2003, 4, 1041–1047. [Google Scholar] [CrossRef]
- Wendt, S.; Sprunger, P.T.; Lira, E.; Madsen, G.K.H.; Li, Z.; Hansen, J.O.; Matthiesen, J.; Blekinge-Rasmussen, A.; Laegsgaard, E.; Hammer, B.; et al. The Role of Interstitial Sites in the Ti3d Defect State in the Band Gap of Titania. Science 2008, 320, 1755–1759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tachikawa, T.; Tojo, S.; Fujitsuka, M.; Sekino, T.; Majima, T. Photoinduced Charge Separation in Titania Nanotubes. J. Phys. Chem. B 2006, 110, 14055–14059. [Google Scholar] [CrossRef] [PubMed]
- Corrent, S.; Cosa, G.; Scaiano, J.C.; Galletero, M.S.; Alvaro, M.; Garcia, H. Intrazeolite Photochemistry. 26. Photophysical Properties of Nanosized TiO2 Clusters Included in Zeolites, Y., β, and Mordenite. Chem. Mater. 2001, 13, 715–722. [Google Scholar] [CrossRef]
- Huber, R.; Spörlein, S.; Moser, J.E.; Grätzel, M.; Wachtveitl, J. The Role of Surface States in the Ultrafast Photoinduced Electron Transfer from Sensitizing Dye Molecules to Semiconductor Colloids. J. Phys. Chem. B 2000, 104, 8995–9003. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, A.I.; Kameneva, O.; Rozes, L.; Sanchez, C.; Bityurin, N.; Kanaev, A. Extinction of Photo-Induced Ti3+ Centres in Titanium Oxide Gels and Gel-Based oxo-PHEMA Hybrids. Chem. Phys. Lett. 2006, 429, 523–527. [Google Scholar] [CrossRef]
- Yamada, Y.; Kanemitsu, Y. Determination of Electron and Hole Lifetimes of Rutile and Anatase TiO2 Single Crystals. Appl. Phys. Lett. 2012, 101, 133907. [Google Scholar] [CrossRef] [Green Version]
- Sa, J.; Friedli, P.; Geiger, R.; Lerch, P.; Rittmann-Frank, M.H.; Milne, C.J.; Szlachetko, J.; Santomauro, F.G.; Van Bokhoven, J.A.; Chergui, M.; et al. Transient Mid-IR Study of Electron Dynamics in TiO2 Conduction Band. Analyst 2013, 138, 1966–1970. [Google Scholar] [CrossRef]
- Peiró, A.M.; Colombo, C.; Doyle, G.; Nelson, J.; Mills, A.; Durrant, J.R. Photochemical Reduction of Oxygen Adsorbed to Nanocrystalline TiO2 Films: A Transient Absorption and Oxygen Scavenging Study of Different TiO2 Preparations. J. Phys. Chem. B 2006, 110, 23255–23263. [Google Scholar] [CrossRef] [PubMed]
- Kormann, C.; Bahnemann, D.W.; Hoffmann, M.R. Preparation and Characterization of Quantum-Size Titanium Dioxide. J. Phys. Chem. 1988, 92, 5196–5201. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Kameneva, O.; Alexandrov, A.; Bityurin, N.; Marteau; Chhor, K.; Sanchez, C.; Kanaev, A. Light-Induced Charge Separation and Storage in Titanium Oxide Gels. Phys. Rev. E 2005, 71, 021403. [Google Scholar] [CrossRef] [PubMed]
- Bityurin, N.; Kuznetsov, A.I.; Kanaev, A. Kinetics of UV-Induced Darkening of Titanium-Oxide Gels. Appl. Surf. Sci. 2005, 248, 86–90. [Google Scholar] [CrossRef]
- Wang, H.; He, J.; Boschloo, G.; Lindström, H.; Hagfeldt, A.; Lindquist, S.-E. Electrochemical Investigation of Traps in a Nanostructured TiO2 Film. J. Phys. Chem. B 2001, 105, 2529–2533. [Google Scholar] [CrossRef]
- Katoh, R.; Murai, M.; Furube, A. Electron–Hole Recombination in the Bulk of a Rutile TiO2 Single Crystal Studied by Sub-Nanosecond Transient Absorption Spectroscopy. Chem. Phys. Lett. 2008, 461, 238–241. [Google Scholar] [CrossRef]
- Kerisit, S.; Deskins, N.A.; Rosso, K.M.; Dupuis, M. A Shell Model for Atomistic Simulation of Charge Transfer in Titania. J. Phys. Chem. C 2008, 112, 7678–7688. [Google Scholar] [CrossRef]
- Shapovalov, V.; Stefanovich, E.V.; Truong, T.N. Nature of the Excited States of the Rutile TiO2(110) Surface with Adsorbed Water. Surf. Sci. 2002, 498, L103–L108. [Google Scholar] [CrossRef]
- Dimitrijevic, N.M.; Saponjic, Z.V.; Rabatic, B.M.; Poluektov, O.G.; Rajh, T. Effect of Size and Shape of Nanocrystalline TiO2 on Photogenerated Charges. An EPR Study. J. Phys. Chem. C 2007, 111, 14597–14601. [Google Scholar] [CrossRef]
- Coronado, J.M.; Javier Maira, A.; Martínez-Arias, A.; Conesa, J.C.; Soria, J. EPR Study of the Radicals Formed upon UV Irradiation of Ceria-Based Photocatalysts. J. Photochem. Photobiol. Chem. 2002, 150, 213–221. [Google Scholar] [CrossRef]
- Berger, T.; Sterrer, M.; Diwald, O.; Knözinger, E.; Panayotov, D.; Thompson, T.L.; Yates, J.T. Light-Induced Charge Separation in Anatase TiO2 Particles. J. Phys. Chem. B 2005, 109, 6061–6068. [Google Scholar] [CrossRef] [PubMed]
- Berger, T.; Sterrer, M.; Diwald, O.; Knzinger, E. Charge Trapping and Photoadsorption of O2 on Dehydroxylated TiO2 Nanocrystals?An Electron Paramagnetic Resonance Study. ChemPhysChem 2005, 6, 2104–2112. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Tamai, N. How Fast Is Interfacial Hole Transfer? In Situ Monitoring of Carrier Dynamics in Anatase TiO2 Nanoparticles by Femtosecond Laser Spectroscopy. Phys. Chem. Chem. Phys. 2001, 3, 3393–3398. [Google Scholar] [CrossRef]
- Tamaki, Y.; Furube, A.; Murai, M.; Hara, K.; Katoh, R.; Tachiya, M. Direct Observation of Reactive Trapped Holes in TiO2 Undergoing Photocatalytic Oxidation of Adsorbed Alcohols: Evaluation of the Reaction Rates and Yields. J. Am. Chem. Soc. 2006, 128, 416–417. [Google Scholar] [CrossRef]
- Tamaki, Y.; Furube, A.; Murai, M.; Hara, K.; Katoh, R.; Tachiya, M. Dynamics of Efficient Electron–Hole Separation in TiO2 Nanoparticles Revealed by Femtosecond Transient Absorption Spectroscopy under the Weak-Excitation Condition. Phys. Chem. Chem. Phys. 2007, 9, 1453–1460. [Google Scholar] [CrossRef]
- Yoshihara, T.; Katoh, R.; Furube, A.; Tamaki, Y.; Murai, M.; Hara, K.; Murata, S.; Arakawa, H.; Tachiya, M. Identification of Reactive Species in Photoexcited Nanocrystalline TiO2 Films by Wide-Wavelength-Range (400−2500 nm) Transient Absorption Spectroscopy. J. Phys. Chem. B 2004, 108, 3817–3823. [Google Scholar] [CrossRef]
- Rams, J.; Tejeda, A.; Cabrera, J.M. Refractive Indices of Rutile as a Function of Temperature and Wavelength. J. Appl. Phys. 1997, 82, 994–997. [Google Scholar] [CrossRef]
- DeVore, J.R. Refractive Indices of Rutile and Sphalerite. J. Opt. Soc. Am. JOSA 1951, 41, 416–419. [Google Scholar] [CrossRef]
- Jellison, G.E.; Boatner, L.A.; Budai, J.D.; Jeong, B.-S.; Norton, D.P. Spectroscopic Ellipsometry of Thin Film and Bulk Anatase (TiO2). J. Appl. Phys. 2003, 93, 9537. [Google Scholar] [CrossRef]
- Saha, D.; Ajimsha, R.S.; Rajiv, K.; Mukherjee, C.; Gupta, M.; Misra, P.; Kukreja, L.M. Spectroscopic Ellipsometry Characterization of Amorphous and Crystalline TiO2 Thin Films Grown by Atomic Layer Deposition at Different Temperatures. Appl. Surf. Sci. 2014, 315, 116–123. [Google Scholar] [CrossRef]
- Cronemeyer, D.C. Infrared Absorption of Reduced Rutile TiO2 Single Crystals. Phys. Rev. 1959, 113, 1222–1226. [Google Scholar] [CrossRef]
- Glassford, K.M.; Chelikowsky, J.R. Optical Properties of Titanium Dioxide in the Rutile Structure. Phys. Rev. B 1992, 45, 3874–3877. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Prasad, K.; Sanjinès, R.; Schmid, P.E.; Lévy, F. Electrical and Optical Properties of TiO2 Anatase Thin Films. J. Appl. Phys. 1994, 75, 2042–2047. [Google Scholar] [CrossRef]
- Tang, H.; Berger, H.; Schmid, P.E.; Lévy, F. Optical Properties of Anatase (TiO2). Solid State Commun. 1994, 92, 267–271. [Google Scholar] [CrossRef]
- Tang, H.; Lévy, F.; Berger, H.; Schmid, P.E. Urbach Tail of Anatase TiO2. Phys. Rev. B 1995, 52, 7771–7774. [Google Scholar] [CrossRef] [PubMed]
- Sekiya, T.; Igarashi, M.; Kurita, S.; Takekawa, S.; Fujisawa, M. Structure Dependence of Reflection Spectra of TiO2 Single Crystals. J. Electron Spectrosc. Relat. Phenom. 1998, 92, 247–250. [Google Scholar] [CrossRef]
- Tanemura, S.; Miao, L.; Jin, P.; Kaneko, K.; Terai, A.; Nabatova-Gabain, N. Optical Properties of Polycrystalline and Epitaxial Anatase and Rutile TiO2 Thin Films by Rf Magnetron Sputtering. Appl. Surf. Sci. 2003, 212–213, 654–660. [Google Scholar] [CrossRef]
- Itoh, C.; Iwahashi, K.; Kan’no, K. Photogeneration of Charge Carriers in Titanium Oxides. Nucl. Instrum. Methods Phys. Res. Sect. Beam Interact. Mater. At. 2002, 191, 271–274. [Google Scholar] [CrossRef]
- Sumita, T.; Yamaki, T.; Yamamoto, S.; Miyashita, A. Photo-Induced Surface Charge Separation of Highly Oriented TiO2 Anatase and Rutile Thin Films. Appl. Surf. Sci. 2002, 200, 21–26. [Google Scholar] [CrossRef]
- Amtout, A.; Leonelli, R. Optical Properties of Rutile near Its Fundamental Band Gap. Phys. Rev. B 1995, 51, 6842–6851. [Google Scholar] [CrossRef]
- Wang, Z.; Helmersson, U.; Käll, P.-O. Optical Properties of Anatase TiO2 Thin Films Prepared by Aqueous Sol–Gel Process at Low Temperature. Thin Solid Films 2002, 405, 50–54. [Google Scholar] [CrossRef]
- Hosaka, N.; Sekiya, T.; Fujisawa, M.; Satoko, C.; Kurita, S. UV Reflection Spectra of Anatase TiO2. J. Electron Spectrosc. Relat. Phenom. 1996, 78, 75–78. [Google Scholar] [CrossRef]
- Kurita, D.; Ohta, S.; Sugiura, K.; Ohta, H.; Koumoto, K. Carrier Generation and Transport Properties of Heavily Nb-Doped Anatase TiO2 Epitaxial Films at High Temperatures. J. Appl. Phys. 2006, 100, 096105. [Google Scholar] [CrossRef]
- Ambrosone, G.; Coscia, U.; Lettieri, S.; Maddalena, P.; Minarini, C. Optical, Structural and Electrical Properties of Μc-Si:H Films Deposited by SiH4+H2. Mater. Sci. Eng. 2003, 101, 236–241. [Google Scholar] [CrossRef]
- Asahi, R.; Taga, Y.; Mannstadt, W.; Freeman, A.J. Electronic and Optical Properties of Anatase TiO2. Phys. Rev. B 2000, 61, 7459–7465. [Google Scholar] [CrossRef]
- Satoh, N.; Nakashima, T.; Kamikura, K.; Yamamoto, K. Quantum Size Effect in TiO2 Nanoparticles Prepared by Finely Controlled Metal Assembly on Dendrimer Templates. Nat. Nanotechnol. 2008, 3, 106–111. [Google Scholar] [CrossRef]
- Serpone, N.; Lawless, D.; Khairutdinov, R. Size Effects on the Photophysical Properties of Colloidal Anatase TiO2 Particles: Size Quantization versus Direct Transitions in This Indirect Semiconductor? J. Phys. Chem. 1995, 99, 16646–16654. [Google Scholar] [CrossRef]
- Monticone, S.; Tufeu, R.; Kanaev, A.V.; Scolan, E.; Sanchez, C. Quantum Size Effect in TiO2 Nanoparticles: Does It Exist? Appl. Surf. Sci. 2000, 162–163, 565–570. [Google Scholar] [CrossRef]
- Ricciardi, C.; Ballarini, V.; Galli, M.; Liscidini, M.; Andreani, L.C.; Losurdo, M.; Bruno, G.; Lettieri, S.; Gesuele, F.; Maddalena, P.; et al. Amorphous Silicon Nitride: A Suitable Alloy for Optical Multilayered Structures. J. Non-Cryst. Solids 2006, 352, 1294–1297. [Google Scholar] [CrossRef]
- Passoni, L.; Criante, L.; Fumagalli, F.; Scotognella, F.; Lanzani, G.; Di Fonzo, F. Self-Assembled Hierarchical Nanostructures for High-Efficiency Porous Photonic Crystals. ACS Nano 2014, 8, 12167–12174. [Google Scholar] [CrossRef]
- Chiarello, G.L.; Zuliani, A.; Ceresoli, D.; Martinazzo, R.; Selli, E. Exploiting the Photonic Crystal Properties of TiO2 Nanotube Arrays To Enhance Photocatalytic Hydrogen Production. ACS Catal. 2016, 6, 1345–1353. [Google Scholar] [CrossRef]
- Chiarello, G.L.; Aguirre, M.H.; Selli, E. Hydrogen Production by Photocatalytic Steam Reforming of Methanol on Noble Metal-Modified TiO2. J. Catal. 2010, 273, 182–190. [Google Scholar] [CrossRef]
- Carotta, M.C.; Fioravanti, A.; Gherardi, S.; Malagù, C.; Sacerdoti, M.; Ghiotti, G.; Morandi, S. (Ti,Sn) Solid Solutions as Functional Materials for Gas Sensing. Sens. Actuators Chem. 2014, 194, 195–205. [Google Scholar] [CrossRef]
- Yu, J.; Lei, J.; Wang, L.; Zhang, J.; Liu, Y. TiO2 Inverse Opal Photonic Crystals: Synthesis, Modification, and Applications - A Review. J. Alloys Compd. 2018, 769, 740–757. [Google Scholar] [CrossRef]
- Qi, D.; Lu, L.; Xi, Z.; Wang, L.; Zhang, J. Enhanced Photocatalytic Performance of TiO2 Based on Synergistic Effect of Ti3+ Self-Doping and Slow Light Effect. Appl. Catal. Environ. 2014, 160–161, 621–628. [Google Scholar] [CrossRef]
- Corn, R.M.; Higgins, D.A. Optical Second Harmonic Generation as a Probe of Surface Chemistry. Chem. Rev. 1994, 94, 107–125. [Google Scholar] [CrossRef]
- Borbone, F.; Carella, A.; Caruso, U.; Roviello, G.; Tuzi, A.; Dardano, P.; Lettieri, S.; Maddalena, P.; Barsella, A. Large Second-Order NLO Activity in Poly(4-Vinylpyridine) Grafted with PdII and CuII Chromophoric Complexes with Tridentate Bent Ligands Containing Heterocycles. Eur. J. Inorg. Chem. 2008, 2008, 1846–1853. [Google Scholar] [CrossRef]
- Shen, Y.R. Basic Theory of Surface Sum-Frequency Generation. J. Phys. Chem. C 2012, 116, 15505–15509. [Google Scholar] [CrossRef]
- Rubano, A.; Scigaj, M.; Sánchez, F.; Herranz, G.; Paparo, D. Optical Second Harmonic Generation from LaAlO3/SrTiO3 Interfaces with Different in-Plane Anisotropies. J. Phys. Condens. Matter 2020, 32, 135001. [Google Scholar] [CrossRef]
- Anpo, M.; Shima, T.; Kubokawa, Y. ESR and Photoluminescence Evidence for the Photocatalytic Formation of Hydroxyl Radicals on Small TiO2 Particles. Chem. Lett. 1985, 14, 1799–1802. [Google Scholar] [CrossRef] [Green Version]
- Anpo, M.; Aikawa, N.; Kubokawa, Y.; Che, M.; Louis, C.; Giamello, E. Photoluminescence and Photocatalytic Activity of Highly Dispersed Titanium Oxide Anchored onto Porous Vycor Glass. J. Phys. Chem. 1985, 89, 5017–5021. [Google Scholar] [CrossRef]
- Anpo, M.; Yamada, Y.; Kubokawa, Y. Photoluminescence and Photocatalytic Activity of MgO Powders with Co-Ordinatively Unsaturated Surface Ions. J. Chem. Soc. Chem. Commun. 1986, 714. [Google Scholar] [CrossRef]
- Anpo, M.; Yamada, Y. Photoluminescence and Photocatalytic Activity of MgO Powders. Mater. Chem. Phys. 1988, 18, 465–484. [Google Scholar] [CrossRef]
- Anpo, M.; Tomonari, M.; Fox, M.A. In Situ Photoluminescence of Titania as a Probe of Photocatalytic Reactions. J. Phys. Chem. 1989, 93, 7300–7302. [Google Scholar] [CrossRef]
- Yu, P.Y.; Cardona, M. Fundamentals of Semiconductors; Graduate Texts in Physics; Springer: Heidelberg, Germany, 2010; ISBN 978-3-642-00709-5. [Google Scholar]
- Forss, L.; Schubnell, M. Temperature Dependence of the Luminescence of TiO2 Powder. Appl. Phys. B 1993, 56, 363–366. [Google Scholar] [CrossRef]
- Ghosh, H.N.; Adhikari, S. Trap State Emission from TiO2 Nanoparticles in Microemulsion Solutions. Langmuir 2001, 17, 4129–4130. [Google Scholar] [CrossRef]
- Susha, A.S.; Lutich, A.A.; Liu, C.; Xu, H.; Zhang, R.; Zhong, Y.; Wong, K.S.; Yang, S.; Rogach, A.L. Comparative Optical Study of Colloidal Anatase Titania Nanorods and Atomically Thin Wires. Nanoscale 2013, 5, 1465. [Google Scholar] [CrossRef] [Green Version]
- Cleary, O.; Purcell-Milton, F.; Vandekerckhove, A.; Gun’ko, Y.K. Chiral and Luminescent TiO2 Nanoparticles. Adv. Opt. Mater. 2017, 5, 1601000. [Google Scholar] [CrossRef] [Green Version]
- Paul, K.K.; Jana, S.; Giri, P.K. Tunable and High Photoluminescence Quantum Yield from Self-Decorated TiO2 Quantum Dots on Fluorine Doped Mesoporous TiO2 Flowers by Rapid Thermal Annealing. Part. Part. Syst. Charact. 2018, 35, 1800198. [Google Scholar] [CrossRef]
- Gfroerer, T.H. Photoluminescence in Analysis of Surfaces and Interfaces. Encycl. Anal. Chem. 2000. [Google Scholar]
- Lettieri, S.; Santamaria Amato, L.; Maddalena, P.; Comini, E.; Baratto, C.; Todros, S. Recombination Dynamics of Deep Defect States in Zinc Oxide Nanowires. Nanotechnology 2009, 20, 175706. [Google Scholar] [CrossRef] [PubMed]
- Dozzi, M.V.; D’Andrea, C.; Ohtani, B.; Valentini, G.; Selli, E. Fluorine-Doped TiO2 Materials: Photocatalytic Activity vs Time-Resolved Photoluminescence. J. Phys. Chem. C 2013, 117, 25586–25595. [Google Scholar] [CrossRef]
- Anpo, M.; Che, M. Applications of Photoluminescence Techniques to the Characterization of Solid Surfaces in Relation to Adsorption, Catalysis, and Photocatalysis. Adv. Catal. 1999, 44, 119–257. [Google Scholar]
- Zhang, W.F.; Tang, J.; Ye, J. Photoluminescence and Photocatalytic Properties of SrSnO3 Perovskite. Chem. Phys. Lett. 2006, 418, 174–178. [Google Scholar] [CrossRef]
- Liqiang, J.; Yichun, Q.; Baiqi, W.; Shudan, L.; Baojiang, J.; Libin, Y.; Wei, F.; Honggang, F.; Jiazhong, S. Review of Photoluminescence Performance of Nano-Sized Semiconductor Materials and Its Relationships with Photocatalytic Activity. Sol. Energy Mater. Sol. Cells 2006, 90, 1773–1787. [Google Scholar] [CrossRef]
- Bohle, D.S.; Spina, C.J. Cationic and Anionic Surface Binding Sites on Nanocrystalline Zinc Oxide: Surface Influence on Photoluminescence and Photocatalysis. J. Am. Chem. Soc. 2009, 131, 4397–4404. [Google Scholar] [CrossRef]
- Coscia, U.; Ambrosone, G.; Lettieri, S.; Maddalena, P.; Rigato, V.; Restello, S.; Bobeico, E.; Tucci, M. Preparation of Microcrystalline Silicon–Carbon Films. Sol. Energy Mater. Sol. Cells 2005, 87, 433–444. [Google Scholar] [CrossRef]
- Ruiz Peralta, M.D.L.; Pal, U.; Zeferino, R.S. Photoluminescence (PL) Quenching and Enhanced Photocatalytic Activity of Au-Decorated ZnO Nanorods Fabricated through Microwave-Assisted Chemical Synthesis. ACS Appl. Mater. Interfaces 2012, 4, 4807–4816. [Google Scholar] [CrossRef] [PubMed]
- Mercado, C.; Seeley, Z.; Bandyopadhyay, A.; Bose, S.; McHale, J.L. Photoluminescence of Dense Nanocrystalline Titanium Dioxide Thin Films: Effect of Doping and Thickness and Relation to Gas Sensing. ACS Appl. Mater. Interfaces 2011, 3, 2281–2288. [Google Scholar] [CrossRef]
- Knorr, F.J.; McHale, J.L. Spectroelectrochemical Photoluminescence of Trap States of Nanocrystalline TiO2 in Aqueous Media. J. Phys. Chem. C 2013, 117, 13654–13662. [Google Scholar] [CrossRef]
- Setaro, A.; Lettieri, S.; Diamare, D.; Maddalena, P.; Malagù, C.; Carotta, M.C.; Martinelli, G. Nanograined Anatase Titania-Based Optochemical Gas Detection. New J. Phys. 2008, 10, 053030. [Google Scholar] [CrossRef] [Green Version]
- Williams, R.T.; Song, K.S. The Self-Trapped Exciton. J. Phys. Chem. Solids 1990, 51, 679–716. [Google Scholar] [CrossRef]
- Varley, J.B.; Janotti, A.; Franchini, C.; Van de Walle, C.G. Role of Self-Trapping in Luminescence and p-Type Conductivity of Wide-Band-Gap Oxides. Phys. Rev. B 2012, 85, 081109. [Google Scholar] [CrossRef] [Green Version]
- Pallotti, D.K.; Passoni, L.; Maddalena, P.; Di Fonzo, F.; Lettieri, S. Photoluminescence Mechanisms in Anatase and Rutile TiO2. J. Phys. Chem. C 2017, 121, 9011–9021. [Google Scholar] [CrossRef]
- Mascaretti, L.; Russo, V.; Zoppellaro, G.; Lucotti, A.; Casari, C.S.; Kment, Š.; Naldoni, A.; Li Bassi, A. Excitation Wavelength- and Medium-Dependent Photoluminescence of Reduced Nanostructured TiO2 Films. J. Phys. Chem. C 2019, 123, 11292–11303. [Google Scholar] [CrossRef]
- Cavigli, L.; Bogani, F.; Vinattieri, A.; Faso, V.; Baldi, G. Volume versus Surface-Mediated Recombination in Anatase TiO2 Nanoparticles. J. Appl. Phys. 2009, 106, 053516. [Google Scholar] [CrossRef]
- Pallotti, D.K.; Orabona, E.; Amoruso, S.; Aruta, C.; Bruzzese, R.; Chiarella, F.; Tuzi, S.; Maddalena, P.; Lettieri, S. Multi-Band Photoluminescence in TiO2 Nanoparticles-Assembled Films Produced by Femtosecond Pulsed Laser Deposition. J. Appl. Phys. 2013, 114, 043503. [Google Scholar] [CrossRef]
- Setaro, A.; Bismuto, A.; Lettieri, S.; Maddalena, P.; Comini, E.; Bianchi, S.; Baratto, C.; Sberveglieri, G. Optical Sensing of NO2 in Tin Oxide Nanowires at Sub-Ppm Level. Sens. Actuators Chem. 2008, 130, 391–395. [Google Scholar] [CrossRef]
- Rex, R.E.; Yang, Y.; Knorr, F.J.; Zhang, J.Z.; Li, Y.; McHale, J.L. Spectroelectrochemical Photoluminescence of Trap States in H-Treated Rutile TiO2 Nanowires: Implications for Photooxidation of Water. J. Phys. Chem. C 2016, 120, 3530–3541. [Google Scholar] [CrossRef] [Green Version]
- McHale, J.L.; Rich, C.C.; Knorr, F.J. Trap State Photoluminescence of Nanocrystalline and Bulk TiO2,: Implications for Carrier Transport. MRS Proc. 2010, 1268, EE03–EE08. [Google Scholar] [CrossRef]
- Pallotti, D.; Orabona, E.; Amoruso, S.; Maddalena, P.; Lettieri, S. Modulation of Mixed-Phase Titania Photoluminescence by Oxygen Adsorption. Appl. Phys. Lett. 2014, 105, 031903. [Google Scholar] [CrossRef] [Green Version]
- Pallotti, D.K.; Amoruso, S.; Orabona, E.; Maddalena, P.; Lettieri, S. Biparametric Optical Sensing of Oxygen by Titanium Dioxide. Sens. Actuators B Chem. 2015, 221, 515–520. [Google Scholar] [CrossRef]
- Orabona, E.; Pallotti, D.; Fioravanti, A.; Gherardi, S.; Sacerdoti, M.; Carotta, M.C.; Maddalena, P.; Lettieri, S. On Mechanism of NO2 Detection by ZnO Excitonic Luminescence. Sens. Actuators B Chem. 2015, 210, 706–711. [Google Scholar] [CrossRef]
- Carotta, M.C.; Cervi, A.; Gherardi, S.; Guidi, V.; Malagu’, C.; Martinelli, G.; Vendemiati, B.; Sacerdoti, M.; Ghiotti, G.; Morandi, S.; et al. (Ti, Sn)O2 Solid Solutions for Gas Sensing: A Systematic Approach by Different Techniques for Different Calcination Temperature and Molar Composition. Sens. Actuators B Chem. 2009, 139, 329–339. [Google Scholar] [CrossRef]
- Baratto, C.; Todros, S.; Faglia, G.; Comini, E.; Sberveglieri, G.; Lettieri, S.; Santamaria, L.; Maddalena, P. Luminescence Response of ZnO Nanowires to Gas Adsorption. Sens. Actuators B Chem. 2009, 140, 461–466. [Google Scholar] [CrossRef]
- Lettieri, S.; Bismuto, A.; Maddalena, P.; Baratto, C.; Comini, E.; Faglia, G.; Sberveglieri, G.; Zanotti, L. Gas Sensitive Light Emission Properties of Tin Oxide and Zinc Oxide Nanobelts. J. Non-Cryst. Solids 2006, 352, 1457–1460. [Google Scholar] [CrossRef]
- Lettieri, S.; Causà, M.; Setaro, A.; Trani, F.; Barone, V.; Ninno, D.; Maddalena, P. Direct Role of Surface Oxygen Vacancies in Visible Light Emission of Tin Dioxide Nanowires. J. Chem. Phys. 2008, 129, 244710. [Google Scholar] [CrossRef] [Green Version]
- Lettieri, S.; Setaro, A.; Baratto, C.; Comini, E.; Faglia, G.; Sberveglieri, G.; Maddalena, P. On the Mechanism of Photoluminescence Quenching in Tin Dioxide Nanowires by NO2 Adsorption. New J. Phys. 2008, 10, 043013. [Google Scholar] [CrossRef]
- Trani, F.; Causà, M.; Lettieri, S.; Setaro, A.; Ninno, D.; Barone, V.; Maddalena, P. Role of Surface Oxygen Vacancies in Photoluminescence of Tin Dioxide Nanobelts. Microelectron. J. 2009, 40, 236–238. [Google Scholar] [CrossRef]
- Valerini, D.; Cretì, A.; Caricato, A.P.; Lomascolo, M.; Rella, R.; Martino, M. Optical Gas Sensing through Nanostructured ZnO Films with Different Morphologies. Sens. Actuators B Chem. 2010, 145, 167–173. [Google Scholar] [CrossRef]
- Cretì, A.; Valerini, D.; Taurino, A.; Quaranta, F.; Lomascolo, M.; Rella, R. Photoluminescence Quenching Processes by NO2 Adsorption in ZnO Nanostructured Films. J. Appl. Phys. 2012, 111, 073520. [Google Scholar] [CrossRef]
- Morandi, S.; Fioravanti, A.; Cerrato, G.; Lettieri, S.; Sacerdoti, M.; Carotta, M.C. Facile Synthesis of ZnO Nano-Structures: Morphology Influence on Electronic Properties. Sens. Actuators B Chem. 2017, 249, 581–589. [Google Scholar] [CrossRef]
- Lettieri, S.; Gargiulo, V.; Alfè, M.; Amati, M.; Zeller, P.; Maraloiu, V.-A.; Borbone, F.; Pavone, M.; Muñoz-García, A.B.; Maddalena, P. Simple Ethanol Refluxing Method for Production of Blue-Colored Titanium Dioxide with Oxygen Vacancies and Visible Light-Driven Photocatalytic Properties. J. Phys. Chem. C 2020, 124, 3564–3576. [Google Scholar] [CrossRef]
- Santara, B.; Giri, P.K.; Imakita, K.; Fujii, M. Evidence for Ti Interstitial Induced Extended Visible Absorption and Near Infrared Photoluminescence from Undoped TiO2 Nanoribbons: An In Situ Photoluminescence Study. J. Phys. Chem. C 2013, 117, 23402–23411. [Google Scholar] [CrossRef]
- Nakato, Y.; Akanuma, H.; Magari, Y.; Yae, S.; Shimizu, J.-I.; Mori, H. Photoluminescence from a Bulk Defect near the Surface of an n-TiO2 (Rutile) Electrode in Relation to an Intermediate of Photooxidation Reaction of Water. J. Phys. Chem. B 1997, 101, 4934–4939. [Google Scholar] [CrossRef]
- Nakamura, R.; Nakato, Y. Primary Intermediates of Oxygen Photoevolution Reaction on TiO2 (Rutile) Particles, Revealed by in Situ FTIR Absorption and Photoluminescence Measurements. J. Am. Chem. Soc. 2004, 126, 1290–1298. [Google Scholar] [CrossRef] [PubMed]
- Imanishi, A.; Okamura, T.; Ohashi, N.; Nakamura, R.; Nakato, Y. Mechanism of Water Photooxidation Reaction at Atomically Flat TiO2 (Rutile) (110) and (100) Surfaces: Dependence on Solution PH. J. Am. Chem. Soc. 2007, 10. [Google Scholar] [CrossRef] [PubMed]
- Vequizo, J.J.M.; Kamimura, S.; Ohno, T.; Yamakata, A. Oxygen Induced Enhancement of NIR Emission in Brookite TiO2 Powders: Comparison with Rutile and Anatase TiO2 Powders. Phys. Chem. Chem. Phys. 2018, 20, 3241–3248. [Google Scholar] [CrossRef]
- Ma, S.; Reish, M.E.; Zhang, Z.; Harrison, I.; Yates, J.T. Anatase-Selective Photoluminescence Spectroscopy of P25 TiO2 Nanoparticles: Different Effects of Oxygen Adsorption on the Band Bending of Anatase. J. Phys. Chem. C 2017, 121, 1263–1271. [Google Scholar] [CrossRef]
- Onishi, H.; Iwasawa, Y. Dynamic Visualization of a Metal-Oxide-Surface/Gas-Phase Reaction: Time-Resolved Observation by Scanning Tunneling Microscopy at 800 K. Phys. Rev. Lett. 1996, 76, 791–794. [Google Scholar] [CrossRef]
- Lettieri, S.; Pallotti, D.K.; Gesuele, F.; Maddalena, P. Unconventional Ratiometric-Enhanced Optical Sensing of Oxygen by Mixed-Phase TiO2. Appl. Phys. Lett. 2016, 109, 031905. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, S.; Dionysiou, D.D.; Pillai, S.C. Self-Cleaning Applications of TiO2 by Photo-Induced Hydrophilicity and Photocatalysis. Appl. Catal. B Environ. 2015, 176–177, 396–428. [Google Scholar] [CrossRef] [Green Version]
- Martin, S.T.; Herrmann, H.; Choi, W.; Hoffmann, M.R. Time-Resolved Microwave Conductivity. Part 1—TiO2 Photoreactivity and Size Quantization. J. Chem. Soc. Faraday Trans. 1994, 90, 3315–3322. [Google Scholar] [CrossRef] [Green Version]
- Martin, S.T.; Herrmann, H.; Hoffmann, M.R. Time-Resolved Microwave Conductivity. Part 2—Quantum-Sized TiO2 and the Effect of Adsorbates and Light Intensity on Charge-Carrier Dynamics. J. Chem. Soc. Faraday Trans. 1994, 90, 3323–3330. [Google Scholar] [CrossRef] [Green Version]
- Schneider, J.; Matsuoka, M.; Takeuchi, M.; Zhang, J.; Horiuchi, Y.; Anpo, M.; Bahnemann, D.W. Understanding TiO2 Photocatalysis: Mechanisms and Materials. Chem. Rev. 2014, 114, 9919–9986. [Google Scholar] [CrossRef]
- Dong, S.; Feng, J.; Fan, M.; Pi, Y.; Hu, L.; Han, X.; Liu, M.; Sun, J.; Sun, J. Recent Developments in Heterogeneous Photocatalytic Water Treatment Using Visible Light-Responsive Photocatalysts: A Review. RSC Adv. 2015, 5, 14610–14630. [Google Scholar] [CrossRef]
- Fragalà, M.E.; Malandrino, G.; Giangregorio, M.M.; Losurdo, M.; Bruno, G.; Lettieri, S.; Amato, L.S.; Maddalena, P. Structural, Optical, and Electrical Characterization of ZnO and Al-Doped ZnO Thin Films Deposited by MOCVD. Chem. Vapor Depos. 2009, 15, 327–333. [Google Scholar] [CrossRef]
- Gerischer, H. Electron-Transfer Kinetics of Redox Reactions at the Semiconductor/Electrolyte Contact. A New Approach. J. Phys. Chem. 1991, 95, 1356–1359. [Google Scholar] [CrossRef]
- Wang, C.M.; Heller, A.; Gerischer, H. Palladium Catalysis of O2 Reduction by Electrons Accumulated on TiO2 Particles during Photoassisted Oxidation of Organic Compounds. J. Am. Chem. Soc. 1992, 114, 5230–5234. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Carraway, E.R.; Hoffmann, M.R. Photocatalytic Production of H2O2 and Organic Peroxides on Quantum-Sized Semiconductor Colloids. Environ. Sci. Technol. 1994, 28, 776–785. [Google Scholar] [CrossRef]
- Ollis, D. Heterogeneous Photoassisted Catalysis: Conversions of Perchloroethylene, Dichloroethane, Chloroacetic Acids, and Chlorobenzenes. J. Catal. 1984, 88, 89–96. [Google Scholar] [CrossRef]
- Augugliaro, V.; Palmisano, L.; Sclafani, A.; Minero, C.; Pelizzetti, E. Photocatalytic Degradation of Phenol in Aqueous Titanium Dioxide Dispersions. Toxicol. Environ. Chem. 1988, 16, 89–109. [Google Scholar] [CrossRef]
- Turchi, C. Mixed Reactant Photocatalysis: Intermediates and Mutual Rate Inhibition. J. Catal. 1989, 119, 483–496. [Google Scholar] [CrossRef]
- Turchi, C. Photocatalytic Degradation of Organic Water Contaminants: Mechanisms Involving Hydroxyl Radical Attack. J. Catal. 1990, 122, 178–192. [Google Scholar] [CrossRef]
- Jaeger, C.D.; Bard, A.J. Spin Trapping and Electron Spin Resonance Detection of Radical Intermediates in the Photodecomposition of Water at Titanium Dioxide Particulate Systems. J. Phys. Chem. 1979, 83, 3146–3152. [Google Scholar] [CrossRef]
- Mao, Y.; Schoeneich, C.; Asmus, K.D. Identification of Organic Acids and Other Intermediates in Oxidative Degradation of Chlorinated Ethanes on Titania Surfaces En Route to Mineralization: A Combined Photocatalytic and Radiation Chemical Study. J. Phys. Chem. 1991, 95, 10080–10089. [Google Scholar] [CrossRef]
- Draper, R.B.; Fox, M.A. Titanium Dioxide Photosensitized Reactions Studied by Diffuse Reflectance Flash Photolysis in Aqueous Suspensions of TiO2 Powder. Langmuir 1990, 6, 1396–1402. [Google Scholar] [CrossRef]
- Carraway, E.R.; Hoffman, A.J.; Hoffmann, M.R. Photocatalytic Oxidation of Organic Acids on Quantum-Sized Semiconductor Colloids. Envir. Sci. Technol. 1994, 28, 786–793. [Google Scholar] [CrossRef]
- Lettieri, S.; Gargiulo, V.; Pallotti, D.K.; Vitiello, G.; Maddalena, P.; Alfè, M.; Marotta, R. Evidencing Opposite Charge-Transfer Processes at TiO2/Graphene-Related Materials Interface through a Combined EPR, Photoluminescence and Photocatalysis Assessment. Catal. Today 2018, 315, 19–30. [Google Scholar] [CrossRef]
- Li, X.; Yu, J.; Jaroniec, M.; Chen, X. Cocatalysts for Selective Photoreduction of CO2 into Solar Fuels. Chem. Rev. 2019, 218. [Google Scholar]
- Pan, X.; Yang, M.-Q.; Fu, X.; Zhang, N.; Xu, Y.-J. Defective TiO2 with Oxygen Vacancies: Synthesis, Properties and Photocatalytic Applications. Nanoscale 2013, 5, 3601. [Google Scholar] [CrossRef] [PubMed]
- Katal, R.; Masudy-Panah, S.; Tanhaei, M.; Farahani, M.H.D.A.; Jiangyong, H. A Review on the Synthesis of the Various Types of Anatase TiO2 Facets and Their Applications for Photocatalysis. Chem. Eng. J. 2020, 384, 123384. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, L.; Yu, J.; Wageh, S.; Al-Ghamdi, A.A.; Jaroniec, M. Direct Z-Scheme Photocatalysts: Principles, Synthesis, and Applications. Mater. Today 2018, 21, 1042–1063. [Google Scholar] [CrossRef]
- Chen, X.; Liu, L.; Yu, P.Y.; Mao, S.S. Increasing Solar Absorption for Photocatalysis with Black Hydrogenated Titanium Dioxide Nanocrystals. Science 2011, 331, 746–750. [Google Scholar] [CrossRef] [PubMed]
- Naldoni, A.; Allieta, M.; Santangelo, S.; Marelli, M.; Fabbri, F.; Cappelli, S.; Bianchi, C.L.; Psaro, R.; Dal Santo, V. Effect of Nature and Location of Defects on Bandgap Narrowing in Black TiO2 Nanoparticles. J. Am. Chem. Soc. 2012, 134, 7600–7603. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, L.; Huang, F. Black Titanium Dioxide (TiO2) Nanomaterials. Chem. Soc. Rev. 2015, 44, 1861–1885. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Liu, N.; Schmuki, P. Photocatalysis with TiO2 Nanotubes: “Colorful” Reactivity and Designing Site-Specific Photocatalytic Centers into TiO2 Nanotubes. ACS Catal. 2017, 7, 3210–3235. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Chen, Q.; Dai, W.; Ren, Y.; Zhou, Y.; Yang, J.; Xie, S.; Shen, Y.; Wu, J.; Chen, W.; et al. Oxygen-Deficient Blue TiO2 for Ultrastable and Fast Lithium Storage. Adv. Energy Mater. 2020, 10, 1903107. [Google Scholar] [CrossRef]
- Liu, N.; Steinrück, H.-G.; Osvet, A.; Yang, Y.; Schmuki, P. Noble Metal Free Photocatalytic H2 Generation on Black TiO2: On the Influence of Crystal Facets vs. Crystal Damage. Appl. Phys. Lett. 2017, 5. [Google Scholar] [CrossRef]
- Pore, V.; Ritala, M.; Leskelä, M.; Areva, S.; Järn, M.; Järnström, J. H2 S Modified Atomic Layer Deposition Process for Photocatalytic TiO2 Thin Films. J. Mater. Chem. 2007, 17, 1361–1371. [Google Scholar] [CrossRef]
- Liu, N.; Schneider, C.; Freitag, D.; Hartmann, M.; Venkatesan, U.; Müller, J.; Spiecker, E.; Schmuki, P. Black TiO2 Nanotubes: Cocatalyst-Free Open-Circuit Hydrogen Generation. Nano Lett. 2014, 14, 3309–3313. [Google Scholar] [CrossRef]
- Liu, N.; Häublein, V.; Zhou, X.; Venkatesan, U.; Hartmann, M.; Mačković, M.; Nakajima, T.; Spiecker, E.; Osvet, A.; Frey, L.; et al. “Black” TiO2 Nanotubes Formed by High-Energy Proton Implantation Show Noble-Metal-co-Catalyst Free Photocatalytic H2-Evolution. Nano Lett. 2015, 15, 6815–6820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, N.; Schneider, C.; Freitag, D.; Zolnhofer, E.M.; Meyer, K.; Schmuki, P. Noble-Metal-Free Photocatalytic H2 Generation: Active and Inactive ‘Black’ TiO2 Nanotubes and Synergistic Effects. Chem. Eur. J. 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Zhou, X.; Nguyen, N.T.; Peters, K.; Zoller, F.; Hwang, I.; Schneider, C.; Miehlich, M.E.; Freitag, D.; Meyer, K.; et al. Black Magic in Gray Titania: Noble-Metal-Free Photocatalytic H2 Evolution from Hydrogenated Anatase. ChemSusChem 2017, 10, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Huang, F.; Zhao, M.; Xu, J.; Zhou, J.; Wang, Y. Ultra-Small Yellow Defective TiO2 Nanoparticles for co-Catalyst Free Photocatalytic Hydrogen Production. Nano Energy 2016, 24, 63–71. [Google Scholar] [CrossRef]
- Kong, L.; Jiang, Z.; Wang, C.; Wan, F.; Li, Y.; Wu, L.; Zhi, J.-F.; Zhang, X.; Chen, S.; Liu, Y. Simple Ethanol Impregnation Treatment Can Enhance Photocatalytic Activity of TiO2 Nanoparticles under Visible-Light Irradiation. ACS Appl. Mater. Interfaces 2015, 7, 7752–7758. [Google Scholar] [CrossRef]
- Wang, L.; Cai, Y.; Liu, B.; Dong, L. A Facile Synthesis of Brown Anatase TiO2 Rich in Oxygen Vacancies and Its Visible Light Photocatalytic Property. Solid State Ion. 2021, 361, 115564. [Google Scholar] [CrossRef]
- Jiang, N.; Du, Y.; Liu, S.; Du, M.; Feng, Y.; Liu, Y. Facile Preparation of Flake-like Blue TiO2 Nanorod Arrays for Efficient Visible Light Photocatalyst. Ceram. Int. 2019, 45, 9754–9760. [Google Scholar] [CrossRef]
- Zheng, J.; Ji, G.; Zhang, P.; Cao, X.; Wang, B.; Yu, L.; Xu, Z. Facile Aluminum Reduction Synthesis of Blue TiO2 with Oxygen Deficiency for Lithium-Ion Batteries. Chem. Eur. J. 2015, 21, 18309–18315. [Google Scholar] [CrossRef]
- Ariyanti, D.; Mills, L.; Dong, J.; Yao, Y.; Gao, W. NaBH4 Modified TiO2: Defect Site Enhancement Related to Its Photocatalytic Activity. Mater. Chem. Phys. 2017, 199, 571–576. [Google Scholar] [CrossRef]
- Ullattil, S.G.; Narendranath, S.B.; Pillai, S.C.; Periyat, P. Black TiO2 Nanomaterials: A Review of Recent Advances. Chem. Eng. J. 2018, 343, 708–736. [Google Scholar] [CrossRef]
- Mun Wong, K.; Alay-e-Abbas, S.M.; Fang, Y.; Shaukat, A.; Lei, Y. Spatial Distribution of Neutral Oxygen Vacancies on ZnO Nanowire Surfaces: An Investigation Combining Confocal Microscopy and First Principles Calculations. J. Appl. Phys. 2013, 114, 034901. [Google Scholar] [CrossRef] [Green Version]
- Ohno, T.; Sarukawa, K.; Matsumura, M. Crystal Faces of Rutile and Anatase TiO2 Particles and Their Roles in Photocatalytic Reactions. New J. Chem. 2002, 26, 1167–1170. [Google Scholar] [CrossRef] [Green Version]
- Lazzeri, M.; Vittadini, A.; Selloni, A. Structure and Energetics of Stoichiometric TiO2 Anatase Surfaces. Phys. Rev. B 2001, 63, 155409. [Google Scholar] [CrossRef]
- Yang, H.G.; Sun, C.H.; Qiao, S.Z.; Zou, J.; Liu, G.; Smith, S.C.; Cheng, H.M.; Lu, G.Q. Anatase TiO2 Single Crystals with a Large Percentage of Reactive Facets. Nature 2008, 453, 638–641. [Google Scholar] [CrossRef] [Green Version]
- Dinh, C.-T.; Nguyen, T.-D.; Kleitz, F.; Do, T.-O. Shape-Controlled Synthesis of Highly Crystalline Titania Nanocrystals. ACS Nano 2009, 3, 3737–3743. [Google Scholar] [CrossRef] [PubMed]
- D’Arienzo, M.; Carbajo, J.; Bahamonde, A.; Crippa, M.; Polizzi, S.; Scotti, R.; Wahba, L.; Morazzoni, F. Photogenerated Defects in Shape-Controlled TiO2 Anatase Nanocrystals: A Probe To Evaluate the Role of Crystal Facets in Photocatalytic Processes. J. Am. Chem. Soc. 2011, 133, 17652–17661. [Google Scholar] [CrossRef]
- Pan, J.; Liu, G.; Lu, G.Q.M.; Cheng, H.-M. On the True Photoreactivity Order of {001}, {010}, and {101} Facets of Anatase TiO2 Crystals. Angew. Chem. Int. Ed. 2011, 50, 2133–2137. [Google Scholar] [CrossRef]
- Tachikawa, T.; Yamashita, S.; Majima, T. Evidence for Crystal-Face-Dependent TiO2 Photocatalysis from Single-Molecule Imaging and Kinetic Analysis. J. Am. Chem. Soc. 2011, 133, 7197–7204. [Google Scholar] [CrossRef]
- Wu, X.; Chen, Z.; Lu, G.Q.M.; Wang, L. Nanosized Anatase TiO2 Single Crystals with Tunable Exposed (001) Facets for Enhanced Energy Conversion Efficiency of Dye-Sensitized Solar Cells. Adv. Funct. Mater. 2011, 21, 4167–4172. [Google Scholar] [CrossRef]
- Dozzi, M.; Selli, E. Specific Facets-Dominated Anatase TiO2: Fluorine-Mediated Synthesis and Photoactivity. Catalysts 2013, 3, 455–485. [Google Scholar] [CrossRef]
- Ong, W.-J.; Tan, L.-L.; Chai, S.-P.; Yong, S.-T.; Mohamed, A.R. Facet-Dependent Photocatalytic Properties of TiO2-Based Composites for Energy Conversion and Environmental Remediation. ChemSusChem 2014, 7, 690–719. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Low, J.; Xiao, W.; Zhou, P.; Jaroniec, M. Enhanced Photocatalytic CO2-Reduction Activity of Anatase TiO2 by Coexposed {001} and {101} Facets. J. Am. Chem. Soc. 2014, 136, 8839–8842. [Google Scholar] [CrossRef]
- D’Arienzo, M.; Dozzi, M.V.; Redaelli, M.; Credico, B.D.; Morazzoni, F.; Scotti, R.; Polizzi, S. Crystal Surfaces and Fate of Photogenerated Defects in Shape-Controlled Anatase Nanocrystals: Drawing Useful Relations to Improve the H2 Yield in Methanol Photosteam Reforming. J. Phys. Chem. C 2015, 119, 12385–12393. [Google Scholar] [CrossRef]
- Kashiwaya, S.; Toupance, T.; Klein, A.; Jaegermann, W. Fermi Level Positions and Induced Band Bending at Single Crystalline Anatase (101) and (001) Surfaces: Origin of the Enhanced Photocatalytic Activity of Facet Engineered Crystals. Adv. Energy Mater. 2018, 8, 1802195. [Google Scholar] [CrossRef]
- Peng, Y.-K.; Tsang, S.C.E. Facet-Dependent Photocatalysis of Nanosize Semiconductive Metal Oxides and Progress of Their Characterization. Nano Today 2018, 18, 15–34. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, J.; Liu, M.; Jing, D.; Guo, L. Photocatalytic Reforming of Glucose under Visible Light over Morphology Controlled Cu 2 O: Efficient Charge Separation by Crystal Facet Engineering. Chem. Commun. 2014, 50, 192–194. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H.; Gao, G.; Butburee, T.; Lyu, M.; Thaweesak, S.; Yun, J.-H.; Du, A.; Liu, G.; Wang, L. Synergistic Crystal Facet Engineering and Structural Control of WO3 Films Exhibiting Unprecedented Photoelectrochemical Performance. Nano Energy 2016, 24, 94–102. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Zhang, F.; Wang, D.; Yang, J.; Li, M.; Zhu, J.; Zhou, X.; Han, H.; Li, C. Spatial Separation of Photogenerated Electrons and Holes among {010} and {110} Crystal Facets of BiVO4. Nat. Commun. 2013, 4, 1432. [Google Scholar] [CrossRef] [Green Version]
- Michaelson, H.B. The Work Function of the Elements and Its Periodicity. J. Appl. Phys. 1977, 48, 6. [Google Scholar] [CrossRef] [Green Version]
- Nørskov, J.K.; Bligaard, T.; Logadottir, A.; Kitchin, J.R.; Chen, J.G.; Pandelov, S.; Stimming, U. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005, 5. [Google Scholar] [CrossRef] [Green Version]
- Kavitha, R.; Kumar, S.G. A Review on Plasmonic Au-ZnO Heterojunction Photocatalysts: Preparation, Modifications and Related Charge Carrier Dynamics. Mater. Sci. Semicond. Process. 2019, 93, 59–91. [Google Scholar] [CrossRef]
- Truppi, A.; Petronella, F.; Placido, T.; Margiotta, V.; Lasorella, G.; Giotta, L.; Giannini, C.; Sibillano, T.; Murgolo, S.; Mascolo, G.; et al. Gram-Scale Synthesis of UV–Vis Light Active Plasmonic Photocatalytic Nanocomposite Based on TiO2/Au Nanorods for Degradation of Pollutants in Water. Appl. Catal. B Environ. 2019, 243, 604–613. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, A.; Cao, S.-W.; Bosman, M.; Li, S.; Xue, C. Direct Evidence of Plasmon Enhancement on Photocatalytic Hydrogen Generation over Au/Pt-Decorated TiO2 Nanofibers. Nanoscale 2014, 6, 5217–5222. [Google Scholar] [CrossRef]
- Tanaka, A.; Sakaguchi, S.; Hashimoto, K.; Kominami, H. Preparation of Au/TiO2 with Metal Cocatalysts Exhibiting Strong Surface Plasmon Resonance Effective for Photoinduced Hydrogen Formation under Irradiation of Visible Light. ACS Catal. 2013, 3, 79–85. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Cao, S.-W.; Xue, C. Au/Pt Nanoparticle-Decorated TiO2 Nanofibers with Plasmon-Enhanced Photocatalytic Activities for Solar-to-Fuel Conversion. J. Phys. Chem. C 2013, 117, 25939–25947. [Google Scholar] [CrossRef]
- Chen, C.; Kuai, L.; Chen, Y.; Wang, Q.; Kan, E.; Geng, B. Au/Pt Co-Loaded Ultrathin TiO2 Nanosheets for Photocatalyzed H2 Evolution by the Synergistic Effect of Plasmonic Enhancement and co-Catalysis. RSC Adv. 2015, 5, 98254–98259. [Google Scholar] [CrossRef]
- Bera, S.; Lee, J.E.; Rawal, S.B.; Lee, W.I. Size-Dependent Plasmonic Effects of Au and Au@SiO2 Nanoparticles in Photocatalytic CO2 Conversion Reaction of Pt/TiO2. Appl. Catal. B Environ. 2016, 199, 55–63. [Google Scholar] [CrossRef]
- Lalitha, K.; Sadanandam, G.; Kumari, V.D.; Subrahmanyam, M.; Sreedhar, B.; Hebalkar, N.Y. Highly Stabilized and Finely Dispersed Cu2 O/TiO2: A Promising Visible Sensitive Photocatalyst for Continuous Production of Hydrogen from Glycerol:Water Mixtures. J. Phys. Chem. C 2010, 114, 22181–22189. [Google Scholar] [CrossRef]
- Li, L.; Xu, L.; Shi, W.; Guan, J. Facile Preparation and Size-Dependent Photocatalytic Activity of Cu2O Nanocrystals Modified Titania for Hydrogen Evolution. Int. J. Hydrog. Energy 2013, 38, 816–822. [Google Scholar] [CrossRef]
- Xi, Z.; Li, C.; Zhang, L.; Xing, M.; Zhang, J. Synergistic Effect of Cu2O/TiO2 Heterostructure Nanoparticle and Its High H2 Evolution Activity. Int. J. Hydrog. Energy 2014, 39, 6345–6353. [Google Scholar] [CrossRef]
- Minami, T.; Nishi, Y.; Miyata, T. Cu2 O-Based Solar Cells Using Oxide Semiconductors. J. Semicond. 2016, 37, 014002. [Google Scholar] [CrossRef]
- Luévano-Hipólito, E.; Torres-Martínez, L.M.; Sánchez-Martínez, D.; Alfaro Cruz, M.R. Cu2O Precipitation-Assisted with Ultrasound and Microwave Radiation for Photocatalytic Hydrogen Production. Int. J. Hydrog. Energy 2017, 42, 12997–13010. [Google Scholar] [CrossRef]
- Huang, L.; Peng, F.; Wang, H.; Yu, H.; Li, Z. Preparation and Characterization of Cu2O/TiO2 Nano–Nano Heterostructure Photocatalysts. Catal. Commun. 2009, 10, 1839–1843. [Google Scholar] [CrossRef]
- Muscetta, M.; Andreozzi, R.; Clarizia, L.; Di Somma, I.; Marotta, R. Hydrogen Production through Photoreforming Processes over Cu2O/TiO2 Composite Materials: A Mini-Review. Int. J. Hydrog. Energy 2020, 45, 28531–28552. [Google Scholar] [CrossRef]
- Zhai, Q.; Xie, S.; Fan, W.; Zhang, Q.; Wang, Y.; Deng, W.; Wang, Y. Photocatalytic Conversion of Carbon Dioxide with Water into Methane: Platinum and Copper (I) Oxide Co-Catalysts with a Core-Shell Structure. Angew. Chem. Int. Ed. 2013, 52, 5776–5779. [Google Scholar] [CrossRef]
- Xiong, Z.; Lei, Z.; Kuang, C.-C.; Chen, X.; Gong, B.; Zhao, Y.; Zhang, J.; Zheng, C.; Wu, J.C.S. Selective Photocatalytic Reduction of CO2 into CH4 over Pt-Cu2O TiO2 Nanocrystals: The Interaction between Pt and Cu2O Cocatalysts. Appl. Catal. Environ. 2017, 202, 695–703. [Google Scholar] [CrossRef]
- Sinatra, L.; LaGrow, A.P.; Peng, W.; Kirmani, A.R.; Amassian, A.; Idriss, H.; Bakr, O.M. A Au/Cu2O–TiO2 System for Photo-Catalytic Hydrogen Production. A pn-Junction Effect or a Simple Case of in Situ Reduction? J. Catal. 2015, 322, 109–117. [Google Scholar] [CrossRef]
- Cheng, W.-Y.; Yu, T.-H.; Chao, K.-J.; Lu, S.-Y. Cu2 O-Decorated Mesoporous TiO2 Beads as a Highly Efficient Photocatalyst for Hydrogen Production. ChemCatChem 2014, 6, 293–300. [Google Scholar] [CrossRef]
- Zhen, W.; Jiao, W.; Wu, Y.; Jing, H.; Lu, G. The Role of a Metallic Copper Interlayer during Visible Photocatalytic Hydrogen Generation over a Cu/Cu2O/Cu/TiO2 Catalyst. Catal. Sci. Technol. 2017, 7, 5028–5037. [Google Scholar] [CrossRef]
- Choi, J.; Song, J.T.; Jang, H.S.; Choi, M.-J.; Sim, D.M.; Yim, S.; Lim, H.; Jung, Y.S.; Oh, J. Interfacial Band-Edge Engineered TiO2 Protection Layer on Cu2O Photocathodes for Efficient Water Reduction Reaction. Electron. Mater. Lett. 2017, 13, 57–65. [Google Scholar] [CrossRef]
- Majeed, I.; Nadeem, M.A.; Badshah, A.; Kanodarwala, F.K.; Ali, H.; Khan, M.A.; Stride, J.A.; Nadeem, M.A. Titania Supported MOF-199 Derived Cu–Cu2O Nanoparticles: Highly Efficient Non-Noble Metal Photocatalysts for Hydrogen Production from Alcohol–Water Mixtures. Catal. Sci. Technol. 2017, 7, 677–686. [Google Scholar] [CrossRef]
- Uddin, M.T.; Nicolas, Y.; Olivier, C.; Jaegermann, W.; Rockstroh, N.; Junge, H.; Toupance, T. Band Alignment Investigations of Heterostructure NiO/TiO2 Nanomaterials Used as Efficient Heterojunction Earth-Abundant Metal Oxide Photocatalysts for Hydrogen Production. Phys. Chem. Chem. Phys. 2017, 19, 19279–19288. [Google Scholar] [CrossRef]
- Chen, C.-J.; Liao, C.-H.; Hsu, K.-C.; Wu, Y.-T.; Wu, J.C.S. P–N Junction Mechanism on Improved NiO/TiO2 Photocatalyst. Catal. Commun. 2011, 12, 1307–1310. [Google Scholar] [CrossRef]
- Chen, J.; Wang, M.; Han, J.; Guo, R. TiO2 Nanosheet/NiO Nanorod Hierarchical Nanostructures: P–n Heterojunctions towards Efficient Photocatalysis. J. Colloid Interface Sci. 2020, 562, 313–321. [Google Scholar] [CrossRef]
- Teter, D.M.; Hemley, R.J. Low-Compressibility Carbon Nitrides. Science 1996, 271, 53–55. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, S.-P. Band Gap of C3N4 in the GW Approximation. Int. J. Hydrog. Energy 2012, 37, 11072–11080. [Google Scholar] [CrossRef]
- Zheng, Y.; Lin, L.; Wang, B.; Wang, X. Graphitic Carbon Nitride Polymers toward Sustainable Photoredox Catalysis. Angew. Chem. Int. Ed. 2015, 54, 12868–12884. [Google Scholar] [CrossRef]
- Wang, X.; Maeda, K.; Thomas, A.; Takanabe, K.; Xin, G.; Carlsson, J.M.; Domen, K.; Antonietti, M. A Metal-Free Polymeric Photocatalyst for Hydrogen Production from Water under Visible Light. Nat. Mater. 2009, 8, 76–80. [Google Scholar] [CrossRef]
- Wang, A.; Wang, C.; Fu, L.; Wong-Ng, W.; Lan, Y. Recent Advances of Graphitic Carbon Nitride-Based Structures and Applications in Catalyst, Sensing, Imaging, and LEDs. Nano-Micro Lett. 2017, 9, 47. [Google Scholar] [CrossRef]
- Acharya, R.; Parida, K. A Review on TiO2/g-C3N4 Visible-Light-Responsive Photocatalysts for Sustainable Energy Generation and Environmental Remediation. J. Environ. Chem. Eng. 2020, 8, 103896. [Google Scholar] [CrossRef]
- Wei, S.; Wang, F.; Yan, P.; Dan, M.; Cen, W.; Yu, S.; Zhou, Y. Interfacial Coupling Promoting Hydrogen Sulfide Splitting on the Staggered Type II G-C3N4/r-TiO2 Heterojunction. J. Catal. 2019, 377, 122–132. [Google Scholar] [CrossRef]
- Lin, Y.; Shi, H.; Jiang, Z.; Wang, G.; Zhang, X.; Zhu, H.; Zhang, R.; Zhu, C. Enhanced Optical Absorption and Photocatalytic H2 Production Activity of G-C3N4/TiO2 Heterostructure by Interfacial Coupling: A DFT+U Study. Int. J. Hydrog. Energy 2017, 42, 9903–9913. [Google Scholar] [CrossRef]
- Zhou, B.-X.; Ding, S.-S.; Wang, Y.; Wang, X.-R.; Huang, W.-Q.; Li, K.; Huang, G.-F. Type-II/Type-II Band Alignment to Boost Spatial Charge Separation: A Case Study of g-C3N4 Quantum Dots/a-TiO2/r-TiO2 for Highly Efficient Photocatalytic Hydrogen and Oxygen Evolution. Nanoscale 2020, 12, 6037–6046. [Google Scholar] [CrossRef] [PubMed]
- Sharma, K.; Sharma, V.; Sharma, S.S. Dye-Sensitized Solar Cells: Fundamentals and Current Status. Nanoscale Res. Lett. 2018, 13, 381. [Google Scholar] [CrossRef] [PubMed]
- Zani, L.; Melchionna, M.; Montini, T.; Fornasiero, P. Design of Dye-Sensitized TiO2 Materials for Photocatalytic Hydrogen Production: Light and Shadow. J. Phys. Energy 2021. [Google Scholar] [CrossRef]
- Chatterjee, D. Effect of Excited State Redox Properties of Dye Sensitizers on Hydrogen Production through Photo-Splitting of Water over TiO2 Photocatalyst. Catal. Commun. 2010, 11, 336–339. [Google Scholar] [CrossRef]
- Choi, S.K.; Yang, H.S.; Kim, J.H.; Park, H. Organic Dye-Sensitized TiO2 as a Versatile Photocatalyst for Solar Hydrogen and Environmental Remediation. Appl. Catal. B Environ. 2012, 121–122, 206–213. [Google Scholar] [CrossRef]
- Armaroli, N.; Balzani, V. Solar Electricity and Solar Fuels: Status and Perspectives in the Context of the Energy Transition. Chem. Eur. J. 2016, 22, 32–57. [Google Scholar] [CrossRef]
- Warnan, J. Solar Electricity and Fuel Production with Perylene Monoimide Dye-Sensitised TiO2 in Water. Chem. Sci. 2019, 9. [Google Scholar]
- Manfredi, N.; Monai, M.; Montini, T.; Peri, F.; De Angelis, F.; Fornasiero, P.; Abbotto, A. Dye-Sensitized Photocatalytic Hydrogen Generation: Efficiency Enhancement by Organic Photosensitizer–Coadsorbent Intermolecular Interaction. ACS Energy Lett. 2018, 3, 85–91. [Google Scholar] [CrossRef]
- Watanabe, M. Dye-Sensitized Photocatalyst for Effective Water Splitting Catalyst. Sci. Technol. Adv. Mater. 2017, 18, 705–723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, J.; Lei, Y.; Luo, T.; Liu, J. Photocatalytic H 2 Production from Water by Metal-free Dye-sensitized TiO2 Semiconductors: The Role and Development Process of Organic Sensitizers. ChemSusChem 2020, 13, 5863–5895. [Google Scholar] [CrossRef] [PubMed]
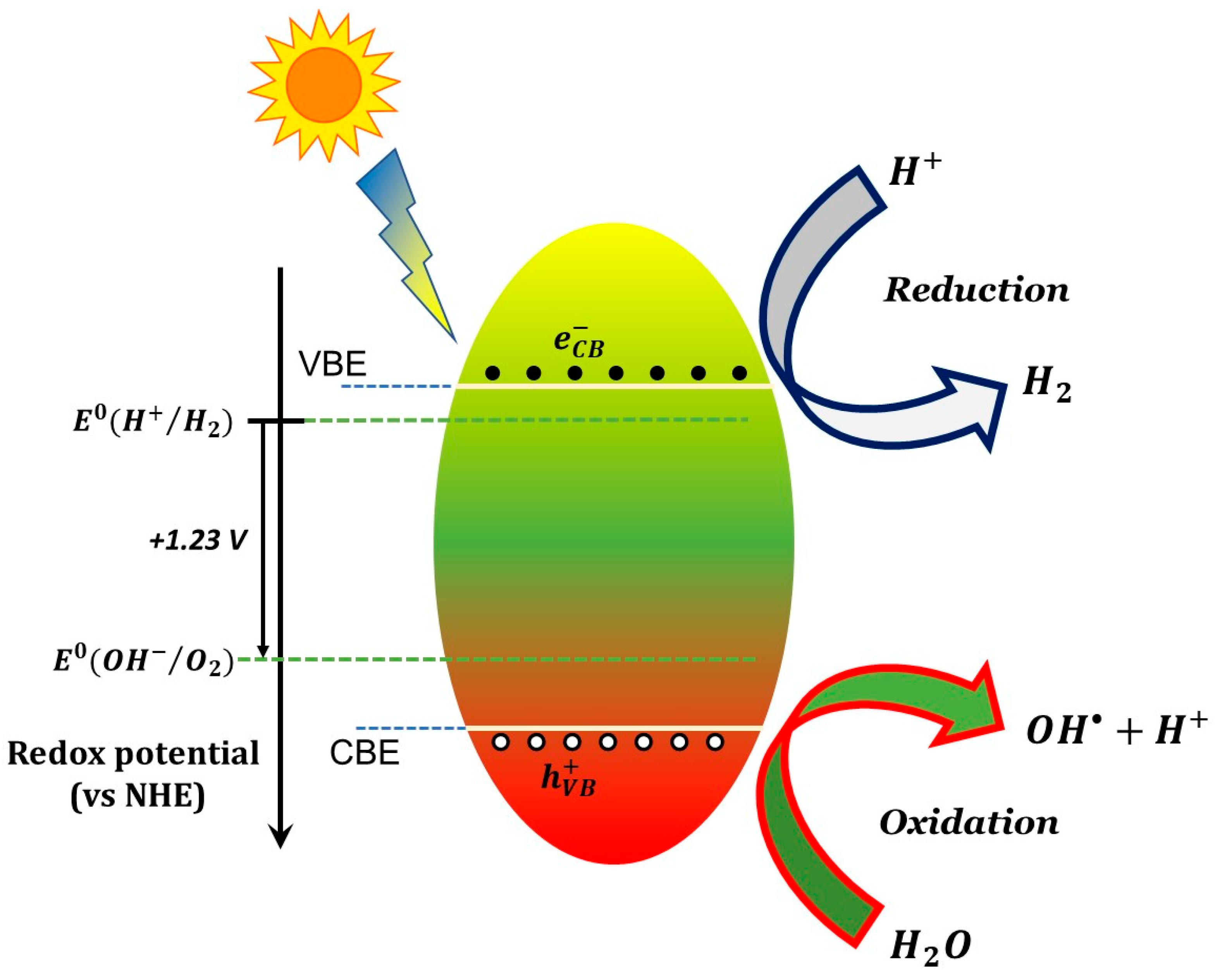



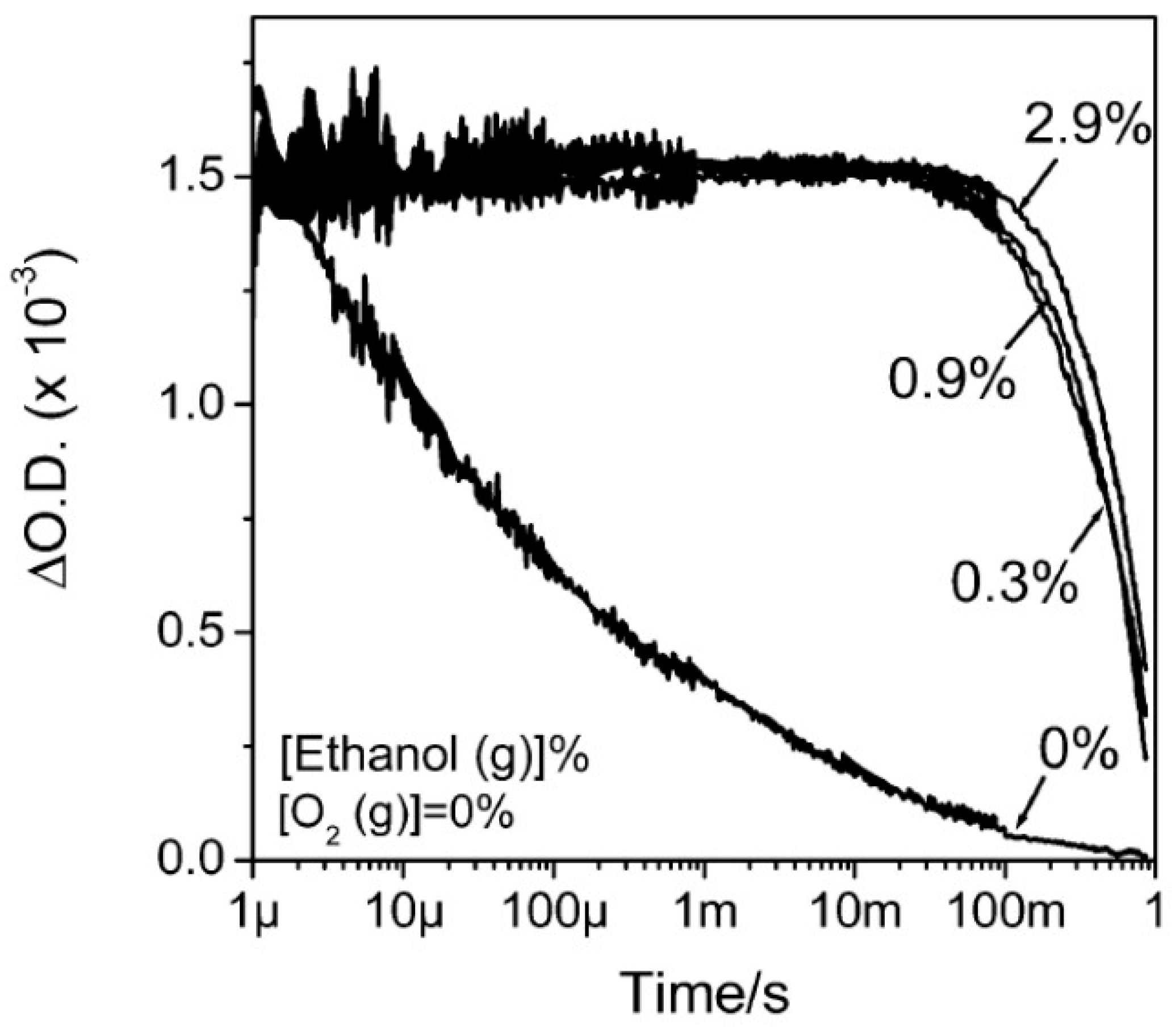


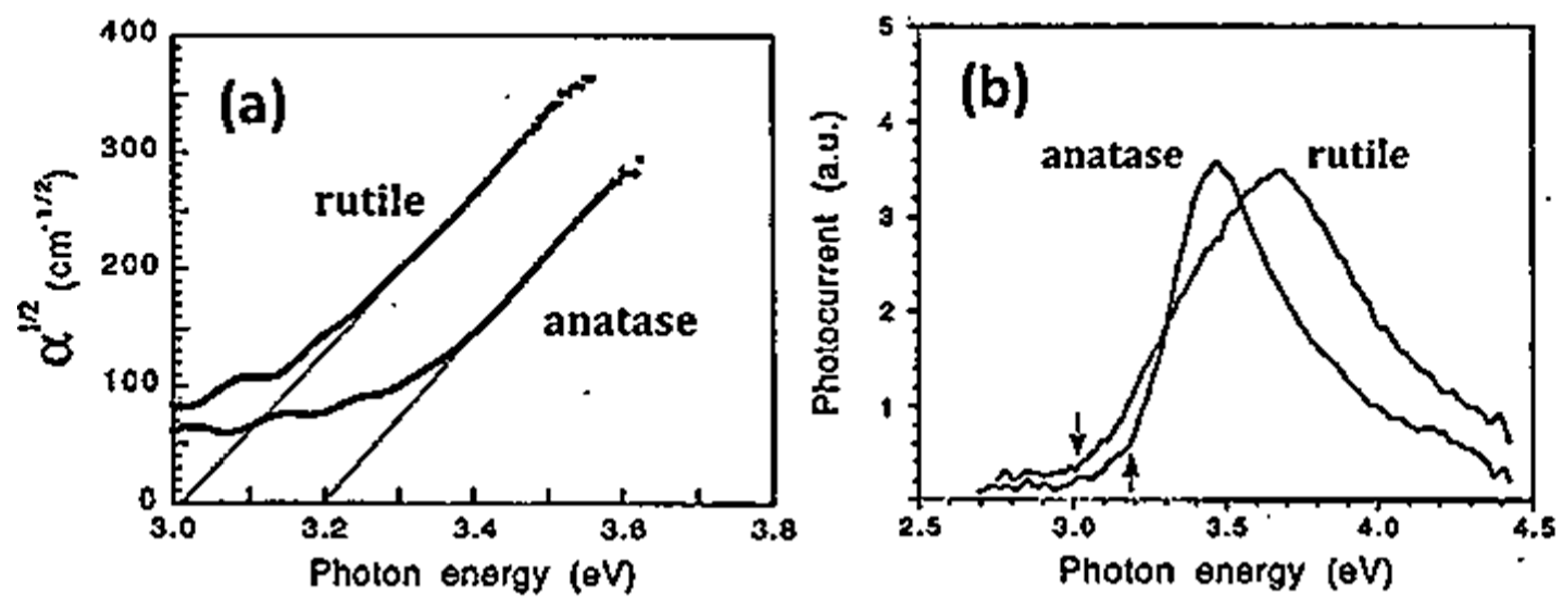
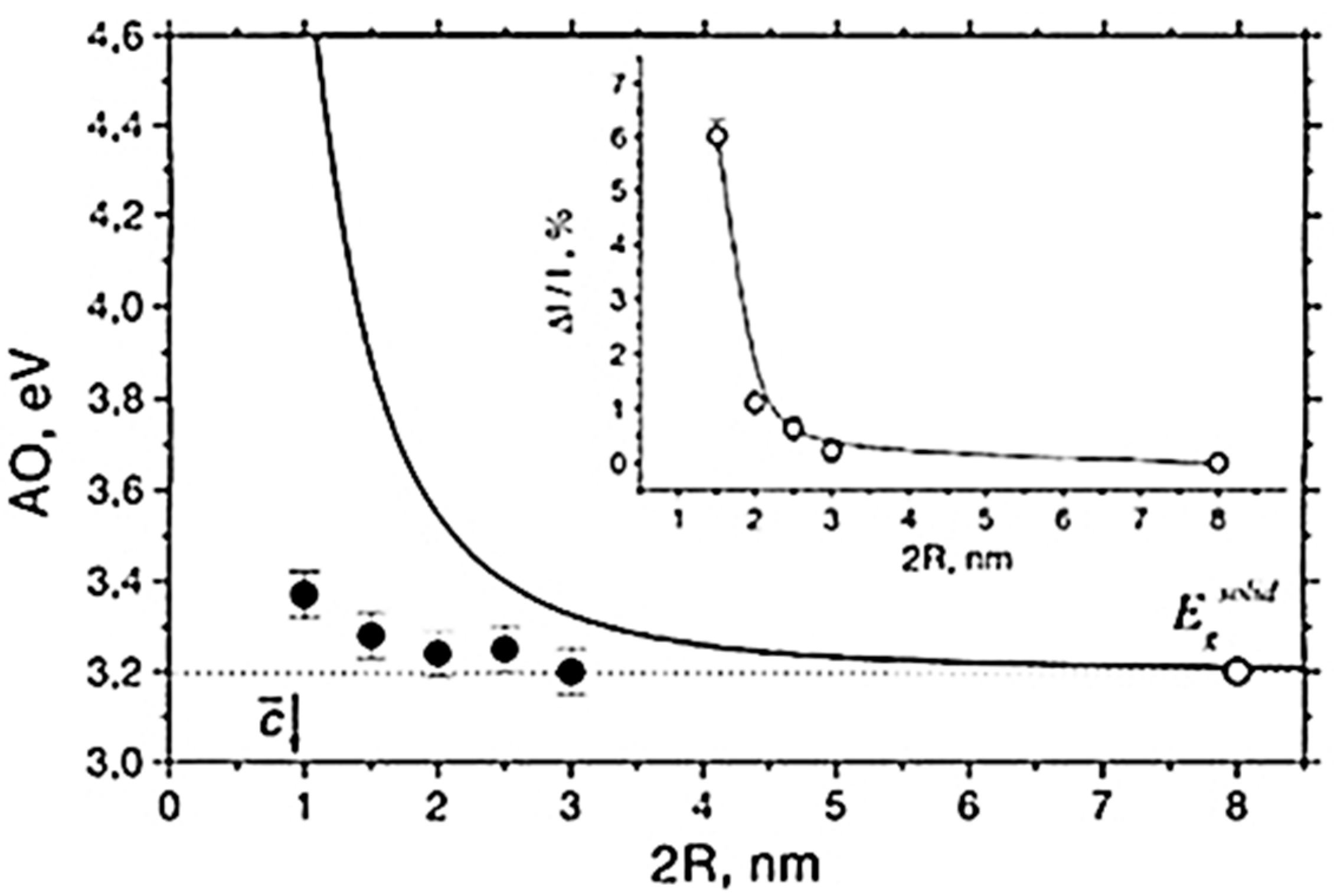
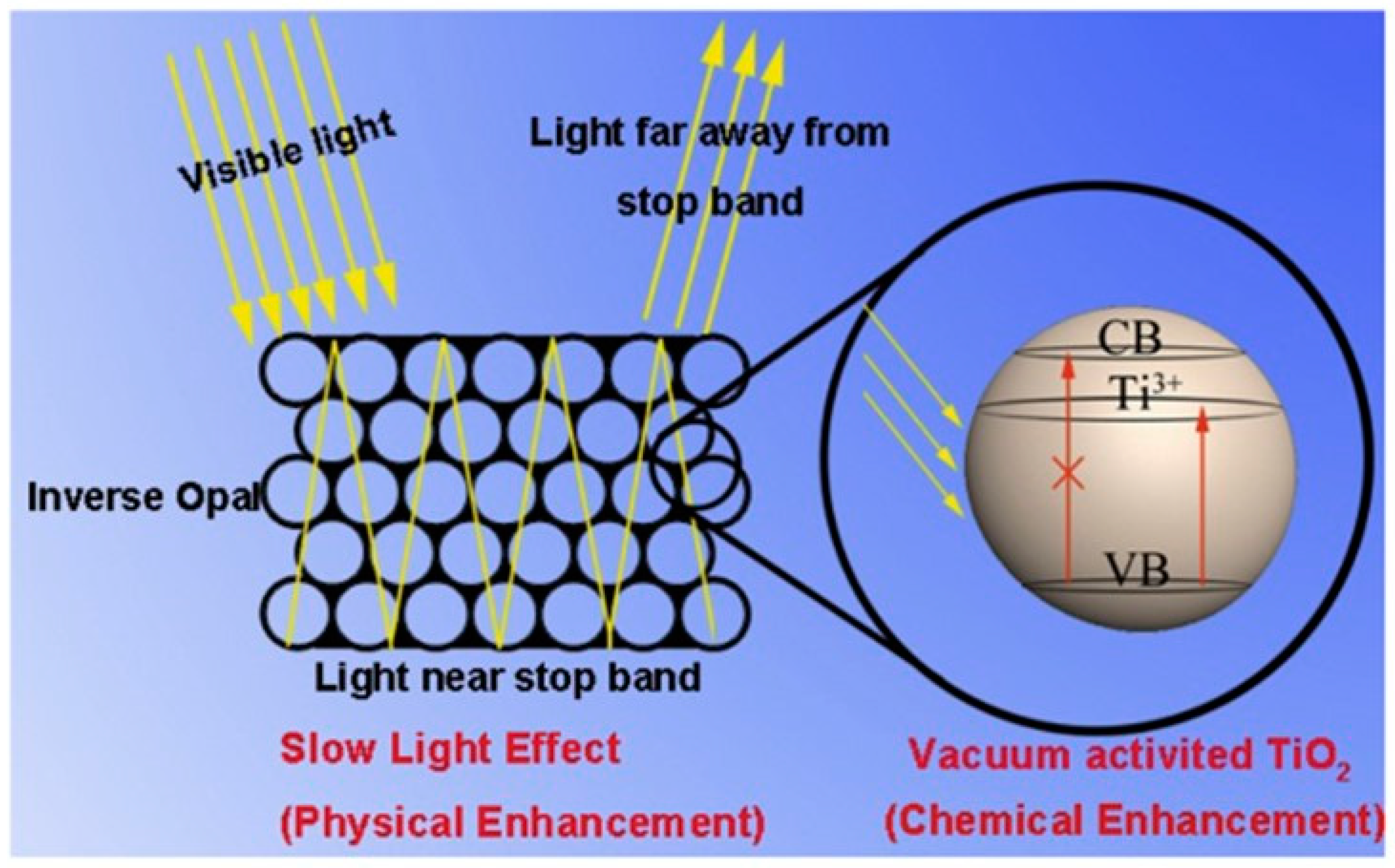
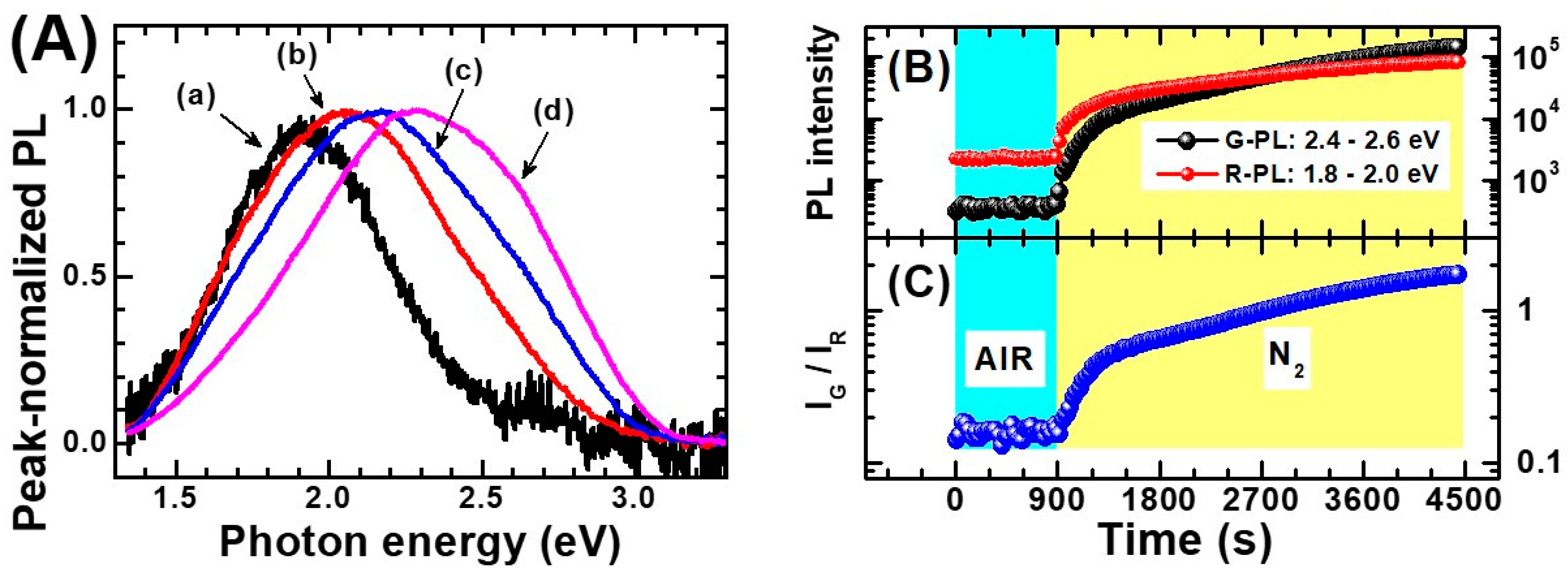
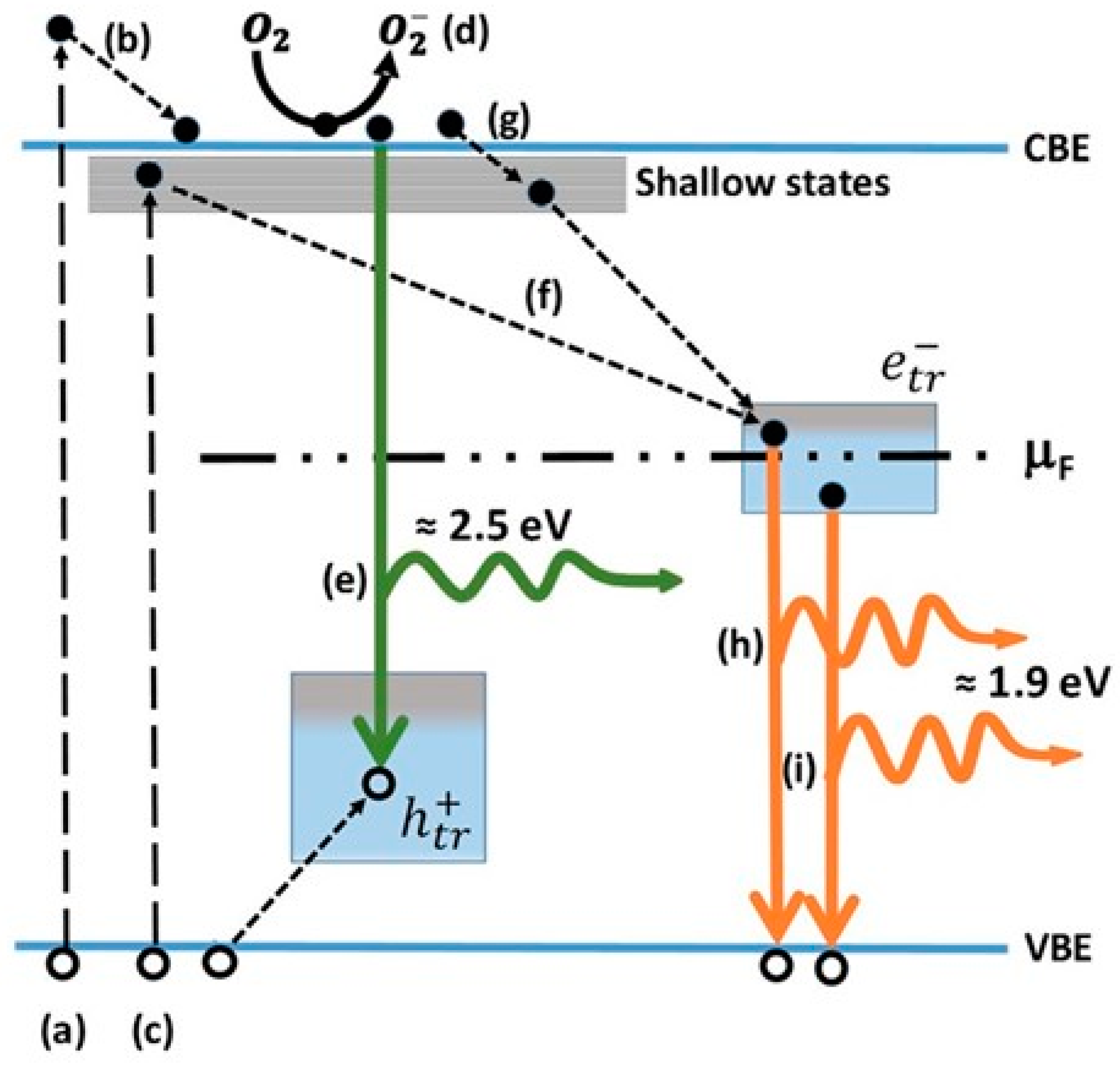

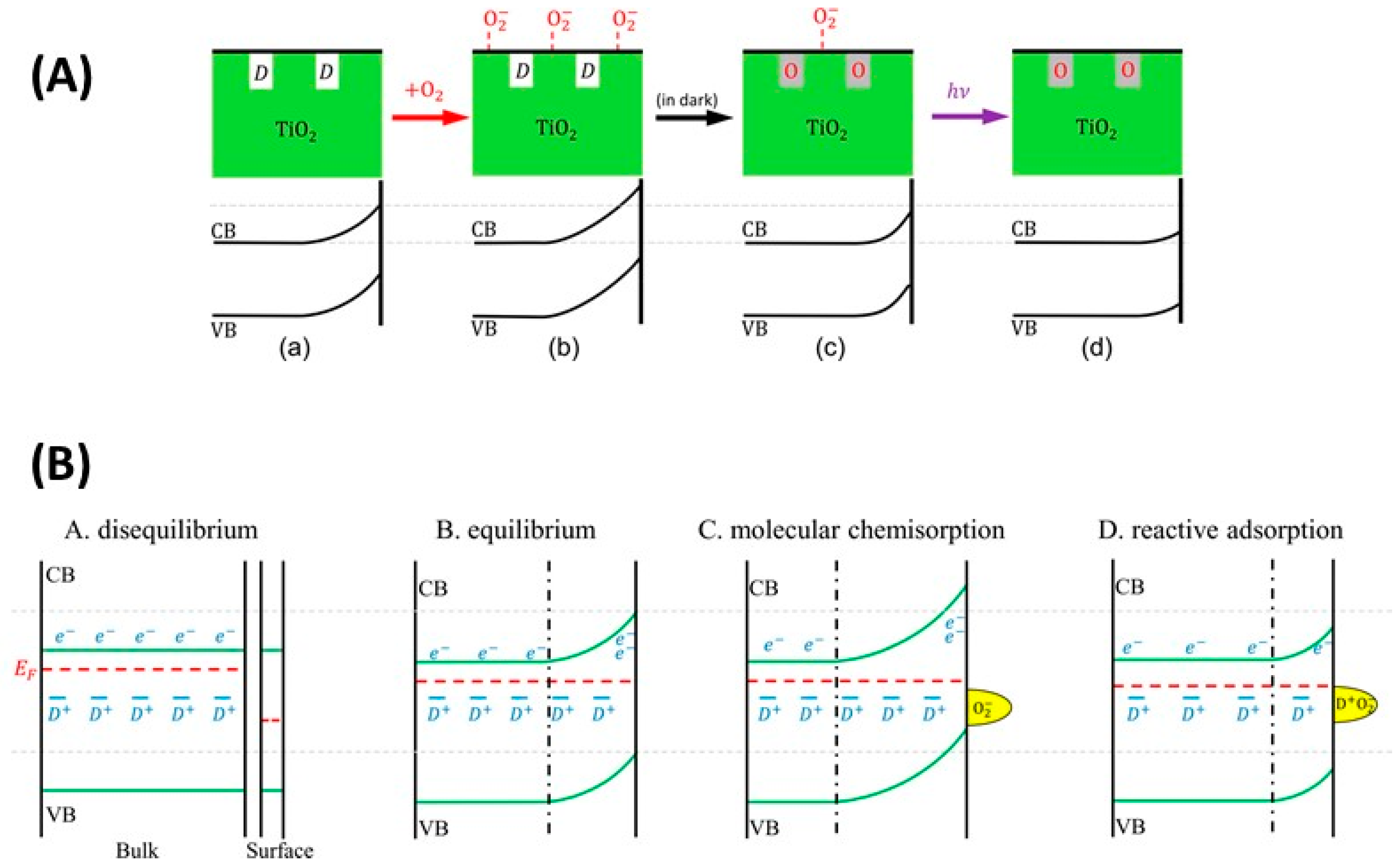
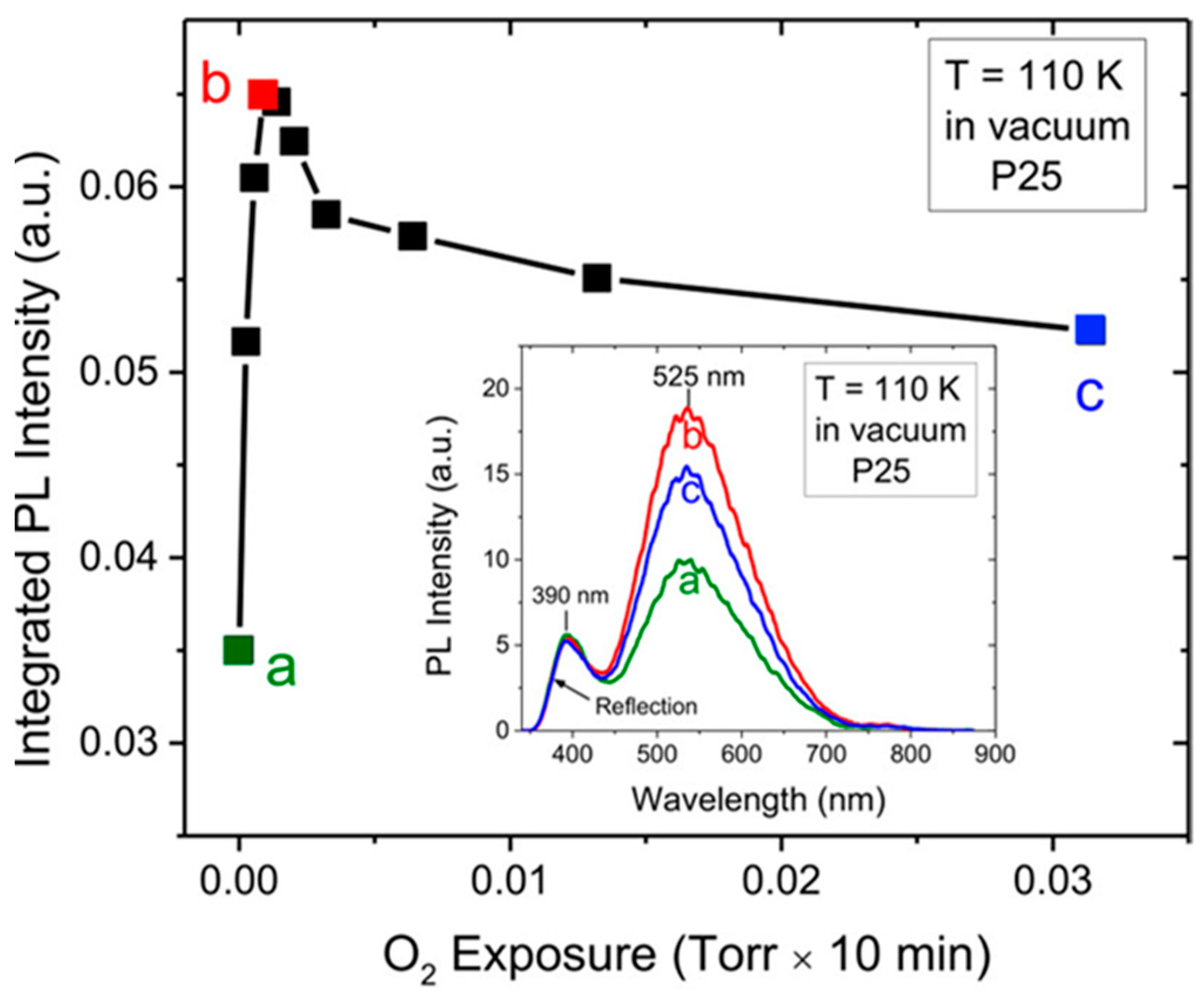
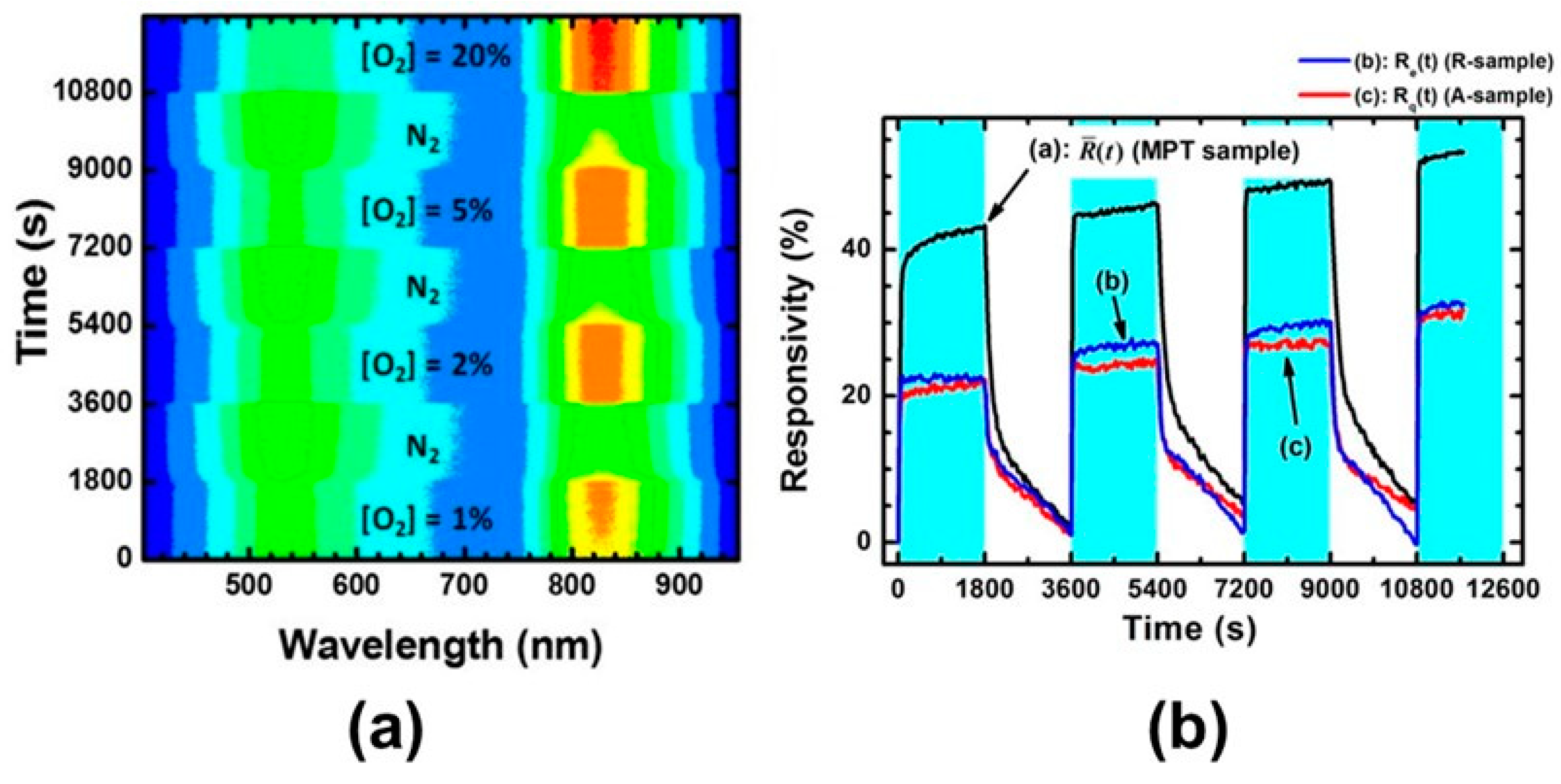
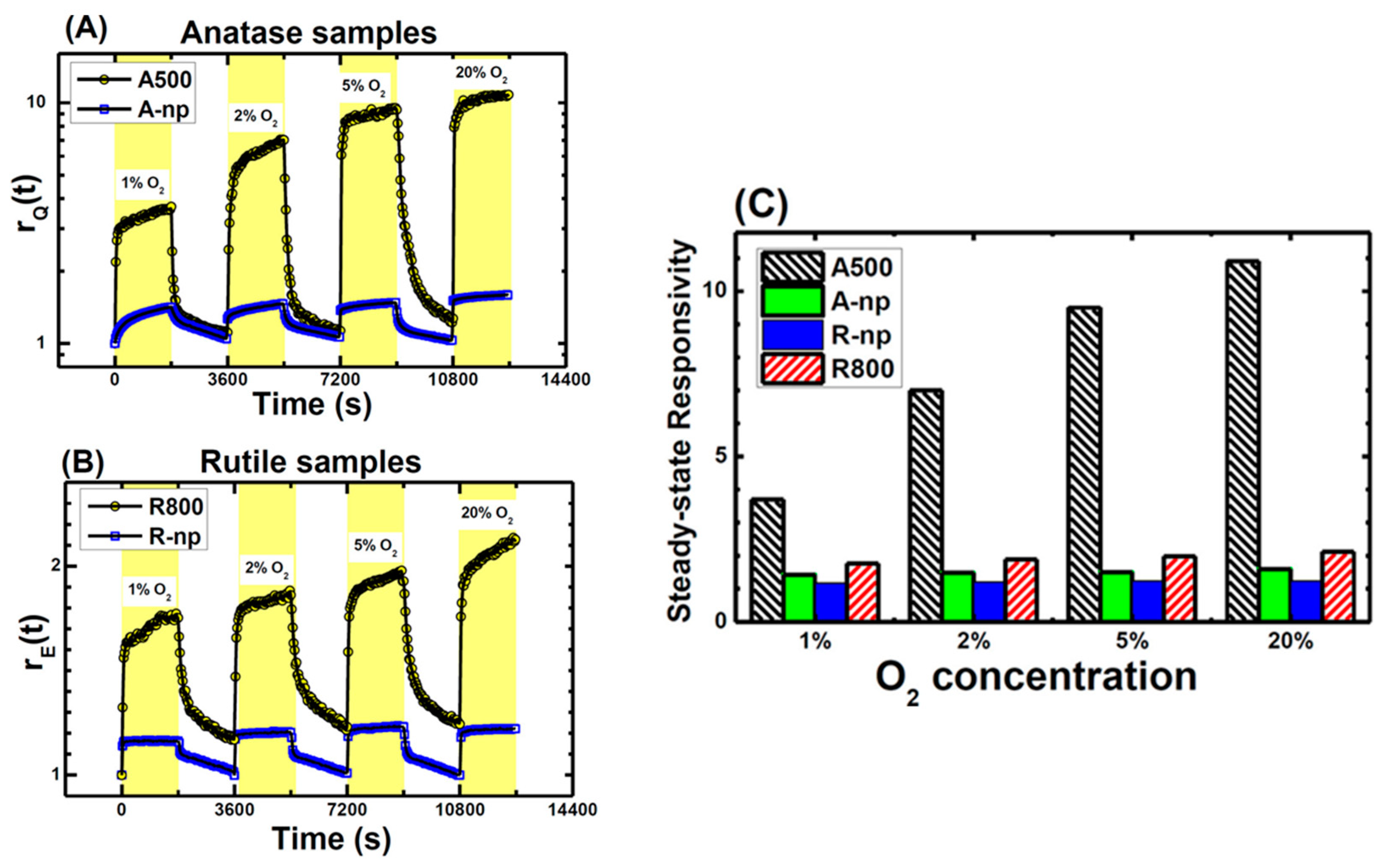
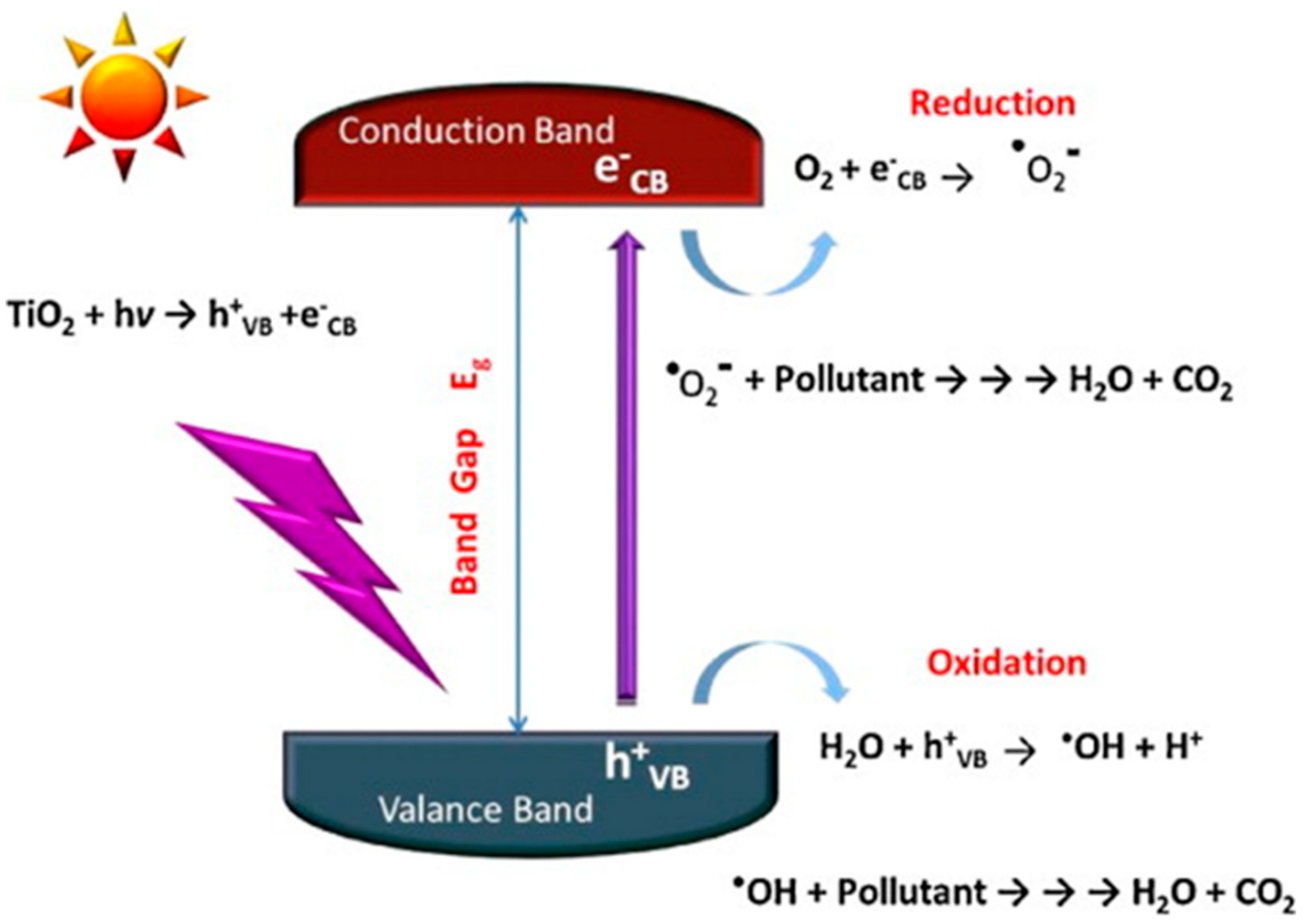

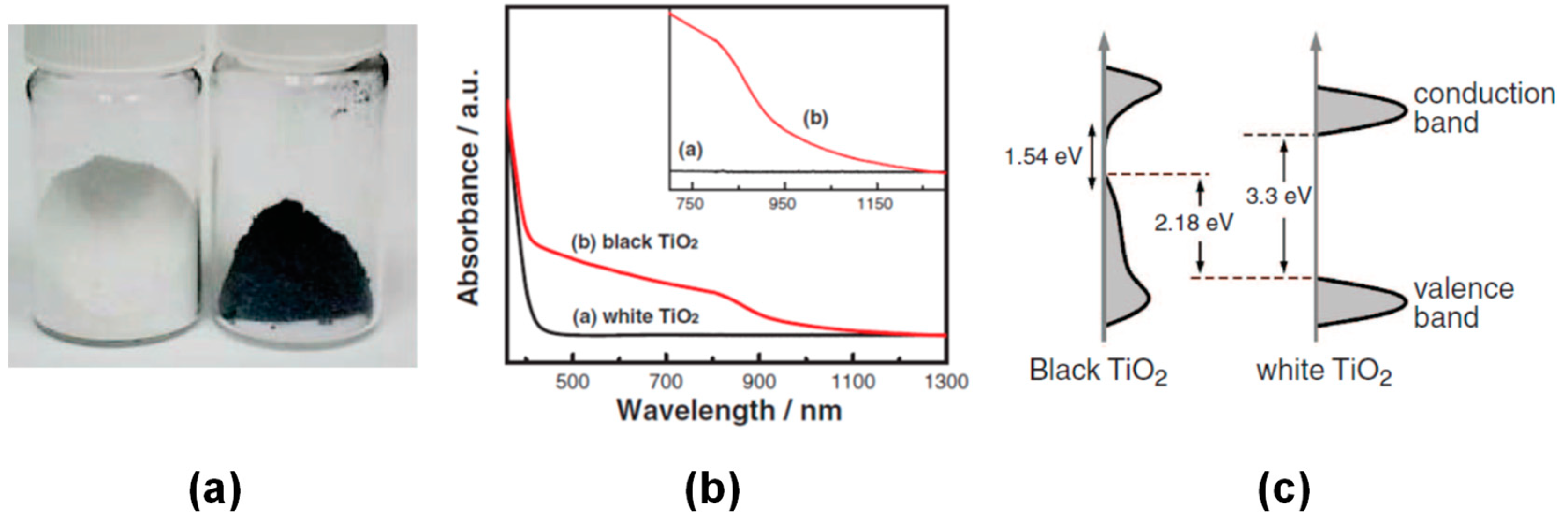
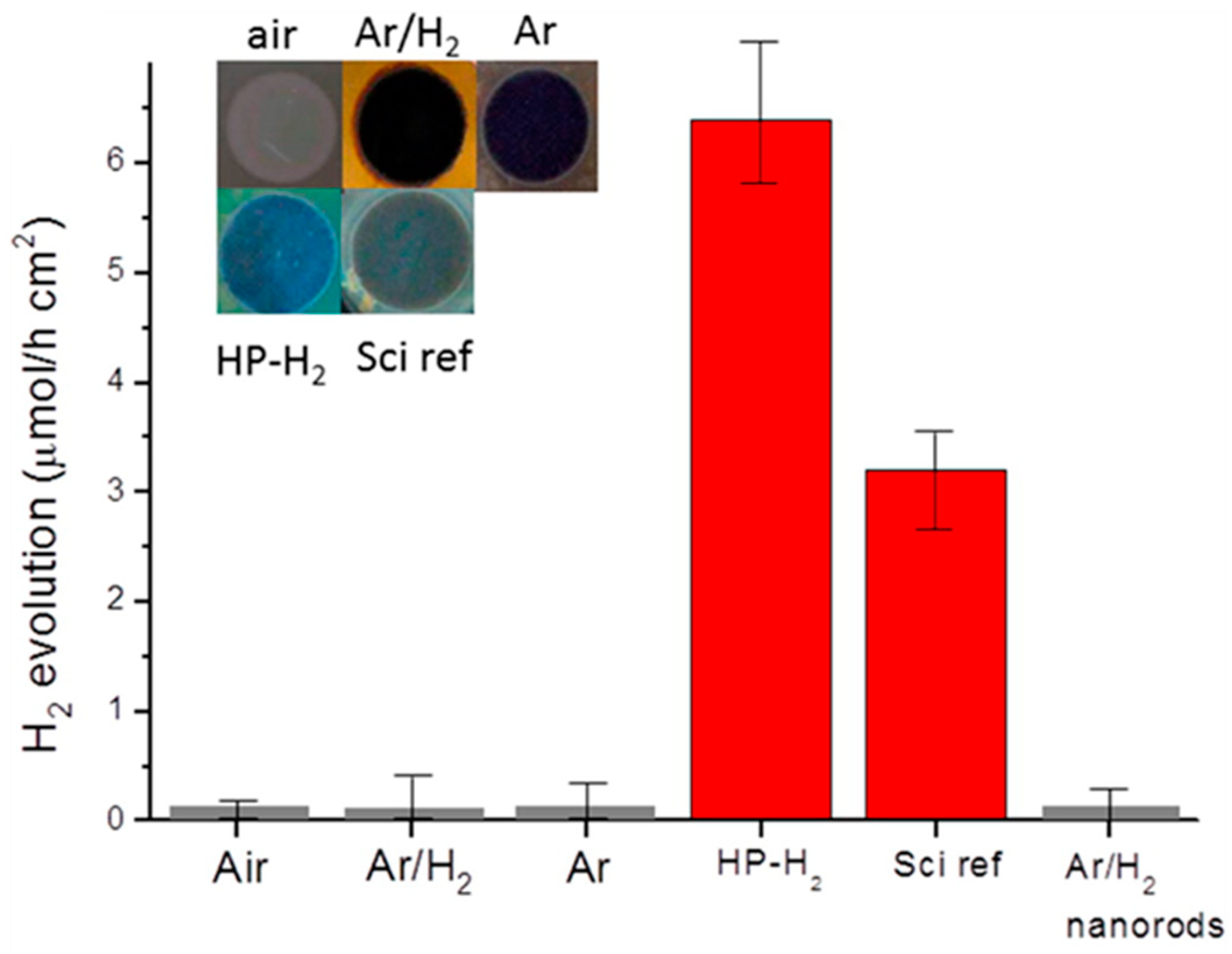

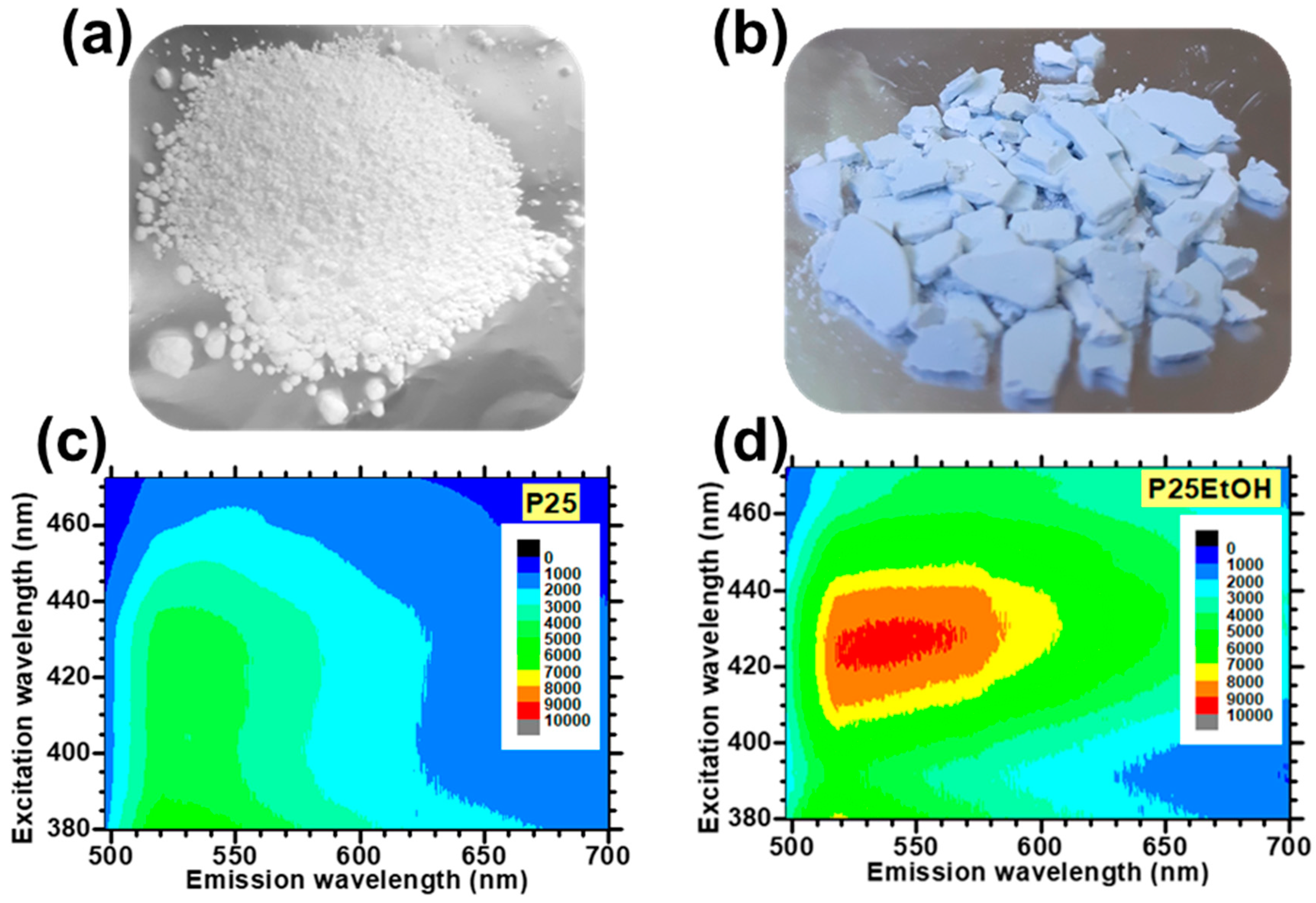

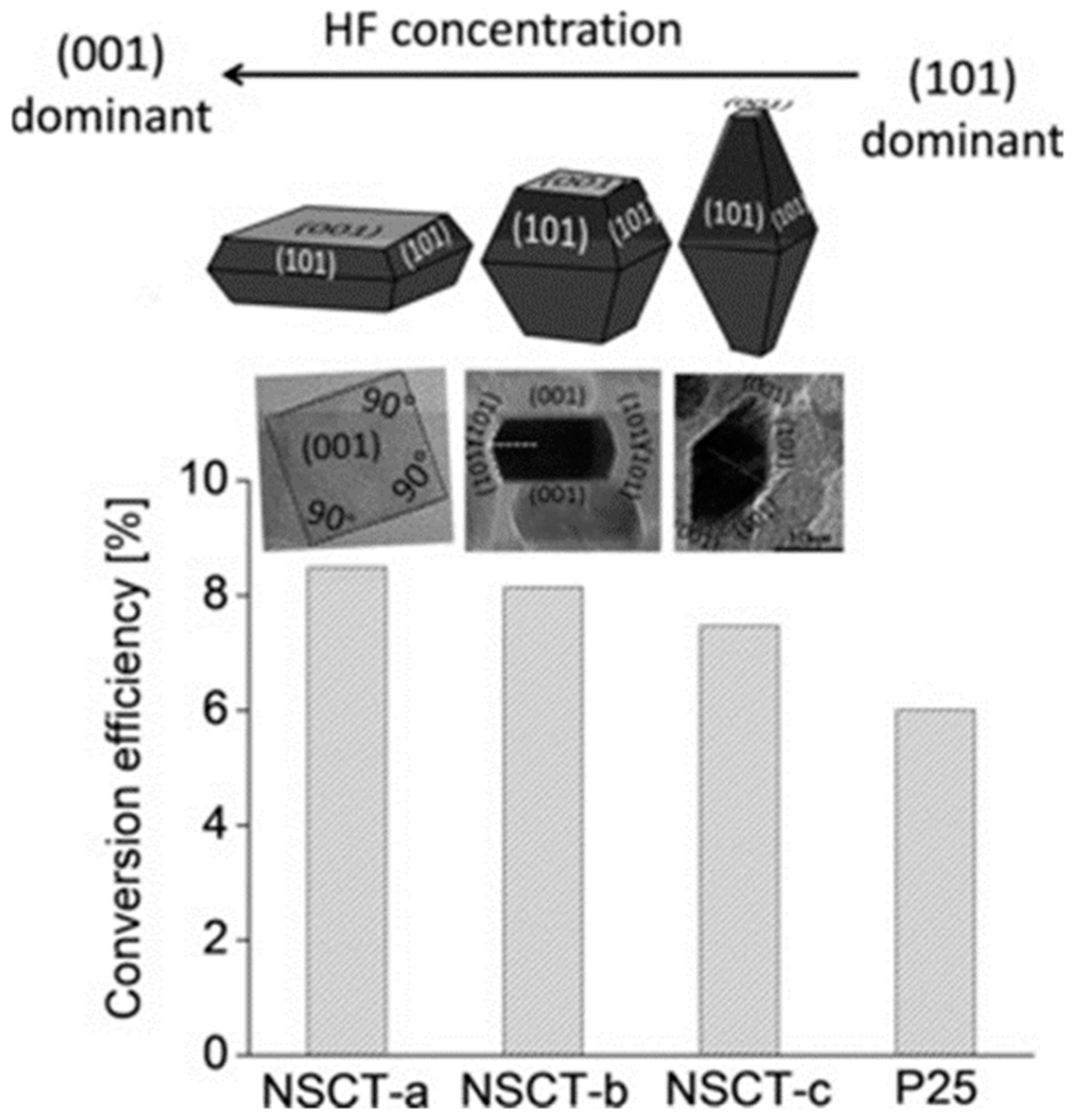
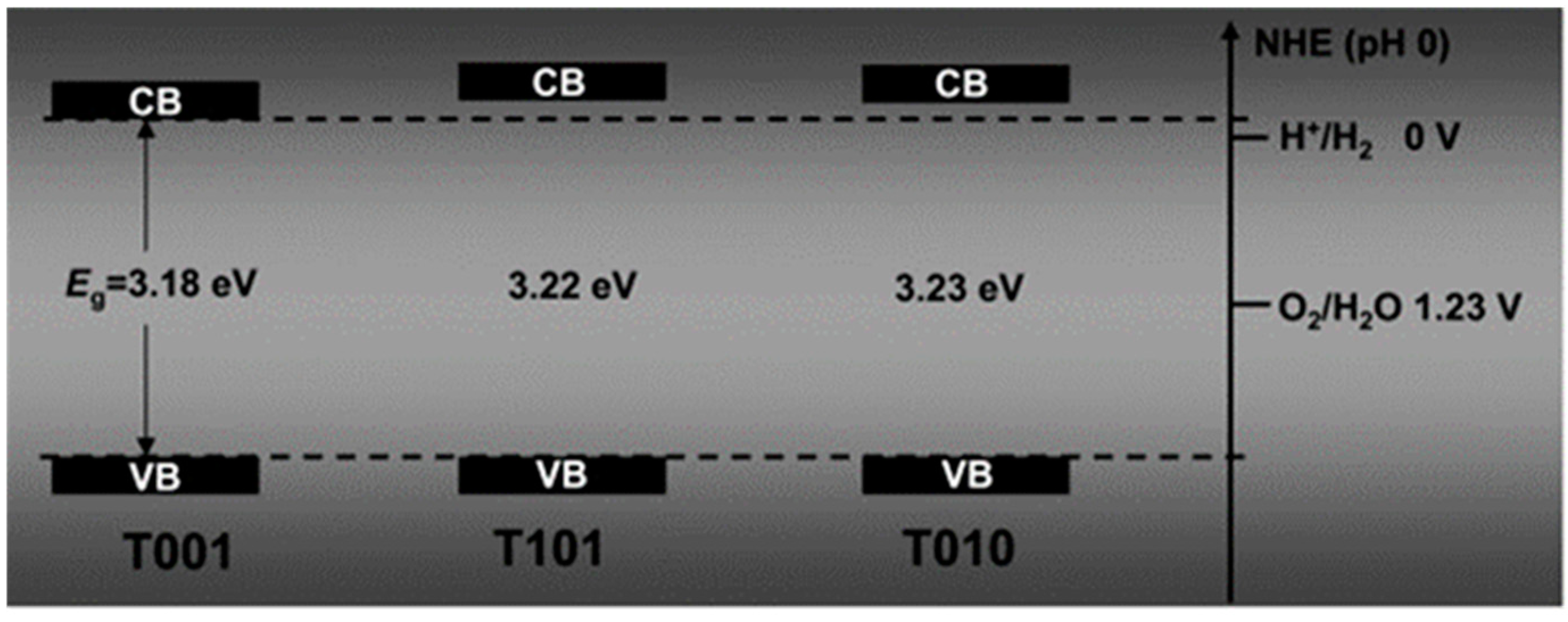
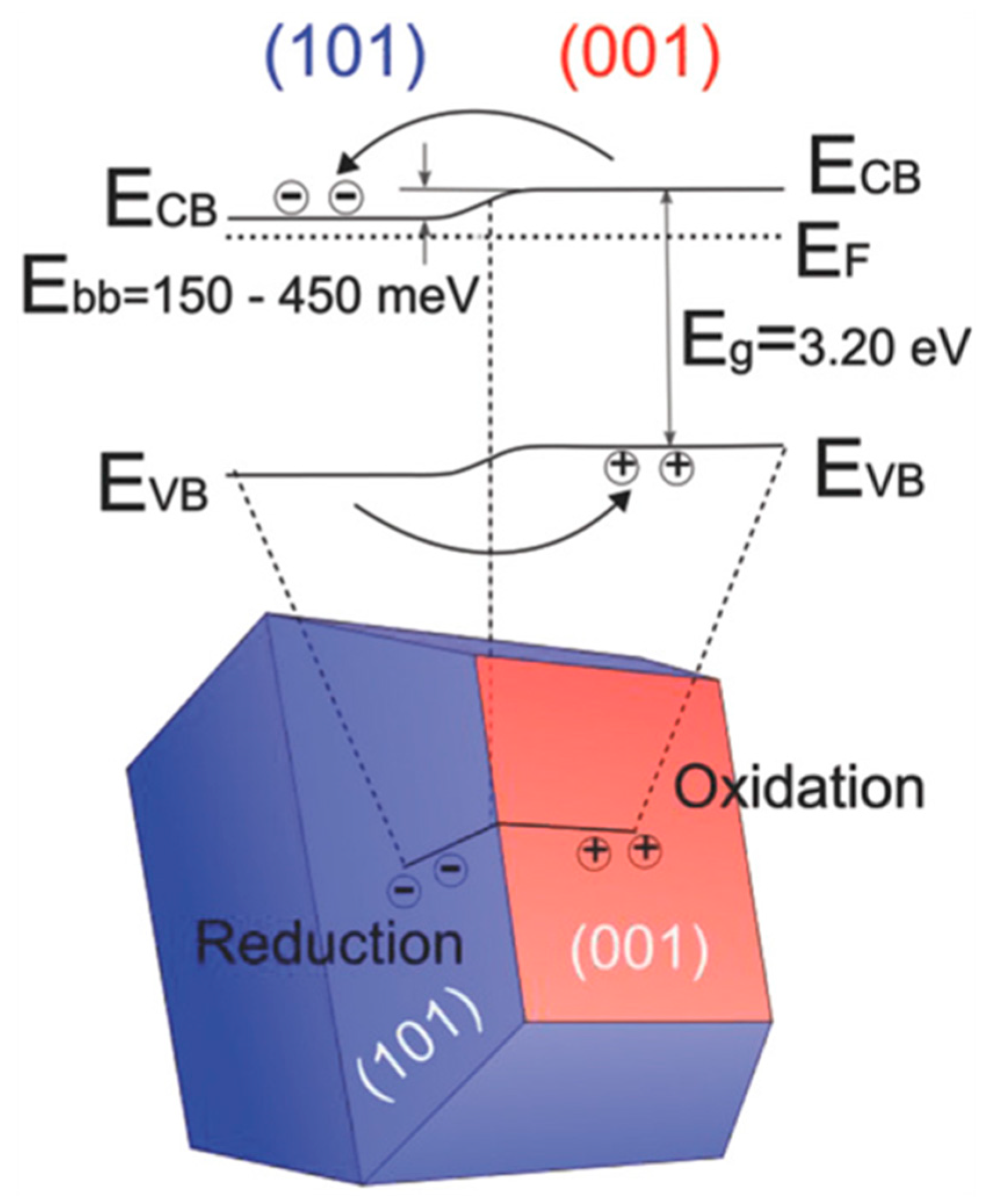
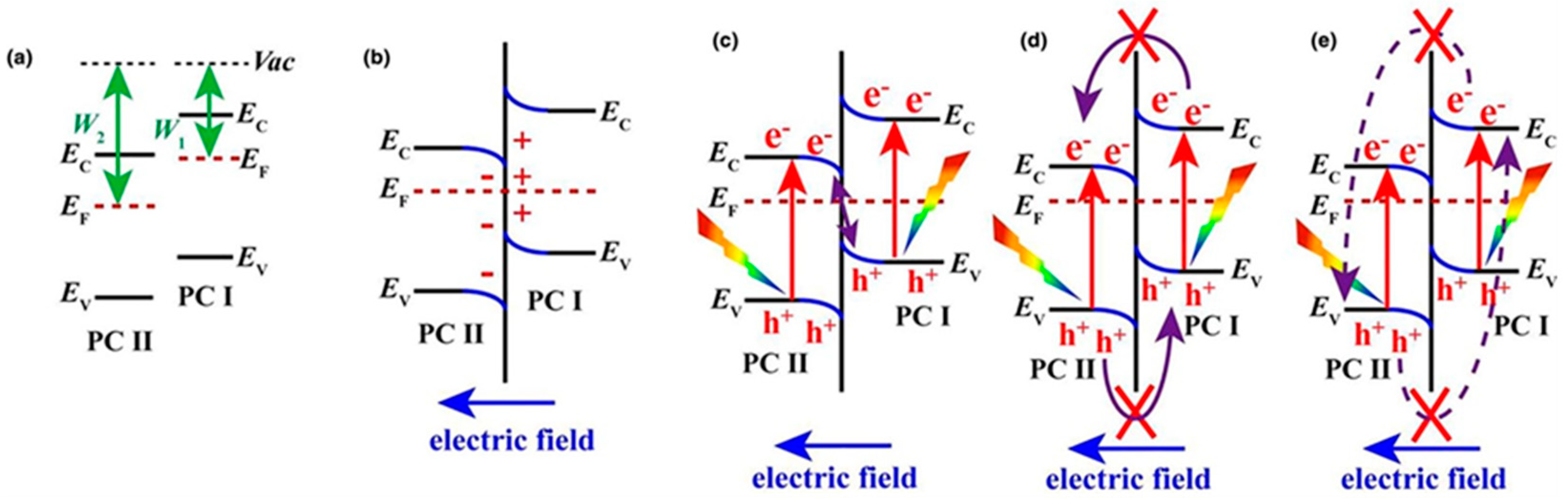

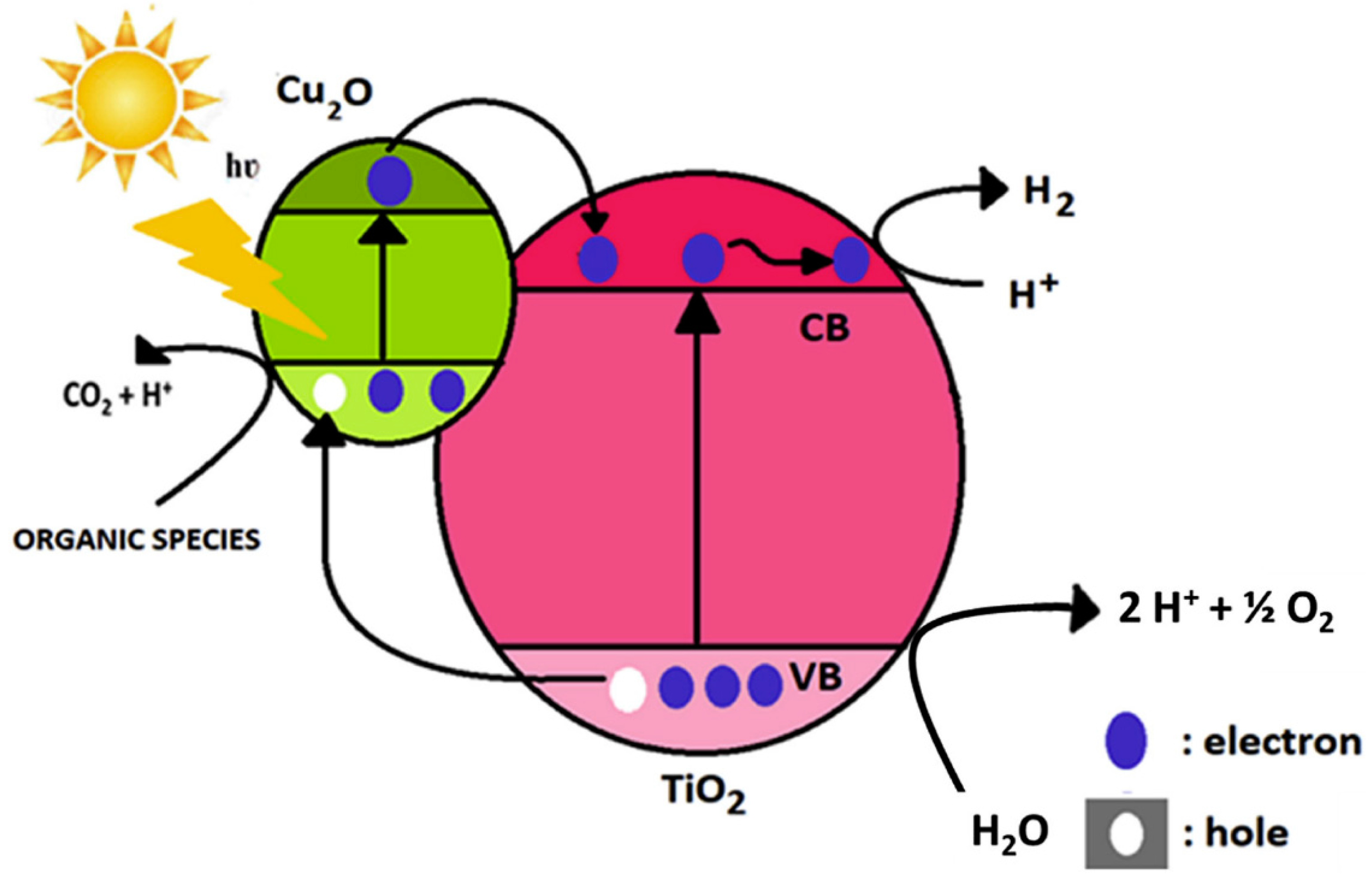
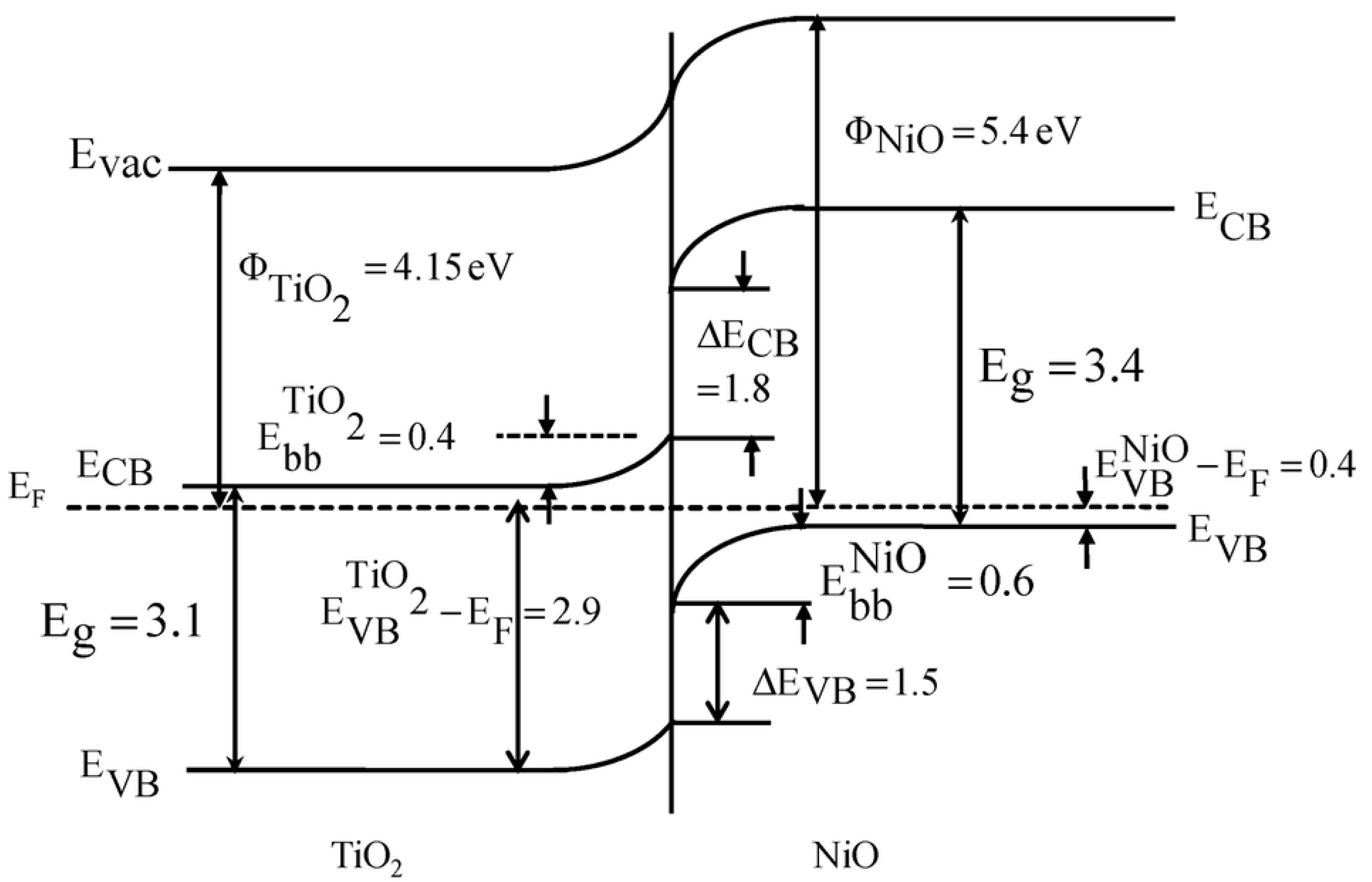


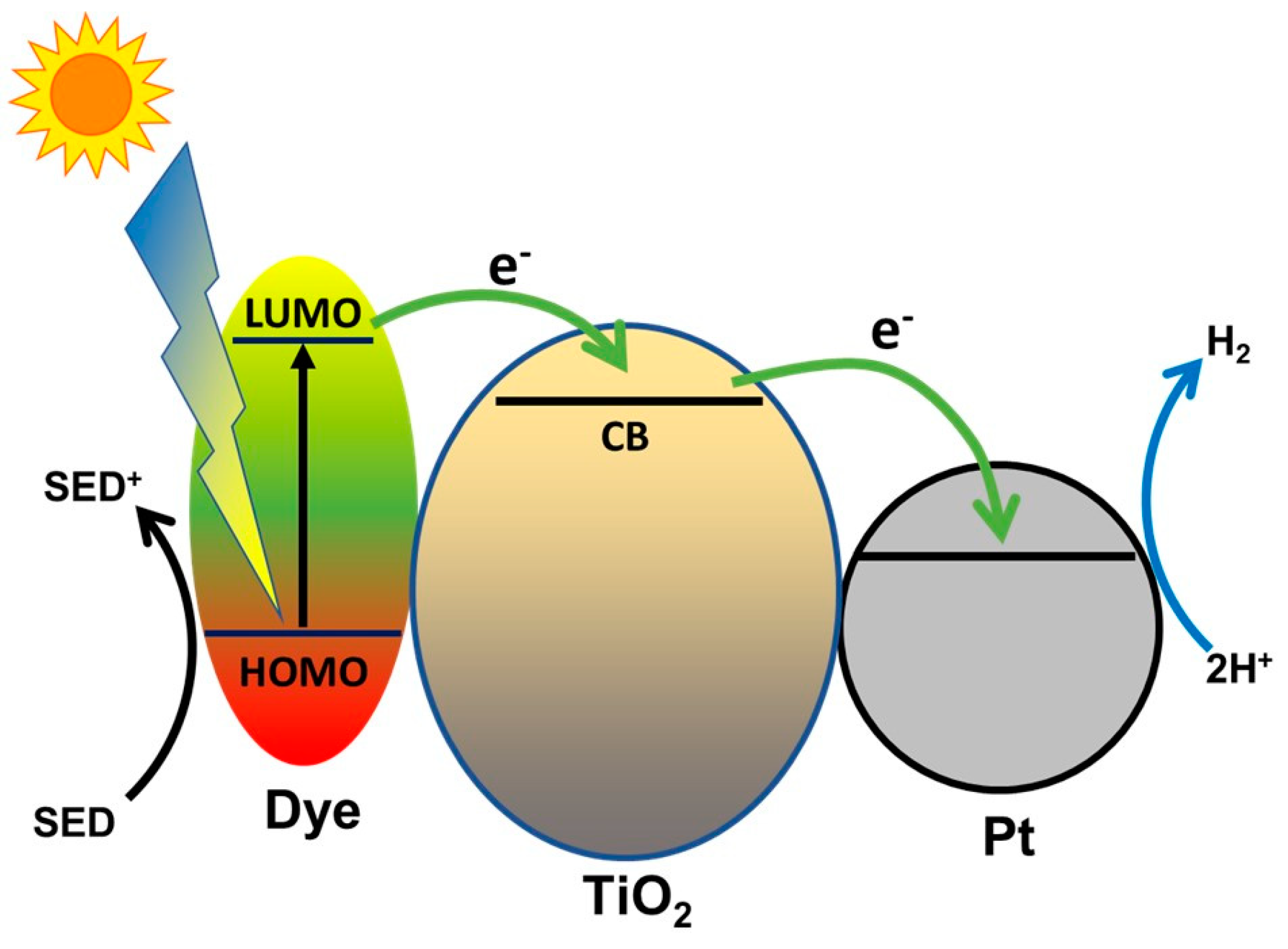

| Atomic Radius (nm) | Density (g/cm3) | ||||
|---|---|---|---|---|---|
| O: | 0.066 (covalent) | Rutile | 4.24 | ||
| Ti: | 0.146 (metallic) | Anatase | 3.83 | ||
| Ionic radius (nm) | Brookite | 4.17 | |||
| O (−2) | 0.14 nm | ||||
| Ti (+4) | 0.064 nm | ||||
| Crystal structure | Lattice constants (nm) | ||||
| System | Space group | a | b | c | |
| Rutile | Tetragonal | P42/mnm (group #136) | 0.4584 | - | 0.2953 |
| Anatase | Tetragonal | I41/amd (group #141) | 0.3733 | - | 0.937 |
| Brookite | Orthorhombic | Pbca (group #61) | 0.5436 | 0.9166 | 0.5135 |
| Energy bandgap (eV) | Electron mobility m (cm2/Vs) | Dielectric constant (at room T) | |||
| Rutile | 3.0 (indirect) | Rutile: ~1 (Reference [75]) | Frequency (Hz) | Value | |
| Anatase | 3.2 (indirect) | Anatase: ~10 (Reference [75]) | Rutile, | 108 | 86 |
| 104 | 160 | ||||
| Rutile, | 108 | 170 | |||
| 107 | 100 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lettieri, S.; Pavone, M.; Fioravanti, A.; Santamaria Amato, L.; Maddalena, P. Charge Carrier Processes and Optical Properties in TiO2 and TiO2-Based Heterojunction Photocatalysts: A Review. Materials 2021, 14, 1645. https://doi.org/10.3390/ma14071645
Lettieri S, Pavone M, Fioravanti A, Santamaria Amato L, Maddalena P. Charge Carrier Processes and Optical Properties in TiO2 and TiO2-Based Heterojunction Photocatalysts: A Review. Materials. 2021; 14(7):1645. https://doi.org/10.3390/ma14071645
Chicago/Turabian StyleLettieri, Stefano, Michele Pavone, Ambra Fioravanti, Luigi Santamaria Amato, and Pasqualino Maddalena. 2021. "Charge Carrier Processes and Optical Properties in TiO2 and TiO2-Based Heterojunction Photocatalysts: A Review" Materials 14, no. 7: 1645. https://doi.org/10.3390/ma14071645
APA StyleLettieri, S., Pavone, M., Fioravanti, A., Santamaria Amato, L., & Maddalena, P. (2021). Charge Carrier Processes and Optical Properties in TiO2 and TiO2-Based Heterojunction Photocatalysts: A Review. Materials, 14(7), 1645. https://doi.org/10.3390/ma14071645










