Application of an Arbitrary Lagrangian–Eulerian Method to Modelling the Machining of Rigid Polyurethane Foam
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Measurements of Material Properties of PUR Foam as a Function of Temperature
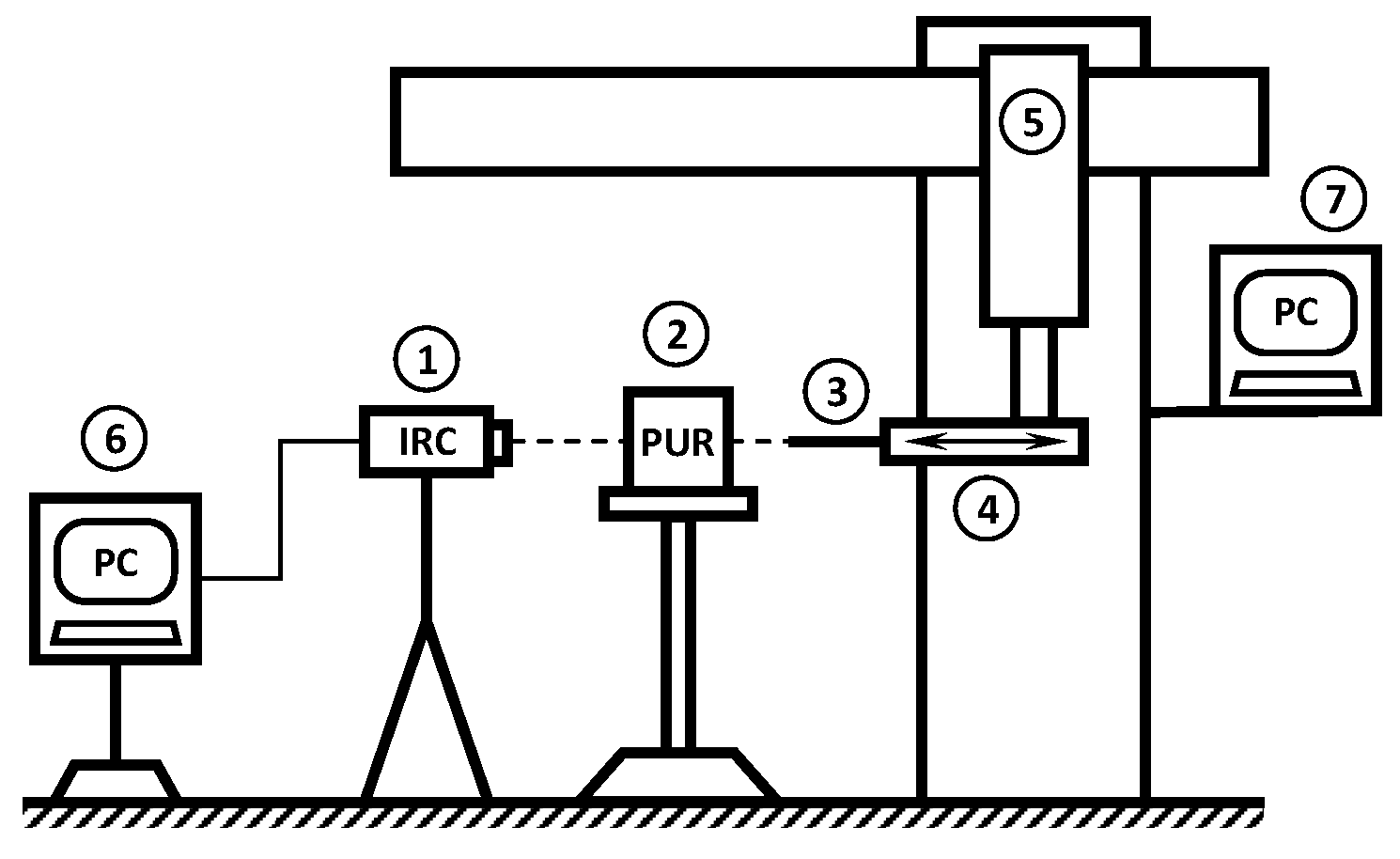
2.2. Experimental Measurement of Temperature on Tool’s Tip during Drilling
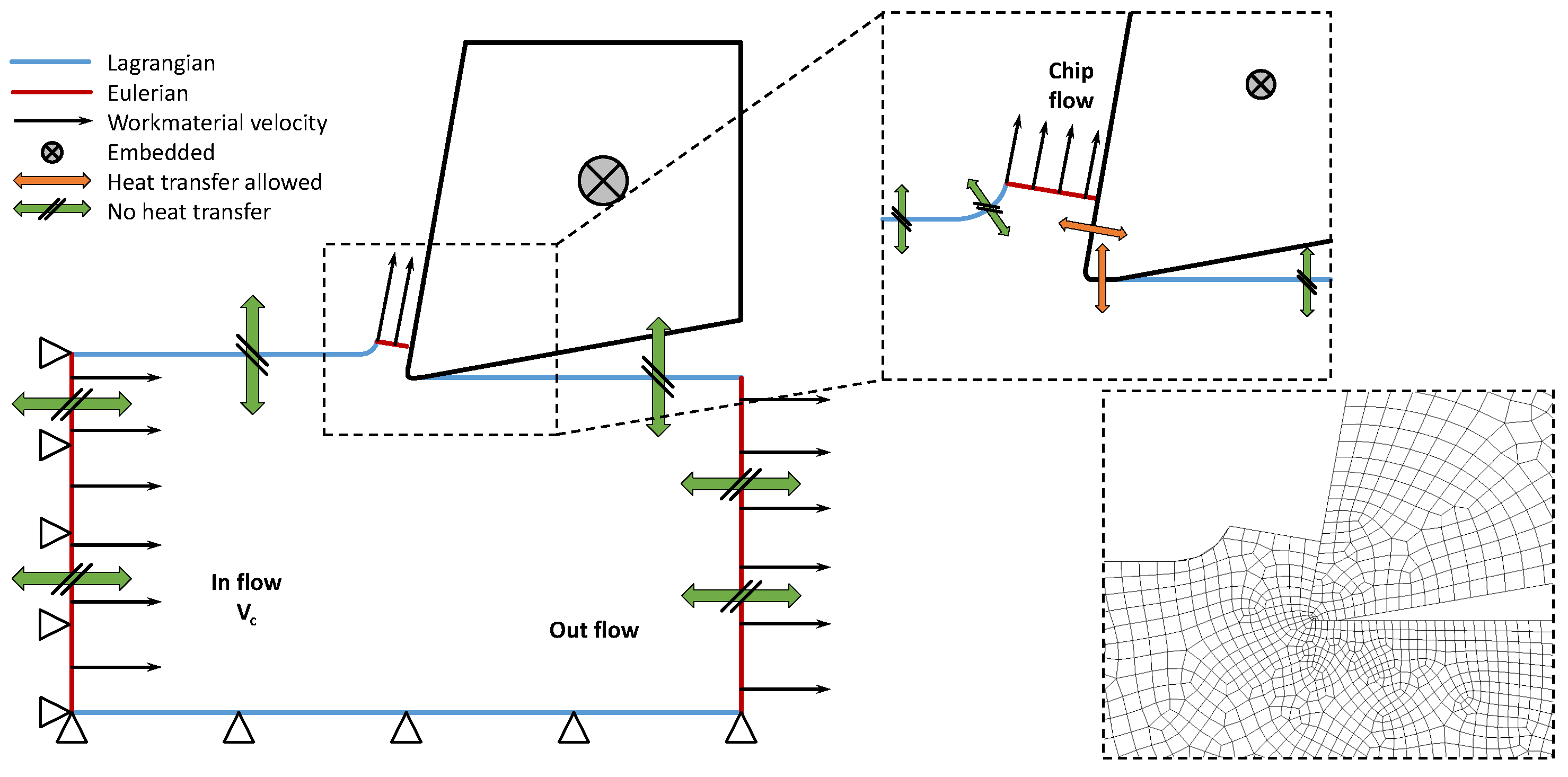
2.3. FE Simulation of the Machining
3. Results
3.1. Material Properties of PUR Foam as a Function of Temperature
3.2. Experimental Measurement of Heat on the Drill during Drilling
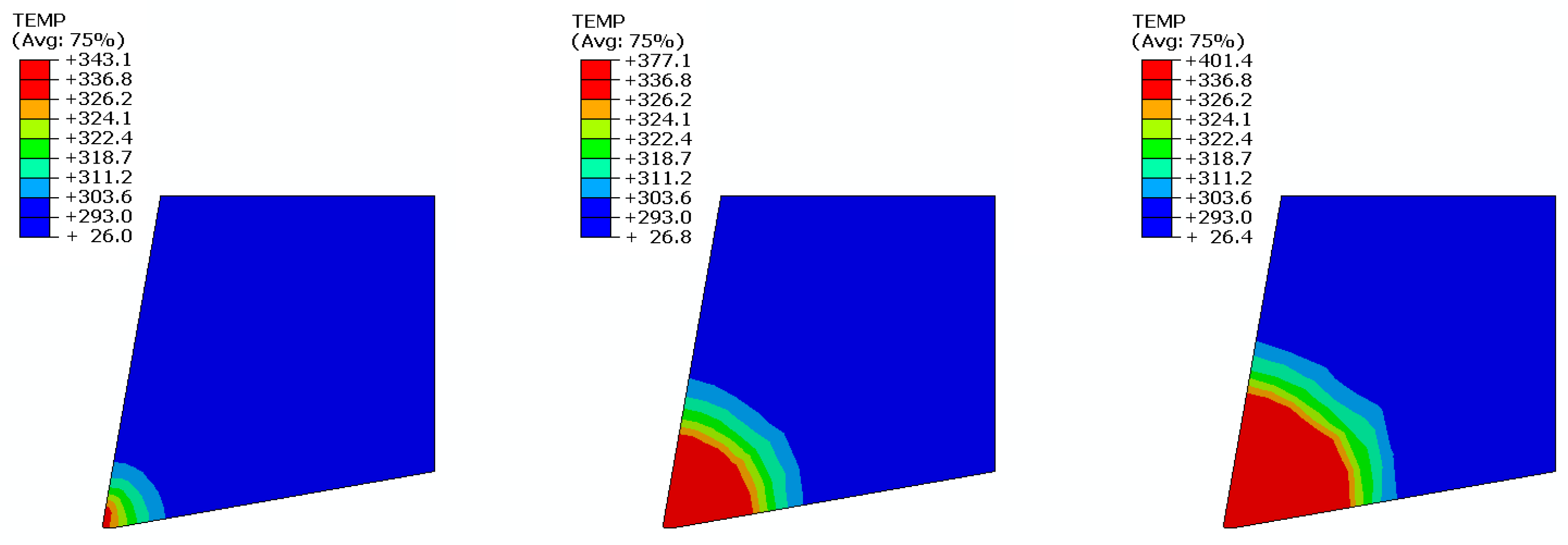
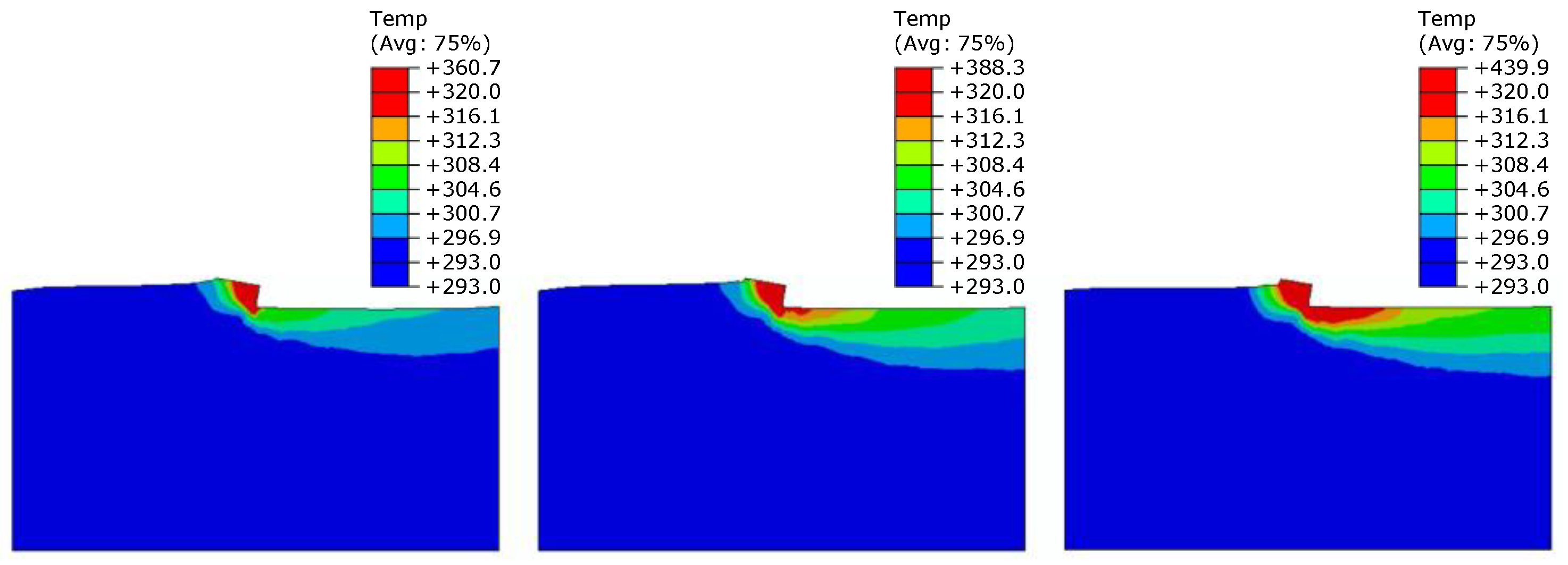
3.3. FE Simulation of the Machining
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| PUR | Rigid polyurethane foam |
| FEM | Finite element |
| ALE | Arbitrary Lagrangian–Eulerian |
| UV | Ultraviolet |
| PCF | Pounds per Cubic Foot |
| CNC | Computer Numeric Control |
| Ductile equivalent plastic strain (-) | |
| Fracture energy () | |
| Density () | |
| Specific heat (J/kg.K) | |
| K | Conductivity (J/m.s.K) |
| IR | Infra red |
| Maximum temperature (K, C ) | |
| Rotation cutting speed (rpm) | |
| Axial cutting speed (mm/min) | |
| t | Chip thickness (mm) |
| f | Friction coefficient (-) |
| k | Conductance (W/m.K) |
| Static yield stress (MPa) | |
| A | Yeld strength (MPa) |
| B | Hardening modulus (MPa) |
| C | Coefficient of strain rate sensitivity (-) |
| n | Hardening coefficient (-) |
| m | Thermal softening coefficient (-) |
| Transition temperature (K) | |
| Melting temperature (K) | |
| Mises equivalent plastic strain (-) | |
| Mises equivalent plastic strain rate | |
| Reference strain rate (1/s) | |
| Stress triaxiality | |
| p | Preasure stress (MPa) |
| q | Mises equivalent stress |
| State variable | |
| Equivalent plastic strain (-) | |
| Equivalent plastic strin at failure (-) | |
| Equivalent plastic displacement at failure (-) | |
| Total energy (mJ) | |
| Total strain energy (mJ) | |
| Viscous dissipated energy (mJ) | |
| Frictional dissipated energy (mJ) | |
| Kinetic energy (mJ) | |
| Internal heat energy (mJ) | |
| Work done by external forces (mJ) | |
| External heat energy (mJ) | |
| Elastic strain energy (mJ) | |
| Inelastic dissipated energy (mJ) | |
| Artificial strain energy (mJ) | |
| Energy dissipated by damage (mJ) |
References
- Gama, N.; Ferreira, A.; Barros-Timmons, A. Polyurethane Foams: Past, Present, and Future. Materials 2018, 11, 1841. [Google Scholar] [CrossRef] [PubMed]
- Harith, I.K. Study on polyurethane foamed concrete for use in structural applications. Case Stud. Constr. Mater. 2018, 8, 79–86. [Google Scholar] [CrossRef]
- Ionescu, M. Chemistry and Technology of Polyols for Polyurethanes; iSmithers Rapra Publishing: Shrewsbury, UK, 2005. [Google Scholar]
- Formela, K.; Hejna, A.; Zedler, L.; Przybysz, M.; Ryl, J.; Saeb, M.R.; Piszczyk, L. Structural, thermal and physico-mechanical properties of polyurethane brewers spent grain composite foams modified with ground tire rubber. Ind. Crops Prod. 2017, 108, 844–852. [Google Scholar] [CrossRef]
- Zhang, M.; Pan, H.; Zhang, L.; Hu, L.; Zhou, Y. Study of the mechanical, thermal properties and flame retardancy of ofrigid polyurethane foams prepared from modified castor-oil-basedpolyols. Ind. Crops Prod. 2014, 59, 1595–1599. [Google Scholar] [CrossRef]
- Chen, W.; Lu, F.; Winfree, N. High-strain-rate Compressive Behavior of a Rigid Polyurethane Foam with Various Densities. Exp. Mech. 2002, 42, 65–73. [Google Scholar] [CrossRef]
- Mane, J.V.; Chandra, S.; Sharma, S.; Ali, H.; Chavan, V.M.; Manjunath, B.S.; Patel, R.J. Mechanical Property Evaluation of Polyurethane Foam under Quasi-static and Dynamic Strain Rates—An Experimental Study. Procedia Eng. 2017, 173, 726–731. [Google Scholar] [CrossRef]
- Burgaz, E.; Kendirlioglu, C. Thermomechanical behavior and thermal stability of polyurethane rigid nanocomposite foams containing binary nanoparticle mixtures. Polym. Test. 2019, 77, 105930. [Google Scholar] [CrossRef]
- Pellizzi, E.; Lattuati-Derieux, A.; Lavedrine, B.; Cheradame, H. Degradation of polyurethane ester foam artifacts: Chemical properties, mechanical properties and comparison between accelerated and natural degradation. Polym. Degrad. Stab. 2014, 107, 255–261. [Google Scholar] [CrossRef]
- Er, M.S.; Altinel, L.; Eroglu, M.; Verim, O.; Demir, T.; Atmaca, H. Suture anchor fixation strength with or without augmentation in osteopenic and severely osteoporotic bones in rotator cuff repair: A biomechanical study on polyurethane foam model. J. Orthop. Surg. Res. 2014, 48, 247–253. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nowak, B. Experimental study on the loosening of pedicle screws implanted to synthetic bone vertebra models and under non-pull-out mechanical loads. J. Mech. Behav. Biomed. 2019, 98, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Hollensteiner, M.; Esterer, B.; Furst, D.; Schrempf, A.; Augat, P. Development of open-cell polyurethane-based bone surrogates for biomechanical testing of pedicle screws. J. Mech. Behav. Biomed. 2019, 97, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Oroszlany, A.; Nagy, P.; Kovacs, J.G. Compressive Properties of Commercially Available PVC Foams Intended for Use as Mechanical Models for Human Cancellous Bone. Acta Polytech. Hung. 2015, 12, 89–101. [Google Scholar]
- Arrazola, P.J.; Ozel, T. Investigations on the effects of friction modeling in finite element simulation of machining. Int. J. Mech. Sci. 2010, 52, 31–42. [Google Scholar] [CrossRef]
- Courbon, C.; Mabrouki, T.; Rech, J.; Mazuyer, D.; D’Eramo, E. On the existence of a thermal contact resistance at the tool-chip interface in dry cutting of AISI 1045: Formation mechanisms and influence on the cutting process. Appl. Therm. Eng. 2013, 50, 1311–1325. [Google Scholar] [CrossRef]
- Pimenov, D.; Guzeev, V. Mathematical model of plowing forces to account for flank wear using FME modeling for orthogonal cutting scheme. Int. J. Adv. Manuf. Technol. 2017, 89, 3149–3159. [Google Scholar] [CrossRef]
- Dhaliwal, G.; Anandan, S.; Chandrashekhara, K.; Lees, J.; Nam, P. Development and characterization of polyurethane foams with substitution of polyether polyol with soy-based polyol. Eur. Polym. J. 2018, 107, 105–117. [Google Scholar] [CrossRef]
- Briody, C.; Duignan, B.; Jerrams, S.; Tiernan, S. The implementation of a visco-hyperelastic numerical material model for simulating the behaviour of polymer foam materials. Comput. Mater. Sci. 2012, 64, 47–51. [Google Scholar] [CrossRef]
- Avevor, Y.; Vincent, J.; Faure, L.; Moufki, A.; Philippon, S. An ALE approach for the chip formation process in high speed machining with transient cutting conditions: Modeling and experimental validation. Int. J. Mech. Sci. 2017, 130, 546–557. [Google Scholar] [CrossRef]
- Haglund, A.; Kishawy, H.; Rogers, R. An exploration of friction models for the chip-tool interface using an Arbitrary Lagrangian–Eulerian finite element model. Wear 2008, 265, 452–460. [Google Scholar] [CrossRef]
- Johnson, G.; Cook, W. A constitutive model and data for metals subjected to large strains high strain rates and high temperatures. In Proceedings of the 7th International Symp. Balistics, Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- ABAQUS Inc. ABAQUS Analysis UserÂ’s Manual, Version 2018; ABAQUS Inc.: London, UK, 2018. [Google Scholar]
- Ducobu, F.; Riviere-Lorphevre, E.; Filippi, E. Application of the Coupled Eulerian-Lagrangian (CEL) method to the modeling of orthogonal cutting. Eur. J. Mech. A-Solid 2016, 59, 58–66. [Google Scholar] [CrossRef]
- Zetterberg, M. A Critical Overview of Machining Simulations in ABAQUS. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2014. [Google Scholar]


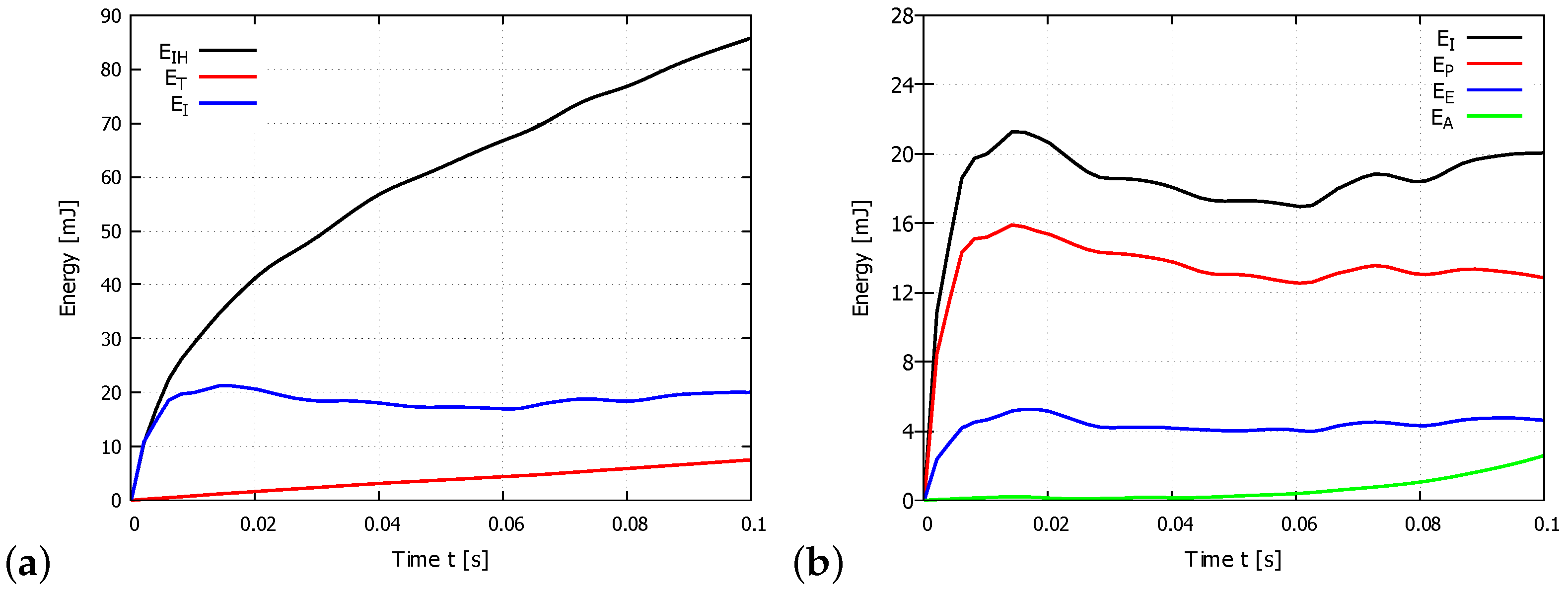
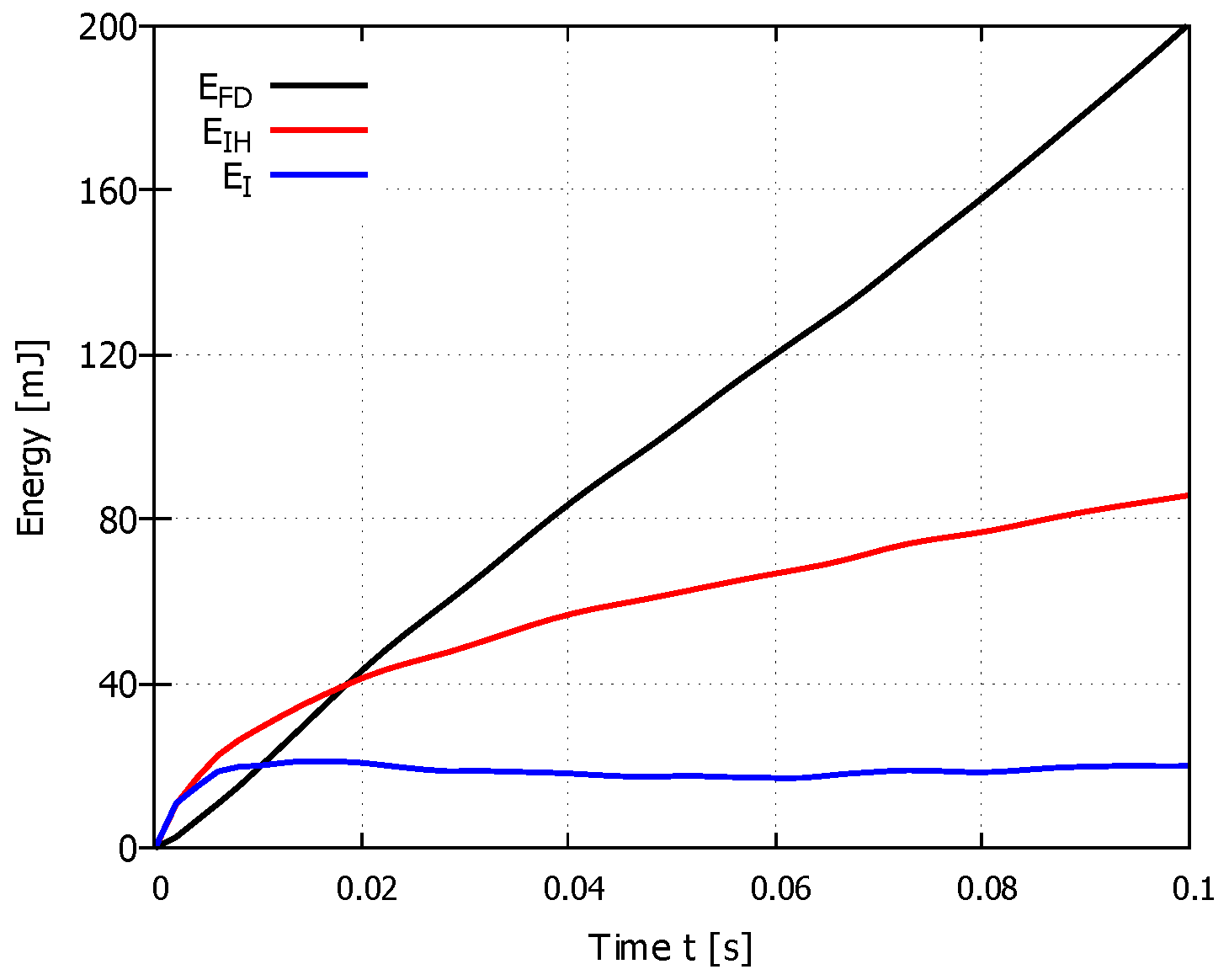
| Equivalent Plastic | Fracture Energy | Density | Specific Heat | Conductivity | |
|---|---|---|---|---|---|
| Strain [-] | [J/mm] | [g/cm] | [J/(kg.K)] | k [J/(m.s.K)] | |
| 40 PCF | |||||
| 298.15 K | 0.0400 | 40.0 | |||
| 363.15 K | 0.0290 | 29.0 | 0.64 | 809 | 0.11 |
| 428.15 K | 0.2242 | 24.2 | |||
| 25 PCF | |||||
| 298.15 K | 0.0155 | 6.23 | |||
| 363.15 K | 0.0323 | 3.28 | 0.40 | 1 400 | 0.06 |
| 428.15 K | 0.1494 | 2.60 | |||
| 10 PCF | |||||
| 298.15 K | 0.0315 | 0.866 | |||
| 363.15 K | 0.0421 | 0.245 | 0.16 | 1 477 | 0.037 |
| 428.15 K | 0.2174 | 0.102 | |||
| Sample | A [MPa] | B [MPa] | n | C | [1/s]] | m | [K] | [K] |
|---|---|---|---|---|---|---|---|---|
| 10 PCF | 1.4670 | 20.6235 | 0.831567 | 0.012 | 1 | 7.5052 | 675.0 | 273.15 |
| 25 PCF | 4.3345 | 169.377 | 0.942053 | 0.012 | 1 | 11.623 | 675.0 | 273.15 |
| 40 PCF | 11.9248 | 92.6822 | 0.686915 | 0.012 | 1 | 8.730 | 675.0 | 273.15 |
| 25 C | 90 C | 155 C | ||||
|---|---|---|---|---|---|---|
| Sample | Tensile | Compressive | Tensile | Compressive | Tensile | Compressive |
| Modulus (MPa) | Modulus (MPa) | Modulus (MPa) | Modulus (MPa) | Modulus (MPa) | Modulus (MPa) | |
| PCF 10 | ||||||
| PCF 25 | ||||||
| PCF 40 | ||||||
| Rotation Speed [rpm] | 800 | 3000 | 5000 |
|---|---|---|---|
| Axial Speed [mm/min] | 10 | 30 | 45 |
| 10 PCF | |||
| 25 PCF | |||
| 40 PCF |
| 500 mm/s | 10 PCF | 25 PCF | 40 PCF |
|---|---|---|---|
| T [C] | 70.0 | 104.0 | 128.3 |
| 40 PCF | 133 mm/s | 500 mm/s | 833 mm/s |
| T [C] | 104.2 | 128.3 | 142.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horak, Z.; Tichy, P.; Dvorak, K.; Vilimek, M. Application of an Arbitrary Lagrangian–Eulerian Method to Modelling the Machining of Rigid Polyurethane Foam. Materials 2021, 14, 1654. https://doi.org/10.3390/ma14071654
Horak Z, Tichy P, Dvorak K, Vilimek M. Application of an Arbitrary Lagrangian–Eulerian Method to Modelling the Machining of Rigid Polyurethane Foam. Materials. 2021; 14(7):1654. https://doi.org/10.3390/ma14071654
Chicago/Turabian StyleHorak, Zdenek, Petr Tichy, Karel Dvorak, and Miloslav Vilimek. 2021. "Application of an Arbitrary Lagrangian–Eulerian Method to Modelling the Machining of Rigid Polyurethane Foam" Materials 14, no. 7: 1654. https://doi.org/10.3390/ma14071654
APA StyleHorak, Z., Tichy, P., Dvorak, K., & Vilimek, M. (2021). Application of an Arbitrary Lagrangian–Eulerian Method to Modelling the Machining of Rigid Polyurethane Foam. Materials, 14(7), 1654. https://doi.org/10.3390/ma14071654






