Modelling Electron Channeling Contrast Intensity of Stacking Fault and Twin Boundary Using Crystal Thickness Effect
Abstract
:1. Introduction
2. Materials and Methods
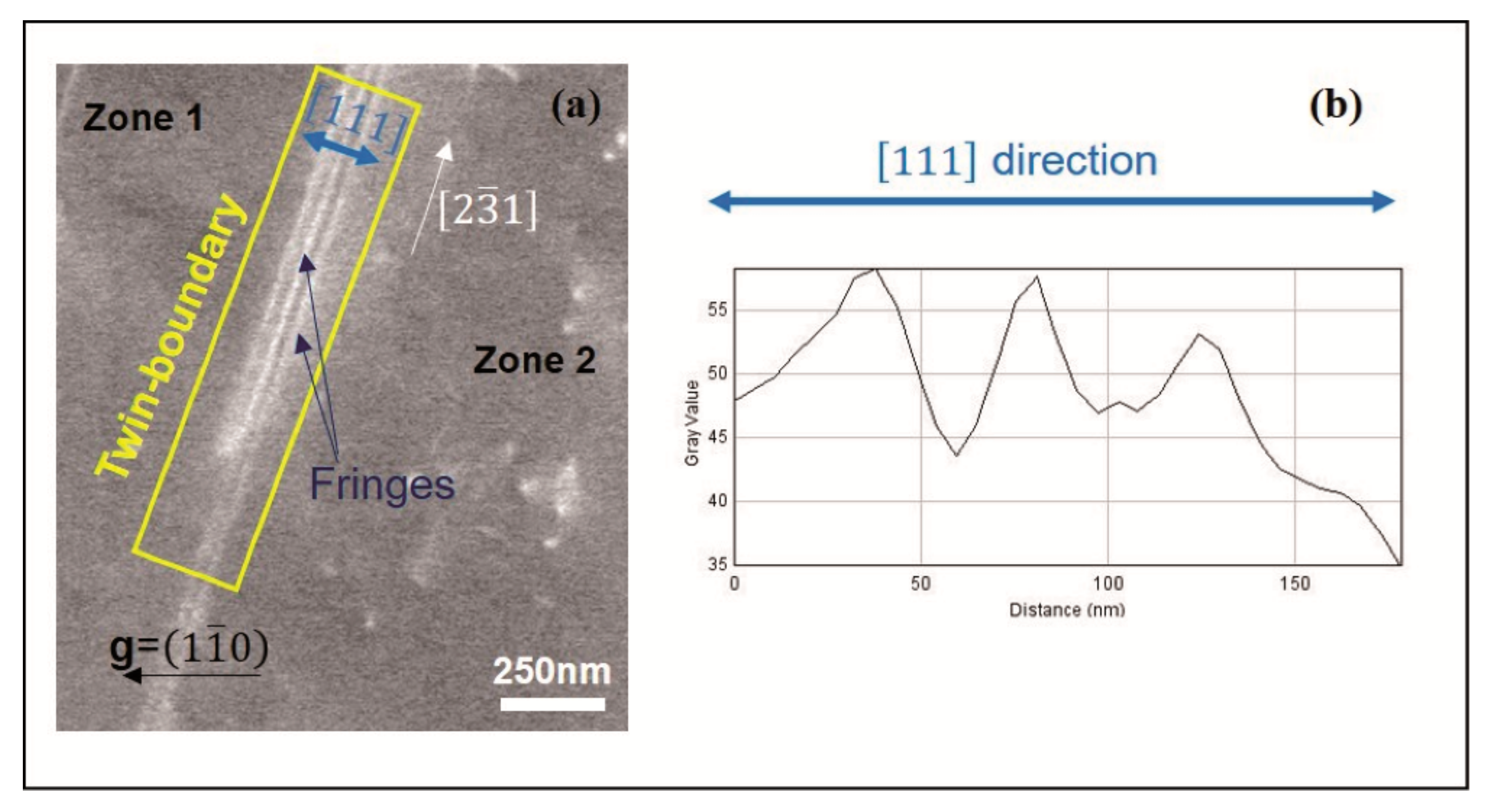
Experimental Analysis of a Special Grain Boundary: Twin-Boundary
3. Theoretical Models
3.1. Contribution of a Thin Perfect Crystal to the BSE Signal
- For a thickness t= 0.12ξg (6 nm), the slight Δη’ variations are between −0.58 (a.u.) and 0.58 (a.u.) as it is shown in Figure 3a. Such variations are due to the slight contribution of the term T(ω).
- For a thickness t = 0.2ξg (10 nm), a larges peak (for negative values of ω) and a hollow (for positive values of ω) appear (see Figure 3b). In addition, it is noted that the more the thickness increases, the more the amplitude of Δη’(ω) increases. These same observations are accentuated for the following thicknesses.
- For the thicknesses t = 0.7ξg (35 nm) and t = ξg (50 nm), the two profiles have, almost, the same appearance: Peak and hollow less spread than those obtained for t = 0.2ξg. In addition, oscillations on the sides of these curves appear (Figure 3c for t = 0.7ξg).
3.2. Modelling the BSE Contrast Generated by a Coherent Twin Boundary
3.2.1. For g.R ≠ 0
3.2.2. For g.R = 0
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Wan, Y.; Jung, D.; Norman, J.; Shang, C.; Li, Q.; May Lau, K.; Gossard, A.; Bowers, J.; Chen, B. Defect characterization of InAs/InGaAs quantum dot p-i-n photodetector grown on GaAs-on-V-grooved-Si substrate. ACS Photonics 2019, 6, 1100–1105. [Google Scholar] [CrossRef]
- Trager-Cowan, C.; Alasmari, A.; Avis, W.; Bruckbauer, J.; Edwards, P.R.; Ferenczi, G.; Hourahine, B.; Kotzai, A.; Kraeusel, S.; Kusch, G.; et al. Structural and luminescence imaging and characterization of semiconductors in the scanning electron microscope. Semicond. Sci. Technol. 2020, 35, 054001. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Zhang, X.; Misra, A. Growth twins and deformation twins in metals. Annu. Rev. Mater. Res. 2014, 44, 329–363. [Google Scholar] [CrossRef]
- Raabe, D.; Sun, B.; Kwiatkowski Da Silva, A.; Gault, B.; Yen, H.W.; Sedighiani, K.; Thoudden Sukumar, P.; Souza Filho, I.R.; Katnagallu, S.; Jägle, E.; et al. Current challenges and opportunities in microstructure-related properties of advanced high-strength steels. Metall. Mater. Trans. A 2020, 51, 5517–5586. [Google Scholar] [CrossRef]
- Naeem, M.; He, H.; Wang, B.; Liu, C.T.; Wang, X.-L. Extremely high dislocation density and deformation pathway of CrMnFeCoNi high entropy alloy at ultralow temperature. Scr. Mater 2020, 188, 21–25. [Google Scholar] [CrossRef]
- Wei, S.; Tasan, C.C. Deformation faulting in a metastable CoCrNiW complex concentrated alloy: A case of negative intrinsic stacking fault energy? Acta Mater. 2020, 200, 992–1007. [Google Scholar] [CrossRef]
- Naresh-Kumar, G.; Thomson, D.; Zhang, Y.; Bai, J.; Jiu, L.; Yu, X.; Gong, P.; Smith, R.M.; Wang, T.; Trager-Cowan, C. Imaging basal plane stacking faults and dislocations in (11-22) GaN using electron channelling contrast imaging. J. Appl. Phys. 2018, 124, 065301. [Google Scholar] [CrossRef] [Green Version]
- Pushkarev, S.S.; Galiev, G.B.; Klimov, E.A.; Kopylov, V.B. Photoluminescence of extended defects in heterostructures with InAlAs metamorphic buffer at different excitation wavelengths. J. Lumin. 2020, 226, 117412. [Google Scholar] [CrossRef]
- Mansour, H.; Guyon, J.; Crimp, M.A.; Gey, N.; Beausir, B.; Maloufi, N. Accurate electron channeling contrast analysis of dislocations in fine grained bulk materials. Scr. Mater. 2014, 84–85, 11–14. [Google Scholar] [CrossRef]
- Mansour, H.; Crimp, M.A.; Gey, N.; Iltis, X.; Maloufi, N. Dislocation analysis of a complex sub-grain boundary in UO2 using accurate electron channelling contrast imaging in a scanning electron microscope. Ceram. Int. 2019, 45, 18666–18671. [Google Scholar] [CrossRef]
- Guyon, J.; Mansour, H.; Gey, N.; Crimp, M.A.; Chalal, S.; Maloufi, N. Sub-micron resolution selected area electron channeling patterns. Ultramicroscopy 2015, 149, 34–44. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kriaa, H.; Guitton, A.; Maloufi, N. Fundamental and experimental aspects of diffraction for characterizing dislocations by electron channeling contrast imaging in scanning electron microscope. Sci. Rep. 2017, 7, 9742. [Google Scholar] [CrossRef] [Green Version]
- Kriaa, H.; Guitton, A.; Maloufi, N. Modeling dislocation contrasts obtained by accurate-Electron Channeling Contrast Imaging for characterizing deformation mechanisms in bulk materials. Materials 2019, 12, 1587. [Google Scholar] [CrossRef] [Green Version]
- Guitton, A.; Kriaa, H.; Bouzy, E.; Maloufi, N. A dislocation-scale characterization of the evolution of deformation microstructures around nanoindentaion imprints in TiAl alloy. Materials 2018, 11, 305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Howie, A.; Whelan, M.J. Diffraction contrast of electron microscope images of crystal lattice defects. II. The development of a dynamical theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1961, 263, 217–237. [Google Scholar]
- Howie, A.; Whelan, M.J. Diffraction contrast of electron microscope images of crystal lattice defects. III. Results and experimental confirmation of the dynamical theory of dislocation image contrast. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 267, 206–230. [Google Scholar]
- Ichinokawa, T.; Nishimura, M.; Wada, H. Contrast reversals of pseudo-Kikuchi band and lines due to detector position in scanning electron microscopy. J. Phys. Soc. Jpn. 1974, 36, 221–226. [Google Scholar] [CrossRef]
- Mendis, B.G.; Barthel, J.; Findlay, S.D.; Allen, L.J. Inelastic Scattering in Electron Backscatter Diffraction and Electron Channeling Contrast Imaging. Microsc. Microanal. 2020, 26, 1147–1157. [Google Scholar] [CrossRef] [PubMed]
- Clarke, D.R.; Howie, A. Calculations of lattice defect images for scanning electron microscopy. Philos. Mag. 1971, 24, 959–971. [Google Scholar] [CrossRef]
- Spencer, J.P.; Humphreys, C.J.; Hirsch, P.B. A dynamical theory for the contrast of perfect and imperfect crystals in the scanning electron microscope using backscattered electrons. Philos. Mag. 1972, 26, 193–213. [Google Scholar] [CrossRef]
- Reimer, L.; Heilers, U.; Saliger, G. Kikuchi band contrast in diffraction patterns recorded by transmitted and backscattered electrons. Scanning 1986, 8, 101–118. [Google Scholar] [CrossRef]
- Wilkinson, A.J.; Hirsch, P.B. Electron diffraction based techniques in scanning electron microscopy of bulk materials. Micron 1997, 28, 279–308. [Google Scholar] [CrossRef] [Green Version]
- Dudarev, S.L.; Rez, P.; Whelan, M.J. Theory of electron backscattering from crystals. Phys. Rev. B Condens. Matter 1995, 51, 3397–3412. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, A. Model mechanisms in Kikuchi pattern formation from crystals. Cryst. Res. Technol. 2017, 52, 1600288. [Google Scholar] [CrossRef]
- Weidner, A.; Martin, S.; Klemm, V.; Martin, U.; Biermann, H. Stacking fault in high alloyed metastable austenitic cast steel observed by electron channeling contrast. Scr. Mater. 2011, 64, 513. [Google Scholar] [CrossRef]
- Williams, D.B.; Carter, C. Transmission Electron Microscopy; Springer: New York, NY, USA, 1996. [Google Scholar]
- Crimp, M.A.; Simkin, B.A.; Ng, B.C. Demonstration of the g center dot b x u=0 edge dislocation invisibility criterion for electron channelling contrast imaging. Phil. Mag. Let. 2001, 81, 833–837. [Google Scholar] [CrossRef]
- Hull, D.; Bacon, D.J. Introduction to Dislocations; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Reimer, L. Scanning Electron Microscopy; Physics of Image Formation and Microanalysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kriaa, H.; Guitton, A.; Maloufi, N. Modelling Electron Channeling Contrast Intensity of Stacking Fault and Twin Boundary Using Crystal Thickness Effect. Materials 2021, 14, 1696. https://doi.org/10.3390/ma14071696
Kriaa H, Guitton A, Maloufi N. Modelling Electron Channeling Contrast Intensity of Stacking Fault and Twin Boundary Using Crystal Thickness Effect. Materials. 2021; 14(7):1696. https://doi.org/10.3390/ma14071696
Chicago/Turabian StyleKriaa, Hana, Antoine Guitton, and Nabila Maloufi. 2021. "Modelling Electron Channeling Contrast Intensity of Stacking Fault and Twin Boundary Using Crystal Thickness Effect" Materials 14, no. 7: 1696. https://doi.org/10.3390/ma14071696
APA StyleKriaa, H., Guitton, A., & Maloufi, N. (2021). Modelling Electron Channeling Contrast Intensity of Stacking Fault and Twin Boundary Using Crystal Thickness Effect. Materials, 14(7), 1696. https://doi.org/10.3390/ma14071696






