Mechanical Behavior and Morphological Study of Polytetrafluoroethylene (PTFE) Composites under Static and Cyclic Loading Condition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods of Testing
3. Results and Discussion
3.1. Characteristics of Fillers
3.2. Static Tests
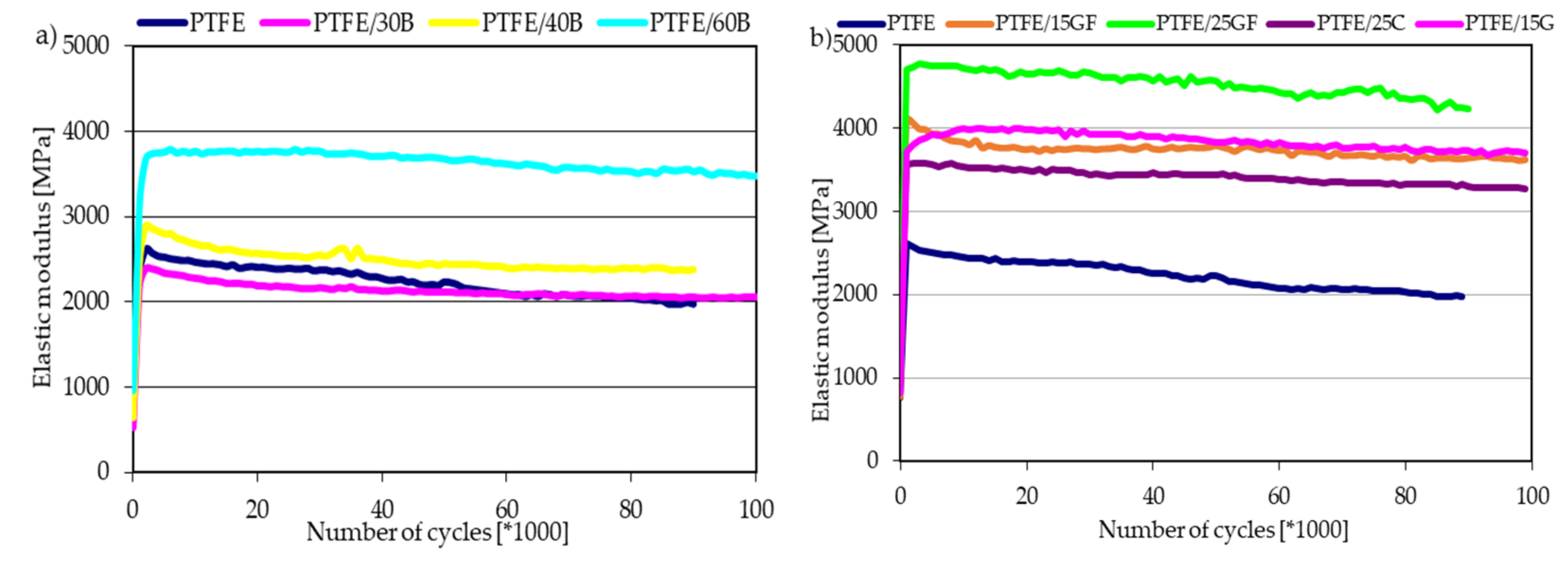
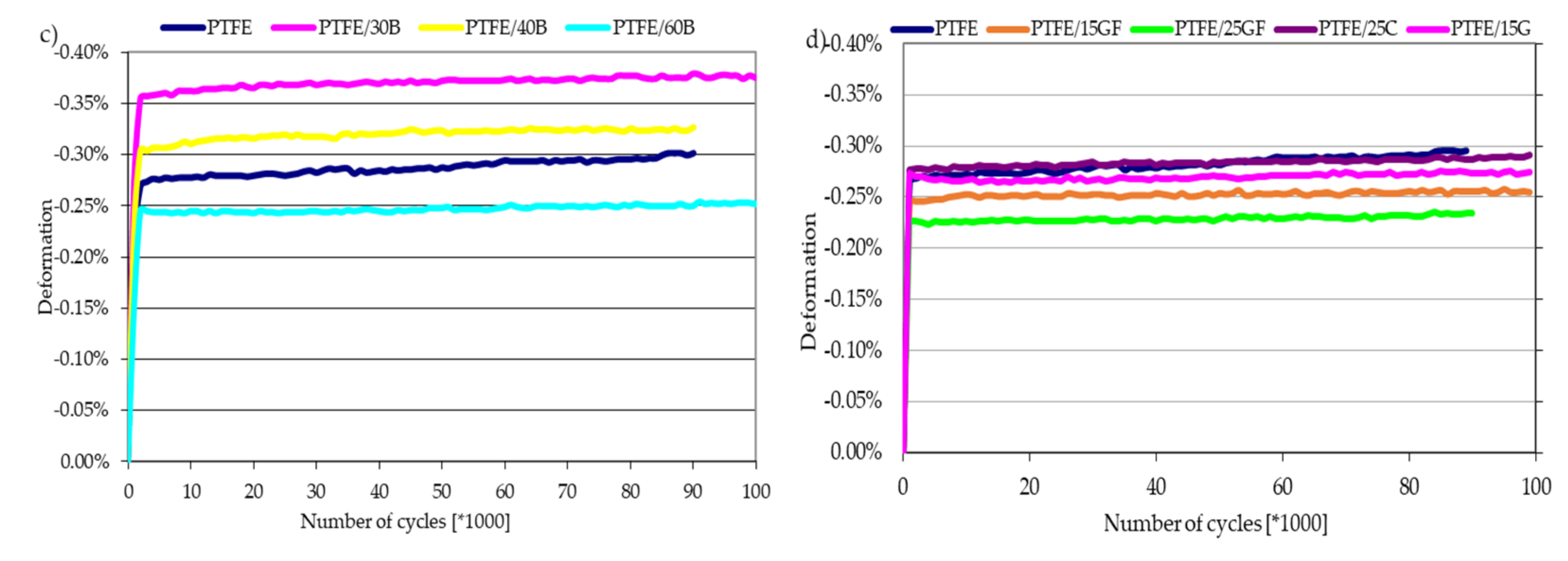
3.3. Dynamic Tests
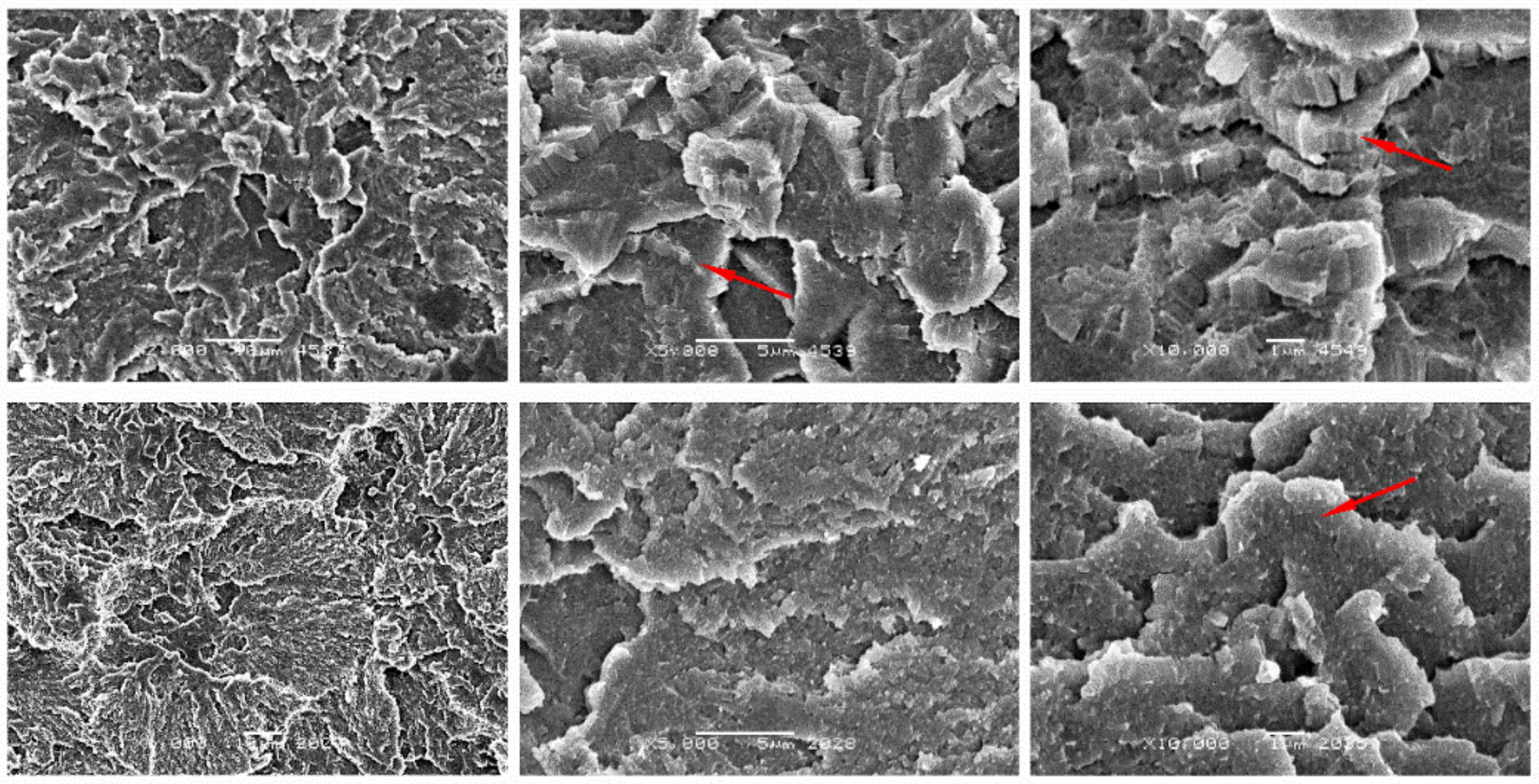
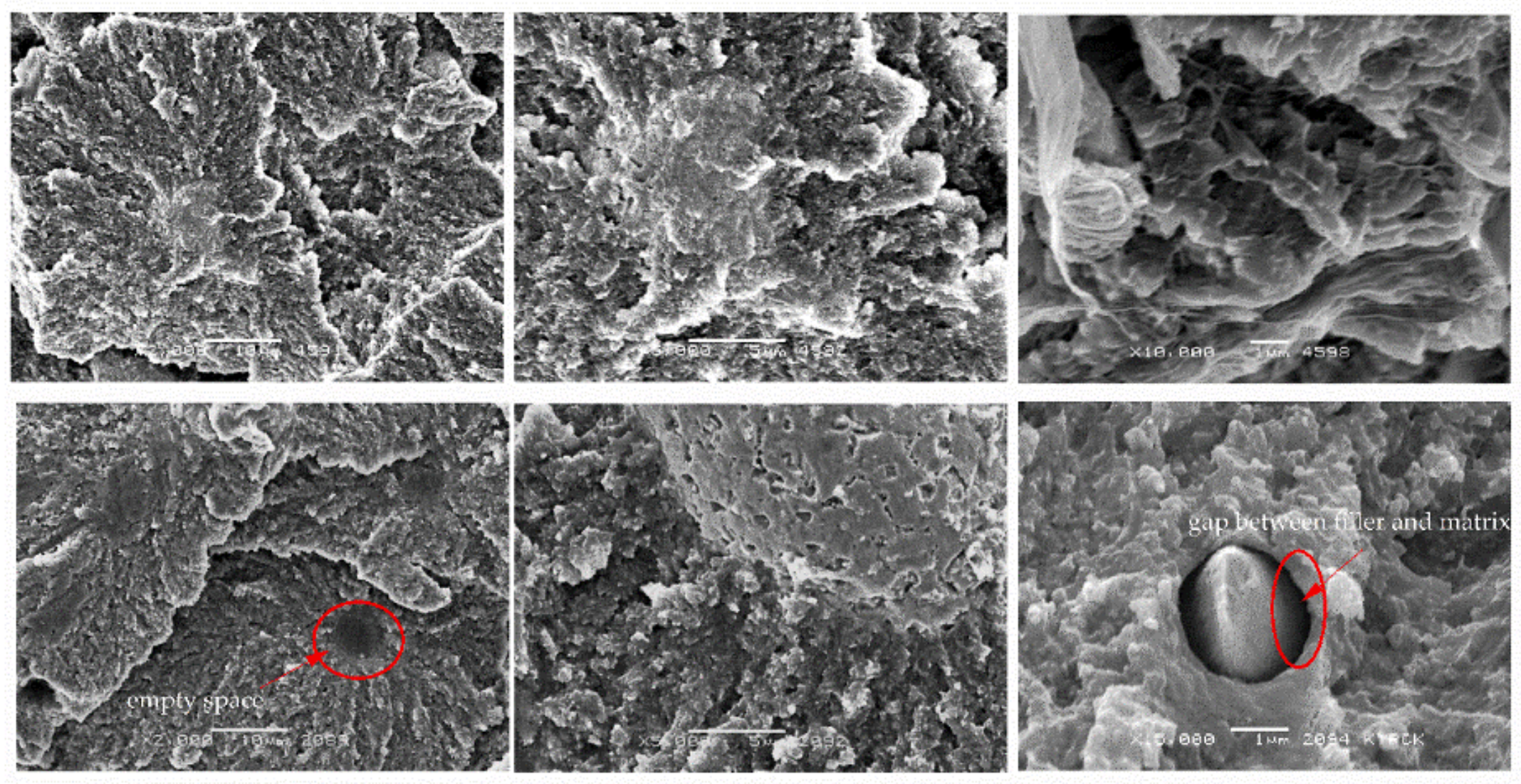
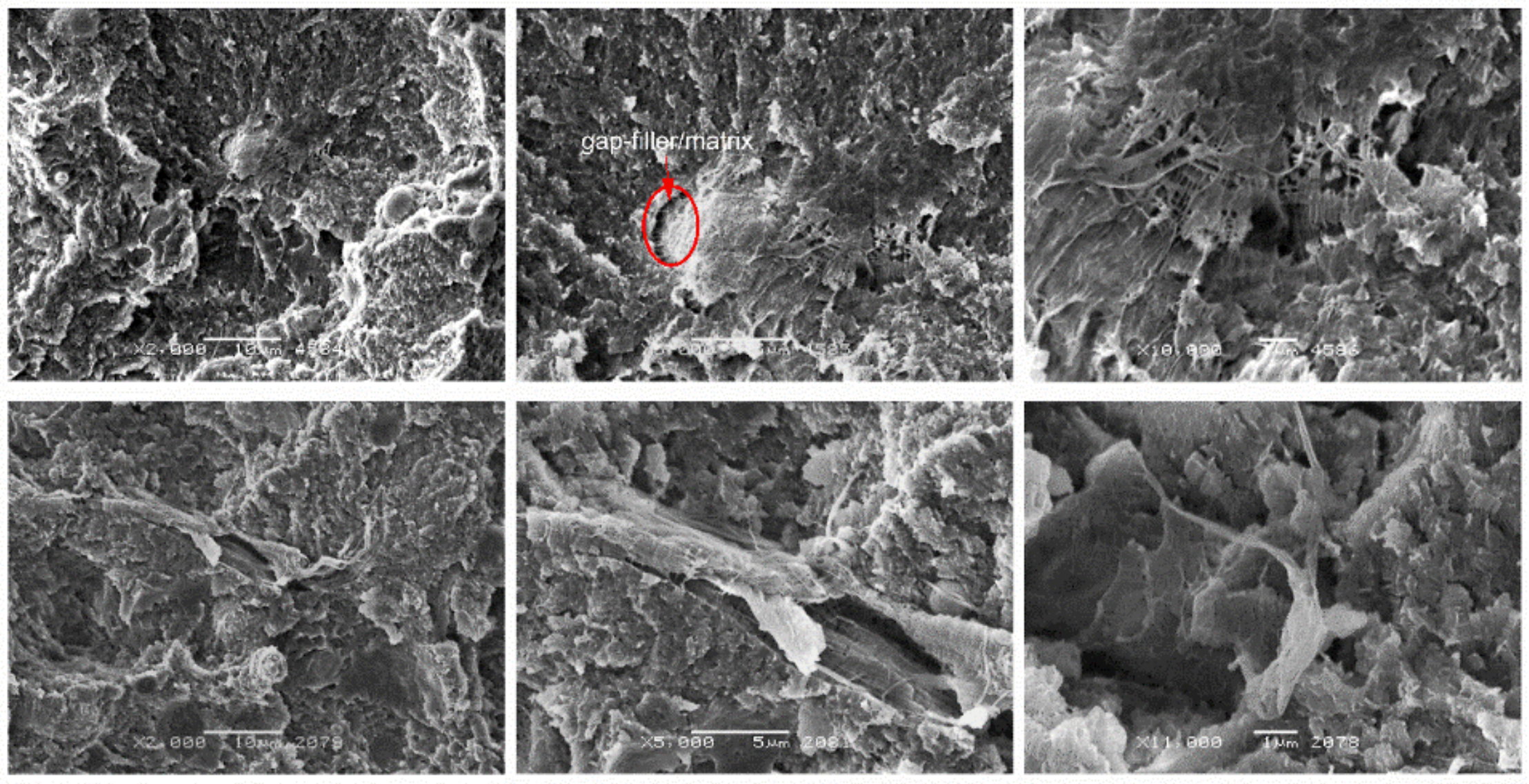
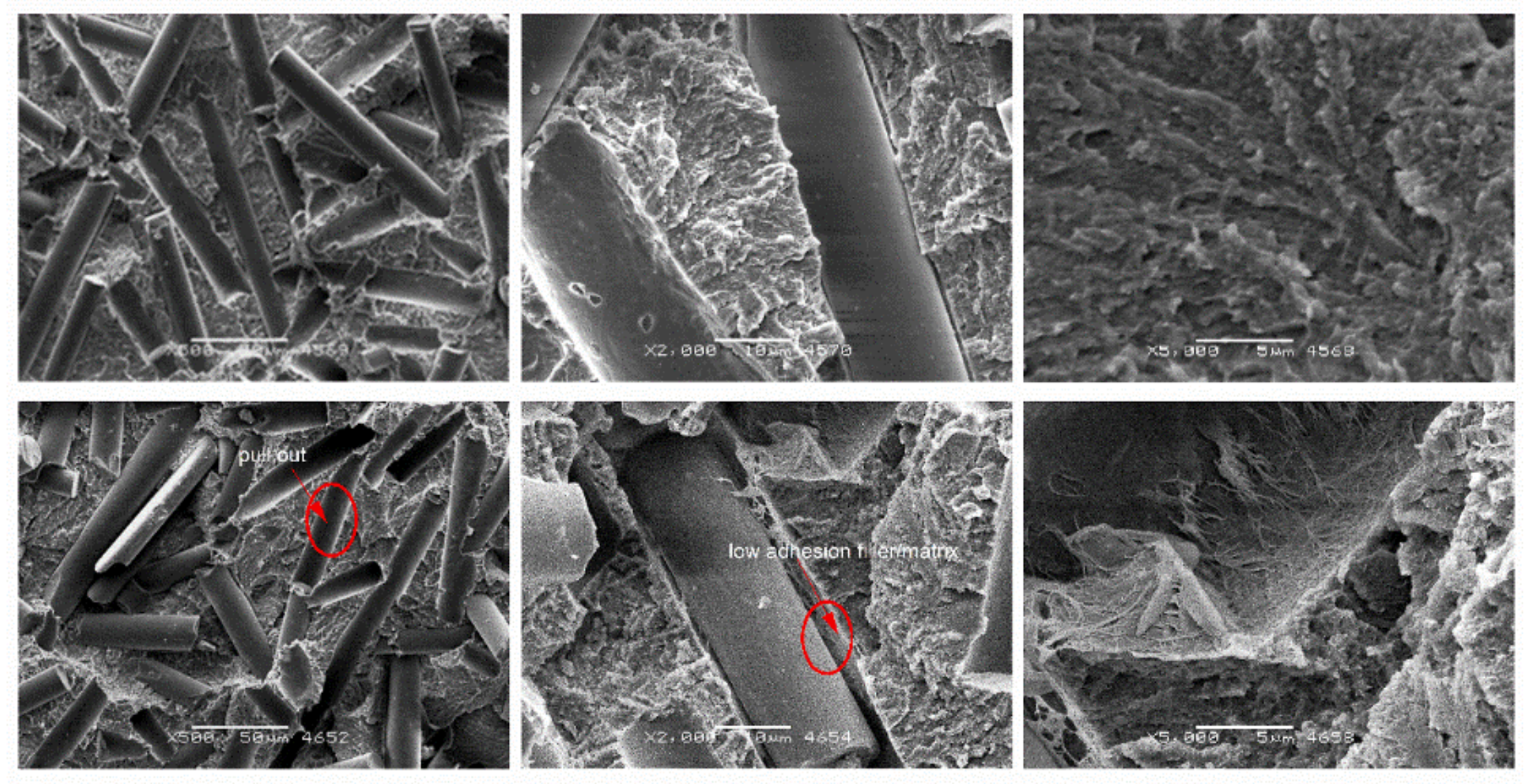
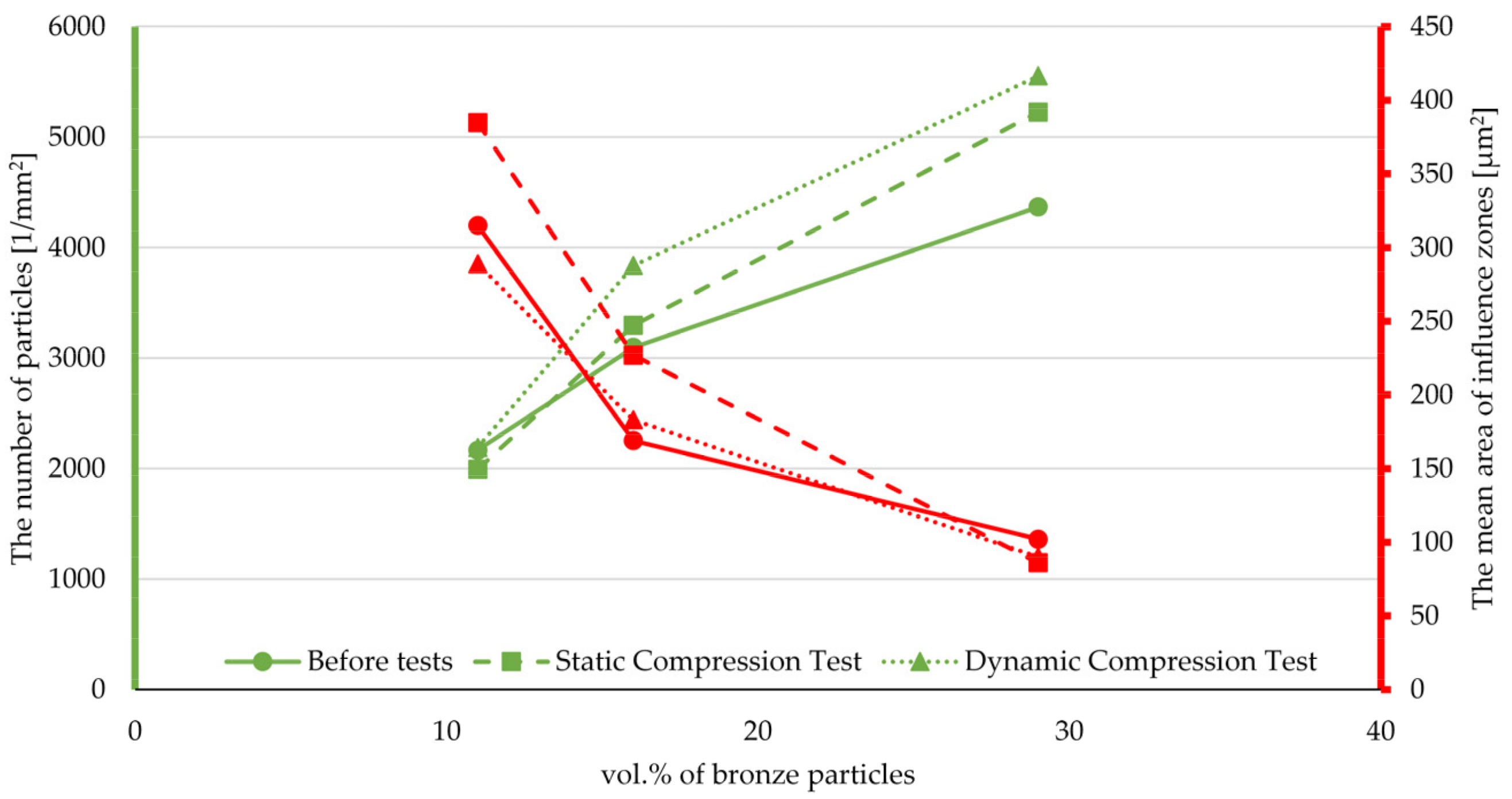
3.4. Morphological Analysis of Composites
4. Conclusions
- The addition of fillers had a positive effect on the obtained values during the static compression test: force at 2% and 15% of deformation increased from 3% (PTFE/30B) to 66% (PTFE/25C) and Young’s modulus increased for composites with mineral fillers max. by 69%;
- Larger particles with elongated shape caused a higher increase of Young’s modulus: PTFE/15G—802 MPa; PTFE/25GF—1291 MPa, where for small bronze particles—534 MPa;
- As the volume of the fillers content increased, the tendency for plastic deformation decreased;
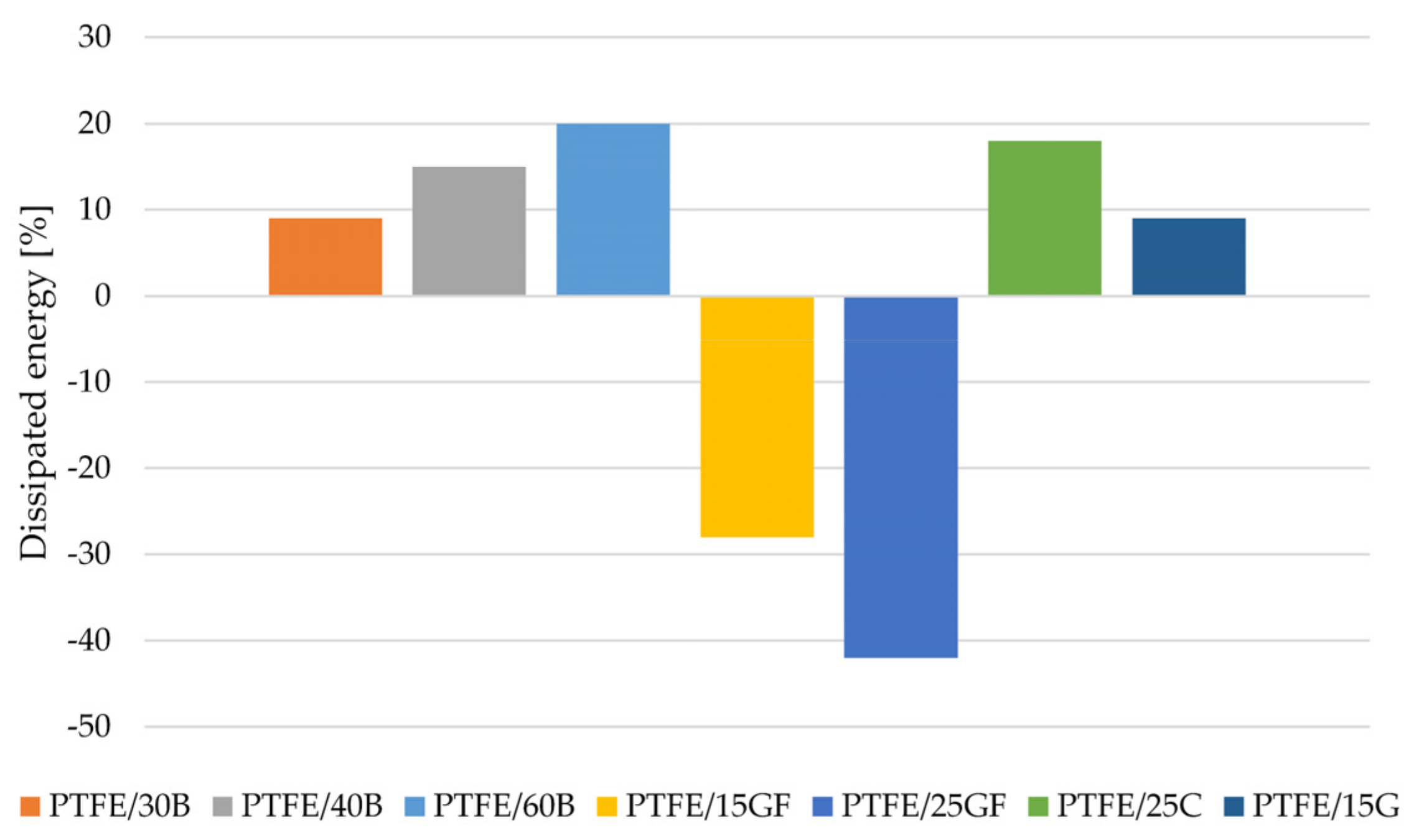
- Mechanical energy dissipation tests for high stress levels (100,000 cycles) have shown that pure PTFE has the surprising ability to increase its ability to dissipate mechanical energy with increasing number of cycles.
- The addition of bronze powder to PTFE further improves the ability of such composites to dissipate energy with increasing mass fractions of the filler. This confirms the possibility of their use in friction junctions.
- The addition of chopped glass fiber reduces the natural creep tendency of PTFE more than graphite or coke, especially under long-term loads, while increasing the values of their modulus of elasticity and compressive strength for such composites.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, B.H.; Yin, J.P.; Cui, Z.Q.; Liu, T.X. Improved Dynamic Mechanical Properties of Modified PTFE Jet Penetrating Charge with Shell. Strength Mater. 2016, 48, 82–89. [Google Scholar] [CrossRef]
- Theiler, G.; Hübner, W.; Gradt, T.; Klein, P.; Friedrich, K. Friction and wear of PTFE composites at cryogenic temperatures. Tribol. Int. 2002, 35, 449–458. [Google Scholar] [CrossRef]
- Elaboudi, I.; Mdarhri, A.; Brosseau, C.; Nourdine, A.; Rzaizi, M.; Servant, L. Comparing the sorption kinetics of poly-tetrafluoroethylene processed either by extrusion or spark plasma sintering. Polymer 2020, 190, 122192. [Google Scholar] [CrossRef]
- Wang, H.; Qi, X.; Zhang, W.; Dong, Y.; Fan, B.; Zhang, Y. Tribological properties of PTFE/Kevlar fabric composites under heavy loading. Tribol. Int. 2020, 151, 106507. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, N.; Wang, Y.; Yao, Y.; Xiao, H.; Jia, J.; Lv, H.; Zhang, D. Preparation and tribological properties of hybrid PTFE/Kevlar fabric self-lubricating composites. Surf. Coat. Technol. 2019, 361, 196–205. [Google Scholar] [CrossRef]
- Conte, M.; Igartua, A. Study of PTFE composites tribological behavior. Wear 2012, 296, 568–574. [Google Scholar] [CrossRef]
- Tevruz, T. Tribological behaviours of bronze-filled polytetrafluoroethylene dry journal bearings. Wear 1999, 230, 61–69. [Google Scholar] [CrossRef]
- Barylski, A.; Swinarew, A.S.; Aniołek, K.; Kaptacz, S.; Gabor, J.; Stanula, A.; Waśkiewicz, Z.; Knechtle, B. Tribological and Mechanical Behavior of Graphite Composites of Polytetrafluoroethylene (PTFE) Irradiated by the Electron Beam. Polymer 2020, 12, 1676. [Google Scholar] [CrossRef]
- Suh, J.; Bae, D. Mechanical properties of polytetrafluoroethylene composites reinforced with graphene nanoplatelets by solid-state processing. Compos. Part B Eng. 2016, 95, 317–323. [Google Scholar] [CrossRef]
- Zhang, Y.; Kou, K.; Pan, C.; Li, Z.; Ji, T. Effect of tensile rates on thermal and mechanical properties of porous PTFE composites. J. Appl. Polym. Sci. 2019, 136. [Google Scholar] [CrossRef]
- Vasilev, A.P.; Struchkova, T.S.; Nikiforov, L.A.; Okhlopkova, A.A.; Grakovich, P.N.; Le Shim, E.; Cho, J.-H. Mechanical and Tribological Properties of Polytetrafluoroethylene Composites with Carbon Fiber and Layered Silicate Fillers. Molecules 2019, 24, 224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shanmugam, V.; Das, O.; Babu, K.; Marimuthu, U.; Veerasimman, A.; Johnson, D.J.; Neisiany, R.E.; Hedenqvist, M.S.; Ramakrishna, S.; Berto, F. Fatigue behaviour of FDM-3D printed polymers, polymeric composites and architected cellular materials. Int. J. Fatigue 2021, 143, 106007. [Google Scholar] [CrossRef]
- Shah, Q.M.Z.; Chowdhury, M.A.; Kowser, A. Failure Mechanism of Polytetrafluoroethylene Under Friction Fatigue. J. Fail. Anal. Prev. 2019, 19, 245–249. [Google Scholar] [CrossRef]
- Kumar, V.; Wu, R.-R.; Lee, D.-J. Morphological aspects of carbon nanofillers and their hybrids for actuators and sensors. Polym. Compos. 2019, 40, E373–E382. [Google Scholar] [CrossRef]
- Qing, H. The Influence of Particle Shapes on Strength and Damage Properties of Metal Matrix Composites. J. Nanosci. Nanotechnol. 2015, 15, 5741–5748. [Google Scholar] [CrossRef]
- Lebar, A.; Aguiar, R.; Oddy, A.; Petel, O.E. Particle surface effects on the spall strength of particle-reinforced polymer matrix composites. Int. J. Impact Eng. 2021, 150, 103801. [Google Scholar] [CrossRef]
- Kumar, V.; Lee, G.; Singh, K.; Choi, J.; Lee, D.-J. Structure-property relationship in silicone rubber nanocomposites reinforced with carbon nanomaterials for sensors and actuators. Sens. Actuators A Phys. 2020, 303, 111712. [Google Scholar] [CrossRef]
- Wojnar, L. Struktura i Właściwości Kompozytów na Osnowie Termoplastów; Politechnika Krakowska: Krakow, Poland, 2005. [Google Scholar]
- Österle, W.; Dmitriev, A.; Wetzel, B.; Zhang, G.; Häusler, I.; Jim, B. The role of carbon fibers and silica nanoparticles on friction and wear reduction of an advanced polymer matrix composite. Mater. Des. 2016, 93, 474–484. [Google Scholar] [CrossRef]
- Frick, A.; Sich, D.; Heinrich, G.; Stern, C.; Gössi, M.; Tervoort, T.A. Relationship between Structure and Mechanical Properties of Melt Processable PTFE: Influence of Molecular Weight and Comonomer Content. Macromol. Mater. Eng. 2012, 298, 954–966. [Google Scholar] [CrossRef]
- Kuciel, S.; Bazan, P.; Liber-Kneć, A.; Gądek-Moszczak, A. Physico-Mechanical Properties of the Poly(oxymethylene) Composites Reinforced with Glass Fibers under Dynamical Loading. Polymer 2019, 11, 2064. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aglan, H.; Gan, Y.; El-Hadik, M.; Faughnan, P.; Bryan, C. Evaluation of the fatigue fracture resistance of unfilled and filled polytetrafluoroethylene materials. J. Mater. Sci. 1999, 34, 83–97. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, J.; Zhu, Y.; Wang, X.; Jin, Y. Microstructure and Properties of Polytetrafluoroethylene Composites Modified by Carbon Materials and Aramid Fibers. Coatings 2020, 10, 1103. [Google Scholar] [CrossRef]
- Rae, P.; Brown, E. The properties of poly(tetrafluoroethylene) (PTFE) in tension. Polymer 2005, 46, 8128–8140. [Google Scholar] [CrossRef]
- Nunes, L.; Paciornik, S.; D’Almeida, J. Evaluation of the damaged area of glass-fiber-reinforced epoxy-matrix composite materials submitted to ballistic impacts. Compos. Sci. Technol. 2004, 64, 945–954. [Google Scholar] [CrossRef]
- Schubert, D.W.; Werner, S.; Hahn, I.; Solovieva, V. Effect of particle size and size distribution on the permeability of soft magnetic liquid silicone rubber composites. Compos. Sci. Technol. 2019, 177, 26–33. [Google Scholar] [CrossRef]

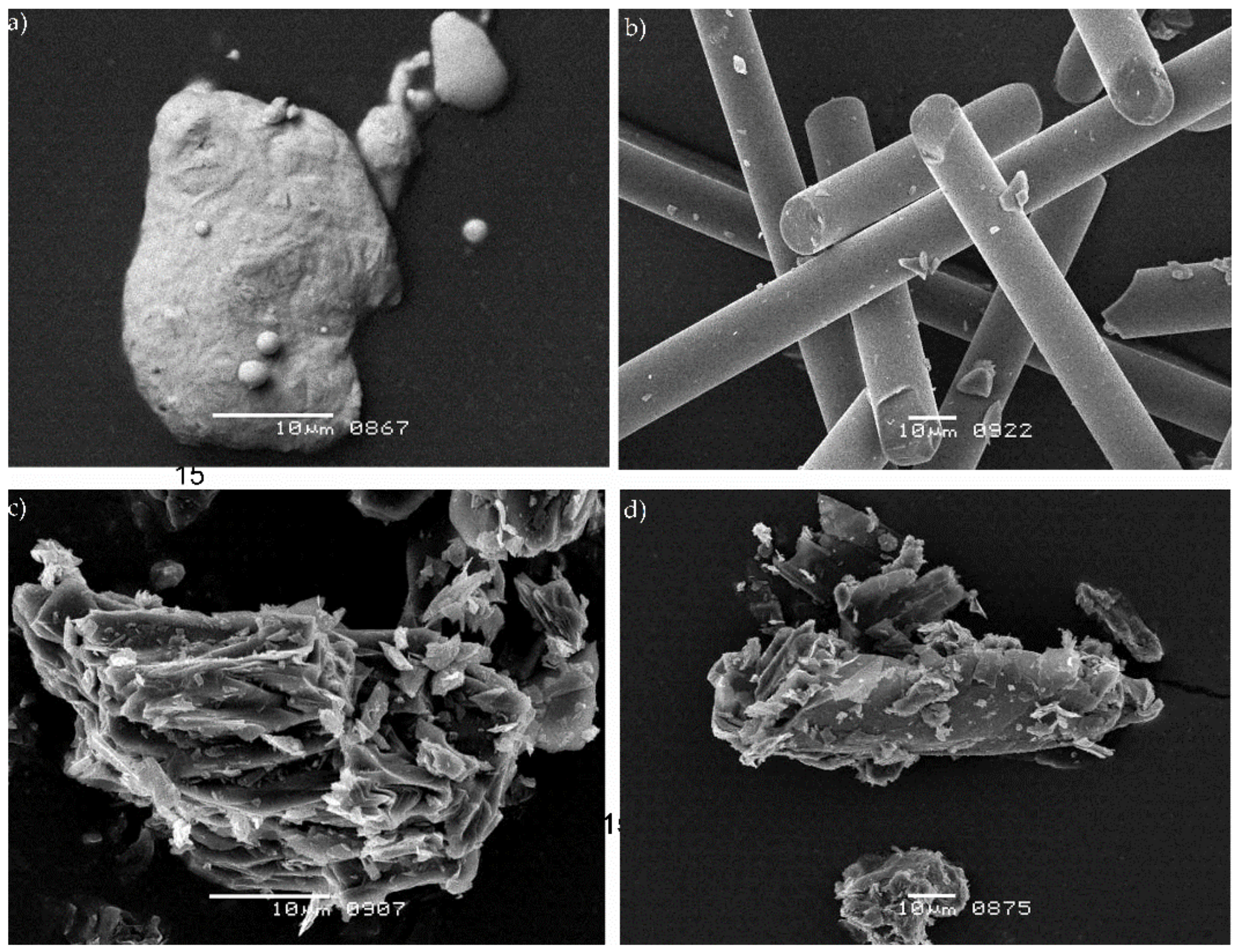




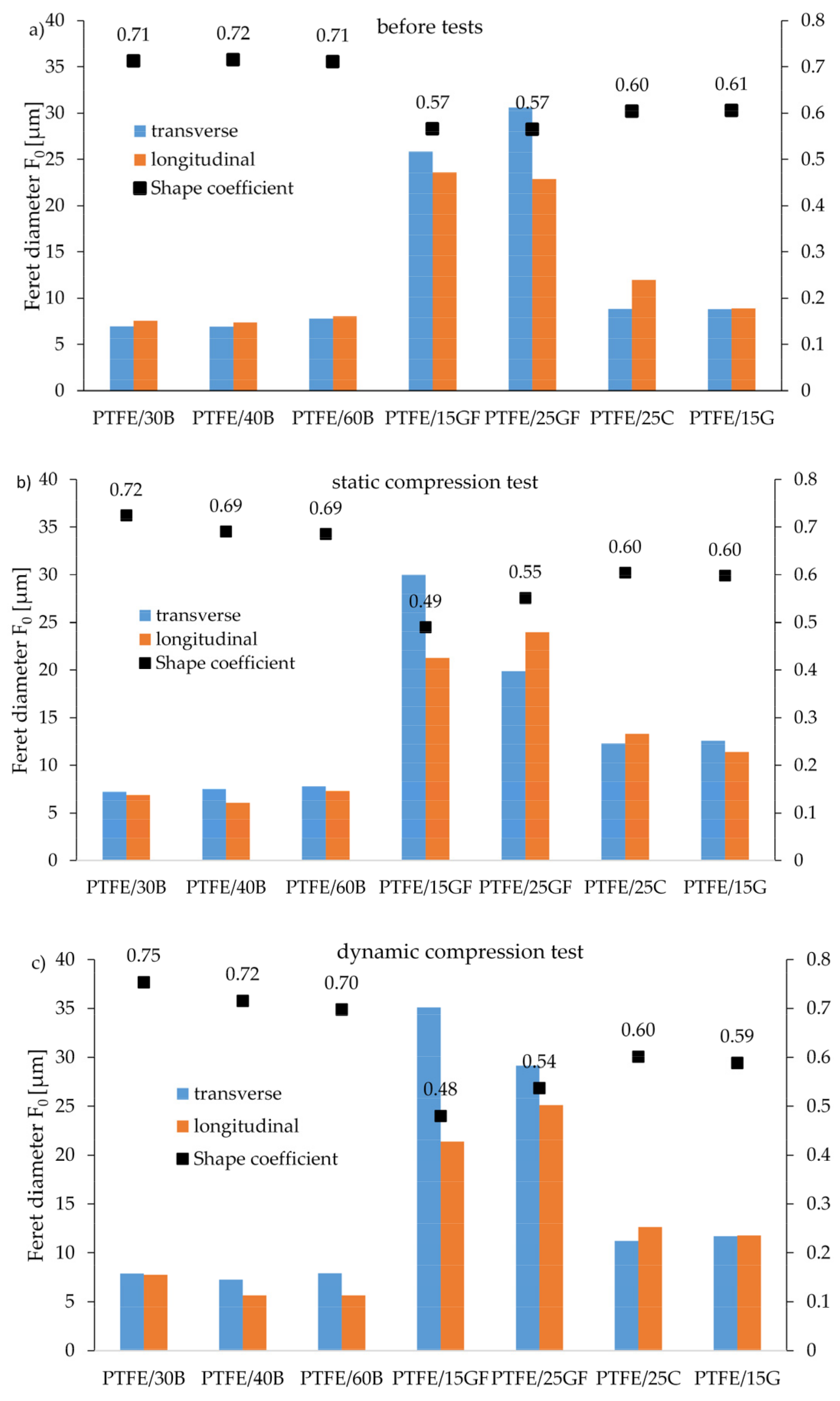
| Abbreviation | Composition |
|---|---|
| PTFE | 100 wt.% polytetrafluoroethylene |
| PTFE/30B | 70 wt.% polytetrafluoroethylene + 30 wt.% (11 vol.%) bronze particles |
| PTFE/40B | 60 wt.% polytetrafluoroethylene + 40 wt.% (16 vol.%) bronze particles |
| PTFE/60B | 40 wt.% polytetrafluoroethylene + 60 wt.% (29 vol.%) bronze particles |
| PTFE/15GF | 85 wt.% polytetrafluoroethylene + 15 wt.% (14 vol.%) glass fibers |
| PTFE/25GF | 75 wt.% polytetrafluoroethylene + 25 wt.% (23 vol.%) glass fibers |
| PTFE/25C | 75 wt.% polytetrafluoroethylene + 25 wt.% (29 vol.%) coke flakes |
| PTFE/15G | 85 wt.% polytetrafluoroethylene + 15 wt.% (15 vol.%) graphite particles |
| Type | Static Compression Test | Static Tensile Test | ||||
|---|---|---|---|---|---|---|
| Young’s Modulus, MPa | Force at 2% Deformation, kN | Force at 15% Deformation, kN | Breaking Stress, MPa | Strain at Break, % | Breaking Stress, MPa | |
| PTFE | 766 ± 29 | 2.22 ± 0.10 | 3.38 ± 0.14 | 30.0 ± 1.2 | 416 ± 20 | 766 ± 29 |
| PTFE/30B | 534 ± 23 | 2.28 ± 0.09 | 3.25 ± 0.13 | 39.9 ± 1.7 | 383 ± 17 | 534 ± 23 |
| PTFE/40B | 634 ± 28 | 2.55 ± 0.11 | 3.75 ± 0.16 | 32.4 ± 1.4 | 367 ± 15 | 634 ± 28 |
| PTFE/60B | 963 ± 45 | 3.15 ± 0.13 | 4.80 ± 0.20 | 22.0 ± 0.9 | 181 ± 8 | 963 ± 45 |
| PTFE/15GF | 781 ± 37 | 2.68 ± 0.11 | 4.11 ± 0.19 | 17.0 ± 0.7 | 250 ± 11 | 781 ± 37 |
| PTFE/25GF | 1291 ± 61 | 2.46 ± 0.11 | 3.65 ± 0.17 | 15.0 ± 0.7 | 200 ± 8 | 1291 ± 61 |
| PTFE/25C | 952 ± 42 | 3.22 ± 0.14 | 5.6 ± 0.25 | 12.0 ± 0.5 | 100 ± 4 | 952 ± 42 |
| PTFE/15G | 802 ± 38 | 3.17 ± 0.13 | 5.25 ± 0.23 | 13.0 ± 0.5 | 200 ± 9 | 802 ± 38 |
| Type | The Number of Particles (1/mm2) | Influence Zones (µm2) | ||||
|---|---|---|---|---|---|---|
| Before Test | Static Compression Test | Dynamic Compression Test | Before Test | Static Compression Test | Dynamic Compression Test | |
| PTFE/30B | 2167 | 1993 | 2192 | 315 | 385 | 289 |
| PTFE/40B | 3097 | 3297 | 3836 | 169 | 227 | 183 |
| PTFE/60B | 4368 | 5226 | 5552 | 102 | 86 | 90 |
| PTFE/15GF | 184 | 148 | 198 | 3328 | 4525 | 3401 |
| PTFE/25GF | 240 | 331 | 293 | 2762 | 1786 | 1992 |
| PTFE/25C | 1672 | 2064 | 1800 | 218 | 147 | 189 |
| PTFE/15G | 1326 | 2301 | 1600 | 269 | 125 | 227 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazur, K.; Gądek-Moszczak, A.; Liber-Kneć, A.; Kuciel, S. Mechanical Behavior and Morphological Study of Polytetrafluoroethylene (PTFE) Composites under Static and Cyclic Loading Condition. Materials 2021, 14, 1712. https://doi.org/10.3390/ma14071712
Mazur K, Gądek-Moszczak A, Liber-Kneć A, Kuciel S. Mechanical Behavior and Morphological Study of Polytetrafluoroethylene (PTFE) Composites under Static and Cyclic Loading Condition. Materials. 2021; 14(7):1712. https://doi.org/10.3390/ma14071712
Chicago/Turabian StyleMazur, Karolina, Aneta Gądek-Moszczak, Aneta Liber-Kneć, and Stanisław Kuciel. 2021. "Mechanical Behavior and Morphological Study of Polytetrafluoroethylene (PTFE) Composites under Static and Cyclic Loading Condition" Materials 14, no. 7: 1712. https://doi.org/10.3390/ma14071712
APA StyleMazur, K., Gądek-Moszczak, A., Liber-Kneć, A., & Kuciel, S. (2021). Mechanical Behavior and Morphological Study of Polytetrafluoroethylene (PTFE) Composites under Static and Cyclic Loading Condition. Materials, 14(7), 1712. https://doi.org/10.3390/ma14071712







