A 95-Year-Old Concrete Arch Bridge: From Materials Characterization to Structural Analysis
Abstract
1. Introduction
2. Materials and Methods
3. Laboratory Test Results and Discussion
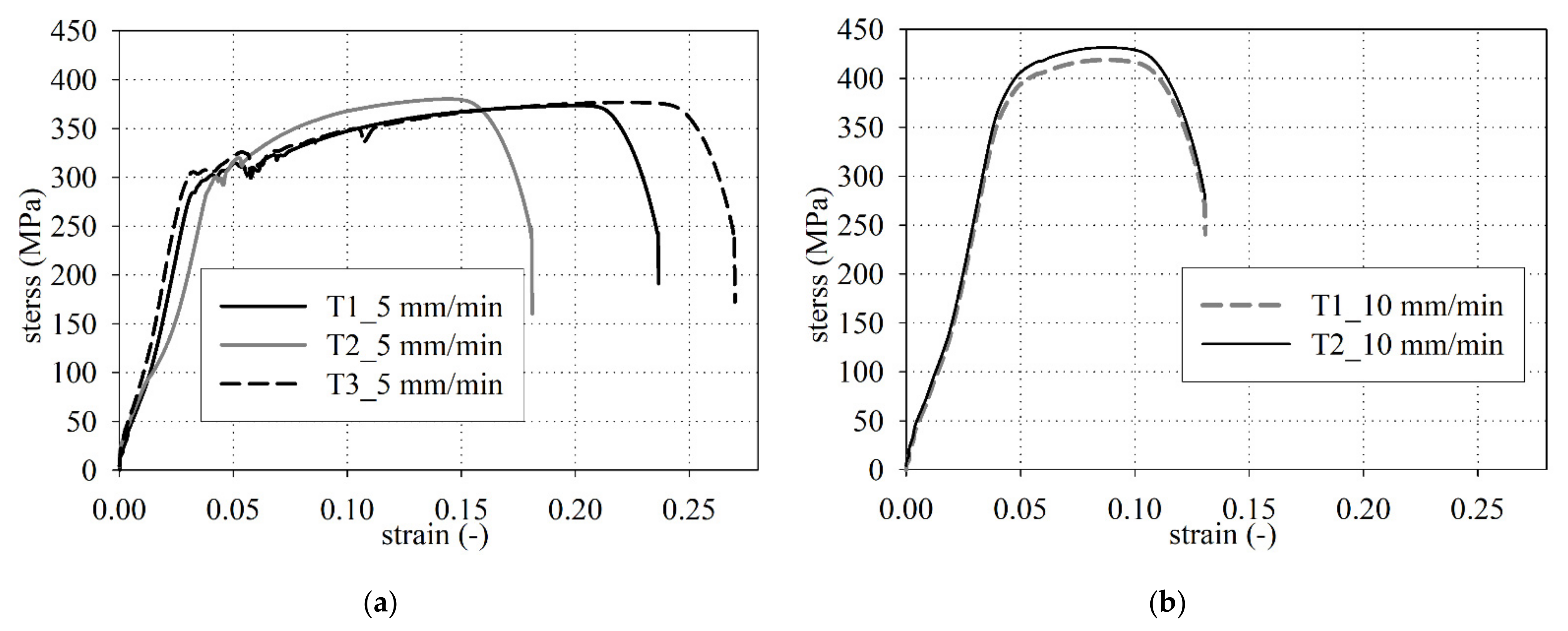
3.1. Reinforced Steel Tensile Tests
3.2. Uniaxial Compressive Tests and Dry Density
3.3. Modulus of Elasticity and Durability
4. Structural Analysis
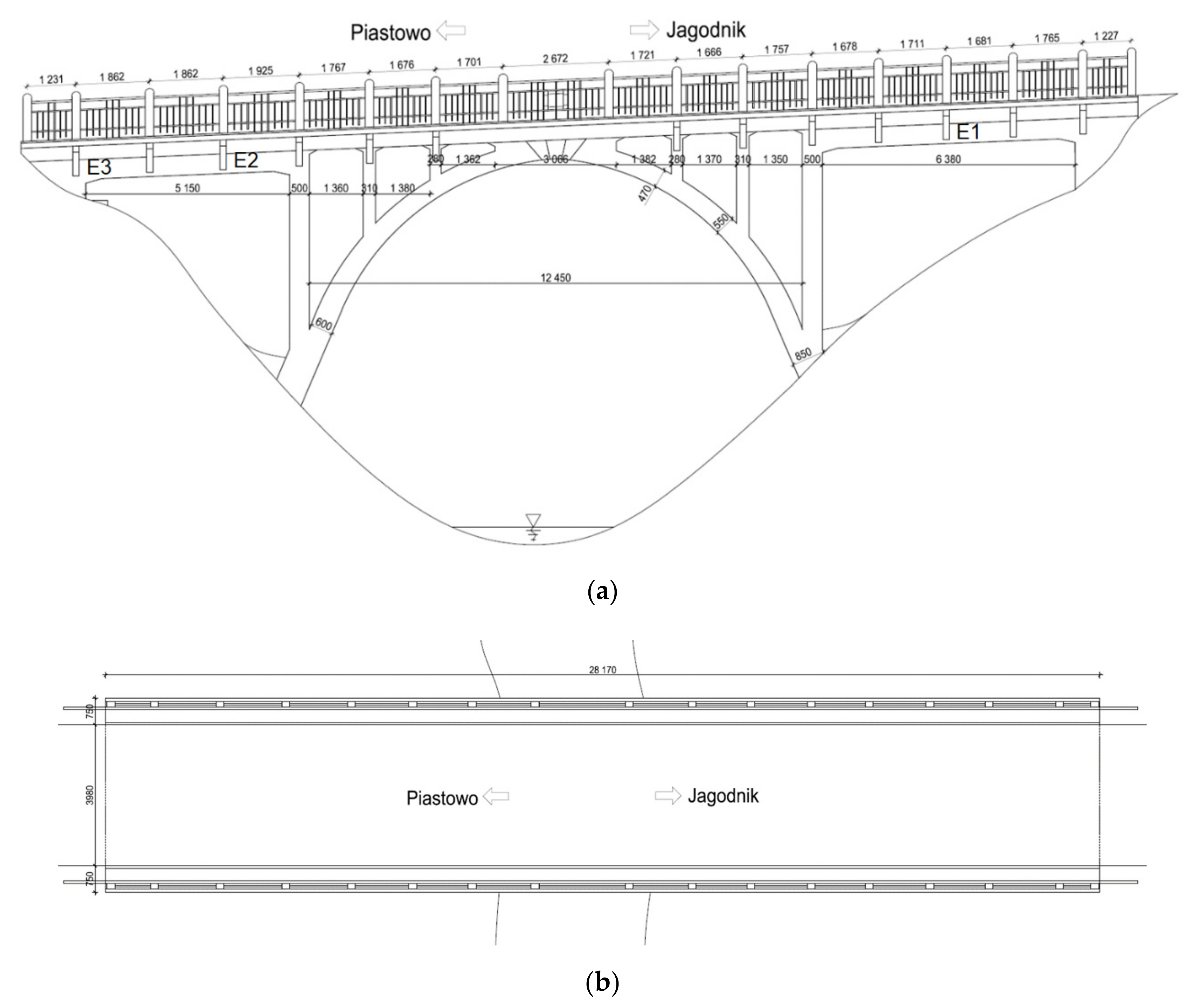
4.1. Description of FEM Model
4.2. Results of Structural Analysis
5. Conclusions
- The investigated core samples of the 95-year-old concrete exhibit a high compressive strength scatter from 14.9 MPa to 29.7 MPa, see Table 1. These results serve as evidence of the very non-homogenous distribution of concrete strength in the old concrete arch bridge.
- The concrete specimens tested in compression show that there is a large number of impurities in the old concrete (i.e., pieces of timber and clay, coarse aggregates, large stones) with cavities and soft pockets. The scatter in the mechanical properties is, therefore, due to either very low quality-control in the building phase or very poor concrete technology based on portable concrete mixers and hand-made proportioning of concrete constituents.
- The in-situ compressive cube strength fck,is,cube equals 16.9 MPa, according to EN 13791 [41] standard. Calculated and applied in structural analysis, the design compressive strength of 95-year-old concrete fcd equals 9.7 MPa.
- The reinforced steel tensile tests confirm that the characteristic yield strength specified in laboratory tests (fyk = 291 ± 7 MPa) corresponds to the guidelines [36] issued in the time of the 95-year-old arch bridge construction.
- The highest stress in steel rebars of structural cross-section is approximately equal to 57% of the design yield strength of reinforcement, the maximum compressive stress in the original parts of the arch bridge is approximately equal to 96% of the design compressive strength of concrete.
- The largest displacement under the SLS combination of the traffic loadings satisfies the SLS condition according to o PN-S-10042 [66] standard. The determined largest deflections are five times less than the permissible deflection.
- The structural analysis confirmed the validity of the adopted design solutions. On top of the existing old deck structure, a new deck slab with pavement covers is designed and the entire surface of the old concrete is protected with repair mortars. The task of the new deck slab is not only to strengthen the structure but also to increase the resistance to present environmental influences and also the shear capacity of the deck slab. The higher strength class of concrete is designed and used to fulfill the EN 206 [47] standard requirement of the present exposure classes.
- The 95-year-old arch bridge satisfies bearing capacity (ULS) and SLS conditions, capable of carrying designed traffic loads class C according to PN-S-10030 [56] in extended working life.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. FEM Calculation Results

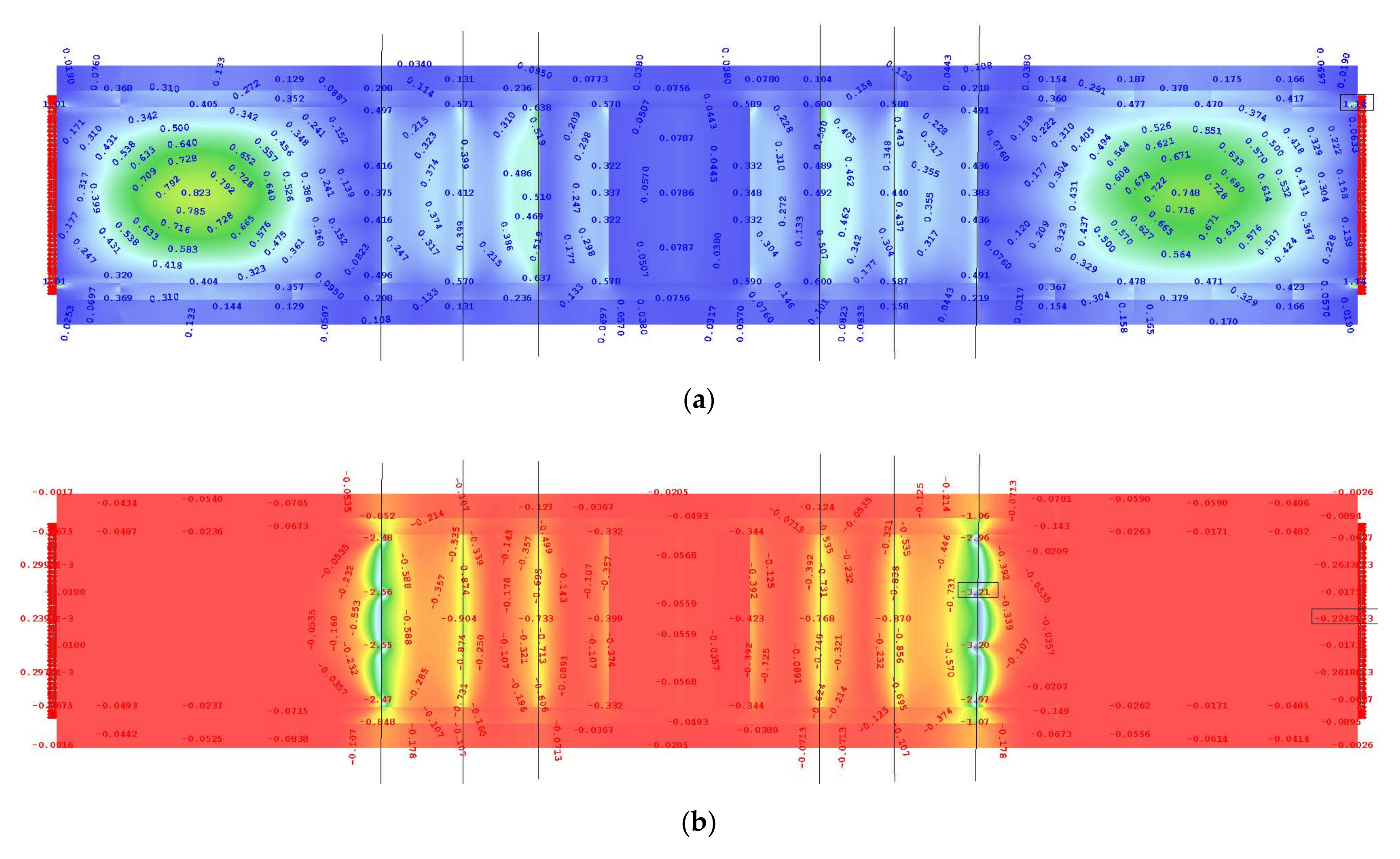

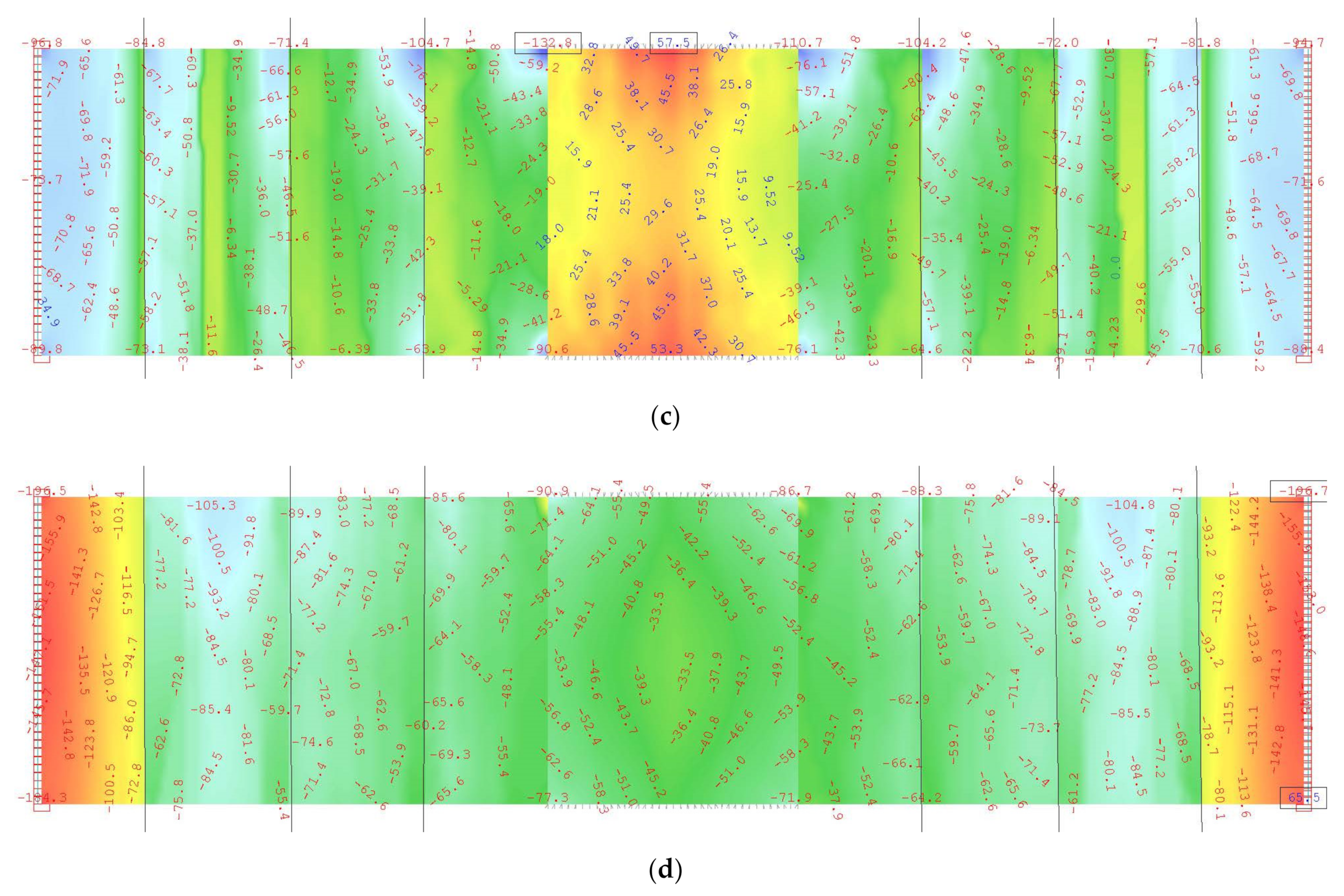
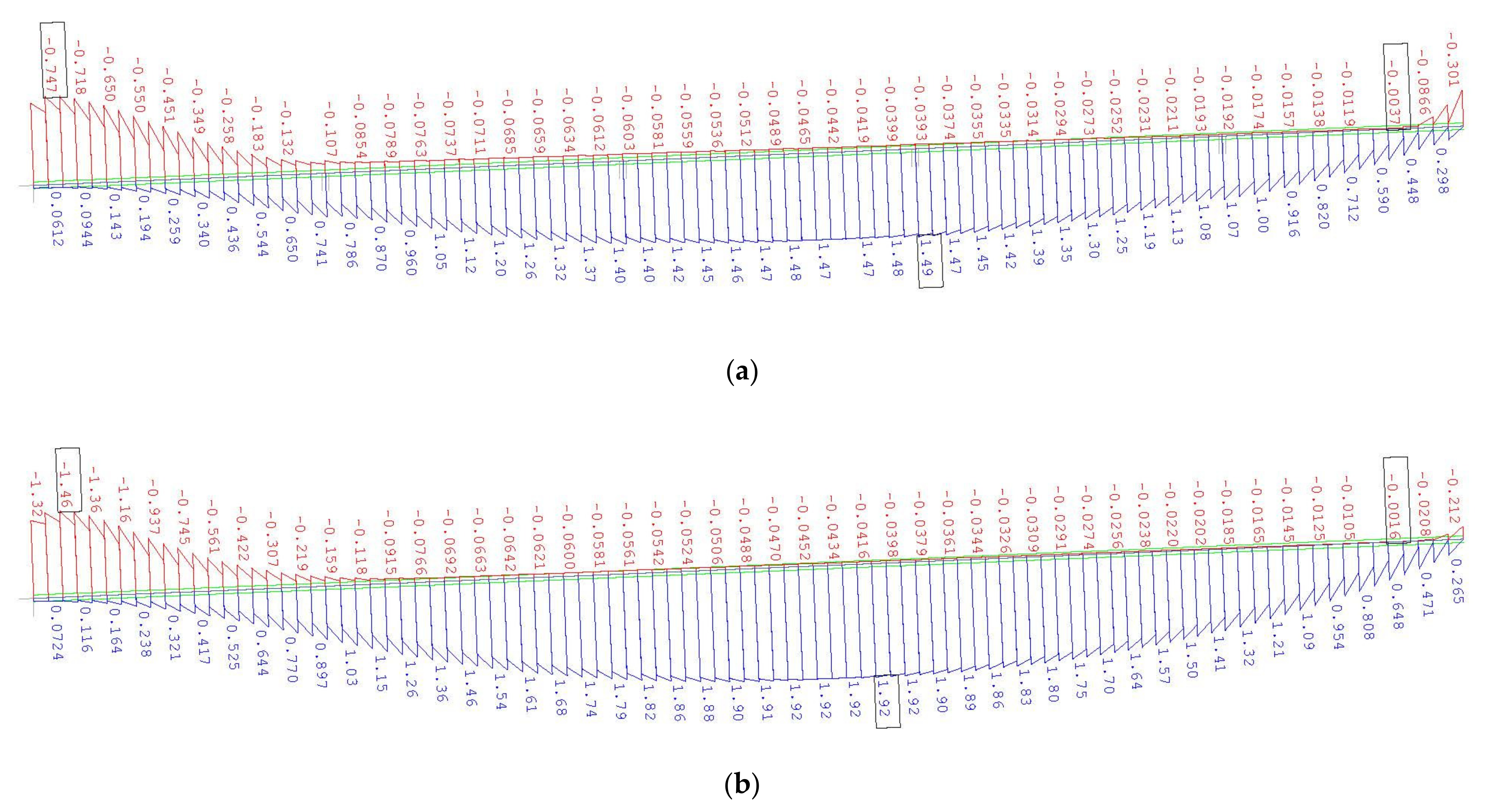


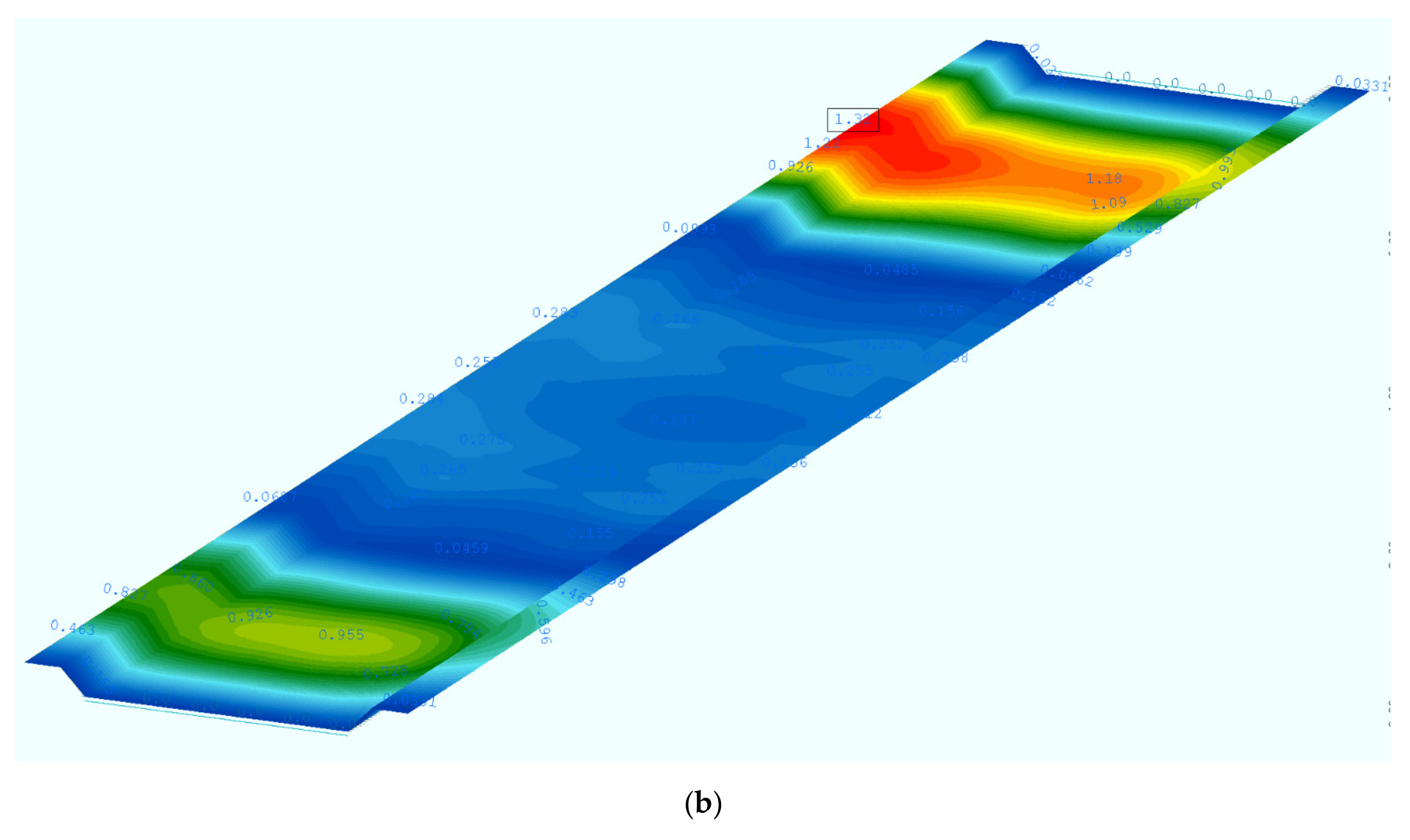
References
- Chen, B.; Su, J.; Lin, S.; Chen, G.; Zhuang, Y.; Tabatabai, H. Development and application of concrete arch bridges in China. J. Asian Concr. Fed. 2017, 3, 12–19. [Google Scholar] [CrossRef]
- Radić, J.; Kindij, A.; Mandić, A. History of Concrete Application in Development of Concrete and Hybriad Arch Bridges. In Proceedings of the Chinese-Croatian Joint Colloquium on Long Arch Bridges, Brijuni Islands, Croatia, 10–14 July 2008; Radić, J., Chen, B., Eds.; SECON HDGK: Zagreb, Croatia, 2008; Volume LONG ARCH, pp. 9–118. [Google Scholar]
- Omar, T.; Nehdi, M. Condition Assessment of Reinforced Concrete Bridges: Current Practice and Research Challenges. Infrastructures 2018, 3, 36. [Google Scholar] [CrossRef]
- Paulík, P.; Bačuvčík, M.; Brodňan, M.; Koteš, P.; Vičan, J. Reconstruction of the Oldest Reinforced Concrete Bridge in Slovakia in Krásno nad Kysucou. Procedia Eng. 2016, 156, 334–339. [Google Scholar] [CrossRef]
- Witzany, J.; Zigler, R. Rehabilitation Design of a Historic Concrete Arch Bridge in Prague from the Early 20th Century. J. Perform. Constr. Facil. 2020, 34, 04020056. [Google Scholar] [CrossRef]
- Hellebois, A.; Espion, B. Concrete properties of a 1904 Hennebique reinforced concrete viaduct. WIT Trans. Built Environ. 2011, 118, 589–600. [Google Scholar] [CrossRef]
- Sena-Cruz, J.; Ferreira, R.M.; Ramos, L.F.; Fernandes, F.; Miranda, T.; Castro, F. Luiz bandeira bridge: Assessment of a historical reinforced concrete (RC) bridge. Int. J. Archit. Herit. 2013, 7, 628–652. [Google Scholar] [CrossRef]
- Wolert, P.J.; Kolodziejczyk, M.K.; Stallings, J.M.; Nowak, A.S. Non-destructive Testing of a 100-Year-Old Reinforced Concrete Flat Slab Bridge. Front. Built Environ. 2020, 6, 1–12. [Google Scholar] [CrossRef]
- Czaderski, C.; Motavalli, M. 40-Year-old full-scale concrete bridge girder strengthened with prestressed CFRP plates anchored using gradient method. Compos. Part B Eng. 2007, 38, 878–886. [Google Scholar] [CrossRef]
- Pettigrew, C.S.; Barr, P.J.; Maguire, M.; Halling, M.W. Behavior of 48-Year-Old Double-Tee Bridge Girders Made with Lightweight Concrete. J. Bridg. Eng. 2016, 21, 04016054. [Google Scholar] [CrossRef]
- Gebauer, J.; Harnik, A.B. Microstructure and composition of the hydrated cement paste of an 84 year old concrete bridge construction. Cem. Concr. Res. 1975, 5, 163–169. [Google Scholar] [CrossRef]
- Papé, T.M.; Melchers, R.E. The effects of corrosion on 45-year-old pre-stressed concrete bridge beams. Struct. Infrastruct. Eng. 2011, 7, 101–108. [Google Scholar] [CrossRef]
- Dasar, A.; Hamada, H.; Sagawa, Y.; Yamamoto, D. Deterioration progress and performance reduction of 40-year-old reinforced concrete beams in natural corrosion environments. Constr. Build. Mater. 2017, 149, 690–704. [Google Scholar] [CrossRef]
- Khan, I.; François, R.; Castel, A. Structural performance of a 26-year-old corroded reinforced concrete beam. Eur. J. Environ. Civ. Eng. 2012, 16, 440–449. [Google Scholar] [CrossRef]
- Shu, J.; Bagge, N.; Nilimaa, J. Field Destructive Testing of a Reinforced Concrete Bridge Deck Slab. J. Bridg. Eng. 2020, 25, 04020067. [Google Scholar] [CrossRef]
- Turker, T. Structural evaluation of Aspendos (Belkis) Masonry Bridge. Struct. Eng. Mech. 2014, 50, 419–439. [Google Scholar] [CrossRef]
- Orlando, M.; Spinelli, P.; Vignoli, A. Structural analysis for the reconstruction design of the old bridge of Mostar. Adv. Archit. 2003, 15, 617–626. [Google Scholar]
- Domede, N.; Sellier, A.; Stablon, T. Structural analysis of a multi-span railway masonry bridge combining in situ observations, laboratory tests and damage modelling. Eng. Struct. 2013, 56, 837–849. [Google Scholar] [CrossRef]
- Pipinato, A.; Modena, C. Structural Analysis and Fatigue Reliability Assessment of the Paderno Bridge. Pract. Period. Struct. Des. Constr. 2010, 15, 109–124. [Google Scholar] [CrossRef]
- Cardinale, G.; Orlando, M. Structural Evaluation and Strengthening of a Reinforced Concrete Bridge. J. Bridg. Eng. 2004, 9, 35–42. [Google Scholar] [CrossRef]
- Richard, B.; Epaillard, S.; Cremona, C.; Elfgren, L.; Adelaide, L. Nonlinear finite element analysis of a 50 years old reinforced concrete trough bridge. Eng. Struct. 2010, 32, 3899–3910. [Google Scholar] [CrossRef]
- Zhang, J.; Li, C.; Xu, F.; Yu, X. Test and Analysis for Ultimate Load-Carrying Capacity of Existing Reinforced Concrete Arch Ribs. J. Bridg. Eng. 2007, 12, 4–12. [Google Scholar] [CrossRef]
- Lubowiecka, I.; Armesto, J.; Arias, P.; Lorenzo, H. Historic bridge modelling using laser scanning, ground penetrating radar and finite element methods in the context of structural dynamics. Eng. Struct. 2009, 31, 2667–2676. [Google Scholar] [CrossRef]
- Lõhmus, H.; Ellmann, A.; Märdla, S.; Idnurm, S. Terrestrial laser scanning for the monitoring of bridge load tests—Two case studies. Surv. Rev. 2018, 50, 270–284. [Google Scholar] [CrossRef]
- Valença, J.; Puente, I.; Júlio, E.; González-Jorge, H.; Arias-Sánchez, P. Assessment of cracks on concrete bridges using image processing supported by laser scanning survey. Constr. Build. Mater. 2017, 146, 668–678. [Google Scholar] [CrossRef]
- Riveiro, B.; González-Jorge, H.; Varela, M.; Jauregui, D.V. Validation of terrestrial laser scanning and photogrammetry techniques for the measurement of vertical underclearance and beam geometry in structural inspection of bridges. Measurement 2013, 46, 784–794. [Google Scholar] [CrossRef]
- Binczyk, M.; Kalitowski, P.; Szulwic, J.; Tysiac, P. Nondestructive Testing of the Miter Gates Using Various Measurement Methods. Sensors 2020, 20, 1749. [Google Scholar] [CrossRef] [PubMed]
- Ziolkowski, P.; Szulwic, J.; Miskiewicz, M. Deformation Analysis of a Composite Bridge during Proof Loading Using Point Cloud Processing. Sensors 2018, 18, 4332. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, M.; Mohammadi, M.; Sadeghlou Kivi, S.; Abdolvand, M.M.; Truong-Hong, L.; Samali, B. A Decade of Modern Bridge Monitoring Using Terrestrial Laser Scanning: Review and Future Directions. Remote Sens. 2020, 12, 3796. [Google Scholar] [CrossRef]
- Ambroziak, A.; Haustein, E.; Niedostatkiewicz, M. Chemical, Physical, and Mechanical Properties of 95-Year-Old Concrete Built-In Arch Bridge. Materials 2020, 14, 20. [Google Scholar] [CrossRef]
- Lockemann, T. Elbing; Deutscher Architectur und Industrie—Verlag: Berlin-Halensee, Germany, 1926. [Google Scholar]
- EN 12504-1 Testing Concrete in Structures—Part 1: Cored Specimens—Taking, Examining and Testing in Compression; CEN (European Committee for Standardization): Brussels, Belgium, 2009.
- EN 12390-3 Testing Hardened Concrete. Compressive Strength of Test Specimens; CEN (European Committee for Standardization): Brussels, Belgium, 2019. [Google Scholar]
- EN 12390-7 Testing Hardened Concrete—Part 7: Density of Hardened Concrete; CEN (European Committee for Standardization): Brussels, Belgium, 2019.
- ISO (International Organization for Standardization) ISO 6892-1 Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature; ISO: Geneva, Switzerland, 2019.
- Rules for the Construction and Maintenance of Road Bridges (Przepisy o Budowie i Utrzymaniu Mostów Drogowych); Pomorska Drukarnia Rolnicza, S.A.: Warszawa, Poland, 1926.
- PN-B-195 Concrete and Reinforced Concrete Structures. Structural Analysis and Design; PKN (Polish Committee for Standardization): Warsaw, Poland, 1945. [Google Scholar]
- Ambroziak, A. Application of elasto-viscoplastic Bodner-Partom constitutive equations in finite element analysis. Comput. Assist. Mech. Eng. Sci. 2007, 14, 405–429. [Google Scholar]
- Brunarski, L.; Dohojda, M. An approach to in-situ compressive strength of concrete. Bull. Polish Acad. Sci. Tech. Sci. 2016, 64, 687–695. [Google Scholar] [CrossRef]
- Domagała, L. Size Effect in Compressive Strength Tests of Cored Specimens of Lightweight Aggregate Concrete. Materials 2020, 13, 1187. [Google Scholar] [CrossRef]
- EN 13791 Assessment of In-Situ Compressive Strength in Tructures and Precast Concrete Components; CEN (European Committee for Standardization): Brussels, Belgium, 2019.
- Ambroziak, A.; Ziolkowski, P. Concrete compressive strength under changing environmental conditions during placement processes. Materials 2020, 13, 4577. [Google Scholar] [CrossRef]
- Bestimmungen für die Ausführung von Bauwerken aus Eisenbeton; DAfStB (Deutscher Ausschuss für Stahlbeton): Berlin, Germany, 1916.
- Deutsche Institut für Normung. DIN 1045:1925-09 Bestimmungen für Ausführung von Bauwerken aus Eisenbeton; Deutsche Institut für Normung: Berlin, Germany, 1925. [Google Scholar]
- Hallauer, O. Die Entwicklung der Zusammensetzung von Beton für Wasserbauten. Mtteilungsblaetter Bundesanstalt für Wasserbaut. 1989, 1988, 39–56. [Google Scholar]
- PN-B-195 Concrete and Reinforced Concrete Structures. Structural Analysis and Design; PKN (Polish Committee for Standardization): Warsaw, Poland, 1934. [Google Scholar]
- EN 206:2013 + A1:2016 Concrete—Specification, Performance, Production and Conformity; CEN (European Committee for Standardization): Brussels, Belgium, 2016.
- ACI 318-19 Building Code Requirements for Structural Concrete; ACI (American Concrete Institute): Farmington Hills, MI, USA, 2019; ISBN 9781641950565.
- EN 1992-1-1 Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; CEN (European Committee for Standardization): Brussels, Belgium, 2004.
- ASTM C469M-14 Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression; ASTM International (American Society for Testing and Materials): West Conshohocken, PA, USA, 2014.
- Żółtowski, K.J. Bridge over Vistula river in Kiezmark. Practical application of nonlinear shell FEM system. In Shell Structures: Theory and Applications; Pietraszkiewicz, W., Szymczak, C., Eds.; Taylor & Francis Group: Abingdon, UK, 2005; pp. 521–525. [Google Scholar]
- Siwowski, T.; Rajchel, M.; Kulpa, M. Design and field evaluation of a hybrid FRP composite—Lightweight concrete road bridge. Compos. Struct. 2019, 230, 111504. [Google Scholar] [CrossRef]
- Siwowski, T.; Wysocki, A. Horizontal Rotation via Floatation as an Accelerated Bridge Construction for Long-Span Footbridge Erection: Case Study. J. Bridg. Eng. 2015, 20, 05014014. [Google Scholar] [CrossRef]
- Erdenebat, D.; Waldmann, D. Application of the DAD method for damage localisation on an existing bridge structure using close-range UAV photogrammetry. Eng. Struct. 2020, 218, 110727. [Google Scholar] [CrossRef]
- Skokandić, D.; Mandić Ivanković, A. Value of additional traffic data in the context of bridge service-life management. Struct. Infrastruct. Eng. 2020, 1–20. [Google Scholar] [CrossRef]
- PN-S-10030 Bridges. Loads; PKN (Polish Committee for Standardization): Warsaw, Poland, 1985. [Google Scholar]
- Malinowski, M.; Banas, A.; Jeszka, M.; Sitarski, A. Imaginative footbridge in Mikolajki, Poland. Stahlbau 2018, 87, 248–255. [Google Scholar] [CrossRef]
- Malinowski, M.; Banas, A.; Cywiński, Z.; Jeszka, M.; Sitarski, A. Zur Wiedergeburt einer historischen Gitterbrücke. Stahlbau 2017, 86, 789–796. [Google Scholar] [CrossRef]
- Imperatore, S.; Lavorato, D.; Nuti, C.; Santini, S.; Sguerri, L. Numerical Modeling of Existing RC Beams Strengthened in Shear with FRP U-sheets. In Proceedings of the 6th International Conference on FRP, Composites in Civil Engineering, CICE 2012, Rome, Italy, 13–15 June 2012; pp. 1–8. [Google Scholar]
- El-Gamal, S.E. Finite Element Analysis of Concrete Bridge Slabs Reinforced with Fiber Reinforced Polymer Bars. J. Eng. Res. 2014, 11, 50. [Google Scholar] [CrossRef]
- Ahmed, H.; La, H.M.; Tran, K. Rebar detection and localization for bridge deck inspection and evaluation using deep residual networks. Autom. Constr. 2020, 120, 103393. [Google Scholar] [CrossRef]
- Erdogmus, E.; Garcia, E.; Amiri, A.S.; Schuller, M. A Novel Structural Health Monitoring Method for Reinforced Concrete Bridge Decks Using Ultrasonic Guided Waves. Infrastructures 2020, 5, 49. [Google Scholar] [CrossRef]
- Asadi, P.; Gindy, M.; Alvarez, M. A Machine Learning Based Approach for Automatic Rebar Detection and Quantification of Deterioration in Concrete Bridge Deck Ground Penetrating Radar B-scan Images. KSCE J. Civ. Eng. 2019, 23, 2618–2627. [Google Scholar] [CrossRef]
- Kobaka, J.; Katzer, J.; Ponikiewski, T. A Combined Electromagnetic Induction and Radar-Based Test for Quality Control of Steel Fibre Reinforced Concrete. Materials 2019, 12, 3507. [Google Scholar] [CrossRef] [PubMed]
- PN-EN 1992-1-1 Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; PKN (Polish Committee for Standardization): Warsaw, Poland, 2008.
- PN-S-10042 Bridges -Concrete, Reinforced Concrete and Prestressed Concrete Structures—Design; PKN (Polish Committee for Standardization): Warsaw, Poland, 1991.
- Karas, S. Unique Hennebique Bridges in Lublin, Poland. Am. J. Civ. Eng. Archit. 2013, 1, 47–51. [Google Scholar] [CrossRef]
- Banas, A.; Jankowski, R. Experimental and Numerical Study on Dynamics of Two Footbridges with Different Shapes of Girders. Appl. Sci. 2020, 10, 4505. [Google Scholar] [CrossRef]
- Nowak, A.S.; Eom, J.; Sanli, A. Control of Live Load on Bridges. Transp. Res. Rec. J. Transp. Res. Board 2000, 1696, 136–143. [Google Scholar] [CrossRef]
- Kilikevičius, A.; Bačinskas, D.; Jurevičius, M.; Kilikevičienė, K.; Fursenko, A.; Jakaitis, J.; Toločka, E. Field testing and dynamic analysis of old continuous truss steel bridge. Balt. J. Road Bridg. Eng. 2018, 13, 54–66. [Google Scholar] [CrossRef]
- Podworna, M.; Klasztorny, M. Vertical vibrations of composite bridge/track structure/high-speed train systems. Part 3: Deterministic and random vibrations of exemplary system. Bull. Polish Acad. Sci. Tech. Sci. 2014, 62, 305–320. [Google Scholar] [CrossRef]
- Law, S.S.; Zhu, X.Q. Dynamic behavior of damaged concrete bridge structures under moving vehicular loads. Eng. Struct. 2004, 26, 1279–1293. [Google Scholar] [CrossRef]
- Biliszczuk, J.; Barcik, W.; Onysyk, J.; Toczkiewicz, R.; Tukendorf, A. The two largest Polish concrete bridges—Design and construction. Proc. Inst. Civ. Eng. Bridg. Eng. 2016, 169, 298–308. [Google Scholar] [CrossRef]






| Specimens No. | Compressive Strength MPa | Dry Density kg/m3 |
|---|---|---|
| Results Obtained by Ambroziak et al. [30] | 14.9 | 2166 |
| 20.0 | 2171 | |
| 19.1 | 2132 | |
| 18.6 | 2184 | |
| 22.0 | 2155 | |
| 19.9 | 2064 | |
| 19.5 | 2180 | |
| 16.1 | 2174 | |
| 18.9 | 2147 | |
| 1_1 | 24.3 | 2157 |
| 1_2 | 21.6 | 2186 |
| 1_3 | 24.5 | 2207 |
| 2_1 | 17.1 | 2173 |
| 2_2 | 25.3 | 2170 |
| 3_1 | 29.7 | 2193 |
| 3_2 | 17.0 | 2179 |
| mean | 20.5 ± 1 | 2165 ± 8 |
| median | 19.7 | 2172.1 |
| The Amount of Cement (kg) in 1 m3 of Aggregate | Forecast Compressive Strength MPa (kg/cm2) |
|---|---|
| 500 | 19.6 (200) |
| 400 | 16.7 (170) |
| 300 | 13.7 (140) |
| 200 | 9.8 (100) |
| 100 | 5.9 (60) |
| Volume Ratios | The Amount of Cement (kg) in 1 m3 of Concrete Mix | Liquid Consistency | Plastic Consistency | Rammed Consistency |
|---|---|---|---|---|
| Sand to gravel 1:1 or sand to stone gravel 1:0.8 | 200 | 0 (0) | 2.9 (30) | 5.9 (60) |
| 300 | 4.9 (50) | 8.8 (90) | 11.8 (120) | |
| 400 | 9.8 (100) | 13.7 (140) | 15.7 (160) | |
| Sand to gravel 1:2 or sand to stone gravel 1:1.6 | 200 | 3.9 (40) | 8.8 (90) | 11.8 (120) |
| 300 | 9.8 (100) | 13.7 (140) | 15.7 (160) | |
| 400 | 13.7 (140) | 17.7 (180) | 19.6 (200) |
| Loads | Right Span | Left Span | Slab and Arch | ||||
|---|---|---|---|---|---|---|---|
| Outer Girder | Inner Girder | Outer Girder | Inner Girder | Center Deck Plate | Arch | ||
| M kNm | M kNm | M kNm | M kNm | M kNm | M kNm | N kN | |
| L1—characteristic load by dead-weight | 9.8 | 10.0 | 8.4 | 3.7 | 1.4 | 56.3 | 560.4 |
| L2—characteristic load by bridge equipment’s | 5.1 | 6.1 | 4.5 | 2.5 | 0.9 | 16.2 | 115.0 |
| L3—characteristic live load, standard load q type | 1.5 | 1.9 | 1.4 | 0.8 | 0.5 | 6.8 | 37.4 |
| L4—characteristic live load, standard load K typewithout the dynamic factor ϕ | 17.0 | 15.3 | 16.0 | 6.5 | 9.2 | 38.7 | 196.8 |
| Sum: L1 ÷ L4 | 33.4 | 33.3 | 30.3 | 13.5 | 12 | 118 | 909.6 |
| dynamic factor ϕ | 1.318 | 1.324 | 1.325 | 1.284 | |||
| design value with dynamic factor ϕ | 55.1 | 53.8 | 50.4 | 22.3 | 21.7 | 172.6 | 1280.3 |
| Properties | Left Span | Right Span | Slab and Arch | |||
|---|---|---|---|---|---|---|
| Outer Girder | Inner Girder | Outer Girder | Inner Girder | Deck Plate | Arch | |
| Steel rebar’s (bottom) | 6#20 | 6#20 | 14#12/m | 5#12/m | ||
| Design yield strength of reinforcement | fyk | |||||
| Design compressive strength of concrete | fck,is,cube | |||||
| Determined largest stress in steel rebar’s, MPa | 32.7 | 31.9 | 38.1 | 16.8 | 78.6 | 145.6 |
| Determined highest stress in concrete, MPa | 2.2 | 2.2 | 3.0 | 1.3 | 3.3 | 9.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambroziak, A.; Malinowski, M. A 95-Year-Old Concrete Arch Bridge: From Materials Characterization to Structural Analysis. Materials 2021, 14, 1744. https://doi.org/10.3390/ma14071744
Ambroziak A, Malinowski M. A 95-Year-Old Concrete Arch Bridge: From Materials Characterization to Structural Analysis. Materials. 2021; 14(7):1744. https://doi.org/10.3390/ma14071744
Chicago/Turabian StyleAmbroziak, Andrzej, and Maciej Malinowski. 2021. "A 95-Year-Old Concrete Arch Bridge: From Materials Characterization to Structural Analysis" Materials 14, no. 7: 1744. https://doi.org/10.3390/ma14071744
APA StyleAmbroziak, A., & Malinowski, M. (2021). A 95-Year-Old Concrete Arch Bridge: From Materials Characterization to Structural Analysis. Materials, 14(7), 1744. https://doi.org/10.3390/ma14071744







