Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects
Abstract
1. Introduction
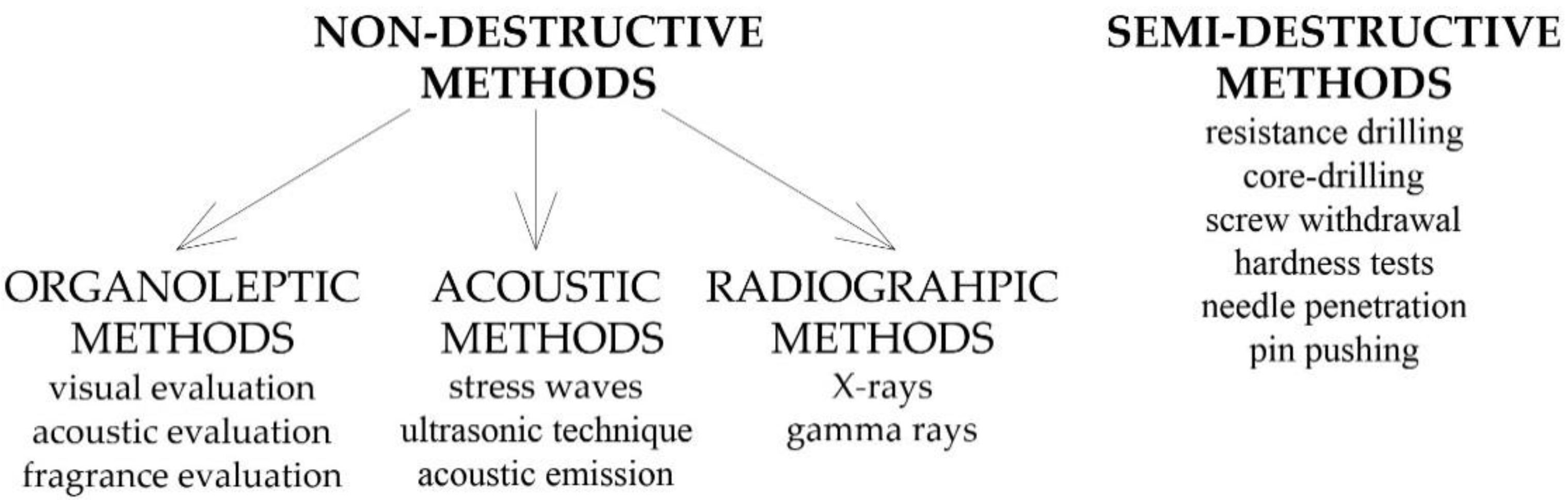
2. Selected Methods for Estimation Wood Structural Properties
2.1. Selected Standard Procedures and Tests
2.2. Mechanical Properties Assessment Based on Visual Grading
| The Classification Basis | KW (Choice Class) | KS (Middle Quality Class) | KG (Lower Quality Class) | |||
|---|---|---|---|---|---|---|
| Variant 1 | Variant 2 | Variant 1 | Variant 2 | |||
| Knots, regardless of quality, expressed as a knotting index USM | ≤1/4 | ≤1/4 | ≤1/2 | ≤1/2 | >1/2 | |
| Over the entire cross-section of timber USC | ≤1/4 | ≤1/3 | ≤1/4 | ≤1/2 | ≤1/3 | |
| Slope of grain (diagonal grain path) | ≤7% (1:14) | ≤10% (1:10) | ≤16% (1:6) | |||
| Cracks, resin pockets, bark pockets and catfaces | Deep, not crossing to the face, sides and opposite plane (not including defects less than 300 mm in length) | Permissible, length up to ¼ of the piece length and not longer than 600 mm | Permissible, length up to ¼ of the piece length and not longer than 600 mm | Permissible, length up to ¼ of the piece length and not longer than 900 mm | ||
| Frontal non-crossing, crossing and circular | Depth up to 1/3 of the piece thickness | Depth up to 1/2 of the piece thickness | Depth up to 2/3 of the piece thickness | |||
| Decay | Impermissible | Impermissible | Impermissible | |||
| Insect damage | Impermissible | Impermissible | Impermissible | |||
| Sapstain | Permissible | Permissible | Permissible | |||
| Reaction wood (compression wood) | Permissible up to 1/5 of the girth | Permissible up to 2/5 of the girth | Permissible up to 3/5 of the girth | |||
| Growth ring index | ≤4 mm | ≤6 mm | ≤10 mm | |||
| Minimum density of timber at a moisture content of 20% | ≥450 kg/m3 | ≥420 kg/m3 | ≥400 kg/m3 | |||
| Wane is permitted along the entire length of two edges of one plane or on side, occupying a total of | Up to ¼ thickness and ¼ width of timber piece | Up to ¼ thickness and ¼ width of timber piece | (a) at a distance of up to 300 mm from faces up to 1/3 of the thickness and 1/3 of the piece width (b) at a distance of more than 300 mm from faces up to 1/2 of the thickness and 1/3 of the piece width | |||
| Bow-longitudinal curvature of planes | ≤10 mm | ≤10 mm | ≤20 mm | |||
| Spring-longitudinal curvature of the sides | ≤8 mm | ≤8 mm | ≤12 mm | |||
| Twist in relation up to width | ≤1 mm/25 mm | ≤1 mm/25 mm | ≤2 mm/25 mm | |||
| Cup-cross curvature to width | ≤1 mm/25 mm | ≤1 mm/25 mm | ≤2 mm/25 mm | |||
| Cracks, kerf waviness | Permissible within the thickness and width deviations specified for basic dimensions | |||||
| Parallelism of planes and sides | Planes should be parallel to each other; sides of edged timber should be perpendicular to planes; deviations from parallelism should be within the limits of acceptable thickness and width deviations specified for the basic dimensions | |||||
| Non-perpendicularity of faces | Faces should be perpendicular to planes and sides; deviations from perpendicularity should be within the permissible deviations in timber length | |||||
| Tree Species | Thickness | KW (Choice Class) | KS (Middle Quality Class) | KG (Lower Quality Class) |
|---|---|---|---|---|
| Scots pine (Pinus sylvestris) | ≥22 mm | C35 | C24 | C20 |
| European spruce (Picea abies) | C30 | C24 | C18 | |
| European silver fir (Abies alba) | C22 | C18 | C14 | |
| European larch (Larix decidua) | C35 | C30 | C24 |
2.3. Mechanical Properties Assessment Based on the Determination of the Dynamic Modulus of Elasticity
| Wood Species | Vibration Method | Acoustic Method |
|---|---|---|
| Scots pine (Pinus sylvestris) | ||
| Radiata Pine (Pinus radiata) |
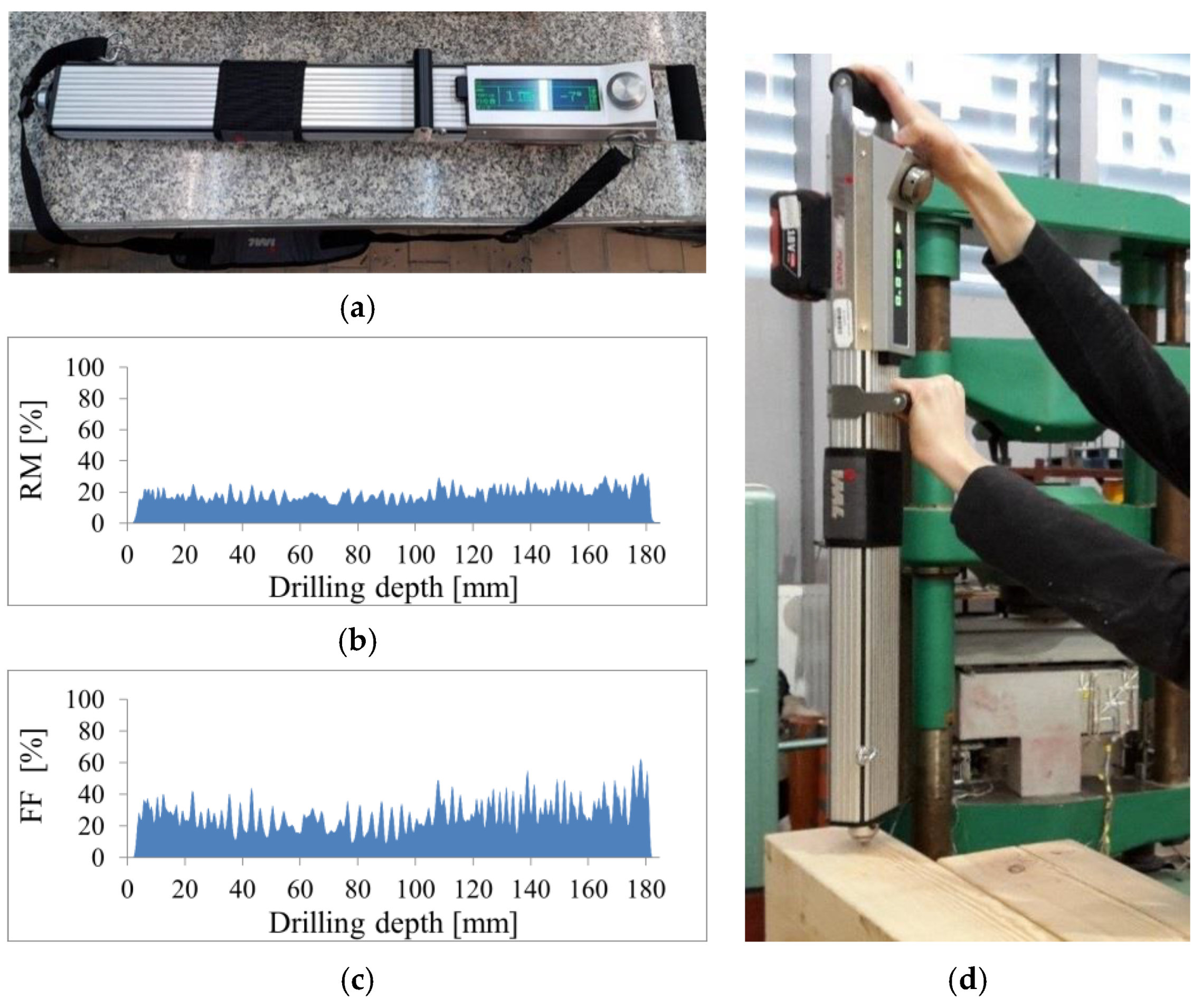
2.4. Mechanical Properties Assessment Based on the Resistance Drilling Method
2.5. Mechanical Properties Assessment Based on Small Clear Wood Specimens Tests
| Wood Property | Coefficient of Variation V [%] | ||
|---|---|---|---|
| ISO 3129 [59] | Krzysik [60] | Wood Handb. [61] | |
| Number of growth rings in 1 cm | 37 | - | - |
| Percentage of late wood | 28 | 28 | - |
| Density | 10 | 10 | 10 |
| Equilibrium moisture content | 5 | - | - |
| Coefficient of shrinkage: linear | 28 | 28 | - |
| Coefficient of shrinkage: volumetric | 16 | 16 | - |
| Ultimate compressive strength parallel to grain | 13 | 13 | 18 |
| Ultimate strength in static bending | 15 | 15 | 16 |
| Ultimate shearing strength parallel to grain | 20 | 19 | 14 |
| Modulus of elasticity in static bending | 20 | 20 | 22 |
| Proportional limit (conventional ultimate strength) in compression perpendicular to grain | 20 | 30 | 28 |
| Ultimate tensile strength parallel to grain | 20 | 20 | 25 |
| Ultimate tensile strength perpendicular to grain | 20 | - | - |
| Impact strength in bending | 32 | 32 | 25 |
| Hardness | 17 | 17 | 20 |
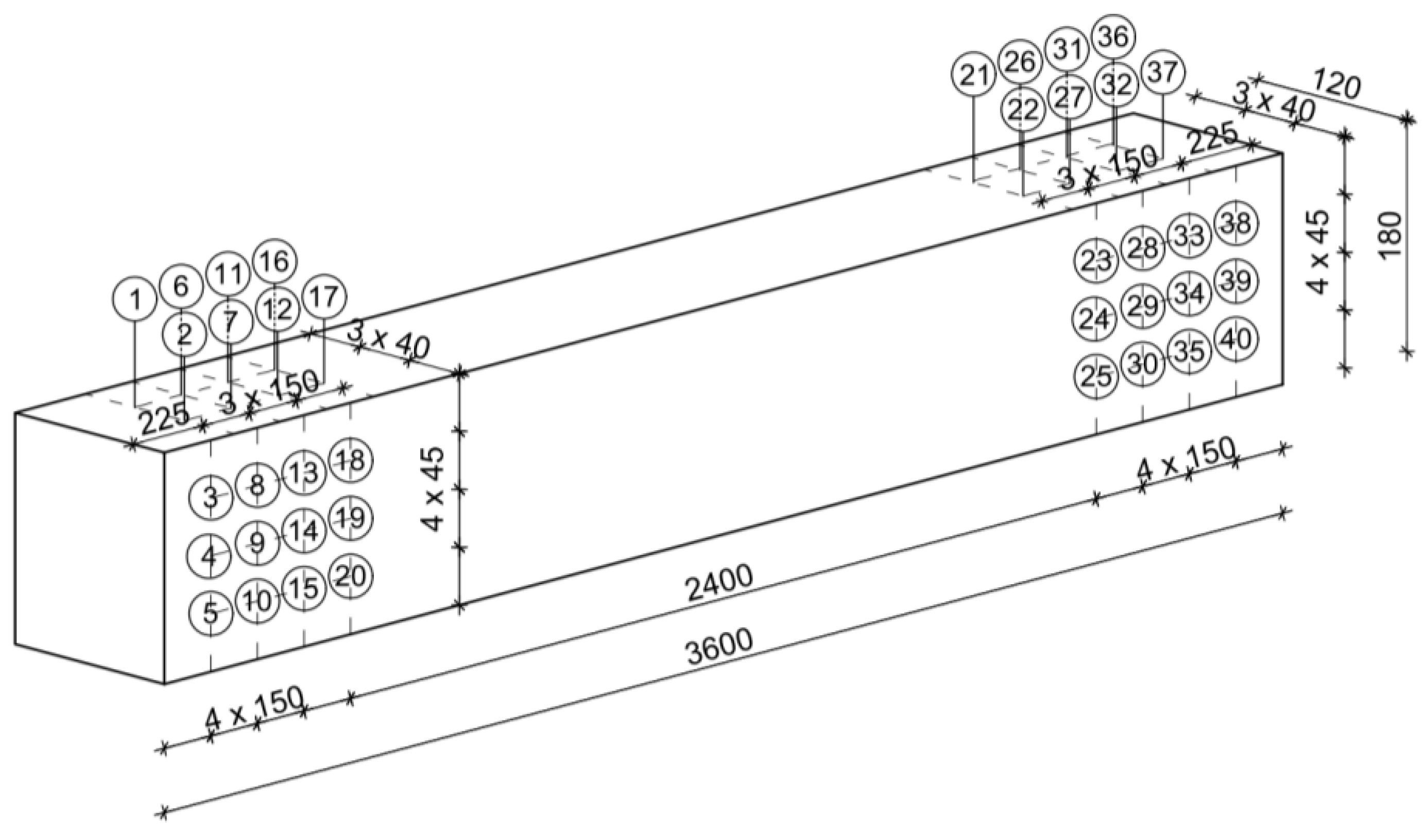
3. Materials and Methods
4. Results
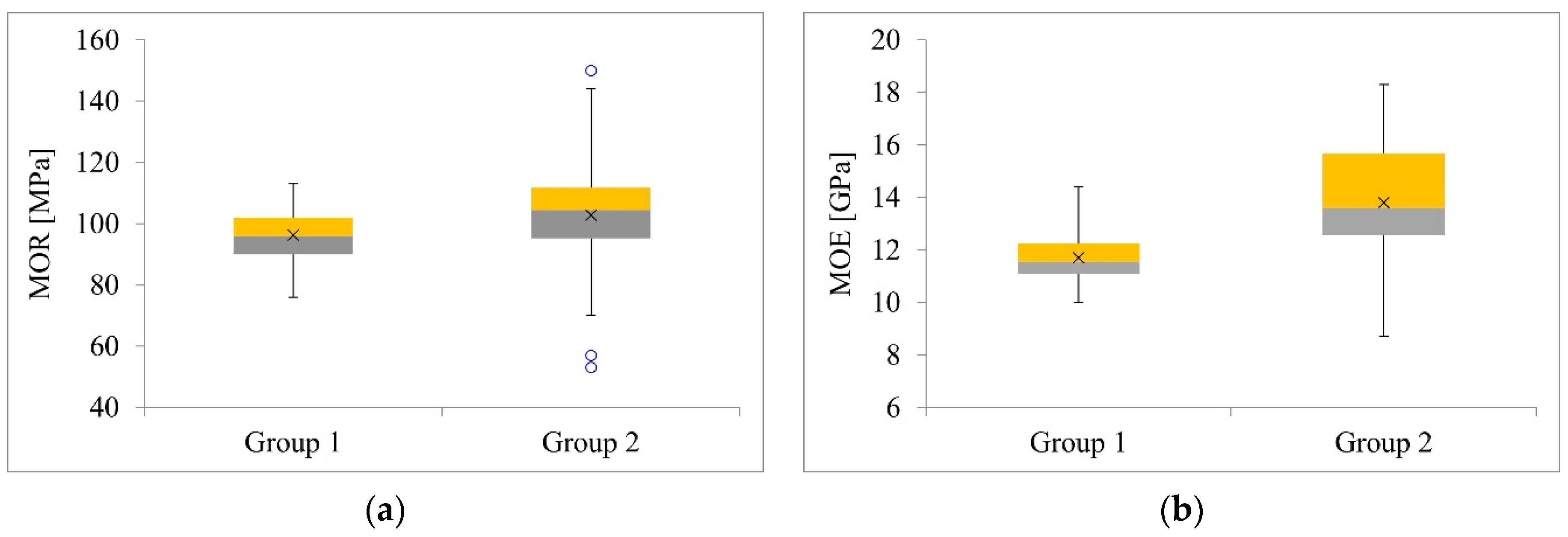
4.1. Results of Destructive Testing of Technical Scale Beams and Density Determination
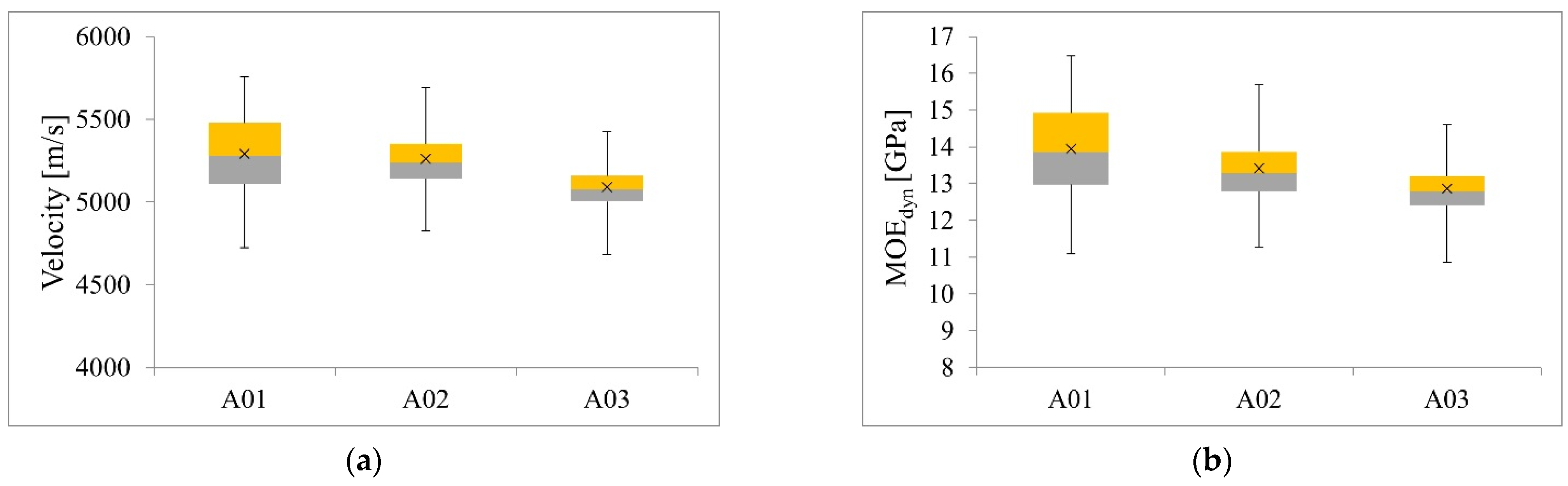
4.2. Results of Tests with Acoustic Method
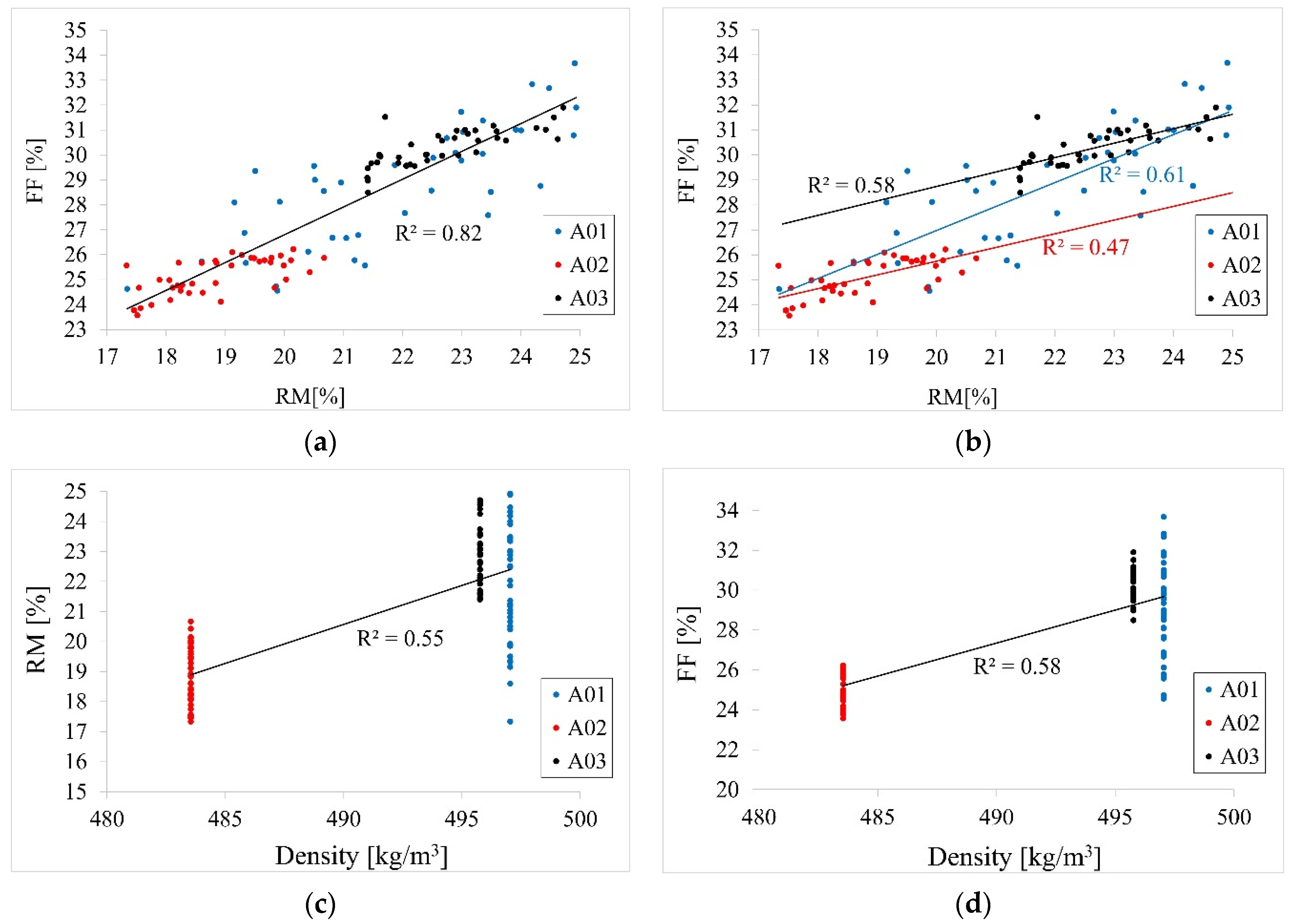
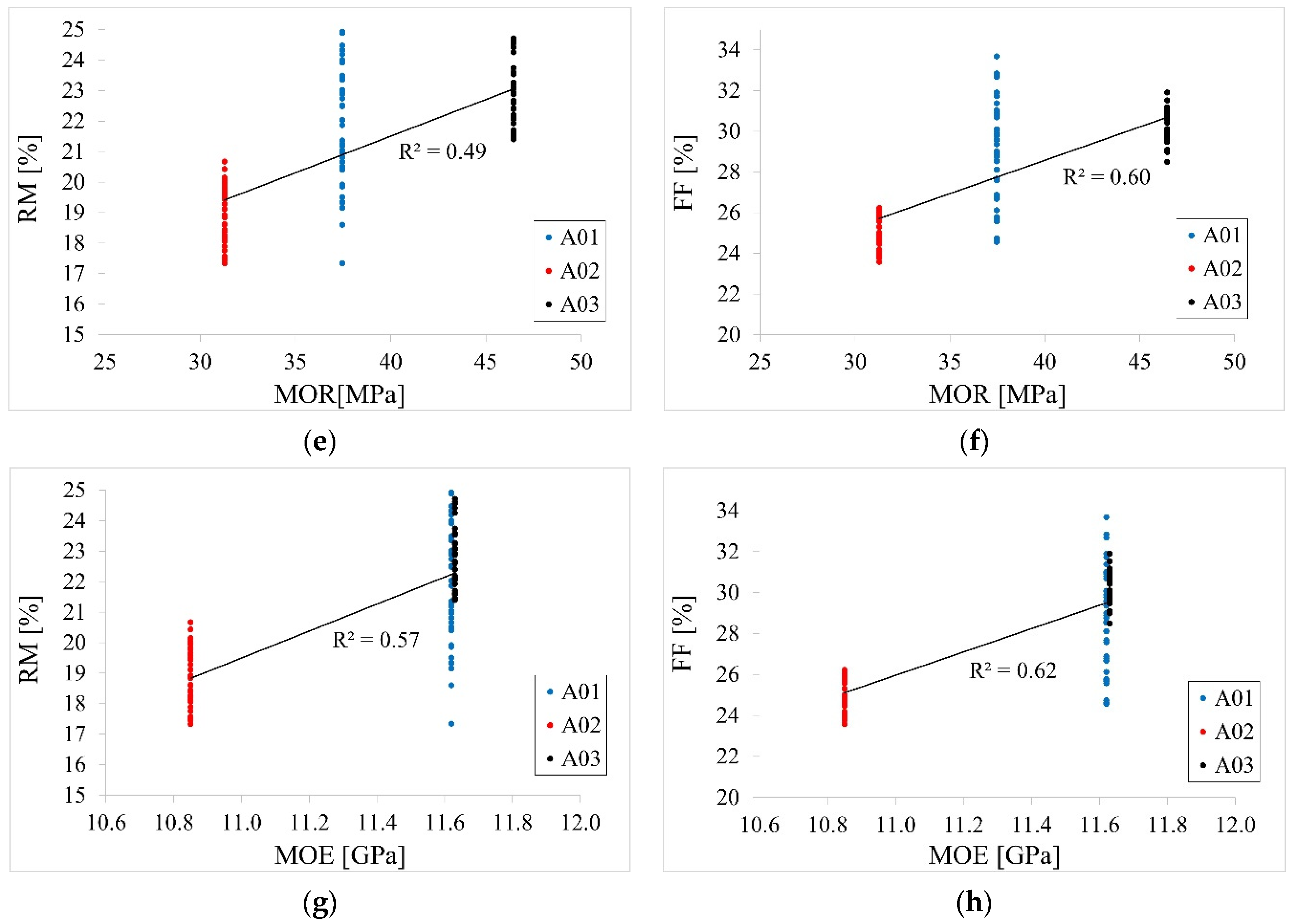
4.3. Results of Test with Drilling Resistance Method
4.4. Results of Tests of Small Clear Specimens and Their Adjustment to Structural Size Beams
| Beam A01 | Beam A02 | Beam A03 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 1 | Group 2 | Group 1 | Group 2 | |||||||
| MOR | MOE | MOR | MOE | MOR | MOE | MOR | MOE | MOR | MOE | MOR | MOE | |
| Mean [MPa] | 96 | 11,700 | 103 | 13,800 | 96 | 11,700 | 103 | 13,800 | 96 | 11,700 | 103 | 13,800 |
| 5% exclusion value (MPa) | 80 | 9800 | 66 | 9400 | 80 | 9800 | 66 | 9400 | 80 | 9800 | 66 | 9400 |
| Special factor kp 1 [-] | 0.68 | - | 0.78 | - | 0.68 | - | 0.78 | - | 0.68 | - | 0.78 | - |
| Factor kd 2 [-] | 0.60 | 1.0 | 0.60 | 1.0 | 0.53 | 0.90 | 0.53 | 0.90 | 0.75 | 1.00 | 0.75 | 1.00 |
| 5% exclusion value [MPa] “Characteristic" | 33 | - | 31 | - | 29 | - | 27 | - | 41 | - | 39 | - |
| [MPa] “Mean” | 39 | 11,700 | 48 | 13,800 | 35 | 10500 | 43 | 12,400 | 49 | 11,700 | 60 | 13,800 |
5. Discussion
6. Conclusions
- In the conducted research, very good correlations were obtained between MOEstat from the acoustic method and MOE from beams on the technical scale. Nevertheless, the difference in the value of the modulus determined by the acoustic method may be high enough to result in an incorrect assignment of wood class.
- In the drilling resistance test, statistically significant correlations were observed between the density, MOR and MOE as predictors and FF or RM as the response (R2 = 0.49–0.62). However, it is considered that resistance drilling should be used for qualitative rather than quantitative evaluation of timber.
- In the conducted study, the MOE values determined in accordance with the ASTM standard, based on the results for small clear specimens, correspond very well with the actual values from the technical scale element tests.
- The failure of the technical scale beams in the bending tests was observed in the areas of occurrence of defects considered by ASTM D245 [44] to be critical for load-bearing capacity.
- It is recommended to use different methods in parallel, as no single method is sufficiently reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Šubic, B.; Fajdiga, G.; Lopatič, J. Bending stiffness, load-bearing capacity and flexural rigidity of slender hybrid wood-based beams. Forests 2018, 9, 703. [Google Scholar] [CrossRef]
- Nowak, T.; Karolak, A.; Sobótka, M.; Wyjadłowski, M. Assessment of the condition of wharf timber sheet wall material by means of selected non-destructive methods. Materials 2019, 12, 1532. [Google Scholar] [CrossRef] [PubMed]
- Baño, V.; Arriaga, F.; Guaita, M. Determination of the influence of size and position of knots on load capacity and stress distribution in timber beams of Pinus sylvestris using finite element model. Biosyst. Eng. 2013, 114, 214–222. [Google Scholar] [CrossRef]
- Vavrusova, K.; Lokaj, A.; Mikolasek, D.; Sucharda, O. Analysis of longitudinal timber beam joints loaded with simple bending. Sustainability 2020, 12, 9288. [Google Scholar] [CrossRef]
- Oliveira, J.; Xavier, J.; Pereira, F.; Morais, J.; de Moura, M. Direct evaluation of mixed mode I+II cohesive laws of wood by coupling MMB test with DIC. Materials 2021, 14, 374. [Google Scholar] [CrossRef] [PubMed]
- Piazza, M.; Riggio, M. Visual strength-grading and NDT of timber in traditional structures. J. Build. Apprais. 2008, 3, 267–296. [Google Scholar] [CrossRef]
- Ilharco, T.; Lechner, T.; Nowak, T. Assessment of timber floors by means of non-destructive testing methods. Constr. Build. Mater. 2015, 101, 1206–1214. [Google Scholar] [CrossRef]
- Lechner, T.; Nowak, T.; Kliger, R. In situ assessment of the timber floor structure of the Skansen Lejonet fortification, Sweden. Constr. Build. Mater. 2014, 58, 85–93. [Google Scholar] [CrossRef]
- Riggio, M.; Anthony, R.; Augelli, F.; Kasal, B.; Lechner, T.; Muller, W.; Tannert, T. In situ assessment of structural timber using non-destructive techniques. Mater. Struct. 2014, 47, 749–766. [Google Scholar] [CrossRef]
- Dackermann, U.; Crews, K.; Kasal, B.; Li, J.; Riggio, M.; Rinn, F.; Tannert, T. In situ assessment of structural timber using stress-wave measurements. Mater. Struct. 2014, 47, 787–803. [Google Scholar] [CrossRef]
- Tannert, T.; Anthony, R.; Kasal, B.; Kloiber, M.; Piazza, M.; Riggio, M.; Rinn, F.; Widmann, R.; Yamaguchi, N. In situ assessment of structural timber using semi-destructive techniques. Mater. Struct. 2014, 47, 767–785. [Google Scholar] [CrossRef]
- Kloiber, M.; Tippner, J.; Hrivnák, J. Mechanical properties of wood examined by semi-destructive devices. Mater. Struct. 2014, 47, 199–212. [Google Scholar] [CrossRef]
- Kasal, B. Semi-destructive method for in-situ evaluation of compressive strength of wood structural members. For. Prod. J. 2003, 53, 55–58. [Google Scholar]
- Jaskowska-Lemanska, J.; Przesmycka, E. Semi-destructive and non-destructive tests of timber structure of various moisture contents. Materials 2021, 14, 96. [Google Scholar] [CrossRef]
- Dolwin, J.A.; Lonsdale, D.; Barnett, J. Detection of decay in trees. Arboric. J. 1999, 23, 139–149. [Google Scholar] [CrossRef]
- ISO 13822:2010—Bases for Design of Structures—Assessment of Existing Structures; International Organization for Standardization: Geneva, Switzerland, 2010.
- PN-EN 17121:2020-01—Conservation of Cultural Heritage. Historic Timber Structures. Guidelines for the On-Site Assessment of Load-Bearing Timber Structures; Polish Committee for Standarization: Warsaw, Poland, 2020.
- UNI 11119:2004—Cultural Heritage—Wooden Artefacts—Load-Bearing Structures—On Site Inspections for the Diagnosis of Timber Members; Ente Nazionale Italiano di Unificazione (UNI): Milano, Italy, 2004.
- UNI 11138:2004—Cultural Heritage—Wooden Artefacts—Building Load Bearing Structures—Criteria for the Preliminary Evaluation, the Design and the Execution of Works; Ente Nazionale Italiano di Unificazione (UNI): Milano, Italy, 2004.
- SIA 269/5:2011—Existing Structures—Timber Structures; Swiss Society of Engineers and Architects (SIA): Zurich, Switzerland, 2011.
- Perria, E.; Sieder, M. Six-steps process of structural assessment of heritage timber structures: Definition based on the state of the art. Buildings 2020, 10, 109. [Google Scholar] [CrossRef]
- Jasieńko, J.; Nowak, T.; Hamrol, K. Selected methods of diagnosis of historic timber structures—Principles and possibilities of assessment. Adv. Mater. Res. 2013, 778, 225–232. [Google Scholar] [CrossRef]
- Sanabria, S.; Furrer, R.; Neuenschwander, J.; Niemz, P.; Sennhauser, U. Air-coupled ultrasound inspection of glued laminated timber. Holzforschung 2011, 65, 377–387. [Google Scholar] [CrossRef]
- As, N.; Senalik, C.A.; Ross, R.J.; Wang, X.; Farber, B. Nondestructive Evaluation of the Tensile Properties of Structural Lumber from the Spruce-Pine-Fir Species Grouping: Relationship between Modulus of Elasticity and Ultimate Tension Stress; Research Note FPL-RN-0383; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2020; p. 12.
- Divos, F.; Tanaka, T. Relation between static and dynamic modulus of elasticity of wood. Acta Silv. Lign. Hung. 2005, 1, 105–110. [Google Scholar]
- Nowak, T.; Jasieńko, J.; Hamrol-Bielecka, K. In situ assessment of structural timber using the resistance drilling method—Evaluation of usefulness. Constr. Build. Mater. 2016, 102, 403–415. [Google Scholar] [CrossRef]
- Jasieńko, J.; Nowak, T.; Bednarz, Ł. Wrocław University’s Leopoldinum Auditorium—Tests of its ceiling and a conservation and strengthening concept. Adv. Mater. Res. 2010, 133, 265–270. [Google Scholar] [CrossRef]
- PN-EN 384+A1:2018—Structural Timber. Determination of Characteristic Values of Mechanical Properties and Density; Polish Committee for Standardization: Warsaw, Poland, 2018.
- PN-EN 408+A1: 2012—Structural Timber and Glued Laminated Timber. Determination of Some Physical and Mechanical Properties; Polish Committee for Standardization: Warsaw, Poland, 2012.
- ISO 13061-3—Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 3: Determination of Ultimate Strength in Static Bending; International Organization for Standardization: Geneva, Switzerland, 2014.
- ISO 13061-4—Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens—Part 4: Determination of Modulus of Elasticity in Static Bending; International Organization for Standardization: Geneva, Switzerland, 2014.
- PN-77/D-04103—Wood. Determination of Static Bending Strength; Polish Committee for Standardization: Warsaw, Poland, 1977.
- ASTM D143-14—Standard Test Method for Small Clear Specimen of Timber; American Society for Testing Material Standard: West Conshohocken, PA, USA, 2014.
- PN-63/D-04117—Physical and Mechanical Properties of Wood. Determination of the Elasticity Coefficient for Static Bending; Polish Committee for Standardization: Warsaw, Poland, 1963.
- BS 373:1957—Methods of Testing Small Clear Specimens of Timber; British Standards Institution: London, UK, 1957.
- ISO 3133:1975—Wood—Determination of Ultimate Strength in Static Bending; International Organization for Standardization: Geneva, Switzerland, 1975.
- Hu, W.; Wan, H.; Guan, H. Size effect on the elastic mechanical properties of beech and its application in finite element analysis of wood structures. Forests 2019, 10, 783. [Google Scholar] [CrossRef]
- Straže, A.; Gorišek, Z. Analysis of size effect on determination of mechanical properties of Norway spruce wood. In Proceedings of the 22nd International Scientific Conference on Wood is Good-EU Pre Accession Challenges of the Sector, Zagreb, Croatia, 21 October 2011; pp. 183–190. [Google Scholar]
- Madsen, B.; Tomoi, M. Size effects occurring in defect-free spruce-pine-fir bending specimens. Can. J. Civ. Eng. 1991, 18, 637–643. [Google Scholar] [CrossRef]
- Madsen, B.; Nielsen, P.C. In-Grade Testing: Size Investigation on Lumber Subjected to Bending; Structural Research Series; Report No. 15; Department of Civil Engineering, University of British Columbia: Vancouver, BC, Canada, 1976; p. 10. [Google Scholar]
- Fotsing, J.A.; Foudjet, A. Size effect of two Cameroonian hardwoods in compression and bending parallel to the Grain. Holzforschung 1995, 49, 376–378. [Google Scholar] [CrossRef]
- Zhou, H.B.; Ren, H.Q.; Lu, J.X. Size effect of length on flexural strength of Chinese fir dimension lumber used in wood structure. J. Build. Mater. 2009, 12, 501–504. (In Chinese) [Google Scholar]
- Zhou, H.B.; Han, L.Y.; Ren, H.Q.; Lu, J.X. Size effect on strength properties of Chinese larch dimension lumber. BioResources 2015, 10, 3790–3797. [Google Scholar] [CrossRef]
- ASTM D245-06(2019)—Standard Practice for Establishing Structural Grades and Related Allowable Properties for Visually Graded Lumber; ASTM International: West Conshohocken, PA, USA, 2019.
- PN-EN 14081-1:2016—Timber Structures. Strength Graded Structural Timber with Rectangular Cross Section. Part 1: General Requirements; Polish Committee for Standardization: Warsaw, Poland, 2016.
- PN-EN 338: 2016—Structural Timber. Strength Classes; Polish Committee for Standardization: Warsaw, Poland, 2016.
- PN-D-94021:2013—Strength Graded Structural Timber; Polish Committee for Standardization: Warsaw, Poland, 2013.
- Wdowiak, A.; Brol, J. Methods of strength grading of structural timber—Comparative analysis of visual and machine grading on the example of scots pine timber from four natural forest regions of Poland. Struct. Environ. 2019, 11, 210–224. [Google Scholar] [CrossRef]
- PN-EN 1995-1-1:2010—Eurocode 5: Design of Timber Structures—Part 1: General-Common Rules and Rules for Buildings; Polish Committee for Standardization: Warsaw, Poland, 2010.
- Kasal, B.; Lear, G.; Tannert, T. Stress waves. In In Situ Assessment of Structural Timber. RILEM State-of-the-Art Reports; Kasal, B., Tannert, T., Eds.; Springer: Dordrecht, The Netherlands, 2010; Volume 7, pp. 5–24. ISBN 978-94-007-0559-3. [Google Scholar]
- Wang, X.; Divos, F.; Pilon, C.; Brashaw, B.K.; Ross, R.J.; Pellerin, R.F. Assessment of Decay in Standing Timber Using Stress Wave Timing Nondestructive Evaluation Tools: A Guide for Use and Interpretation; Gen. Tech. Rep. FPL-GTR-147; US Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2004.
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Íñiguez- González, G. Clasificación Mediante Técnicas no Destructivas y Evaluación de las Propiedades Mecánicas de la Madera Aserrada de Coníferas de Gran Escuadría Para uso Structural. Ph.D. Thesis, Universidad Politécnica de Madrid, ETS de Ingenieros de Montes, Madrid, Spain, 2007. (In Spanish). [Google Scholar]
- Rinn, F. Basics of micro-resistance drilling for timber inspection. Holztechnologie 2012, 53, 24–29. [Google Scholar]
- Anthony, R.W. Nondestructive evaluation: Wood. APT Bull. 2010, 41, 1–6. [Google Scholar]
- Feio, A.O.; Lourenço, P.B.; Machado, J.S. Testing and modeling of a traditional timber mortise and tenon joint. Mater. Struct. 2014, 47, 213–225. [Google Scholar] [CrossRef]
- Feio, A.O.; Machado, J.S.; Lourenço, P.B. Compressive behavior and NDT correlations for chestnut wood (Castanea sativa Mill.). In Proceedings of the 4th International Seminar on Structural Analysis of Historical Constructions, Padova, Italy, 10–13 November 2004; pp. 369–375. [Google Scholar]
- PN-EN 384:2011—Structural Timber. Determination of Characteristic Values of Mechanical Properties and Density; Polish Committee for Standardization: Warsaw, Poland, 2011.
- ISO 3129:2019—Wood—Sampling Methods and General Requirements for Physical and Mechanical Testing of Small Clear Wood Specimens; International Organization for Standardization: Geneva, Switzerland, 2019.
- Krzysik, F. Nauka o Drewnie (Wood Science); PWN: Warsaw, Poland, 1978. (In Polish) [Google Scholar]
- Ross, R.J. Wood Handbook: Wood as an Engineering Material, Centennial Edition; U.S. Dept. of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010.
- Lokaj, A.; Dobes, P.; Sucharda, O. Effects of loaded end distance and moisture content on the behavior of bolted connections in squared and round timber subjected to tension parallel to the grain. Materials 2020, 13, 5525. [Google Scholar] [CrossRef] [PubMed]
- ISO 12491:1997—Statistical Methods for Quality Control of Building Materials and Components; International Organization for Standardization: Geneva, Switzerland, 2010.
- PN-EN 14358:2016-08—Timber Structures. Calculation and Verification of Characteristic Values; Polish Committee for Standardization: Warsaw, Poland, 2016.
- PN-EN 1990:2004—Basis of Structural Design; Polish Committee for Standardization: Warsaw, Poland, 2004.
- Mirski, R.; Dziurka, D.; Chuda-Kowalska, M.; Wieruszewski, M.; Kawalerczyk, J.; Trociński, A. The usefulness of pine timber (Pinus sylvestris L.) for the production of structural elements. Part I: Evaluation of the quality of the pine timber in the bending test. Materials 2020, 13, 3957. [Google Scholar] [CrossRef] [PubMed]





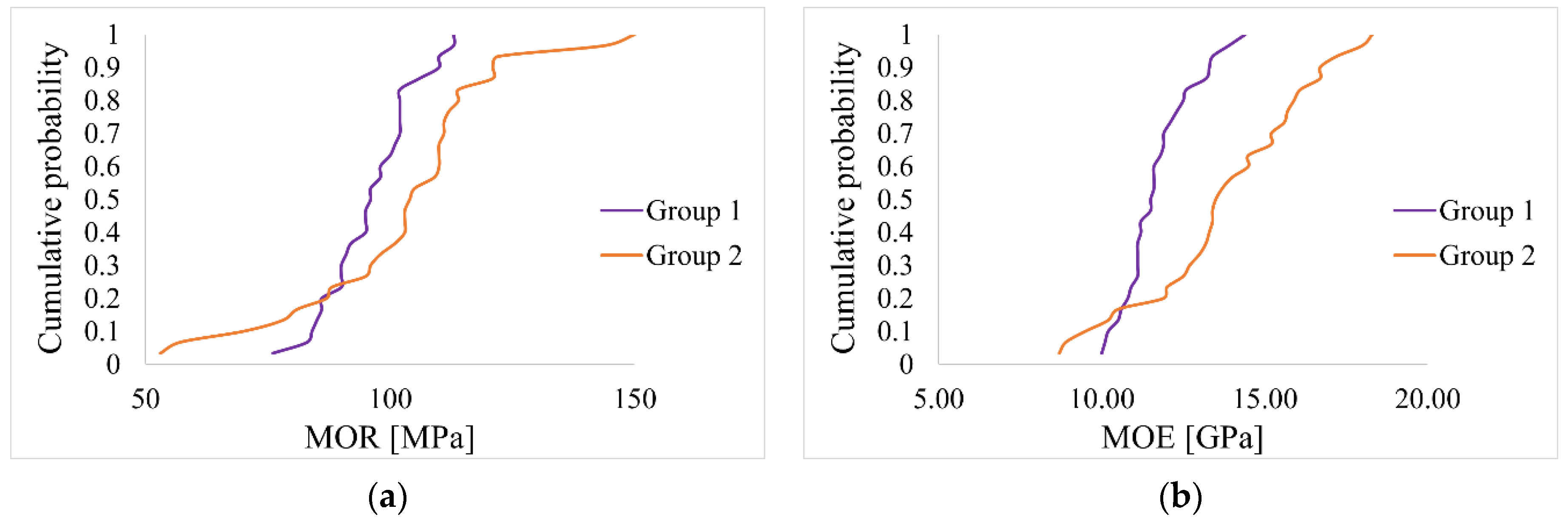
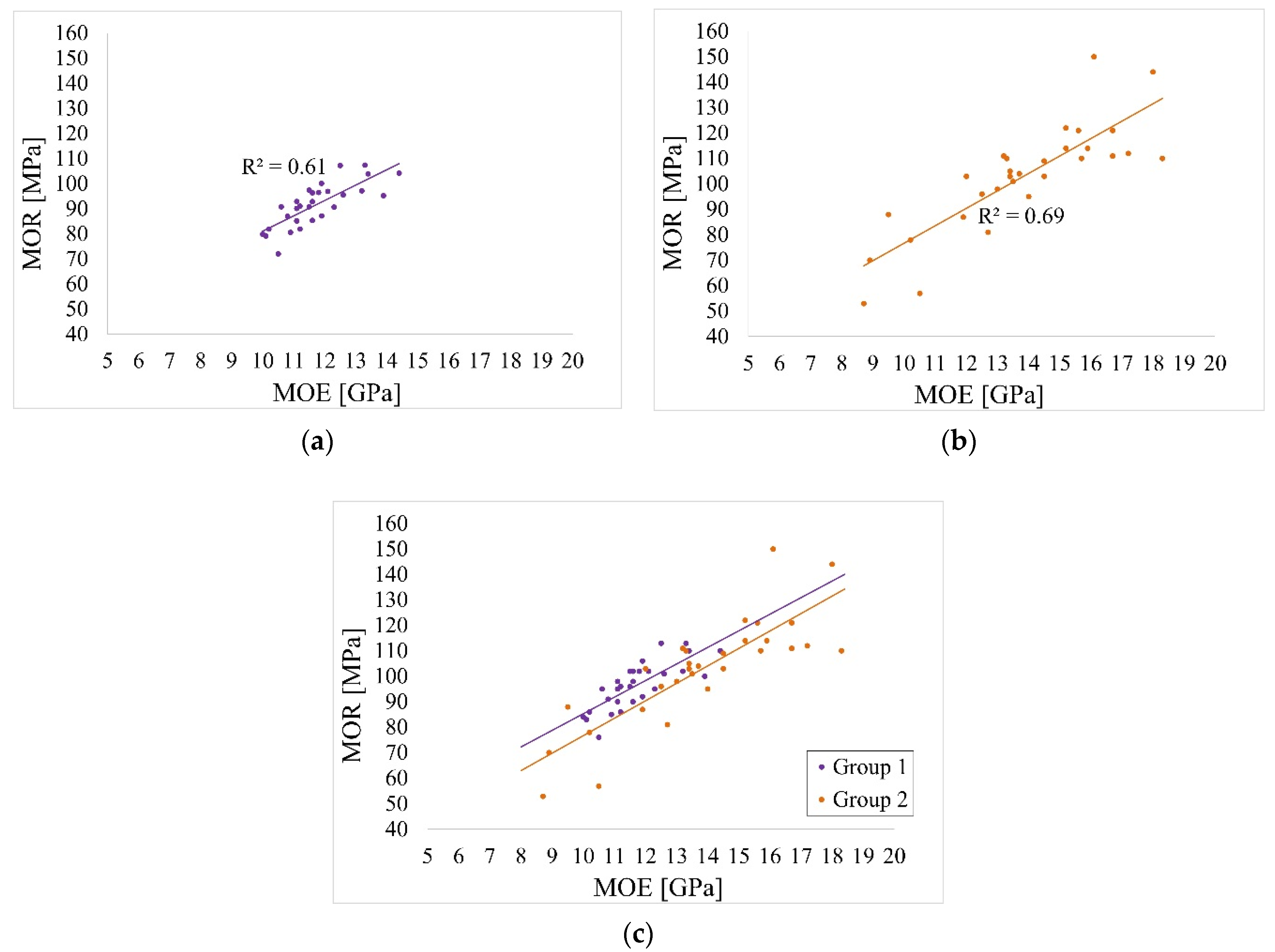

| MOR | MOE | |
|---|---|---|
| Number of samples | 30 | 30 |
| Coefficient of variation according to ISO 3129 | 15% | 20% |
| Confidence level | 0.95 | 0.95 |
| Estimated test accuracy rate | 5.37% | 7.16% |
| Beam | MOR | MOE | Density [kg/m3] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Value [MPa] | Mean [MPa] | Standard Deviation [MPa] | Variation Coefficient ν [%] | Value [GPa] | Mean [GPa] | Standard Deviation [GPa] | Variation Coefficient ν [%] | ||
| A01 | 37.46 | 38.39 | 6.23 | 16.23 | 11.62 | 11.36 | 0.37 | 3.23 | 497 |
| A02 | 31.27 | 10.85 | 484 | ||||||
| A03 | 46.45 | 11.63 | 496 | ||||||
| Beam | Direction Relative to Grain | Velocity [m/s] | MOEdyn [GPa] | MOEstat 1 [GPa] | |||
|---|---|---|---|---|---|---|---|
| Fakkop MS | Sylvatest Trio | Fakkop MS | Sylvatest Trio | Fakkop MS | Sylvatest Trio | ||
| A01 | parallel | 5292 | 5134 | 13.95 2Δ = 20.1% | 13.10 Δ = 12.7% | 11.11 Δ = 4.4% | 10.47 Δ = 9.9% |
| perpendicular | 1689 | 1617 | 1.42 | 1.31 | 1.65 | 1.57 | |
| A02 | parallel | 5262 | 5155 | 13.41 Δ = 23.6% | 12.87 Δ = 18.6% | 10.70 Δ = 1.4% | 10.29 Δ = 5.1% |
| perpendicular | 1742 | 1559 | 1.47 | 1.18 | 1.69 | 1.47 | |
| A03 | parallel | 5090 | 5038 | 12.86 Δ = 10.6% | 12.59 Δ = 8.3% | 10.29 Δ = 11.6% | 10.08 Δ = 13.3% |
| perpendicular | 1668 | 1573 | 1.38 | 1.23 | 1.62 | 1.51 | |
| Beam | Number of Measurements | Resistance Measure RM [%] | |||
|---|---|---|---|---|---|
| Mean | Range | Standard Deviation | Coefficient of Variation | ||
| A01 | 40 | 21.86 | 17.34–24.93 | 1.96 | 8.99 |
| A02 | 40 | 18.84 | 17.33–20.67 | 0.95 | 5.04 |
| A03 | 40 | 22.66 | 22.66–21.40 | 0.99 | 4.38 |
| Summary | 120 | 21.12 | 17.33–24.93 | 2.15 | 10.17 |
| Beam | Number of Measurements | Feed Force FF [%] | |||
|---|---|---|---|---|---|
| Mean | Range | Standard Deviation | Coefficient of Variation | ||
| A01 | 40 | 28.76 | 24.56–33.68 | 2.41 | 8.39 |
| A02 | 40 | 25.11 | 23.57–26.22 | 0.76 | 3.02 |
| A03 | 40 | 30.28 | 28.49–31.90 | 0.75 | 2.48 |
| Summary | 120 | 28.05 | 23.57–33.68 | 2.65 | 9.44 |
| Beam | Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|---|
| A01 | Intercept | 7.79 | 2.73 | .007 |
| RM | 0.96 | 0.12 | <.001 | |
| A02 | Intercept | 14.78 | 1.78 | <.001 |
| RM | 0.55 | 0.09 | <.001 | |
| A03 | Intercept | 17.19 | 1.80 | <.001 |
| RM | 0.58 | 0.08 | <.001 |
| Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|
| Intercept | 7.79 | 1.76 | <.001 |
| RM | 0.96 | 0.08 | <.001 |
| Beam A02 vs. A01 | 6.99 | 3.58 | .053 |
| Beam A03 vs. A01 | 9.40 | 4.00 | .021 |
| RM: beam A02 vs. A01 | −0.41 | 0.18 | .027 |
| RM: beam A03 vs. A01 | −0.38 | 0.18 | .034 |
| Feed Force/Resistance Measure | Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|---|
| FF | Intercept | −148.28 | 13.79 | <.001 |
| Density | 0.36 | 0.03 | <.001 | |
| RM | Intercept | −117.11 | 11.68 | <.001 |
| Density | 0.28 | 0.02 | <.001 |
| Feed Force/Resistance Measure | Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|---|
| FF | Intercept | 15.47 | 0.96 | <.001 |
| MOR | 0.33 | 0.02 | <.001 | |
| RM | Intercept | 11.90 | 0.88 | <.001 |
| MOR | 0.24 | 0.02 | <.001 |
| Feed Force/Resistance Measure | Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|---|
| FF | Intercept | −36.78 | 4.64 | <.001 |
| MOE | 5.70 | 0.41 | <.001 | |
| RM | Intercept | −29.19 | 4.01 | <.001 |
| MOE | 4.43 | 0.35 | <.001 |
| Group 1 | Group 2 | |||
|---|---|---|---|---|
| MOR | MOE | MOR | MOE | |
| Number of specimens | 30 pieces | 30 pieces | ||
| Mean value | 96 MPa | 11.7 GPa | 103 MPa | 13.8 GPa |
| Standard deviation | 9.3 MPa | 1.11 GPa | 21.2 MPa | 2.57 GPa |
| Coefficient of variation | 9.6% | 9.5% | 20.2% | 18.3% |
| Confidence interval for the mean (0.95) | 92.7–99.3 MPa | 11.43–12.23 GPa | 95.1–110.3 MPa | 12.88–14.72 GPa |
| 5% exclusion limit | 80 MPa | 9.8 GPa | 66 MPa | 9.4 GPa |
| Group | Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|---|
| Group 1 | Intercept | 19.99 | 11.52 | 0.094 |
| MOE | 6.52 | 0.98 | <0.001 | |
| Group 2 | Intercept | 8.08 | 12.07 | 0.509 |
| MOE | 6.86 | 0.86 | <0.001 |
| Variable | Estimate | Standard Error | p-Value |
|---|---|---|---|
| Intercept | 19.99 | 18.44 | 0.283 |
| MOE | 6.52 | 2.07 | <0.001 |
| Group 2 vs. 1 | −11.91 | 20.75 | 0.568 |
| MOE * Group | 0.33 | 1.71 | 0.846 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowak, T.; Patalas, F.; Karolak, A. Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects. Materials 2021, 14, 1941. https://doi.org/10.3390/ma14081941
Nowak T, Patalas F, Karolak A. Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects. Materials. 2021; 14(8):1941. https://doi.org/10.3390/ma14081941
Chicago/Turabian StyleNowak, Tomasz, Filip Patalas, and Anna Karolak. 2021. "Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects" Materials 14, no. 8: 1941. https://doi.org/10.3390/ma14081941
APA StyleNowak, T., Patalas, F., & Karolak, A. (2021). Estimating Mechanical Properties of Wood in Existing Structures—Selected Aspects. Materials, 14(8), 1941. https://doi.org/10.3390/ma14081941






