Theoretical Local Buckling Behavior of Thin-Walled UHPC Flanges Subjected to Pure Compressions
Abstract
:1. Introduction


2. Material Properties of UHPC
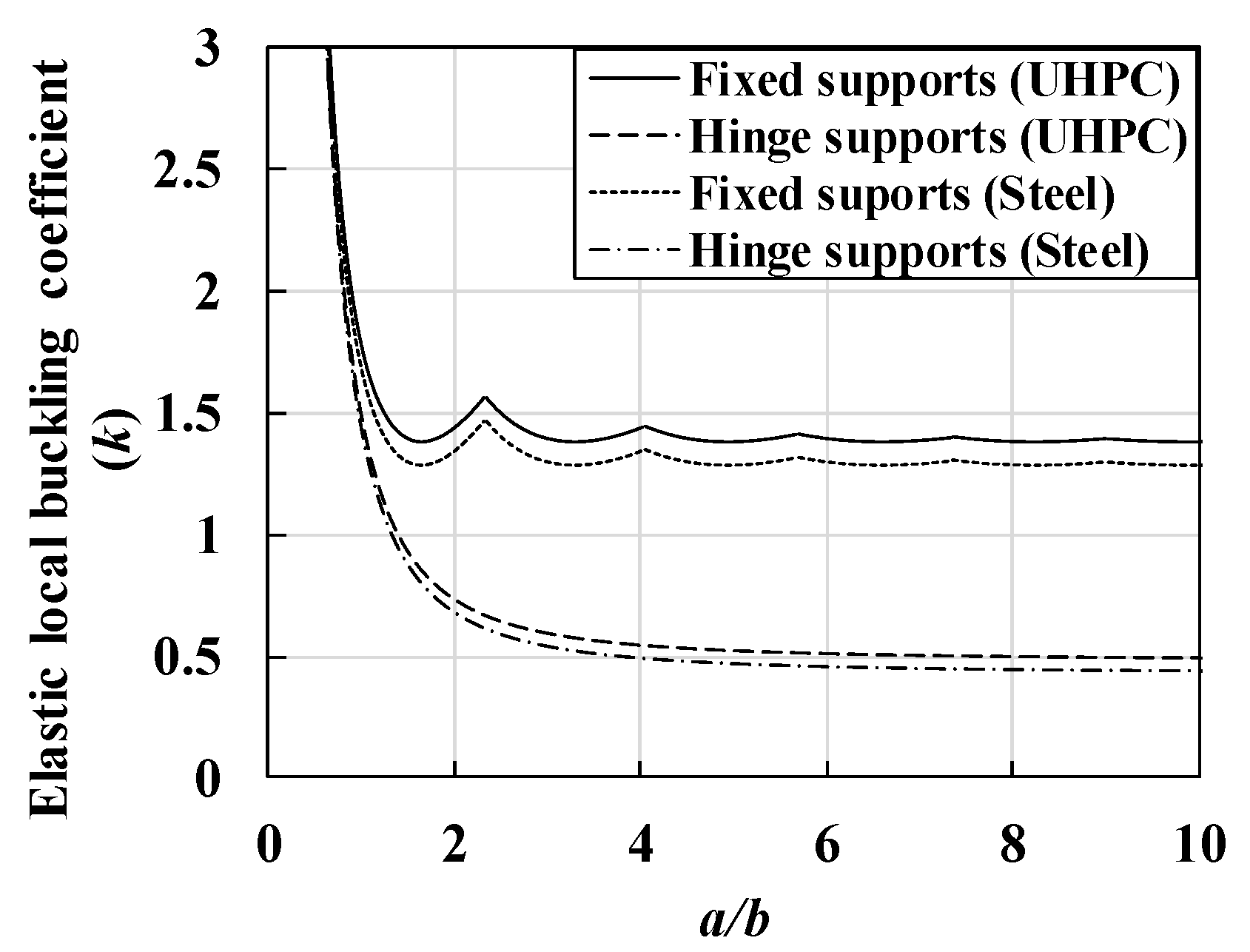
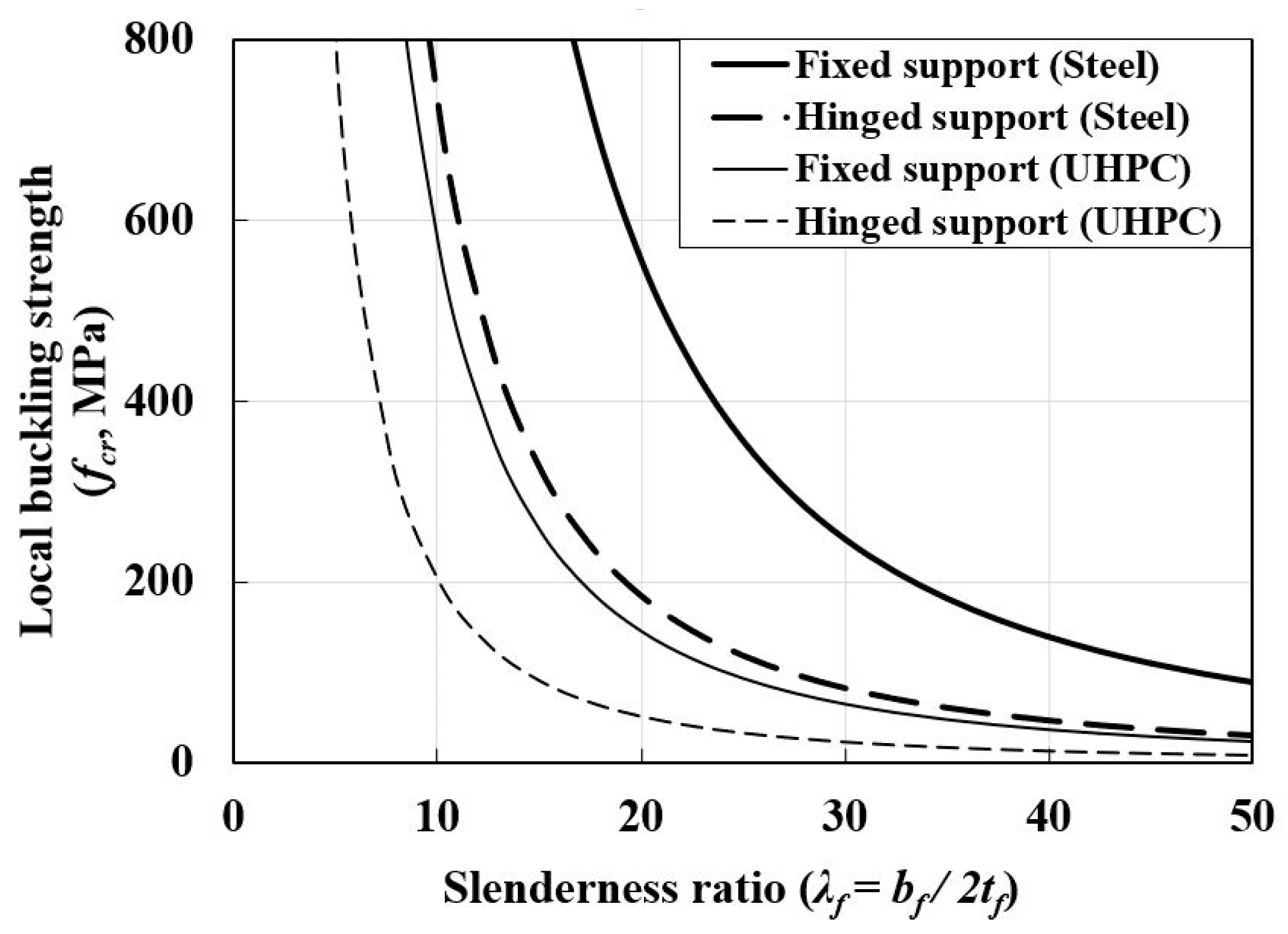
3. Theoretical Elastic Local Buckling Strength of Thin-Walled UHPC Flanges
4. Inelastic Local Buckling of Thin-Walled UHPC Flanges Based on FEA
4.1. Overview of FEA
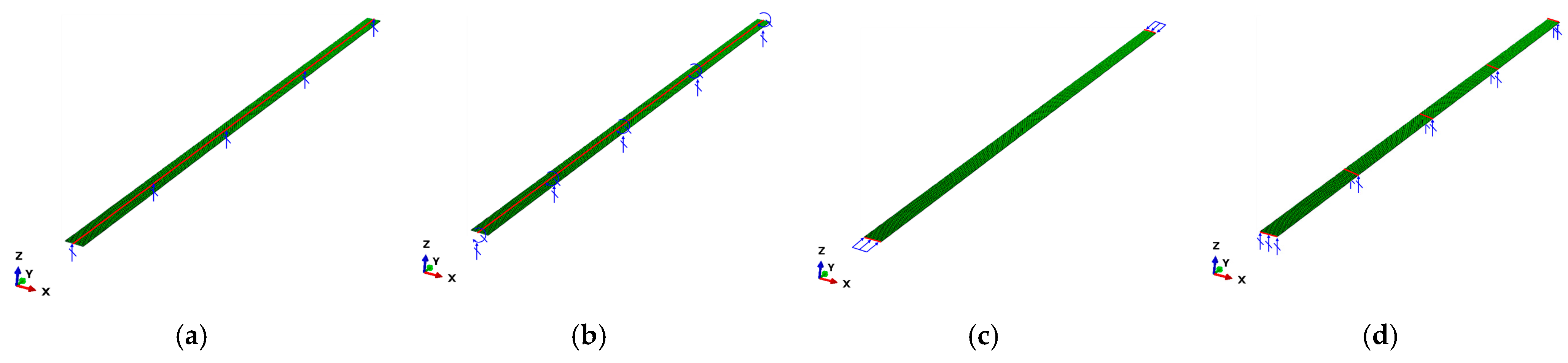
4.1.1. FEA Models
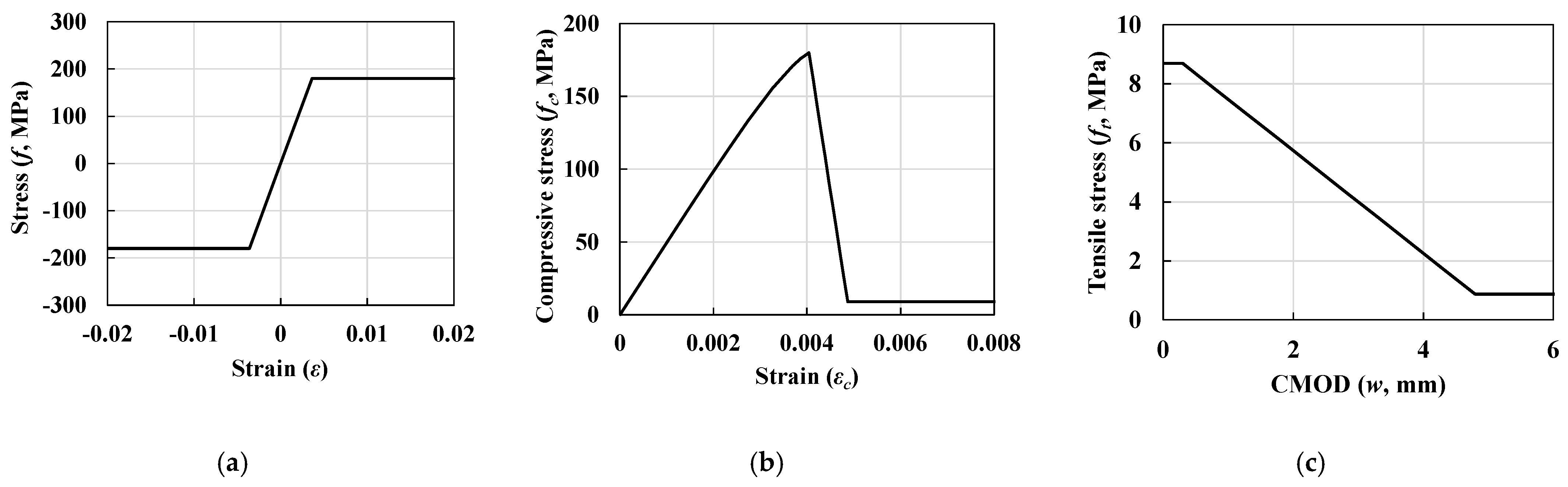
4.1.2. Material Properties for FEA
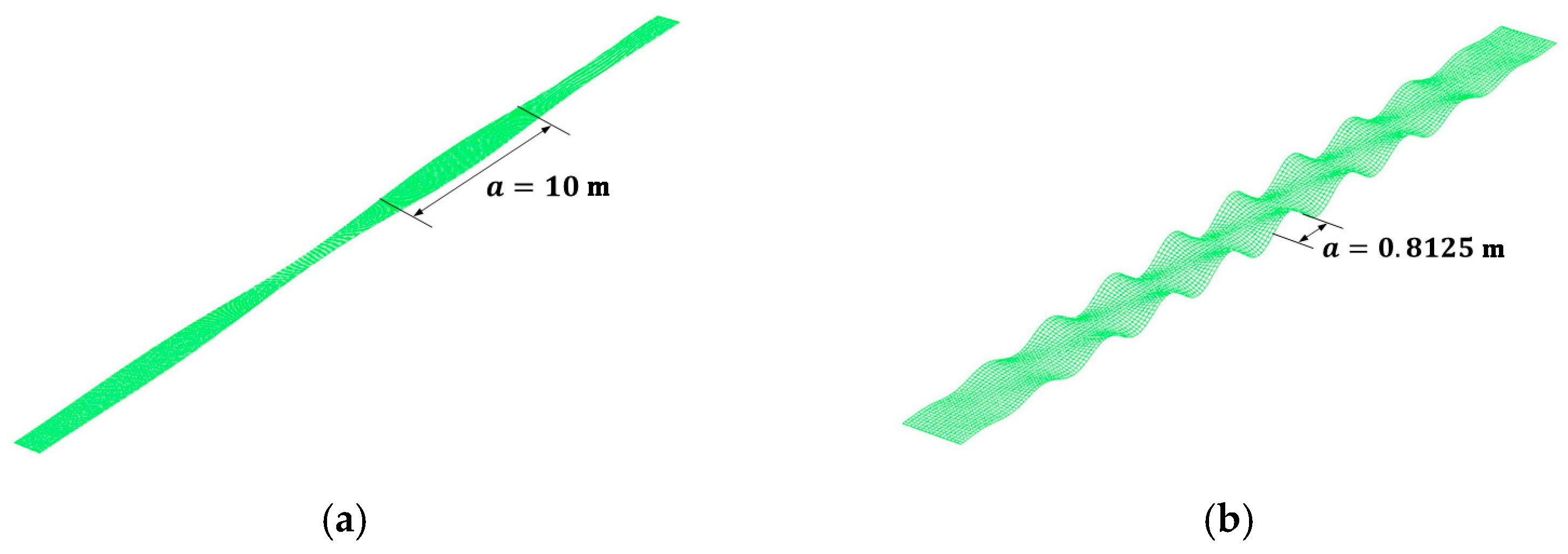
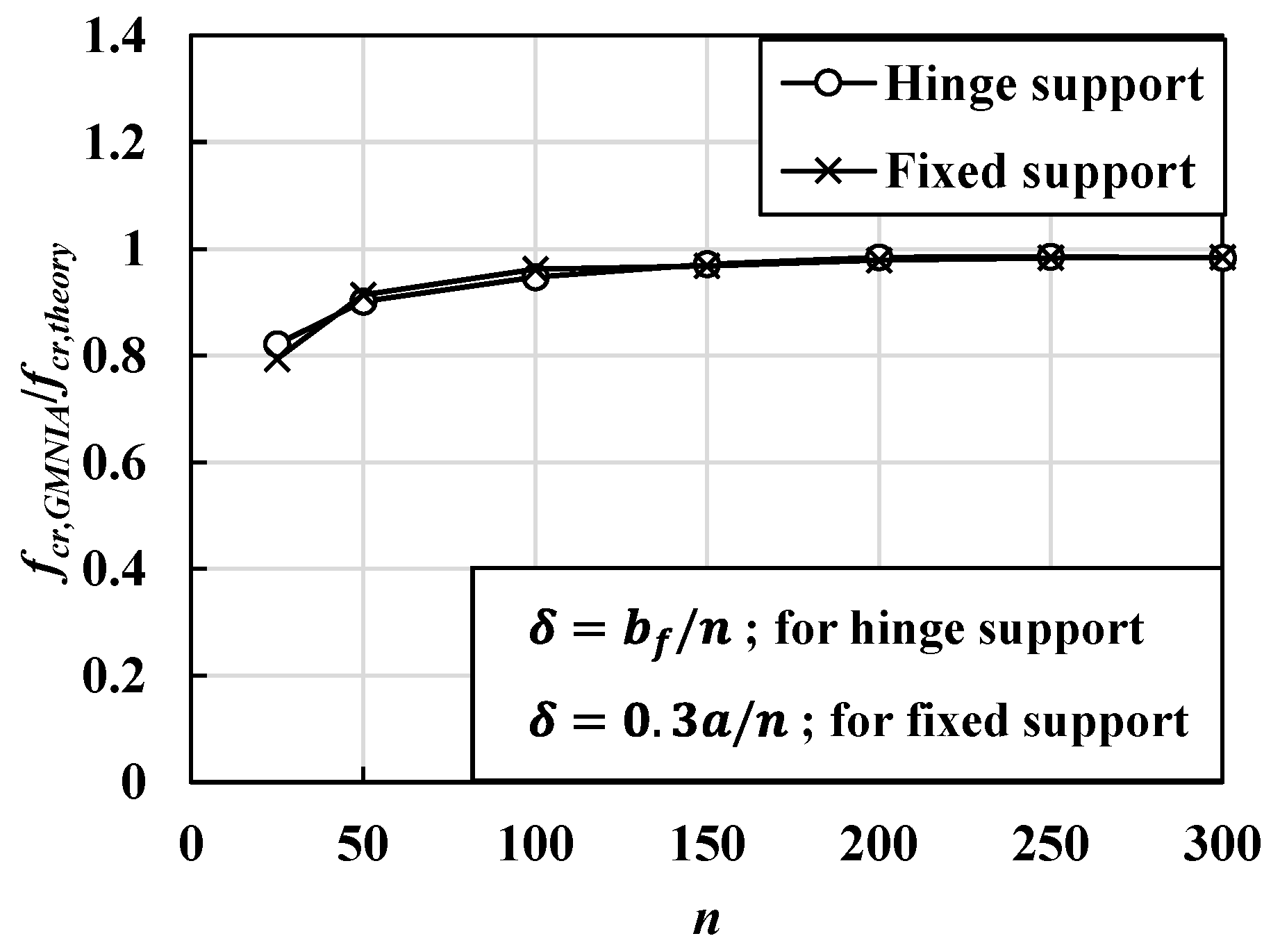
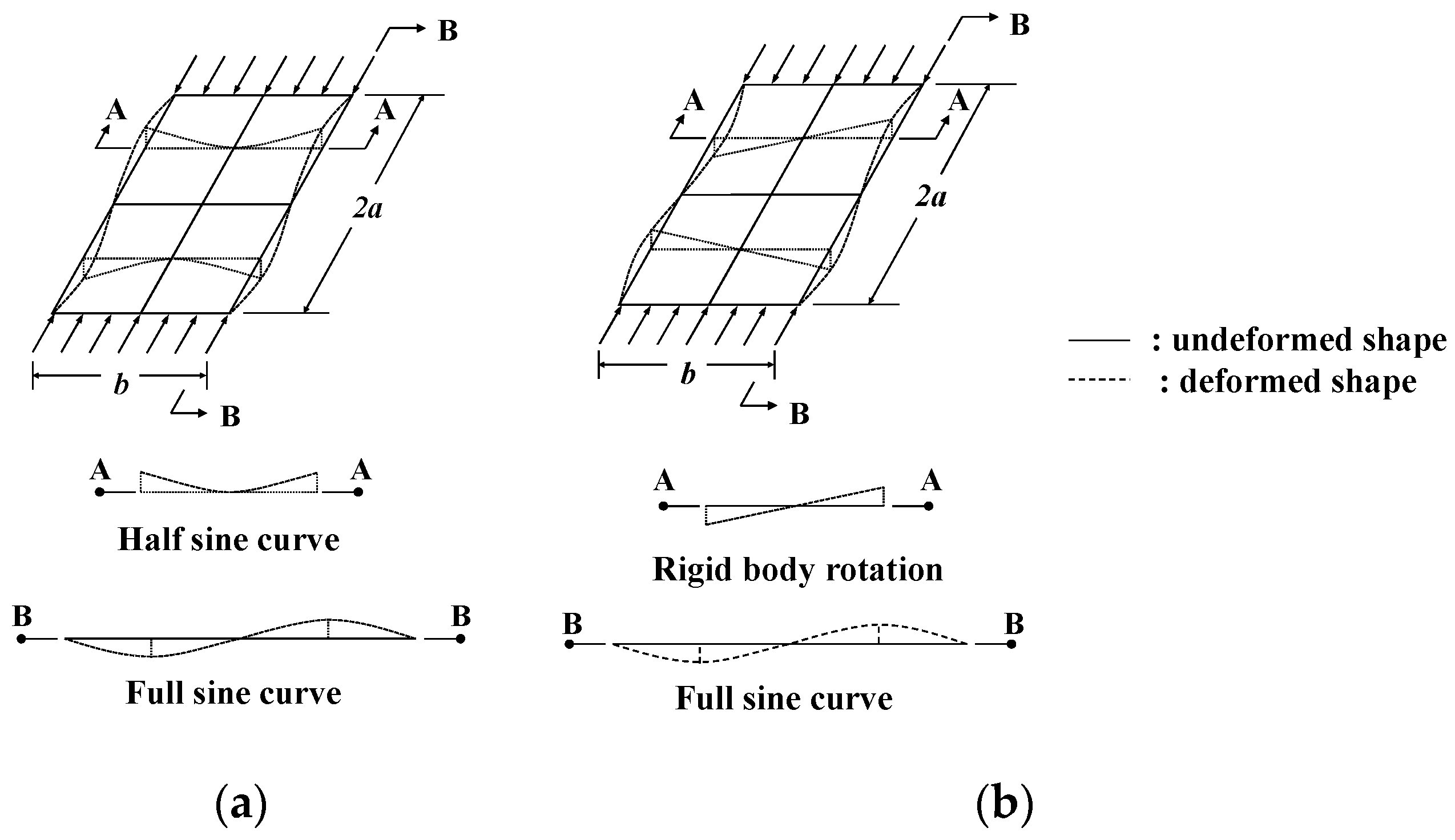
4.1.3. Initial Imperfections
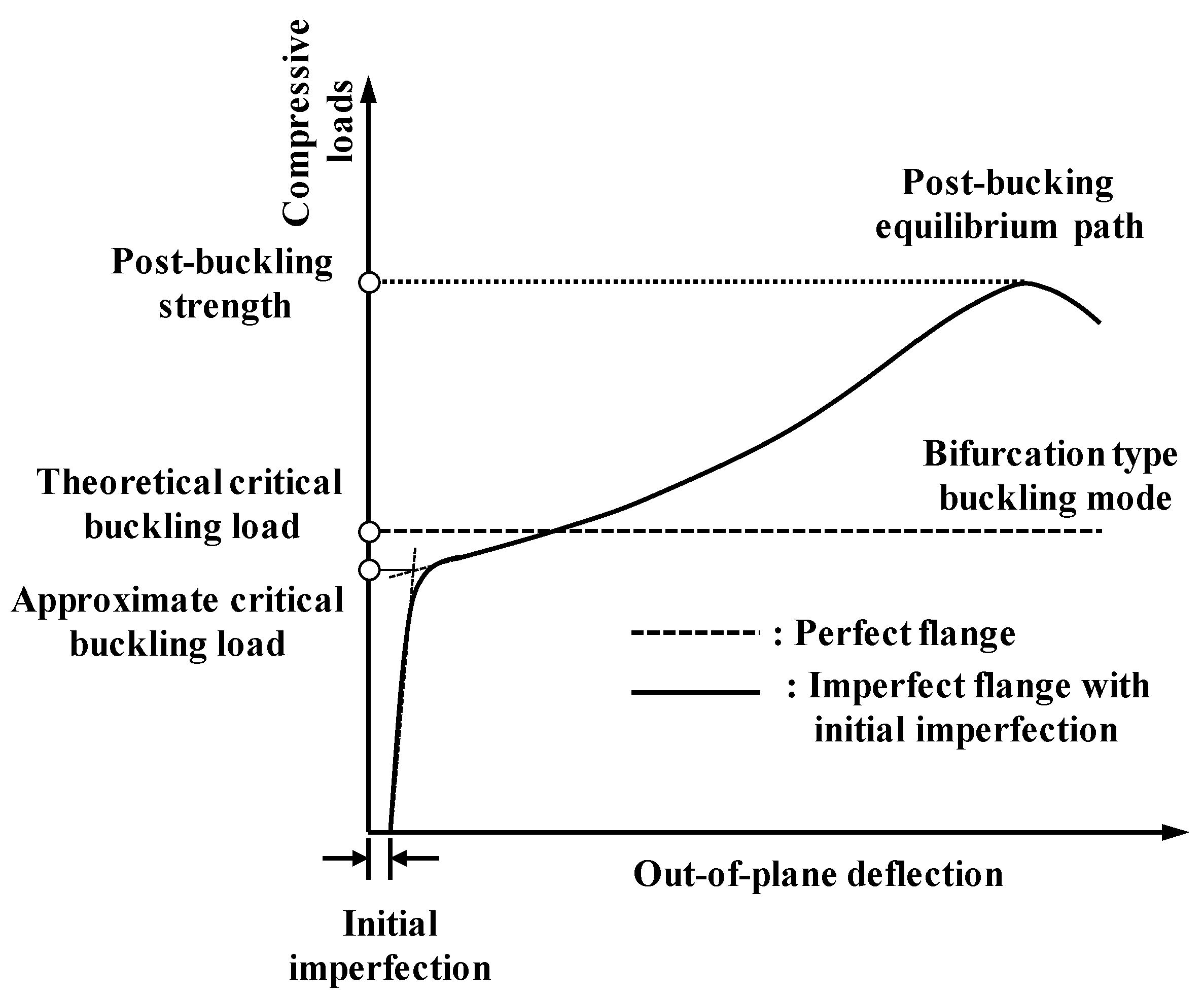
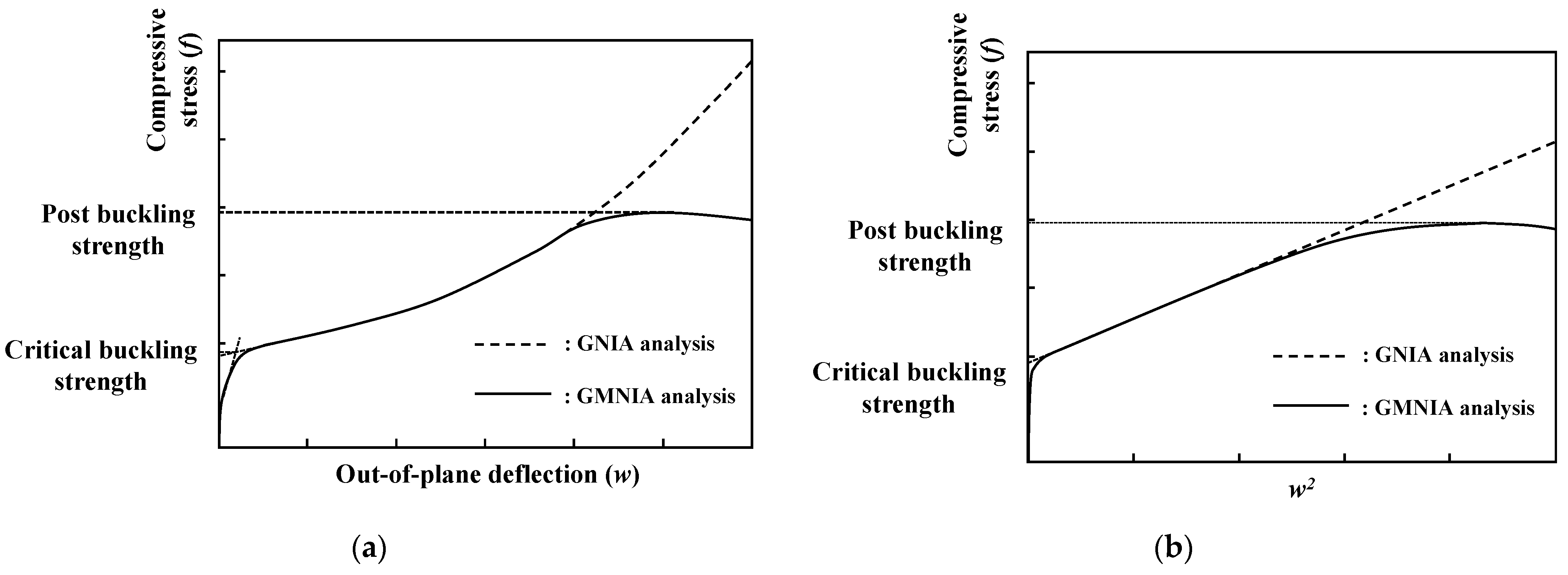
4.1.4. Definition of Critical and Post-Buckling Strength
4.2. Estimation of Inelastic Local Buckling Strength of Thin-Walled UHPC Flanges
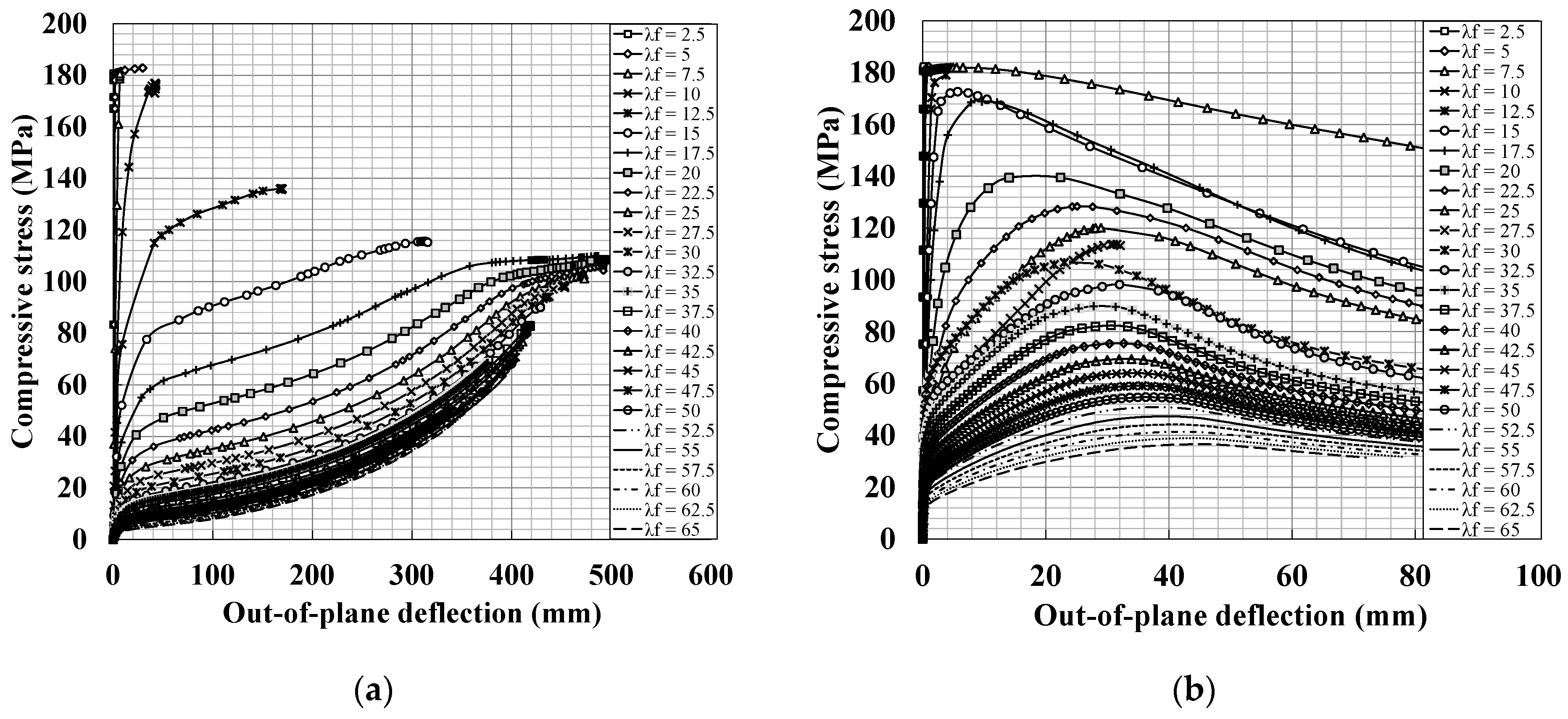
4.2.1. Axial Compressive Strength and Out-of-Plane Displacement Relationships
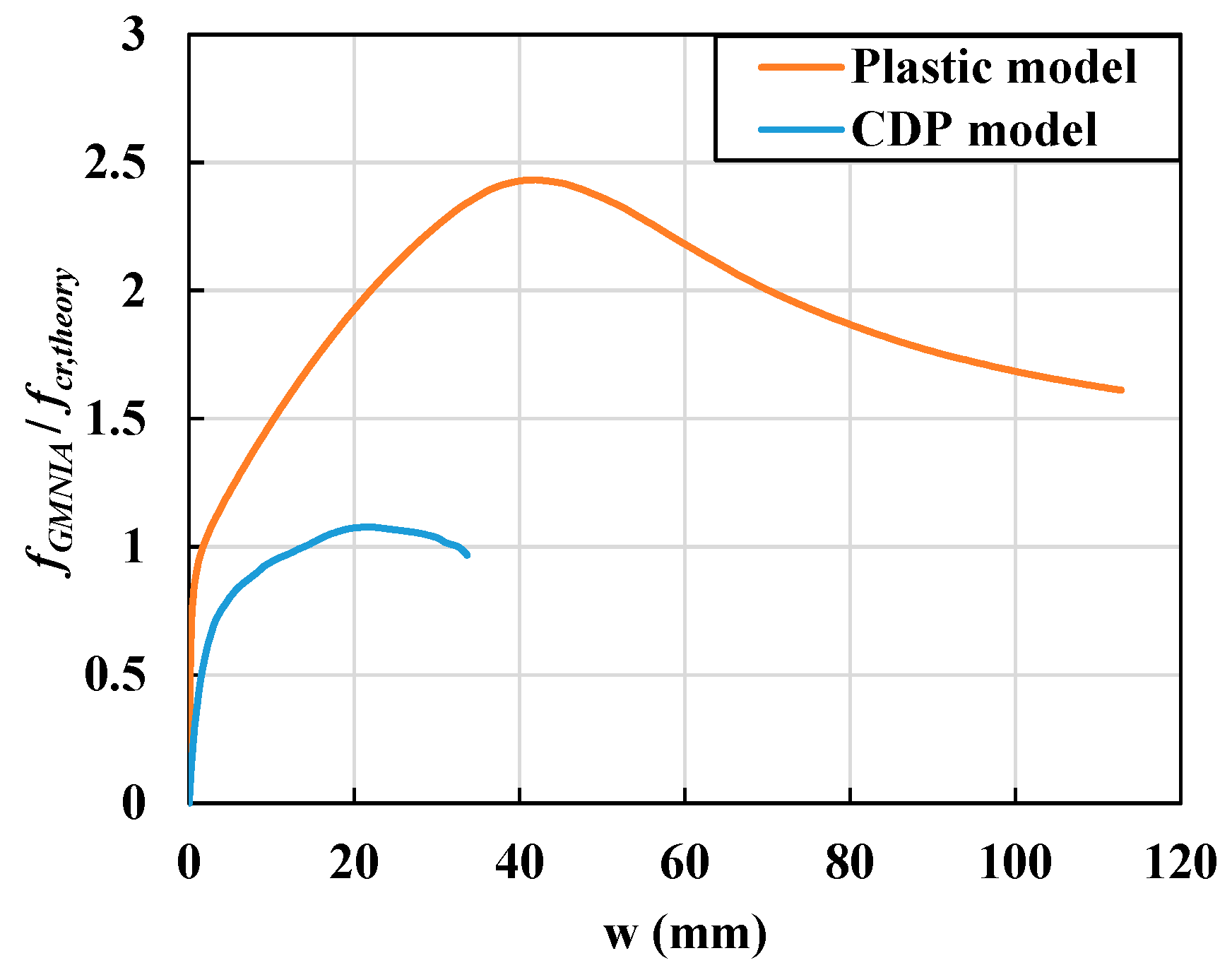
- Elastic-Perfectly Plastic Model: Steel Flanges
- CDP Model: UHPC Flanges
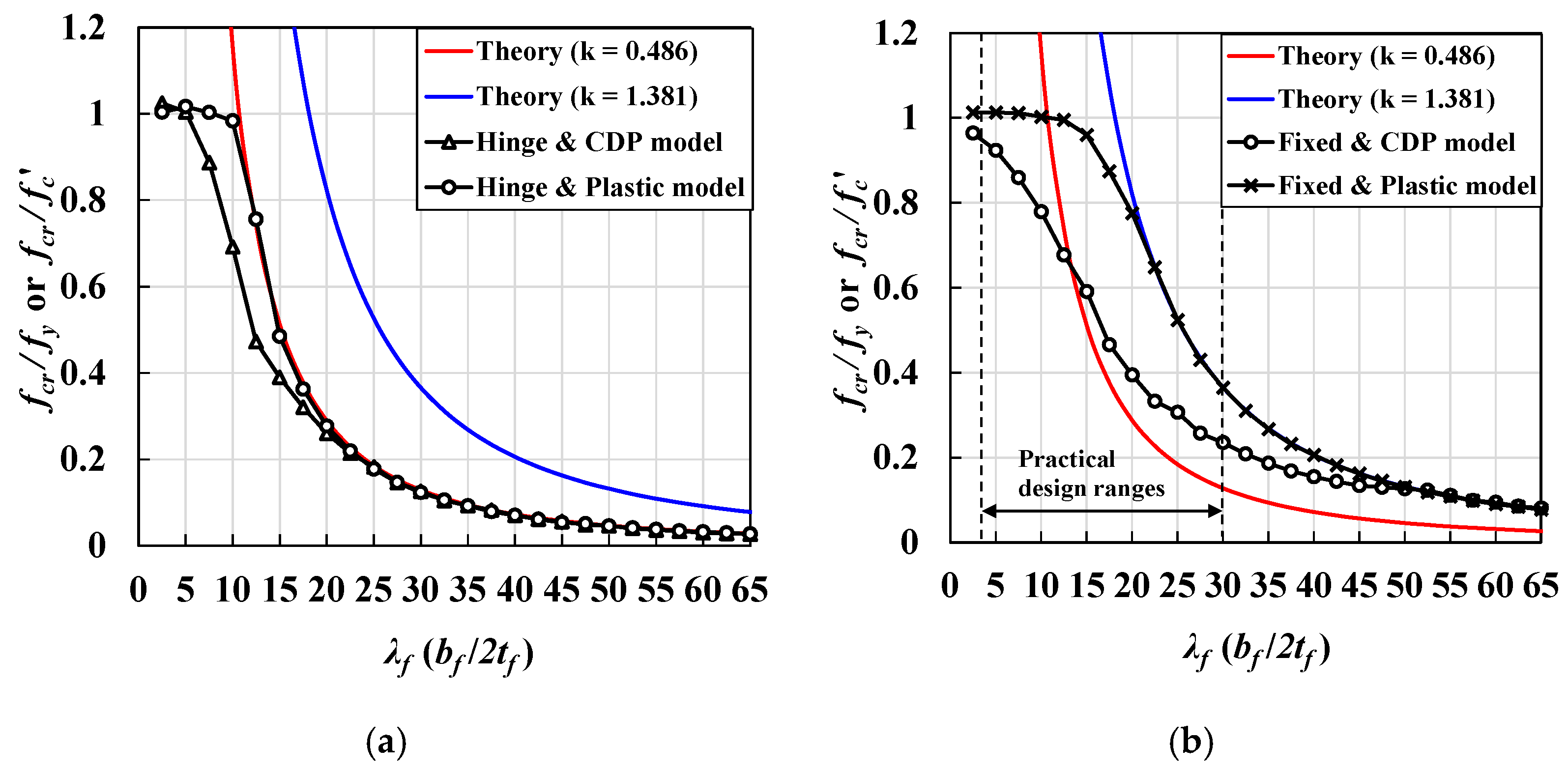
4.2.2. Inelastic Local Buckling Strength of UHPC Flanges
5. Evaluation of FEA Approaches Based on Test Data
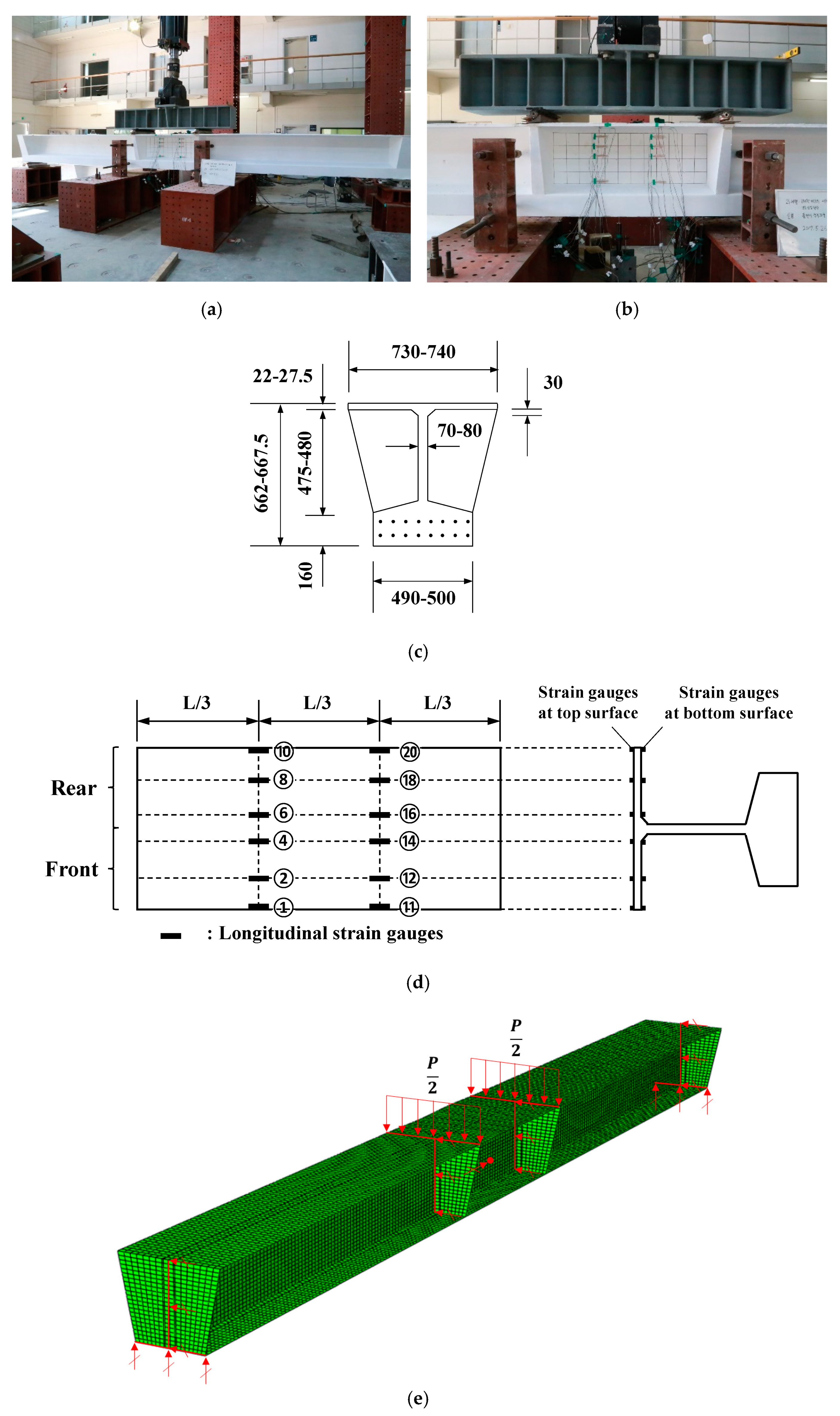
5.1. Summary of the Experimental Test in the Literature
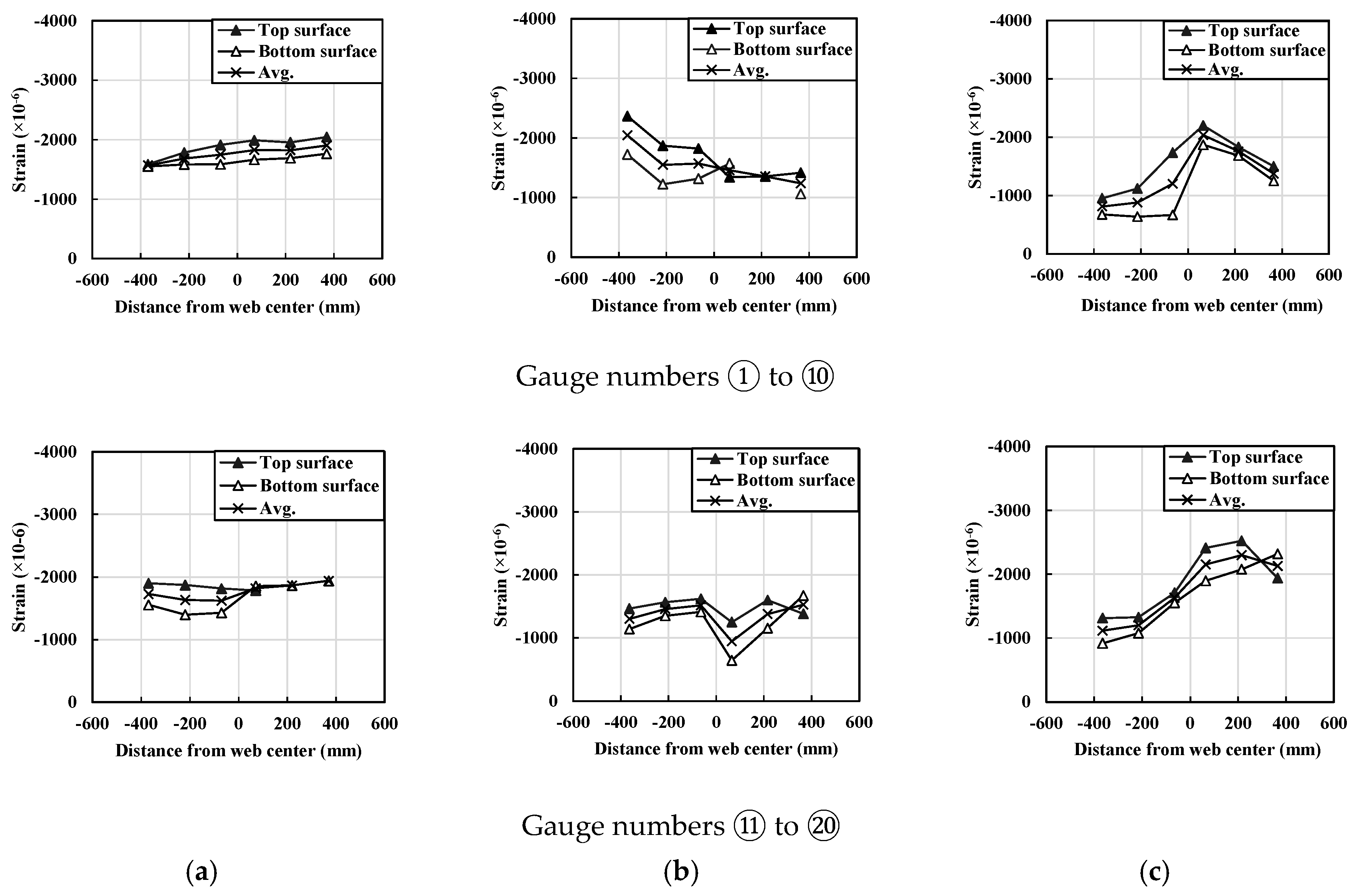
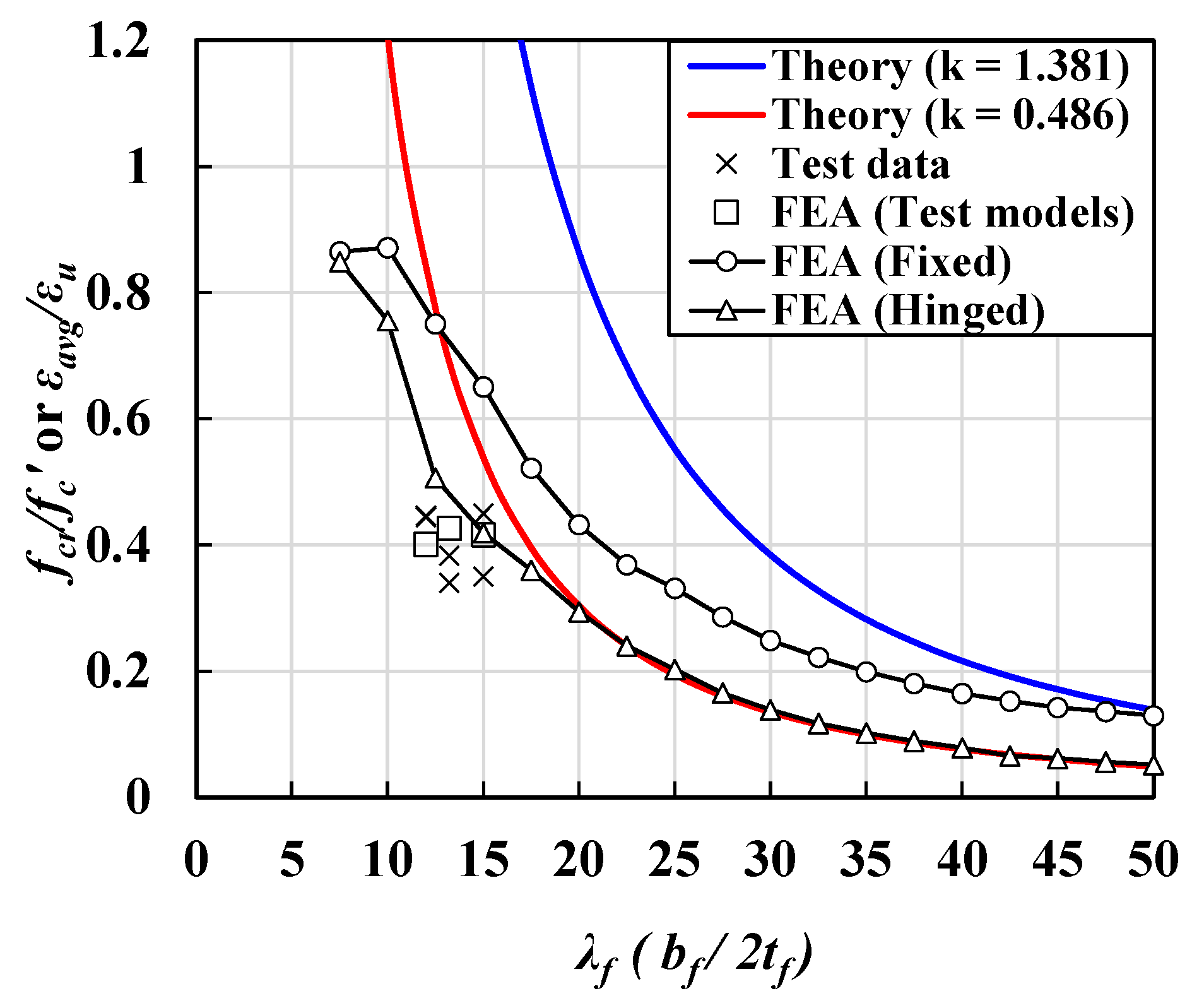
5.2. Comparisions between FEA and Test Data
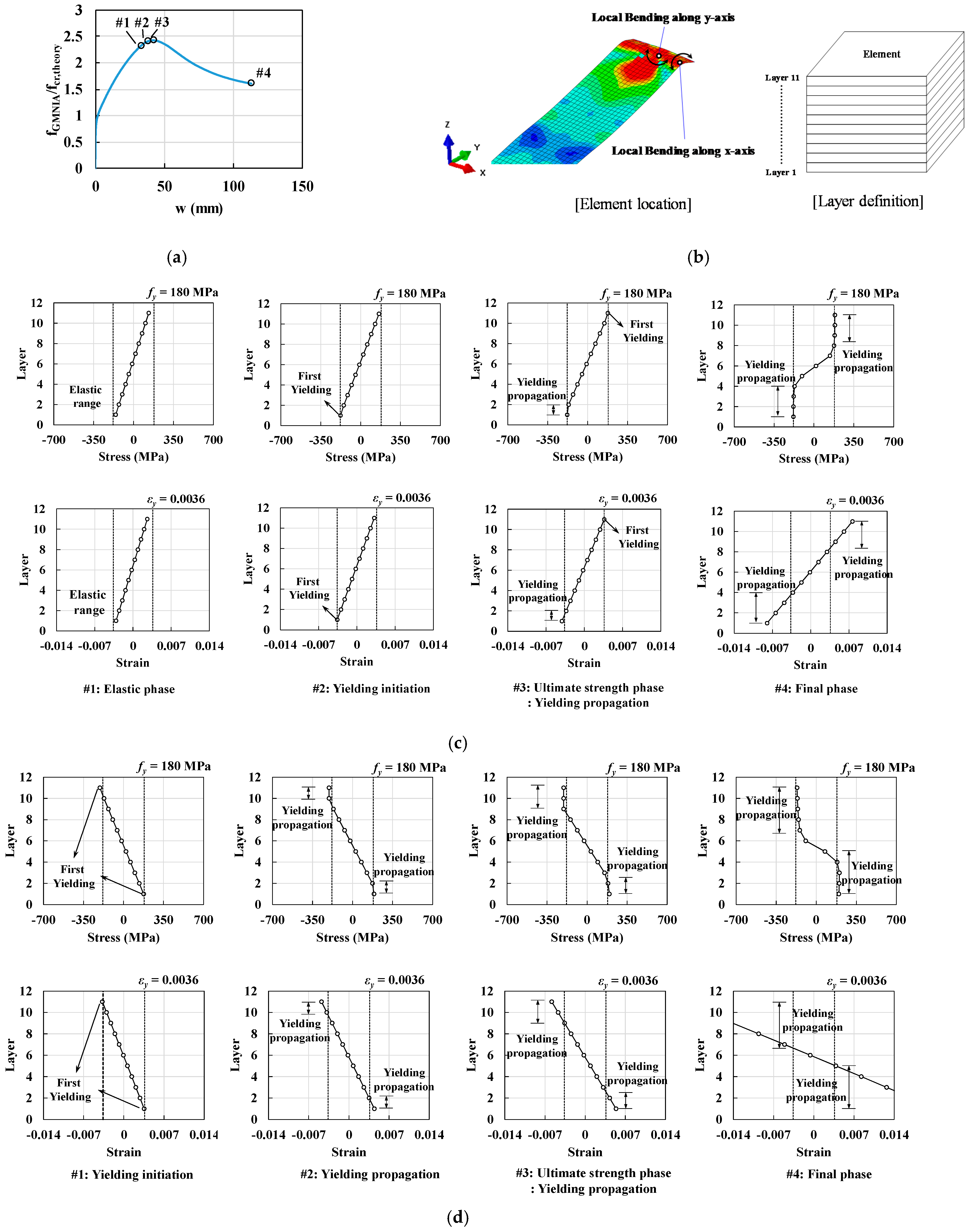
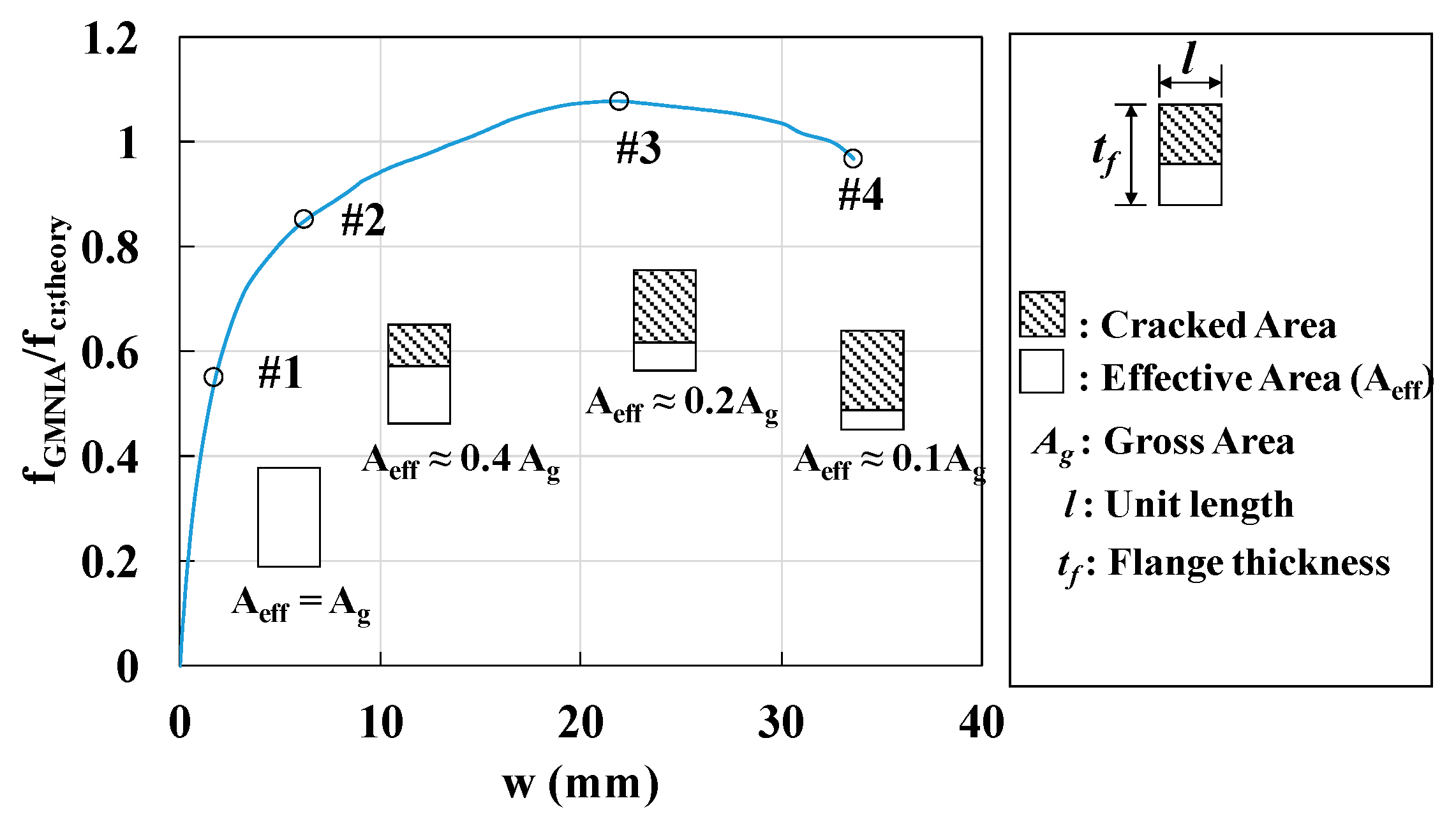
6. Characteristic of Local Buckling Behavior of Thin-Walled UHPC Flanges
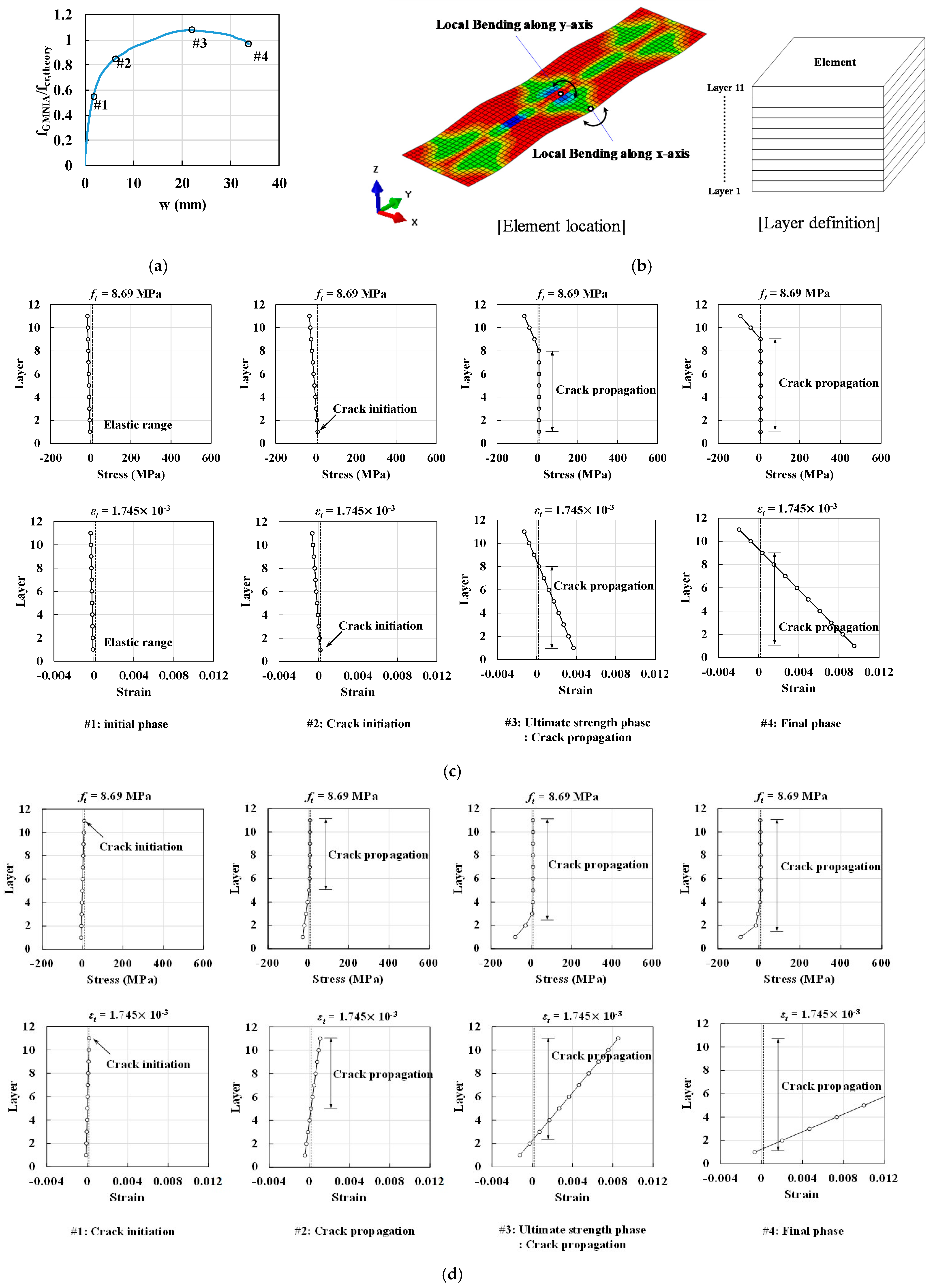
6.1. Inelastic Local Buckling Behavior of UHPC Flanges
6.2. Estimation of Local Buckling Behavior of UHPC Flanges
7. Conclusions
- The elastic buckling strength of UHPC flanges was affected by boundary conditions and Poisson’s ratio. Although the UHPC flanges exhibited a higher elastic buckling coefficient than the steel flanges, the buckling strength of UHPC flanges possessed ¼ times lower values than that of the steel flanges.
- Nonlinear finite element analysis strategies to simulate the local buckling behavior of UHPC flanges were established based on geometric and material nonlinear analysis with imperfections (GMNIA). It was verified based on test data conducted in the literature. The finite element analysis results and test data show good correlations in accordance with maximum average strain values along with the longitudinal directions.
- The post-buckling strength of UHPC flanges was found to be considerably lower than that of the reference steel flanges, under both hinged and fixed support conditions. Particularly, UHPC flanges with fixed support conditions were susceptible to a considerable reduction in post-buckling strength because these flanges underwent local bending and tensile cracks caused by simultaneous longitudinal and transverse stress components.
- Considering practical deck designs, local buckling of the UHPC flange deck could potentially exist within the design range with severe cases. In these cases, realistic buckling modes may be considered as the inelastic local buckling instead of elastic local buckling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Larrard, F.; Sedran, T. Optimization of Ultra-High-Performance Concrete by the Use of a Packing Model. Cem. Concr. Res. 1994, 24, 997–1008. [Google Scholar] [CrossRef]
- Richard, P.; Cheyrezy, M. Composition of Reactive Powder Concrete. Cem. Concr. Res. 1995, 25, 1501–1511. [Google Scholar] [CrossRef]
- Graybeal, B.A. Material Property Characterization of Ultra-High Performance Concrete; FHWA: Washington, WA, USA, 2006.
- Rossi, P.; Arca, A.; Parant, E.; Fakhri, P. Bending and Compressive Behaviours of a new cement composite. Cem. Concr. Res. 2005, 35, 27. [Google Scholar] [CrossRef]
- KICT. SUPER Bridge 200/Development of Economic and Durable Hybrid Cable Stayed Bridges; Korea Istitute of Construction Technology: Goyang-si, Korea, 2012. [Google Scholar]
- SETRA-AFGC. Ultra High Performance Fibre-Reinforced Concretes, interim Recommendations; AFGC Groupe de Travail BUP: Paris, France, 2002. [Google Scholar]
- JSCE. Recommendations for Design and Consruction of Ultra High Strength Fiber Reinforced Concrete Structures (Draft); Japan Society of Civil Engineers: Tokyo, Japan, 2004. [Google Scholar]
- KCI. Design Guidelines for K-UHPC; Korea Concrete Institute: Seoul, Korea, 2014. [Google Scholar]
- SAA. Australian Standard: Concrete Structures, 2nd ed.; Vols. AS3600-94; SAA: Sydney, Australia, 1996. [Google Scholar]
- Marshall, W.T. The Lateral Stability of Reinforced Concrete Beams. J. Inst. Civ. Eng. 1948, 30, 194–196. [Google Scholar] [CrossRef]
- Hansel, W.; Winter, G. Lateral Stability of Reinforced Concrete Beams. Am. Concr. Inst. J. 1959, 56, 193–214. [Google Scholar]
- Sant, J.K.; Bletzacker, R.W. Experimental Study of Lateral Stability of Reinforced Concrete Beams. Am. Concr. Inst. J. 1961, 58, 713–736. [Google Scholar]
- Massey, C. Lateral Instability of Reinforced Concrete Beams under Uniform Bending Moments. Am. Concr. Inst. J. 1967, 64, 164–172. [Google Scholar]
- Revathi, P.; Menon, D. Estimation of Critical Buckling Moments in Slender Reinforced Concrete Beams. Am. Concr. Inst. J. 2006, 103, 296–303. [Google Scholar]
- Girija, K.; Menon, D. Reduction in Flexural Strength in Rectangular RC Beams due to Slenderness. Eng. Struct. 2011, 33, 2398–2406. [Google Scholar] [CrossRef]
- Hurff, J.B.; Kahn, L.F. Lateral-Torsional Buckling of Structural Concrete Beams: Experimental and Analytical Study. J. Struct. Eng. 2012, 138, 1138–1148. [Google Scholar] [CrossRef]
- Kalkan, I. Lateral Torsional Buckling of Rectangular Reinforced Concrete Beams with Initial Imperfections. Aci Struct. J. 2014, 111, 71–81. [Google Scholar]
- Kalkan, I.; Bocek, M.; Aykac, S. Lateral Stability of Reinforced-Concrete Beams with Initial Imperfections. Proc. Inst. Civ. Eng. Strut. Build. 2016, 169, 727–740. [Google Scholar] [CrossRef]
- ACI. ACI 318-14: Building Code Requirements for Structural Concrete and Commentary; American Concrete Institution: Indianapolis, IN, USA, 2014. [Google Scholar]
- Illich, G.; Tue, N.V.; Freytag, B. Schlanke vorgespannte Stützen aus UHPC-Experimentelle Untersuchung und Nachrechnung”. Beton Stahlbetonbau 2014, 109, 534–543. [Google Scholar] [CrossRef]
- Lee, K.; Andrawes, B.; Lee, J.; Kang, Y.J. Lateral Torsional Buckling of Ultra-High-Performance-Fibrereinforced Concrete Girders. Mag. Concr. Res. 2020, 72, 820–836. [Google Scholar] [CrossRef]
- Lee, J. Inelastic Flange Local Buckling Strength of Ultra High Performence Concrete I-Girders; Korea University: Seoul, Korea, 2018. [Google Scholar]
- Lee, J.; Byun, N.J.; Lee, Y.W.; Kang, S.Y.; Kang, Y.J. Experimental and Numerical Evaluations of Local Buckling in Thin-walled UHPFRC Flanges. Thin-Walled Struct. 2021, 163, 107662. [Google Scholar] [CrossRef]
- Ma, J.; Dehn, F.; Tue, N.V.; Orgass, M.; Schmidt, D. Comparative Investigations on Ultra-high Performance Concrete with and without Coarse Aggregates. In Proceedings of International Symposium on Ultra High Performance Concrete (UHPC); Kassel University Press: Kassel, Germany, 2004. [Google Scholar]
- AASHTO. Aashto Lrfd Bridge Design Specifications, 8th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2020. [Google Scholar]
- Lundquist, E.E.; Stowell, E.Z. Critical Compressive Stress for Outstanding Flanges; NACA Technical Report, Report No. 734; US Government Printing Office: Washington, DC, USA, 1 April 1941.
- SIMULIA. ABAQUS Manual 6.18; SIMULIA: Johnston, RI, USA, 2018. [Google Scholar]
- Kappos, A.J.; Konstantinidis, D. Statistical Analysis of Confined High Strength Concrete. Mater. Struct. 1999, 32, 734. [Google Scholar] [CrossRef]
- AWS. Bridge Welding Code, ANSI/AASHTO/AWS L1.5-95; Joint Publication of American Association of State and High-Way Transportation Officials and American Welding Society; American Welding Society: Miami, FL, USA, 1995. [Google Scholar]
- Roorda, J.; Venkataramaiah, K.R. Analysis of Local Plate Buckling Experimental Data. In Proceedings of International Specialty Conference on Cold-formed Steel Structures; Missouri S&T: Rolla, MO, USA, 1982. [Google Scholar]



| W/B | Cement | Fine Sand | Silica Fume | Glass Powder | Water Reducer | Steel Fiber (Volume) |
|---|---|---|---|---|---|---|
| 0.18 | 1 | 0.92 | 0.25 | 0.25 | 0.0108 | 0.22–0.31 |
| Cases | ||||
|---|---|---|---|---|
| Hinge Support | Fixed Support | |||
| Steel | 205,000 | 0.3 | 0.426 | 1.289 |
| UHPC | 49,790 | 0.2 | 0.486 | 1.381 |
| Cases | (MPa) | or (MPa) | or (MPa) | (mm) | ||
|---|---|---|---|---|---|---|
| Steel | 205,000 | 0.3 | 180 | 180 | 1000 | 2.5–65 (26 cases at 2.5 intervals) |
| UHPC | 49,790 | 0.2 | 8.7 |
| (MPa) | (MPa) | (MPa) | (mm) | (mm) | |
|---|---|---|---|---|---|
| 49,790 | 180 | 0.0042 | 8.67 | 0.3 | 5.3 |
| (MPa) | (MPa) | (MPa) | (mm) | (mm) | |
|---|---|---|---|---|---|
| 47,166 | 162 | 0.00396 | 8.24 | 0.22 | 6.43 |
| Specimens | (mm) | (mm) | Test | FEA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
( = 1.7) | ||||||||||||
| Gauges ① to ⑩ |
Gauges ① to ⑩ |
Gauges ① to ⑩ |
Gauges ① to ⑩ | |||||||||
| Specimen #1 | 730 | 27.5 | 12 | 2221 | 1103 | 0.497 | 0.00396 | 0.001766 | 0.00176 | 0.446 | 0.444 | 0.401 |
| Specimen #2 | 730 | 25 | 13.2 | 2056 | 1005 | 0.489 | 0.00396 | 0.001516 | 0.001346 | 0.383 | 0.34 | 0.426 |
| Specimen #3 | 740 | 22 | 15 | 1984 | 1111 | 0.56 | 0.00396 | 0.001387 | 0.001779 | 0.35 | 0.45 | 0.416 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, S.; Lee, K.; Kang, Y.J. Theoretical Local Buckling Behavior of Thin-Walled UHPC Flanges Subjected to Pure Compressions. Materials 2021, 14, 2130. https://doi.org/10.3390/ma14092130
Lee J, Kim S, Lee K, Kang YJ. Theoretical Local Buckling Behavior of Thin-Walled UHPC Flanges Subjected to Pure Compressions. Materials. 2021; 14(9):2130. https://doi.org/10.3390/ma14092130
Chicago/Turabian StyleLee, Jeonghwa, Seungjun Kim, Keesei Lee, and Young Jong Kang. 2021. "Theoretical Local Buckling Behavior of Thin-Walled UHPC Flanges Subjected to Pure Compressions" Materials 14, no. 9: 2130. https://doi.org/10.3390/ma14092130
APA StyleLee, J., Kim, S., Lee, K., & Kang, Y. J. (2021). Theoretical Local Buckling Behavior of Thin-Walled UHPC Flanges Subjected to Pure Compressions. Materials, 14(9), 2130. https://doi.org/10.3390/ma14092130








