Benchmark for the Coupled Magneto-Mechanical Boundary Value Problem in Magneto-Active Elastomers
Abstract
:1. Introduction
2. Benchmark Problem
2.1. Setup
2.2. Governing Equations
2.3. Constitutive Behavior
3. Numerical Approaches
3.1. Finite Element Approach
3.2. Grid-Based Spectral Approach
4. Results
4.1. Influence of the Sample Size
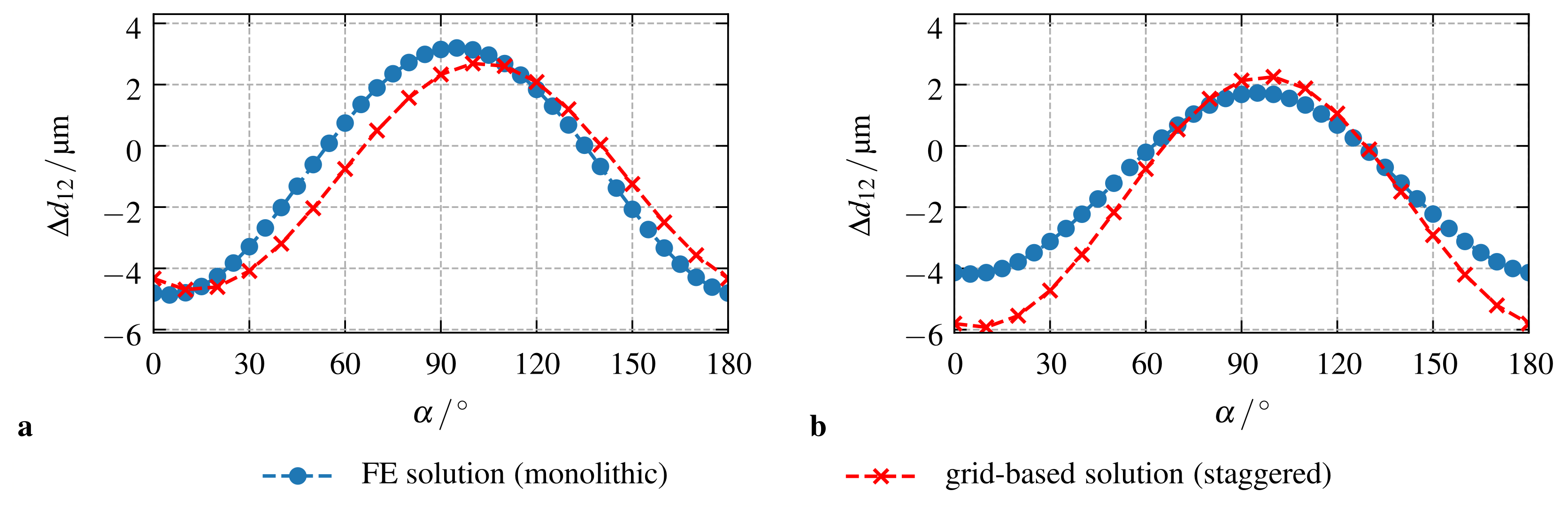
4.2. Comparison of the Numerical Simulation Frameworks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markert, B. Weak or Strong: On Coupled Problems in Continuum Mechanics. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2010. [Google Scholar] [CrossRef]
- Ashby, M.F. Physical Modelling of Materials Problems. Mater. Sci. Technol. 1992, 8, 102–111. [Google Scholar] [CrossRef]
- Larché, F.C.; Cahn, J.W. Overview No. 41 The Interactions of Composition and Stress in Crystalline Solids. Acta Metall. 1985, 33, 331–357. [Google Scholar] [CrossRef]
- Brigadnov, I.A.; Dorfmann, A. Mathematical Modeling of Magneto-Sensitive Elastomers. Int. J. Solids Struct. 2003, 40, 4659–4674. [Google Scholar] [CrossRef]
- Dargahi, A.; Sedaghati, R.; Rakheja, S. On the Properties of Magnetorheological Elastomers in Shear Mode: Design, Fabrication and Characterization. Compos. Part B Eng. 2019, 159, 269–283. [Google Scholar] [CrossRef]
- Becker, T.I.; Stolbov, O.V.; Borin, D.Y.; Zimmermann, K.; Raikher, Y.L. Basic Magnetic Properties of Magnetoactive Elastomers of Mixed Content. Smart Mater. Struct. 2020, 29, 075034. [Google Scholar] [CrossRef]
- Metsch, P.; Schmidt, H.; Sindersberger, D.; Kalina, K.A.; Brummund, J.; Auernhammer, G.K.; Monkman, G.J.; Kästner, M. Field-Induced Interactions in Magneto-Active Elastomers—A Comparison of Experiments and Simulations. Smart Mater. Struct. 2020, 29, 085026. [Google Scholar] [CrossRef]
- Park, J.; Darvishi Kamachali, R.; Kim, S.D.; Kim, S.H.; Oh, C.S.; Schwarze, C.; Steinbach, I. First Evidence for Mechanism of Inverse Ripening from Insitu TEM and Phasefield Study of δ-Precipitation in an AlLi Alloy. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Darvishi Kamachali, R.; Schwarze, C.; Lin, M.; Diehl, M.; Shanthraj, P.; Prahl, U.; Steinbach, I.; Raabe, D. Numerical Benchmark of Phasefield Simulations with Elastic Strains: Precipitation in the Presence of Chemomechanical Coupling. Comput. Mater. Sci. 2018, 155. [Google Scholar] [CrossRef] [Green Version]
- Ginder, J.M.; Clark, S.M.; Schlotter, W.F.; Nichols, M.E. Magnetostrictive Phenomena in Magnetorheological Elastomers. Int. J. Mod. Phys. B 2002, 16, 2412–2418. [Google Scholar] [CrossRef]
- Guan, X.; Dong, X.; Ou, J. Magnetostrictive Effect of Magnetorheological Elastomer. J. Magn. Magn. Mater. 2008, 320, 158–163. [Google Scholar] [CrossRef]
- Bodelot, L.; Voropaieff, J.P.; Pössinger, T. Experimental Investigation of the Coupled Magneto-Mechanical Response in Magnetorheological Elastomers. Exp. Mech. 2017, 58, 207–221. [Google Scholar] [CrossRef] [Green Version]
- Metsch, P.; Romeis, D.; Kalina, K.A.; Raßloff, A.; Saphiannikova, M.; Kästner, M. Magneto-Mechanical Coupling in Magneto-Active Elastomers. Materials 2021, 14, 434. [Google Scholar] [CrossRef]
- Varga, Z.; Filipcsei, G.; Zrínyi, M. Magnetic Field Sensitive Functional Elastomers with Tuneable Elastic Modulus. Polymer 2006, 47, 227–233. [Google Scholar] [CrossRef]
- Borin, D.Y.; Stepanov, G.V.; Odenbach, S. Tuning the Tensile Modulus of Magnetorheological Elastomers with Magnetically Hard Powder. J. Phys. Conf. Ser. 2013, 412, 012040. [Google Scholar] [CrossRef]
- Kalina, K.A.; Metsch, P.; Kästner, M. Microscale Modeling and Simulation of Magnetorheological Elastomers at Finite Strains: A Study on the Influence of Mechanical Preloads. Int. J. Solids Struct. 2016, 102–103, 286–296. [Google Scholar] [CrossRef]
- Borin, D.; Odenbach, S.; Stepanov, G. Stress Induced by the Striction of Hybrid Magnetoactive Elastic Composites. J. Magn. Magn. Mater. 2019, 470, 85–88. [Google Scholar] [CrossRef]
- Roache, P.J. Code Verification by the Method of Manufactured Solutions. J. Fluids Eng. 2002, 124, 4–10. [Google Scholar] [CrossRef]
- Münch, I. Error Measurement and FEM Benchmark for Phase Field Modeling. PAMM 2015, 15, 599–600. [Google Scholar] [CrossRef]
- Jokisaari, A.M.; Voorhees, P.W.; Guyer, J.E.; Warren, J.; Heinonen, O.G. Benchmark Problems for Numerical Implementations of Phase Field Models. Comput. Mater. Sci. 2017, 126, 139–151. [Google Scholar] [CrossRef] [Green Version]
- Schröder, J.; Wick, T.; Reese, S.; Wriggers, P.; Müller, R.; Kollmannsberger, S.; Kästner, M.; Schwarz, A.; Igelbüscher, M.; Viebahn, N.; et al. A Selection of Benchmark Problems in Solid Mechanics and Applied Mathematics. Arch. Comput. Methods Eng. 2021, 28, 713–751. [Google Scholar] [CrossRef]
- Ginder, J.M.; Nichols, M.E.; Elie, L.D.; Tardiff, J.L. Magnetorheological Elastomers: Properties and Applications. In Smart Structures and Materials 1999: Smart Materials Technologies; Wuttig, M.R., Ed.; SPIE: Belingham, WA, USA, 1999; Volume 3675, pp. 131–138. [Google Scholar] [CrossRef]
- Abramchuk, S.; Kramarenko, E.; Stepanov, G.; Nikitin, L.V.; Filipcsei, G.; Khokhlov, A.R.; Zrínyi, M. Novel Highly Elastic Magnetic Materials for Dampers and Seals: Part I. Preparation and Characterization of the Elastic Materials. Polym. Adv. Technol. 2007, 18, 883–890. [Google Scholar] [CrossRef]
- Pössinger, T. Experimental Characterization, Modeling and Simulation of Magneto-Rheological Elastomers. Ph.D. Thesis, École Polytechnique, Palaiseau, France, 2015. [Google Scholar]
- Moffett, M.B.; Clark, A.E.; Wun-Fogle, M.; Linberg, J.; Teter, J.P.; McLaughlin, E.A. Characterization of Terfenol-D for Magnetostrictive Transducers. J. Acoust. Soc. Am. 1991, 89, 1448–1455. [Google Scholar] [CrossRef]
- Domenjoud, M.; Berthelot, E.; Galopin, N.; Corcolle, R.; Bernard, Y.; Daniel, L. Characterization of Giant Magnetostrictive Materials under Static Stress: Influence of Loading Boundary Conditions. Smart Mater. Struct. 2019, 28, 095012. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Y.; Chen, K.; Dai, Z.; Ma, T.; Wang, Y.; Ren, S.; Deng, J.; Zhang, R.; Tian, F.; et al. Improved Magnetostriction in Galfenol Alloys by Aligning Crystal Growth Direction along Easy Magnetization Axis. Sci. Rep. 2020, 10, 20055. [Google Scholar] [CrossRef]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic Soft Continuum Robots. Sci. Robot. 2019, 4, 1–15. [Google Scholar] [CrossRef]
- Said, M.M.; Yunas, J.; Bais, B.; Hamzah, A.A.; Majlis, B.Y. The Design, Fabrication, and Testing of an Electromagnetic Micropump with a Matrix-Patterned Magnetic Polymer Composite Actuator Membrane. Micromachines 2017, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Skalski, P.; Kalita, K. Role of Magnetorheological Fluids and Elastomers in Today’s World. Acta Mech. Autom. 2017, 11, 267. [Google Scholar] [CrossRef] [Green Version]
- Volkova, T.; Böhm, V.; Kaufhold, T.; Popp, J.; Becker, F.; Borin, D.; Stepanov, G.; Zimmermann, K. Motion Behaviour of Magneto-Sensitive Elastomers Controlled by an External Magnetic Field for Sensor Applications. J. Magn. Magn. Mater. 2016. [Google Scholar] [CrossRef]
- Becker, T.I.; Böhm, V.; Chavez Vega, J.; Odenbach, S.; Raikher, Y.L.; Zimmermann, K. Magnetic-Field-Controlled Mechanical Behavior of Magneto-Sensitive Elastomers in Applications for Actuator and Sensor Systems. Arch. Appl. Mech. 2019, 89, 133–152. [Google Scholar] [CrossRef]
- Schubert, G. Manufacture, Characterisation and Modelling of Magneto-Rheological Elastomers. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2014. [Google Scholar]
- Carlson, J.D.; Jolly, M.R. MR Fluid, Foam and Elastomer Devices. Mechatronics 2000, 10, 555–569. [Google Scholar] [CrossRef]
- Guðmundsson, Í. A Feasibility Study of Magnetorheological Elastomers for a Potential Application in Prosthetic Devices. Ph.D. Thesis, University of Iceland, Reykjavyk, Iceland, 2011. [Google Scholar]
- Bíró, O.; Preis, K. On the Use of the Magnetic Vector Potential in the Finite Element Analysis of Three-Dimensional Eddy Currents. IEEE Trans. Magn. 1989, 25, 3145–3159. [Google Scholar] [CrossRef]
- Fetzer, J.; Haas, M.; Kurz, S. Numerische Berechnung Elektromagnetischer Felder; Kontakt & Studium; Expert-Verlag: Tübingen, Deutschland, 2002; Volume 627. [Google Scholar]
- Dorfmann, A.; Ogden, R.W. Nonlinear Magnetoelastic Deformations. Q. J. Mech. Appl. Math. 2004, 57, 599–622. [Google Scholar] [CrossRef]
- Metsch, P.; Kalina, K.A.; Brummund, J.; Kästner, M. Two- and Three-Dimensional Modeling Approaches in Magneto-Mechanics: A Quantitative Comparison. Arch. Appl. Mech. 2018, 89, 47–62. [Google Scholar] [CrossRef]
- Kalina, K.; Raßloff, A.; Wollner, M.; Metsch, P.; Brummund, J.; Kästner, M. Multiscale Modeling and Simulation of Magneto-Active Elastomers Based on Experimental Data. Phys. Sci. Rev. 2020, in press. [Google Scholar]
- De Groot, S.R.; Suttorp, L.G. Foundations of Electrodynamics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Metsch, P.; Kalina, K.A.; Spieler, C.; Kästner, M. A Numerical Study on Magnetostrictive Phenomena in Magnetorheological Elastomers. Comput. Mater. Sci. 2016, 124, 364–374. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Alnæs, M.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. The FEniCS Project Version 1.5. Arch. Numer. Softw. 2015, 3, 9–23. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Hu, S.Y.; Chen, L.Q. A Phase-Field Model for Evolving Microstructures with Strong Elastic Inhomogeneity. Acta Mater. 2001, 49, 1879–1890. [Google Scholar] [CrossRef]
- Interdisciplinary Centre for Advanced Materials Simulation, Ruhr-Universität Bochum. OpenPhase. 2021. Available online: http://www.icams.de/content/software-development/openphase/ (accessed on 28 April 2021).
- Tegeler, M.; Shchyglo, O.; Kamachali, R.D.; Monas, A.; Steinbach, I.; Sutmann, G. Parallel Multiphase Field Simulations with OpenPhase. Comput. Phys. Commun. 2017, 215, 173–187. [Google Scholar] [CrossRef]
- Vogel, F.; Pelteret, J.P.; Kaessmair, S.; Steinmann, P. Magnetic Force and Torque on Particles Subject to a Magnetic Field. Eur. J. Mech. A Solids 2014, 48, 23–37. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metsch, P.; Schiedung, R.; Steinbach, I.; Kästner, M. Benchmark for the Coupled Magneto-Mechanical Boundary Value Problem in Magneto-Active Elastomers. Materials 2021, 14, 2380. https://doi.org/10.3390/ma14092380
Metsch P, Schiedung R, Steinbach I, Kästner M. Benchmark for the Coupled Magneto-Mechanical Boundary Value Problem in Magneto-Active Elastomers. Materials. 2021; 14(9):2380. https://doi.org/10.3390/ma14092380
Chicago/Turabian StyleMetsch, Philipp, Raphael Schiedung, Ingo Steinbach, and Markus Kästner. 2021. "Benchmark for the Coupled Magneto-Mechanical Boundary Value Problem in Magneto-Active Elastomers" Materials 14, no. 9: 2380. https://doi.org/10.3390/ma14092380






