2. Critical Analysis of the Present Knowledge
The complete thin-walled folded shells transformed into central sectors of hyperbolic paraboloids were investigated by many researchers. The main geometric and mechanical properties of folded sheeting deformed into corrugated hyperbolic paraboloid shells were presented by Nilson [
7]. The Winter’s team [
8] confirmed Nilson’s results and expanded on the scope of the performed tests and analysis. Parker analyzed structures composed of a few quarters of right hyperbolic paraboloids made of two layers of sheets located orthogonally in the same shell.
McDermott [
9] described the behaviour of a central sector of a folded steel hyperbolic paraboloid stiffened with a circumferential frame. Parallel studies related to the static-strength work single and complex hyperbolic paraboloid shells were conducted by Egger et al. [
10] based on the conventional analysis and analytical calculations of strength and critical loads. Gergely et al. [
11] carried out a detailed analysis of the static-strength work of the single and complex profiled hyperbolic paraboloid shells composed of two orthogonal layers, which enables these research studies to analyze the shells as isotropic.
Gioncu and Petcu [
12] developed the novel HYPBUCK computer program for calculating the critical loads. Davis and Bryan [
13] pointed out the most important geometric and mechanical characteristics of the transformed shell folds, to make it easier for the designer to shape the transformed shells. Finally, they stated that theoretically it is possible to shape many different types of the transformed folded shell sheeting. Practically, it is possible to build only cylindrical and shallow corrugated hyperbolic paraboloid roofs due to the available engineering technology. In summary, all the investigated shells underwent forced shape transformations, causing relatively big initial stresses, because the fold’s longitudinal axes were adapted to the selected rulings of the adopted hyperbolic paraboloids. Therefore, the initial stresses had to be restricted, for example, by limiting the transformation degree. As a result, only shallow hyperbolic-paraboloid shells called hypars can be created (
Figure 4).
Biswas and Iffland [
14] presented a few concepts of shaping continuous regular roof structures composed of many identical hyperbolic paraboloid segments made up of transformed folded steel sheets. They arranged many complete shell sectors on a sphere to increase the span of the designed free form building.
The thin-walled corrugated shell steel roofs transformed freely are shaped by Reichhart [
15] and simply modeled with various right hyperbolic paraboloids (
Figure 5) and other deeply ruled surfaces [
16]. For geometric engineering developments, each shell sheeting can be modeled with a smooth sector of a ruled undevelopable surface called a warped surface [
1] (
Figure 1) including hyperbolic paraboloid [
17] (
Figure 2).
In order to create a method for shaping corrugated shells transformed rationally, Abramczyk has proposed a condition requiring the contraction of a single shell to pass halfway along the length of each shell fold [
1] (
Figure 3). Abramczyk’s method employs some specific geometric properties of regular warped surfaces, primarily their lines of striction. The second condition utilized by Abramczyk relates to determining certain surface areas of the created smooth shell models corresponding to the compressing and stretching zones of each transformed fold [
3]. These two conditions are based on the results of his experimental tests and computer simulations (
Figure 1 and
Figure 3).
The quarters of the hyperbolic paraboloid shells are often arranged symmetrically in different configurations to increase the expected roof spans. In order to create diversified free form building structures roofed with complex corrugated shells characterized by medium spans, Prokopska and Abramczyk [
18,
19] analyzed the so-called reference tetrahedrons to model a complete free form covered with oblique plane elevations and roofed with many transformed complete corrugated shell sectors arranged regularly in the three dimensional space [
20].
Each single shell segment is modeled by Abramczyk for the engineering developments [
1] with a sector of a warped surface [
21] (
Figure 6a), limited by a closed spatial line composed of four segments contained in the planes of a so-called reference network [
22]. The planes of the reference network divide the complete shell segments of the designed shell roof structure. They are helpful in defining roof directrices (
Figure 6b). In the present article, all directrices
e and
f are straight sections.
Abramczyk [
23] developed a method for shaping axis symmetric polyhedral networks based on rigid motions of all vertices of these networks (
Figure 7). Four adjacent planes of each reference network limit one tetrahedral mesh. A parameterization of the reference networks enables one to shape various configurations of attractive complex building free forms and innovative structural systems intended for these free forms by means of computer technique.
The above-mentioned method allows one to transform the shapes of various types of building structures proposed by Abdel and Mungan [
24] and Saitoh [
25]. Free-form shell bar structures are presented by Obrębski [
26]. Structural bar systems for several types of the corrugated roofs were developed by Rębielak [
27]. Free-form buildings and their constructions were analyzed by Reichhart [
28] and Wei-Wen [
29]. Samyn suggests interesting aluminium hypar forms [
30].
The most general method of architectural shaping of polyhedral shell structures was developed by Pottmann et al. [
31,
32]. The designed geometry of these structures does not result from the orthotropic properties, rectangular shapes of the folded sheets and the shape transformations of the designed roof shells.
The folded steel sheeting transformed elastically or plastically can be used as a structural shell unit supporting appropriate roof covers [
33]. The classical theory of elasticity proposed by Green and Lindsay has been extended by Marin et al. [
34] to cover the theory of thermoelasticity for dipolar bodies. A specific method of unique solution of a mixed problem in the dynamical case is proposed using a reciprocal theorem [
35]. These fundamental results were obtained under not very restrictive conditions.
4. The Method’s Concept
The process of shaping the built environment by means of diverse unconventional building forms requires one to solve many interdisciplinary issues in the field of town planning, architecture, morphology, civil engineering, constructions and computer support. Each issue is considered at different levels of accuracy, which further complicates the process of conducting the relevant analysis. The complex design process must therefore be divided into many steps related to the function, arrangement and type of the components of the building shaped, as well as the level of the modeling accuracy and execution of these elements.
The relation between the formation of the urban space and the social experience of the human self must be taken into account [
36]. The formation of the space investigating its physical form and cultural patterns into a whole spatial system is very important.
The design syntax of urban greenways should also be explicitly discussed. In this way, mathematics-based graph studies to analyze patterns and shapes, photography based thermal, material and morphology studies, and section analyses to make imagery-derived deductions on the design syntax are carried out [
37].
The morphological shaping of buildings plays a significant role in the design process, by using features specific for architectural, industrial and structural design [
38]. Morphology is a study of the forms taking account of the adopted interrelationships between the function, structure, internal and external texture, static-strength work and comfort conditions ascribed to the designed building object.
In each of the above mentioned aspects of the design process, a strict ordering of the objects characteristic for the considered step must be carried out. Therefore, according to the deliberated step, the general model is divided into many consistent individual elements and then into sub-elements arranged in a strictly defined order. These elements are adapted to the utilized concept, in accordance with the production technology and the assembly technique.
Thorough research and tests allow one to create appropriate geometric and static-strength models used in the search and development of the new concepts and techniques. The created unconventional new forms result from various innovative approaches to the shaping and ordering of their individual elements, for example in the three-dimensional Euclidean space.
Systematic morphology is defined by Eekhout as “the study of the system, rules and principles of form has led to the interpretation of the study of the geometry of regular three-dimensional bodies or forms, usually known as polyhedra.” [
38]. Analogous systems of planes called polyhedral reference networks are used in the present article. These are sums of many regular tetrahedrons arranged regularly in the three-dimensional space.
Wester defined structural morphology as “the Study of Form” [
39]. A detailed description of the issues related to the morphology of the structure is presented by Qingpeng [
40]. In this article, the study is limited to the geometric shaping of complex building structures roofed with free-form transformed corrugated shell structures arranged regularly in the three-dimensional space. The arrangement of the complete roof shell sectors is carried out by means of plane systems called polyhedral reference networks. The individual planes of each system separate single roof shells and contain the directrices of these shells. The diversification of the shape and mutual position of each pair of the adjacent directrices enables one to shape various innovative transformed forms of the complete corrugated shells.
The following factors have a decisive impact on the geometric properties of the investigated reference networks: (1) the regularity of the shapes and arrangement of the designed roof structures, (2) the rectangular shapes of the utilized folded sheets connected by their longitudinal edges into a single transformed strip, respectively, (3) the shape and mutual position of the roof directrices supporting each individual transformed shell segment, and (4) multi-wall character of the shaped complex facades. The assumed multi-segment nature of each roof structure Ω divided by the specific sets of planes allows all individual shells Ωij to be arranged by joining together along their transverse edges in relation to the fold directions. This way of connection results in specific ribbed roof structures.
Two adjacent shells of a roof structure can be connected along common eaves lines, including directrices (
Figure 2 and
Figure 5), or separated by flat window areas, allowing the sun rays to illuminate the building interior. This method allows the designer to shape freely attractive free forms of the roof structures (
Figure 6b). In the last case, the roof directrices of two adjacent shells are contained in the same plane, which forced development of a specific method for creating the special systems of these planes called polyhedral reference networks.
The quadrilateral nature of each closed edge line Bvij limiting each complete transformed roof shell Ωij results in that each reference network Γ is composed of meshes Γij restricted by tetrads of planes. Due to the rectangular characteristics of the individual sheets and their strips, the meshes are built as specific reference tetrahedrons whose four walls contain four single segments of the edge line Bvij of each single shell Ωij. Thus, all Bvij are closed spatial quadrangles whose all four apex angles are close to right angles.
As a rule, the complete shell segments are variously transformed, because they take relatively different forms depending on the shape and mutual position of their roof directrices adapted to the diversified curvature of the whole roof shell structure. Many special regular single shell sectors
Ωij and complete free forms
∑ij should be located in one polyhedral network mesh
Γij (
Figure 8a). Thus, the respective façade walls, side edges, roof directrices and eaves segments are included in the tetrad of planes of each
Γij. The most general type of the tetrahedral meshes
Γij was adopted in the further analysis (
Figure 8b). Every two adjacent planes of the same mesh
Γij intersect in a side edge
aij,
bij,
cij or
dij, however, two of its opposite planes intersect in one axis
uij or
vij. The side edges and axes are defined by means of four vertices
WABij,
WCDij,
WADij and
WBCij, adopted initially or created previously for
Γij (
Figure 8b).
Subsequently, tetrads of points
SAij,
SBij,
SCij and
SDij are determined on four side edges
aij,
bij,
cij,
dij in relation to four adopted vertices
WABij,
WCDij,
WADij and
WBCij of
Γij, (
i = 2,
j = 1) (
Figure 8a). The constructed points are the vertices of a quadrangle
SAijSBijSCijSDij constituting a plane mesh of an auxiliary multi-plane edge net determining a reference surface
ωr. In relation to the reference surface
ωr, four vertices
Aij,
Bij,
Cij,
Dij of the quadrilateral eaves net
Bvij are determined. Other tetrads of points
PAij,
PBij,
PCij and
PDij defining a flat horizontal base of the sought-after free form
∑ are also constructed in relation to four vertices
WABij,
WCDij,
WADij and
WBCij. The complex free form
∑ determined by the reference network
Γ is a sum of all individual free forms
∑ij roofed with
Ωij.
To construct the subsequent shell sectors Ωij of different curvature in two orthogonal directions, the axes uij and vij must be mutual skew. The greater the curvature diversity of Ωij in two orthogonal directions, the greater the distance between the uij and vij axes must be adopted. To build the diversified shells Ωij as sectors of warped surfaces, many pairs of directrices must be modeled with the help of skew straight or curved lines contained in opposite walls of each tetrahedron Γij.
The parameterization proposed in the present article regarding the geometric process of shaping such free forms
∑ is based on an adoption of a finite set of independent variables entering into the proposed novel computer application in the form of division coefficients of the respective pairs of the investigated
Γ’s vertices. The algorithm of the activities leading to the creation of
Γ and
∑ is presented in
Section 5.
5. Results—The Methods Algorithm
The first step of the method’s algorithm relates to the determination of all vertices of the subsequent reference tetrahedrons
Γij, constituting the meshes of a reference network
Γ. The first mesh
Γ11 is created so that the positions of its four vertices
WAB11,
WCD11,
WAD11 and
WBC11 are defined. For that purpose, a global coordinate system [
x,y,z] with the origin
O was taken (
Figure 9a). A first set of the initial data concerning the creation of
Γ11 is formed from the coordinates of these vertices. A few ways of determination of the vertices belonging to the investigated reference networks were developed by Abramczyk [
1,
17,
21]. If we want a sought-after mesh to be symmetric, then its vertices must be arranged either symmetrically, in accordance with the principal planes (
x,z) and (
y,z), or in these planes. After defining the vertices
WAB11,
WCD11,
WAD11 and
WBC11, we can determine four straight side edges
a11,
b11,
c11 and
d11 of
Γ11.
The second reference tetrahedron
Γ12 is located along the (
x,z)-plane in one of two principal orthogonal directions relative to
Γ11 (
Figure 9b). Its vertex
WAB12 is identical to
WCD11 introduced previously, so the second set of the initial data is composed of the coordinates of three other vertices
WCD12,
WAD12 and
WBC12 of
Γ12. These vertices can be determined as follows. The positions of the vertices
WBC12,
WAD12 have to be defined on two side edges
b12 =
c11,
a12 =
d11, by means of two division coefficients of the pairs (
WCD11,
WBC11) and (
WCD11,
WAD11) by these vertices. The division coefficients constitute the elements of the second set of the initial data instead of the coordinates of these points.
The position of vertex
WCD12 is obtained as a result of a rotation of the triangle
WAB12WBC12WAD12 about the axis
v12(
WAD12,
WBC12) into the position of the triangle
WCD12WBC12WAD12 (
Figure 9b). If
Γ12 is to be symmetrical towards the (
x,z)-plane,
WBC12 and
WAD12 have to be identical to each other with respect to this plane. The point
O12 helpful in programming, is the middle point of
WAD12WBC12. Four vertices
WAB12,
WCD12,
WAD12 and
WBC12 determine four straight side edges:
a12,
b12,
c12 and
d12 of
Γ12. The remaining tetrahedrons
Γ1j (for
j > 2) arranged symmetrically along the (
x,z)-plane are determined in an analogous manner.
The third reference tetrahedron
Γ21 is located in the second of two principal orthogonal directions of
Γ11, that is, along the (
y,z)-plane (
Figure 10a). The third set of the initial data is composed of the coordinates of only three vertices
WAB21,
WCD21 and
WBC21 of
Γ21 because the other vertex
WAD21 =
WBC11. The positions of the vertices
WAB21 and
WCD21 are defined on two side edges
a21 =
b11,
d21 =
c11 with the help of two division coefficients belonging to the third set of initial data instead of the coordinates of these points. The position of vertex
WBC21 is obtained as a result of a rotation of the triangle
WAD21WCD21WAB21 about the axis
u21(
WCD21,
WAB21) into the position of the triangle
WBC21WCD21WAB21. If (
y,z) is to be the plane of symmetry of
Γ21, then
WCD21 and
WAB21 have to be isentical to each other in relation to this plane. In addition, the point
O21, helpful in programming, has to be taken as the middle point of
WCD21WAB21. Four vertices—
WAB21,
WCD21,
WAD21 and
WBC21—determine four straight side edges—
a21,
b21,
c21 and
d21 of
Γ21. The remaining tetrahedrons
Γi1 (for
i > 2) arranged along the (
y,z)-plane are determined in an analogous manner.
The fourth reference tetrahedron
Γ22 is located diagonally in relation to
Γ11 (
Figure 10b). The fourth set of the initial data should be composed of the coordinates of only two vertices
WCD22 and
WBC22 because
WAD22 =
WBC12 and
WAB22 =
WCD21. The positions of
WCD22 and
WBC22 are defined on two side edges
d22 =
c12,
b22 =
c21 with the help of two division coefficients belonging to the fourth set of the initial data, instead of the coordinates of these points. Four vertices—
WAB22,
WCD22,
WAD22 and
WBC22—determine four straight side edges
a22,
b22,
c22 and
d22 and two axes
u22 and
v22 of
Γ22. The remaining tetrahedrons
Γij (for
i,j > 2) arranged diagonally in relation to
Γ11 are determined in an analogous manner.
Let us follow some selected instructions characteristic of the AutoLISP language of programming the AutoCAD graphic editor used in the novel application to create the investigated reference networks. The procedure presented in Line 1 instructs the displacement of a local coordinate system to the position of the global coordinate system [x,y,z]. Line 2 contains the instruction giving the WAB12 point coordinates identical to the coordinates of the point WCD11. Instructions of Lines 3 and 4 calculate the coordinates of the points WAD12 and WBC12 on the side edges b12 = c11(WCD11,WBC11) and a12 = d11(WCD11,WAD11) by means of two division coefficients—dWBC12 and dWAD12—of the pairs (WCD11,WBC11) and (WCD11,WAD11) by WBC12 and WAD12.
- Line 1:
(command “luw” “g”)
- Line 2:
(setq WAB12 (cal “WCD11+Oo”))
- Line 3:
(setq WBC12 (cal “plt(WCD11,WBC11,dWBC12)”))
- Line 4:
(setq WAD12 (cal “plt(WCD11,WAD11,dWAD12)”))
- Line 5:
(setq O12 (cal “plt(WBC12,WAD12,0.5)”))
- Line 6:
(command “luw” “3” WBC12 WAD12 WAB12)
- Line 7:
(setq O12u (cal “w2u(O12)”))
- Line 8:
(command “luw” “_o” O12u)
- Line 9:
(command “luw” “x” alfCD12)
- Line 10:
(setq WCD12u (list 0.0 jcd12 0.0) WCD12 (cal “u2w(WCD12u)”))
By means of the instruction from Line 6, a local clockwise coordinate system [
xL,
yL,
zL] with the origin at
WBC12 is created so that the positive half axis
xL is determined by the points
WBC12 and
WAD12, and the positive half axis
yL is contained in the plane (
WBC12,
WAD12,
WAB12), where the point
WAB12 determines its positive course. The axis
zL passes through
WBC12 perpendicularly to the plane (
xL,
yL), so that, the system [
xL,
yL,
zL] is clockwise. Then, [
xL,
yL,
zL] is moved into a new position [
xL1,
yL1,
zL1] according to the instruction assigned to Line 8. After executing this instruction, the origin of [
xL1,
yL1,
zL1] is located in the middle point
O12 of
WBC12WAD12 (
Figure 9b).
Since the translation of the old system [xL,yL,zL] to its new position [xL1,yL1,zL1] has to be performed, the coordinates of the point O12 must be transformed into the new system. This action is initiated by the procedure shown in Line 7. The instruction given in Line 9 rotates the system [xL1,yL1,zL1] to its new position [xL2,yL2,zL2]. The point WCD12u takes the coordinates (0.0 jcd12 0.0) in its new position, according to the instruction given in Line 10. The height of the triangle WAB12WBC12WAD12, passed from the point WAB12 is equal to jcd12. In the second part of Line 10, the coordinates of WCD12 are transformed from the local system [xL2,yL2,zL2] to the global system [x,y,z].
The code of the presented application contains two main instructions (while...) for creating subsequent meshes Γij located in two orthogonal directions, that is, in i rows and j columns of the network Γ. The selection function (cond...) makes it possible to distinguish and determine four sets of these meshes. The first set relates to the first mesh Γ11. The subsequent two sets concern the meshes located in two orthogonal directions passing along the planes (x,z) and (y,z). The last set of meshes is related to the diagonal directions relative to Γ11.
(setq i 0) |
(while (<= i iN) |
(setq j 0) |
(setq i (+ i 1)) |
(while (<= j jN) |
(setq j (+ j 1)) |
(cond ((and (= i 1) (= j 1)) (progn … creation of the first Γ11)) |
((and (= i 1) (> j 1)) (progn … creation of the first type of orthogonal reference tetrahedrons Γ1j)) |
((and (> i 1) (= j 1)) (prong … creation of the second type of orthogonal reference tetrahedrons Γi1)) |
((and (> i 1) (> j 1)) (progn … creation of diagonal reference tetrahedrons Γij) |
);cond |
);while. |
);while |
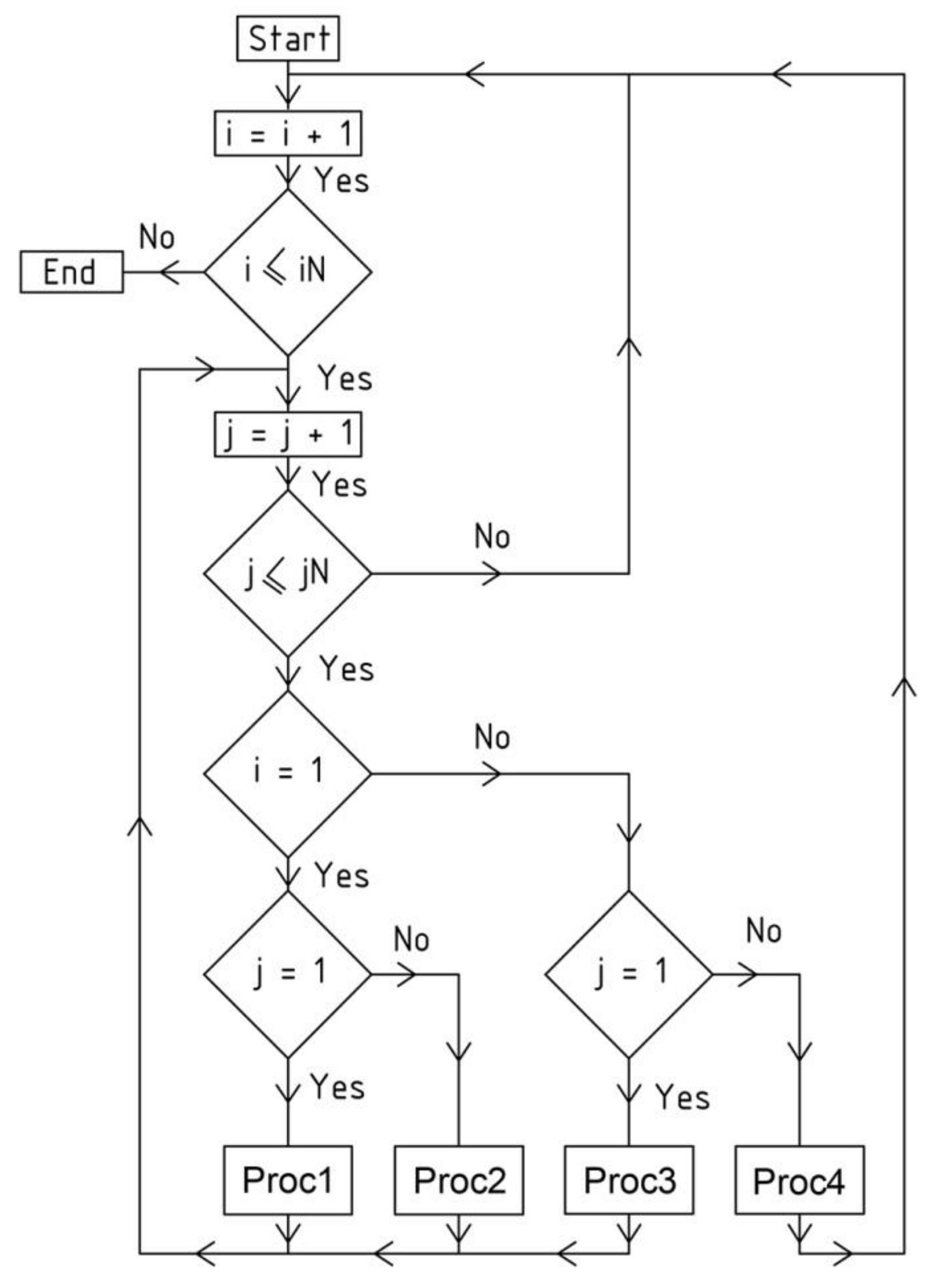
The above-mentioned procedures are represented by the block scheme shown in
Figure 11. They are the main part of the method’s algorithm presented in this article.
To determine four points
SA11,
SB11,
SC11 and
SD11 (
Figure 12a) defining a sector of a reference surface, four division coefficients constituting four elements of the first set of the initial data must be employed. Subsequently, four auxiliary points of the reference surface must be determined on the side edges of
Γ12 so that two of them
SB12 =
SC11,
SA12 =
SD11 belong to
b12 =
c11 and
a12 =
d11, and the other two—
SC12 and
SD12—are determined on two side edges
c12 and
d12 using two division coefficients constituting two elements of the second set of the initial data adopted earlier (
Figure 12b). Tetrads of points
SA1j,
SB1j,
SC1j and
SD1j belonging to the remaining tetrahedrons
Γ1j (for
j > 2) arranged along the (
x,z)-plane are determined in an analogous manner.
At the subsequent step of the method’s algorithm, four auxiliary points
SA21,
SB21,
SC21 and
SD21 of the reference surface must be determined on the side edges of
Γ21, so that two of them are
SA21 =
SB11,
SD21 =
SC11, and the other two
SC21 and
SB21 are determined on two side edges
c21 and
b21 (
Figure 13), using two division coefficients of the third set of the initial data.
At the end of this step, four auxiliary points f the
ωr reference surface are determined on the side edges of
Γ22. Three of these points are determined on
a22 =
b12,
b22 =
c21, and
d22 =
c12, so that
SA22 =
SB12,
SB22 =
SC21 and
SD22 =
SC12 (
Figure 14). The last one belongs to
c22 determined by
WCD22 and
WBC22, using a division coefficient constituting one element of the fourth set of the initial data.
Tetrads of points
SAij,
SBij,
SCij and
SDij belonging to the remaining tetrahedrons
Γij (for
i,j > 2) arranged diagonally in relation to
Γ11 have to be determined in an analogous manner. On the basis of the auxiliary quadrilateral net having vertices located at the points
SAij,
SBij,
SCij and
SDij of
Γij, the
ωr surface is defined (
Figure 14).
Some procedures related to the determination of the aforementioned points SAij, SBij, SCij and SDij are presented and analyzed below. The procedures shown in Lines 11 to 14 realize the calculations of the coordinates of the above points. The procedure given in Line 15 creates the plane quadrangle SA11SB11SC11SD11 in the three-dimensional computer space.
- Line 11:
(setq SA11 (cal “plt(WAB11,WAD11,dSA11)”))
- Line 12:
(setq SB11 (cal “plt(WAB11,WBC11,dSB11)”))
- Line 13:
(setq SD11 (cal “plt(WCD11,WAD11,dSD11)”))
- Line 14:
(setq SC11 (cal “plt(WCD11,WBC11,dSC11)”))
- Line 15:
(command “linia” SA11 SB11 SC11 SD11 SA11 ““)
The instructions assigning the values of the coordinates of the previously determined points SD11 and SC11 to the coordinates of SA12 and SB12 are presented in Lines 16 and 17. The procedure from Line 18 calculates the division coefficient of the pair (WAB12,WAD12) by SA12 using an internal novel function (wspolcz...) written by the author. The next instruction located in Line 19 assigns the value calculated by the function (wspolcz...) to the division coefficient dSA12.
The analogous procedures resulting in the calculation of the coefficient dSB12 of the pair (WAB12,WBC12) by SB12 are given in Lines 20 and 21. The instructions from Lines 22 and 23 calculate the coordinates of the points SC12 and SD12 positioned on the straight lines (WCD12,WBC12) and (WCD12,WAD12), using the division coefficients dWBC12 and dWAD12 of the aforementioned pairs by SC12 and SD12. The procedure shown in Line 24 creates a quadrangle SA12SB12SC12 SD12 in the three-dimensional computer space.
- Line 16:
(setq SA12 (cal “SD11 + Oo”))
- Line 17:
(setq SB12 (cal “SC11 + Oo”))
- Line 18:
(wspolcz SA12 WAB12 WAD12)
- Line 19:
(setq dSA12 wspcz)
- Line 20:
(wspolcz SB12 WAB12 WBC12)
- Line 21:
(setq dSB12 wspcz)
- Line 22:
(setq SC12 (cal “plt(WCD12,WBC12,dSC12)”))
- Line 23:
(setq SD12 (cal “plt(WCD12,WAD12,dSD12)”))
- Line 24:
(command “linia” SA12 SB12 SC12 SD12 SA12 ““)
The procedures calculating the coordinates of SA22, SB22, SC22 and SD22 are analogous to those presented earlier for Γ11 and Γ12. The internal function (wspolcz...) must be used three times to calculate the coordinates of the above three points. In the case of Γ22, the value of the calculated division coefficient dSA22 of (WAB22,WAD22) by SC11 have to be assigned to the division coefficient dSC22 of (WCD22,WBC22) by SC2.
It is worth paying attention to the following properties of the reference network Γ built so far. All vertices of each reference tetrahedron Γij designate four side edges aij, bij, cij and dij and four planes of Γ. Each new reference tetrahedron Γi+1j or Γij+1 is created as a spatial mesh with two sought-after vertices defined on two side edges of two previously constructed tetrahedrons Γij, so the subsequent pairs of adjacent meshes of Γ have to have common planes. The roof directrices of each Γij should be positioned in these planes.
To calculate the coordinates of
A11,
B11,
C11 and
D11 of a closed spatial eaves quadrangle
Bv11, four division coefficients constituting four elements of the first set of the initial data, used for
Γ11, have to be adopted. These points belong to four side edges
a11(
WAB11,
WAD11),
b11(
WAB11,
WBC11),
c11(
WBC11,
WCD11) and
d11(
WCD11,
WAD11) and should be positioned in accordance with
ωr by means of the respective division coefficients (
Figure 15a). Subsequently, four vertices—
A12,
B12,
C12 and
D12 of
Bv12—have to be determined on the side edges
a12,
b12,
c12 and
d12 of
Γ12 in relation to
ωr. Two of these vertices are
A12 =
C11,
B12 =
D11. The other two
C12 and
D12 have to be determined on two side edges
c12(
WBC12,
WCD12) and
d12(
WCD12,
WAD12) using two division coefficients constituting two elements of the second set of the initial data. The tetrads of points
A1j,
B1j,
C1j and
D1j belonging to the side edges of the remaining tetrahedrons
Γ1j (for
j > 2) and constituting the vertices of the remaining spatial quadrangles
Bv1j located along the (
x,z)-plane are determined in an analogous manner.
Four vertices
A21,
B21,
C21 and
D21 of the eaves
Bv21 have to be determined on the side edges
a21,
b21,
c21 and
d21 of
Γ21 in accordance with
ωr (
Figure 15a). Two of these vertices are
A21 =
B11,
D21 =
C11. The other two
C21 and
B21 have to be determined on two side edges
c21 (
WBC21,
WCD21) and
b21(
WAB21,
WBC21), using two division coefficients constituting two elements of the third set of the initial data. The points
Ai1,
Bi1,
Ci1 and
Di1 belonging to the other tetrahedrons
Γi1 and constituting the vertices of the spatial quadrangles
Bvi1 (for
i > 2) arranged along the (
y,z)-plane are determined in an analogous manner.
Four vertices
A22,
B22,
C22 and
D22 of the quadrangle
Bv22 have to be determined on the side edges
a22(
WAB22,
WAD22),
b22(
WAB22,
WBC22),
c22(
WBC22,
WCD22) and
d22(
WCD22,
WAD22) of
Γ22 relative to
ωr (
Figure 15a). Three of these points are determined on
a22 =
c11,
b22 =
c21, and
d22 =
c12 so that
A22 =
C11,
B22 =
C21 and
D22 =
C12. The last one
C22 belongs to
c22(
WCD22,
WBC22). It is determined by means of one division coefficient constituting an element of the fourth set of the initial data. The tetrads of points
Aij,
Bij,
Cij and
Dij belonging to the remaining tetrahedrons
Γij (for
i,j > 2) arranged diagonally with regard to
Γ22 can be determined in an analogous manner.
In order to determine a horizontal plane base of the free form
∑, one its point, for example,
PD12 has to be defined on
d12 (
Figure 15b). The value of the division coefficient of the pair (
WCD12,
WAD12) by this point is an element of the second set of the initial data. Another point of the plane base is the intersection of the horizontal base plane passing through
PD12 with the subsequent tetrads of side edges of
Γ11,
Γ12, etc.
The result of adding up the four reference tetrahedrons Γij is a subnet Γ1 constituting a quarter of the resultant reference network Γ. The other three parts of Γ can be built using a z-axis symmetry and two (x,z)-plane and (y,z)-plane symmetries, called 3D-mirrors, in the way described in the next section on an example of a more complex reference network.
Similarly, four tetrahedrons ∑ij create a subnet ∑1 constituting one-fourth of the designed building free form ∑. Four eaves quadrangles Bvij create a subnet Bv1 constituting one-fourth of the network Bv. On the basis of Bv, the roof structure Ω composed of many sectors Ωij is created.
In summary, for the case of creating reference tetrahedrons Γ1j or Γi1 (for j > 2 or i > 2 and i, j different from (1) located in two orthogonal directions of planes (x,z) and (y,z), one vertex of each of these tetrahedrons must be located outside the side edges of the already created subnet of Γ. The vertex determines a new plane of Γ passing through the already constructed axis of the designed tetrahedron. Two of its subsequent vertices ought to be determined on two side edges of the previously created subnet of Γ with the help of two division coefficients. The location of the fourth vertex is identical with one of the vertices of Γ constructed earlier. In the case of the diagonal directions of Γ11, each new reference tetrahedron Γij has two vertices identical to two previously constructed vertices of Γ. However, its new vertices have to be determined on two side edges of the previously created subnet of Γ by means of the respective division coefficients.
This way of constructing the subsequent reference tetrahedrons located in the orthogonal and diagonal courses of each reference network Γ is characterized by the fact that each inner side edge of Γ is shared by four adjacent reference tetrahedrons and eight vertices of these four tetrahedrons belong to the same side edge of Γ. In a general case, these eight vertices occupy four different positions, in pairs. This topic is going to be presented in further publications. The example of using the proposed algorithm for determining the parametric reference polyhedral networks Γ and eaves nets Bv is given in next section.
6. Results—Parametric Shaping of the Reference Networks
Two ways of shaping of the investigated networks
Γ and
Bv can be carried out in scientific and engineering problems. One of these ways is based on the stiff-motions such as translations and rotations of several initially adopted or calculated points edges and planes determining the other vertices and side edges of these nets [
22]. The second way, presented in this article, is more intuitive, because it enables one to create parametric models by means of the division coefficients expressing very specific relations between the main elements of the designed building free-forms. To make this method easy for many designers, a novel computer application written in the AutoLISP language of programming the AutoCAD visual editor was developed.
The last way requires a little more operations related to the division coefficients of the respective pairs of the determined vertices of the investigated reference polyhedral Γ and the quadrilateral Bv networks. The coefficients define the positions of: (1) the vertices of the sought-after reference network Γ with respect to a few intuitively adopted specific points of Γ, (2) the planes of Γ, (3) the points SAij, SBij, SCij, and SDij belonging to ωr, and (4) the vertices Aij Bij, Cij and Dij of Bv determining the multi-shell roof structure Ω.
In the example presented below, a usage of the method for computational determining one quarter
Γ1 of a reference network
Γ (
Figure 16) based on some adopted proportions is discussed. All vertices of three other quarters
Γ2L,
Γ3p,
Γ4r of
Γ are determined using: (1)
z-axial symmetry for the case of
Γ2L, (2) (
x,z)-plane symmetry called 3D-mirror for
Γ3p, and (3) (
y,z)-plane symmetry for the case of
Γ4r. A description of creating the symmetric nets
Γ2L,
Γ3p,
Γ4r is not presented in this article.
Creating one quarter
Γ1 of an
z-axially symmetric network
Γ is started by defining the first
z-axis-symmetric mesh
Γ11 (
Figure 17a). It is continued for subsequent meshes
Γij arranged orthogonally (
Figure 17b) and, next, diagonally with respect to
Γ11, following the algorithm presented in the previous section. To obtain the first tetrahedron
Γ11, four of its vertices—
WAB11,
WCD11,
WAD11 and
WBC11—are defined by means of their coordinates listed in
Table 1.
The positions of the points SA11, SB11, SC11 and SD11 of ωr are defined with the following division coefficients (WAB11,WAD11)\SA11, (WAB11,WBC11)\SB11, (WCD11,WBC11)\SC11 and (WCD11,WAD11)\SD11, where
(WAB11,WAD11)\SA11 = /
(WAB11,WBC11)\SB11 = /
(WCD11,WBC11)\SC11 = /
(WCD11,WAD11)\SD11 = /
and
is the vector starting with
WAB11 and ending at
WAD11, m(
) is the measure of
,
is the vector with the starting point at
WAB11 and the ending point at
SA11, etc. The values of the above ratios are listed in
Table 2. The subsequent points
SA11, SB11,
SC11 and
SD11 define the spatial quadrangle determining a respective segment of
ωr.
The locations of the vertices
A11,
B11,
C11 and
D11 of
Γ11 (
Figure 17c) are defined by means of the aforementioned vertices of
Γ11 and the following proportions
(WAB11,WAD11)\A11 = /
(WAB11, WBC11)\B11 = /
(WCD11, WBC11)\C11 = /
(WCD11, WAD11)\D11 = /
where is the vector defined by the starting point at WAB11 and the ending point A11, etc. The points A11, B11, C11 and D11 determine the spatial quadrangle Bv11 limiting the single smooth shell segment Ω11 of the complex roof structure Ω. Subsequently, the values of four division coefficients (WAB11,WAD11)\(SA11,A11), (WAB11,WBC11)\(SB11,B11), (WCD11,WBC11)\(SC11,C11) and (WCD11,WAD11)\(SD11,D11) must be adopted as follows
(WAB11,WAD11)\(SA11,A11) = / = (WAB11,WAD11)\A11-(WAB11,WAD11)\SA11
(WAB11,WBC11)\(SB11,B11) = / = (WAB11,WBC11)\B11–(WAB11,WBC11)\SB11
(WCD11,WBC11)\(SC11,C11) = / = (WCD11,WBC11)\C11-(WCD11,WBC11)\SC11
(WCD11,WAD11)\(SD11,D11) = / = (WCD11,WAD11)\D11-(WCD11,WAD11)\SD11
The above constants have positive or negative signs depending on whether the points
A11,
B11,
C11 and
D11 lie above or below
ωr defined by means of the quadrangle
SA11SB11SC11SD11 (
Figure 17a).
If we transform the above formulas, the division ratios (WAB11,WAD11)\A11, (WAB11,WBC11)\B11, (WCD11,WBC11)\C11 and (WCD11,WAD11)\D11 can be calculated as follows
(WAB11,WAD11)\A11 = (WAB11,WAD11)\SA11 + (WAB11,WAD11)\(SA11,A11)
(WAB11,WBC11)\B11 = (WAB11,WBC11)\SB11 + (WAB11,WBC11)\(SB11,B11)
(WCD11,WBC11)\C11 = (WCD11,WBC11)\SC11 + (WCD11,WBC11)\(SC11,C11)
(WCD11,WAD11)\D11 = (WCD11,WAD11)\SD11 + (WCD11,WAD11)\(SD11,D11)
The values of the division coefficients used in the example are given in
Table 2.
In order to create the tetrahedron
Γ12, four of its vertices—
WAB12,
WCD12,
WAD12 and
WBC12—were defined by means of the coordinates listed in
Table 3.
The positions of the points SA12, SB12, A12 and B12 are similar to the positions of SD11, SC11, D11 and C11, so the following division coefficients have to be calculated as follows
(WAB12,WAD12)\SA12 = (WCD11,WAD11)\SD11/(WCD11,WAD11)\WAD12
(WAB12,WBC12)\SB12 = (WCD11,WBC11)\SC11/(WCD11,WBC11)\WBC12
(WAB12,WAD12)\A12 = (WCD11,WAD11)\D11/(WCD11,WAD11)\WAD12
(WAB12,WBC12)\B12 = (WCD11,WBC11)\C11/(WCD11,WBC11)\WBC12
where the spaces before and behind the slash denote that we have common division of two numbers. Other division ratios related to Γ12 and Bv12 are adopted as follows.
(WCD12,WBC12)\SC12 = (WAB12,WAD12)\SA12
(WCD12,WAD12)\SD12 = (WAB12,WBC12)\SB12
(WCD12,WBC12)\C12 = (WAB12,WAD12)\A12
(WCD12,WAD12)\D12 = (WAB12,WBC12)\B12
The calculated values of these division coefficients are given in
Table 4.
The positions of the points: (1)
SA13,
SB13,
SC13,
SD13,
A13,
B13,
C13 and
D13, (2)
SA21,
SB21,
SC21,
SD21,
A21,
B21,
C21 and
D21, (3)
SA31,
SB31,
SC31,
SD31,
A31,
B31,
C31 and
D31 can be defined or calculated in an analogous way, as for
SA12,
SB12,
SC12,
SD12,
A12,
B12,
C12 and
D12. The values of the coordinates of all aforementioned points are given in
Table A2 and
Table A3, posted in
Appendix A.
To determine the last tetrahedron
Γ22 investigated in our example, four of its vertices—
WAB22,
WCD22,
WAD22 and
WBC22 (
Figure 18)—are initially defined by means of the coordinates listed in
Table 5.
To construct the quadrangle
Bv22 (
Figure 18), the values of the vertices
SA22, SB22,
SC22,
SD22,
A22,
B22,
C22 and
D22 must be calculated in the following way. The positions of the points
SA22, SB22,
SD22,
A22,
B22 and
D22 are similar to the positions of
SC11,
SC21,
SC12,
C11,
C21 and
C12 determined previously for
Γ11,
Γ21,
Γ12,
Bv11,
Bv21 and
Bv12.
To achieve the coordinates of the aforementioned points of ωr and Bv, the following division coefficients should be calculated
(WAB22,WAD22)\SA22 =
(WAB22,WAD22)\A22 =
(WAB22,WAD22)\(SA22,A22) = (WAB22,WAD22)\A22 (WAB22,WAD22)\SA22
(WAB22,WBC22)\SB22 = (WCD21,WBC21)\SC21/(WCD21,WBC21)\WBC22
(WAB22,WBC22)\B22 = (WCD21,WBC21)\C21/(WCD21,WBC21)\WBC22
(WAB22,WBC22)\(SB22,B22) = (WAB22,WBC22)\B22 (WAB22,WBC22)\SB22
(WCD22,WAD22)\SD22 = (WCD12,WAD12)\SC12/(WBC12,WCD12)\WCD22
(WCD22,WAD22)\D22 = (WCD12,WAD12)\C12/(WBC12,WCD12)\WCD22
(WCD22,WAD22)\(SD22,D22) = (WCD22,WAD22)\D22 (WCD22,WAD22)\SD22
A detailed description of a mutual position of the vertices belonging to one exemplary configuration of a polygonal
Bv net and a polyhedral net
Γ is presented by Abramczyk using the method based on stiff motions [
22]. In the present article, the extensive method of parametric shaping of the regular roof shell structures by means of the orthotropic properties of the corrugated shell sectors is developed based on the division coefficients.
The spaces before and after slash/depict if a usual division is used. In contrast, a division ratio is expressed if there are not spaces before and after the backslash\. On the basis of the above division coefficients, the following can be calculated
(WCD22,WBC22)\SC22 = (WAB22,WAD22)\SA22
(WCD22,WBC22)\C22 = (WAB22,WAD22)\A22
(WCD22,WBC22)\(SC22,C22) = (WCD22,WBC22)\C22(WCD22,WBC22)\SC22
The values of these division coefficients are given in
Table 6.
Analogous proportions as for the quadrangle
Γ22 can be defined for other meshes located diagonally with respect to
Γ11, including for
Γ23,
Γ32, and
Γ33. The subnet
Γ1 constituting a sum of
Γij (for
i,j = 1 to 3) is located between the planes (
x,z) and (
y,z) in the dihedral angle containing the positive axis
y and the negative axis
x (
Figure 19). It is about one quarter of the designed resultant
z-axis-symmetric
Γ (
Figure 16).
7. Discussion
The first basic goal accomplished by the proposed novel method is to create a relatively simple and regular spatial arrangement of many simple complete free forms connected to each other into one complex building free-form with oblique plane elevations and a transformed multi-segment shell roof structure. The individual free forms are roofed with single ruled shells whose shapes result from the expected shape transformations of thin-walled folded sheets. The simplicity of the method’s algorithm is to build a system of planes that, when intersected, isolate many spatial meshes creating a reference network adaptable to various boundary conditions. These complete meshes also define the facade walls of the designed complete free-forms. In these planes, common directrices of the shell segments roofing adjacent single free-forms are included. In the article, mutual skew straight lines are investigated as the roof directrices.
The regularity of numerous arrangements of many individual roof shell segments is ensured by the specific geometric shaping of these segments, based on the reference surface and division coefficients related to the intersecting point of respective planes and side edges of the reference networks. The most important steps of the method’s algorithm leading to the achievement of the above assumed goal by means of a parameterization based on the aforementioned division coefficients are presented in
Figure 11 and
Figure 20. The multitude and complexity of the activities and objects realized by the algorithm need to use computer technology to program the calculations and create the required geometric models.
The second main goal implemented by the method is the possibility of a relatively free and intuitive shaping of complex building free-form structures and their easy modification to the requirements and expectations of the designer.
To build a complex building form, the presented method’s algorithm instructs the iterative activities and objects presented by means of the block scheme shown in
Figure 11. At the beginning of each
Γ’s and
Bv’s shaping process, a set of numbers defining the locations of the vertices
WABij,
WCDij,
WADij and
WBCij of all subsequent reference tetrahedrons
Γij of
Γ is adopted. The numbers are the division coefficients of the proper pairs of the already constructed vertices belonging to
Γij by the other sought-after vertices belonging to the subsequently determined tetrahedrons
Γi+1j,
Γij+1 and
Γi+1j+1.
To create tetrahedrons Γ1j and Γi1 forming two principal orthogonal strips of Γ, a specific set of numbers constituting dependent or independent variables has to be adopted. To determine four vertices of each new reference tetrahedron located in one of these orthogonal strips, the following relations must be taken. Each tetrahedron has to have one common wall and two common side edges with one of the previously built reference tetrahedrons. Three other walls and two remaining side edges of this new reference tetrahedron are determined by means of two searched and two known vertices.
In order to determine the diagonal strips of the network Γ, a new set of parameters defining the location of four vertices of each tetrahedron Γij located diagonally has to be adopted, so that: (1) two its walls and three side edges have to be common with some tetrahedrons constructed previously, and (2) one of these side edges must also be common with one of the previously constructed tetrahedrons of the same diagonal strip. Based on the above set, the locations of the remaining fourth side edge and two walls of this diagonal reference tetrahedron, for example Γ22, are sought by means of two sought-after points belonging to two different side edges created previously.
Subsequently, the points
SAij,
SBij,
SCij and
SDij of a reference surface
ωr and the vertices of all
Bvij meshes are determined on the basis of the reference network
Γ and the adopted sets of initial data. These parameters are single-division coefficients and double-division coefficients of the subsequently selected pairs of the
Γ’s vertices by: (1) the points
SAij,
SBij,
SCij and
SDij, (2) the vertices
Aij,
Bij,
Cij and
Dij of
Bvij, and (3) the points
PAij,
PBij,
PCij and
PDij of the base of the free-form-shaped building. In the example presented in the previous section, the calculated values of the division coefficients related to the positions of the aforementioned vertices are listed in
Table 7.
The main step of the method’s algorithm is accomplished by means of the activities assigned to the sections Proc
k, where
k = 1 to 3 (
Figure 20) depending on the location of
Γij in
Γ. There are four configurations of these procedures, supporting the activities requiring different input data and various type and number of the functions used to determine the
Γ’s and
Bv’s vertices. The common actions assigned to all configurations are presented in the container called Procedure
k shown in
Figure 21. The activities are implemented in the innovative computer application written in the AutoLISP programming language.
The actions of the section Proc1 (for k = 1) concern the first constructed meshes of networks Γ and Bv and the sectors of structures Ω and ∑, where i = j = 1. The activities referred to the section Proc2 (for k = 2), relating to the meshes of the first of two orthogonal strips of Γ, Bv, Ω and ∑ running along the plane (x,z), for which i = 1 and j different from 1. The activities of the section Proc3 (for k = 3) relate to the meshes of the second orthogonal strip passing along the plane (y,z), for which j = 1 and i is different from 1. The activities assigned to the section Proc4 (for k = 4) refer to all meshes of the diagonal strips of Γ, Bv, Ω and ∑, for which i and j are different from 1. A novel computer-aided method is proposed due to the complexity of the above operations and geometric objects.
The division coefficients adopted initially to define the characteristic points of Γ, ωr and Bv are also used for assessing the curvature of the reference surface ωr and the roughness of the eaves net Bv. The expected curvature of the ωr’s area corresponding to the single mesh Γij can be shaped by means of four division coefficients (WABij,WADij)\SAij, (WABij,WBCij)\SBij, (WCDij,WBCij)\SCij and (WCDij,WADij)\SDij determining the positions of the points SAij, SBij, SCij and SDij on the side edges aij, bij, cij and dij. Since the points are created for a finite number of subsequent meshes Γij, then the curves located on ωr can be defined in an approximate way on the basis of these points. These curves also define ωr in an approximate way.
For the considered networks Γ and Bv and structures Ω and ∑, roughness of the Bv network also plays an important role. The roughness is determined by means of division coefficients of the respective pairs of the Γ’s vertices by the selected ωr’s points and Bv’s vertices. The roughness describes the disturbances in the smoothness of the network Bv in relation to the smooth surface ωr. The disturbances result from the forced mutual inclination of each pair of the adjacent roof directrices designed for all complete meshes Bvij to realize the shape transformations of the complete corrugated roof shells. On the one hand, the roughness can have a positive effect on the attractiveness and span of the complex roof free forms Ω and entire building ∑. On the other hand, the edges between the adjacent meshes Bvij can reduce the visual attractiveness of the building shaped by disturbing the smoothness of the shell roof rib structure.
The maximum and minimum values of the absolute and relative roughness of the entire network Bv and the proportions between these values can be defined as double- and triple-division coefficients if the need exists. This problem also goes beyond the scope of the article.
The division coefficients of the selected pairs of the
Γij’s vertices by the points
SAij,
SBij,
SCij and
SDij affect the
ωr’s curvature. If the values of the above coefficients are greater than 1, convex roof free forms with positive Gaussian curvatures are shaped (
Figure 22a). If the values of the above coefficients are greater than 0 and less than 1, then concave roof shell forms with negative Gaussian curvature are shaped (
Figure 22b). If the values of the above coefficients are from the range (-∞,0), concave roof free forms with positive Gaussian curvature are shaped. These forms have oblique facades tapering upwards in contrast to the forms widening upwards, e.g., the one presented in
Figure 22a. A possibility of modifying the reference networks
Γ by changing some division coefficients defining their shapes and the positions of their vertices allows one to optimize the curvature of
ωr and the roughness of
Bv according to the demands referring to the attractiveness of the shaped building free-forms.
The third basic goal realized by means of the method is attractiveness and rationality of the final complex building free forms ∑, which is associated with the properties of the investigated networks Γ and Bv, and surface ωr. The main elements determining the attractiveness are: (1) the ωr’s curvature in two orthogonal and diagonal directions, (2) the positions of the Γ’s planes, and (3) the positions of the Bv’s vertices on the Γ’s side edges with respect to ωr. Modifications of these elements enable us to maintain the expected shape and slope of the designed multi-plane facades and multi-segment shell roof structure, as well as their geometric coherence with the entire building free form.
The main elements determining the rationality of the investigated geometric structures are: (1) the mutual consistency and regular arrangement of all individual forms ∑ij, (2) the mutual consistency and the regular arrangement of all individual roof forms Ωij, (3) the consistency of the entire roof and facade forms, (4) the regularity of the distribution of all Γij relative to ωr, and (5) the location of the contraction of each effectively transformed fold along its length, induced by the mutual position and slope of the Bvij’s and Ωij’s directrices. The rationality is defined by means of the respective division coefficients or proportions between the selected elements of the investigated networks and structures.