Numerical Investigation of the Composite Action of Axially Compressed Concrete-Filled Circular Aluminum Alloy Tubular Stub Columns
Abstract
:1. Introduction
2. FE Model of CFCAT Stub Columns
2.1. Modeling of CFCAT Stub Columns
2.1.1. Mesh Size and Element Type
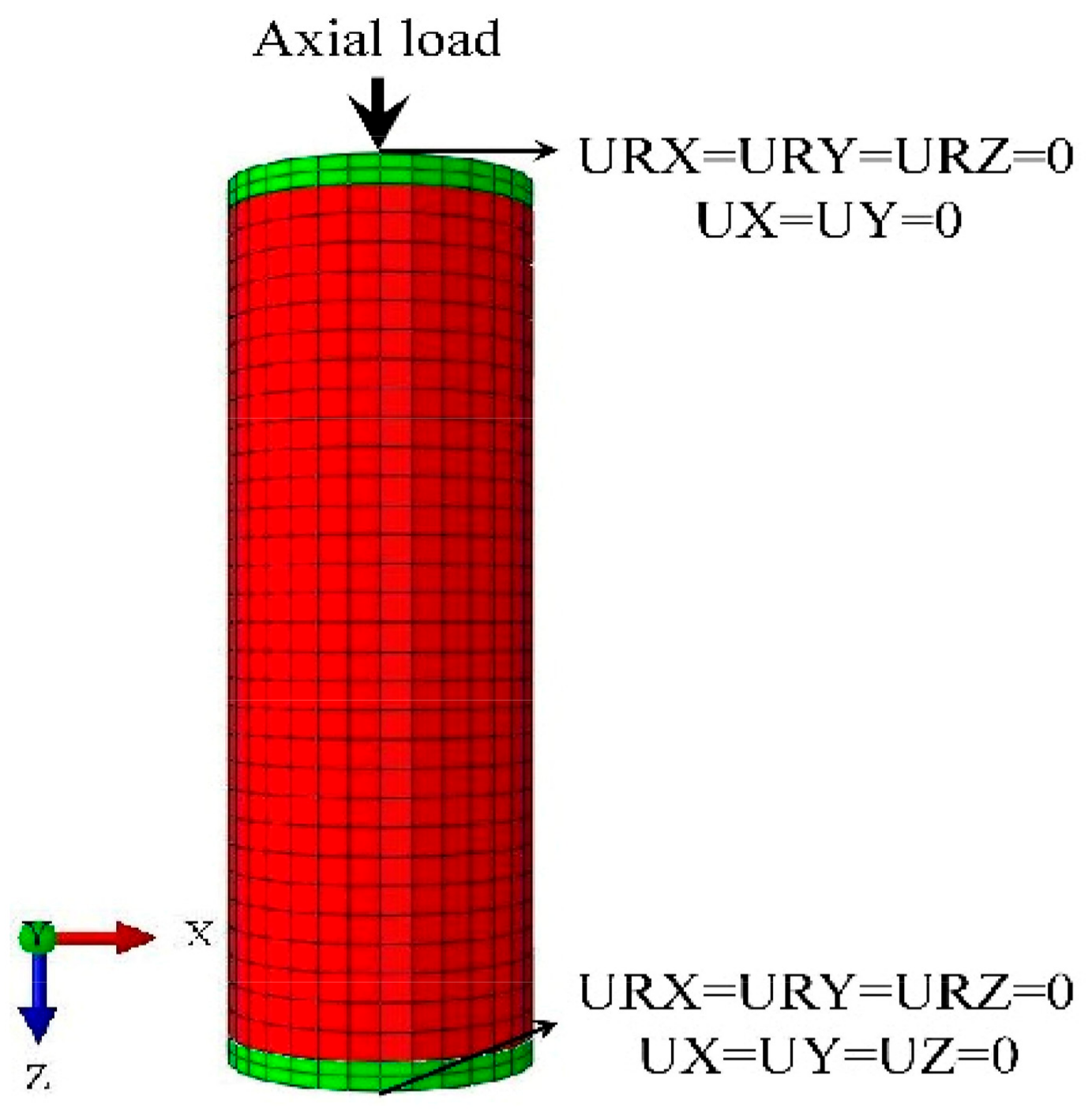
2.1.2. Loading and Boundary Conditions
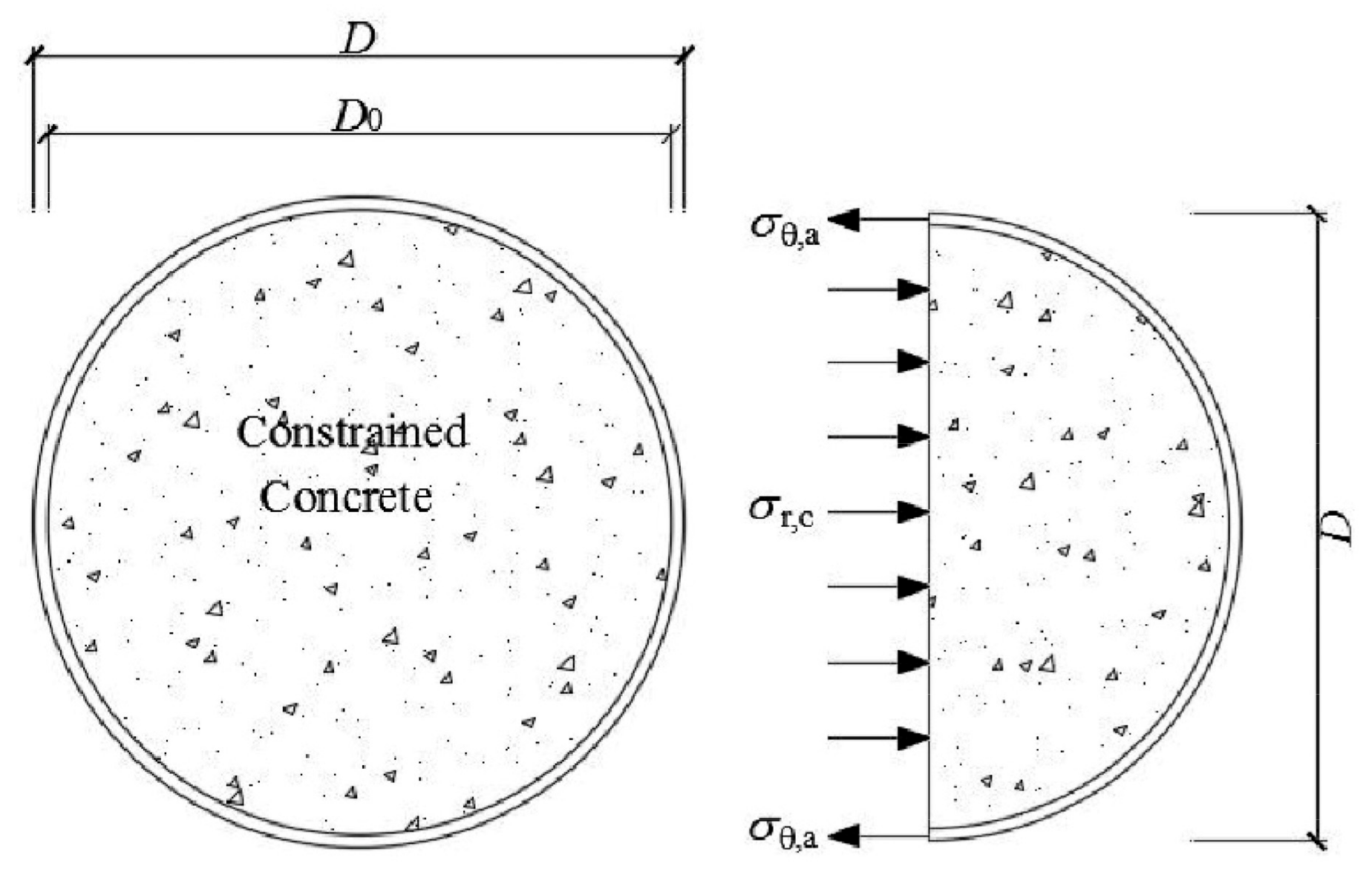
2.1.3. Interaction of the Aluminum Alloy Tubes and the Infilled Concrete
2.2. Constitutive Models of Infilled Concrete
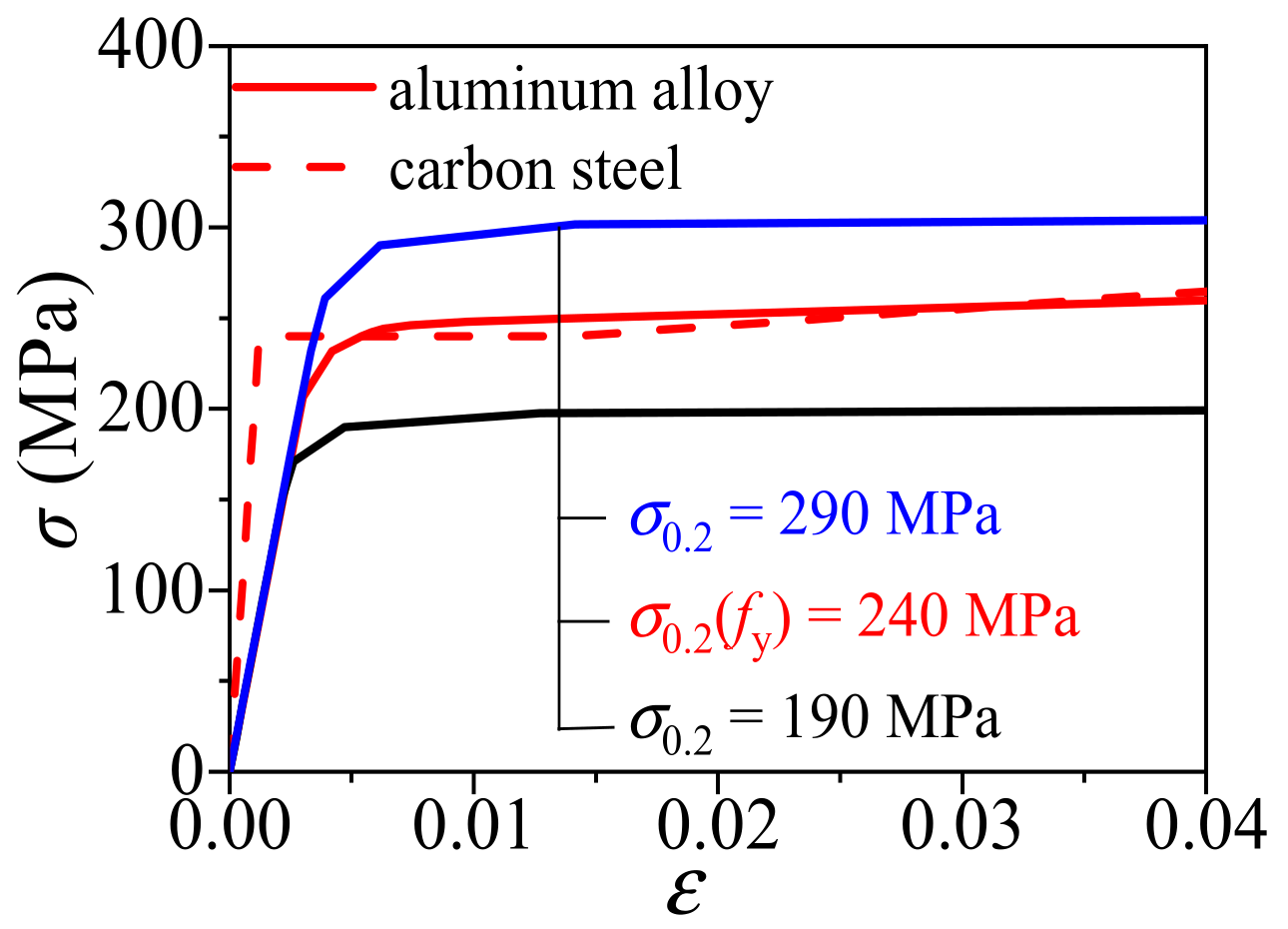
2.3. Constitutive Models of Aluminum Alloy Tube
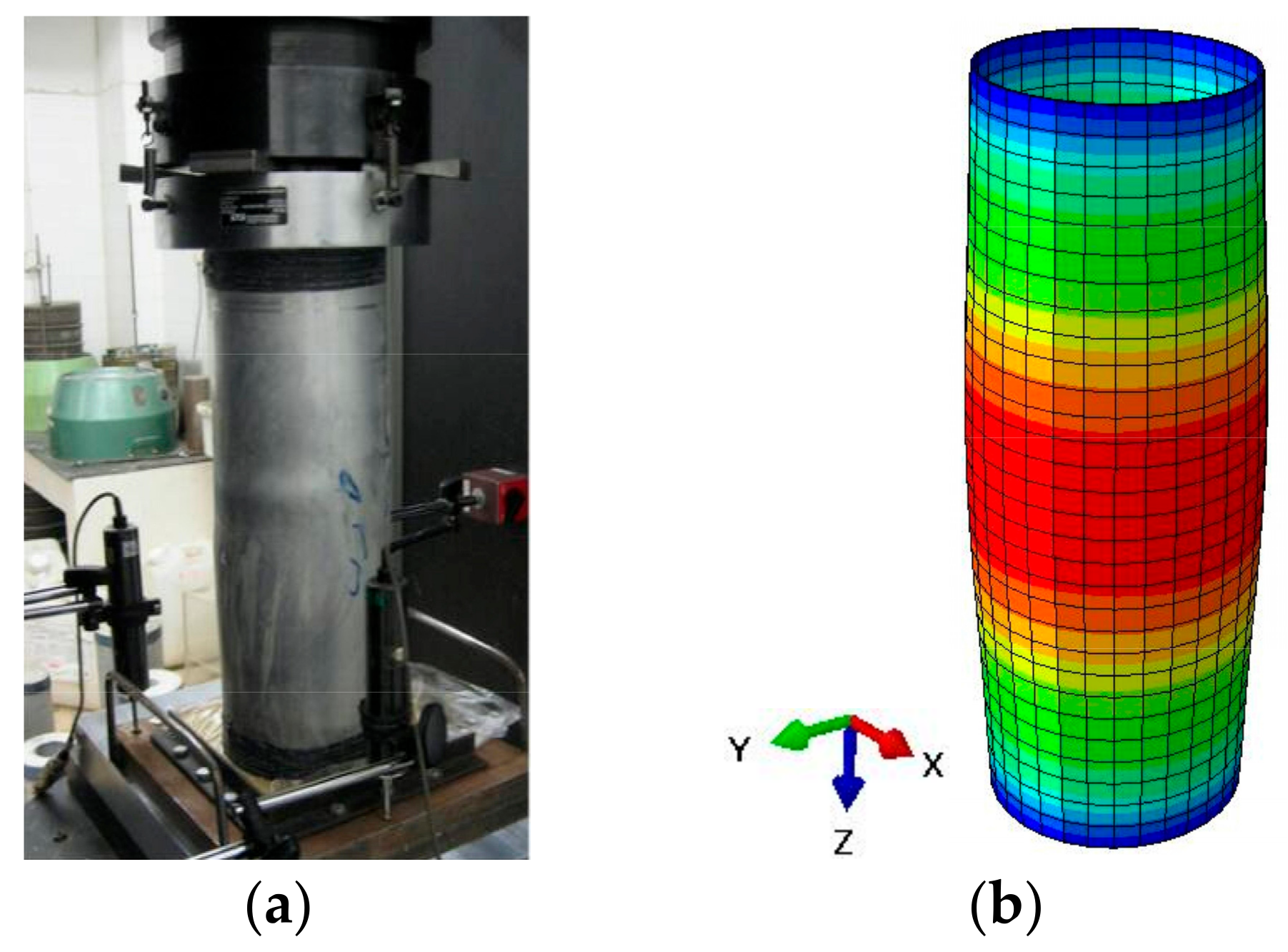
2.4. Geometric Imperfection
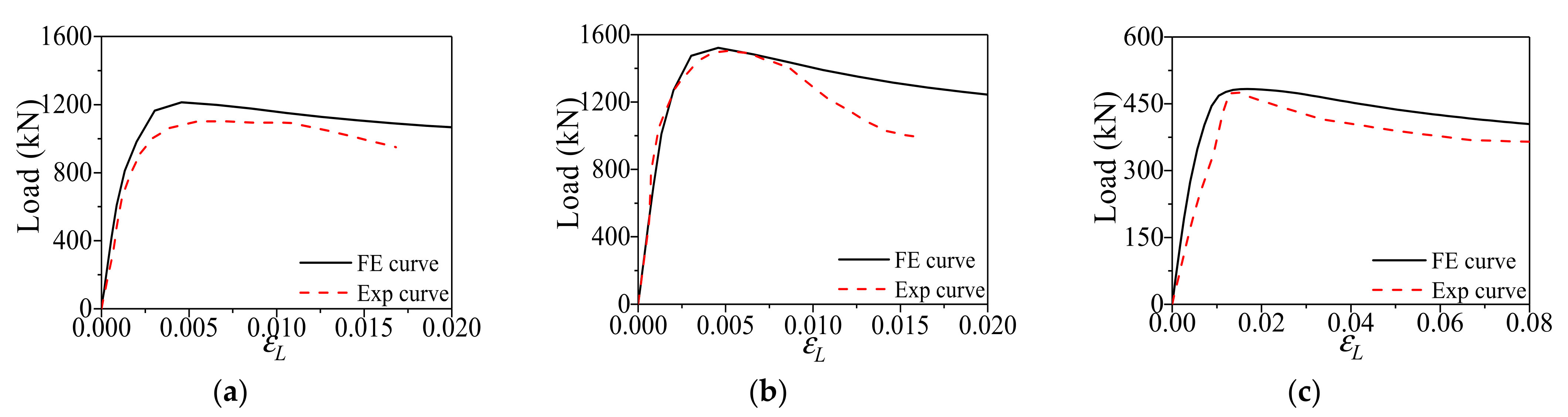
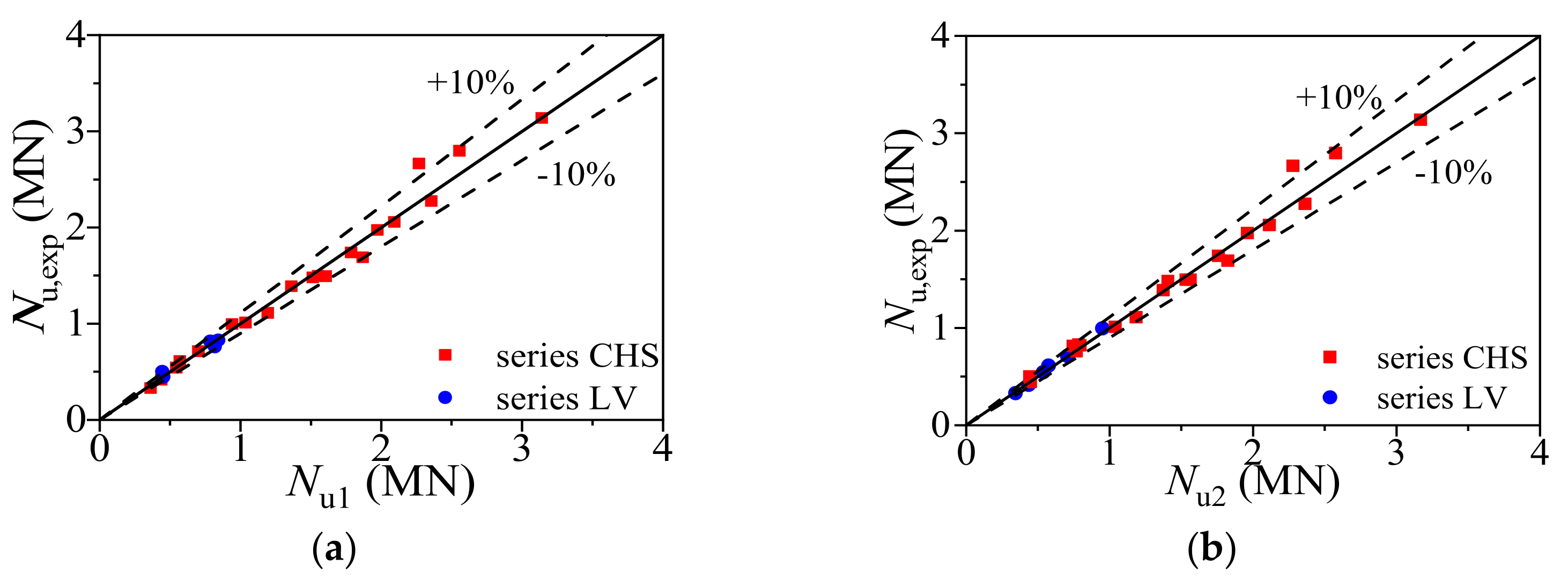
2.5. Model Validation
3. Numerical Investigation of CFCAT Stub Columns Subjected Axial Loading
3.1. Parametric Study
3.2. Composite Action of CFCAT Stub Columns
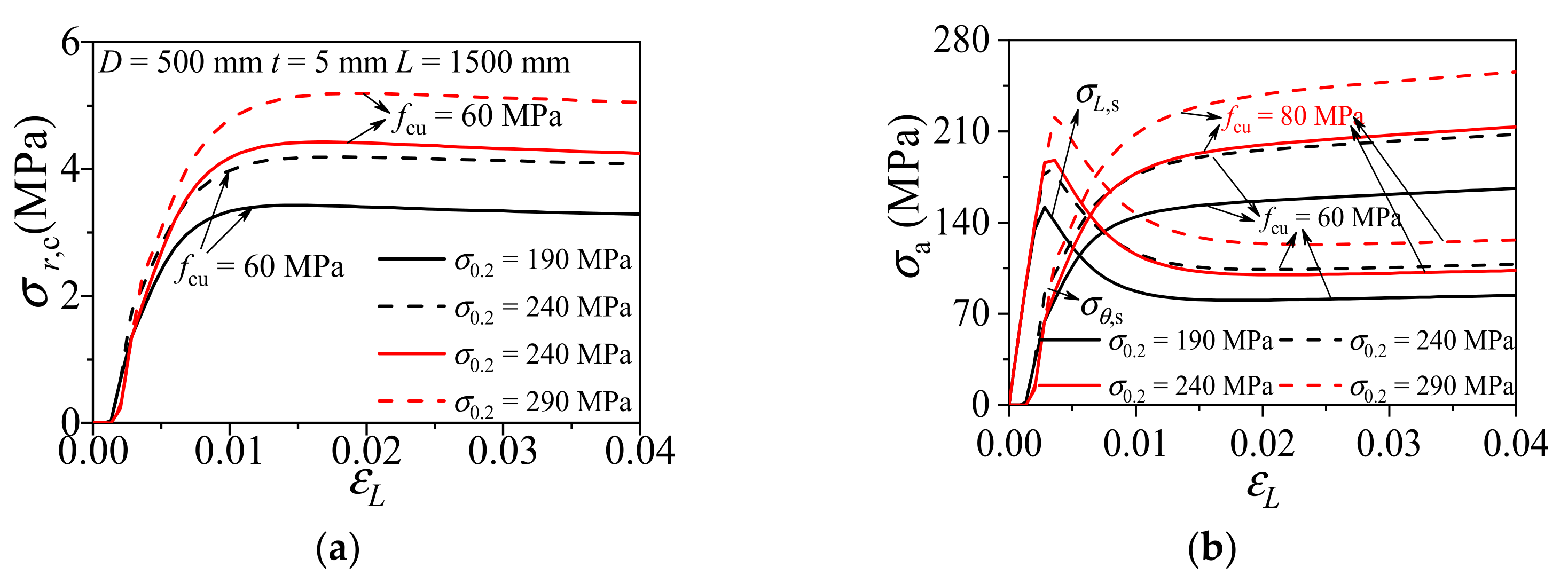
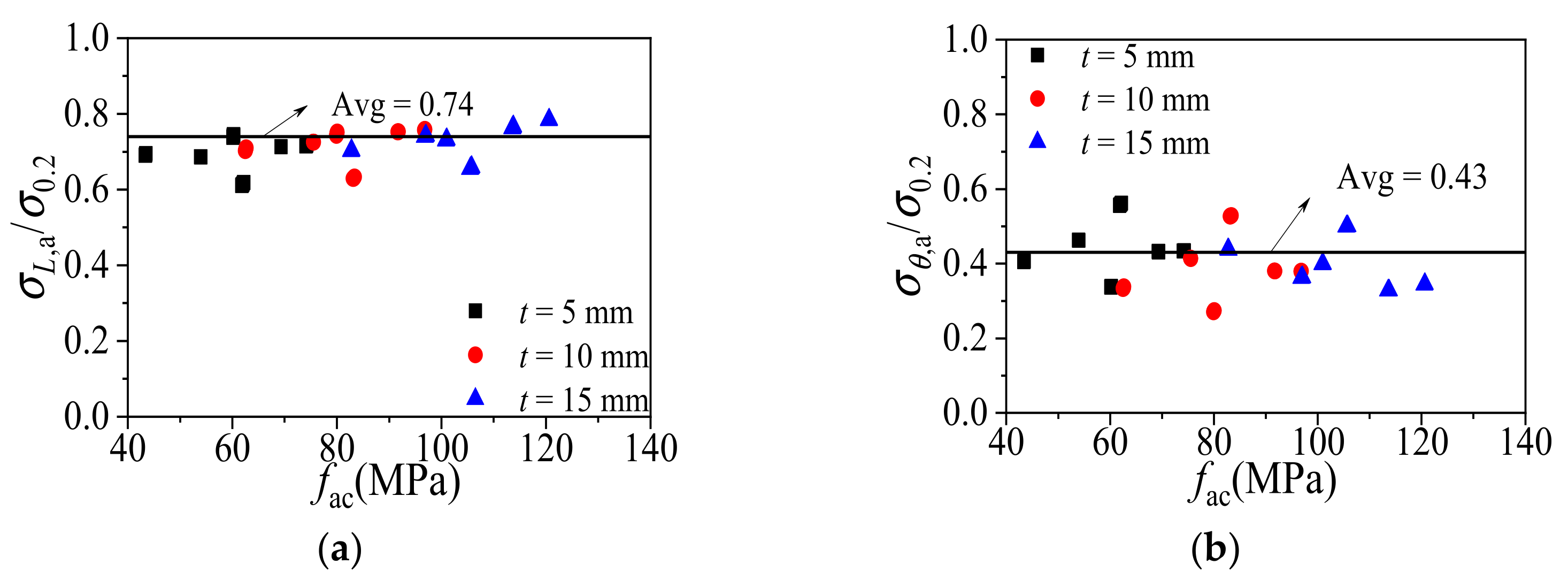
3.2.1. Concrete Strength
3.2.2. Yielding Strength of Aluminum Alloy
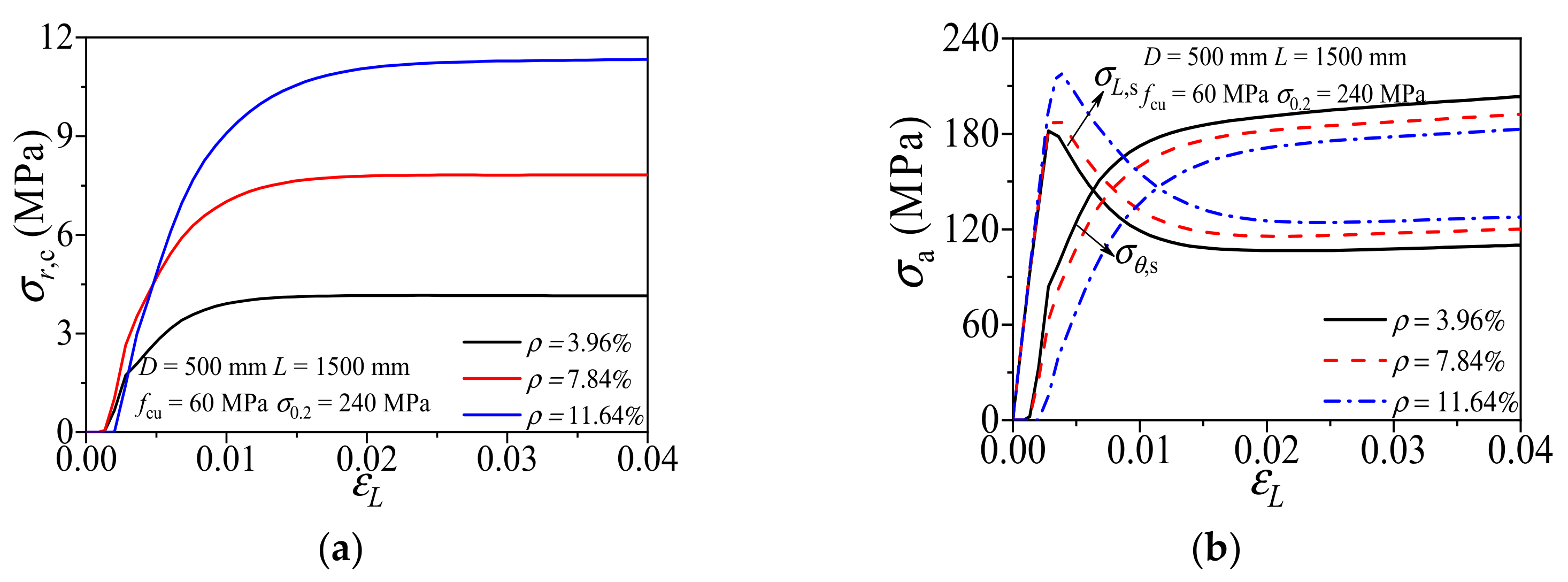
3.2.3. Aluminum Ratio
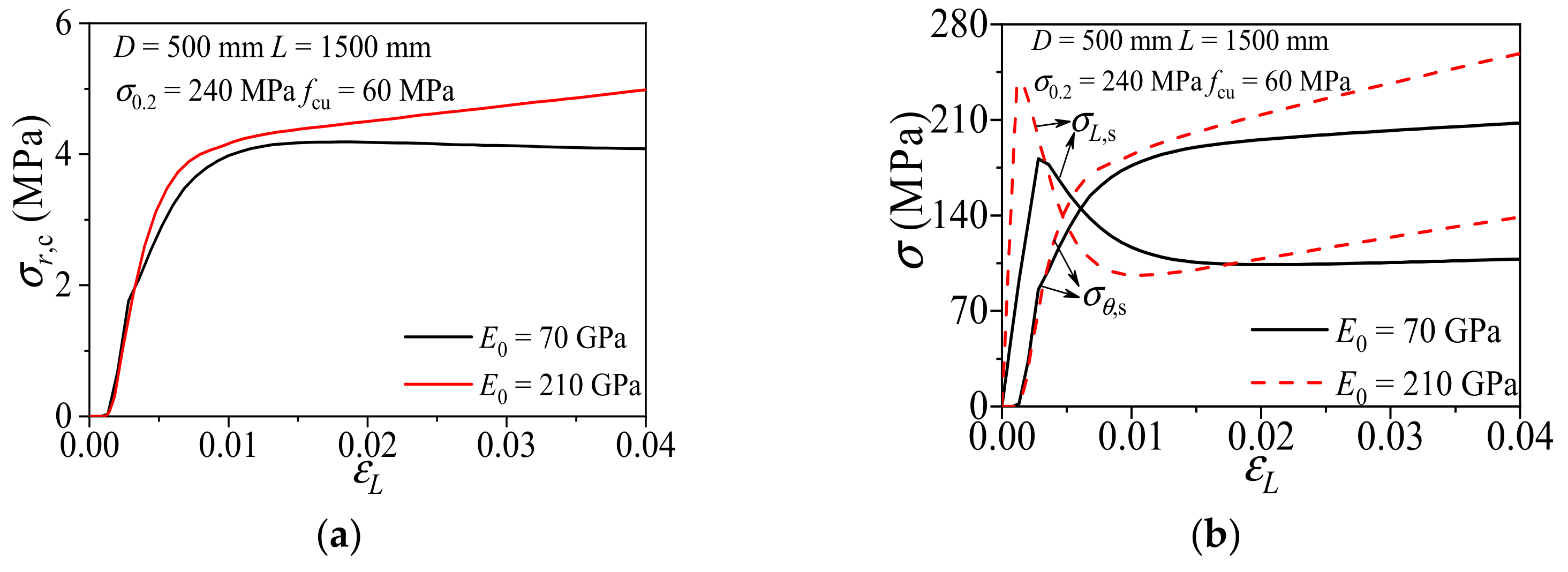
3.2.4. Elastic Modulus
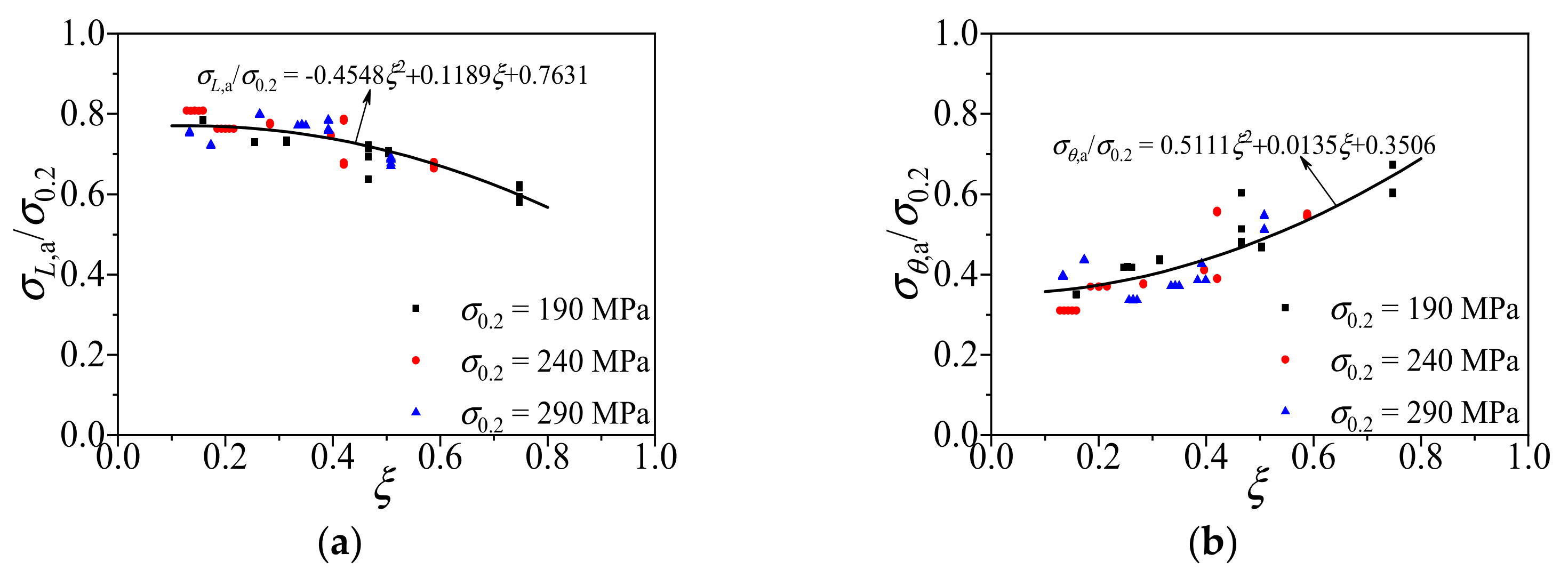
4. Composite Action Model of CFCAT Stub Columns
5. Practical Design Formula for Axial Load-Bearing Capacity of CFCAT Stub Columns
5.1. Model Simplification
5.2. Derivation of Design Formula of CFCAT Stub Columns
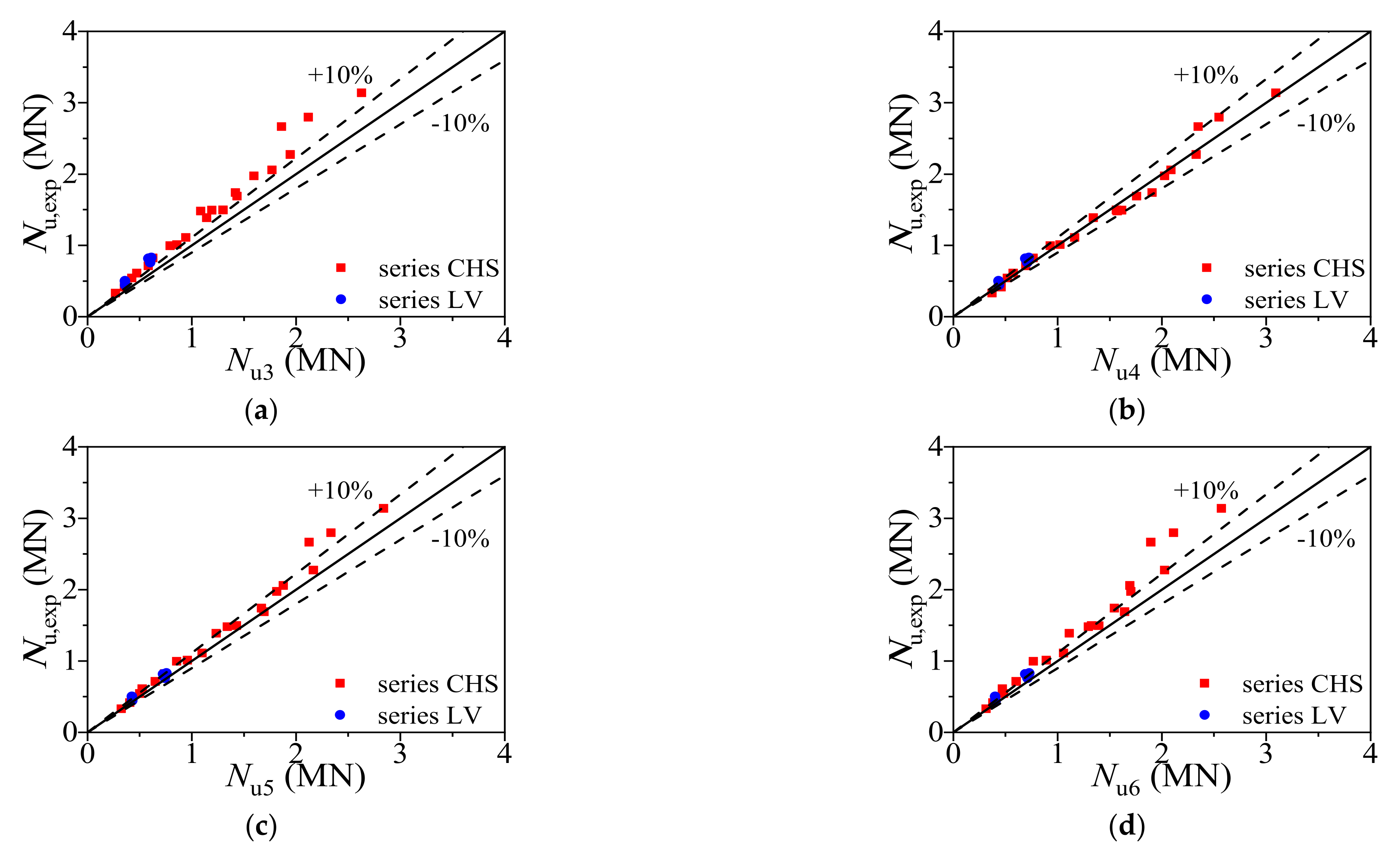
5.3. Formula Validation
6. Conclusions
- A fine-meshed finite 3D solid element model of CFCAT under axial compression was established based on the tri-axial plastic-damage constitutive model of concrete and elastoplastic constitutive model of the aluminum alloy. The FE analytical results coincide well with the experimental results.
- Based on the validated FE modeling technique, 90 full-scale FE models were established for parametric study. The numerical results revealed that the higher aluminum alloy strength and ratio lead to a better confinement effect and a weakened enhancement effect. As a result, the compatibility of the strength and dimension of the aluminum alloy and concrete should be noticed in the design, rather than only seeking better confinement.
- Regression models of the longitudinal stress and transverse stress of the aluminum alloy tube at the ultimate state of the columns were proposed, respectively. This model considered the three-dimensional stress state of the outer tube and is a more authentic expression when the column reached its ultimate state.
- A design formula was proposed to estimate the ultimate bearing capacity of CFCAT stub columns under axial compression. An enhancement factor which reflects the level of composite action of CFCAT stub columns is calculated. The obtained value of 1.47, which is smaller than the confinement coefficient of 1.62 of CFCST stub columns. The proposed formula that was evaluated has a higher accuracy compared with some current design methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, Z.Y.; Guo, X.N.; Li, Y.Q. State of the arts of research on aluminium alloy structures. J. Build. Struct. 2007, 28, 100–109. [Google Scholar]
- Das, S. Development of aluminium alloy composites for engineering applications. Trans. Indian Inst. Met. 2004, 57, 325–334. [Google Scholar]
- Blatnický, M.; Sága, M.; Dižo, J.; Bruna, M. Application of Light Metal Alloy EN AW 6063 to Vehicle Frame Construction with an Innovated Steering Mechanism. Materials 2020, 13, 817. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.; Feng, R.; Gong, W. Flexural behavior of concrete-filled aluminum alloy circular hollow section tubes. Constr. Build. Mater. 2018, 165, 173–186. [Google Scholar] [CrossRef]
- Szumigała, M.; Polus, Ł. Applications of Aluminium and Concrete Composite Structures. Procedia Eng. 2015, 108, 544–549. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Young, B. Tests of concrete-filled aluminum stub columns. Thin-Walled Struct. 2008, 46, 573–583. [Google Scholar] [CrossRef]
- Zhou, F.; Young, B. Concrete-filled aluminum circular hollow section column tests. Thin-Walled Struct. 2009, 47, 1272–1280. [Google Scholar] [CrossRef]
- Zhou, F.; Young, B. Concrete-filled double-skin aluminum circular hollow section stub columns. Thin-Walled Struct. 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Zhu, J.-H.; Young, B. Experimental investigation of aluminum alloy circular hollow section columns. Eng. Struct. 2006, 28, 207–215. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameter. Technical Notes No. 902. 1943. Available online: https://ntrs.nasa.gov/citations/19930081614 (accessed on 20 April 2021).
- Ding, F.X.; Wang, W.J.; Liu, X.M.; Wang, L.P.; Sun, Y. Mechanical behavior of outer square inner circular concrete filled dual steel tubular stub columns. Steel Compos. Struct. 2021, 38, 305–317. [Google Scholar] [CrossRef]
- Lu, D.-R.; Wang, W.-J.; Ding, F.-X.; Liu, X.-M.; Fang, C.-J. The impact of stirrups on the composite action of concrete-filled steel tubular stub columns under axial loading. Structures 2021, 30, 786–802. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Zhang, S. Static behaviors of reinforcement-stiffened square concrete-filled steel tubular columns. Thin-Walled Struct. 2012, 58, 18–31. [Google Scholar] [CrossRef]
- Qu, X.; Chen, Z.; Sun, G. Axial behaviour of rectangular concrete-filled cold-formed steel tubular columns with different loading methods. Steel Compos. Struct. 2015, 18, 71–90. [Google Scholar] [CrossRef]
- Nasser, K.Z. Structural Behavior of Concrete Filled Aluminum Tubular Columns. Basrah J. Eng. Sci. 2012, 12, 46–59. [Google Scholar]
- Resan, F. Experimental Investigation of Aluminium-Lightweight Concrete Composite Columns. Basrah J. Eng. Sci. 2014, 14, 13–25. [Google Scholar]
- Aluminium Association. Aluminium Design Manual—Part I: Specification for Aluminium Structures; Aluminium Association: Washington, DC, USA, 2005. [Google Scholar]
- ACI. ACI 318-08: Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Detroit, MI, USA, 2008. [Google Scholar]
- Australia/New Zealand Strandard. Aluminium Structures Part 1: Limit State Design; AS/NZS 1664.1-1997; Standards Australia: Sydney, NSW, Australia, 1997.
- Australian Standard AS3600. Concrete Structures; AS3600-2001; Standards Australia: Sydney, NSW, Australia, 2001. [Google Scholar]
- Zhou, F.; Young, B. Numerical analysis and design of concrete-filled aluminum circular hollow section columns. Thin-Walled Struct. 2012, 50, 45–55. [Google Scholar] [CrossRef]
- Wang, F.-C.; Zhao, H.-Y.; Han, L.-H. Analytical behavior of concrete-filled aluminum tubular stub columns under axial compression. Thin-Walled Struct. 2019, 140, 21–30. [Google Scholar] [CrossRef] [Green Version]
- Hibbitt, B.K.D.; Sorensen, P. ABAQUS Standard User’s and Reference Manuals; Version 6.14; Dassault Systèmes: Providence, RI, USA, 2014. [Google Scholar]
- Wang, F.C.; Zhao, H.Y.; Han, L.H. Analytical Behavior of Concrete-Filled Aluminum Tubular Stub Columns Under Axial Compression. In Proceedings of the 12th International Conference on Advances in Steel-Concrete Composite Structures—ASCCS 2018, Valencia, Spain, 27–29 June 2018. [Google Scholar]
- Idan, F.K. Finite element analysis of concrete-filled aluminium tube columns. Int. J. Appl. Eng. Res. 2017, 12, 3054–3062. [Google Scholar]
- Patel, V.I.; Liang, Q.Q.; Hadi, M.N. Numerical study of circular double-skin concrete-filled aluminum tubular stub columns. Eng. Struct. 2019, 197, 109418. [Google Scholar] [CrossRef]
- Liu, Y.; Lyu, F.; Ding, F.; Wang, E.; Xu, Y.; Yuan, T.; Deng, C.; Luo, C. Numerical Study on Confinement Effect and Efficiency of Concentrically Loaded RACFRST Stub Columns. Front. Mater. 2021, 8. [Google Scholar] [CrossRef]
- Bencardino, F.; Nisticò, M.; Verre, S. Experimental Investigation and Numerical Analysis of Bond Behavior in SRG-Strengthened Masonry Prisms Using UHTSS and Stainless-Steel Fibers. Fibers 2020, 8, 8. [Google Scholar] [CrossRef] [Green Version]
- Fortunato, G.; Funari, M.F.; Lonetti, P. Survey and seismic vulnerability assessment of the Baptistery of San Giovanni in Tumba (Italy). J. Cult. Herit. 2017, 26, 64–78. [Google Scholar] [CrossRef]
- Ding, F.; Ying, X.; Zhou, L.; Yu, Z. Unified calculation method and its application in determining the uniaxial mechanical properties of concrete. Front. Arch. Civ. Eng. China 2011, 5, 381–393. [Google Scholar] [CrossRef]
- Jankowiak, T.; Lodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Ding, F.-X.; Yin, Y.-X.; Mao, J.-F.; Wang, L.-P.; Yu, Y.-J.; Luo, L.; Yu, Z.-W. Analytical behaviors of concrete-filled circular stainless steel tubular (CFCSST) stub columns under axial loading. Structures 2019, 19, 277–285. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhu, J.Q.; Wu, P.G. High-Strength Concrete and its Applications; Tsinghua University Press: Beijing, China, 1992. [Google Scholar]
- Gardner, L.; Ashraf, M. Structural design for non-linear metallic materials. Eng. Struct. 2006, 28, 926–934. [Google Scholar] [CrossRef]
- EU. Eurocode 9 (EC9) EN 1999-1-1:2007, Design of Aluminium Structures-General Structure Rules. In Edict of Government; CEN: Brussels, Belgium, 2013. [Google Scholar]
- Wang, F.-C.; Han, L.-H.; Li, W. Analytical behavior of CFDST stub columns with external stainless steel tubes under axial compression. Thin-Walled Struct. 2018, 127, 756–768. [Google Scholar] [CrossRef]
- Ashraf, M.; Gardner, L.; Nethercot, D.A. Finite element modelling of structural stainless steel cross-sections. Thin-Walled Struct. 2006, 44, 1048–1062. [Google Scholar] [CrossRef]
- Gardner, L.; Nethercot, D.A. Numerical Modeling of Stainless Steel Structural Components—A Consistent Approach. J. Struct. Eng. 2004, 130, 1586–1601. [Google Scholar] [CrossRef]
- Ellobody, E.; Young, B. Structural performance of cold-formed high strength stainless steel columns. J. Constr. Steel Res. 2005, 61, 1631–1649. [Google Scholar] [CrossRef]
- Tao, Z.; Uy, B.; Liao, F.-Y.; Han, L.-H. Nonlinear analysis of concrete-filled square stainless steel stub columns under axial compression. J. Constr. Steel Res. 2011, 67, 1719–1732. [Google Scholar] [CrossRef]
- Gong, Y.L. Experimental and Theoretical Research on Mechanical Property of Common Concrete Filled Metal Tubes Columns; Harbin Institute of Technology: Harbin, China, 2011. [Google Scholar]
- Sakino, K.; Nakahara, H.; Morino, S.; Nishiyama, I. Behavior of Centrally Loaded Concrete-Filled Steel-Tube Short Columns. J. Struct. Eng. 2004, 130, 180–188. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D. Numerical model for the behavior and capacity of circular CFT columns, Part I: Theory. Eng. Struct. 2008, 30, 1573–1578. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, S.; Zhang, X.; Guo, L. Behavior and strength of circular tube confined reinforced-concrete (CTRC) columns. J. Constr. Steel Res. 2009, 65, 1447–1458. [Google Scholar] [CrossRef]
- Mei, H.; Kiousis, P.D.; Ehsani, M.R.; Saadatmanesh, H. Confinement effects on highstrength concrete. Struct. J. 2001, 98, 548–553. [Google Scholar]
- Ding, F.-X.; Yu, Z.-W.; Bai, Y.; Gong, Y.-Z. Elasto-plastic analysis of circular concrete-filled steel tube stub columns. J. Constr. Steel Res. 2011, 67, 1567–1577. [Google Scholar] [CrossRef]
- Wei, Y.; Jiang, C.; Wu, Y.-F. Confinement effectiveness of circular concrete-filled steel tubular columns under axial compression. J. Constr. Steel Res. 2019, 158, 15–27. [Google Scholar] [CrossRef]
- Zha, X.X.; Gong, Y.L. Behavior study of new-type concrete filled metal tubular (CFMT) columns Ⅰ: Strength capacity of axially compressed short columns. Prog. Steel Build. Struct. 2012, 14, 12–18. [Google Scholar]




| Specimens | Ref. | L (mm) | E0 (MPa) | σ0.2 (MPa) | n | fcu (MPa) | Nu,exp (kN) | Nu,FE (kN) | Nu,exp/Nu,FE |
|---|---|---|---|---|---|---|---|---|---|
| CHS4-C40 | [7] | 76.1 2.06 228 | 64,900 | 237.0 | 23.70 | 56.0 | 329.9 | 383.5 | 0.860 |
| CHS4-C70 | 76.0 2.06 228 | 64,900 | 237.0 | 23.70 | 80.2 | 415.7 | 450.2 | 0.923 | |
| CHS4-C100 | 76.1 2.05 228 | 64,900 | 237.0 | 23.70 | 114.0 | 611.4 | 599.5 | 1.020 | |
| CHS5-C40 | 99.7 2.02 300 | 65,600 | 244.3 | 24.43 | 56.0 | 543.6 | 557.5 | 0.975 | |
| CHS5-C70 | 99.8 2.06 300 | 65,600 | 244.3 | 24.43 | 80.2 | 712.0 | 692.8 | 1.028 | |
| CHS5-C100 | 100 2.05 300 | 65,600 | 244.3 | 24.43 | 114.0 | 995.8 | 947.0 | 1.052 | |
| CHS6-C40 | 119.8 2.49 360 | 66,500 | 253.1 | 25.31 | 56.0 | 822.8 | 826.3 | 0.996 | |
| CHS6-C70 | 120 2.55 360 | 66,500 | 253.1 | 25.31 | 80.2 | 1010.3 | 1023.9 | 0.987 | |
| CHS6-C100 | 119.6 2.48 360 | 66,500 | 253.1 | 25.31 | 114.0 | 1388.7 | 1377.2 | 1.008 | |
| CHS7-C40 | 150.1 2.53 450 | 64,900 | 267.9 | 26.79 | 56.0 | 1111.1 | 1212.2 | 0.917 | |
| CHS7-C70 | 150.1 2.54 451 | 64,900 | 267.9 | 26.79 | 80.2 | 1496.4 | 1520.4 | 0.984 | |
| CHS7-C100 | 149.9 2.53 450 | 64,900 | 267.9 | 26.79 | 114.0 | 2057.8 | 2108.4 | 0.976 | |
| CHS8-C40 | 150.2 5.03 228 | 65,800 | 216.9 | 21.69 | 56.0 | 1481.9 | 1432.7 | 1.034 | |
| CHS8-C70 | 150.2 5.04 450 | 65,800 | 216.9 | 21.69 | 80.2 | 1740.6 | 1661.9 | 1.047 | |
| CHS8-C100 | 150.2 5.03 450 | 65,800 | 216.9 | 21.69 | 114.0 | 2666.1 | 2171.0 | 1.228 | |
| CHS9-C40 | 160.1 4.03 480 | 66,600 | 254.2 | 25.42 | 56.0 | 1494.1 | 1544.9 | 0.967 | |
| CHS9-C70 | 160.5 4.07 480 | 66,600 | 254.2 | 25.42 | 80.2 | 1974.4 | 1928.0 | 1.024 | |
| CHS9-C100 | 160.5 4.06 480 | 66,600 | 254.2 | 25.42 | 114.0 | 2797.3 | 2551.6 | 1.096 | |
| CHS10-C40 | 180.0 3.71 540 | 68,700 | 264.9 | 26.49 | 56.0 | 1690.2 | 1913.1 | 0.883 | |
| CHS10-C70 | 180.4 3.69 540 | 68,700 | 264.9 | 26.49 | 80.2 | 2274.2 | 2339.5 | 0.972 | |
| CHS10-C100 | 180.5 3.75 540 | 68,700 | 264.9 | 26.49 | 114.0 | 3139.2 | 3172.0 | 0.990 | |
| LV100-1 | [41] | 100 2 300 | 89,752 | 186.4 | 18.64 | 50.08 | 443.6 | 483.0 | 0.918 |
| LV100-2 | 100 2 300 | 86,956 | 187.8 | 18.78 | 50.08 | 448.85 | 485.3 | 0.923 | |
| LV100-3 | 100 2 300 | 90,878 | 182.0 | 18.20 | 50.08 | 502.3 | 479.5 | 1.048 | |
| LV120-1 | 120 4 360 | 105,661 | 170.8 | 17.08 | 50.08 | 815.9 | 811.3 | 1.005 | |
| LV120-2 | 120 4 360 | 92,593 | 188.8 | 18.88 | 50.08 | 829.7 | 862.7 | 0.962 | |
| LV120-3 | 120 4 360 | 91,863 | 181.1 | 18.11 | 50.08 | 761.5 | 839.6 | 0.907 | |
| Mean | 0.996 | ||||||||
| Cov | 0.073 |
| D (mm) | L (mm) | t (mm) | n | fcu (MPa) | σ0.2 (MPa) |
|---|---|---|---|---|---|
| 500 | 1500 | 5 | 23–31 | 40, 60 | 190 |
| 5 | 23–31 | 60, 80 | 240 | ||
| 5 | 23–31 | 80, 100 | 290 | ||
| 10 | 23–31 | 40, 60 | 190 | ||
| 10 | 23–31 | 60, 80 | 240 | ||
| 10 | 23–31 | 80, 100 | 290 | ||
| 15 | 23–31 | 40, 60 | 190 | ||
| 15 | 23–31 | 60, 80 | 240 | ||
| 15 | 23–31 | 80, 100 | 290 |
| No. | Ref. | Formula | Limitations |
|---|---|---|---|
| Equation (19) | ACI 318 [18] | - | |
| Equation (20) | Zhou, F. [21] | ||
| Equation (21) | Wang, F.C. [22] | ||
| Equation (22) | Zha, X.X. [48] | - |
| Specimens | Ref. | Nu,exp (kN) | Nu2 (kN) | Nu3 (kN) | Nu4 (kN) | Nu5 (kN) | Nu6 (kN) | Nu,exp/ Nu2 | Nu,exp/ Nu3 | Nu,exp/ Nu4 | Nu,exp/ Nu5 | Nu,exp/ Nu6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CHS4-C40 | [7] | 329.9 | 345.1 | 286.6 | 371.3 | 323.9 | 314.5 | 1.046 | 0.814 | 1.126 | 0.982 | 0.953 |
| CHS4-C70 | 415.7 | 436.8 | 383.8 | 458.3 | 407.0 | 379.6 | 1.051 | 0.855 | 1.102 | 0.979 | 0.913 | |
| CHS4-C100 | 611.4 | 574.7 | 515.0 | 574.8 | 524.6 | 471.9 | 0.940 | 0.773 | 0.940 | 0.858 | 0.772 | |
| CHS5-C40 | 543.6 | 537.2 | 457.1 | 518.7 | 501.5 | 482.3 | 0.988 | 0.782 | 0.954 | 0.922 | 0.887 | |
| CHS5-C70 | 712 | 705.8 | 633.7 | 695.7 | 650.3 | 603.5 | 0.991 | 0.819 | 0.977 | 0.913 | 0.848 | |
| CHS5-C100 | 995.8 | 951.3 | 867.3 | 929.5 | 854.4 | 768.1 | 0.955 | 0.796 | 0.933 | 0.858 | 0.771 | |
| CHS6-C40 | 822.8 | 794.7 | 672.6 | 765.3 | 739.7 | 715.0 | 0.966 | 0.761 | 0.930 | 0.899 | 0.869 | |
| CHS6-C70 | 1010.3 | 1040.3 | 929.2 | 1022.5 | 957.3 | 892.3 | 1.030 | 0.848 | 1.012 | 0.947 | 0.883 | |
| CHS6-C100 | 1388.7 | 1375.2 | 1250.1 | 1342.4 | 1234.0 | 1112.9 | 0.990 | 0.823 | 0.967 | 0.889 | 0.801 | |
| CHS7-C40 | 1111.1 | 1185.2 | 1016.9 | 1163.5 | 1099.6 | 1056.0 | 1.067 | 0.849 | 1.047 | 0.990 | 0.950 | |
| CHS7-C70 | 1496.4 | 1563.3 | 1416.3 | 1563.0 | 1427.9 | 1325.4 | 1.045 | 0.869 | 1.045 | 0.954 | 0.886 | |
| CHS7-C100 | 2057.8 | 2114.6 | 1940.7 | 2087.0 | 1878.5 | 1693.7 | 1.028 | 0.860 | 1.014 | 0.913 | 0.823 | |
| CHS8-C40 | 1481.9 | 1406.5 | 1153.5 | 1571.8 | 1340.2 | 1294.2 | 0.949 | 0.732 | 1.061 | 0.904 | 0.873 | |
| CHS8-C70 | 1740.6 | 1759.2 | 1526.1 | 1906.3 | 1668.8 | 1545.3 | 1.011 | 0.815 | 1.095 | 0.959 | 0.888 | |
| CHS8-C100 | 2666.1 | 2279.1 | 2020.5 | 2347.6 | 2124.7 | 1893.3 | 0.855 | 0.698 | 0.881 | 0.797 | 0.710 | |
| CHS9-C40 | 1494.1 | 1533.0 | 1274.3 | 1615.1 | 1428.4 | 1394.6 | 1.026 | 0.798 | 1.081 | 0.956 | 0.933 | |
| CHS9-C70 | 1974.4 | 1961.0 | 1723.5 | 2026.8 | 1813.9 | 1701.9 | 0.993 | 0.808 | 1.027 | 0.919 | 0.862 | |
| CHS9-C100 | 2797.3 | 2575.5 | 2307.8 | 2547.2 | 2334.5 | 2113.1 | 0.921 | 0.757 | 0.911 | 0.835 | 0.755 | |
| CHS10-C40 | 1690.2 | 1824.1 | 1539.1 | 1757.7 | 1691.5 | 1642.6 | 1.079 | 0.849 | 1.040 | 1.001 | 0.972 | |
| CHS10-C70 | 2274.2 | 2362.8 | 2109.6 | 2328.8 | 2166.4 | 2025.5 | 1.039 | 0.855 | 1.024 | 0.953 | 0.891 | |
| CHS10-C100 | 3139.2 | 3169.5 | 2872.6 | 3092.7 | 2839.1 | 2570.5 | 1.010 | 0.837 | 0.985 | 0.904 | 0.819 | |
| LV100-1 | [41] | 443.6 | 448.2 | 390.2 | 438.2 | 428.4 | 404.8 | 1.010 | 0.816 | 0.988 | 0.966 | 0.913 |
| LV100-2 | 448.85 | 449.4 | 391.0 | 439.4 | 429.4 | 406.0 | 1.001 | 0.808 | 0.979 | 0.957 | 0.905 | |
| LV100-3 | 502.3 | 444.2 | 387.5 | 434.4 | 425.4 | 401.0 | 0.884 | 0.715 | 0.865 | 0.847 | 0.798 | |
| LV120-1 | 815.9 | 746.3 | 623.8 | 690.5 | 725.5 | 689.8 | 0.915 | 0.717 | 0.846 | 0.889 | 0.845 | |
| LV120-2 | 829.7 | 784.8 | 650.0 | 723.6 | 756.2 | 727.5 | 0.946 | 0.737 | 0.872 | 0.911 | 0.877 | |
| LV120-3 | 761.5 | 768.3 | 638.8 | 709.5 | 743.1 | 711.4 | 1.009 | 0.788 | 0.932 | 0.976 | 0.934 | |
| Mean | 0.991 | 0.799 | 0.986 | 0.921 | 0.864 | |||||||
| Cov | 0.055 | 0.061 | 0.077 | 0.056 | 0.076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, F.; Liao, C.; Wang, E.; Lyu, F.; Xu, Y.; Liu, Y.; Feng, Y.; Shang, Z. Numerical Investigation of the Composite Action of Axially Compressed Concrete-Filled Circular Aluminum Alloy Tubular Stub Columns. Materials 2021, 14, 2435. https://doi.org/10.3390/ma14092435
Ding F, Liao C, Wang E, Lyu F, Xu Y, Liu Y, Feng Y, Shang Z. Numerical Investigation of the Composite Action of Axially Compressed Concrete-Filled Circular Aluminum Alloy Tubular Stub Columns. Materials. 2021; 14(9):2435. https://doi.org/10.3390/ma14092435
Chicago/Turabian StyleDing, Faxing, Changbin Liao, En Wang, Fei Lyu, Yunlong Xu, Yicen Liu, Yuan Feng, and Zhihai Shang. 2021. "Numerical Investigation of the Composite Action of Axially Compressed Concrete-Filled Circular Aluminum Alloy Tubular Stub Columns" Materials 14, no. 9: 2435. https://doi.org/10.3390/ma14092435







