Blood Particulate Analogue Fluids: A Review
Abstract
:1. Introduction
2. RBC Templates
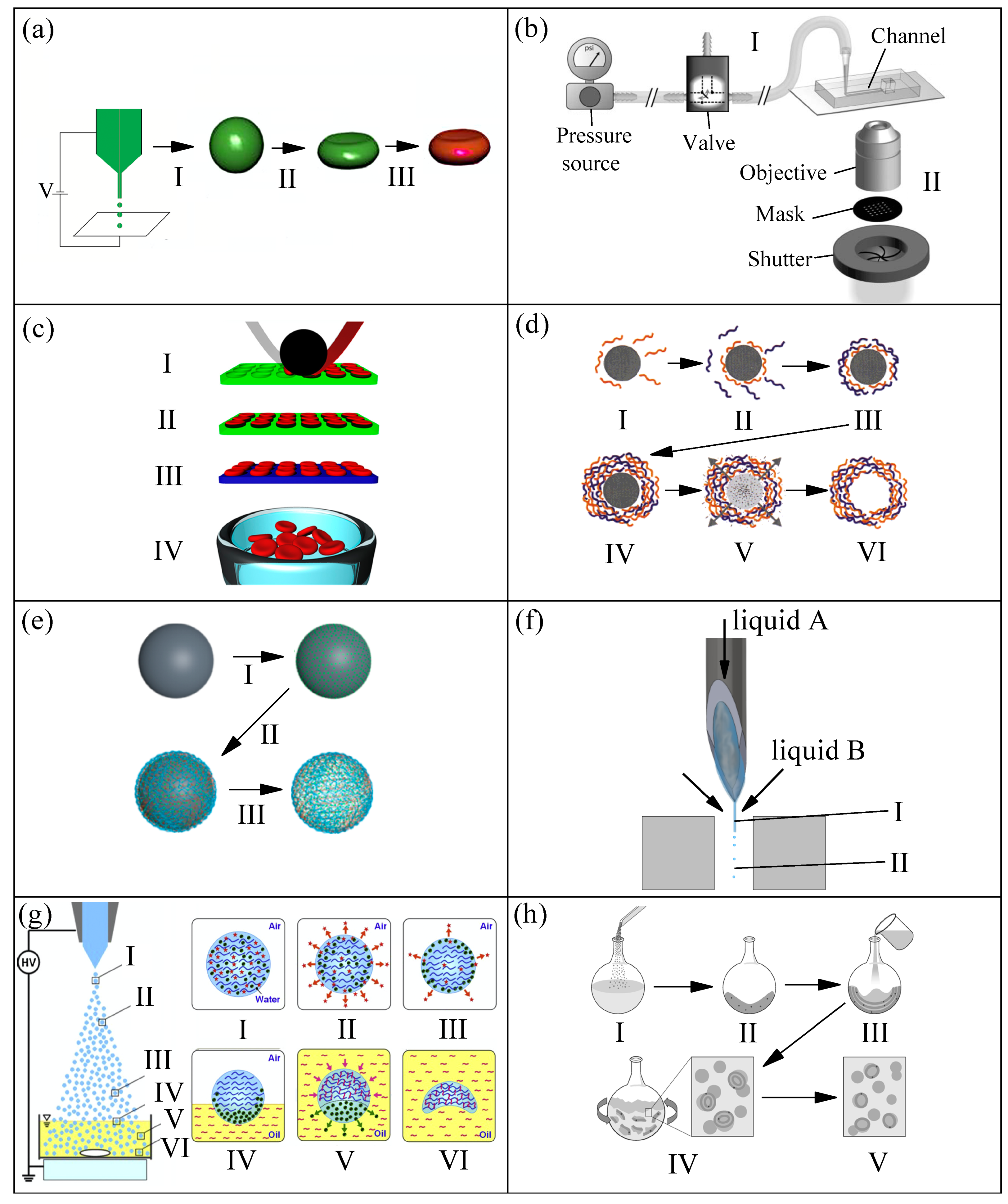
2.1. Production Methods, Size, and Shape
2.2. Deformability
2.3. Biological Functionalities
3. Dynamic Flow of Particulate Fluids
3.1. Rheology: Shear and Extensional
3.1.1. Shear Flow Measurement: Steady and Oscillatory
3.1.2. Extensional Flow Measurement
- The limitation faced by the slow retraction method used, which differs from Ref. [52] to Ref. [81]. The relaxation time in Ref. [52] was determined by a commercialized CaBER device that allows a reliable measurement down to 240 μs, while it was down to 100 μs in Ref. [81]. The extensional device used in Ref. [81] was a custom-made setup developed by Sousa et al. [83] that allows the use of an outer silicone oil bath to avoid evaporation effects, and to visualize the blood cells in the filament. The relaxation time measured using blood samples surrounded by silicone oil was around = 259 ± 47 μs. In addition, the fluid sample was stretched at a constant speed down to 10 μm/s, while these data were around 65 μm/s for the commercial CaBER used in Ref. [52].
3.2. Cell Free Layer
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sebastian, B.; Dittrich, P.S. Microfluidics to mimic blood flow in health and disease. Annu. Rev. Fluid Mech. 2018, 50, 483–504. [Google Scholar] [CrossRef]
- Kang, Y.J.; Lee, S.J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Carvalho, V.; Gonçalves, I.M.; Teixeira, S.; Lima, R. Visualization and Measurements of Blood Cells Flowing in Microfluidic Systems and Blood Rheology: A Personalized Medicine Perspective. J. Pers. Med. 2020, 10, 249. [Google Scholar] [CrossRef]
- Abkarian, M.; Faivre, M.; Horton, R.; Smistrup, K.; Best-Popescu, C.A.; Stone, H.A. Cellular-scale hydrodynamics. Biomed. Mater. 2008, 3, 034011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sousa, P.C.; Pinho, F.T.; Oliveira, M.S.N.; Alves, M.A. Extensional flow of blood analog solutions in microfluidic devices. Biomicrofluidics 2011, 5, 014108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, T.T.; Biadillah, Y.; Mongrain, R.; Brunette, J.; Tardif, J.C.; Bertrand, O.F. A Method for Matching the Refractive Index and Kinematic Viscosity of a Blood Analog for Flow Visualization in Hydraulic Cardiovascular Models. J. Biomech. Eng. 2004, 126, 529–535. [Google Scholar] [CrossRef] [PubMed]
- Gray, J.D.; Owen, I.; Escudier, M.P. Dynamic scaling of unsteady shear-thinning non-Newtonian fluid flows in a large-scale model of a distal anastomosis. Exp. Fluids 2007, 43, 535–546. [Google Scholar] [CrossRef]
- Akagawa, E.; Lee, H.; Tatsumi, E.; Homma, A.; Tsukiya, T.; Taenaka, Y. Flow visualization for different port angles of a pulsatile ventricular assist device. J. Artif. Organs 2012, 15, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Deplano, V.; Knapp, Y.; Bailly, L.; Bertrand, E. Flow of a blood analogue fluid in a compliant abdominal aortic aneurysm model: Experimental modelling. J. Biomech. 2014, 47, 1262–1269. [Google Scholar] [CrossRef]
- Anastasioua, A.D.; Spyrogiannia, A.S.; Koskinasb, K.C.; Giannoglou, G.D.; Paras, S.V. Experimental investigation of the flow of a blood analogue fluid in a replica of a bifurcated small artery. Med. Eng. Phys. 2012, 34, 211–218. [Google Scholar] [CrossRef]
- Gijsen, F.J.H.; Allanic, E.; Vosse, F.V.D.; Janssen, J. The influence of the non-Newtonian properties of blood on the flow in large arteries: Unsteady flow in a 90° curved tube. J. Biomech. 1999, 32, 705–713. [Google Scholar] [CrossRef]
- Doutel, E.; Carneiro, J.; Oliveira, M.S.N.; Campos, J.B.L.M.; Miranda, J.M. Fabrication of 3d mili-scale channels for hemodynamic studies. J. Mech. Med. Biol. 2015, 15, 1550004. [Google Scholar] [CrossRef]
- Buchmann, N.A.; Atkinson, C.; Jeremy, M.C.; Soria, J. Tomographic particle image velocimetry investigation of the flow in a modeled human carotid artery bifurcation. Exp. Fluids 2011, 50, 1131–1151. [Google Scholar] [CrossRef]
- Yousif, M.Y.; Holdsworth, D.W.; Poepping, T.L. A blood-mimicking fluid for particle image velocimetry with silicone vascular models. Exp. Fluids 2011, 50, 769–774. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Pinho, D.; Bento, D.; Lima, R.; Ribeiro, J. Wall expansion assessment of an intracranial aneurysm model by a 3D digital image correlation system measurement. Measurement 2016, 88, 262–270. [Google Scholar] [CrossRef] [Green Version]
- Campo-Deaño, L.; Dullens, R.P.A.; Aarts, D.G.A.L.; Pinho, F.T.; Oliveira, M.S.N. Viscoelasticity of blood and viscoelastic blood analogues for use in polydymethylsiloxane in vitro models of the circulatory system. Biomicrofluidics 2013, 7, 034102. [Google Scholar] [CrossRef] [Green Version]
- Vlastos, G.; Lerche, D.; Koch, B. he superposition of steady on oscillatory shear and its effect on the viscoelasticity of human blood and a blood-like model fluid. Biorheology 1997, 34, 19–36. [Google Scholar] [CrossRef]
- Vlastos, G.; Lerche, D.; Koch, B.; Samba, O.; Pohl, M. The effect of parallel combined steady and oscillatory shear flows on blood and polymer solutions. Rheol. Acta 1997, 36, 160–172. [Google Scholar] [CrossRef]
- Completo, C.; Geraldes, V.; Semiao, V. Rheological and dynamical characterization of blood analogue flows in a slit. Int. J. Heat Fluid Flow 2014, 46, 17–28. [Google Scholar] [CrossRef]
- Najjari, M.R.; Hinke, J.A.; Bulusu, K.V.; Plesniak, M.W. On the rheology of refractive-index-matched, non-Newtonian blood-analog fluids for PIV experiments. Exp. Fluids 2016, 57, 96. [Google Scholar] [CrossRef]
- Brindise, M.C.; Busse, M.M.; Vlachos, P.P. Density-and viscosity-matched Newtonian and non-Newtonian blood-analog solutions with PDMS refractive index. Exp. Fluids 2018, 59, 173. [Google Scholar] [CrossRef]
- Sousa, P.C.; Pinho, F.T.; Alves, M.A.; Oliveira, M.S.N. A review of hemorheology: Measuring techniques and recent advances. Korea-Aust. Rheol. J. 2016, 28, 1–22. [Google Scholar] [CrossRef]
- Maeda, N. Erythrocyte rheology in microcirculation. Jpn. J. Physiol. 1996, 46, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brust, M.; Schaefer, C.; Doerr, R.; Pan, L.; Garcia, M.; Arratia, P.E.; Wagner, C. Rheology of human blood plasma: Viscoelastic versus Newtonian behavior. Phys. Rev. Lett. 2013, 110, 078305. [Google Scholar] [CrossRef] [Green Version]
- Ramnarine, K.V.; Nassiri, D.K.; Hoskins, P.R.; Lubbers, J. Validation of a new blood-mimicking fluid for use in Doppler flow test objects. Ultrasound Med. Biol. 1998, 24, 451–459. [Google Scholar] [CrossRef]
- Oglat, A.A.; Suardi, N.; Matjafri, M.Z.; Oqlat, M.A.; Abdelrahman, M.A.; Oqlat, A.A. A review of suspension-scattered particles used in blood-mimicking fluid for doppler ultrasound imaging. J. Med. Ultrasound 2018, 26, 2. [Google Scholar]
- Turgeon, M.L. Clinical Hematology: Theory and Procedures; Lippincott Williams & Wilkins: Baltimore, MD, USA, 2004. [Google Scholar]
- Robertson, A.M.; Sequeira, A.; Kameneva, M.V. Hemorheology; Chapter Hemodynamical Flows; Birkhäuser: Basel, Switzerland, 2008; pp. 63–120. [Google Scholar]
- Fukada, E.; Seaman, G.V.F.; Liepsch, D.; Lee, M.; Friis-Baastad, L. Blood modeling using polystyrene microspheres. Biorheology 1989, 26, 401–413. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, K.; Ono, K.; Suzuki, H.; Sawada, M.; Moriya, M.; Sakamoto, W.; Yogo, T. Electrosprayed Synthesis of Red-Blood-Cell-Like Particles with Dual Modality for Magnetic Resonance and Fluorescence Imaging. Small 2010, 6, 2384–2391. [Google Scholar] [CrossRef] [PubMed]
- Park, C.H.; Chung, N.; Lee, J. Monodisperse red blood cell-like particles via consolidation of charged droplets. J. Colloid Interface Sci. 2011, 361, 423–428. [Google Scholar] [CrossRef]
- Kozlovskaya, V.; Alexander, J.F.; Wang, Y.; Kuncewicz, T.; Liu, X.; Godin, B.; Kharlampieva, E. Internalization of Red Blood Cell-Mimicking Hydrogel Capsules with pH-Triggered Shape Responses. ACS Nano 2014, 8, 5725–5737. [Google Scholar] [CrossRef] [PubMed]
- Roh, K.H.; Martin, D.C.; Lahann, J. Biphasic Janus particles with nanoscale anisotropy. Nat. Mater. 2005, 4, 759–763. [Google Scholar] [CrossRef] [PubMed]
- Doshi, N.; Zahr, A.S.; Bhaskar, S.; Lahann, J.; Mitragotri, S. Red blood cell-mimicking synthetic biomaterial particles. Proc. Natl. Acad. Sci. USA 2009, 106, 21495–21499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haghgooie, R.; Toner, M.; Doyle, P.S. Squishy Non-Spherical Hydrogel Microparticlesa. Macromol. Rapid Commun. 2010, 31, 128–134. [Google Scholar]
- Dendukuri, D.; Gu, S.S.; Pregibon, D.C.; Hatton, T.A.; Doyle, P.S. Stop-flow lithography in a microfluidic device. Lab Chip 2007, 7, 818–828. [Google Scholar] [CrossRef]
- Merkel, T.J.; Jones, S.W.; Herlihy, K.P.; Kersey, F.R.; Shields, A.R.; Napier, M.; Luft, J.C.; Wu, H.; Zamboni, W.C.; Wang, A.Z.; et al. Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles. Proc. Natl. Acad. Sci. USA 2011, 108, 586–591. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Merkel, T.J.; Pandya, A.; Napier, M.E.; Luft, J.C.; Daniel, W.; Sheiko, S.; Desimone, J.M. Low modulus biomimetic microgel particles with high loading of hemoglobin. Biomacromolecules 2012, 13, 2748–2759. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Q.; Wang, X.; Liu, J.; Yang, J. The Preparation and Forming Mechanism of the Red Blood Cell-Shaped Microspheres via Electrospraying. J. Appl. Polym. Sci. 2011, 122, 2552–2556. [Google Scholar] [CrossRef]
- Donath, E. Novel Hollow Polymer Shells by Colloid-Tem- plated Assembly of Polyelectrolytes. Oxf. Econ. Pap. 1998, 50, 534–562. [Google Scholar]
- She, S.; Li, Q.; Shan, B.; Tong, W.; Gao, C. Fabrication of red-blood-cell-like polyelectrolyte microcapsules and their deformation and recovery behavior through a microcapillary. Adv. Mater. 2013, 25, 5814–5818. [Google Scholar] [CrossRef] [PubMed]
- Cui, J.; Björnmalm, M.; Liang, K.; Xu, C.; Best, J.P.; Zhang, X.; Caruso, F. Super-soft hydrogel particles with tunable elasticity in a microfluidic blood capillary model. Adv. Mater. 2014, 26, 7295–7299. [Google Scholar] [CrossRef]
- Sun, H.; Björnmalm, M.; Cui, J.; Wong, E.H.H.; Dai, Y.; Dai, Q.; Qiao, G.G.; Caruso, F. Structure governs the deformability of polymer particles in a microfluidic blood capillary model. ACS Macro Lett. 2015, 4, 1205–1209. [Google Scholar] [CrossRef]
- Muñoz-Sánchez, B.N.; Silva, S.F.; Pinho, D.; Vega, E.J.; Lima, R. Generation of micro-sized PDMS particles by a flow focusing technique for biomicrofluidics applications. Biomicrofluidics 2016, 10, 14122. [Google Scholar] [CrossRef] [Green Version]
- Anes, C.F.; Pinho, D.; Muñoz-Sánchez, B.N.; Vega, E.J.; Lima, R. Shrinkage and colour in the production of micro-sized PDMS particles for microfluidic applications. J. Micromech. Microeng. 2018, 28, 075002. [Google Scholar] [CrossRef] [Green Version]
- Pinho, D.; Muñoz-Sánchez, B.N.; Anes, C.F.; Vega, E.J.; Lima, R. Flexible PDMS microparticles to mimic RBCs in blood particulate analogue fluids. Mech. Res. Commun. 2019, 100, 103399. [Google Scholar] [CrossRef] [Green Version]
- Ju, X.; Wang, X.; Liu, Z.; Xie, R.; Wang, W.; Chu, L. Red-blood-cell-shaped chitosan microparticles prepared by electrospraying. Particuology 2017, 30, 151–157. [Google Scholar] [CrossRef]
- Lasic, D.D. Liposomes. Sci. Am. Sci. Med. 1996, 3, 34–43. [Google Scholar]
- Carvalho, D.A.M.; Rodrigues, A.R.O.; Faustino, V.; Pinho, D.; Castanheira, E.M.S.; Lima, R. Microfluidic deformability study of an innovative blood analogue fluid based on giant unilamellar vesicles. J. Funct. Biomater. 2018, 9, 70. [Google Scholar] [CrossRef] [Green Version]
- López, M.; Rubio, M.; Sadek, S.H.; Vega, E.J. A simple emulsification technique for the production of micro-sized flexible powder of polydimethylsiloxane (PDMS). Powder Technol. 2020, 366, 610–616. [Google Scholar] [CrossRef]
- Kim, C.M.; Choi, H.J.; Kim, G.M. 512-Channel Geometric Droplet-Splitting Microfluidic Device by Injection of Premixed Emulsion for Microsphere Production. Polymers 2020, 12, 776. [Google Scholar] [CrossRef] [Green Version]
- Carneiro, J.; Lima, R.; Campos, J.B.L.M.; Miranda, J.M. Microparticle blood analogue suspension matching blood rheology. Soft Matter 2021, 17, 3963–3974. [Google Scholar] [CrossRef]
- Tong, W.; Gao, C.; Möhwald, H. Single Polyelectrolyte Microcapsules Fabricated By Glutaraldehyde-Mediated Covalent Layer-By-Layer Assembly. Macromol. Rapid Commun. 2006, 27, 2078–2083. [Google Scholar] [CrossRef]
- Calejo, J.; Pinho, D.; Galindo-Rosales, F.J.; Lima, R.; Campo-Deaño, L. Particulate Blood Analogues Reproducing the Erythrocytes Cell Free Layer in a Microfluidic Device Containing a Hyperbolic Contraction. Micromachines 2016, 7, 4. [Google Scholar] [CrossRef]
- Pinho, D.; Campo-Deaño, L.; Lima, R.; Pinho, F.T. In vitro particulate analogue fluids for experimental studies of rheological and hemorheological behavior of glucose-rich RBC suspensions. Biomicrofluidics 2017, 11, 054105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gañán-Calvo, A.M.; Montanero, J.M.; Martín-Banderas, L.; Flores-Mosquera, M. Building functional materials for health care and pharmacy from microfluidic principles and Flow Focusing. Adv. Drug Deliv. Rev. 2013, 65, 1447–1469. [Google Scholar] [CrossRef] [PubMed]
- Montanero, J.M.; Gañán-Calvo, A.M. Dripping, jetting and tip streaming. Rep. Prog. Phys. 2020, 83, 097001. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.X.; Ju, X.J.; Sun, S.X.; Xie, R.; Wang, W.; Liua, Z.; Chu, L.Y. Monodis-perse erythrocyte-sized and acid-soluble chitosan microspheres prepared viaelectrospraying. RSC Adv. 2015, 5, 34243–34250. [Google Scholar] [CrossRef]
- Lima, R.; Vega, E.J.; Moita, A.S.; Miranda, J.M.; Pinho, D.; Moreira, A.L.N. Fast, flexible and low cost multiphase blood analogue for biomedical and energy applications. Exp. Fluids 2020, 61, 231. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, K.; Park, Y. Measurement Techniques for Red Blood Cell Deformability: Recent Advances. In Blood Cell; Moschandreou, T.E., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 10. [Google Scholar] [CrossRef] [Green Version]
- Ciasca, G.; Papi, M.; Claudio, S.D.; Chiarpotto, M.; Palmieri, V.; Maulucci, G.; Nocca, G.; Rossi, C.; Spirito, M.D. Mapping viscoelastic properties of healthy and pathological red blood cells at the nanoscale level. Nanoscale 2015, 7, 17030–17037. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, Y.; Wan, J.; Chen, H. Enhanced separation of aged RBCs by designing channel cross section. Biomicrofluidics 2018, 12, 024106. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Han, Y.; Hua, W.; Wang, Y.; You, G.; Li, P.; Liao, F.; Zhao, L.; Ding, Y. Improved flowing behaviour and gas exchange of stored red blood cells by a compound porous structure. Artif. Cell. Nanomed. B. 2019, 47, 1888–1897. [Google Scholar] [CrossRef] [Green Version]
- Barns, S.; Balanant, M.A.; Sauret, E.; Flower, R.; Saha, S.; Gu, Y. Investigation of red blood cell mechanical properties using AFM indentation and coarse-grained particle method. BioMed. Eng. Online 2017, 16, 140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lamzin, I.M.; Khayrullin, R. The Quality Assessment of Stored Red Blood Cells Probed Using Atomic-Force Microscopy. Anat. Res. Int. 2014, 2014, 869683. [Google Scholar] [CrossRef]
- Maciaszek, J.L.; Lykotrafitis, G. Sickle cell trait human erythrocytes are significantly stiffer than normal. J. Biomech. 2011, 44, 657–661. [Google Scholar] [CrossRef]
- Bremmell, K.E.; Evans, A.; Prestidge, C.A. Deformation and nano-rheology of red blood cells: An AFM investigation. Colloid Surf. B Biointerfaces 2006, 50, 43–48. [Google Scholar] [CrossRef]
- Dulińska, I.; Targosz, M.; Strojny, W.; Lekka, M.; Czuba, P.; Balwierz, W.; Szymoński, M. Stiffness of normal and pathological erythrocytes studied by means of atomic force microscopy. J. Biochem. Biophys. Methods 2006, 66, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Rubio, A.; Faustino, V.; Cabezas, M.G.; Lima, R.; Vega, E.J. Fire-shaped cylindrical glass micronozzles to measure cell deformability. J. Micromech. Microeng. 2019, 29, 105001. [Google Scholar] [CrossRef]
- Ochsner, M.; Dusseiller, M.R.; Grandin, H.M.; Luna-Morris, S.; Textor, M.; Vogel, V.; Smith, M.L. Micro-well arrays for 3D shape control and high resolution analysis of single cells. Lab Chip 2007, 7, 1074–1077. [Google Scholar] [CrossRef]
- Akbari, S.; Pirbodaghi, T.; Kamm, R.D.; Hammond, P.T. A versatile microfluidic device for high throughput production of microparticles and cell microencapsulation. Lab Chip 2017, 17, 2067–2075. [Google Scholar] [CrossRef]
- Jiang, K.; Thomas, P.C.; Forry, S.P.; DeVoe, D.L.; Raghavan, S.R. Microfluidic synthesis of monodisperse PDMS microbeads as discrete oxygen sensors. Soft Matter 2012, 8, 923–926. [Google Scholar] [CrossRef]
- Choi, Y.H.; Chung, K.H.; Hong, H.B.; Lee, W. Production of PDMS microparticles by emulsification of two phases and their potential biological application. Int. J. Polym. Mater. Polym. 2018, 67, 686–692. [Google Scholar] [CrossRef]
- Kim, H.W.; Greenburg, A.G. Artificial oxygen carriers as red blood cell substitutes: A selected review and current status. Artif. Organs 2004, 28, 813–828. [Google Scholar] [CrossRef]
- Henkel-Hanke, T.; Oleck, M. Artificial oxygen carriers: A current review. AANA J. 2007, 75, 205–211. [Google Scholar]
- Tsuchida, E.; Sou, K.; Nakagawa, A.; Sakai, H.; Komatsu, T.; Kobayashi, K. Artificial oxygen carriers, hemoglobin vesicles and albumin-hemes, based on bioconjugate chemistry. Bioconjug. Chem. 2009, 20, 1419–1440. [Google Scholar] [CrossRef] [PubMed]
- Simoni, J. New Approaches in Commercial Development of Artificial Oxygen Carriers. Artif. Organs 2014, 38, 8. [Google Scholar] [CrossRef] [PubMed]
- Keyhanian, S.; Ebrahimifard, M.; Zandi, M. Investigation on artificial blood or substitute blood replace the natural blood. IPHOS 2014, 14, 2. [Google Scholar]
- Varchanis, S.; Dimakopoulos, Y.; Wagner, C.; Tsamopoulos, J. How viscoelastic is human blood plasma? Soft Matter 2018, 14, 4238–4251. [Google Scholar] [CrossRef] [PubMed]
- Sousa, P.C.; Carneiro, J.; Vaz, R.; Cerejo, A.; Pinho, F.T.; Alves, M.A.; Oliveira, M.S.N. Shear viscosity and nonlinear behavior of whole blood under large amplitude oscillatory shear. Biorheology 2013, 50, 269–282. [Google Scholar] [CrossRef] [Green Version]
- Sousa, P.C.; Vaz, R.; Cerejo, A.; Oliveira, M.S.N.; Alves, M.A.; Pinho, F.T. Rheological behavior of human blood in uniaxial extensional flow. J. Rheol. 2018, 62, 447–456. [Google Scholar] [CrossRef] [Green Version]
- Campo-Deaño, L.; Clasen, C. The slow retraction method (SRM) for the determination of ultra-short relaxation times in capillary breakup extensional rheometry experiments. J. Non-Newton. Fluid Mech. 2010, 165, 1688–1699. [Google Scholar] [CrossRef] [Green Version]
- Sousa, P.C.; Vega, E.J.; Sousa, R.G.; Montanero, J.M.; Alves, M.A. Measurement of relaxation times in extensional flow of weakly viscoelastic polymer solutions. Rheol. Acta 2017, 56, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Catarino, S.O.; Rodrigues, R.O.; Pinho, D.; Miranda, J.M.; Minas, G.; Lima, R. Blood Cells Separation and Sorting Techniques of Passive Microfluidic Devices: From Fabrication to Applications. Micromachines 2019, 10, 593. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, R.O.; Lopes, R.; Pinho, D.; Pereira, A.I.; Garcia, V.; Gassmann, S.; Sousa, P.C.; Lima, R. In vitro blood flow and cell-free layer in hyperbolic microchannels: Visualizations and measurements. Biochip J. 2016, 10, 9–15. [Google Scholar] [CrossRef]
- Bento, D.; Fernandes, C.S.; Miranda, J.M.; Lima, R. In vitro blood flow visualizations and cell-free layer (CFL) measurements in a microchannel network. Exp. Therm. Fluid Sci. 2019, 109, 109847. [Google Scholar] [CrossRef]
- Leble, V.; Lima, R.; Dias, R.; Fernandes, C.; Ishikawa, T.; Imai, Y.; Yamaguchi, T. Asymmetry of red blood cell motions in a microchannel with diverging and converging bifurcation. Biomicrofluidics 2011, 5, 044120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishikawa, T.; Fujiwara, H.; Matsuki, N.; Yoshimoto, T.; Imai, Y.; Ueno, H.; Yamaguchi, T. Asymmetry of blood flow and cancer cell adhesion in a microchannel with symmetric bifurcation and confluence. Biomed. Microdevices 2011, 13, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Bento, D.; Sousa, L.; Yaginuma, T.; Garcia, V.; Lima, R.; Miranda, J.M. Microbubble moving in blood flow in microchannels: Effect on the cell-free layer and cell local concentration. Biomed. Microdevices 2017, 19, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bento, D.; Rodrigues, R.O.; Faustino, V.; Pinho, D.; Fernandes, C.S.; Pereira, A.I.; Garcia, V.; Miranda, J.M.; Lima, R. Deformation of Red Blood Cells, Air Bubbles, and Droplets in Microfluidic Devices: Flow Visualizations and Measurements. Micromachines 2018, 9, 151. [Google Scholar] [CrossRef] [Green Version]
- Lima, R. Integrated Nano-Biomechanics; Chapter Microfluidic Devices Based on Biomechanics; Elsevier: Boston, MA, USA, 2018; pp. 217–263. [Google Scholar]
- Zografos, K.; Pimenta, F.; Alves, M.A.; Oliveira, M.S.N. Microfluidic converging/diverging channels optimised for homogeneous extensional deformation. Biomicrofluidics 2016, 10, 043508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.S.; Yim, Y.; Ahn, K.H.; Lee, S.J. Extensional flow-based assessment of red blood cell deformability using hyperbolic converging microchannel. Biomed. Microdevices 2009, 11, 1021. [Google Scholar] [CrossRef]
- Yaginuma, T.; Oliveira, M.; Lima, R.; Ishikawa, T.; Yamaguchi, T. Human red blood cell behaviour under homogeneous extensional flow in a hyperbolic-shaped microchannel. Biomicrofluidics 2013, 7, 054110. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, R.O.; Bañobre-López, M.; Gallo, J.; Tavares, P.B.; Silva, A.M.T.; Lima, R.; Gomes, H.T. Haemocompatibility of iron oxide nanoparticles synthesized for theranostic applications: A high-sensitivity microfluidic tool. J. Nanopart. Res. 2016, 18, 194. [Google Scholar] [CrossRef] [Green Version]
- Faustino, V.; Pinho, D.; Yaginuma, T.; Calhelha, R.; Ferreira, I.; Lima, R. Extensional flow-based microfluidic device: Deformability assessment of red blood cells in contact with tumor cells. BioChip J. 2014, 8, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Faustino, V.; Rodrigues, R.O.; Pinho, D.; Costa, E.; Santos-Silva, A.; Miranda, V.; Amaral, J.S.; Lima, R. A Microfluidic Deformability Assessment of Pathological Red Blood Cells Flowing in a Hyperbolic Converging Microchannel. Micromachines 2019, 10, 645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D, R.G.; Tse, H.T.K.; Lee, S.A.; Ying, Y.; Lindgren, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Carlo, D.D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar]
- Henon, Y.; Sheard, G.J.; Fouras, A. Erythrocyte deformation in a microfluidic cross-slot channel. RSC Adv. 2014, 4, 36079–36088. [Google Scholar] [CrossRef]
- Guillou, L.; Dahl, J.B.; Lin, J.M.G.; Barakat, A.I.; Husson, J.; Muller, S.J.; Kumar, S. Measuring Cell Viscoelastic Properties Using a Microfluidic Extensional Flow Device. Biophys. J. 2016, 111, 2039–2050. [Google Scholar] [CrossRef] [Green Version]
- Abràmoff, M.D.; Magalhães, P.J.; Ram, S.J. Image processing with ImageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Meijering, E.; Smal, I.; Danuser, G. Tracking in molecular bioimaging. IEEE Signal Process. Mag. 2006, 23, 46–53. [Google Scholar] [CrossRef] [Green Version]
- Pinho, D.; Lima, R.; Pereira, A.I.; Gayubo, F. Automatic tracking of labeled red blood cells in microchannels. Int. J. Numer. Method. Biomed. Eng. 2013, 29, 977–987. [Google Scholar] [CrossRef] [Green Version]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, A.; Bahrami, M. A novel swimming microrobot based on artificial cilia for biomedical applications. J. Intell. Robot. Syst. 2011, 63, 399–416. [Google Scholar] [CrossRef]
- Rodrigues, R.O.; Sousa, P.C.; Gaspar, J.; Bañobre-Lòpez, M.; Lima, R.; Minas, G. Organ-on-a-chip: A Preclinical Microfluidic Platform for the Progress of Nanomedicine. Small 2020, 16, 2003517. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, V.; Maia, I.; Souza, A.; Ribeiro, J.; Costa, P.; Puga, H.; Teixeira, S.; Lima, R.A. In vitro Biomodels in Stenotic Arteries to Perform Blood Analogues Flow Visualizations and Measurements: A Review. Open Biomed. Eng. J. 2020, 14, 87–102. [Google Scholar] [CrossRef]













| Material | Shape | Size | E (Deformability) | Biological Functionality | Production Method | Production Rate | References |
|---|---|---|---|---|---|---|---|
| PLGA | Biconcave discoidal | 7 ± 2 μm (diameter), around 2 μm (thickness) | E = 92.8 ± 42 kPa (high) | Yes | Electrohydrodynamic jetting | 1 g/h | [34] |
| PEG (hydrogel) | Discoidal | 8 ± 0.2 μm (diameter), 2 ± 0.1 μm (thickness) | (High) | No, but possible | Stop flow lithography | 0.01 g/h | [35] |
| HEA (hydrogel) | Discoidal | 5.2–5.9 μm (diameter), 1.22–1.54 μm (thickness) | E≥ 7.8 kPa (high) | No, but possible | PRINT® | - | [37] |
| PES | Spherical, slightly RBC-shaped | 10 μm | E ≈ 2.6 GPa (low) | No | Electrospraying (electrohydrodynamic) | - | [39] |
| TEGA (hydrogel) | Discoidal | 6.3 μm (diameter) × 1.8 μm (thickness) | E≥ 6.5 kPa (high) | Yes | PRINT® | - | [38] |
| PAH+GA | Biconcave discoidal (hollow) | 6.7 μm (diameter) × 2.8 μm (thickness) | E(capsule wall) ≥ 100 MPa (high) | Yes | Layer-by-Layer from solid template | - | [41] |
| PEG (hydrogel) | Spherical | 7–9 μm | 0.2 ≤E≤ 3.3 kPa (high) | No, but possible | Layer-by-Layer from porous template (also called mesoporous silica templating method) | - | [42] |
| HA | Spherical (hollow) | 7 μm | 8.3 ≤E≤ 24.5 kPa (high) | No, but possible | from solid template | - | [43] |
| HA | Spherical | 6–8 μm | 4.3 ≤E≤ 38.3 kPa (high) | No, but possible | from porous template | - | [43] |
| PMMA | Spherical | 6.32 ± 0.118 μm | 3 ≤E≤ 3.3 GPa (low) | No | Unknown (Spheromers® CA 6, Microbeads AS) | - | [50,54] |
| PMMA | Spherical | 10 μm | 3 ≤E≤ 3.3 GPa (low) | No | Unknown (Spheromers® CA 10, Microbeads AS) | - | [55] |
| PDMS (6:4) | Spherical | 7.13 ± 1.34 μm | E ≈ 1300 kPa (high) | No, but possible | Liquid-liquid flow-focusing with a hypodermic needle | 0.01 g/h | [44,45,46] |
| Chitosan | Concave | 7.4 ± 0.74 μm | E ≈ 9 MPa (low) | No, but possible | Electrospray with solvent diffusion | 0.01 g/h | [47] |
| GUV (lipid) | Spherical | 6.15 ± 1.24 μm | (High) | No | Lipid film hydration | 0.01 g/h | [49] |
| PDMS (30:1) | Spherical | 9.05 ± 2.5 μm | E ≈ 90 kPa (high) | No, but possible | Two syringe membrane emulsification | 1 g/h | [50] |
| PS | Spherical | 11.1 ± 0.208 μm | 3 ≤E≤ 3.3 GPa (low) | No | Unknown (Dynoseeds TS10 Microbeads® AS) | - | [50] |
| PLGA | Spherical | 9.23 ± 0.35 μm | E ≈ 4300 MPa (low) | No, but possible | 512-channel geometric droplet-splitting microfluidic device combined with a post array part | 1 g/h | [51] |
| Brij L4 surfactant (micelles) | Spherical | 7.72 ± 3.72 μm | (High) | No | Premix membrane emulsification | 1 g/h | [59] |
| PDMS (6:4) | Spherical | 7.1 ± 1.6 μm | E ≈ 1300 kPa (high) | No, but possible | Premix membrane emulsification | 1 g/h | [52] |
| References | RBC Template Used | Liquid as Plasma | Particle Concentration | Shear Rheology (at Around 22 C) | Extensional Rheology | Other Measurements |
|---|---|---|---|---|---|---|
| [29] | Quasi-rigid PS (around 1 μm) | Distilled water; distilled water + at 0, 10, 20, and 30 mM; Dx70 + at 10 mM | 12, 24, and 32 wt% | Steady shear flow 0 ≤ (s) ≤ 120; Oscillatory shear flow 0.02 ≤ (rad/s) ≤ 0.8 | No | Rouleaux (aggregation) |
| [38] | TEGA (hydrogel) with Hb (around 6 μm) | PBS | 40 vol% | Steady shear flow 0.1 ≤ (s) ≤ 10 | No | No |
| [54] | Quasi-rigid PMMA (around 6 μm) | Dx40 + SDS; Dx40 + XG (115 ppm) + SDS | 5 wt% | Steady shear flow 1 ≤ (s) ≤ 10 | No | CFL, deformability, and Rouleaux (aggregation) |
| [44] | Flexible PDMS 6:4 (around 6 μm) | Dx40 | 1 vol% | Steady shear flow 1 ≤ (s) ≤ 10 | No | No |
| [55] | Quasi-rigid PMMA (around 10 μm) | Dx40; Dx40 + XG (115 ppm) | 5 and 20 wt% | Steady shear flow 1 ≤ (s) ≤ 10; SAOS 0.01 ≤ (rad/s) ≤ 100; LAOS at = 0.1 and 1 (rad/s) | No | CFL, deformability, and Rouleaux (aggregation) |
| [49] | Flexible GUV (around 6 μm) | Tris-HCl buffer solution | 1.6, 2.1 and 2.5 vol% | Steady shear flow 10 ≤ (s) ≤ 10 | No | Deformability |
| [46] | Flexible PDMS 10:1, 8:2, 6:4, black 1:1, and red-dyed 10:1 (around 8 μm) | Dx40 | 8 vol% | Steady shear flow 1 ≤ (s) ≤ 10 | No | CFL and deformability |
| [59] | Flexible micelles of Brij L4 surfactant (around 8 μm) | Pure water | 1, 5, 10, and 20 wt% | Steady shear flow 1 ≤ (s) ≤ 10 | No | CFL and deformability |
| [52] | Flexible PDMS 6:4 (around 7 μm) | Aqueous solution of 4 wt% SDS | 8, 17, 21, 24, and 32 wt% | Steady shear flow 1 ≤ (s) ≤ 3 × 10; LAOS at = 0.158 and 1 (rad/s) | Yes | CFL and deformability |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadek, S.H.; Rubio, M.; Lima, R.; Vega, E.J. Blood Particulate Analogue Fluids: A Review. Materials 2021, 14, 2451. https://doi.org/10.3390/ma14092451
Sadek SH, Rubio M, Lima R, Vega EJ. Blood Particulate Analogue Fluids: A Review. Materials. 2021; 14(9):2451. https://doi.org/10.3390/ma14092451
Chicago/Turabian StyleSadek, Samir Hassan, Manuel Rubio, Rui Lima, and Emilio José Vega. 2021. "Blood Particulate Analogue Fluids: A Review" Materials 14, no. 9: 2451. https://doi.org/10.3390/ma14092451
APA StyleSadek, S. H., Rubio, M., Lima, R., & Vega, E. J. (2021). Blood Particulate Analogue Fluids: A Review. Materials, 14(9), 2451. https://doi.org/10.3390/ma14092451








