Evolution of Hydraulic Conductivity of Unsaturated Compacted Na-Bentonite under Confined Condition—Including the Microstructure Effects
Abstract
:1. Introduction
2. Theory and Methodology
2.1. Pore Evolution of Compacted Bentonite
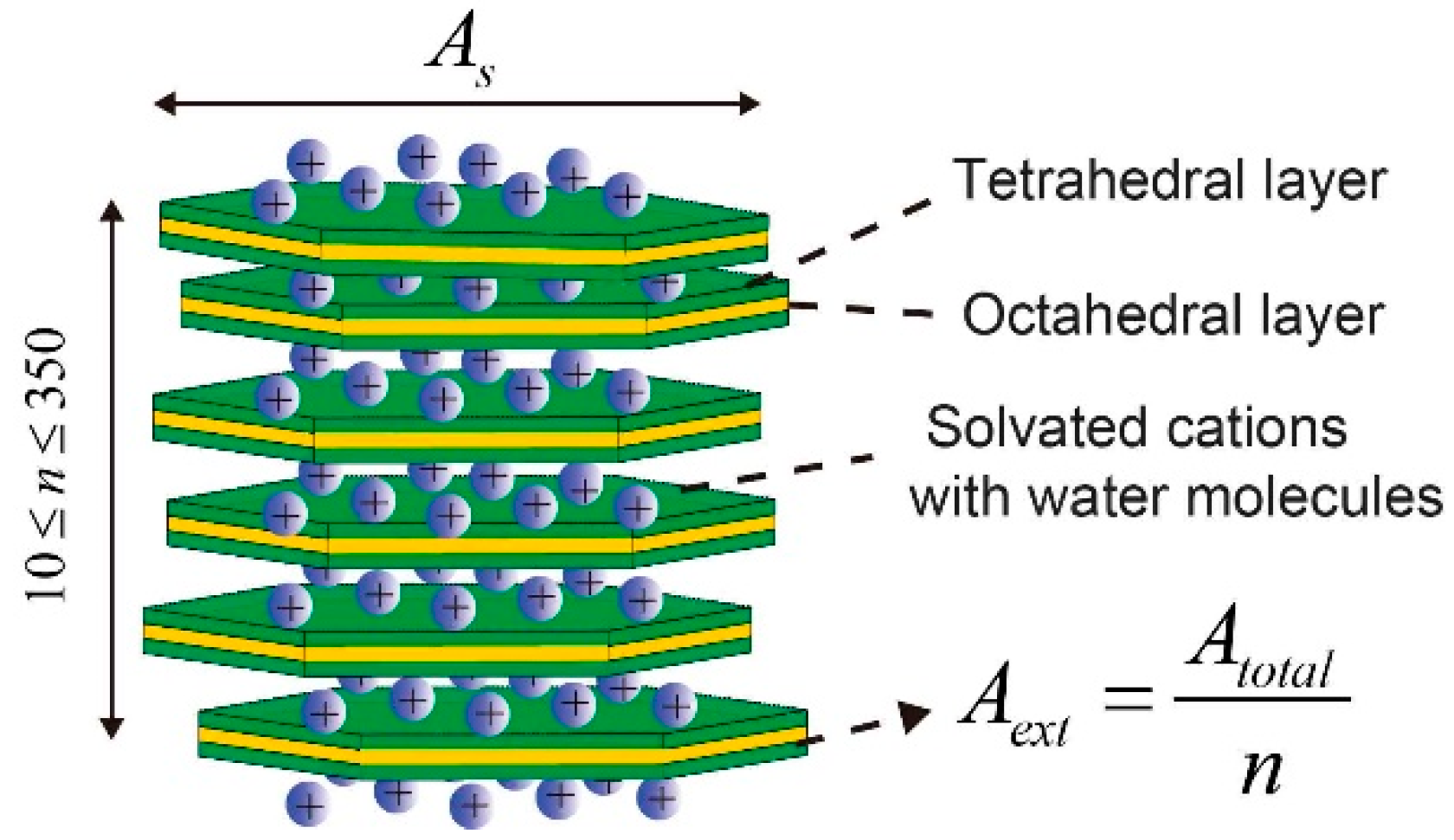
2.1.1. Specific Surface Area
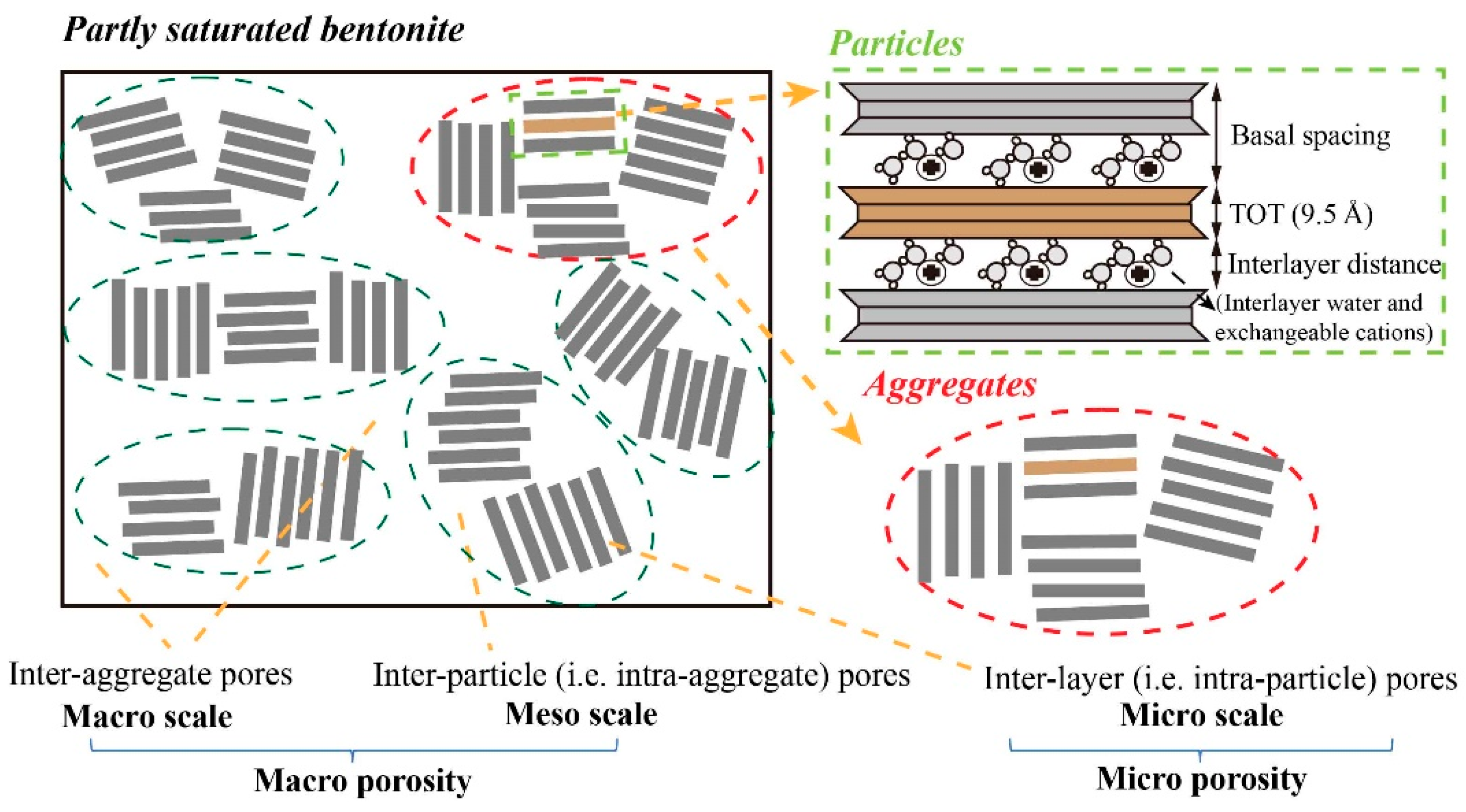
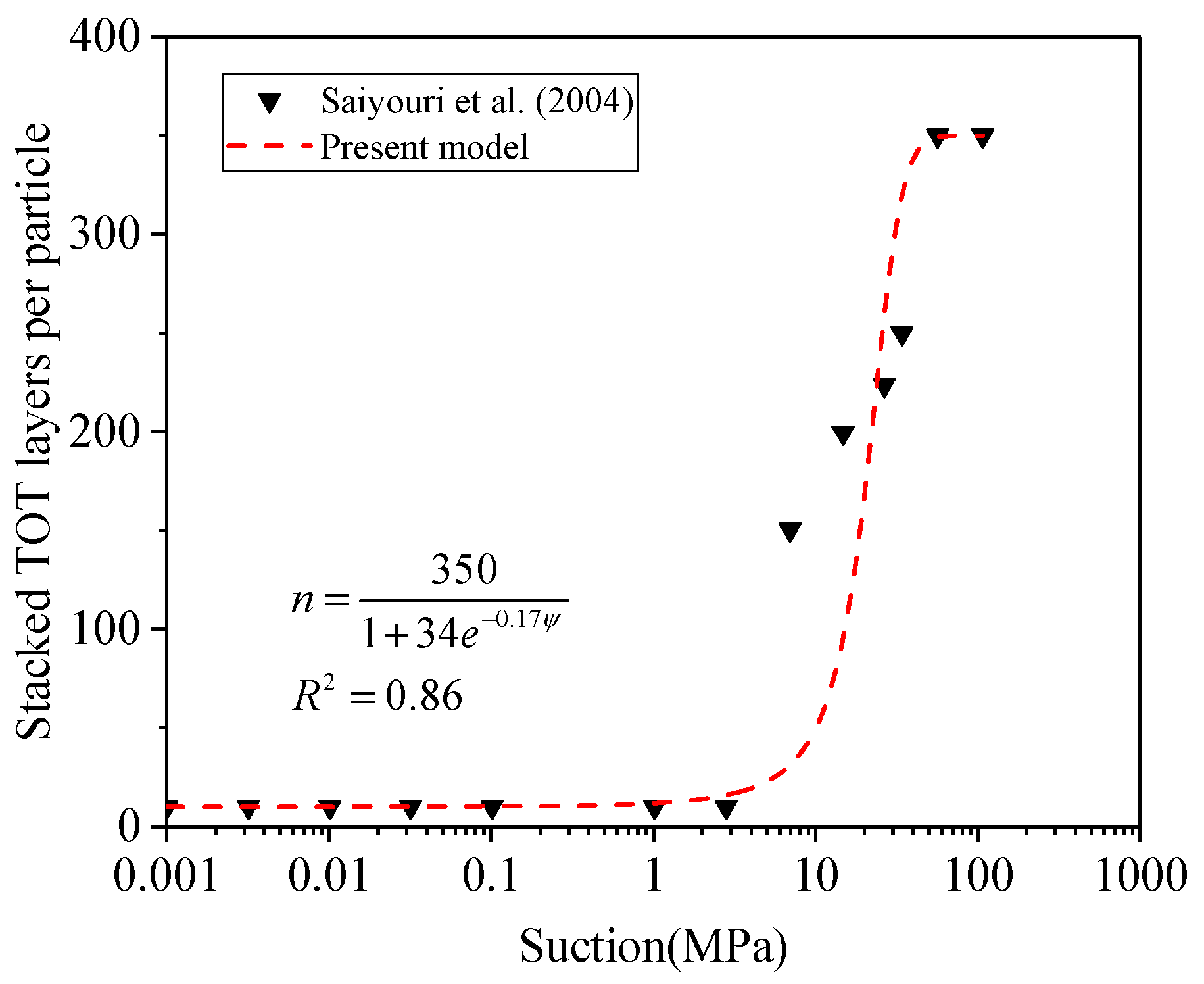
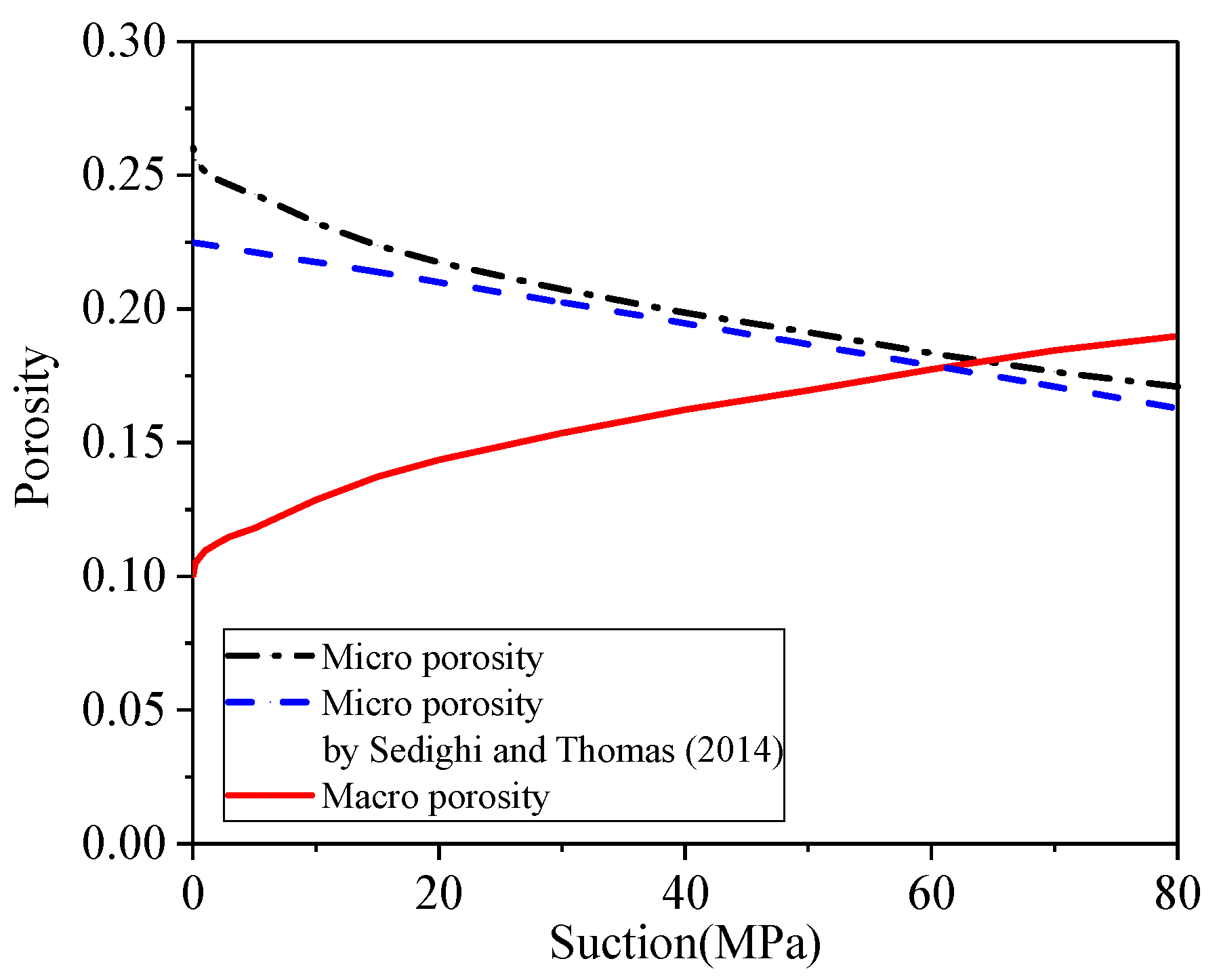
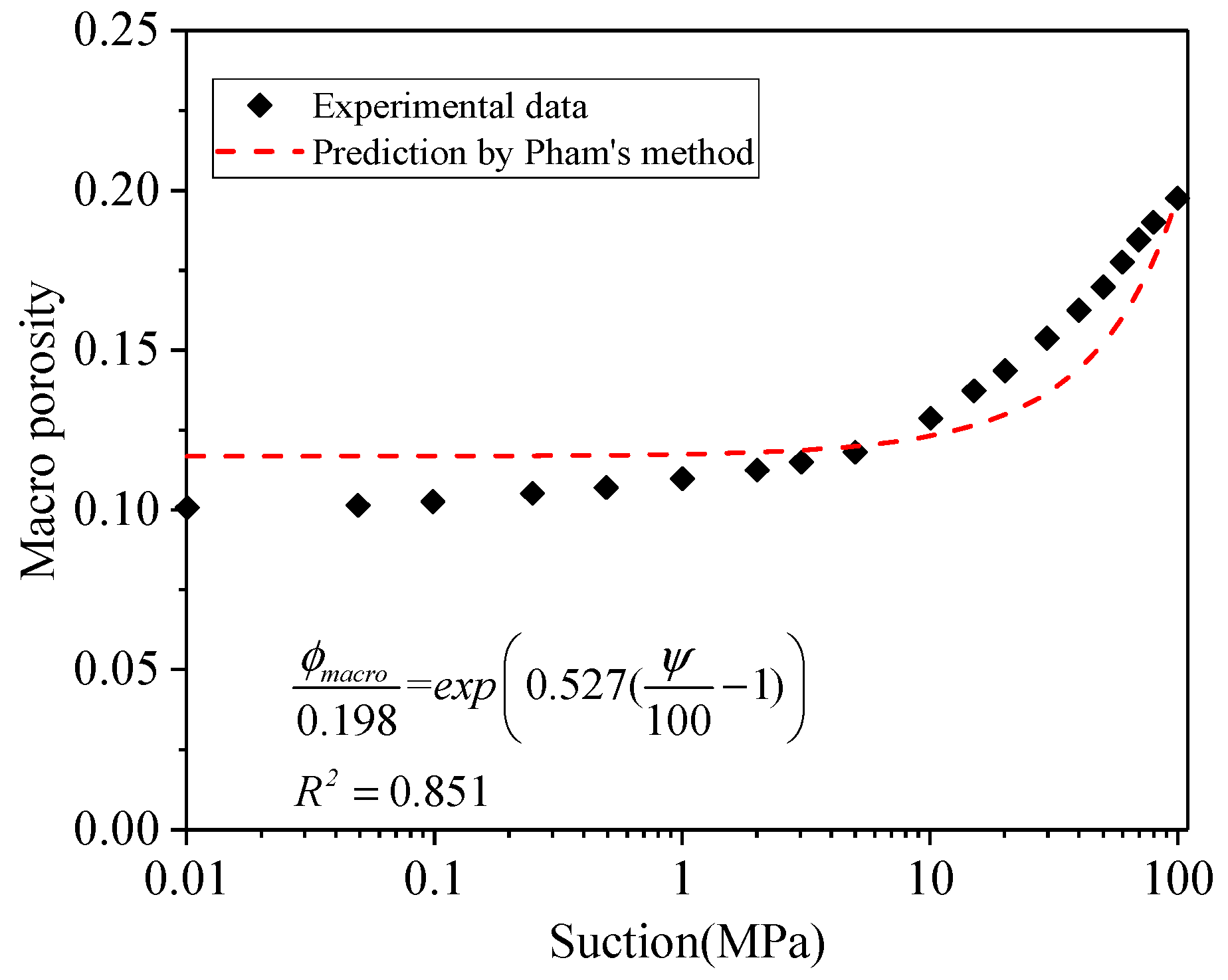
2.1.2. Evolution of Pore System
2.1.3. Tortuosity
2.2. Model for Unsaturated Hydraulic Conductivity
3. Results and Discussion
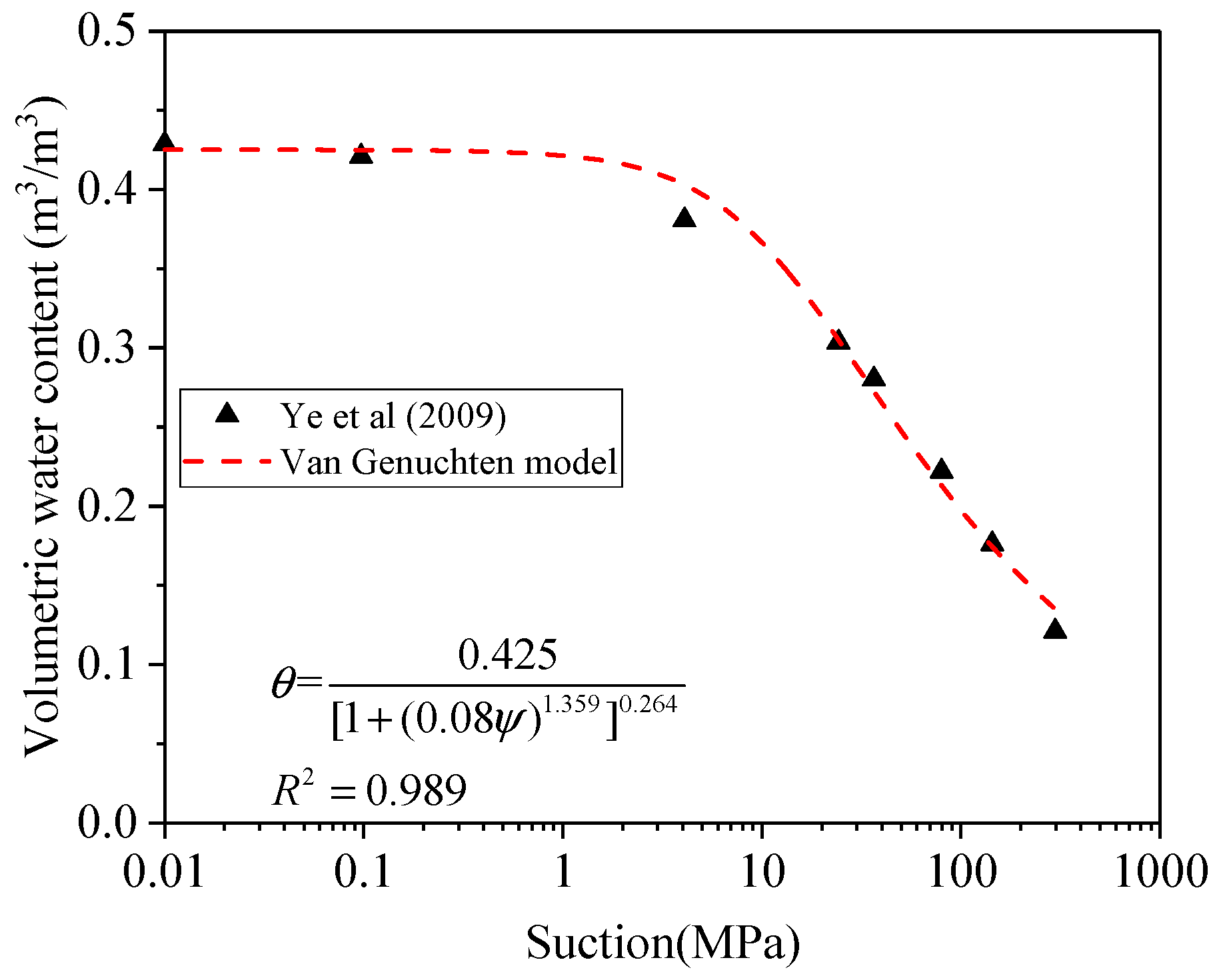
3.1. Experimental Data and Parameters of Model
3.2. Saturated Hydraulic Conductivity
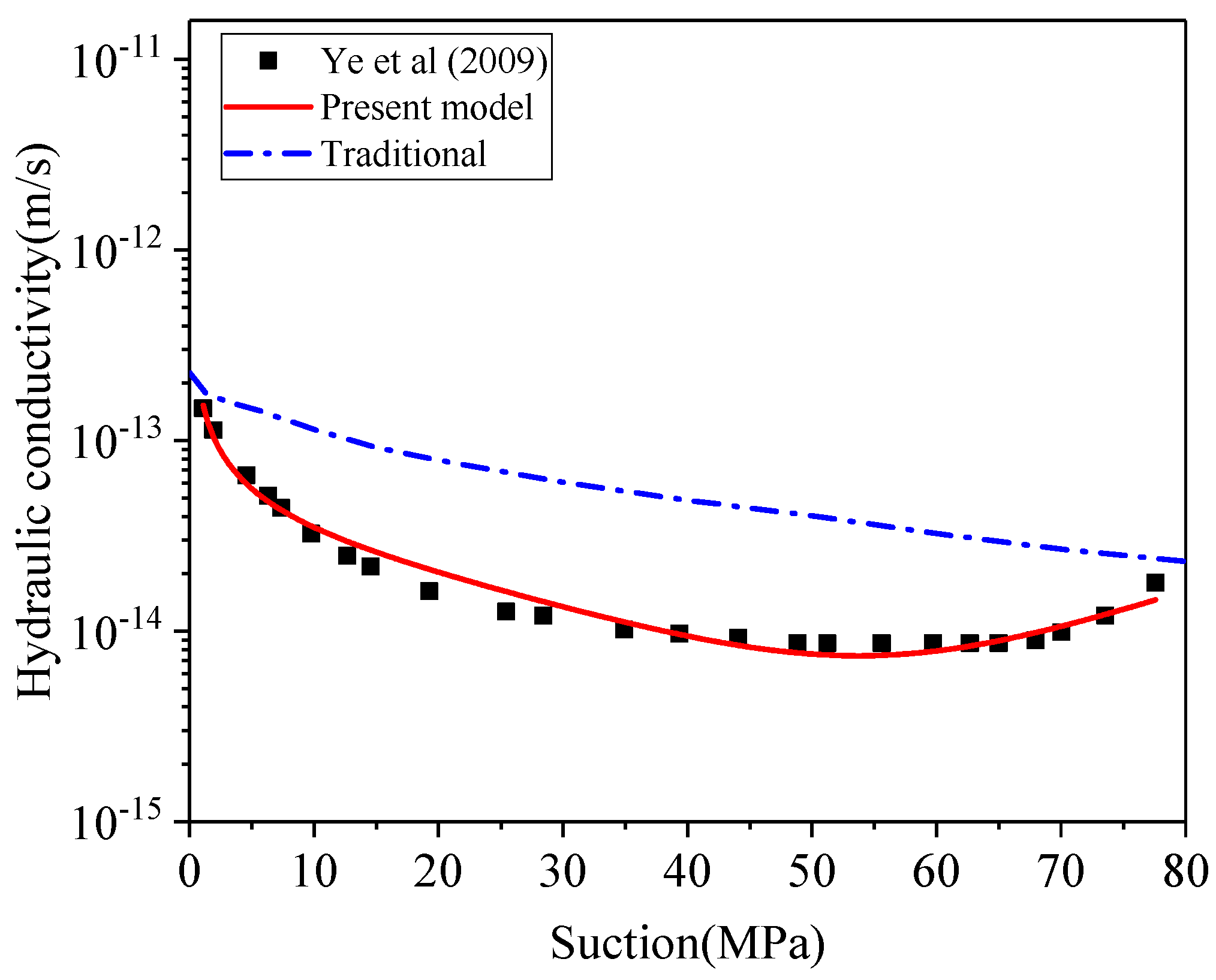
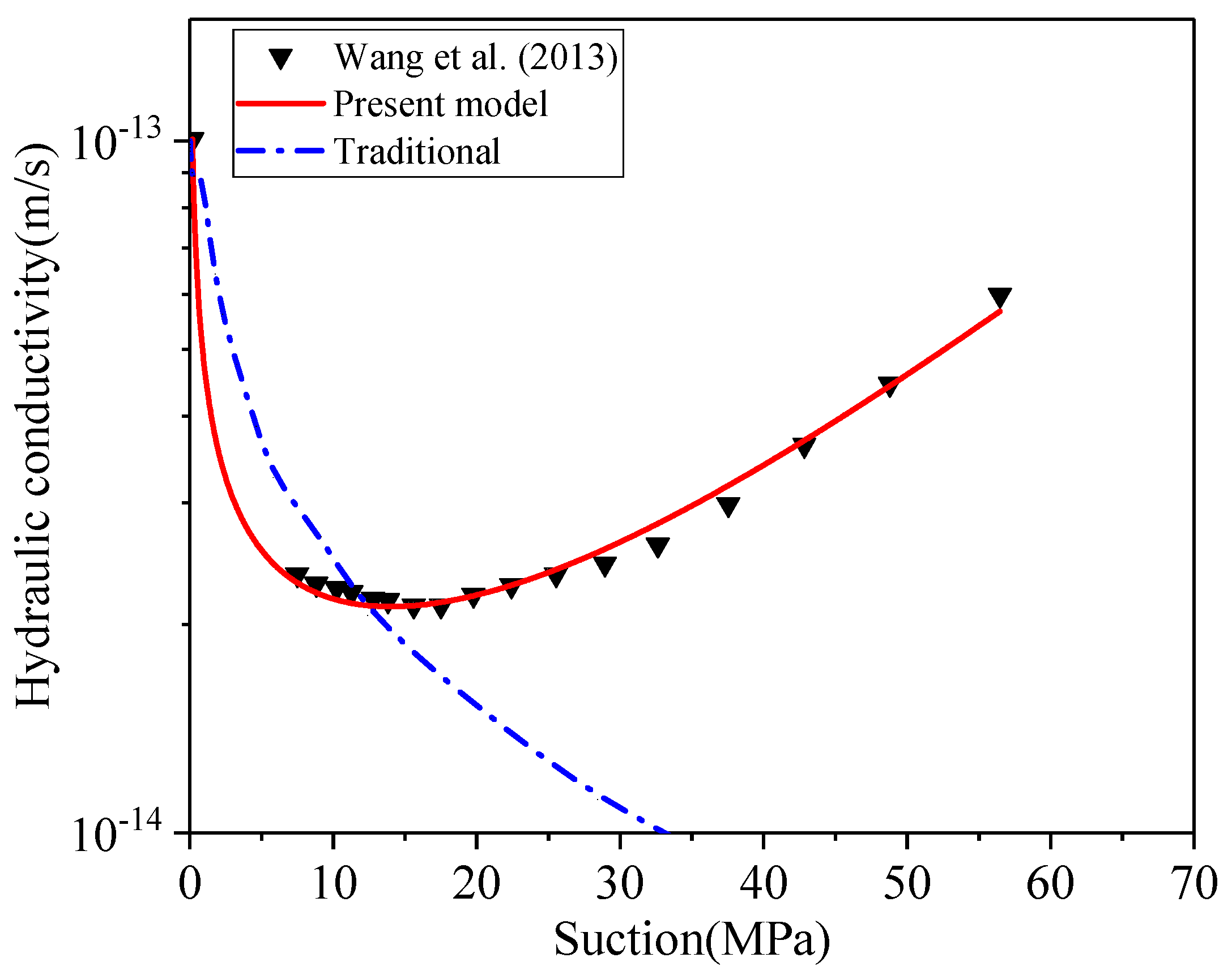
3.3. Unsaturated Hydraulic Conductivity
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| k | Hydraulic permeability (m/s) |
| kr | Relative hydraulic conductivity |
| Proposed relative hydraulic conductivity of compacted bentonite | |
| ksat | The saturated hydraulic conductivity (m/s) |
| kunsat | The unsaturated hydraulic conductivity (m/s) |
| Se | The effective saturation |
| θ | The actual volumetric water content |
| θr | The residual volumetric water content |
| θs | The saturated volumetric water content |
| α | The constant parameter in Mualem [54] |
| μ | A dimensionless number in Burdine [31] |
| Ψ | Suction of soil/bentonite(MPa) |
| Ψd | The air entry value (MPa) |
| λ | A fitting factor related to pore-size distribution |
| Cs | Shape factor |
| τ | Tortuosity |
| γw | Unit weight of water (N/m3) |
| η | Viscosity of water (Pa∙s) |
| SA | Specific surface area (m2/kg) |
| Φ | Porosity |
| ρd | Dry density of soil (kg/m3) |
| Atot | Total specific surface area (m2/kg) |
| n | The number of TOT layers of per particle |
| N | Total number of TOT layers of bentonite sample |
| Aext | External specific surface area of bentonite (m2/g) |
| As | The surface area of a single TOT layer |
| msi | Mass of one particle (kg) |
| msmectite | Mass of smectite (kg) |
| ms | Mass of solid (kg) |
| b C | A constant related to water adsorption rate A correction term |
| ω | Water content (kg/kg) |
| ρw | Density of water (kg/m3) |
| mw | The mass of water (kg) |
| Vt | Total volume of soil sample (m3) |
| Vw | Volume of total water in soil (m3) |
| Dry density of smectite (kg/m3) | |
| dTOT | Thickness of TOT layer (9.5 Å) |
| dt | Basal spacing (Å) |
| hw | Total interlayer water thickness of soil |
| Vimw | Micro pore volume/volume of interlayer water |
| Ve | Macro pore volume/effect pore volume |
| Vs | Volume of solid (m3) |
| diw | Interlayer water thickness between two TOT layers |
| Φmacro | Macro porosity (Effective porosity) |
| Φmicro | Micro porosity (Interlayer porosity) |
| ρs | Density of the solid (kg/m3) |
| ρi | Density of the non-smectite minerals or impurities (kg/m3) |
| Gs | Specific gravity of clay |
| Xsm | The mass fraction of smectite in the bentonite |
| Le | Effective path length of flow |
| L | Sample length |
| ref | The reference case in which measurements are available |
| β | A fitting factor between Φ and Ψ in Pham et al. [92] |
| σ | Coefficient related to porosity and size of pore |
| Xhs | Mole fraction of hydrated smectite |
| Msm | Molar mass of dry smectite (Kg/mol) |
| ζc | The number of moles of waters in the interlayer adsorption or desorption reaction |
| υil | The molar volume of the interlayer water (m3/mol) |
| a, m | Curve-fitting parameters by van Genuchten [24] |
| nmax, nmin | The maximum and minimum number of TOT layers of bentonite particle respectively |
References
- Pusch, R.; Yong, R.N. Microstructure of Smectite Clays and Engineering Performance; Taylor and Francis: New York, NY, USA, 2006. [Google Scholar]
- Kohler, M.; Curtis, G.P.; Kent, D.; Davis, J.A. Experimental Investigation and Modeling of Uranium (VI) Transport Under Variable Chemical Conditions. Water Resour. Res. 1996, 32, 3539–3551. [Google Scholar] [CrossRef]
- Xiong, Q.; Joseph, C.; Schmeide, K.; Jivkov, A.P. Measurement and modelling of reactive transport in geological barriers for nuclear waste containment. Phys. Chem. Chem. Phys. 2015, 17, 30577–30589. [Google Scholar] [CrossRef] [Green Version]
- Gleason, M.H.; Daniel, D.E.; Eykholt, G.R. Calcium and Sodium Bentonite for Hydraulic Containment Applications. J. Geotech. Geoenviron. Eng. 1997, 123, 438–445. [Google Scholar] [CrossRef]
- Yigzaw, Z.G.; Cuisinier, O.; Massat, L.; Masrouri, F. Role of different suction components on swelling behavior of compacted bentonites. Appl. Clay Sci. 2016, 120, 81–90. [Google Scholar] [CrossRef]
- Bouchelaghem, F.; Pusch, R. Fluid flow and effective conductivity calculations on numerical images of bentonite microstructure. Appl. Clay Sci. 2017, 144, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Busch, A.; Alles, S.; Gensterblum, Y.; Prinz, D.; Dewhurst, D.N.; Raven, M.D.; Stanjek, H.; Krooss, B. M Carbon dioxide storage potential of shales. Int. J. Greenh. Gas Control. 2008, 2, 297–308. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Ezeuko, C.; Sen, A.; Grigoryan, A.; Gates, I. Pore-network modeling of biofilm evolution in porous media. Biotechnol. Bioeng. 2011, 108, 2413–2423. [Google Scholar] [CrossRef]
- Chung, E.T.; Efendiev, Y.; Leung, T.; Vasilyeva, M. Coupling of multiscale and multi-continuum approaches. GEM Int. J. Geomath. 2017, 8, 9–41. [Google Scholar] [CrossRef] [Green Version]
- Mather, J.; Chapman, N.; Black, J.; Lintern, B. The geological disposal of high-level radioactive waste-a review of the Institute of Geological Sciences’ research programme. Nucl. Energy 1982, 21, 167–173. [Google Scholar]
- Kutalek, R.; Wewalka, G.; Gundacker, C.; Auer, H.; Wilson, J.; Haluza, D.; Huhulescu, S.; Hillier, S.; Sager, M.; Prinz, A. Geophagy and potential health implications: Geohelminths, microbes and heavy metals. Trans. R. Soc. Trop. Med. Hyg. 2010, 104, 787–795. [Google Scholar] [CrossRef]
- Eisenhour, D.D.; Brown, R.K. Bentonite and its impact on modern life. Elements 2009, 5, 83–88. [Google Scholar] [CrossRef]
- Ye, W.; Cui, Y.; Qian, L.; Chen, B. An experimental study of the water transfer through confined compacted GMZ bentonite. Eng. Geol. 2009, 108, 169–176. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Tang, A.M.; Loiseau, C.; Delage, P. Determining the unsaturated hydraulic conductivity of a compacted sand–bentonite mixture under constant-volume and free-swell conditions. Phys. Chem. Earth Parts A/B/C 2008, 33, S462–S471. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.-J.; Tang, A.M.; Qian, L.-X.; Ye, W.-M.; Chen, B. Thermal-Mechanical Behavior of Compacted GMZ Bentonite. Soils Found. 2011, 51, 1065–1074. [Google Scholar] [CrossRef] [Green Version]
- Ye, W.; Borrell, N.; Zhu, J.; Chen, B.; Chen, Y. Advances on the investigation of the hydraulic behavior of compacted GMZ bentonite. Eng. Geol. 2013, 169, 41–49. [Google Scholar] [CrossRef]
- Ye, W.; Zheng, Z.; Chen, B.; Chen, Y.; Cui, Y.; Wang, J. Effects of pH and temperature on the swelling pressure and hydraulic conductivity of compacted GMZ01 bentonite. Appl. Clay Sci. 2014, 101, 192–198. [Google Scholar] [CrossRef]
- Xiong, Q.; Baychev, T.G.; Jivkov, A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 2016, 192, 101–117. [Google Scholar] [CrossRef]
- Delage, P. Micro-Macro Effects in Bentonite Engineered Barriers for Radioactive Waste Disposal. In Proceedings of the 8th International Congress on Environmental Geotechnics, Hangzhou, China, 28 October–1 November 2019; Springer: Singapore, 2019; Volume 1, pp. 61–80. [Google Scholar]
- Sedighi, M.; Thomas, H.R.; Vardon, P.J. Reactive Transport of Chemicals in Compacted Bentonite under Nonisothermal Water Infiltration. J. Geotech. Geoenviron. Eng. 2018, 144, 04018075. [Google Scholar] [CrossRef] [Green Version]
- Thomas, H.; Cleall, P.; Chandler, N.; Dixon, D.; Mitchell, H. Water infiltration into a large-scale in-situ experiment in an underground research laboratory. Géotechnique 2003, 53, 207–224. [Google Scholar] [CrossRef]
- Liu, H.-H.; Li, L.; Birkholzer, J. Unsaturated properties for non-Darcian water flow in clay. J. Hydrol. 2012, 430–431, 173–178. [Google Scholar] [CrossRef] [Green Version]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Agus, S.; Schanz, T. In Permeability of a heavily compacted bentonite-sand mixture as sealing and buffer element for nuclear waste repository, Unsaturated Soils. In Advances in Geo-Engineering, Proceedings of the 1st European Conference, Durham, UK, 2–4 July 2008; CRC Press: Durham, UK, 2008; pp. 305–311. [Google Scholar]
- Agus, S.; Leong, E.; Schanz, T. Assessment of statistical models for indirect determination of permeability functions from soil–water characteristic curves. Géotechnique 2003, 53, 279–282. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Nielsen, D.C. On describing and predicting the hydraulic properties. Annales Geophysicae 1985, 3, 615–628. [Google Scholar]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Guo, Y.; Pan, B.; Zhang, L.; Fang, C. A new model to predict the relative permeability of wetting phase for tight sandstones. Environ. Fluid Mech. 2017, 17, 1067–1079. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Suits, L.D.; Likos, W.J. Compacted Clay: Difficulties Obtaining Good Laboratory Permeability Tests. Geotech. Test. J. 2017, 40, 20150286. [Google Scholar] [CrossRef]
- Burdine, N. Relative Permeability Calculations from Pore Size Distribution Data. J. Pet. Technol. 1953, 5, 71–78. [Google Scholar] [CrossRef]
- Chen, T.; Sedighi, M.; Jivkov, A.; Seetharam, S. A model for hydraulic conductivity of compacted bentonite—Inclusion of microstructure effects under confined wetting. Géotechnique 2020, 71, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Zhao, Y.; Deng, Q.; Kang, J.; Li, D.; Wang, D. A relation of hydraulic conductivity—Void ratio for soils based on Kozeny-Carman equation. Eng. Geol. 2016, 213, 89–97. [Google Scholar] [CrossRef]
- Yustres, Á.; López-Vizcaíno, R.; Sáez, C.; Cañizares, P.; Rodrigo, M.A.; Navarro, V. Water transport in electrokinetic remediation of unsaturated kaolinite. Experimental and numerical study. Sep. Purif. Technol. 2018, 192, 196–204. [Google Scholar] [CrossRef]
- Srisutthiyakorn, N.; Mavko, G.M. What is the role of tortuosity in the Kozeny-Carman equation? Interpretation 2017, 5, SB57–SB67. [Google Scholar] [CrossRef]
- Katagiri, J.; Konno, Y.; Yoneda, J.; Temma, N. Pore-scale modeling of flow in particle packs containing grain-coating and pore-filling hydrates: Verification of a Kozeny–Carman-based permeability reduction model. J. Nat. Gas Sci. Eng. 2017, 45, 537–551. [Google Scholar] [CrossRef]
- Hilfer, R. Geometric and dielectric characterization of porous media. Phys. Rev. B 1991, 44, 60–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zakirov, T.; Khramchenkov, M. Prediction of permeability and tortuosity in heterogeneous porous media using a disorder parameter. Chem. Eng. Sci. 2020, 227, 115893. [Google Scholar] [CrossRef]
- Carrier, W.D., III. Goodbye, hazen; hello, kozeny-carman. J. Geotech. Geoenviron. Eng. 2003, 129, 1054–1056. [Google Scholar] [CrossRef]
- Bourg, I.C.; Ajo-Franklin, J.B. Clay, Water, and Salt: Controls on the Permeability of Fine-Grained Sedimentary Rocks. Accounts Chem. Res. 2017, 50, 2067–2074. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Zhu, W.; Qian, X.; Wang, S.; Fan, X. Studies on hydraulic conductivity and compressibility of backfills for soil-bentonite cutoff walls. Appl. Clay Sci. 2016, 132–133, 326–335. [Google Scholar] [CrossRef]
- Taylor, D.W. Fundamentals of Soil Mechanics; Chapman and Hall, Limited: New York, NY, USA, 1948. [Google Scholar]
- Molinero-Guerra, A.; Delage, P.; Cui, Y.-J.; Mokni, N.; Tang, A.M.; Aimedieu, P.; Bernier, F.; Bornert, M. Water-retention properties and microstructure changes of a bentonite pellet upon wetting/drying; application to radioactive waste disposal. Géotechnique 2020, 70, 199–209. [Google Scholar] [CrossRef]
- Kozeny, J. Uber kapillare leitung der wasser in boden. R. Acad. Sci. Vienna Proc. Class. I 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1997, 75, S32–S48. [Google Scholar] [CrossRef]
- Carman, P.C. Flow of Gases through Porous Media; Butterworths Publications Ltd.: London, UK, 1956. [Google Scholar]
- Chapuis, R.P.; Aubertin, M. On the use of the Kozeny–Carman equation to predict the hydraulic conductivity of soils. Can. Geotech. J. 2003, 40, 616–628. [Google Scholar] [CrossRef]
- Chapuis, R.; Légaré, P.-P. A simple method for determining the surface area of fine aggregates and fillers in bituminous mixtures. In Effects of Aggregates and Mineral Fillers on Asphalt Mixture Performance; American Society for Testing and Materials: Philadelphia, PA, USA, 1992; pp. 177–186. [Google Scholar]
- Holmboe, M.; Wold, S.; Jonsson, M. Porosity investigation of compacted bentonite using XRD profile modeling. J. Contam. Hydrol. 2012, 128, 19–32. [Google Scholar] [CrossRef]
- Tournassat, C.; Bizi, M.; Braibant, G.; Crouzet, C. Influence of montmorillonite tactoid size on Na–Ca cation exchange reactions. J. Colloid Interface Sci. 2011, 364, 443–454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Likos, W.J.; Wayllace, A. Porosity evolution of free and confined bentonites during interlayer hydration. Clays Clay Miner. 2010, 58, 399–414. [Google Scholar] [CrossRef]
- Sedighi, M.; Thomas, H.R. Micro porosity evolution in compacted swelling clays—A chemical approach. Appl. Clay Sci. 2014, 101, 608–618. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B. Porewater chemistry in compacted re-saturated MX-80 bentonite. J. Contam. Hydrol. 2003, 61, 329–338. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Brooks, R.; Corey, T. Hydraulic Properties of Porous Media; Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Averyanov, S.F. About Permeability of Subsurface Soils in Case of Incomplete Saturation; English Collection Volume 7; The Theory of Ground Water Movement; Princeton University Press: Princeton, NJ, USA, 1950. [Google Scholar]
- Cases, J.M.; Berend, I.; Besson, G.; Francois, M.; Uriot, J.P.; Thomas, F.; Poirier, J.E. Mechanism of adsorption and desorption of water vapor by homoionic montmorillonite. 1. The sodium-exchanged form. Langmuir 1992, 8, 2730–2739. [Google Scholar] [CrossRef]
- Jacinto, A.; Villar, M.V.; Ledesma, A. Influence of water density on the water-retention curve of expansive clays. Geotechnique 2012, 62, 657–667. [Google Scholar] [CrossRef]
- Perdrial, J.; Warr, L.N. Hydration Behavior of MX80 Bentonite in a Confined-Volume System: Implications for Backfill Design. Clays Clay Miner. 2011, 59, 640–653. [Google Scholar] [CrossRef]
- Cases, J.; Bérend, I.; François, M.; Uriot, J.; Michot, L.; Thomas, F. Mechanism of adsorption and desorption of water vapor by homoionic montmorillonite; 3, The Mg (super 2+), Ca (super 2+), and Ba (super 3+) exchanged forms. Clays Clay Miner. 1997, 45, 8–22. [Google Scholar] [CrossRef]
- Zhu, C.-M.; Ye, W.-M.; Chen, Y.; Chen, B.; Cui, Y.-J. Influence of salt solutions on the swelling pressure and hydraulic conductivity of compacted GMZ01 bentonite. Eng. Geol. 2013, 166, 74–80. [Google Scholar] [CrossRef]
- Salles, F.; Douillard, J.-M.; Denoyel, R.; Bildstein, O.; Jullien, M.; Beurroies, I.; Van Damme, H. Hydration sequence of swelling clays: Evolutions of specific surface area and hydration energy. J. Colloid Interface Sci. 2009, 333, 510–522. [Google Scholar] [CrossRef] [PubMed]
- Pusch, R. Bentonite Clay: Environmental Properties and Applications; CRC Press: New York, NY, USA, 2015. [Google Scholar]
- Gens, A. Soil–environment interactions in geotechnical engineering. Géotechnique 2010, 60, 3–74. [Google Scholar] [CrossRef]
- Wersin, P.; Curti, E.; Appelo, C. Modelling bentonite–water interactions at high solid/liquid ratios: Swelling and diffuse double layer effects. Appl. Clay Sci. 2004, 26, 249–257. [Google Scholar] [CrossRef]
- Saiyouri, N.; Tessier, D.; Hicher, P.Y. Experimental study of swelling in unsaturated compacted clays. Clay Miner. 2004, 39, 469–479. [Google Scholar] [CrossRef] [Green Version]
- Hillel, D. Introduction to Environmental Soil Physics; Academic Press, Elsevier Science: San Diego, CA, USA, 2003. [Google Scholar]
- Singh, P.N.; Wallender, W.W. Effects of Adsorbed Water Layer in Predicting Saturated Hydraulic Conductivity for Clays with Kozeny–Carman Equation. J. Geotech. Geoenviron. Eng. 2008, 134, 829–836. [Google Scholar] [CrossRef]
- Jacinto, A.C.; Ledesma, A.; Demagistri, A. Effect of the clay–water interaction in the hydration of compacted bentonite used in engineered barriers. Géoméch. Energy Environ. 2016, 8, 52–61. [Google Scholar] [CrossRef]
- Villar, M.; Gómez-Espina, R.; Gutiérrez-Nebot, L. Basal spacings of smectite in compacted bentonite. Appl. Clay Sci. 2012, 65–66, 95–105. [Google Scholar] [CrossRef]
- Torikai, Y.; Sato, S.; Ohashi, H. Thermodynamic Properties of Water in Compacted Sodium Montmorillonite. Nucl. Technol. 1996, 115, 73–80. [Google Scholar] [CrossRef]
- Pusch, R. The Microstructure of Mx-80 Clay with Respect to Its Bulk Physical Properties under Different Environmental Conditions; SKB: Lund, Sweden, 2001. [Google Scholar]
- Azizian, S. Kinetic models of sorption: A theoretical analysis. J. Colloid Interface Sci. 2004, 276, 47–52. [Google Scholar] [CrossRef]
- Kuroda, Y.; Idemitsu, K.; Furuya, H.; Inagaki, Y.; Arima, T. Diffusion of Technetium in Compacted Bentonites in the Reducing Condition with Corrosion Products of Iron. MRS Online Proc. Libr. Arch. 1996, 465, 909–916. [Google Scholar] [CrossRef]
- Epstein, N. On tortuosity and the tortuosity factor in flow and diffusion through porous media. Chem. Eng. Sci. 1989, 44, 777–779. [Google Scholar] [CrossRef]
- Comiti, J.; Renaud, M. A new model for determining mean structure parameters of fixed beds from pressure drop measurements: Application to beds packed with parallelepipedal particles. Chem. Eng. Sci. 1989, 44, 1539–1545. [Google Scholar] [CrossRef]
- Mauret, E.; Renaud, M. Transport phenomena in multi-particle systems—I. Limits of applicability of capillary model in high voidage beds-application to fixed beds of fibers and fluidized beds of spheres. Chem. Eng. Sci. 1997, 52, 1807–1817. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in Porous Media: A Critical Review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Tjaden, B.; Finegan, D.; Lane, J.; Brett, D.J.; Shearing, P.R. Contradictory concepts in tortuosity determination in porous media in electrochemical devices. Chem. Eng. Sci. 2017, 166, 235–245. [Google Scholar] [CrossRef]
- Allen, R.; Sun, S. Computing and Comparing Effective Properties for Flow and Transport in Computer-Generated Porous Media. Geofluids 2017, 2017, 1–24. [Google Scholar] [CrossRef]
- Carman, P.C. Permeability of saturated sands, soils and clays. J. Agric. Sci. 1939, 29, 262–273. [Google Scholar] [CrossRef]
- Dullien, F.A.L. New network permeability model of porous media. AIChE J. 1975, 21, 299–307. [Google Scholar] [CrossRef]
- Boudreau, B.P. The diffusive tortuosity of fine-grained unlithified sediments. Geochim. Cosmochim. Acta 1996, 60, 3139–3142. [Google Scholar] [CrossRef]
- Weissberg, H.L. Effective Diffusion Coefficient in Porous Media. J. Appl. Phys. 1963, 34, 2636–2639. [Google Scholar] [CrossRef]
- Ho, F.-G.; Striender, W. A variational calculation of the effective surface diffusion coefficient and tortuosity. Chem. Eng. Sci. 1981, 36, 253–258. [Google Scholar] [CrossRef]
- Mbonimpa, M.; Aubertin, M.; Chapuis, R.P.; Bussière, B. Practical pedotransfer functions for estimating the saturated hydraulic conductivity. Geotech. Geol. Eng. 2002, 20, 235–259. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. Predicting the Coefficient of Permeability of Soils Using the Kozeny-Carman Equation; École Polytechnique de Montréal: Montreal, QC, Canada, 2003. [Google Scholar]
- Morandini, T.L.C.; Leite, A.D.L. Characterization and hydraulic conductivity of tropical soils and bentonite mixtures for CCL purposes. Eng. Geol. 2015, 196, 251–267. [Google Scholar] [CrossRef]
- Ye, W.; Wan, M.; Chen, B.; Chen, Y.; Cui, Y.; Wang, J. Temperature effects on the unsaturated permeability of the densely compacted GMZ01 bentonite under confined conditions. Eng. Geol. 2011, 126, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Cui, Y.-J.; Tang, A.M.; Barnichon, J.-D.; Saba, S.; Ye, W.-M. Hydraulic conductivity and microstructure changes of compacted bentonite/sand mixture during hydration. Eng. Geol. 2013, 164, 67–76. [Google Scholar] [CrossRef]
- Leverett, M. Capillary Behavior in Porous Solids. Trans. AIME 1941, 142, 152–169. [Google Scholar] [CrossRef]
- Pham, Q.; Vales, F.; Malinsky, L.; Minh, D.N.; Gharbi, H. Effects of desaturation–resaturation on mudstone. Phys. Chem. Earth Parts A/B/C 2007, 32, 646–655. [Google Scholar] [CrossRef]
- Villar, M.V. Water retention of two natural compacted bentonites. Clays Clay Miner. 2007, 55, 311–322. [Google Scholar] [CrossRef]
- Gailhanou, H.; Van Miltenburg, J.; Rogez, J.; Olives, J.; Amouric, M.; Gaucher, E.C.; Blanc, P. Thermodynamic properties of anhydrous smectite MX-80, illite IMt-2 and mixed-layer illite–smectite ISCz-1 as determined by calorimetric methods. Part I: Heat capacities, heat contents and entropies. Geochim. Cosmochim. Acta 2007, 71, 5463–5473. [Google Scholar] [CrossRef]
- Ransom, B.; Helgeson, H.C. A chemical and thermodynamic model of aluminous dioctahedral 2:1 layer clay minerals in diagenetic processes; regular solution representation of interlayer dehydration in smectite. Am. J. Sci. 1994, 294, 449–484. [Google Scholar] [CrossRef]
- Fan, R.-D.; Du, Y.-J.; Reddy, K.; Liu, S.; Yang, Y. Compressibility and hydraulic conductivity of clayey soil mixed with calcium bentonite for slurry wall backfill: Initial assessment. Appl. Clay Sci. 2014, 101, 119–127. [Google Scholar] [CrossRef]
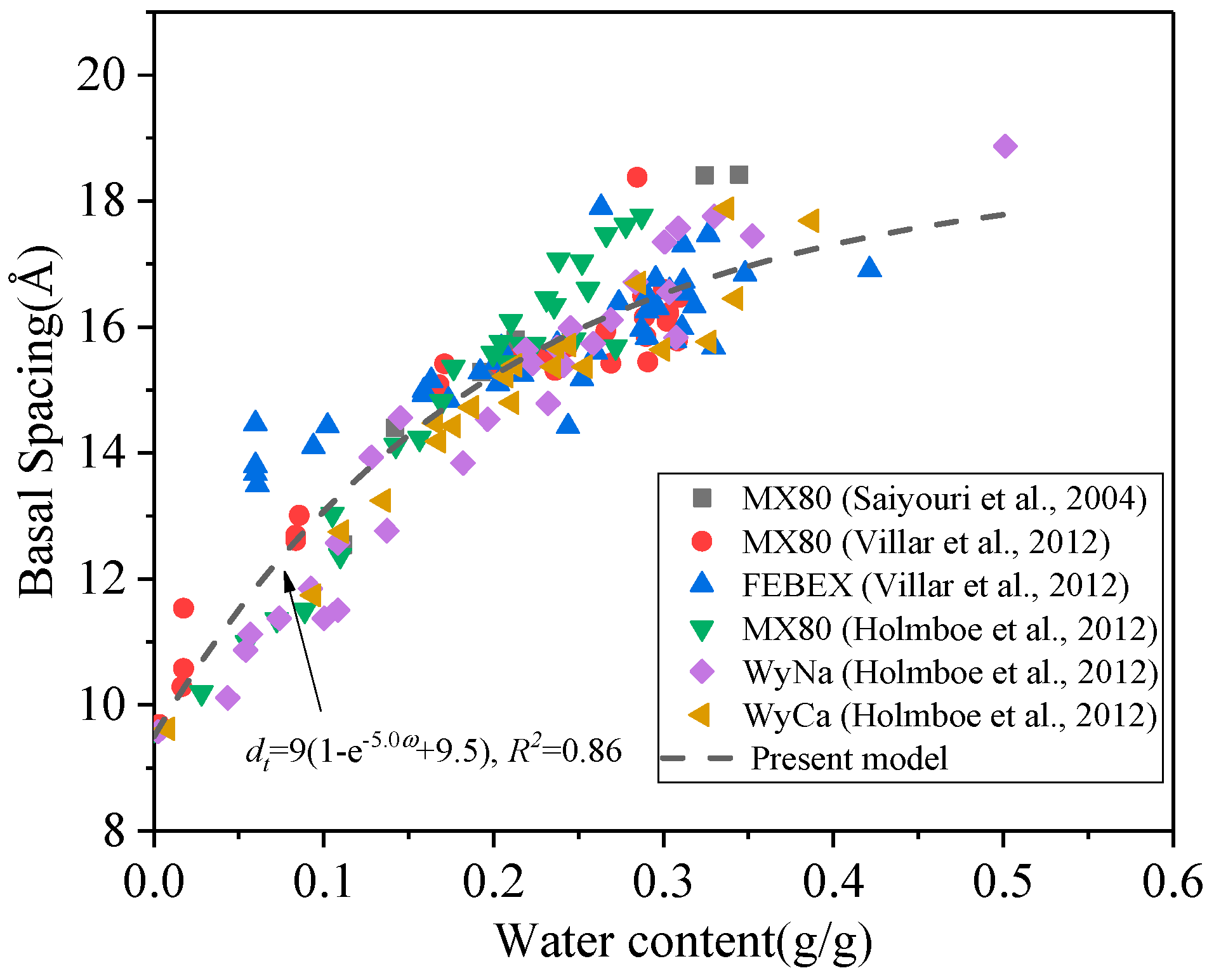
| Water Layers | Basal Spacing (Å) | |||||
|---|---|---|---|---|---|---|
| [69] | [70] | [49] | [66] | |||
| 0 | 9.5 | 10 | 9.5 | 9.5 | 9.2–10.1 | 10 |
| 1 | 12.4 | 12.5 | 12.3 | 12.4 | 12.2–12.7 | 12.6 |
| 2 | 15.4 | 15.5 | 15.0 | 15.6 | 15.2–15.7 | 15.6 |
| 3 | 18.4 | 18.5 | 18.5 | 18.9 | 18.4–19 | 18.6 |
| 4 | 21.6 * | \ | \ | 21.8 * | 21.4–22 * | 21.6 |
| Water Layers | Water Content (g/g, %) | ||||
|---|---|---|---|---|---|
| [71,72] | [70] | [66] | [49] | ||
| 0 | <7 | <8.6 | <11.1 | <10.8 | <8.8 |
| 1 | 7–20 | 8.6–16.8 | 11.1–19.2 | 10.8–23.3 | 8.8–19.7 |
| 2 | 10–20 | 16.8–28.4 | 19.2–32.4 | 23.3–35.4 | 19.7–30.3 |
| 3 | 20–35 | >28.4 | 32.4–69.4 | >35.4 | >30.3 |
| 4 | \ | \ | >69.4 | \ | \ |
| Mineral | GMZ | MX80 |
|---|---|---|
| Montmorillonite (%) | 75.4 1 | 79 1 |
| Particle < 2 μm (%) | 60 1 | 60 1 |
| Specific surface area (m2/g) | 570 1 | 756 4 |
| Gs | 2.66 1 | 2.82 2 |
| CEC (meq/100 g) | 77.3 1 | 82.3 1 |
| WL (%) | 313 1 | 519 1 |
| WP (%) | 38 1 | 35 1 |
| IP | 275 1 | 484 1 |
| Molar mass (g/mol O10(OH)2)) | \ | 378.79 3 |
| 1—[15,17]. 2—[93]. 3—[94]. 4—[49]. | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Du, M.; Yao, Q. Evolution of Hydraulic Conductivity of Unsaturated Compacted Na-Bentonite under Confined Condition—Including the Microstructure Effects. Materials 2022, 15, 219. https://doi.org/10.3390/ma15010219
Chen T, Du M, Yao Q. Evolution of Hydraulic Conductivity of Unsaturated Compacted Na-Bentonite under Confined Condition—Including the Microstructure Effects. Materials. 2022; 15(1):219. https://doi.org/10.3390/ma15010219
Chicago/Turabian StyleChen, Tian, Mao Du, and Qiangling Yao. 2022. "Evolution of Hydraulic Conductivity of Unsaturated Compacted Na-Bentonite under Confined Condition—Including the Microstructure Effects" Materials 15, no. 1: 219. https://doi.org/10.3390/ma15010219





