Experimental and Numerical Investigation of Bond-Slip Behavior of High-Strength Reinforced Concrete at Service Load
Abstract
:1. Introduction
2. Laboratory Experiment
3. Finite Element Modelling
4. Test Results and Analysis
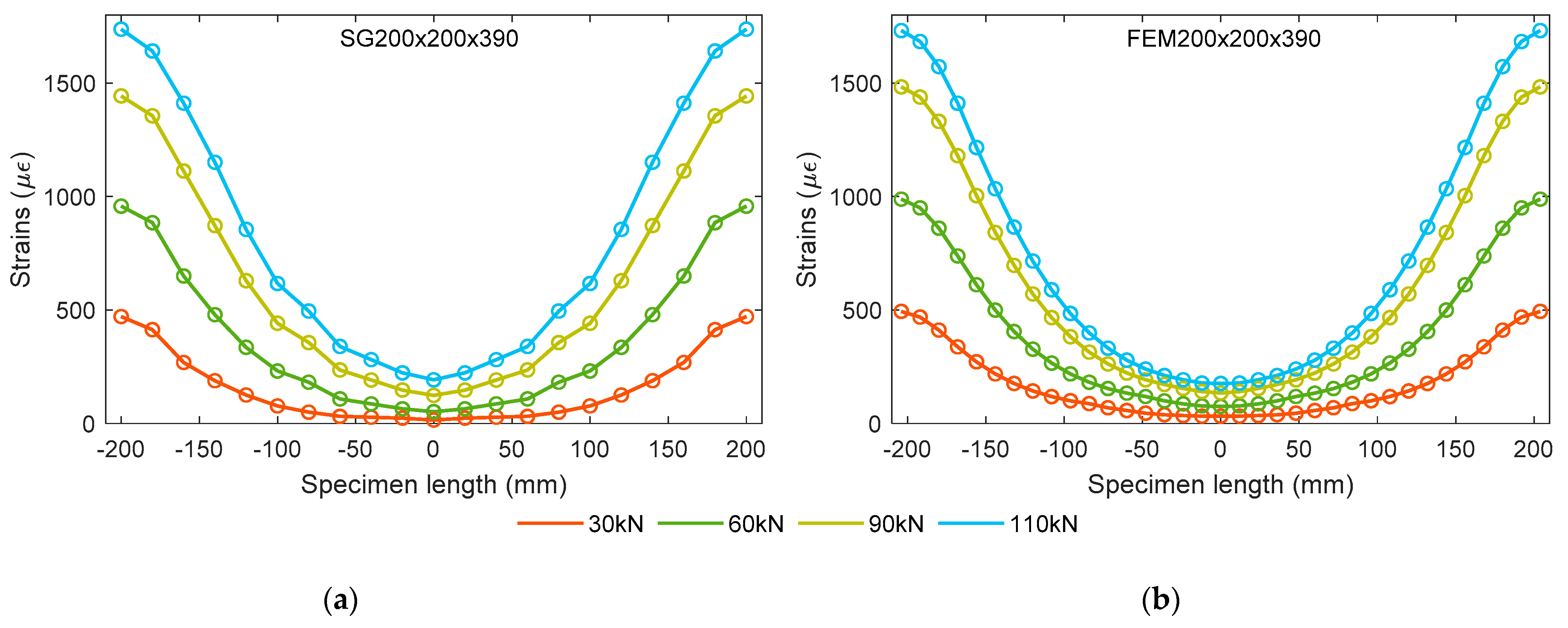
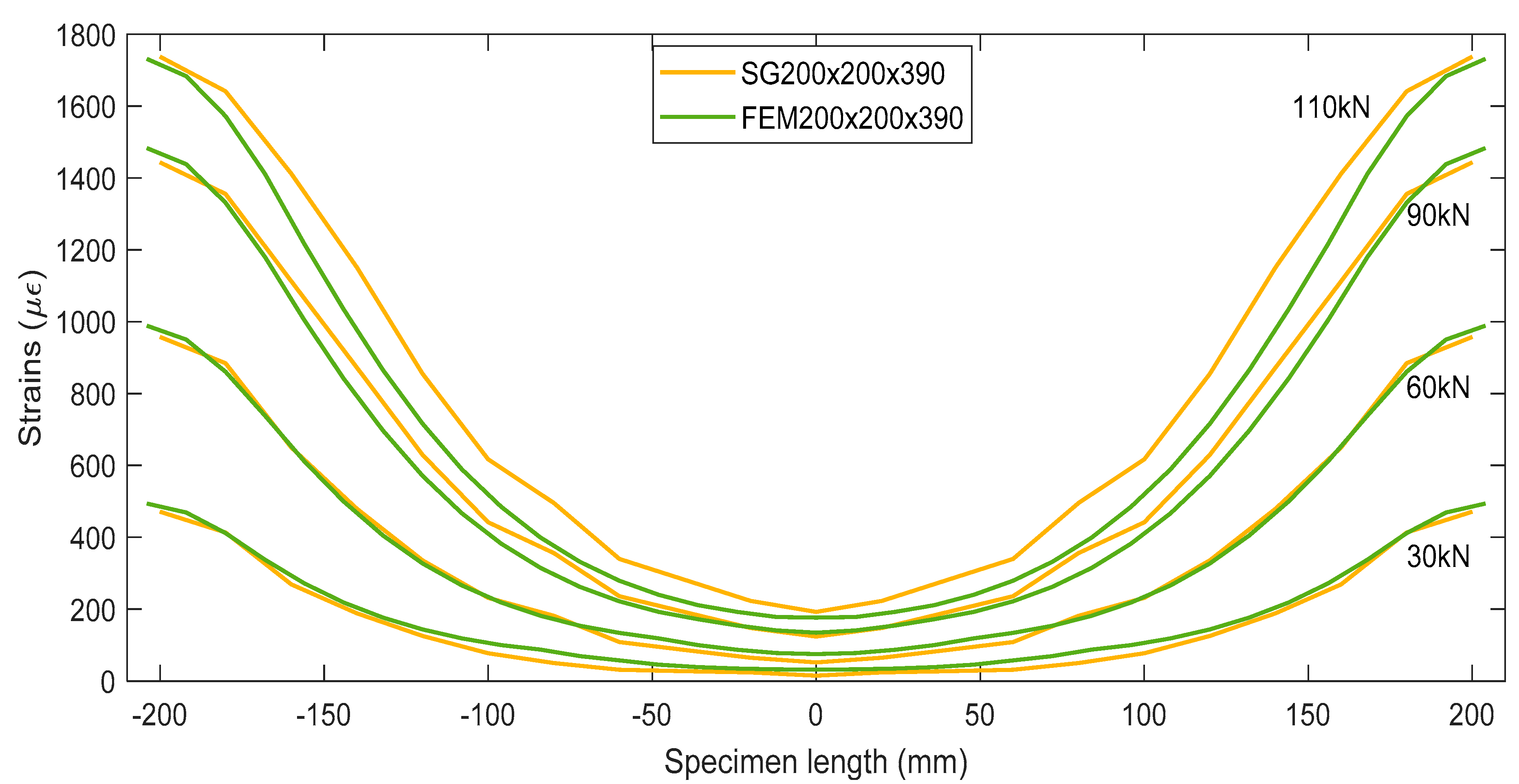
4.1. Strain Profile Results
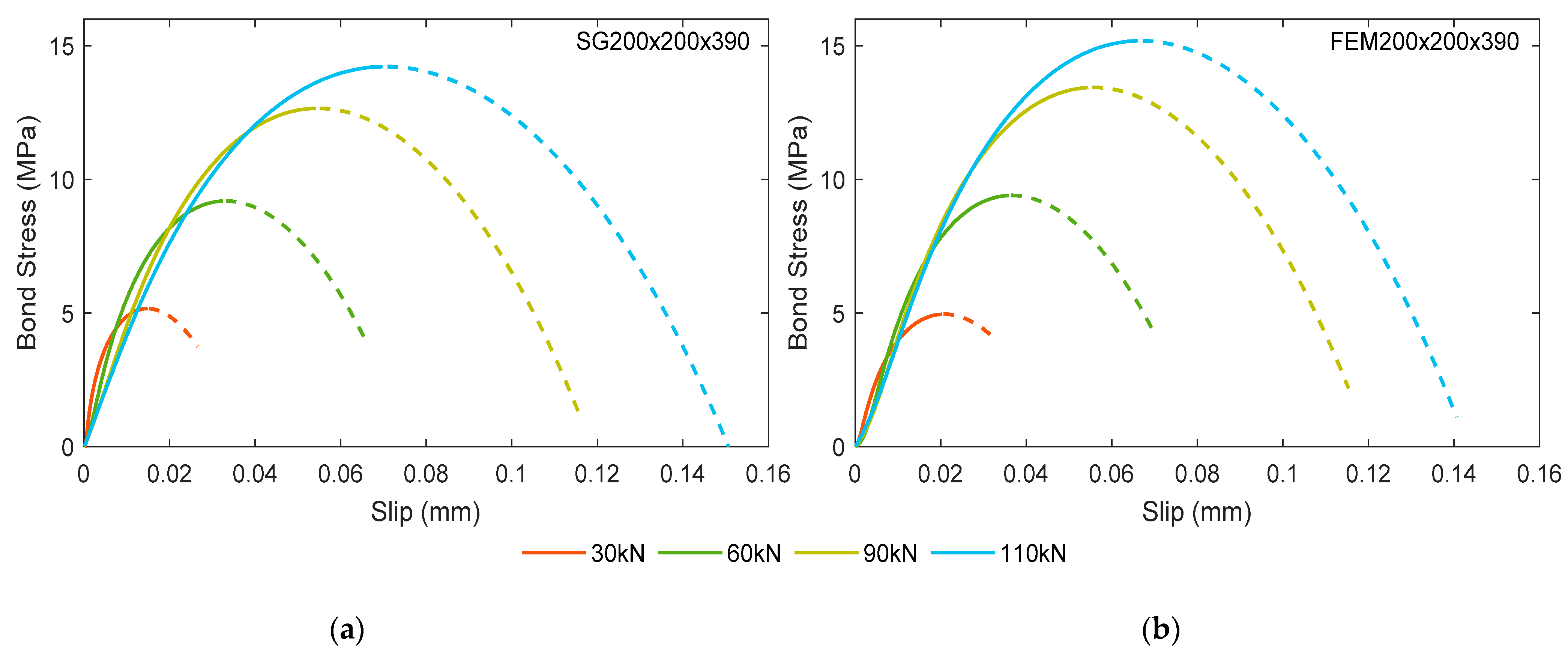
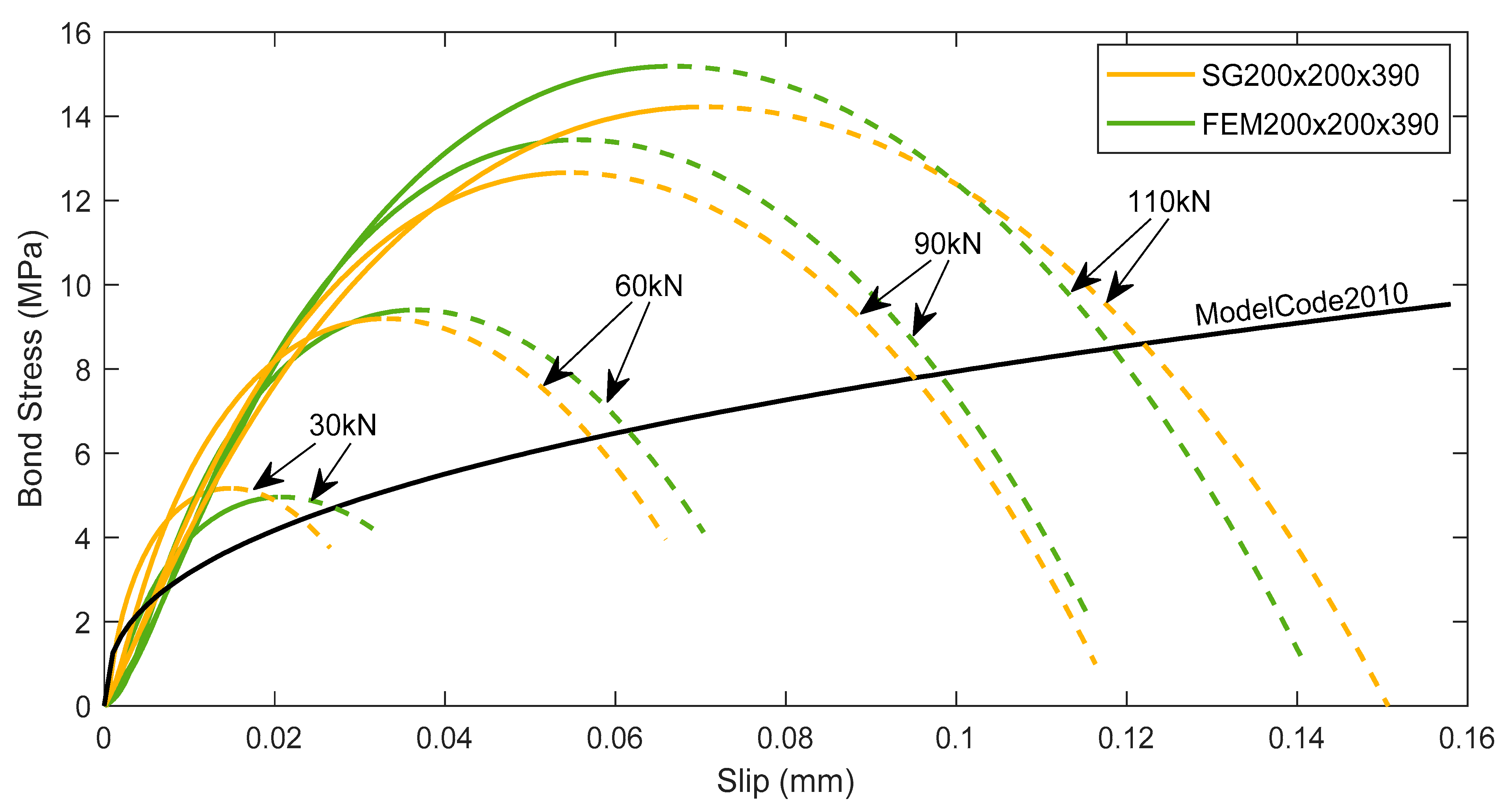
4.2. Bond-Slip Behavior
5. Conclusions
- The reinforcement strain profiles recorded at different load levels had a smooth and regular shape, and also kept symmetry in respect to the mid-section of the members representing zero slip. This implies that the employed reinforcement strain measurement technique based on the strain gauge sensors glued inside a groove of the bar may assure consistent and reliable test results.
- The bond-slip relations derived from the experimental reinforcement strain profiles of short RC ties had an ascending and a descending branch. The ascending branches of bond–slip curves were of a parabolic shape, and were in close agreement with each other at different load levels. This confirms that the same bond–slip relationship may be used for the whole loading analysis. Moreover, the ascending bond–slip branch may be considered to represent the inherent material feature of the reinforcement–concrete interaction, whereas the descending branch signifies the structural effect of cracking on the bond stresses in the close proximity of the cracks.
- In the case of strain monitoring, the numerical model performed extremely good correlation with the experimental one at lower load levels, though a maximum 19.5% disparity in strain data was noticed at the highest load level 110 kN.
- In the criteria of predicting bond-slip behavior, the numerical model has shown a thorough consistency in accordance with the experimental result. Only at higher loads has minor disparity (max. 7%) has been noticed.
- The current investigation demonstrated much stiffer bond response by fast reaching specific bond stress values at a significantly smaller slip compared to the MC2010.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bolborea, B.; Baera, C.; Dan, S.; Gruin, A.; Burduhos-Nergis, D.D.; Vasile, V. Concrete compressive strength by means of ultrasonic pulse velocity and moduli of elasticity. Materials 2021, 14, 7018. [Google Scholar] [CrossRef]
- Windisch, A. A modified pull-out test and new evaluation methods for a more real local bond-slip relationship. Mater. Struct. 1985, 18, 181–184. [Google Scholar] [CrossRef]
- Siempu, R.; Pancharthi, R.K. Bond characteristics of concrete made of recycled aggregates from building demolition waste. Mag. Concr. Res. 2017, 69, 665–682. [Google Scholar] [CrossRef]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local Bond Stress—Slip Relationships of Deformed Bars under Generalized Excitation; University of California, Berkeley: Berkeley, CA, USA, 1982. [Google Scholar]
- Cosenza, B.E.; Realfonzo, R. Beravior and modeling of bond of frp rebars to concrete. J. Compos. Constr. 1997, 1, 40–51. [Google Scholar] [CrossRef]
- Shima, H.; Chou, L.L.; Okamura, H. Micro and macro models for bond in reinforced concrete. J. Fac. Eng. Univ. Tokyo Ser. B 1987, 39, 133–194. [Google Scholar]
- Du Béton, F.I. Bond of reinforcement in concrete: State-of-art report. Bulletin 2000, 10, 160–167. [Google Scholar]
- Jakubovskis, R.; Kaklauskas, G. Damage of bond in reinforced concrete: A detailed finite element analysis. Struct. Concr. 2021, 22, 1–13. [Google Scholar] [CrossRef]
- Scott, R.H.; Gill, P.A.T. Short-term distributions of strain and bond stress along tension reinforcement. Struct. Eng. 1987, 65B, 39–48. [Google Scholar]
- Kaklauskas, G.; Sokolov, A.; Ramanauskas, R.; Jakubovskis, R. Reinforcement strains in reinforced concrete tensile members recorded by strain gauges and FBG sensors: Experimental and numerical analysis. Sensors 2019, 19, 200. [Google Scholar] [CrossRef] [Green Version]
- Bado, M.F.; Casas, J.R.; Kaklauskas, G. Distributed Sensing (DOFS) in Reinforced Concrete members for reinforcement strain monitoring, crack detection and bond-slip calculation. Eng. Struct. 2021, 226, 111385. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R.; Dey, A.; Berrocal, C.G.; Kaklauskas, G.; Fernandez, I.; Rempling, R. Characterization of concrete shrinkage induced strains in internally-restrained RC structures by distributed optical fiber sensing. Cem. Concr. Compos. 2021, 120, 104058. [Google Scholar] [CrossRef]
- Gribniak, V.; Jakubovskis, R.; Rimkus, A.; Ng, P.L.; Hui, D. Experimental and numerical analysis of strain gradient in tensile concrete prisms reinforced with multiple bars. Constr. Build. Mater. 2018, 187, 572–583. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.V.; Herrmann, L.R. Development of a plasticity bond model for steel reinforcement. Mech. Cohesive Frict. Mater. 1998, 180, 155–180. [Google Scholar] [CrossRef]
- Jiang, T.; Wu, Z.; Huang, L.; Ye, H. Three-dimensional nonlinear finite element modeling for bond performance of ribbed steel bars in concrete under lateral tensions. Int. J. Civ. Eng. 2020, 18, 595–617. [Google Scholar] [CrossRef]
- Seok, S.; Haikal, G.; Ramirez, J.A.; Lowes, L.N. High-resolution fi nite element modeling for bond in high-strength concrete beam. Eng. Struct. 2018, 173, 918–932. [Google Scholar] [CrossRef]
- Jakubovskis, R.; Kaklauskas, G. Bond-stress and bar-strain profiles in RC tension members modelled via finite elements. Eng. Struct. 2019, 194, 138–146. [Google Scholar] [CrossRef]
- Wenkenbach, I. Tension Stiffening in Reinforced Concrete Members with Large Diameter Reinforcement. Ph.D. Thesis, Durham University, Durham, UK, 2011. [Google Scholar]
- Bado, M.F.; Casas, J.R.; Dey, A.; Berrocal, C.G. Distributed optical fiber sensing bonding techniques performance for embedment inside reinforced concrete structures. Sensors 2020, 20, 5788. [Google Scholar] [CrossRef] [PubMed]
- Kaklauskas, G.; Ramanauskas, R.; Jakubovskis, R. Mean crack spacing modelling for RC tension elements. Eng. Struct. 2017, 150, 843–851. [Google Scholar] [CrossRef]
- Kaklauskas, G.; Ramanauskas, R.; Ng, P.L. Predicting crack spacing of reinforced concrete tension members using strain compliance approach with debonding. J. Civ. Eng. Manag. 2019, 25, 422–430. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton (Fib). Model Code 2010; International Federation for Structural Concrete, Federal Institute of Technology Lausanne-EPFI: Lausanne, Switzerland, 2013. [Google Scholar]
- ACI Committee. Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- García-Taengua, E.; Martí-Vargas, J.R.; Serna, P. Splitting of concrete cover in steel fiber reinforced concrete: Semi-empirical modeling and minimum confinement requirements. Constr. Build. Mater. 2014, 66, 743–751. [Google Scholar] [CrossRef]
- Cairns, J.; Jones, K. The splitting forces generated by bond. Mag. Concr. Res. 1995, 47, 153–165. [Google Scholar] [CrossRef]
- Stramandinoli, R.S.B.; La Rovere, H.L. An efficient tension-stiffening model for nonlinear analysis of reinforced concrete members. Eng. Struct. 2008, 30, 2069–2080. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Jabareen, M.; Abutbul, A.D. One-dimensional analysis of tension stiffening in reinforced concrete with discrete cracks. Eng. Struct. 2008, 30, 206–217. [Google Scholar] [CrossRef]
- Rolland, A.; Argoul, P.; Benzarti, K.; Quiertant, M.; Chataigner, S. Analytical and numerical modeling of the bond behavior between FRP reinforcing bars and concrete. Constr. Build. Mater. 2020, 231, 117160. [Google Scholar] [CrossRef]
- Ahmed, S.A.S.; Fahmy, M.F.M.; Wu, Z. Experimental Study and Numerical Modeling of Cyclic Bond—Slip Behavior of Basalt FRP Bars in Concrete. J. Compos. Constr. 2018, 22, 04018050. [Google Scholar] [CrossRef] [Green Version]
- Sharabi, M.N. Numerical modeling of reinforced- concrete bond. Nucl. Eng. Des. 1986, 91, 207–216. [Google Scholar] [CrossRef]
- Desir, J.M.; Romdhane, M.R.B.; Ulm, F.; Fairbairn, E.M.R. Steel—Concrete interface: Revisiting constitutive and numerical modeling. Comput. Struct. 1999, 71, 489–503. [Google Scholar] [CrossRef]
- Dehestani, M.; Asadi, A.; Mousavi, S.S. On discrete element method for rebar-concrete interaction. Constr. Build. Mater. 2017, 151, 220–227. [Google Scholar] [CrossRef]
- Chen, G.; Baker, G. Influence of bond slip on crack spacing in numerical modeling of reinforced concrete. J. Struct. Eng. 2004, 129, 1514–1521. [Google Scholar] [CrossRef]
- Červenka, V.; Jendele, L.; Červenka, J. ATENA Program Documentation, Part 1: Theory. Cerv. Consult. Prague 2007, 1–158. [Google Scholar]
- Metelli, G.; Plizzari, G.A. Influence of the relative rib area on bond behaviour. Mag. Concr. Res. 2014, 66, 277–294. [Google Scholar] [CrossRef] [Green Version]
- Goto, Y. Cracks formed in concrete around deformed tension bars. Am. Concr. Inst. 1971, 68, 244–251. [Google Scholar]
- Kanakubo, T.; Sato, Y.; Uchida, Y.; Watanabe, K.; Shima, H. Japan Concrete institute TC activities on bond behavior and constitutive laws in RC (Part 3: Application of constitutive laws for FEA). Bond. Concr. 2012, 2012, 105–112. [Google Scholar]

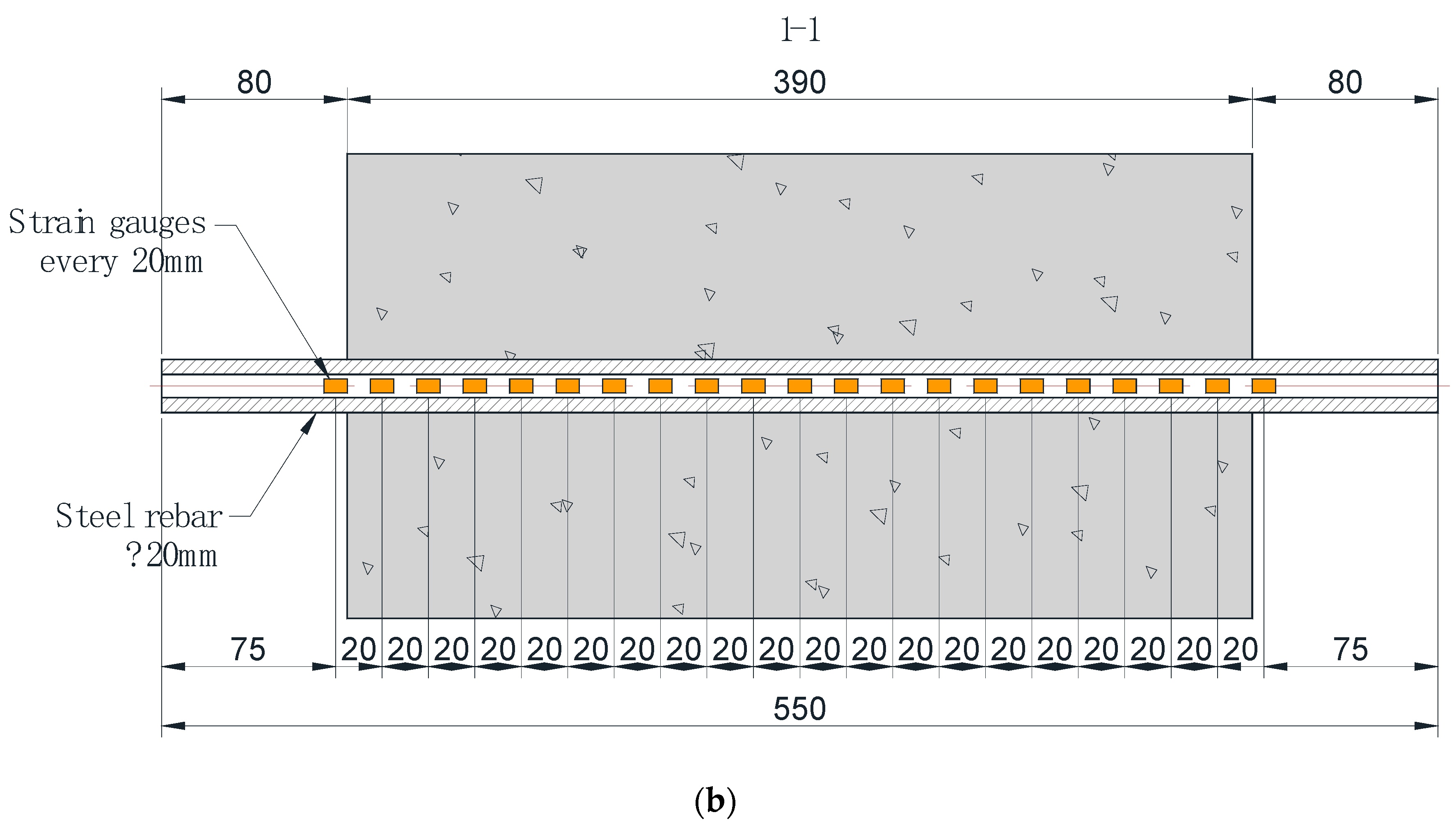


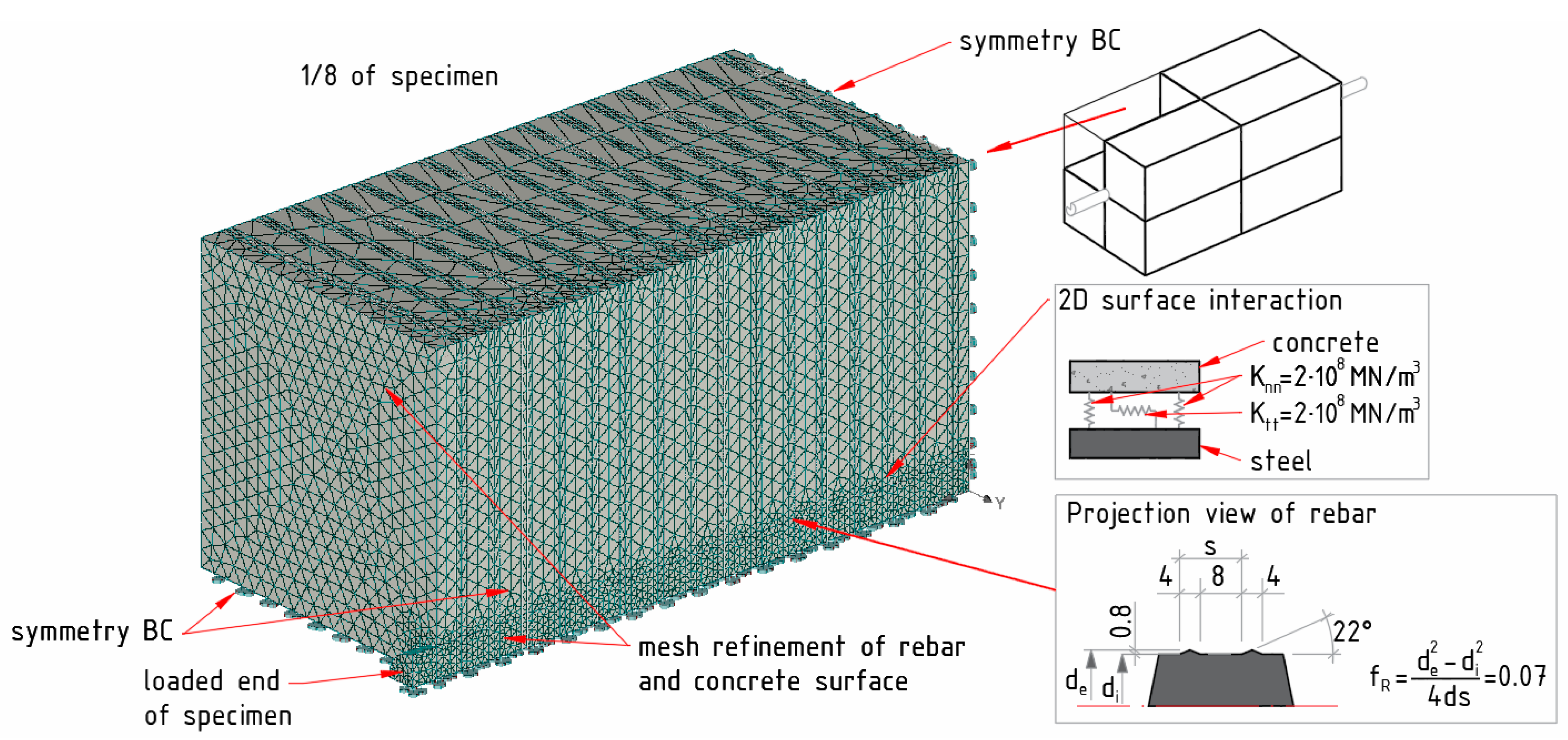
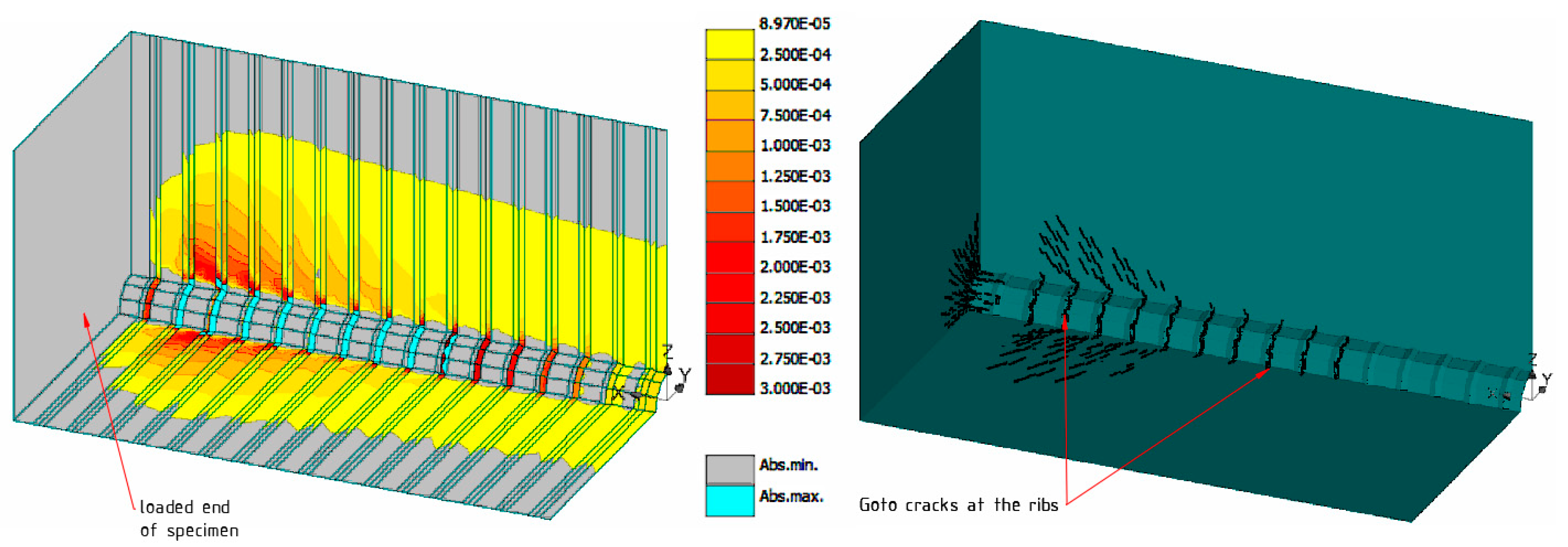
| Chemical Composition | Quantity (kg/m3) | Specific Density (kg/m3) | Bulk Density (kg/m3) |
|---|---|---|---|
| Ordinary Portland Cement (CEM I 42.5 R) | 425 | 3089 | 1100 |
| Water-cement ratio 0.35 | 150 | - | - |
| Fine aggregate 0/4 mm | 1165 | 2650 | 1620 |
| Crushed coarse aggregate 5/8 mm | 715 | 2610 | 1310 |
| Concrete plasticizer (1.0%) | 4.25 | 1060 (density of solution) | |
| Physical Specification | Mechanical Properties | |||
|---|---|---|---|---|
| Specimen Dimension (mm) | 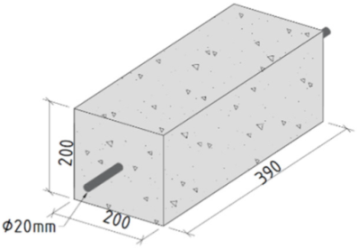 | Concrete | fm,cyl (MPa) | 71.32 |
| fm,sp (MPa) | 4.45 | |||
| fm,fl (MPa) | 6.61 | |||
| Ec (MPa) | 41,526 | |||
| Groove dimension (mm) | 2(2 × 10) | Steel | fy (MPa) | 486 |
| AS (mm2) | 270.8 | Es (MPa) | 201,734 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, A.; Valiukas, D.; Jakubovskis, R.; Sokolov, A.; Kaklauskas, G. Experimental and Numerical Investigation of Bond-Slip Behavior of High-Strength Reinforced Concrete at Service Load. Materials 2022, 15, 293. https://doi.org/10.3390/ma15010293
Dey A, Valiukas D, Jakubovskis R, Sokolov A, Kaklauskas G. Experimental and Numerical Investigation of Bond-Slip Behavior of High-Strength Reinforced Concrete at Service Load. Materials. 2022; 15(1):293. https://doi.org/10.3390/ma15010293
Chicago/Turabian StyleDey, Alinda, Domas Valiukas, Ronaldas Jakubovskis, Aleksandr Sokolov, and Gintaris Kaklauskas. 2022. "Experimental and Numerical Investigation of Bond-Slip Behavior of High-Strength Reinforced Concrete at Service Load" Materials 15, no. 1: 293. https://doi.org/10.3390/ma15010293
APA StyleDey, A., Valiukas, D., Jakubovskis, R., Sokolov, A., & Kaklauskas, G. (2022). Experimental and Numerical Investigation of Bond-Slip Behavior of High-Strength Reinforced Concrete at Service Load. Materials, 15(1), 293. https://doi.org/10.3390/ma15010293






