Transverse Cracking Induced Acoustic Emission in Carbon Fiber-Epoxy Matrix Composite Laminates
Abstract
:1. Introduction
2. Materials and Methods
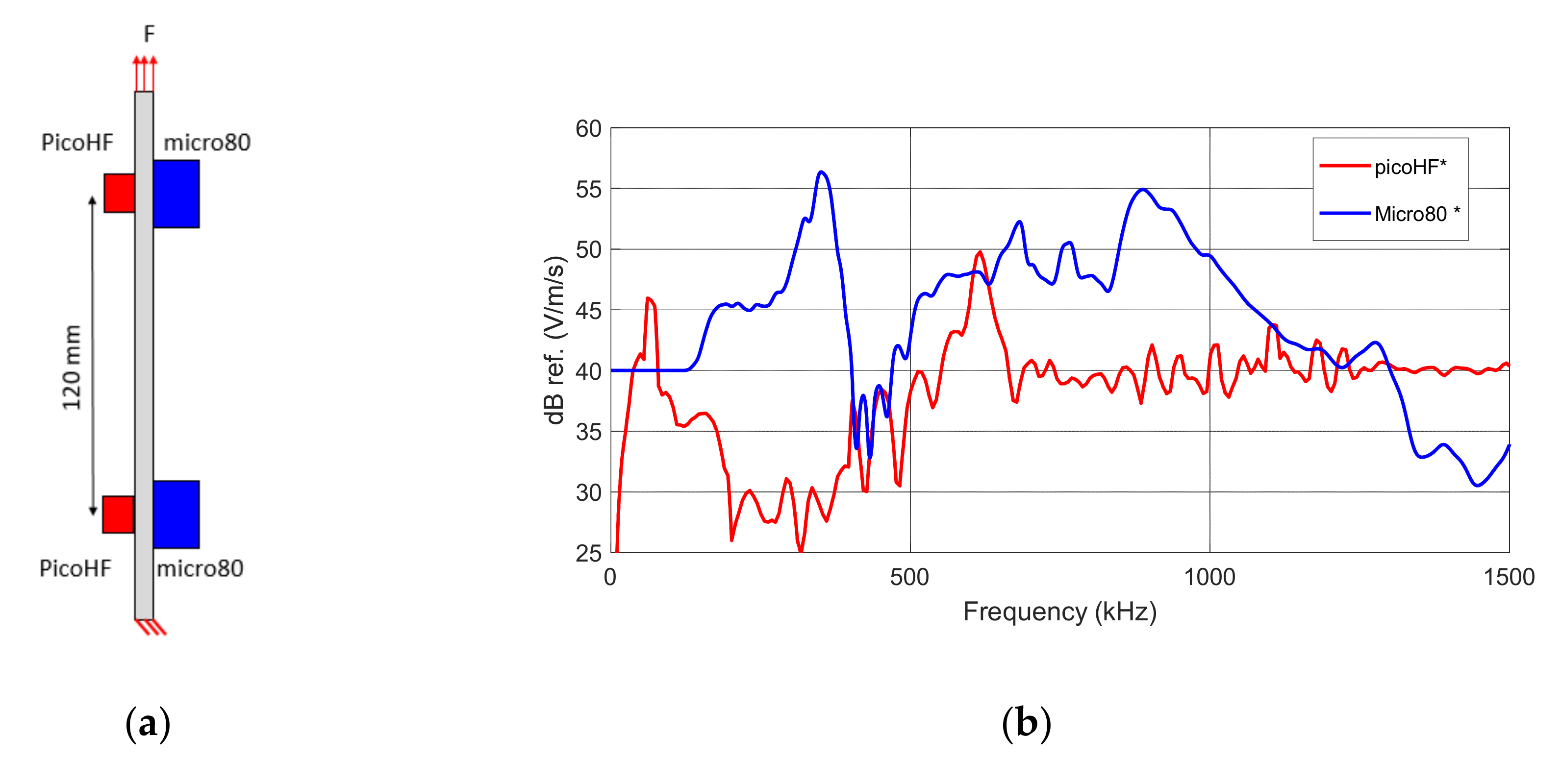
2.1. Experimental Settings
2.2. Simulation Settings
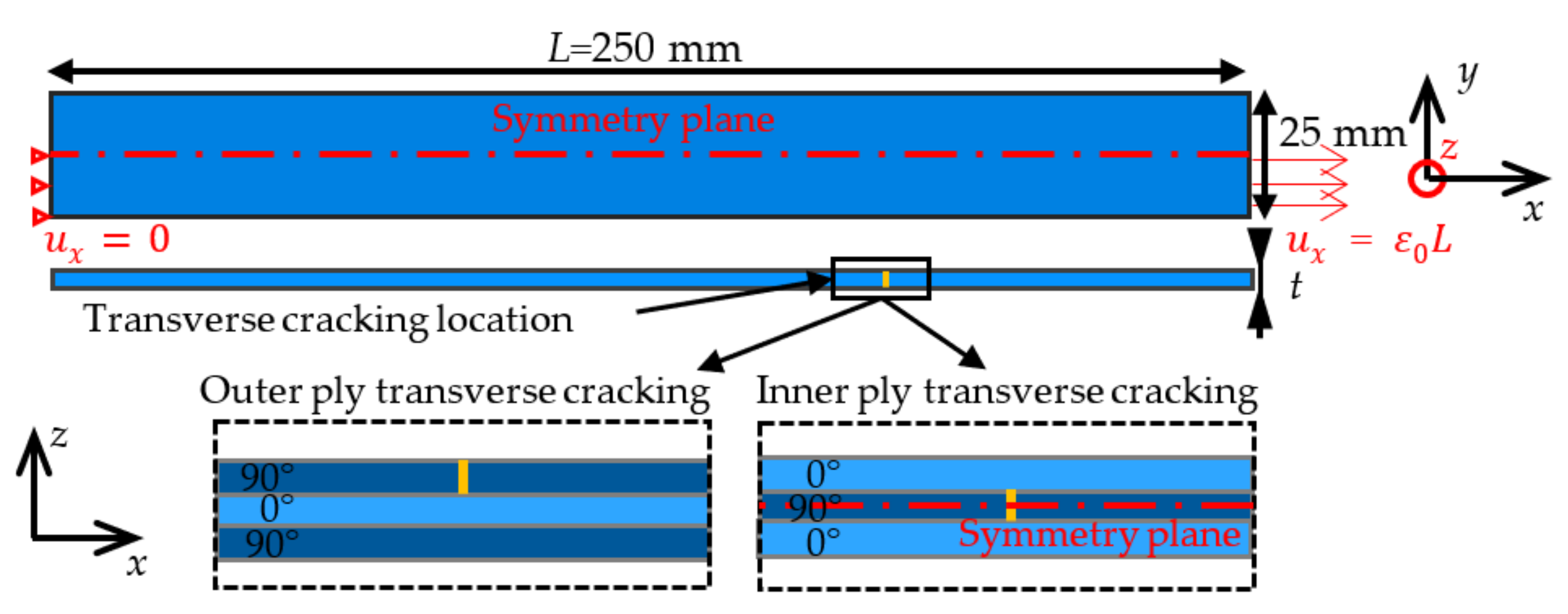
2.2.1. Composite Laminate Model
2.2.2. Transverse Cracking
2.2.3. Acoustic Emission
3. Results
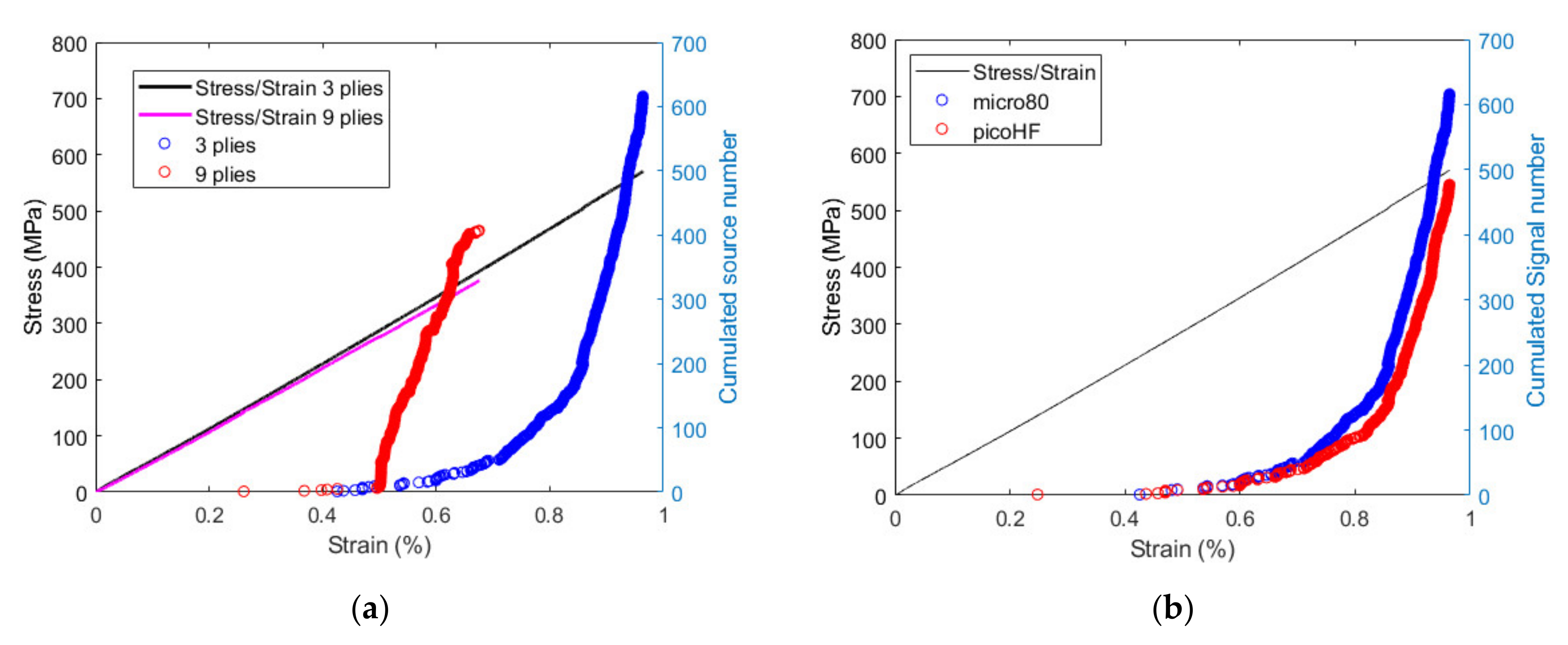
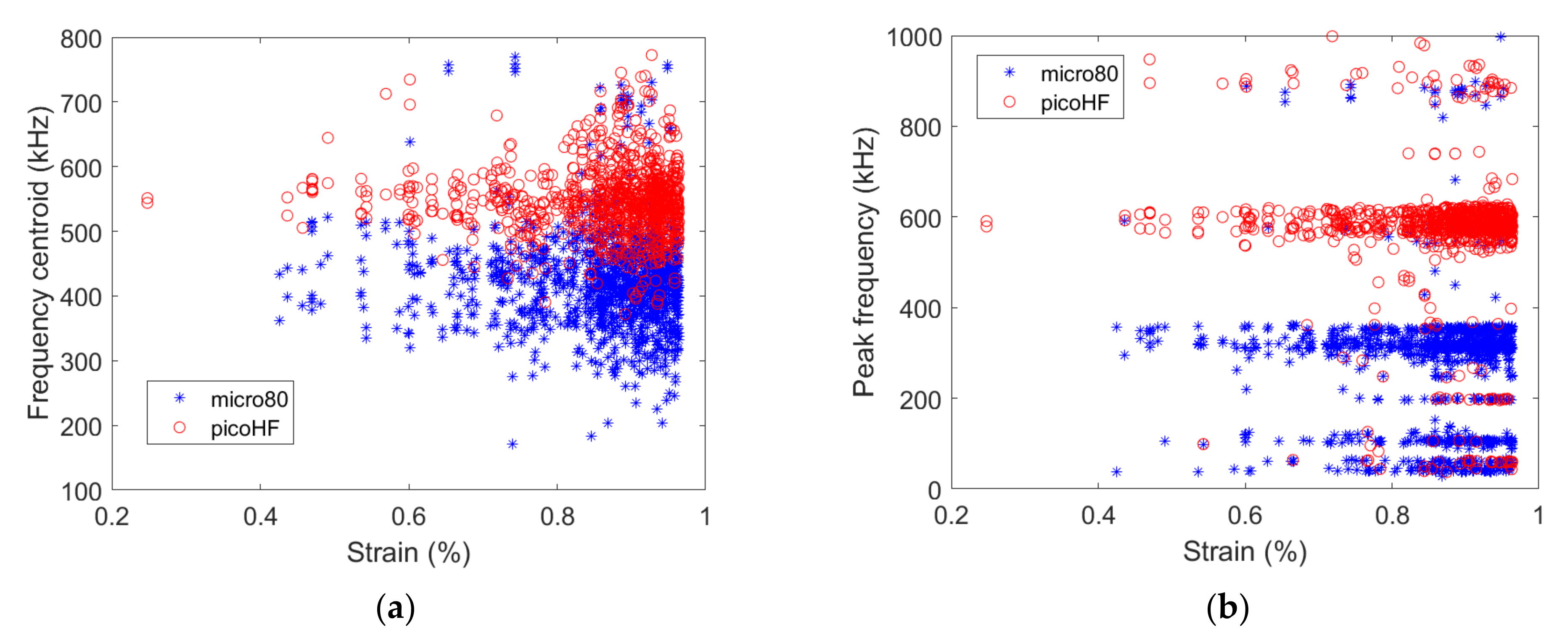
3.1. Experimental Results
3.2. Comparison between Experimental and Simulation Results
- (i)
- [03/903/03] composite with micro80 sensor,
- (ii)
- [0/90/0] composite with micro80 sensor,
- (iii)
- [0/90/0] composite with picoHF sensor.
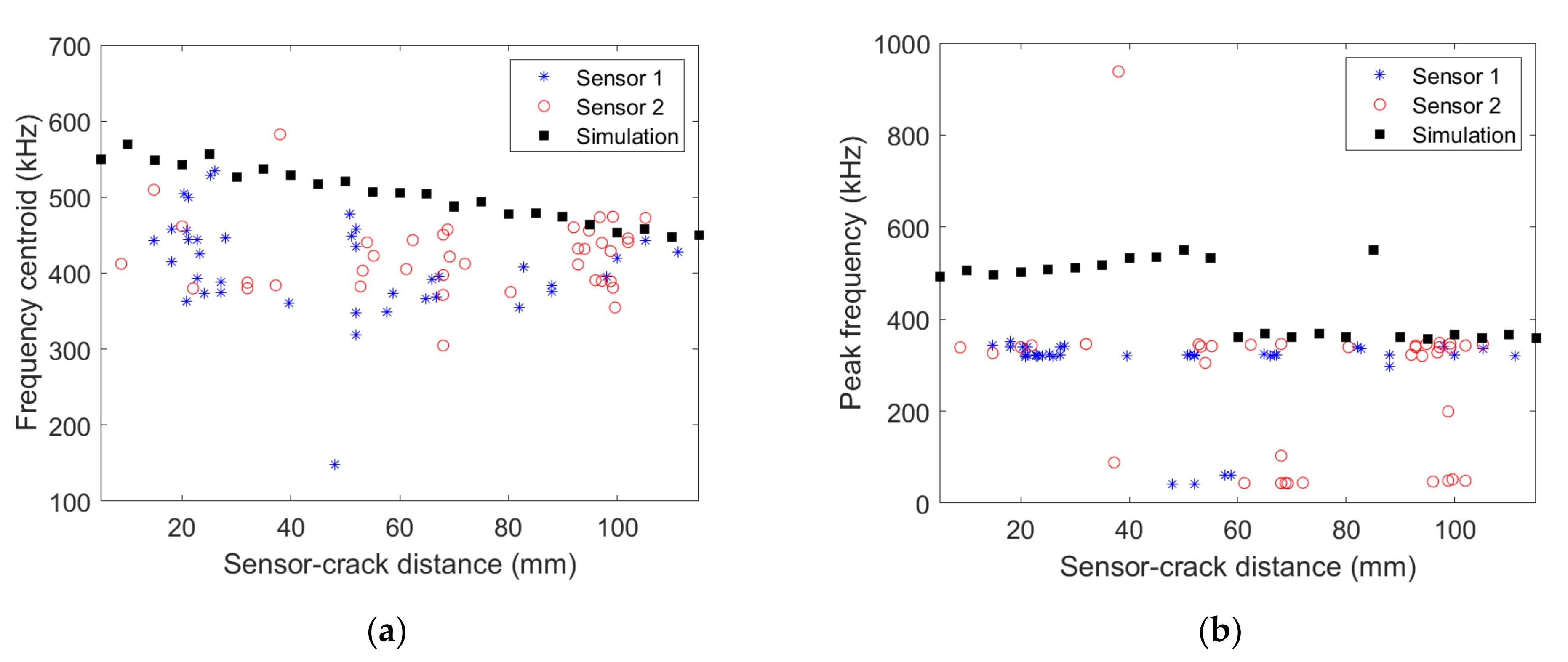
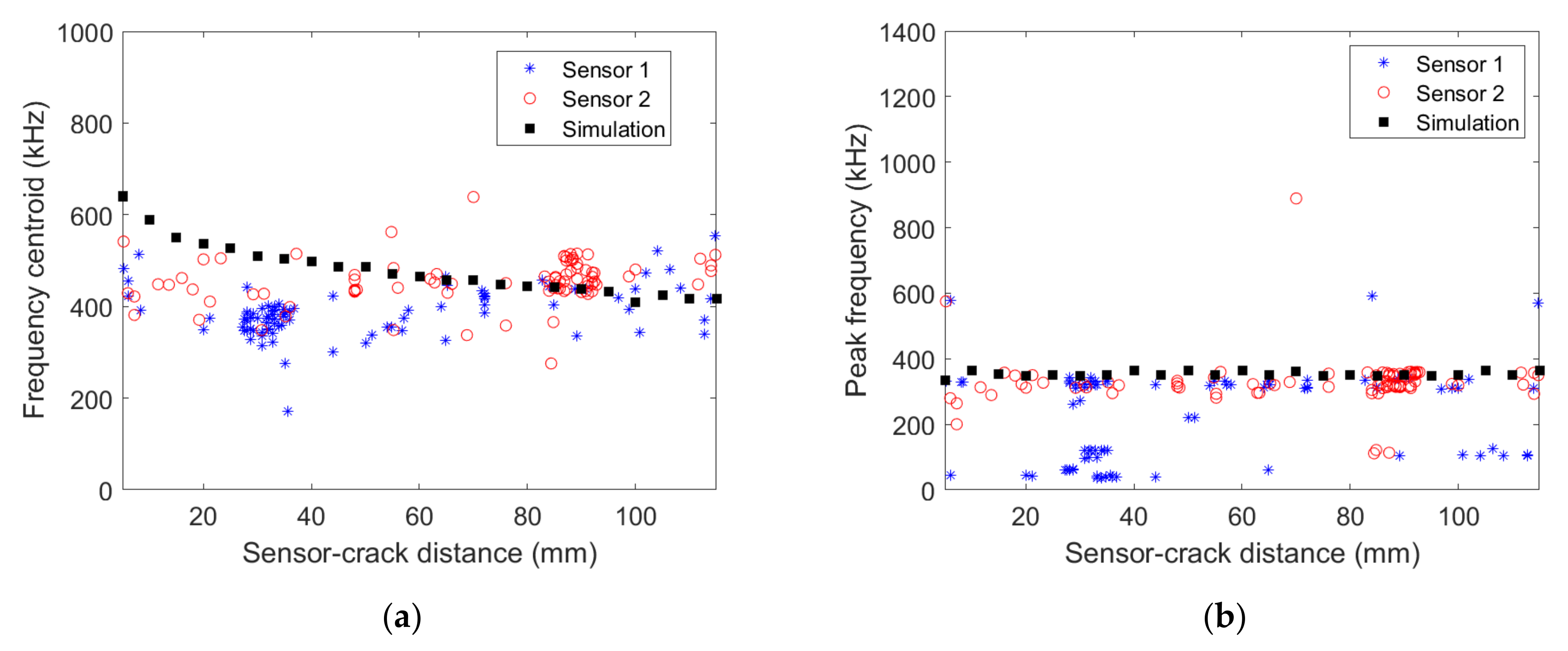
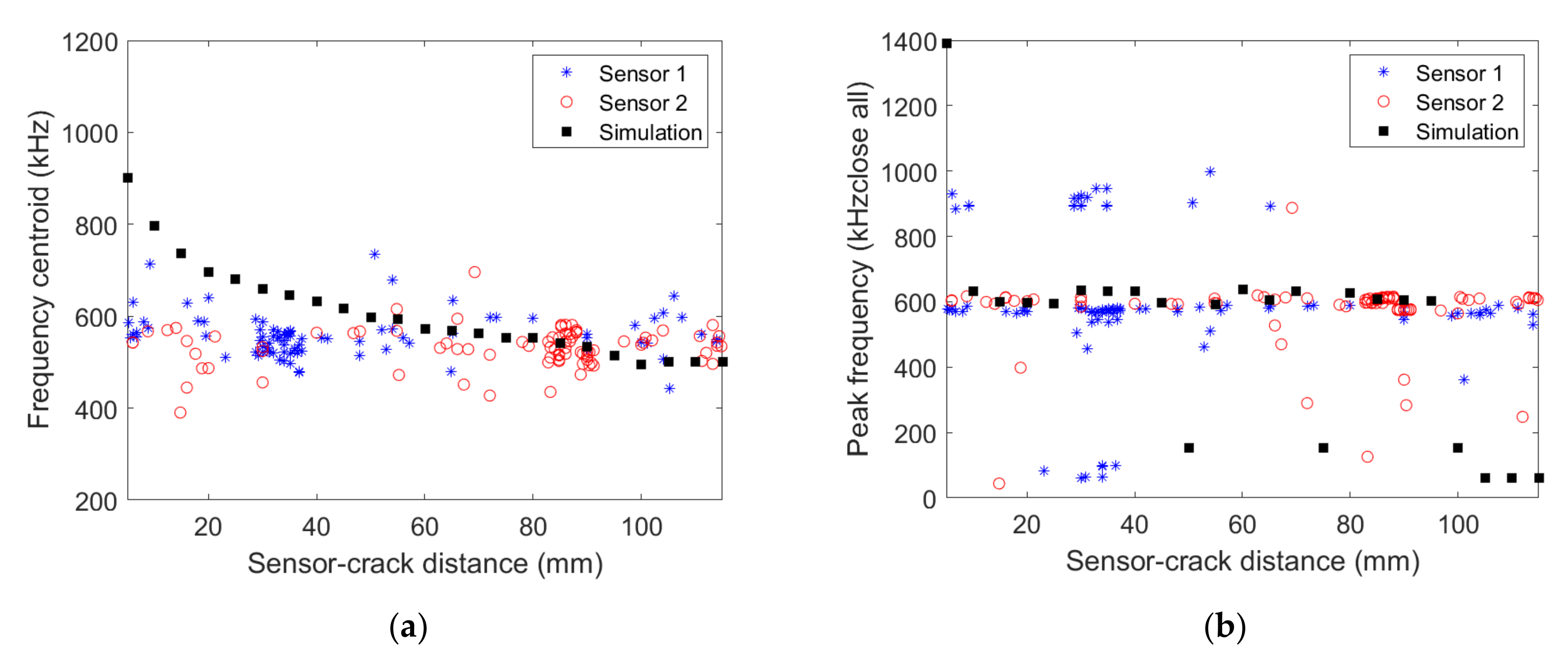
3.2.1. [03/903/03] Composite with micro80 Sensor
3.2.2. [0/90/0] Composite with micro80 Sensor
3.2.3. [0/90/0] Composite with picoHF Sensor
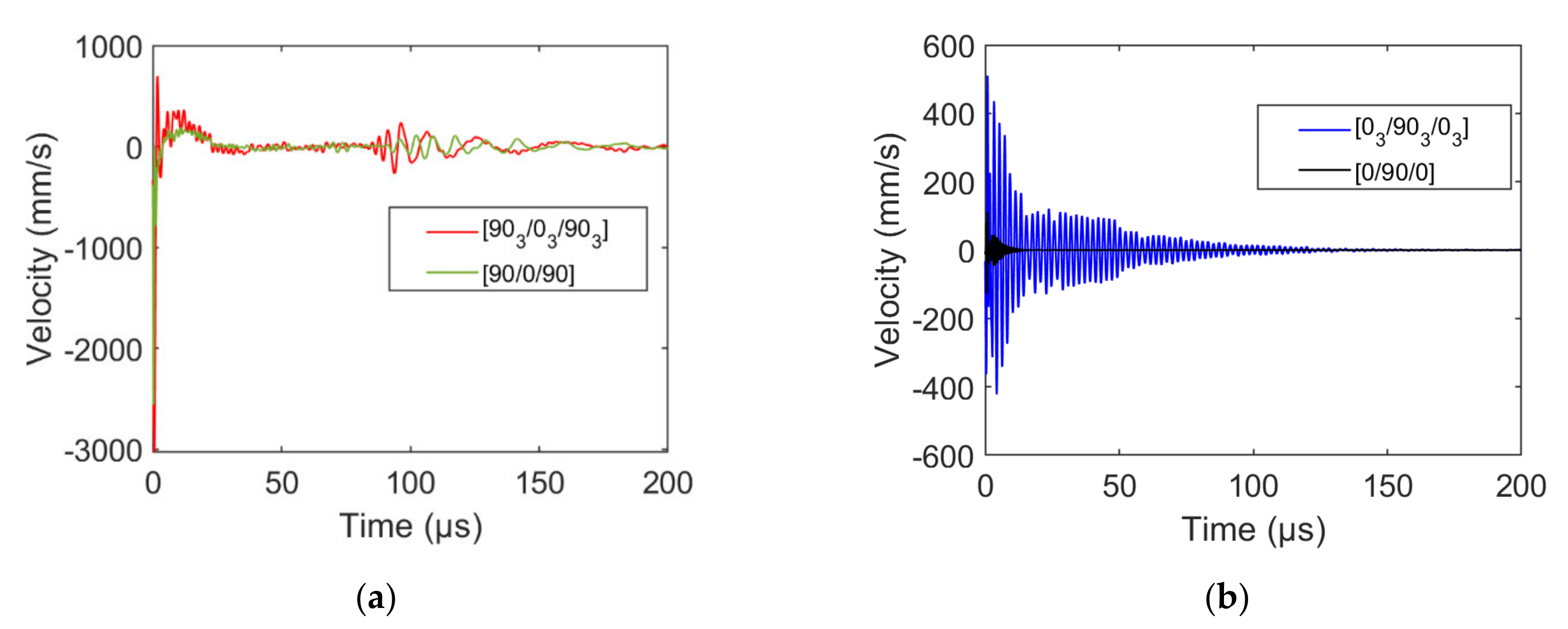
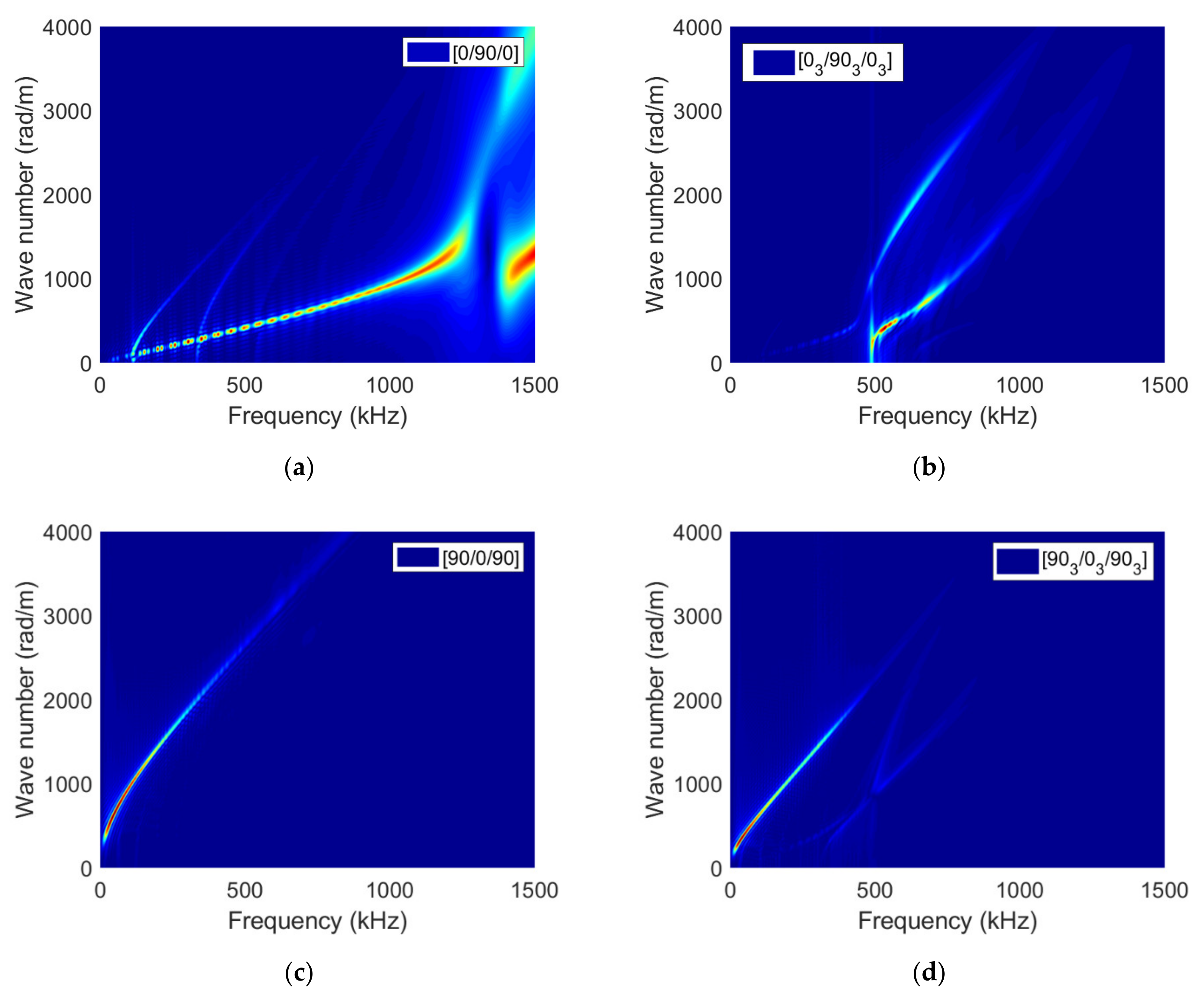
4. Influence of the Ply Thickness, Stacking Sequence
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Hemelrijck, D.; Anastassopoulos, A.A. Non Destructive Testing; Balkema: Rotterdam, The Netherlands, 1996; ISBN 905410595. [Google Scholar]
- Anastassopoulos, A.; Philippidis, T.P. Clustering methodology for the evaluation of acoustic emission from composites. J. Acoust. Emiss. 1995, 13, 11–12. [Google Scholar]
- Ramasso, E.; Placet, V.; Boubakar, M.L. Unsupervised Consensus Clustering of Acoustic Emission Time-Series for Robust Damage Sequence Estimation in Composites. IEEE Trans. Instrum. Meas. 2015, 64, 3297–3307. [Google Scholar] [CrossRef] [Green Version]
- Morscher, G.N.; Godin, N. Use of Acoustic Emission for Ceramic Matrix Composites; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014; pp. 569–590. [Google Scholar] [CrossRef]
- Alia, A.; Fantozzi, G.; Godin, N.; Osmani, H.; Reynaud, P. Mechanical behaviour of jute fibre-reinforced polyester composite: Characterization of damage mechanisms using acoustic emission and microstructural observations. J. Compos. Mater. 2019, 53, 3377–3394. [Google Scholar] [CrossRef]
- Guel, N.; Hamam, Z.; Godin, N.; Reynaud, P.; Caty, O.; Bouillon, F.; Paillassa, A. Data Merging of AE Sensors with Different Frequency Resolution for the Detection and Identification of Damage in Oxide-Based Ceramic Matrix Composites. Materials 2020, 13, 4691. [Google Scholar] [CrossRef]
- Marec, A.; Thomas, J.-H.; El Guerjouma, R. Damage characterization of polymer-based composite materials: Multivariable analysis and wavelet transform for clustering acoustic emission data. Mech. Syst. Signal Process. 2008, 22, 1441–1464. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Application of different acoustic emission descriptors in damage assessment of fiber reinforced plastics: A comprehensive review. Eng. Fract. Mech. 2020, 235, 107083. [Google Scholar] [CrossRef]
- Li, L.; Lomov, S.V.; Yan, X. Correlation of acoustic emission with optically observed damage in a glass/epoxy woven laminate under tensile loading. Compos. Struct. 2015, 123, 45–53. [Google Scholar] [CrossRef]
- Munoz, V.; Valès, B.; Perrin, M.; Pastor, M.L.; Welemane, H.; Cantarel, A.; Karama, M. Damage detection in CFRP by coupling acoustic emission and infrared thermography. Compos. Part B Eng. 2016, 85, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Godin, N.; Reynaud, P.; Fantozzi, G. Challenges and Limitations in the Identification of Acoustic Emission Signature of Damage Mechanisms in Composites Materials. Appl. Sci. 2018, 8, 1267. [Google Scholar] [CrossRef] [Green Version]
- Kharrat, M.; Placet, V.; Ramasso, E.; Boubakar, M. Influence of damage accumulation under fatigue loading on the AE-based health assessment of composite materials: Wave distortion and AE-features evolution as a function of damage level. Compos. Part A Appl. Sci. Manuf. 2018, 109, 615–627. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Accornero, F.; Mpalaskas, A.C.; Matikas, T.E.; Aggelis, D.G. Influence of damage in the acoustic emission parameters. Cem. Concr. Compos. 2013, 44, 9–16. [Google Scholar] [CrossRef]
- Maillet, E.; Baker, C.; Morscher, G.N.; Pujar, V.V.; Lemanski, J.R. Feasibility and limitations of damage identification in composite materials using acoustic emission. Compos. Part A Appl. Sci. Manuf. 2015, 75, 77–83. [Google Scholar] [CrossRef]
- Oz, F.E.; Ersoy, N.; Lomov, S.V. Do high frequency acoustic emission events always represent fibre failure in CFRP laminates? Compos. Part A Appl. Sci. Manuf. 2017, 103, 230–235. [Google Scholar] [CrossRef]
- Aggelis, D.; Shiotani, T.; Papacharalampopoulos, A.; Polyzos, D. The influence of propagation path on elastic waves as measured by acoustic emission parameters. Struct. Health Monit. 2012, 11, 359–366. [Google Scholar] [CrossRef]
- Aggelis, D.; Matikas, T. Effect of plate wave dispersion on the acoustic emission parameters in metals. Comput. Struct. 2012, 98-99, 17–22. [Google Scholar] [CrossRef]
- Baker, C.; Morscher, G.N.; Pujar, V.V.; Lemanski, J.R. Transverse cracking in carbon fiber reinforced polymer composites: Modal acoustic emission and peak frequency analysis. Compos. Sci. Technol. 2015, 116, 26–32. [Google Scholar] [CrossRef]
- Sause, M.G.R.; Richler, S. Finite Element Modelling of Cracks as Acoustic Emission Sources. J. Nondestruct. Eval. 2015, 34, 4. [Google Scholar] [CrossRef] [Green Version]
- Sause, M.G.R.; Horn, S. Simulation of Acoustic Emission in Planar Carbon Fiber Reinforced Plastic Specimens. J. Nondestruct. Eval. 2010, 29, 123–142. [Google Scholar] [CrossRef]
- Zelenyak, A.-M.; Schorer, N.; Sause, M.G. Modeling of ultrasonic wave propagation in composite laminates with realistic discontinuity representation. Ultrasonics 2018, 83, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yalcinkaya, H.; Ozevin, D. Numerical approach to absolute calibration of piezoelectric acoustic emission sensors using multiphysics simulations. Sens. Actuators A Phys. 2017, 256, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.S.; McLaskey, G.C. Broadband Calibration of Acoustic Emission and Ultrasonic Sensors from Generalized Ray Theory and Finite Element Models. J. Nondestruct. Eval. 2018, 37, 8. [Google Scholar] [CrossRef]
- Sause, M.G.; Hamstad, M.A. Numerical modeling of existing acoustic emission sensor absolute calibration approaches. Sens. Actuators A Phys. 2018, 269, 294–307. [Google Scholar] [CrossRef]
- Hamam, Z.; Godin, N.; Fusco, C.; Monnier, T. Modelling of Acoustic Emission Signals Due to Fiber Break in a Model Composite Carbon/Epoxy: Experimental Validation and Parametric Study. Appl. Sci. 2019, 9, 5124. [Google Scholar] [CrossRef] [Green Version]
- Hamam, Z.; Godin, N.; Fusco, C.; Doitrand, A.; Monnier, T. Acoustic Emission Signal Due to Fiber Break and Fiber Matrix Debonding in Model Composite: A Computational Study. Appl. Sci. 2021, 11, 8406. [Google Scholar] [CrossRef]
- Le Gall, T.; Monnier, T.; Fusco, C.; Godin, N.; Hebaz, S.-E. Towards Quantitative Acoustic Emission by Finite Element Modelling: Contribution of Modal Analysis and Identification of Pertinent Descriptors. Appl. Sci. 2018, 8, 2557. [Google Scholar] [CrossRef] [Green Version]
- Dia, S.; Monnier, T.; Godin, N.; Zhang, F. Primary Calibration of Acoustic Emission Sensors by the Method of Reciprocity, Theoretical and Experimental Considerations. J. Acoust. Emiss. 2012, 30, 152–166. [Google Scholar]
- Goujon, L.; Baboux, J.C. Behaviour of acoustic emission sensors using broadband calibration techniques. Meas. Sci. Technol. 2003, 14, 903–908. [Google Scholar] [CrossRef]
- Cervena, O.; Hora, P. Analysis of the conical piezoelectric acoustic emission transducer. Appl. Comput. Mech. 2008, 2, 13–24. [Google Scholar]
- Boulay, N.; Lhémery, A.; Zhang, F. Simulation of the spatial frequency-dependent sensitivities of Acoustic Emission sensors. In Proceedings of the Physical Acoustics Conference, AFPAC 2017, Croydon, UK, 17–19 January 2018; Volume 1017. [Google Scholar]
- Parvizi, A.; Garrett, K.W.; Bailey, J.E. Constrained cracking in glass fibre-reinforced epoxy cross-ply laminates. J. Mater. Sci. 1978, 13, 195–201. [Google Scholar] [CrossRef]
- Leguillon, D. Strength or toughness? A criterion for crack onset at a notch. Eur. J. Mech.—A/Solids 2002, 21, 61–72. [Google Scholar] [CrossRef]
- Doitrand, A.; Martin, E.; Leguillon, D. Numerical implementation of the coupled criterion: Matched asymptotic and full finite element approaches. Finite Elem. Anal. Des. 2020, 168, 103344. [Google Scholar] [CrossRef]
- García, I.; Carter, B.; Ingraffea, A.; Mantic, V. A numerical study of transverse cracking in cross-ply laminates by 3D finite fracture mechanics. Compos. Part B Eng. 2016, 95, 475–487. [Google Scholar] [CrossRef]
- García, I.G.; Mantič, V.; Blázquez, A. The effect of residual thermal stresses on transverse cracking in cross-ply laminates: An application of the coupled criterion of the finite fracture mechanics. Int. J. Fract. 2018, 211, 61–74. [Google Scholar] [CrossRef]
- García, I.; Justo, J.; Simon, A.; Mantič, V. Experimental study of the size effect on transverse cracking in cross-ply laminates and comparison with the main theoretical models. Mech. Mater. 2019, 128, 24–37. [Google Scholar] [CrossRef]
- Barenblatt, G. The formation of equilibrium cracks during brittle fracture. General ideas and hypotheses. Axially-symmetric cracks. J. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Morizet, N.; Godin, N.; Tang, J.; Maillet, E.; Fregonese, M.; Normand, B. Classification of acoustic emission signals using wavelets and Random Forests: Application to localized corrosion. Mech. Syst. Signal Process. 2016, 70–71, 1026–1037. [Google Scholar] [CrossRef]
- Marlett, K. Hexcel 8852 AS4 Unidirectional Prepreg at 190 gsm & 35% RC Qualification Material Property Data Report; Kansas Technical Report CAM-RP-2010-002 Rev A; National Institute for Aviation Research, Wichita State University: Wichita, KS, USA, 2010. [Google Scholar]
- Renart, J.; Blanco, N.; Pajares, E.; Costa, J.; Lazcano, S.; Santacruz, G. Side Clamped Beam (SCB) hinge system for delamination tests in beam-type composite specimens. Compos. Sci. Technol. 2011, 71, 1023–1029. [Google Scholar] [CrossRef]
- Doitrand, A.; Estevez, R.; Leguillon, D. Comparison between cohesive zone and coupled criterion modeling of crack initiation in rhombus hole specimens under quasi-static compression. Theor. Appl. Fract. Mech. 2019, 99, 51–59. [Google Scholar] [CrossRef] [Green Version]
- Doitrand, A.; Estevez, R.; Thibault, M.; Leplay, P. Fracture and Cohesive Parameter Identification of Refractories by Digital Image Correlation Up to 1200 °C. Exp. Mech. 2020, 60, 577–590. [Google Scholar] [CrossRef]



| Sensor | Sensitivity | Gain | Sampling Rate | Threshold | PDT | HDT | HLT | Filter |
|---|---|---|---|---|---|---|---|---|
| Micro80 | 200–900 kHz | dB | 5 MSPS | 38 dB | 25 µs | 50 µs | 1000 µs | 20–1200 kHz |
| PicoHF | 500–1850 kHz | dB | 5 MSPS | 38 dB | 25 µs | 50 µs | 1000 µs | 20–1200 kHz |
| Properties | Values |
|---|---|
| (GPa) | 127 |
| (GPa) | 9.2 |
| 0.302 | |
| 0.4 | |
| (GPa) | 4.8 |
| Gc (J/m2) | 248 |
| (MPa) | 63.9 |
| (kg/m3) | 1500 |
| Configuration | Total Thickness | Strain at First Transverse Crack |
|---|---|---|
| [0/90/0] | 0.9 mm | 0.007 |
| [03/903/03] | 2.7 mm | 0.004 |
| [90/0/90] | 0.9 mm | 0.007 |
| [903/03/903] | 2.7 mm | 0.0025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamam, Z.; Godin, N.; Reynaud, P.; Fusco, C.; Carrère, N.; Doitrand, A. Transverse Cracking Induced Acoustic Emission in Carbon Fiber-Epoxy Matrix Composite Laminates. Materials 2022, 15, 394. https://doi.org/10.3390/ma15010394
Hamam Z, Godin N, Reynaud P, Fusco C, Carrère N, Doitrand A. Transverse Cracking Induced Acoustic Emission in Carbon Fiber-Epoxy Matrix Composite Laminates. Materials. 2022; 15(1):394. https://doi.org/10.3390/ma15010394
Chicago/Turabian StyleHamam, Zeina, Nathalie Godin, Pascal Reynaud, Claudio Fusco, Nicolas Carrère, and Aurélien Doitrand. 2022. "Transverse Cracking Induced Acoustic Emission in Carbon Fiber-Epoxy Matrix Composite Laminates" Materials 15, no. 1: 394. https://doi.org/10.3390/ma15010394
APA StyleHamam, Z., Godin, N., Reynaud, P., Fusco, C., Carrère, N., & Doitrand, A. (2022). Transverse Cracking Induced Acoustic Emission in Carbon Fiber-Epoxy Matrix Composite Laminates. Materials, 15(1), 394. https://doi.org/10.3390/ma15010394







