Quantum Hall Effect across Graphene Grain Boundary
Abstract
:1. Introduction
2. Materials and Methods
2.1. Graphene Growth
2.2. Device Fabrication
2.3. Device Characterization
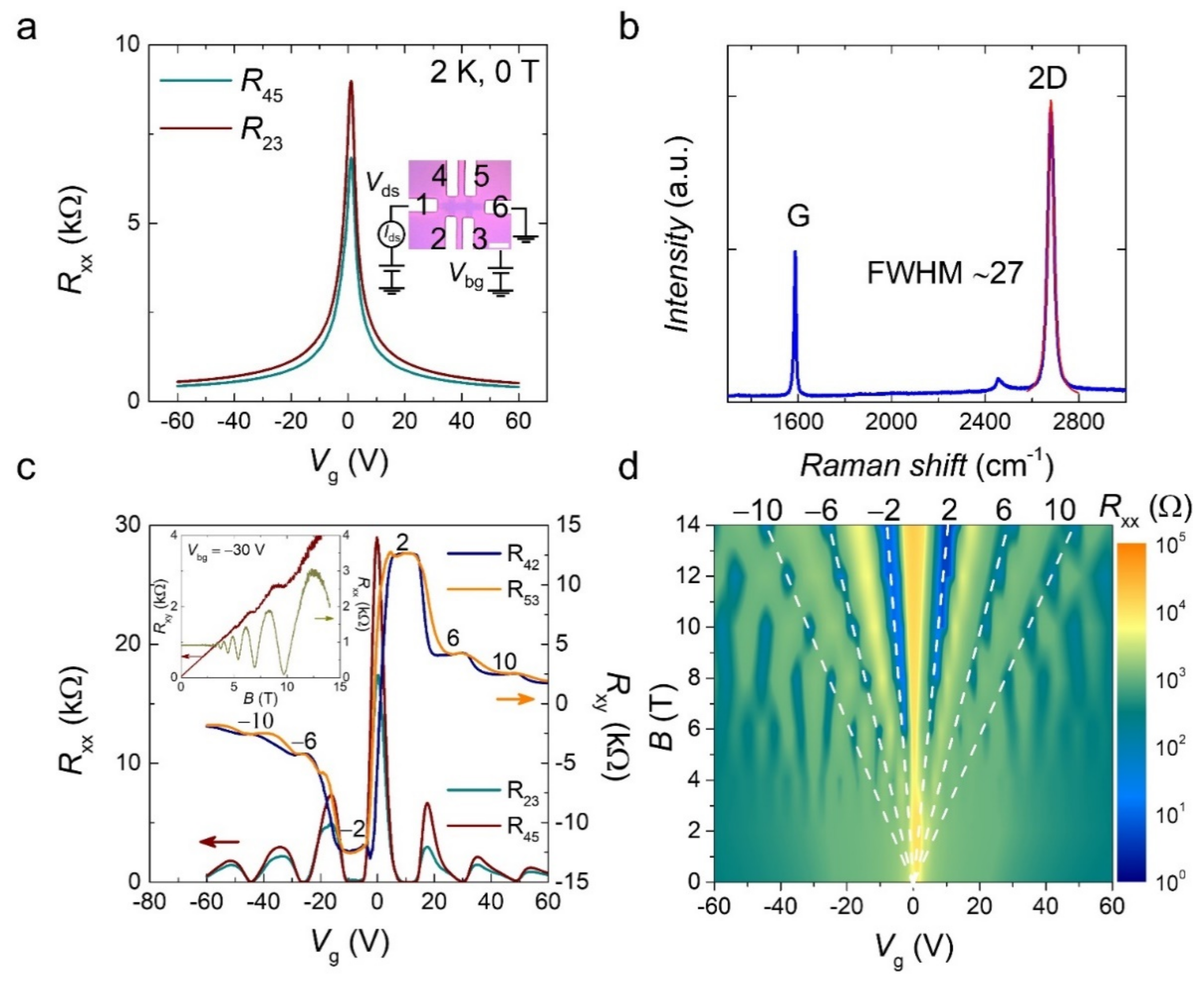
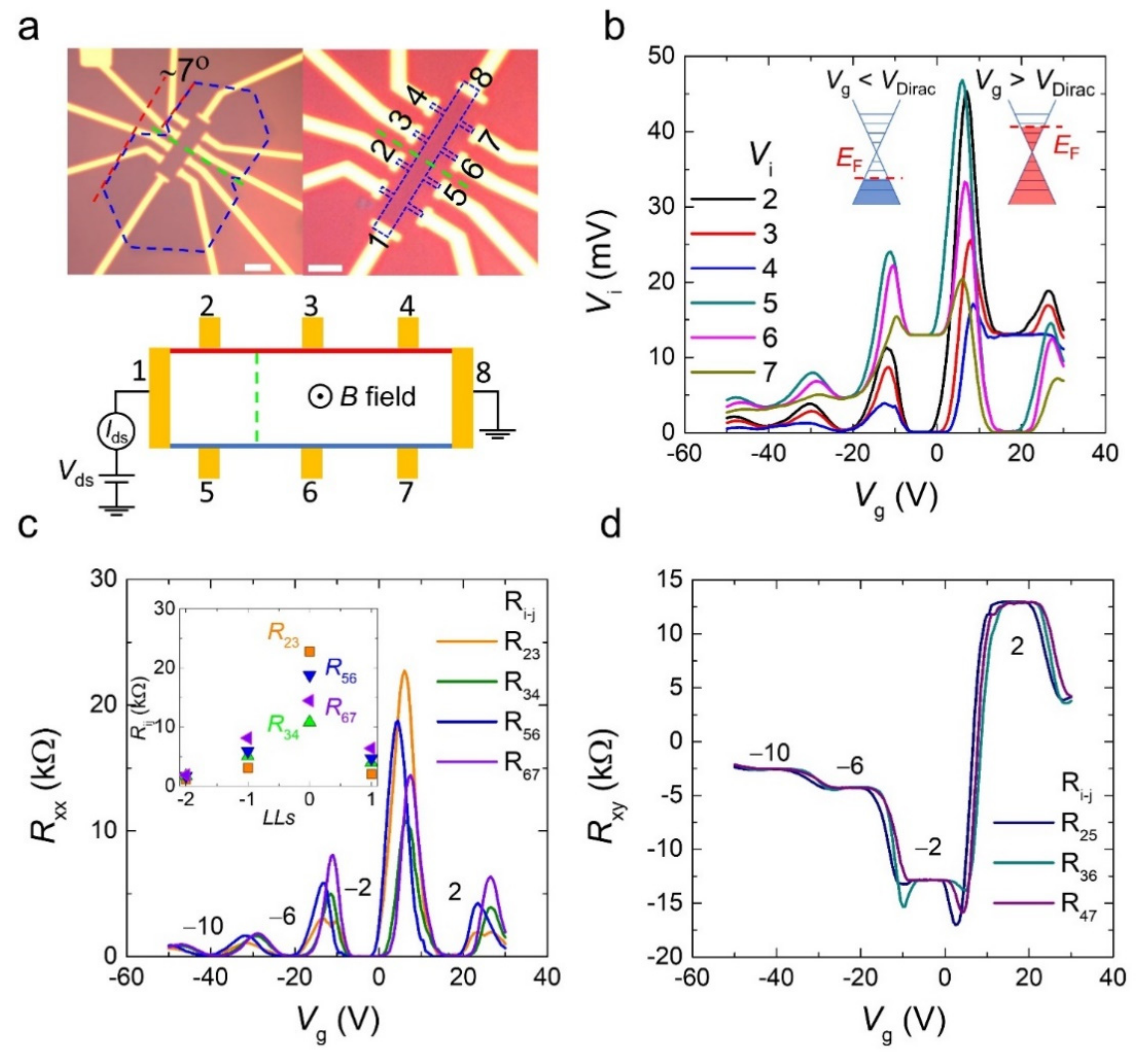
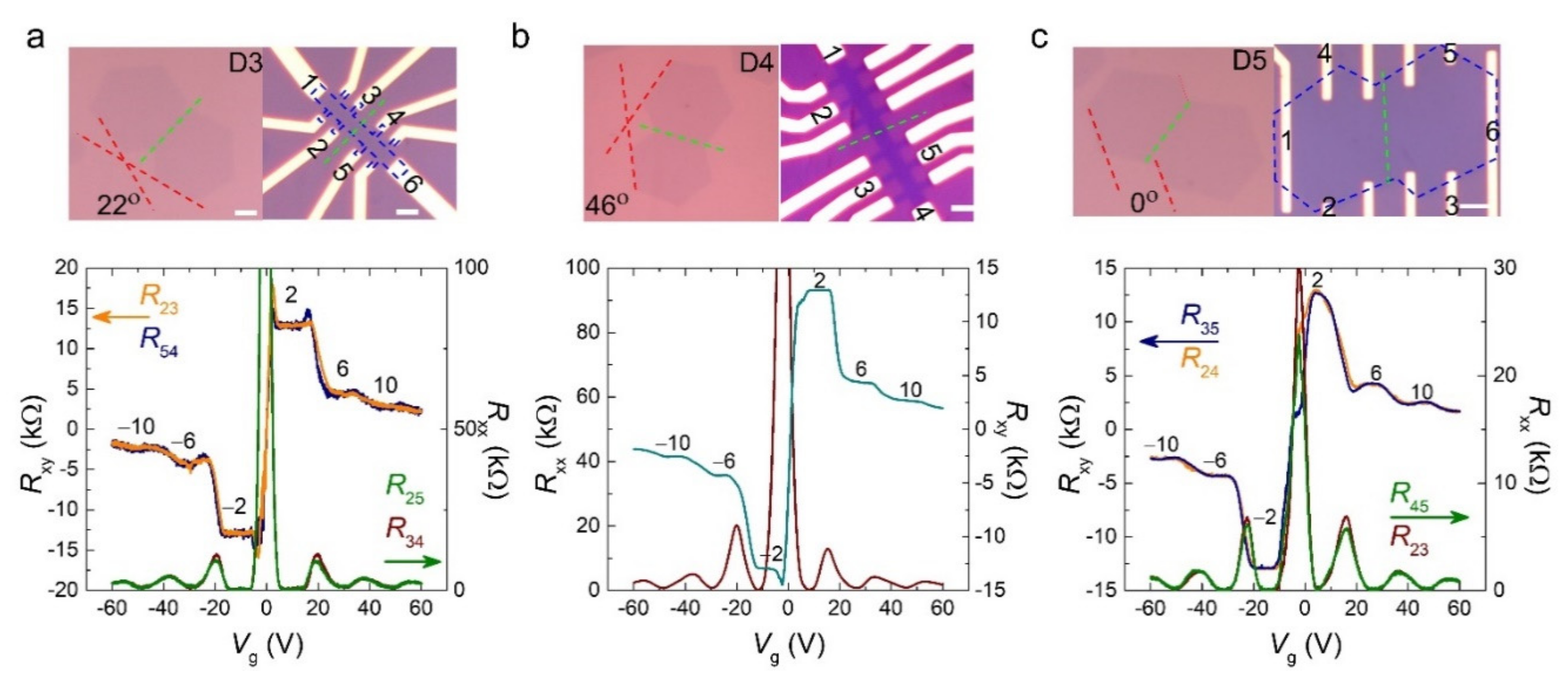
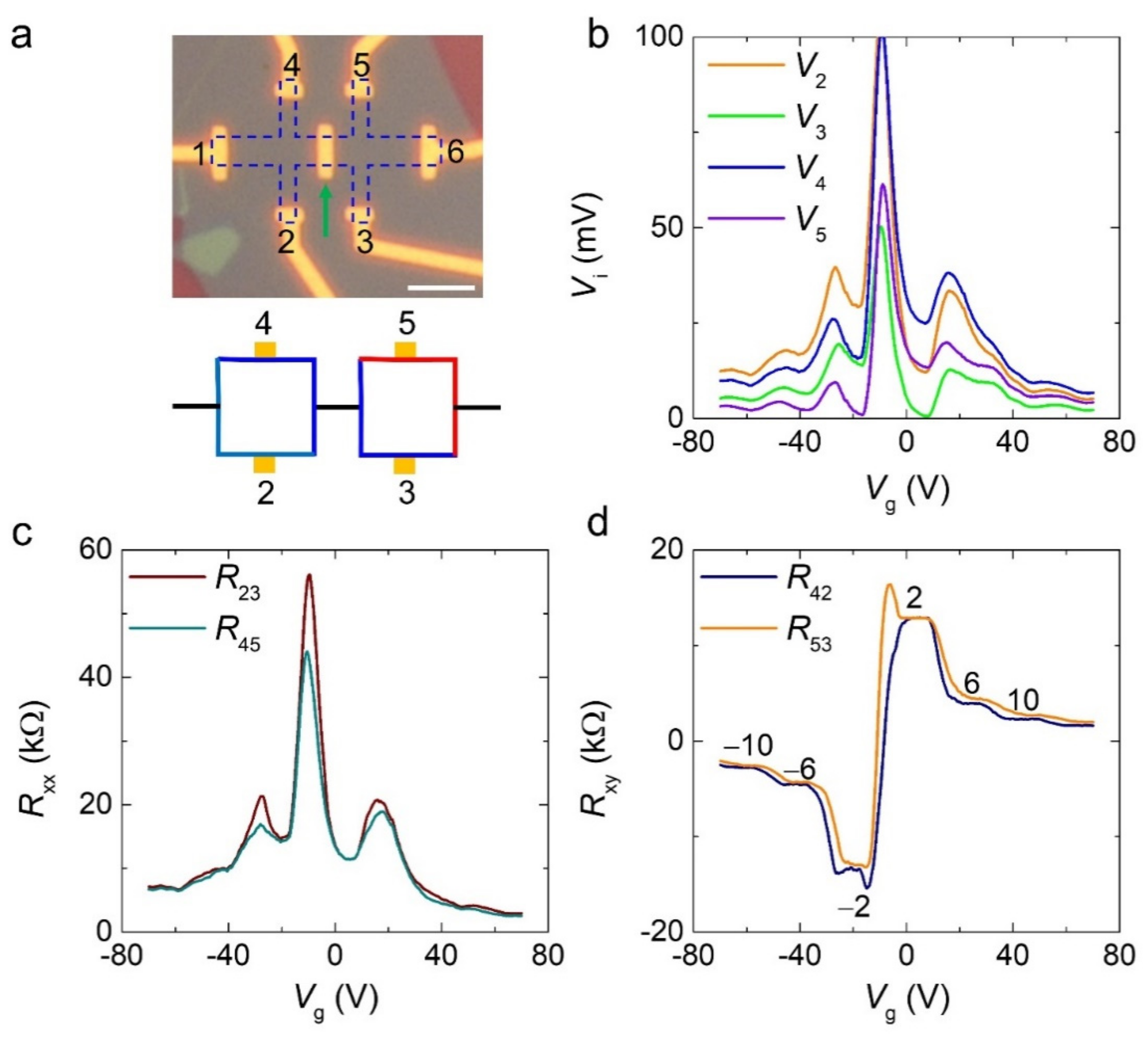
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Koenig, S.P.; Boddeti, N.G.; Dunn, M.L.; Bunch, J.S. Ultrastrong adhesion of graphene membranes. Nat. Nanotechnol. 2011, 6, 543–546. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.-M.; Jenkins, K.A.; Valdes-Garcia, A.; Small, J.P.; Farmer, D.B.; Avouris, P. Operation of graphene transistors at gigahertz frequencies. Nano Lett. 2009, 9, 422–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, Y.B.; Lee, C.S.; Chen, Z.H.; Yuan, G.D.; Kang, Z.H.; Luo, L.B.; Song, H.S.; Liu, Y.; He, Z.B.; Zhang, W.J.; et al. High-quality graphenes via a facile quenching method for field-effect transistors. Nano Lett. 2009, 9, 1374–1377. [Google Scholar] [CrossRef]
- Novoselov, K.S.; McCann, E.; Morozov, S.V.; Fal’ko, V.I.; Katsnelson, M.I.; Zeitler, U.; Jiang, D.; Schedin, F.; Geim, A.K. Unconventional quantum hall effect and berry’s phase of 2π in bilayer graphene. Nat. Phys. 2006, 2, 177–180. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.-W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum hall effect and berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [Green Version]
- Gusynin, V.P.; Sharapov, S.G. Unconventional integer quantum hall effect in graphene. Phys. Rev. Lett. 2005, 95, 146801. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-temperature quantum hall effect in graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Janssen, T.J.; Tzalenchuk, A.; Lara-Avila, S.; Kubatkin, S.; Fal’ko, V.I. Quantum resistance metrology using graphene. Rep. Prog. Phys. 2013, 76, 104501. [Google Scholar] [CrossRef] [PubMed]
- Tzalenchuk, A.; Lara-Avila, S.; Kalaboukhov, A.; Paolillo, S.; Syväjärvi, M.; Yakimova, R.; Kazakova, O.; Janssen, T.J.B.M.; Fal’ko, V.; Kubatkin, S. Towards a quantum resistance standard based on epitaxial graphene. Nat. Nanotechnol. 2010, 5, 186–189. [Google Scholar] [CrossRef]
- Janssen, T.J.B.M.; Rozhko, S.; Antonov, I.; Tzalenchuk, A.; Williams, J.M.; Melhem, Z.; He, H.; Lara-Avila, S.; Kubatkin, S.; Yakimova, R. Operation of graphene quantum hall resistance standard in a cryogen-free table-top system. 2D Mater. 2015, 2, 035015. [Google Scholar] [CrossRef] [Green Version]
- Kang, K.T.; Kang, H.; Park, J.; Suh, D.; Choi, W.S. Quantum conductance probing of oxygen vacancies in srtio3 epitaxial thin film using graphene. Adv. Mater. 2017, 29, 1700071. [Google Scholar] [CrossRef] [PubMed]
- Chau, T.K.; Suh, D.; Kang, H. Detection of hidden localized states by the quantum hall effect in graphene. Curr. Appl. Phys. 2021, 23, 26–29. [Google Scholar] [CrossRef]
- Duong, D.L.; Han, G.H.; Lee, S.M.; Gunes, F.; Kim, E.S.; Kim, S.T.; Kim, H.; Ta, Q.H.; So, K.P.; Yoon, S.J.; et al. Probing graphene grain boundaries with optical microscopy. Nature 2012, 490, 235–239. [Google Scholar] [CrossRef]
- Han, G.H.; Güneş, F.; Bae, J.J.; Kim, E.S.; Chae, S.J.; Shin, H.-J.; Choi, J.-Y.; Pribat, D.; Lee, Y.H. Influence of copper morphology in forming nucleation seeds for graphene growth. Nano Lett. 2011, 11, 4144–4148. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsen, A.W.; Brown, L.; Levendorf, M.P.; Ghahari, F.; Huang, P.Y.; Havener, R.W.; Ruiz-Vargas, C.S.; Muller, D.A.; Kim, P.; Park, J. Tailoring electrical transport across grain boundaries in polycrystalline graphene. Science 2012, 336, 1143–1146. [Google Scholar] [CrossRef] [Green Version]
- Yazyev, O.V.; Louie, S.G. Electronic transport in polycrystalline graphene. Nat. Mater. 2010, 9, 806–809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Tuan, D.; Kotakoski, J.; Louvet, T.; Ortmann, F.; Meyer, J.C.; Roche, S. Scaling properties of charge transport in polycrystalline graphene. Nano Lett. 2013, 13, 1730–1735. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tapasztó, L.; Nemes-Incze, P.; Dobrik, G.; Yoo, K.J.; Hwang, C.; Biró, L.P. Mapping the electronic properties of individual graphene grain boundaries. Appl. Phys. Lett. 2012, 100, 053114. [Google Scholar] [CrossRef] [Green Version]
- Clark, K.W.; Zhang, X.G.; Vlassiouk, I.V.; He, G.; Feenstra, R.M.; Li, A.-P. Spatially resolved mapping of electrical conductivity across individual domain (grain) boundaries in graphene. ACS Nano 2013, 7, 7956–7966. [Google Scholar] [CrossRef] [PubMed]
- Yazyev, O.V.; Louie, S.G. Topological defects in graphene: Dislocations and grain boundaries. Phys. Rev. B 2010, 81, 195420. [Google Scholar] [CrossRef] [Green Version]
- Mesaros, A.; Papanikolaou, S.; Flipse, C.F.J.; Sadri, D.; Zaanen, J. Electronic states of graphene grain boundaries. Phys. Rev. B 2010, 82, 205119. [Google Scholar] [CrossRef] [Green Version]
- Peres, N.M.R.; Guinea, F.; Castro Neto, A.H. Electronic properties of disordered two-dimensional carbon. Phys. Rev. B 2006, 73, 125411. [Google Scholar] [CrossRef] [Green Version]
- Bergvall, A.; Carlsson, J.M.; Löfwander, T. Influence of [1] tilt grain boundaries on the destruction of the quantum hall effect in graphene. Phys. Rev. B 2015, 91, 245425. [Google Scholar] [CrossRef] [Green Version]
- Cummings, A.W.; Cresti, A.; Roche, S. Quantum hall effect in polycrystalline graphene: The role of grain boundaries. Phys. Rev. B 2014, 90, 161401. [Google Scholar] [CrossRef] [Green Version]
- Lafont, F.; Ribeiro-Palau, R.; Han, Z.; Cresti, A.; Delvallée, A.; Cummings, A.W.; Roche, S.; Bouchiat, V.; Ducourtieux, S.; Schopfer, F.; et al. Anomalous dissipation mechanism and hall quantization limit in polycrystalline graphene grown by chemical vapor deposition. Phys. Rev. B 2014, 90, 115422. [Google Scholar] [CrossRef] [Green Version]
- Huang, P.Y.; Ruiz-Vargas, C.S.; van der Zande, A.M.; Whitney, W.S.; Levendorf, M.P.; Kevek, J.W.; Garg, S.; Alden, J.S.; Hustedt, C.J.; Zhu, Y.; et al. Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature 2011, 469, 389–392. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Lee, Z.; Regan, W.; Kisielowski, C.; Crommie, M.F.; Zettl, A. Grain boundary mapping in polycrystalline graphene. ACS Nano 2011, 5, 2142–2146. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y.; Xu, X.; Dubuisson, E.; Bao, Q.; Lu, J.; Loh, K.P. Electrochemical delamination of cvd-grown graphene film: Toward the recyclable use of copper catalyst. ACS Nano 2011, 5, 9927–9933. [Google Scholar] [CrossRef] [PubMed]
- Yoon, D.; Moon, H.; Cheong, H.; Choi, J.S.; Choi, J.A.; Park, B.H. Variations in the raman spectrum as a function of the number of graphene layers. J. Korean Phys. Soc. 2009, 55, 1299–1303. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, Y.; Wang, L.; Ni, Z.; Wang, Z.; Wang, R.; Koo, C.K.; Shen, Z.; Thong, J.T.L. Probing layer number and stacking order of few-layer graphene by raman spectroscopy. Small 2010, 6, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.L.; Shin, B.G.; Duong, D.L.; Kim, S.T.; Perello, D.; Lim, Y.J.; Yuan, Q.H.; Ding, F.; Jeong, H.Y.; Shin, H.S.; et al. Seamless stitching of graphene domains on polished copper (111) foil. Adv. Mater. 2015, 27, 1376–1382. [Google Scholar] [CrossRef]
- Ma, R.; Huan, Q.; Wu, L.; Yan, J.; Guo, W.; Zhang, Y.-Y.; Wang, S.; Bao, L.; Liu, Y.; Du, S.; et al. Direct four-probe measurement of grain-boundary resistivity and mobility in millimeter-sized graphene. Nano Lett. 2017, 17, 5291–5296. [Google Scholar] [CrossRef]
- Cummings, A.W.; Duong, D.L.; Nguyen, V.L.; Van Tuan, D.; Kotakoski, J.; Barrios Vargas, J.E.; Lee, Y.H.; Roche, S. Charge transport in polycrystalline graphene: Challenges and opportunities. Adv. Mater. 2014, 26, 5079–5094. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chau, T.K.; Suh, D.; Kang, H. Quantum Hall Effect across Graphene Grain Boundary. Materials 2022, 15, 8. https://doi.org/10.3390/ma15010008
Chau TK, Suh D, Kang H. Quantum Hall Effect across Graphene Grain Boundary. Materials. 2022; 15(1):8. https://doi.org/10.3390/ma15010008
Chicago/Turabian StyleChau, Tuan Khanh, Dongseok Suh, and Haeyong Kang. 2022. "Quantum Hall Effect across Graphene Grain Boundary" Materials 15, no. 1: 8. https://doi.org/10.3390/ma15010008
APA StyleChau, T. K., Suh, D., & Kang, H. (2022). Quantum Hall Effect across Graphene Grain Boundary. Materials, 15(1), 8. https://doi.org/10.3390/ma15010008






