Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements
Abstract
:1. Introduction
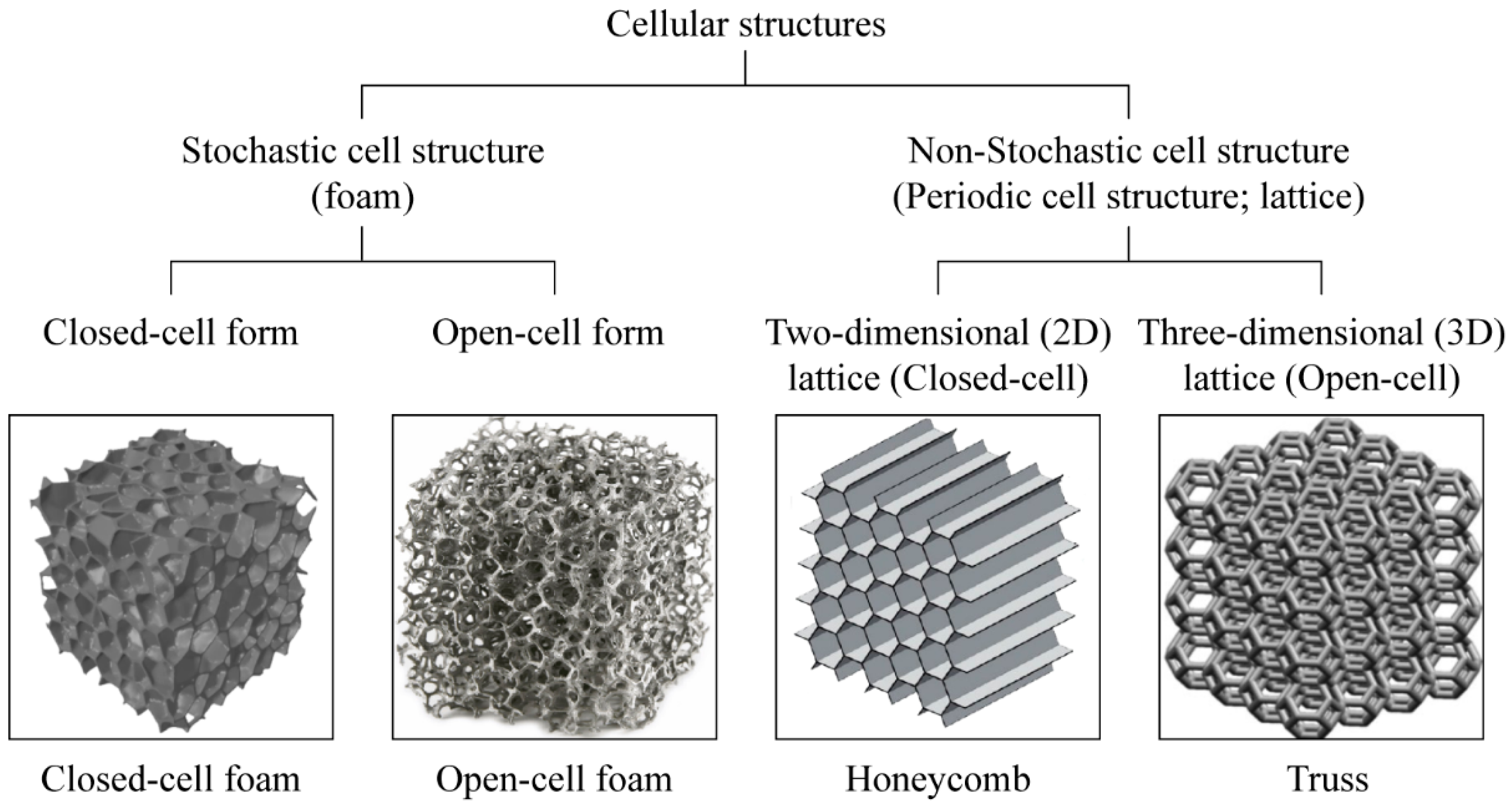
1.1. Structural Lattice
1.2. Additive Manufacturing and Selective Laser Melting
1.3. Research Objectives
- We aimed to develop an approach for the configuration optimization of the lattice structure. AM increases the design freedom, and it remains difficult to design or select an appropriate unit cell topology. In this study, a ground structure topology optimization approach was developed for the unit cell design. Thereafter, we intended to construct and provide a unit cell relative density database according to the box size and circular cross strut radius of the boundary unit cell;
- We aimed to optimize the unit cell arrangement. We modeled the lattice structures by patterning 1 × 1 × 1, 2 × 2 × 2, 3 × 3 × 3, and 4 × 4 × 4 unit cells to derive the yield strength in order to identify the mechanical properties of the lattice structures. In this study, we only focused on lattice structures with dimensions of 20 mm × 20 mm × 20 mm;
- We aimed to derive an optimal lattice structure consisting of the optimal unit cell obtained using the abovementioned steps under axial compressive loading conditions because the choice of the appropriate lattice topology is a major challenge in lattice adoption.
2. Materials and Methods
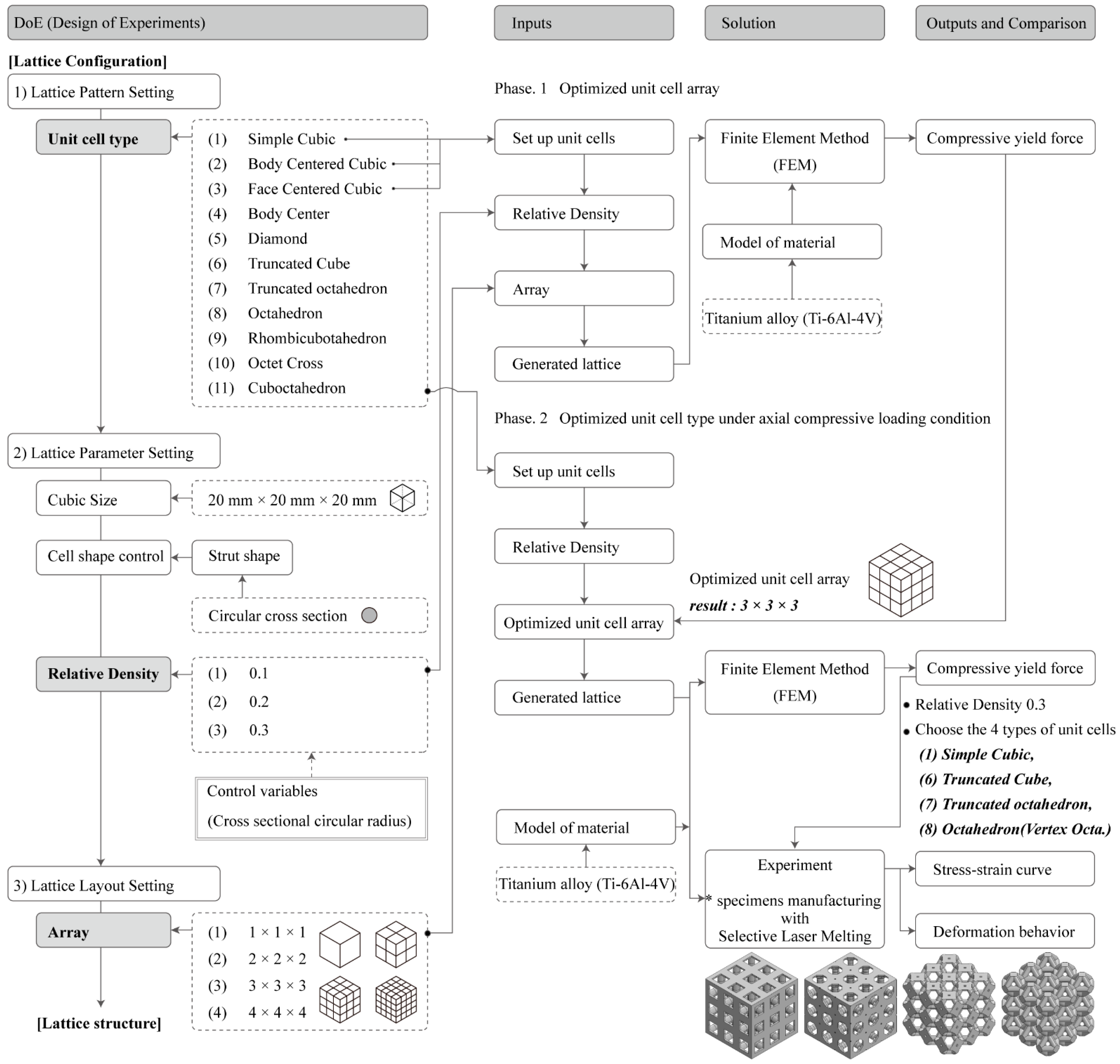
2.1. Lattice Configuration
2.1.1. Lattice Pattern Setting
2.1.2. Lattice Parameter Setting
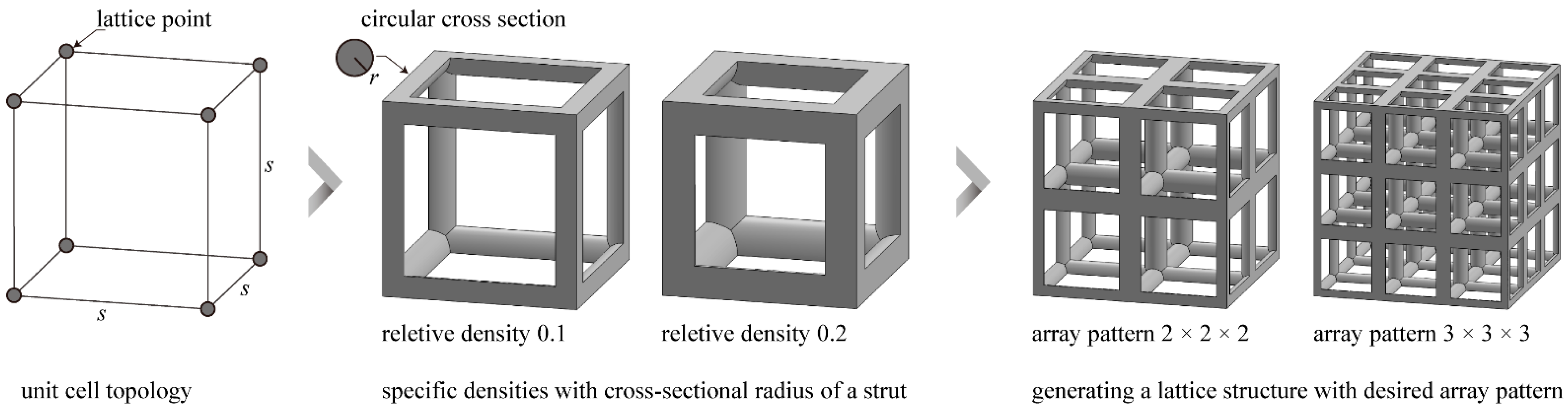
- Lattice-structured cubes with nominal dimensions of 20 mm × 20 mm × 20 mm were designed. A specific unit cell was then designed in the cube ();
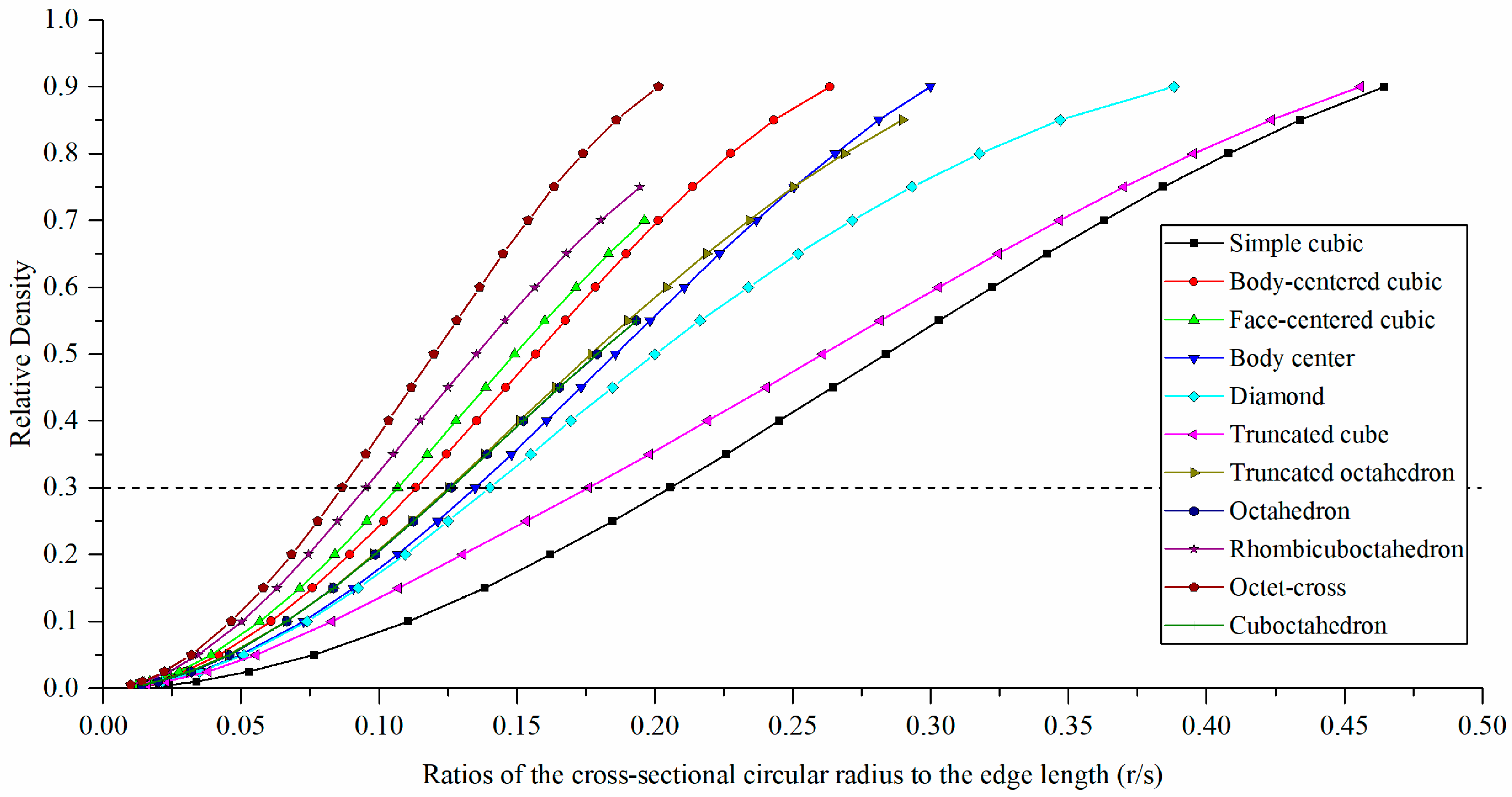
- The unit cell strut was created in a circular cross-section to generate a volume in the lattice structure. Specific relative density was designed by controlling (Figure 3).
2.1.3. Lattice Layout Setting
2.2. Optimizing Unit Cell Array
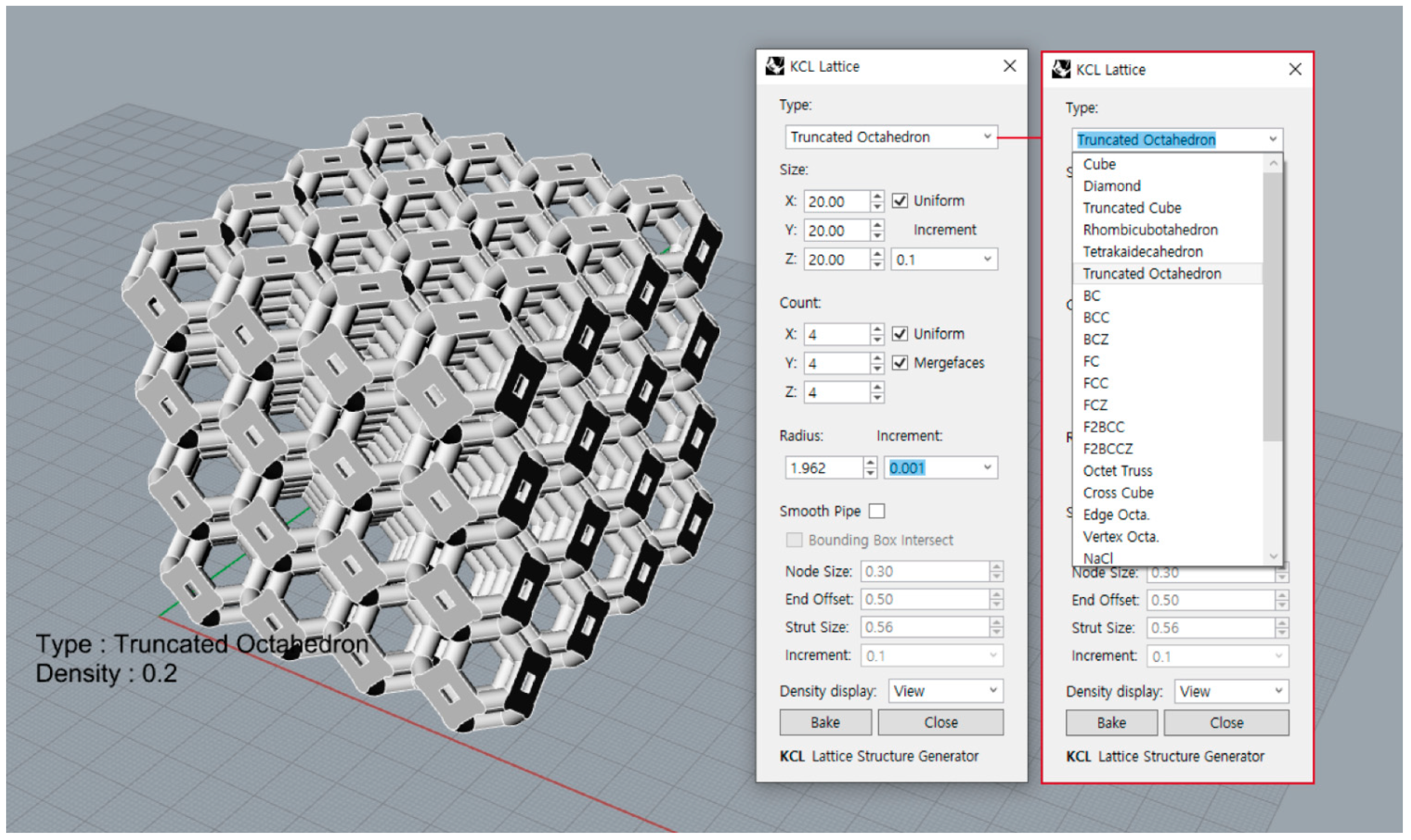
2.2.1. Numerical Modeling
2.2.2. Numerical Simulation
2.3. Optimization of Unit Cell Type under Axial Compressive Loading Condition
2.3.1. Numerical Modeling
2.3.2. Experimental Tests
3. Results and Discussion
3.1. Lattice Configuration
3.2. Optimizing Unit Cell Array
3.3. Optimization of Unit Cell Type under Axial Compressive Loading Condition
4. Conclusions
- 1.
- The unit cell topologies of the lattice structures were designed as described in Section 3.1 by determining ratios. It was possible to control the relative density of the unit cells using the datasheet. The lattice structure was created from an array of repeated unit cells using direct patterning, in which the unit cells were directly generated by repeating the unit cells in three dimensions;
- 2.
- Under the same unit cell type and arrangement conditions, an increase in the relative density significantly enhanced the yield force of the lattice structure;
- 3.
- The yield force of the lattice structure was optimal for the 3 × 3 × 3 pattern. These results indicated that, at a constant relative density, the yield force could be optimized by configuring the lattice structure through the pattern design;
- 4.
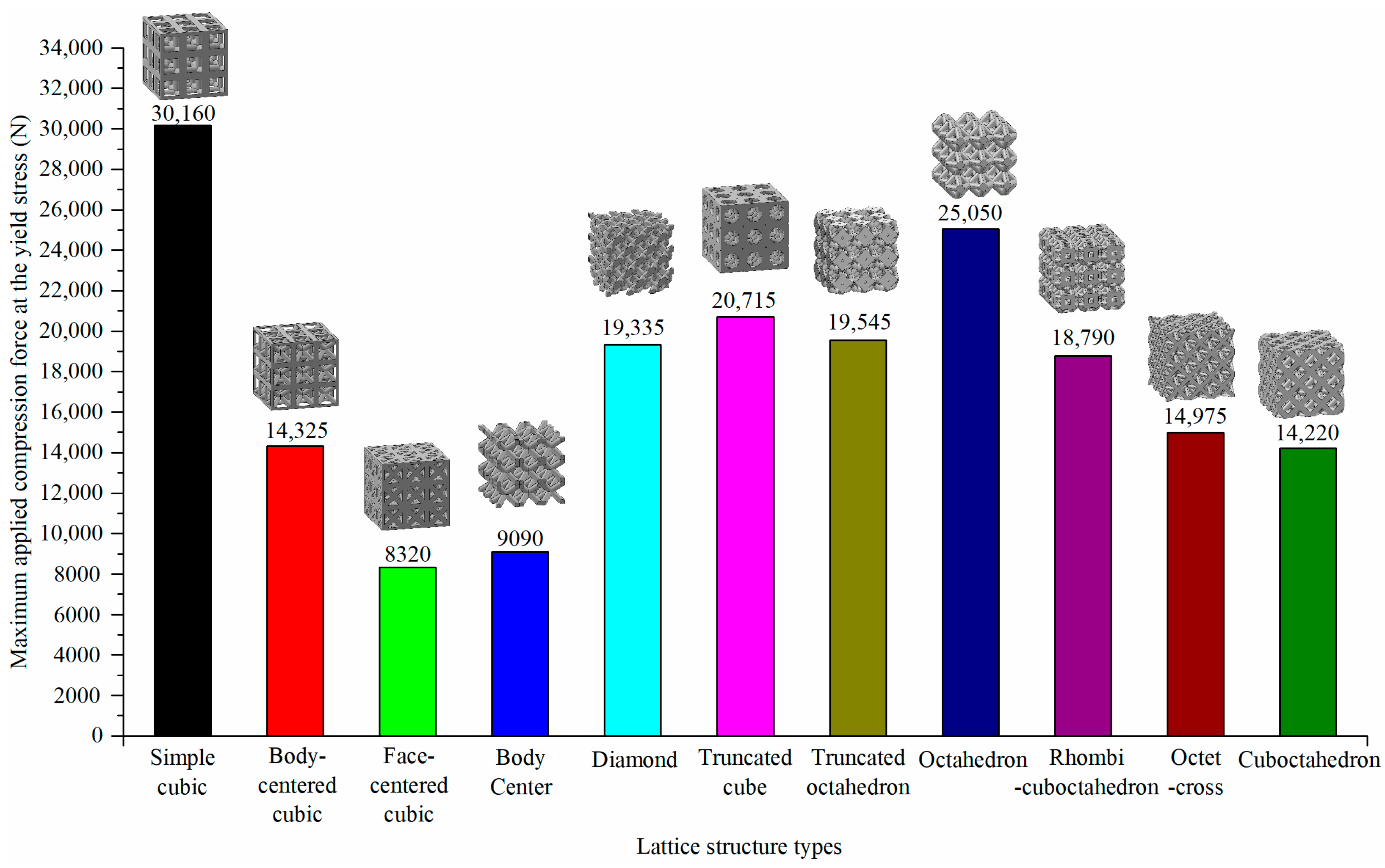
- Simple cubic, octahedron, truncated cube, and truncated octahedron lattice structures exhibited higher axial compression yield forces compared with body-centered cubic, face-centered cubic, body center, diamond, rhombicuboctahedron, octet-cross, and cuboctahedron structures with the same relative density, indicating that these four lattice structures had better mechanical properties under axial compression conditions;
- 5.
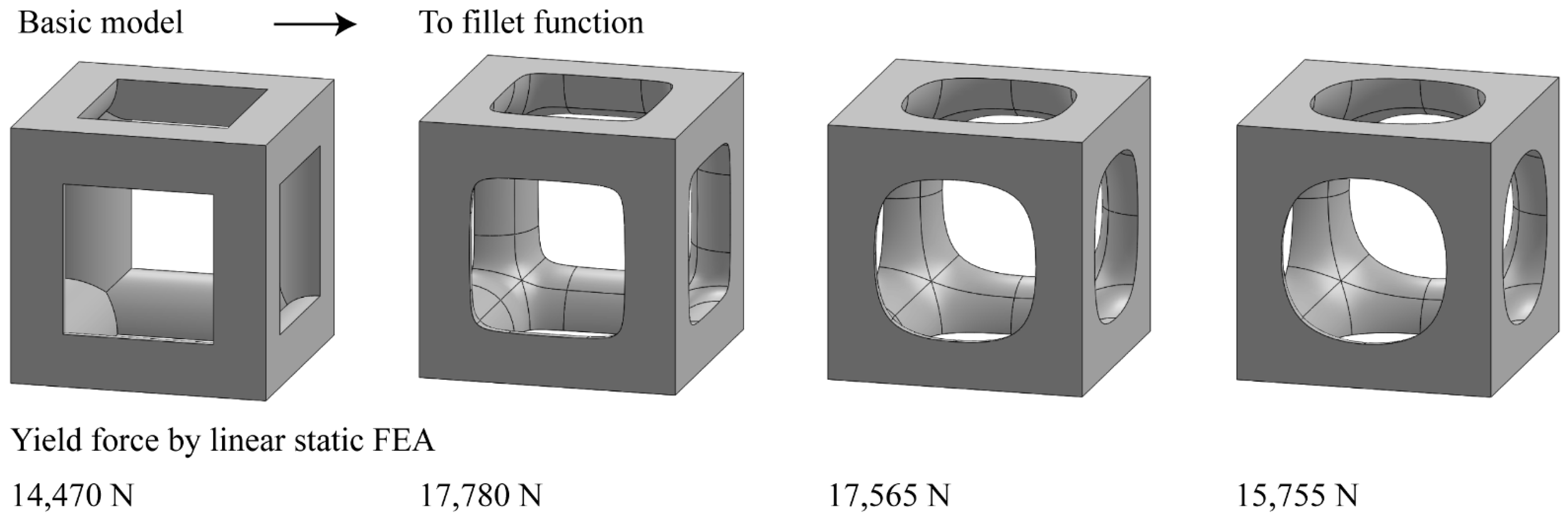
- Under a compressive load, the initial fracture of the lattice structures occurred at the locations where stress was concentrated. Therefore, when nodes and struts were introduced and under conditions of fillet optimization, the stress concentration were released and re-distributed. At the same time, the compressive strength increased with the optimized node, strut, and fillet design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F.; Brendan, A.H. Cellular Materials in Nature and Medicine, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Ma, Q.; Rejab, M.; Siregar, J.; Guan, Z. A Review of the Recent Trends on Core Structures and Impact Response of Sandwich Panels. J. Compos. Mater. 2021, 55, 2513–2555. [Google Scholar] [CrossRef]
- Jin, F.L.; Zhao, M.; Park, M.; Park, S.J. Recent Trends of Foaming in Polymer Processing: A Review. Polymers 2019, 11, 953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarlochan, F. Sandwich Structures for Energy Absorption Applications: A Review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge Solid State Science Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Dossi, M.; Brennan, M.; Moesen, M. A Multi-Physics Study of the Wave Propagation Problem in Open Cell Polyurethane Foams. In Proceedings of the COMSOL International Conference, Rotterdam, The Netherlands, 18–20 October 2017. [Google Scholar]
- Lehmhus, D.; Vesenjak, M.; Schampheleire, S.D.; Fiedler, T. From Stochastic Foam to Designed Structure: Balancing Cost and Performance of Cellular Metals. Met. Mater. 2017, 10, 922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, C.; Han, Y.; Lu, J. Design and Optimization of Lattice Structures: A Review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; McMillan, M.; Sun, S.; Shidid, D.; Brandt, D. Mechanical Properties of Ti6Al4V and AlSi12Mg Lattice Structures Manufactured by Selective Laser Melting (SLM). In Woodhead Publishing Series in Electronic and Optical Materials; Laser Additive Manufacturing; Woodhead Publishing: Cambridge, UK, 2017; Volume 5, pp. 119–161. [Google Scholar] [CrossRef]
- Cao, X.; Duan, S.; Liang, J.; Wen, W.; Fang, D. Mechanical Properties of an Improved 3D-Printed Rhombic Dodecahedron Stainless Steel Lattice Structure of Variable Cross Section. Int. J. Mech. Sci. 2018, 145, 53–63. [Google Scholar] [CrossRef]
- Xiao, D.; Dong, Z.; Li, Y.; Wu, W.; Fang, D. Compression Behavior of the Graded Metallic Auxetic Reentrant Honeycomb: Experiment and Finite Element Analysis. Mater. Sci. Eng. A 2019, 758, 163–171. [Google Scholar] [CrossRef]
- Barynin, V.A.; Bunakov, V.A.; Rasin, A.F.; Vasiliev, V.V. Aerospace Composite Lattice Structures. In Proceedings of the 120th International Conference on Composite Materials, Paris, France, 5–9 July 1999. [Google Scholar]
- Vasiliev, V.V.; Razin, A.F. Anisogrid Composite Lattice Structures for Spacecraft and Aircraft Applications. Compos. Struct. 2006, 76, 182–189. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam Topology: Bending Versus Stretching Dominated Architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Queheillalt, D.T.; Murty, Y.; Wadley, H.N.G. Mechanical Properties of an Extruded Pyramidal Lattice Truss Sandwich Structure. Scr. Mater. 2008, 58, 76–79. [Google Scholar] [CrossRef]
- ASTM F2792-12. Standard Terminology for Additive Manufacturing Technologies; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Alsalla, H.; Hao, L.; Smith, C. Fracture Toughness and Tensile Strength of 316L Stainless Steel Cellular Lattice Structures Manufactured Using the Selective Laser Melting Technique. Mater. Sci. Eng. A 2016, 669, 1–6. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P. Ti–6Al–4V Triply Periodic Minimal Surface Structures for Bone Implants Fabricated via Selective Laser Melting. J. Mech. Behav. Biomed. Mater. 2015, 51, 61–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gong, H.; Rafi, K.; Gu, H.; Janaki Ram, G.D.J.; Starr, T.; Stucker, B. Influence of Defects on Mechanical Properties of Ti–6Al–4 V Components Produced by Selective Laser Melting and Electron Beam Melting. Mater. Des. 2015, 86, 545–554. [Google Scholar] [CrossRef]
- Sterling, A.J.; Torries, B.; Shamsaei, N.; Thompson, S.M.; Seely, D.W. Fatigue Behavior and Failure Mechanisms of Direct Laser Deposited Ti–6Al–4V. Mater. Sci. Eng. A 2016, 655, 100–112. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Bubb, S.L.; Young, P.; Raymont, D. Evaluation of Light-Weight AlSi10Mg Periodic Cellular Lattice Structures Fabricated via Direct Metal Laser Sintering. J. Mater. Process. Technol. 2014, 214, 856–864. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Young, P.; Huang, J.; Zhu, W. Microstructure and Mechanical Properties of Aluminium Alloy Cellular Lattice Structures Manufactured by Direct Metal Laser Sintering. Mater. Sci. Eng. A 2015, 628, 238–246. [Google Scholar] [CrossRef]
- Brandt, M. (Ed.) Laser Additive Manufacturing: Materials, Design, Technologies, and Applications; Woodhead Publishing: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Trupiano, S.; Vivio, F. Multiscale Analysis and Mechanical Characterization of Open-cell Foams by Simplified FE Modeling. Eur. J. Mech. A/Solids 2021, 89, 104291. [Google Scholar] [CrossRef]
- Dumas, M.; Terriault, P.; Brailovski, V. Modelling and Characterization of a Porosity Graded Lattice Structure for Additively Manufactured Biomaterials. Mater. Des. 2017, 121, 383–392. [Google Scholar] [CrossRef]
- De Aquino, D.A.; Maskery, I.; Longhitano, G.A.; Jardini, A.L.; del Conte, E.G. Investigation of Load Direction on the Compressive Strength of Additively Manufactured Triply Periodic Minimal Surface Scaffolds. Int. J. Adv. Manuf. Technol. 2020, 109, 771–779. [Google Scholar] [CrossRef]
- Cutolo, A.; Engelen, B.; Desmet, W.; Van Hooreweder, B. Mechanical Properties of Diamond Lattice Ti–6Al–4V Structures Produced by Laser Powder Bed Fusion: On the Effect of the Load Direction. J. Mech. Behav. Biomed. Mater. 2020, 104, 103656. [Google Scholar] [CrossRef]
- Liu, L.; Kamm, P.; García-Moreno, F.; Banhart, J.; Pasini, D. Elastic and Failure Response of Imperfect Three-Dimensional Metallic Lattices: The Role of Geometric Defects Induced by Selective Laser Melting. J. Mech. Phys. Solids 2017, 107, 160–184. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Yavari, S.A.; Wauthle, R.; Pouran, B.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Additively Manufactured Open-Cell Porous Biomaterials Made from Six Different Space-Filling Unit Cells: The Mechanical and Morphological Properties. Materials 2015, 8, 1871–1896. [Google Scholar] [CrossRef] [Green Version]
- Borleffs, M.S. Finite Element Modeling to Predict Bulk Mechanical Properties of 3D Printed Metal Foams; TU: Delft, The Netherlands, 2012; Available online: http://resolver.tudelft.nl/uuid:551dee76-2301-4f77-ba6e-230d32e8c58f (accessed on 17 December 2021).
- Choy, S.Y.; Sun, C.-N.; Leong, K.F.; Wei, J. Compressive Properties of Ti-6Al-4V Lattice Structures Fabricated by Selective Laser Melting: Design, Orientation and Density. Addit. Manuf. 2017, 16, 213–224. [Google Scholar] [CrossRef]
- Han, C.; Yan, C.; Wen, S.; Xu, T.; Li, S.; Liu, J.; Wei, Q.; Shi, Y. Effects of the Unit Cell Topology on the Compression Properties of Porous Co-Cr Scaffolds Fabricated via Selective Laser Melting. Rapid Prototyp. J. 2017, 23, 16–27. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Hosseini-Toudeshky, H. Comparison of Elastic Properties of Open-Cell Metallic Biomaterials with Different Unit Cell Types. J. Biomed. Mater. Res. B Appl. Biomater. 2018, 106, 386–398. [Google Scholar] [CrossRef] [Green Version]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Effect of Mass Multiple Counting on the Elastic Properties of Open-Cell Regular Porous Biomaterials. Mater. Des. 2016, 89, 9–20. [Google Scholar] [CrossRef]
- Li, S.J.; Xu, Q.S.; Wang, Z.; Hou, W.T.; Hao, Y.L.; Yang, R.; Murr, L.E. Influence of Cell Shape on Mechanical Properties of Ti–6Al–4V Meshes Fabricated by Electron Beam Melting Method. Acta Biomater. 2014, 10, 4537–4547. [Google Scholar] [CrossRef] [PubMed]
- Murr, L.E.; Gaytan, S.M.; Medina, F.; Lopez, H.; Martinez, E.; Machado, B.I.; Hernandez, D.H.; Martinez, L.; Lopez, M.I.; Wicker, R.B.; et al. Next-Generation Biomedical Implants Using Additive Manufacturing of Complex, Cellular and Functional Mesh Arrays. Philos. Trans. R. Soc. Lond. A 2010, 368, 1999–2032. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical Evaluation of Porous Titanium (Ti6Al4V) Structures with Electron Beam Melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Zaharin, H.A.; Abdul Rani, A.M.; Azam, F.I.; Ginta, T.L.; Sallih, N.; Ahmad, A.; Yunus, N.A.; Zulkifli, T.Z.A. Effect of Unit Cell Type and Pore Size on Porosity and Mechanical Behavior of Additively Manufactured Ti6Al4V Scaffolds. Materials 2018, 11, 2402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, S.; Li, S.J.; Hou, W.T.; Hao, Y.L.; Yang, R.; Misra, R.D.K. The Influence of Cell Morphology on the Compressive Fatigue Behavior of Ti-6Al-4V Meshes Fabricated by Electron Beam Melting. J. Mech. Behav. Biomed. Mater. 2016, 59, 251–264. [Google Scholar] [CrossRef]
- Egan, P.F.; Gonella, V.C.; Engensperger, M.; Ferguson, S.J.; Shea, K. Computationally Designed Lattices with Tuned Properties for Tissue Engineering Using 3D Printing. PLoS ONE 2017, 12, e0182902. [Google Scholar] [CrossRef]
- Boniotti, L.; Foletti, S.; Beretta, S.; Patriarca, L. Analysis of Strain and Stress Concentrations in Micro-Lattice Structures Manufactured by SLM. Rapid Prototyp. J. 2019, 26, 370–380. [Google Scholar] [CrossRef]
- Egan, P.; Wang, X.; Greutert, H.; Shea, K.; Wuertz-Kozak, K.; Ferguson, S. Mechanical and Biological Characterization of 3D Printed Lattices. 3D Print. Addit. Manuf. 2019, 6, 73–81. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective Laser Melting (SLM) of AlSi12Mg Lattice Structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Williams, H.; Yang, E.; Alghamdi, A.; Lozanovski, B.; Zhang, X.; Shidid, D.; Farahbod-Sternahl, L.; Witt, G.; et al. Inconel 625 Lattice Structures Manufactured by Selective Laser Melting (SLM): Mechanical Properties, Deformation and Failure Modes. Mater. Des. 2018, 157, 179–199. [Google Scholar] [CrossRef]
- Rehme, O.; Emmelmann, C. Rapid Manufacturing of Lattice Structures with Selective Laser Melting. In Laser-Based Micropackaging, Proceedings of the Lasers and Applications in Science and Engineering, San Jose, CA, USA, 23 February 2006; International Society for Optics and Photonics: San Diego, CA, USA, 2006; p. 61070K. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W. Compressive Behaviour of Stainless Steel Micro-Lattice Structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W.; Karadeniz, S. Static Mechanical Behaviours of Stainless Steel Micro-Lattice Structures under Different Loading Conditions. Mater. Sci. Eng. A 2013, 586, 392–406. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of Compressive Properties of SLM-Fabricated Multi-Layer Lattice Structures by Experimental Test and μ-CT-Based Finite Element Analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Mazur, M.; Leary, M.; Sun, S.; Vcelka, M.; Shidid, D.; Brandt, M. Deformation and Failure Behaviour of Ti-6Al-4V Lattice Structures Manufactured by Selective Laser Melting (SLM). Int. J. Adv. Manuf. Technol. 2016, 84, 1391–1411. [Google Scholar] [CrossRef]
- McKown, S.; Shen, Y.; Brookes, W.K.; Sutcliffe, C.J.; Cantwell, W.J.; Langdon, G.S.; Nurick, G.N.; Theobald, M.D. The quasi-Static and Blast Loading Response of Lattice Structures. Int. J. Impact Eng. 2008, 35, 795–810. [Google Scholar] [CrossRef]
- Mines, R.A.W.; Tsopanos, S.; Shen, Y.; Hasan, R.; McKown, S.T. Drop Weight Impact Behaviour of Sandwich Panels with Metallic Micro Lattice Cores. Int. J. Impact Eng. 2013, 60, 120–132. [Google Scholar] [CrossRef] [Green Version]
- Mullen, L.; Stamp, R.C.; Brooks, W.K.; Jones, E.; Sutcliffe, C.J. Selective Laser Melting: A Regular Unit Cell Approach for the Manufacture of Porous, Titanium, Bone in-Growth Constructs, Suitable for Orthopedic Applications. J. Biomed. Mater. Res. B 2009, 89, 325–334. [Google Scholar] [CrossRef] [PubMed]
- Ptochos, E.; Labeas, G. Elastic Modulus and Poisson’s Ratio Determination of Micro-Lattice Cellular Structures by Analytical, Numerical and Homogenisation Methods. J. Sandw. Struct. Mater. 2012, 14, 597–626. [Google Scholar] [CrossRef]
- Shen, Y.; Mckown, S.; Tsopanos, S.; Sutcliffe, C.J.; Mines, R.A.W.; Cantwell, W.J. The Mechanical Properties of Sandwich Structures Based on Metal Lattice Architectures. J. Sandw. Struct. Mater. 2010, 12, 159–180. [Google Scholar] [CrossRef]
- Smith, M.; Guan, Z.; Cantwell, W.J. Finite Element Modelling of the Compressive Response of Lattice Structures Manufactured Using the Selective Laser Melting Technique. Int. J. Mech. Sci. 2013, 67, 28–41. [Google Scholar] [CrossRef]
- Tsopanos, S.; Mines, R.A.W.; McKown, S.; Shen, Y.; Cantwell, W.J.; Brooks, W.; Sutcliffe, C.J. The Influence of Processing Parameters on the Mechanical Properties of Selectively Laser Melted Stainless Steel Microlattice Structures. J. Manuf. Sci. Eng. 2010, 132, 4. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.J.; Chen, D.H. Prediction of the Mechanical Properties of Micro-Lattice Structures Subjected to Multi-Axial Loading. Int. J. Mech. Sci. 2013, 68, 47–55. [Google Scholar] [CrossRef]
- Ushijima, K.; Cantwell, W.; Mines, R.; Tsopanos, S.; Smith, M. An Investigation into the Compressive Properties of Stainless Steel Micro-Lattice Structures. J. Sandw. Struct. Mater. 2011, 13, 303–329. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [Green Version]
- Heinl, P.; Müller, L.; Körner, C.; Singer, R.F.; Müller, F.A. Cellular Ti–6Al–4V Structures with Interconnected Macro Porosity for Bone Implants Fabricated by Selective Electron Beam Melting. Acta Biomater. 2008, 4, 1536–1544. [Google Scholar] [CrossRef] [PubMed]
- Heinl, P.; Körner, C.; Singer, R.F. Selective Electron Beam Melting of Cellular Titanium: Mechanical Properties. Adv. Eng. Mater. 2008, 10, 882–888. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy Absorption in Lattice Structures in Dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef] [Green Version]
- Van Grunsven, W.; Hernandez-Nava, E.; Reilly, G.C.; Goodall, R. Fabrication and Mechanical Characterisation of Titanium Lattices with Graded Porosity. Metals 2014, 4, 401–409. [Google Scholar] [CrossRef]
- Wauthle, R.; Vrancken, B.; Beynaerts, B.; Jorissen, K.; Schrooten, J.; Kruth, J.P.; Van Humbeeck, J. Effects of Build Orientation and Heat Treatment on the Microstructure and Mechanical Properties of Selective Laser Melted Ti6Al4V Lattice Structures. Addit. Manuf. 2015, 5, 77–84. [Google Scholar] [CrossRef]
- Zadpoor, A.A.; Hedayati, R. Analytical Relationships for Prediction of the Mechanical Properties of Additively Manufactured Porous Biomaterials. J. Biomed. Mater. Res. A 2016, 104, 3164–3174. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.X.; Knott, J.F.; Mills, N.J. Analysis of the Elastic Properties of Open-Cell Foams with Tetrakaidecahedral Cells. J. Mech. Phys. Solids 1997, 45, 319–343. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Analytical Relationships for the Mechanical Properties of Additively Manufactured Porous Biomaterials Based on Octahedral Unit Cells. Appl. Math. Modell. 2017, 46, 408–422. [Google Scholar] [CrossRef] [Green Version]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Mechanics of Additively Manufactured Porous Biomaterials Based on the Rhombicuboctahedron Unit Cell. J. Mech. Behav. Biomed. Mater. 2016, 53, 272–294. [Google Scholar] [CrossRef]
- Arabnejad, S.; Burnett Johnston, R.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-Strength Porous Biomaterials for Bone Replacement: A Strategy to Assess the Interplay between Cell Morphology, Mechanical Properties, Bone Ingrowth and Manufacturing Constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef] [Green Version]
- De Formanoir, C.; Suard, M.; Dendievel, R.; Martin, G.; Godet, S. Improving the Mechanical Efficiency of Electron Beam Melted Titanium Lattice Structures by Chemical Etching. Addit. Manuf. 2016, 11, 71–76. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective Properties of the Octet-Truss Lattice Material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef] [Green Version]
- He, Z.Z.; Wang, F.C.; Zhu, Y.B.; Wu, H.A.; Park, H.S. Mechanical Properties of Copper Octet-Truss Nanolattices. J. Mech. Phys. Solids 2017, 101, 133–149. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively Manufactured Metallic Micro-Lattice Materials for High Specific Energy Absorption under Static and Dynamic Loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- ISO 13314:2011. Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals; The International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- Červinek, O.; Werner, B.; Koutný, D.; Vaverka, O.; Pantělejev, L.; Paloušek, D. Computational Approaches of Quasi-Static Compression Loading of SS316L Lattice Structures Made by Selective Laser Melting. Materials 2021, 14, 2462. [Google Scholar] [CrossRef]
- Amani, Y.; Dancette, S.; Delroisse, P.; Simar, A.; Maire, E. Compression Behavior of Lattice Structures Produced by Selective Laser Melting: X-ray Tomography Based Experimental and Finite Element Approaches. Acta Mater. 2018, 159, 395–407. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Zheng, J.; Yang, J.; Li, K.; Sun, Y. Heterogeneous Compressive Responses of Additively Manufactured Ti-6Al-4V Lattice Structures by Varying Geometric Parameters of Cells. Int. J. Mech. Sci. 2022, 214, 106922. [Google Scholar] [CrossRef]
- ASTM B988-18. Standard Specification for Powder Metallurgy (PM) Titanium and Titanium Alloy Structural Components; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- ASTM F2924-14. Standard Specification for Additive Manufacturing Titanium-6 Aluminum-4 Vanadium with Powder Bed Fusion; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Ashby, M.F. The Properties of Foams and Lattices. Philos. Trans. R. Soc. Lond. A 2006, 364, 15–30. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive Failure Modes and Energy Absorption in Additively Manufactured Double Gyroid Lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]





| Unit Cell Topology | Image 1 | Unit Cell Topology | Image 1 |
|---|---|---|---|
| Simple cubic [29,30,31,32,33,34,35,36,37,38,39] |  | Body-centered cubic [40,41,42] | 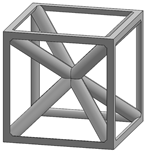 |
| Face-centered cubic [43,44,45] |  | Body center [32,43,44,46,47,48,49,50,51,52,53,54,55,56,57,58,59] |  |
| Diamond [29,30,33,34,60,61,62,63,64] |  | Truncated cube [29,65] |  |
| Truncated octahedron (a.k.a. Kelvin) [30,33,34,65,66] | 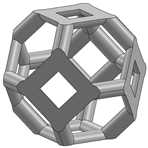 | Octahedron [65,67] |  |
| Rhombicuboctahedron [29,65,68] | 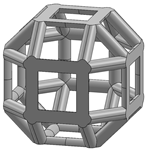 | Octet-cross (a.k.a. octet-truss) [69,70,71,72,73] |  |
| Cuboctahedron [29,65] |  |
| Simple Cubic | Body-Centered Cubic | Face-Centered Cubic | Body Center | Diamond | Truncated Cube | Truncated Octahedron | Octahedron | Rhombicuboctahedron | Octet-cross | Cuboctahedron | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Total nodes | 97,644 | 136,270 | 137,365 | 105,205 | 131,167 | 155,709 | 145,548 | 159,411 | 166,543, | 179,549 | 119,672 |
| Total elements | 57,512 | 77,665 | 77,719 | 60,962 | 78,211 | 96,331 | 83,908 | 98,685 | 93,887 | 100,727 | 68,796 |
| Relative Density | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simple Cubic | Body-centered Cubic | Face-Centered Cubic | Body Center | Diamond | Truncated cube | Truncated Octahedron | Octahedron | Rhombicuboctahedron | Octet-cross | Cuboctahedron | |
| 0.005 | 0.024 | 0.013 | 0.012 | 0.015 | 0.015 | 0.016 | 0.014 | 0.014 | 0.010 | 0.010 | 0.015 |
| 0.010 | 0.034 | 0.018 | 0.017 | 0.022 | 0.022 | 0.023 | 0.020 | 0.020 | 0.015 | 0.014 | 0.020 |
| 0.025 | 0.053 | 0.030 | 0.028 | 0.035 | 0.035 | 0.038 | 0.032 | 0.032 | 0.024 | 0.022 | 0.032 |
| 0.050 | 0.077 | 0.042 | 0.039 | 0.050 | 0.051 | 0.056 | 0.046 | 0.046 | 0.035 | 0.032 | 0.046 |
| 0.100 | 0.111 | 0.061 | 0.057 | 0.073 | 0.074 | 0.083 | 0.067 | 0.067 | 0.050 | 0.047 | 0.067 |
| 0.150 | 0.138 | 0.076 | 0.071 | 0.091 | 0.093 | 0.107 | 0.083 | 0.084 | 0.063 | 0.058 | 0.084 |
| 0.200 | 0.162 | 0.090 | 0.084 | 0.107 | 0.110 | 0.131 | 0.098 | 0.099 | 0.075 | 0.068 | 0.099 |
| 0.250 | 0.185 | 0.102 | 0.096 | 0.121 | 0.125 | 0.154 | 0.112 | 0.113 | 0.085 | 0.078 | 0.113 |
| 0.300 | 0.206 | 0.113 | 0.107 | 0.135 | 0.140 | 0.176 | 0.125 | 0.126 | 0.095 | 0.087 | 0.126 |
| 0.350 | 0.226 | 0.125 | 0.118 | 0.148 | 0.155 | 0.198 | 0.138 | 0.139 | 0.105 | 0.095 | 0.139 |
| 0.400 | 0.245 | 0.135 | 0.128 | 0.161 | 0.170 | 0.219 | 0.151 | 0.152 | 0.115 | 0.104 | 0.152 |
| 0.450 | 0.265 | 0.146 | 0.139 | 0.173 | 0.185 | 0.240 | 0.164 | 0.166 | 0.125 | 0.112 | 0.165 |
| 0.500 | 0.284 | 0.157 | 0.149 | 0.186 | 0.200 | 0.261 | 0.177 | 0.179 | 0.135 | 0.120 | 0.179 |
| 0.550 | 0.303 | 0.168 | 0.160 | 0.198 | 0.216 | 0.282 | 0.190 | 0.193 | 0.146 | 0.128 | 0.193 |
| 0.600 | 0.322 | 0.179 | 0.171 | 0.211 | 0.234 | 0.303 | 0.204 | N/A 1 | 0.157 | 0.137 | N/A |
| 0.650 | 0.342 | 0.190 | 0.183 | 0.224 | 0.252 | 0.325 | 0.219 | N/A | 0.168 | 0.145 | N/A |
| 0.700 | 0.363 | 0.201 | 0.196 | 0.237 | 0.272 | 0.347 | 0.234 | N/A | 0.181 | 0.154 | N/A |
| 0.750 | 0.384 | 0.214 | N/A | 0.251 | 0.293 | 0.370 | 0.250 | N/A | 0.195 | 0.164 | N/A |
| 0.800 | 0.408 | 0.228 | N/A | 0.265 | 0.318 | 0.395 | 0.269 | N/A | N/A | 0.174 | N/A |
| 0.850 | 0.434 | 0.243 | N/A | 0.281 | 0.347 | 0.424 | 0.290 | N/A | N/A | 0.186 | N/A |
| 0.900 | 0.465 | 0.264 | N/A | 0.300 | 0.388 | 0.456 | N/A | N/A | N/A | 0.201 | N/A |
| Simple Cubic | Body-Centered Cubic | Face-Centered Cubic | Body Center | Diamond | Truncated cube | Truncated Octahedron | Octahedron | Rhombicuboctahedron | Octet-cross | Cuboctahedron | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of nodes | 8 | 9 | 14 | 9 | 14 | 24 | 24 | 6 | 24 | 14 | 14 |
| No. of struts | 12 | 20 | 36 | 8 | 12 | 36 | 36 | 12 | 48 | 36 | 24 |
| M-value | −6 | −1 | 0 | −13 | −24 | −30 | −30 | 0 | −18 | 0 | −6 |
| Relative Density | Lattice Structure Yield Forces (N) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simple Cubic | Body-Centered Cubic | Face-Centered Cubic | ||||||||||
| 1 × 1 × 1 | 2 × 2 × 2 | 3 × 3 × 3 | 4 × 4 × 4 | 1 × 1 × 1 | 2 × 2 × 2 | 3 × 3 × 3 | 4 × 4 × 4 | 1 × 1 × 1 | 2 × 2 × 2 | 3 × 3 × 3 | 4 × 4 × 4 | |
| 0.1 | 3070 | 3715 | 4890 | 4860 | 890 | 1065 | 1095 | 1135 | 615 | 815 | 975 | 810 |
| 0.2 | 8400 | 13,200 | 14,880 | 14,095 | 3225 | 4630 | 4350 | 4540 | 2650 | 3195 | 4385 | 2655 |
| 0.3 | 14,470 | 22,200 | 30,160 | 31,315 | 6825 | 11,045 | 14,325 | 15,115 | 4605 | 6080 | 8320 | 9800 |
| Simple Cubic | Truncated Cube | Truncated Octahedron | Octahedron | |
|---|---|---|---|---|
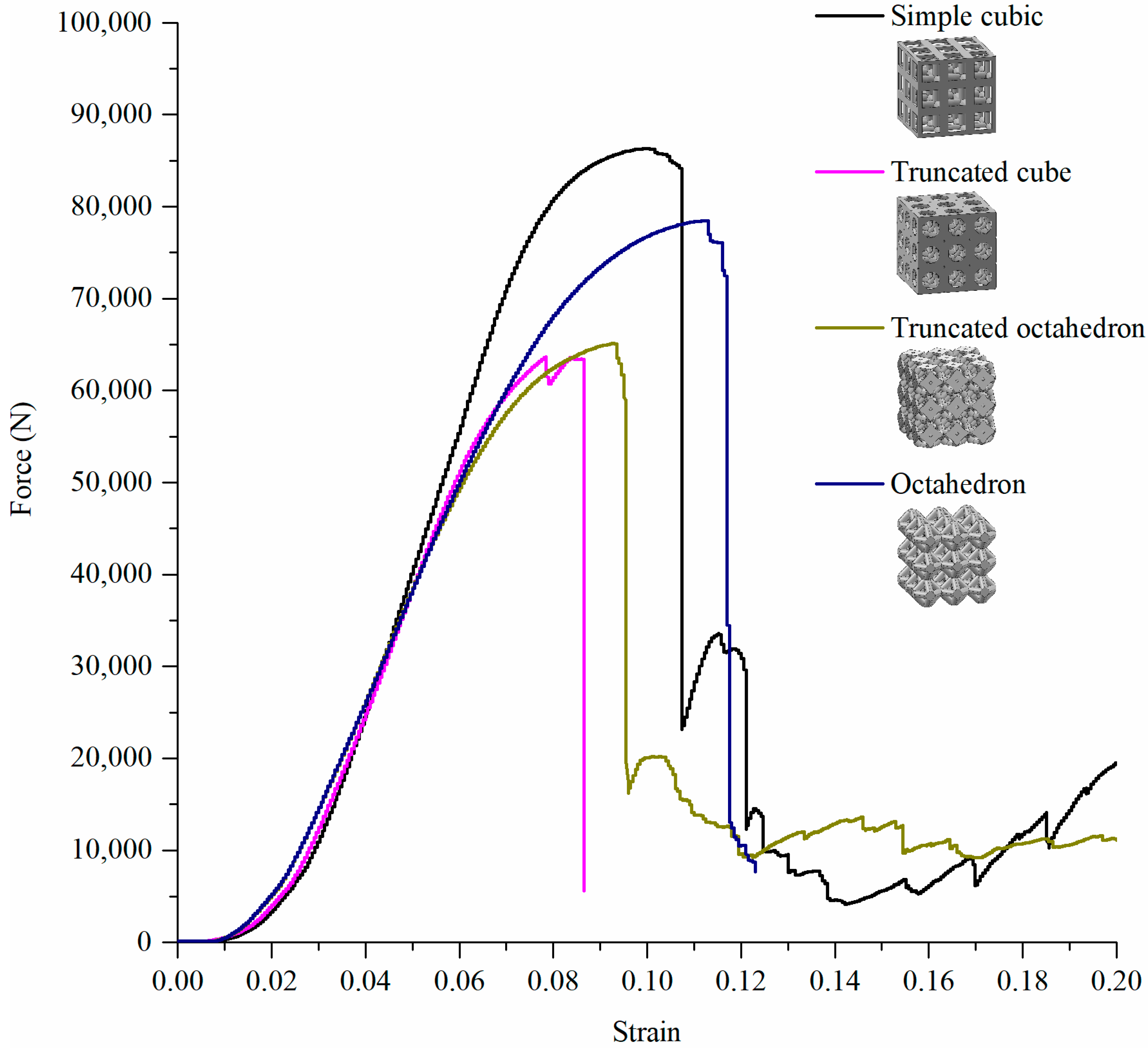
| Yield force by experimental test (N) | 86,300 | 63,680 | 65,120 | 78,470 |
| Yield force by linear static FEA (N) | 30,160 | 20,715 | 19,545 | 25,050 |
| Linear static FEA/experimental test (%) | 34.9 | 32.5 | 30.0 | 31.9 |
| Yield force by nonlinear FEA (N) | 65,250 | 49,750 | 47,350 | 56,800 |
| Nonlinear FEA/experimental test (%) | 75.6 | 78.1 | 72.7 | 72.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.-M.; Min, K.-S.; Roh, Y.-S. Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements. Materials 2022, 15, 97. https://doi.org/10.3390/ma15010097
Park K-M, Min K-S, Roh Y-S. Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements. Materials. 2022; 15(1):97. https://doi.org/10.3390/ma15010097
Chicago/Turabian StylePark, Kwang-Min, Kyung-Sung Min, and Young-Sook Roh. 2022. "Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements" Materials 15, no. 1: 97. https://doi.org/10.3390/ma15010097
APA StylePark, K.-M., Min, K.-S., & Roh, Y.-S. (2022). Design Optimization of Lattice Structures under Compression: Study of Unit Cell Types and Cell Arrangements. Materials, 15(1), 97. https://doi.org/10.3390/ma15010097






