Spin Polarization of Mn Could Enhance Grain Boundary Sliding in Mg
Abstract
:1. Introduction
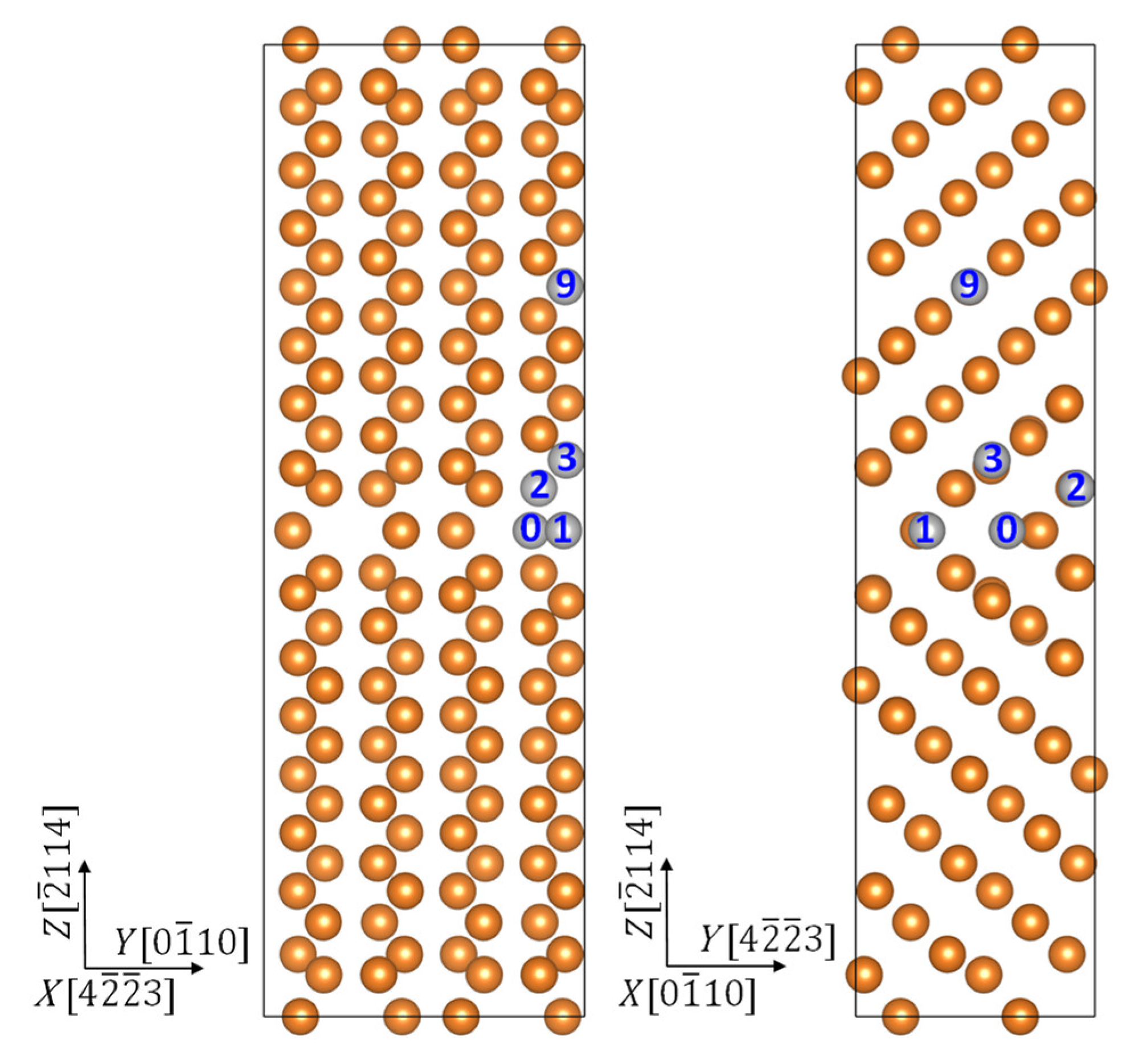
2. Model and Computation
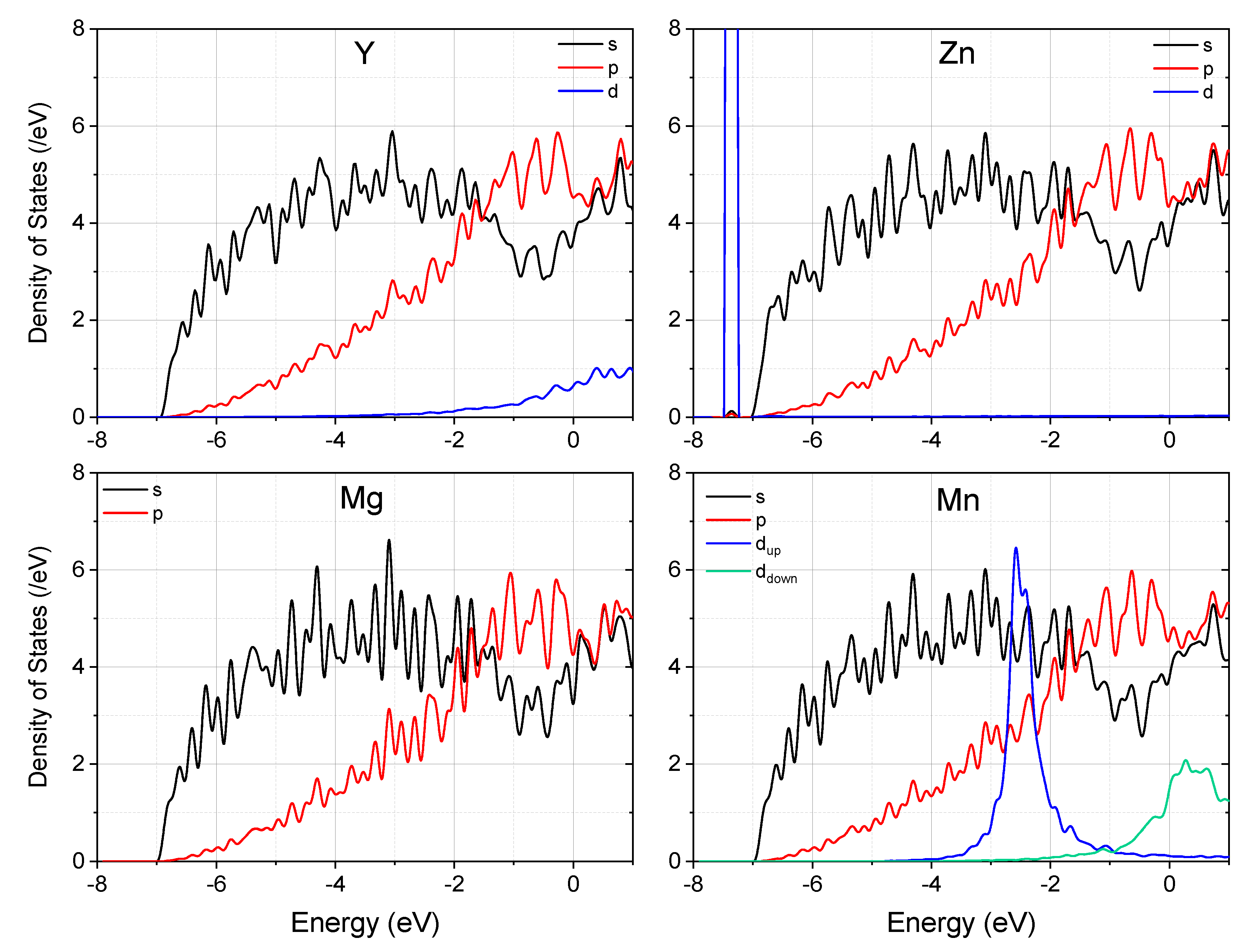
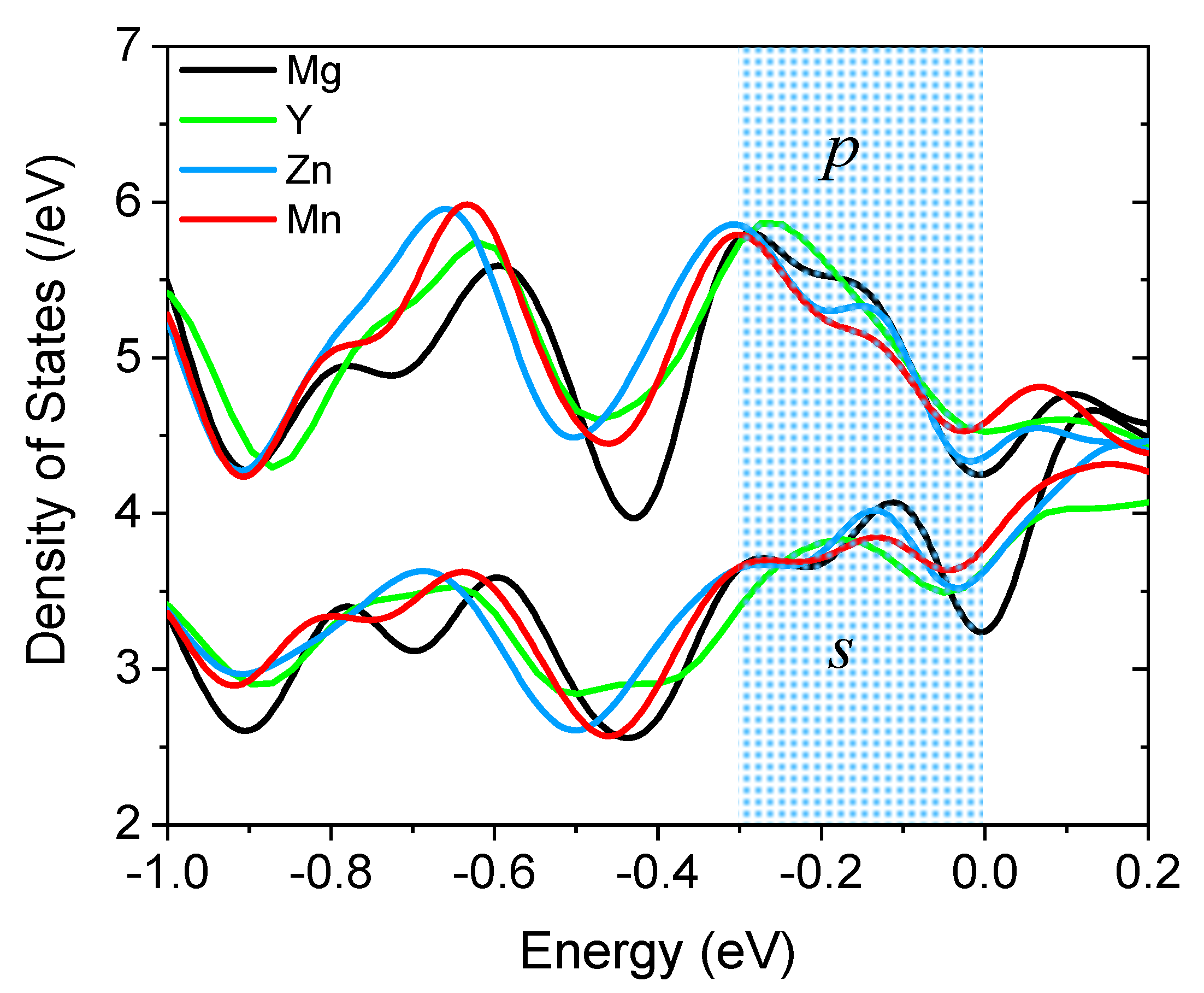
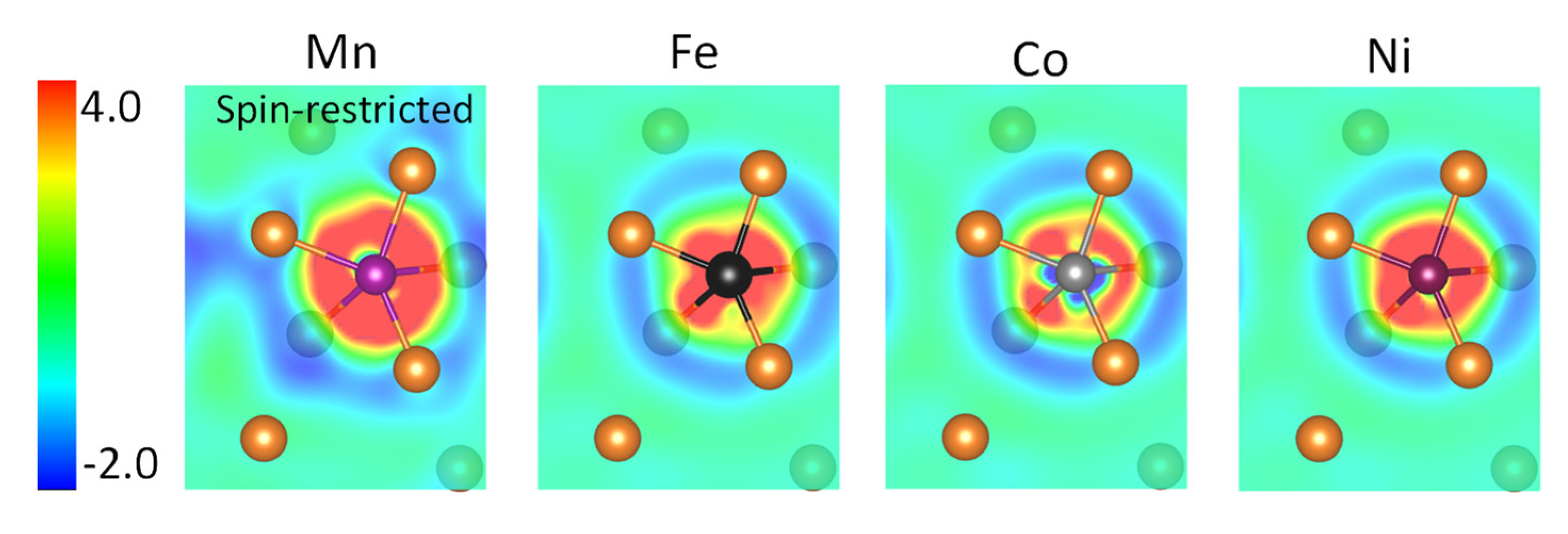
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kubota, K.; Mabuchi, M.; Higashi, K. Review Processing and mechanical properties of fine-grained magnesium alloys. J. Mater. Sci. 1999, 34, 2255–2262. [Google Scholar] [CrossRef]
- Koike, J.; Kobayashi, T.; Mukai, T.; Watanabe, H.; Suzuki, M.; Maruyama, K.; Higashi, K. The activity of non-basal slip systems and dynamic recovery at room temperature in fine-grained AZ31B magnesium alloys. Acta Mater. 2003, 51, 2055–2065. [Google Scholar] [CrossRef]
- Koike, J.; Ohyama, R.; Kobayashi, T.; Suzuki, M.; Maruyama, K. Grain-Boundary Sliding in AZ31 Magnesium Alloys at Room Temperature to 523 K. Mater. Trans. 2003, 44, 445–451. [Google Scholar] [CrossRef] [Green Version]
- Geng, W.T.; Freeman, A.J.; Wu, R.; Geller, C.B.; Raynolds, J.E. Embrittling and strengthening effects of hydrogen, boron, and phosphorus on a Σ5 nickel grain boundary. Phys. Rev. B 1999, 60, 7149–7155. [Google Scholar] [CrossRef]
- McFadden, S.X.; Mukherjee, A.K. Sulfur and superplasticity in electrodeposited ultrafine-grained Ni. Mater. Sci. Eng. A 2005, 395, 265–268. [Google Scholar] [CrossRef]
- Watanabe, H.; Owashi, A.; Uesugi, T.; Takigawa, Y.; Higashi, K. Threshold stress for superplasticity in solid solution magnesium alloys. Philos. Mag. 2012, 92, 787–803. [Google Scholar] [CrossRef]
- Hadorn, J.P.; Hantzsche, K.; Yi, S.B.; Bohlen, J.; Letzig, D.; Wollmershauser, J.A.; Agnew, S.R. Role of Solute in the Texture Modification During Hot Deformation of Mg-Rare Earth Alloys. Met. Mater. Trans. A 2012, 43, 1347–1362. [Google Scholar] [CrossRef]
- Stanford, N.; Sha, G.; Xia, J.H.; Ringer, S.P.; Barnett, M.R. Solute segregation and texture modification in an extruded magnesium alloy containing gadolinium. Scr. Mater. 2011, 65, 919–921. [Google Scholar] [CrossRef]
- Zhang, D.L.; Wen, H.M.; Kumar, M.A.; Chen, F.; Zhang, L.M.; Beyerlein, I.J.; Schoenung, J.M.; Mahajan, S.; Lavernia, E.J. Yield symmetry and reduced strength differential in Mg-2.5Y alloy. Acta Mater. 2016, 120, 75–85. [Google Scholar] [CrossRef] [Green Version]
- Somekawa, H.; Inoue, T.; Tsuzaki, K. Effect of solute atoms on fracture toughness in dilute magnesium alloys. Philos. Mag. 2013, 93, 4582–4592. [Google Scholar] [CrossRef]
- Trang, T.T.T.; Zhang, J.H.; Kim, J.H.; Zargaran, A.; Hwang, J.H.; Suh, B.C.; Kim, N.J. Designing a magnesium alloy with high strength and high formability. Nat. Commun. 2018, 9, 2522. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Li, Y.; Sun, S.; Bian, H.; Huang, H.; Wang, Z.; Koizumi, Y.; Chiba, A. Enhanced damping capacity of magnesium alloys by tensile twin boundaries. Scr. Mater. 2015, 101, 8–11. [Google Scholar] [CrossRef]
- Somekawa, H.; Basha, D.A.; Singh, A.; Tsuru, T.; Yamaguchi, M. Non-Basal Dislocation Nucleation Site of Solid Solution Magnesium Alloy. Mater. Trans. 2020, 61, 1172–1175. [Google Scholar] [CrossRef] [Green Version]
- Nie, J.F.; Zhu, Y.M.; Liu, J.Z.; Fang, X.Y. Periodic Segregation of Solute Atoms in Fully Coherent Twin Boundaries. Science 2013, 340, 957. [Google Scholar] [CrossRef] [PubMed]
- Somekawa, H.; Naito, K.; Watanabe, H. Grain boundary relaxation behavior in meso-grained dilute magnesium alloys. Materialia 2020, 14, 100947. [Google Scholar] [CrossRef]
- Zeng, Z.R.; Zhu, Y.M.; Xu, S.W.; Bian, M.Z.; Davies, C.H.J.; Birbilis, N.; Nie, J.F. Texture evolution during static recrystallization of cold-rolled magnesium alloys. Acta Mater. 2016, 105, 479–494. [Google Scholar] [CrossRef]
- Basu, I.; Al-Samman, T. Triggering rare earth texture modification in magnesium alloys by addition of zinc and zirconium. Acta Mater. 2014, 67, 116–133. [Google Scholar] [CrossRef]
- Guan, D.K.; Liu, X.G.; Gao, J.H.; Ma, L.; Wynne, B.P.; Rainforth, W.M. Exploring the mechanism of “Rare Earth” texture evolution in a lean Mg–Zn–Ca alloy. Sci. Rep. UK 2019, 9, 7152. [Google Scholar] [CrossRef] [Green Version]
- Somekawa, H.; Singh, A.; Mukai, T.; Inoue, T. Effect of alloying elements on room temperature tensile ductility in magnesium alloys. Philos. Mag. 2016, 96, 2671–2685. [Google Scholar] [CrossRef]
- Somekawa, H.; Basha, D.A.; Singh, A. Room temperature grain boundary sliding behavior of fine-grained Mg-Mn alloys. Mater. Sci. Eng. A 2018, 730, 355–362. [Google Scholar] [CrossRef]
- Somekawa, H.; Tsuru, T. Effect of twin boundary on crack propagation behavior in magnesium binary alloys; Experimental and calculation studies. Scr. Mater. 2017, 130, 114–118. [Google Scholar] [CrossRef]
- Hase, T.; Ohtagaki, T.; Yamaguchi, M.; Ikeo, N.; Mukai, T. Effect of aluminum or zinc solute addition on enhancing impact fracture toughness in Mg–Ca alloys. Acta Mater. 2016, 104, 283–294. [Google Scholar] [CrossRef]
- Mahjoub, R.; Basha, D.A.; Singh, A.; Ferry, M.; Stanford, N. The contrasting fracture behaviour of twin boundaries and general boundaries—A first principles study based on experimental observation. Mat. Sci. Eng. A Struct. 2020, 781, 139225. [Google Scholar] [CrossRef]
- Namilae, S.; Chandra, N.; Nieh, T.G. Atomistic simulation of grain boundary sliding in pure and magnesium doped aluminum bicrystals. Scr. Mater. 2002, 46, 49–54. [Google Scholar] [CrossRef]
- Schusteritsch, G.; Kuhne, T.D.; Guo, Z.X.; Kaxiras, E. The effect of Ag, Pb and Bi impurities on grain boundary sliding and intergranular decohesion in Copper. Philos. Mag. 2016, 96, 2868–2886. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.B.; Hu, J.W.; Liu, Y.; Dong, F.; Huang, Y.C. Co-segregation behavior of Sc and Zr solutes and their effect on the Al Σ5 (210) [110] symmetrical tilt grain boundary: A first-principles study. Phys. Chem. Chem. Phys. 2019, 21, 19437–19446. [Google Scholar] [CrossRef]
- Wang, H.; Kohyama, M.; Tanaka, S.; Shiihara, Y. First-principles study of Si and Mg segregation in grain boundaries in Al and Cu: Application of local-energy decomposition. J. Mater. Sci. 2015, 50, 6864–6881. [Google Scholar] [CrossRef]
- Yuasa, M.; Nakazawa, T.; Mabuchi, M. Grain boundary sliding in pure and segregated bicrystals: A molecular dynamics and first principles study. J. Phys. Condens. Mat. 2012, 24, 26570. [Google Scholar] [CrossRef]
- Oliveira, M.I.A.; Rivelino, R.; de Brito Mota, F.; Gueorguiev, G.K. Optical Properties and Quasiparticle Band Gaps of Transition-Metal Atoms Encapsulated by Silicon Cages. J. Phys. Chem. C 2014, 118, 5501–5509. [Google Scholar] [CrossRef] [Green Version]
- Freitas, R.R.Q.; de Brito Mota, F.; Rivelino, R.; de Castilho, C.M.C.; Kakanakova-Georgieva, A.; Gueorguiev, G.K. Spin-orbit-induced gap modification in buckled honeycomb XBi and XBi3 (X = B, Al, Ga, and In) sheets. J. Phys. Condens. Matter 2015, 27, 485306. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Beyerlein, I.J. Atomic Structures of [010] Symmetric Tilt Grain Boundaries in Hexagonal Close-Packed (hcp) Crystals. Metall. Mater. Trans. A 2012, 43, 3556–3569. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Allred, A.L. Electronegativity values from thermochemical data. J. Inorg. Nucl. Chem. 1961, 17, 215–221. [Google Scholar] [CrossRef]
- Somekawa, H. Effect of Alloying Elements on Fracture Toughness and Ductility in Magnesium Binary Alloys; A Review. Mater. Trans. 2020, 61, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Somekawa, H.; Mukai, T. Hall–Petch Breakdown in Fine-Grained Pure Magnesium at Low Strain Rates. Met. Mater. Trans. A 2015, 46, 894–902. [Google Scholar] [CrossRef]
- Zheng, R.X.; Du, J.P.; Gao, S.; Somekawa, H.; Ogata, S.; Tsuji, N. Transition of dominant deformation mode in bulk polycrystalline pure Mg by ultra-grain refinement down to sub-micrometer. Acta Mater. 2020, 198, 35–46. [Google Scholar] [CrossRef]
- Zeng, Z.R.; Nie, J.F.; Xu, S.W.; Davies, C.H.J.; Birbilis, N. Super-formable pure magnesium at room temperature. Nat. Commun. 2017, 8, 972. [Google Scholar] [CrossRef] [PubMed]
- Yagi, T.; Hirayama, T.; Matsuoka, T.; Somekawa, H. Effect of Alloying Elements on Nano-ordered Wear Property of Magnesium Alloys. Metall. Mater. Trans. A 2017, 48, 1366–1374. [Google Scholar] [CrossRef]
- Okamoto, H.; Massalski, T. Binary Alloy Phase Diagrams; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]


| Y-Mg | Zn-Mg | Mg-Mg | Mn-Mg | ||
|---|---|---|---|---|---|
| (010) | Δρmin | −0.141 | −0.021 | −0.004 | −0.002 |
| Δρmax | +0.012 | +0.004 | +0.003 | +0.015 | |
| Δρmax-Δρmin | 0.153 | 0.025 | 0.007 | 0.017 | |
| (114) | Δρmin | −0.004 | −0.005 | −0.004 | −0.002 |
| Δρmax | +0.008 | +0.004 | +0.003 | +0.004 | |
| Δρmax-Δρmin | 0.012 | 0.009 | 0.007 | 0.006 | |
| Mn-Mg Non-Magnetic | Fe-Mg | Co-Mg | Ni-Mg | |
|---|---|---|---|---|
| Δρmin Δρmax Δρmax-Δρmin | −0.012 | −0.014 | −0.010 | −0.023 |
| +0.010 | +0.019 | +0.051 | +0.008 | |
| 0.022 | 0.033 | 0.061 | 0.031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, V.; Du, J.-P.; Somekawa, H.; Ogata, S.; Geng, W.T. Spin Polarization of Mn Could Enhance Grain Boundary Sliding in Mg. Materials 2022, 15, 3483. https://doi.org/10.3390/ma15103483
Wang V, Du J-P, Somekawa H, Ogata S, Geng WT. Spin Polarization of Mn Could Enhance Grain Boundary Sliding in Mg. Materials. 2022; 15(10):3483. https://doi.org/10.3390/ma15103483
Chicago/Turabian StyleWang, Vei, Jun-Ping Du, Hidetoshi Somekawa, Shigenobu Ogata, and Wen Tong Geng. 2022. "Spin Polarization of Mn Could Enhance Grain Boundary Sliding in Mg" Materials 15, no. 10: 3483. https://doi.org/10.3390/ma15103483
APA StyleWang, V., Du, J.-P., Somekawa, H., Ogata, S., & Geng, W. T. (2022). Spin Polarization of Mn Could Enhance Grain Boundary Sliding in Mg. Materials, 15(10), 3483. https://doi.org/10.3390/ma15103483







