Multi-Layer Simulation of the Powder Bed Selective Laser Processing of Alumina for Residual Stress and Distortion Evaluation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Procedure
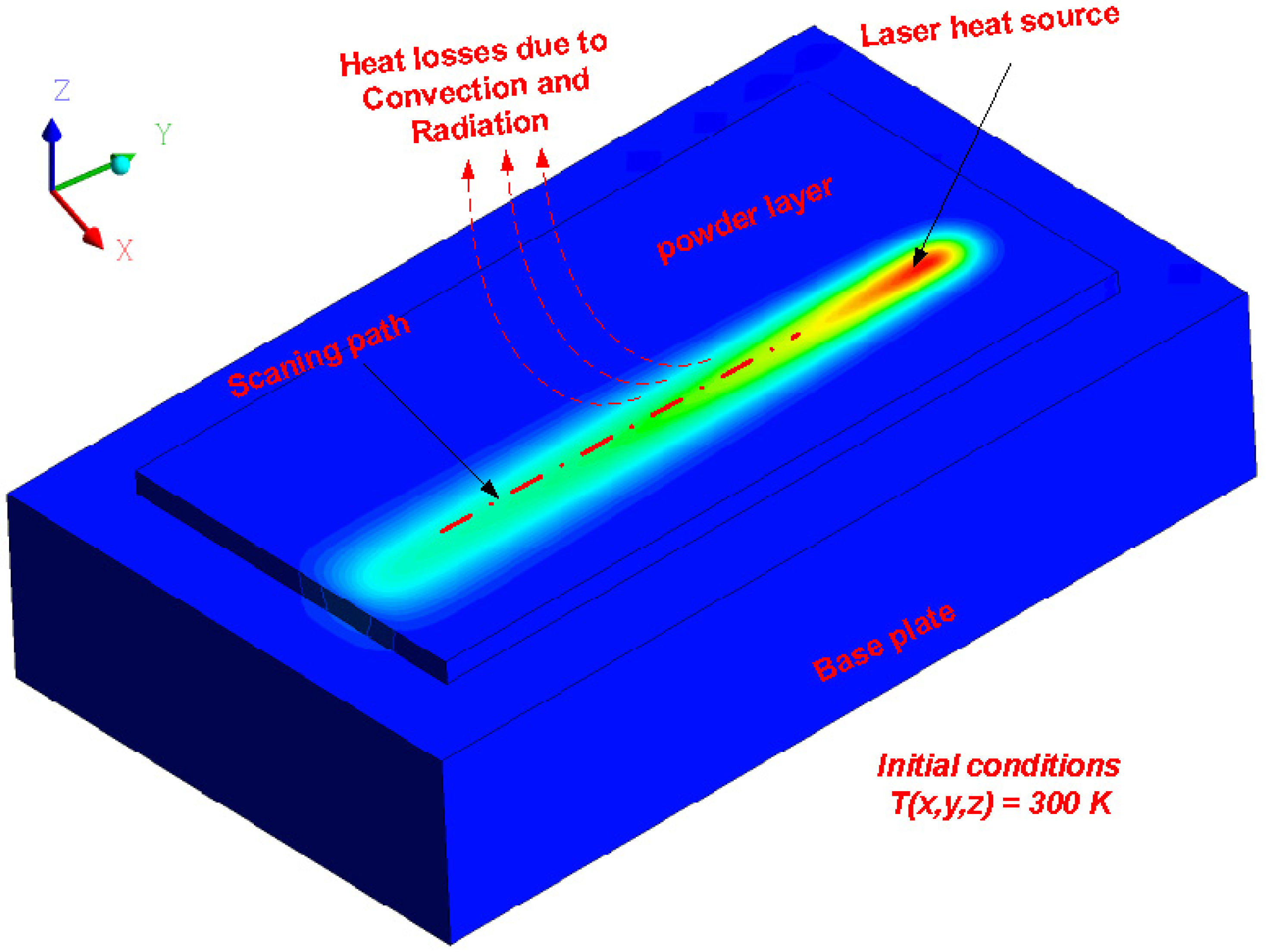
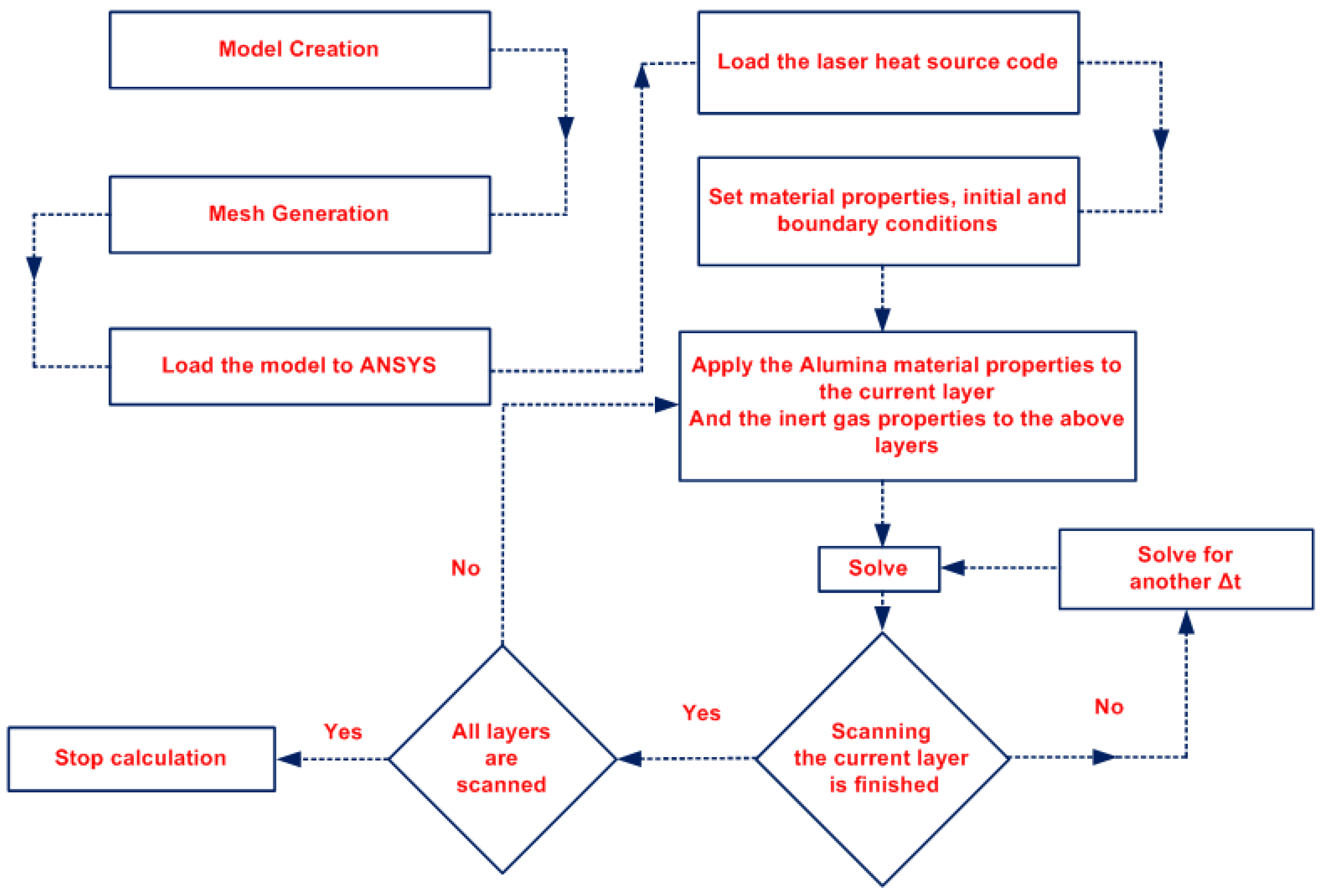
2.1.1. Numerical Model Development
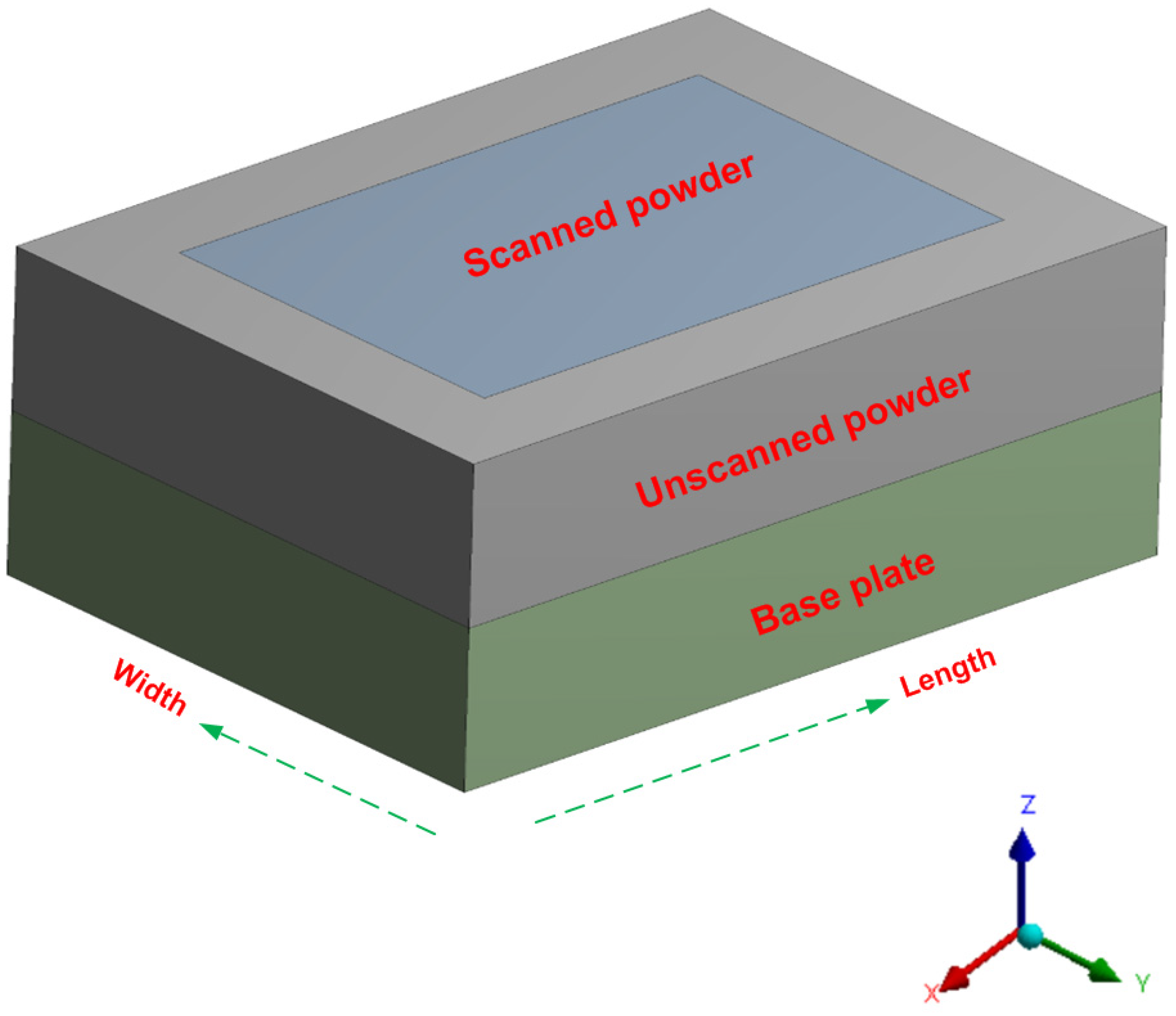
2.1.2. Numerical Model Geometry
2.1.3. Alumina PBSLP Using the CO2 Laser
2.2. Experimental Procedure
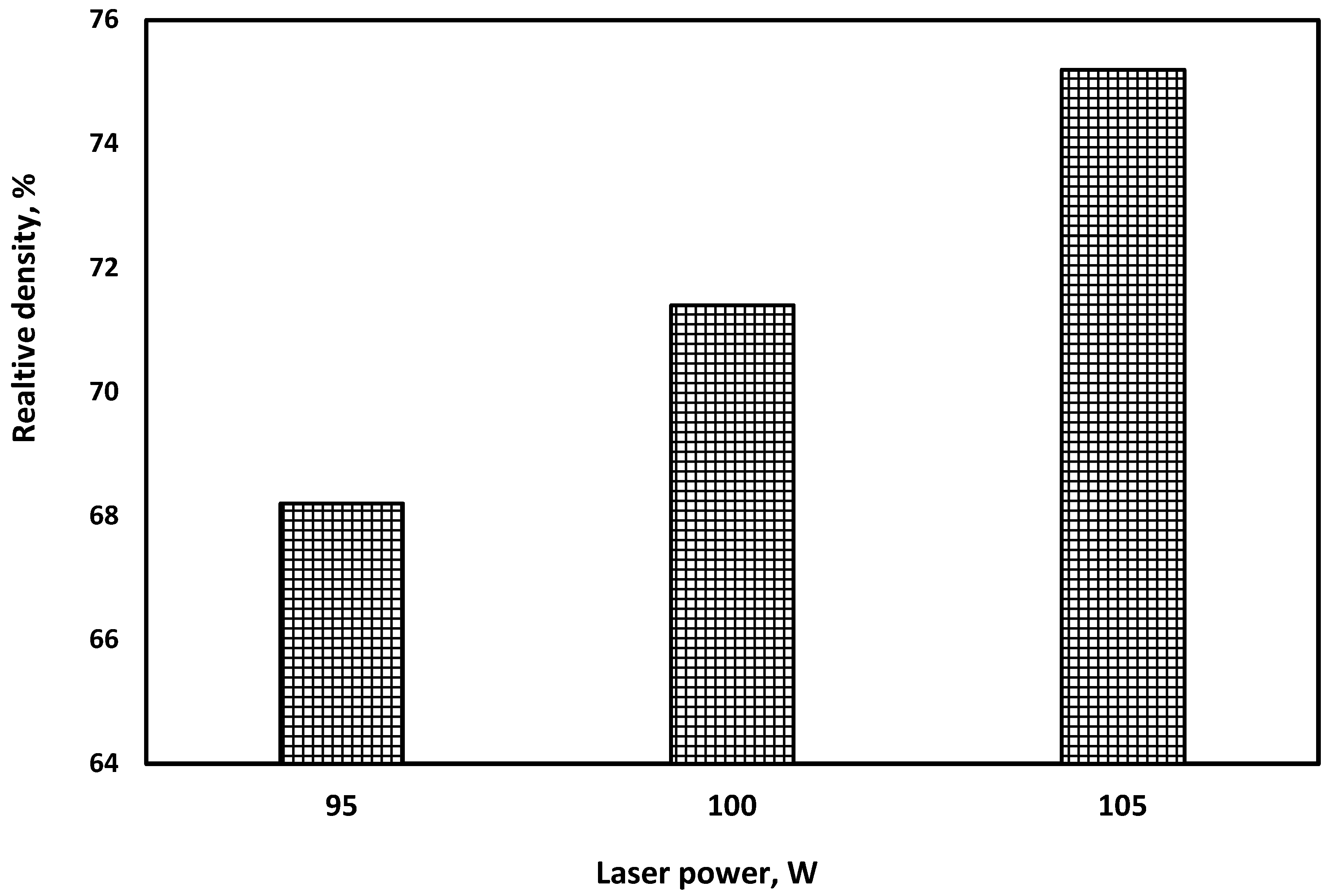
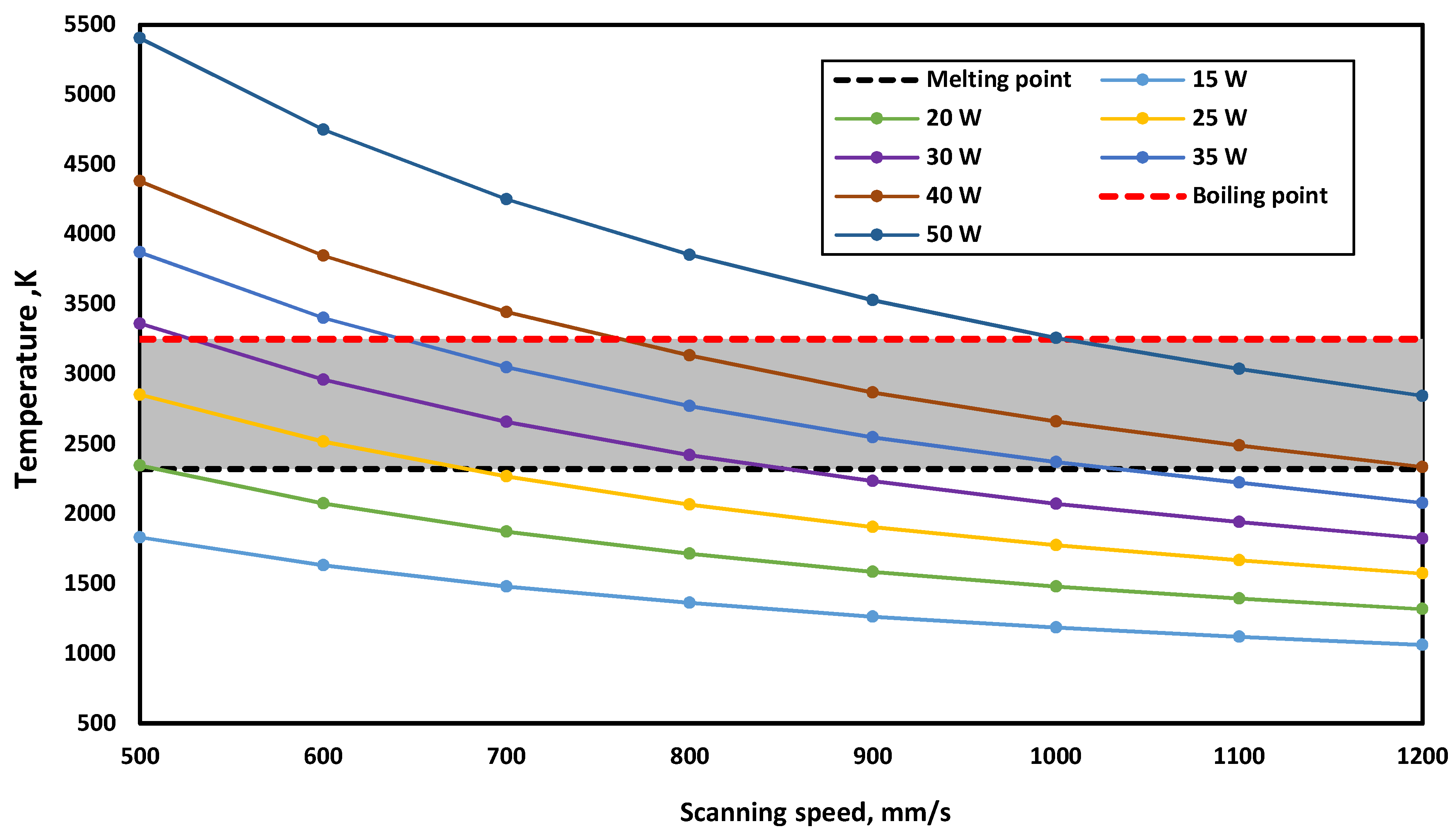
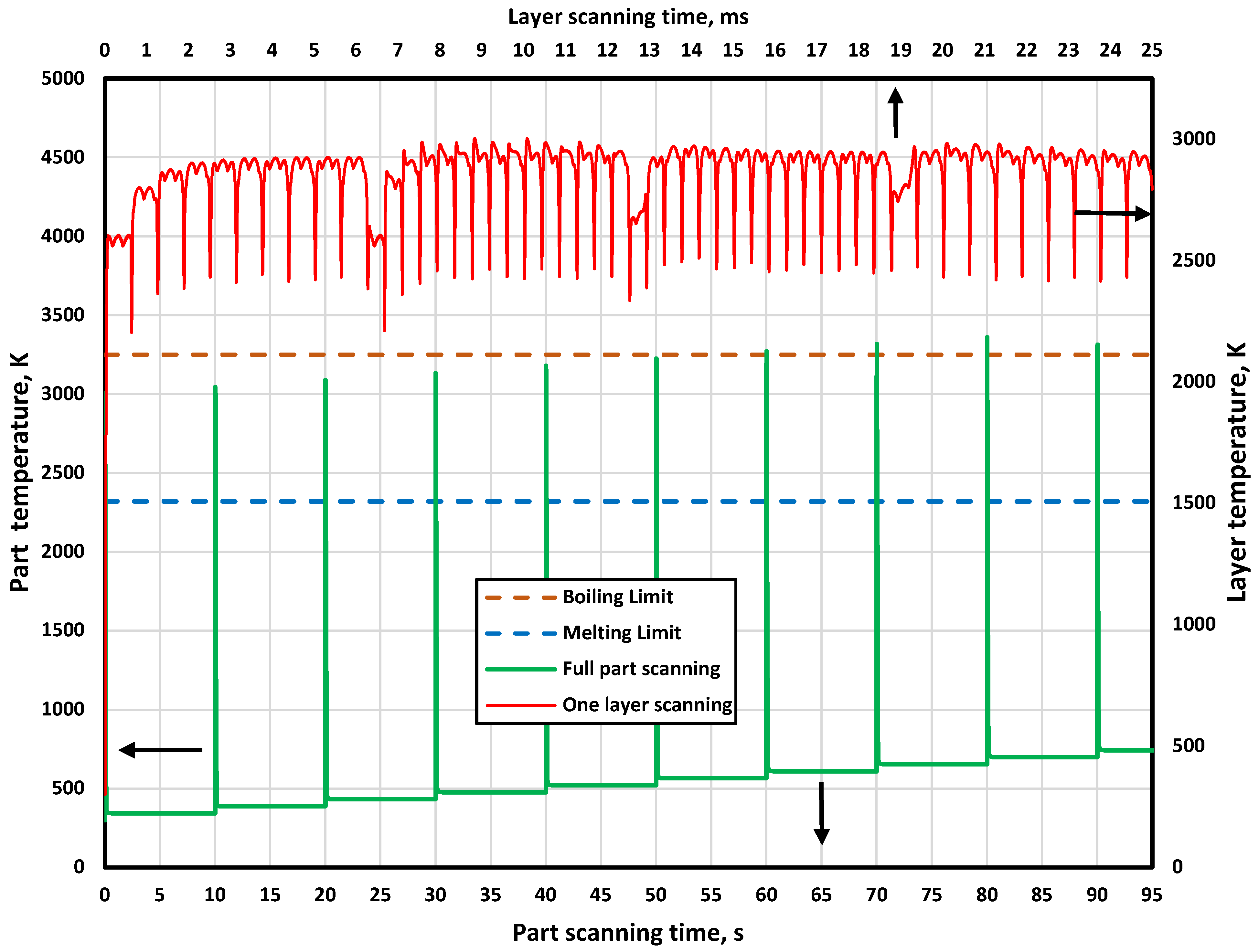
3. Results and Discussion
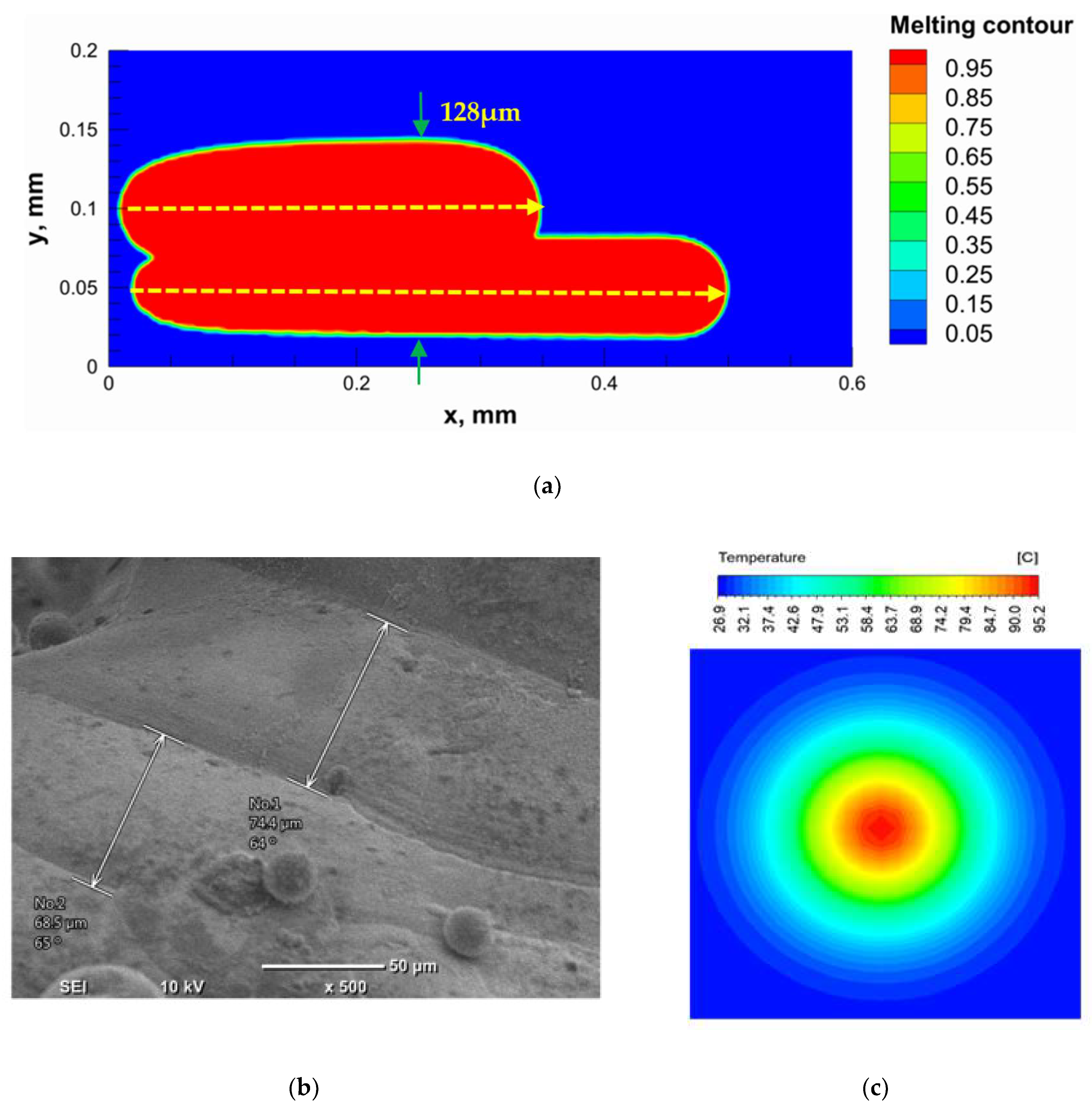
3.1. Numerical Model Validation
3.2. Process Window for the PBSLP of Alumina Using the CO2 Laser
3.3. Temperature History during Part Printing
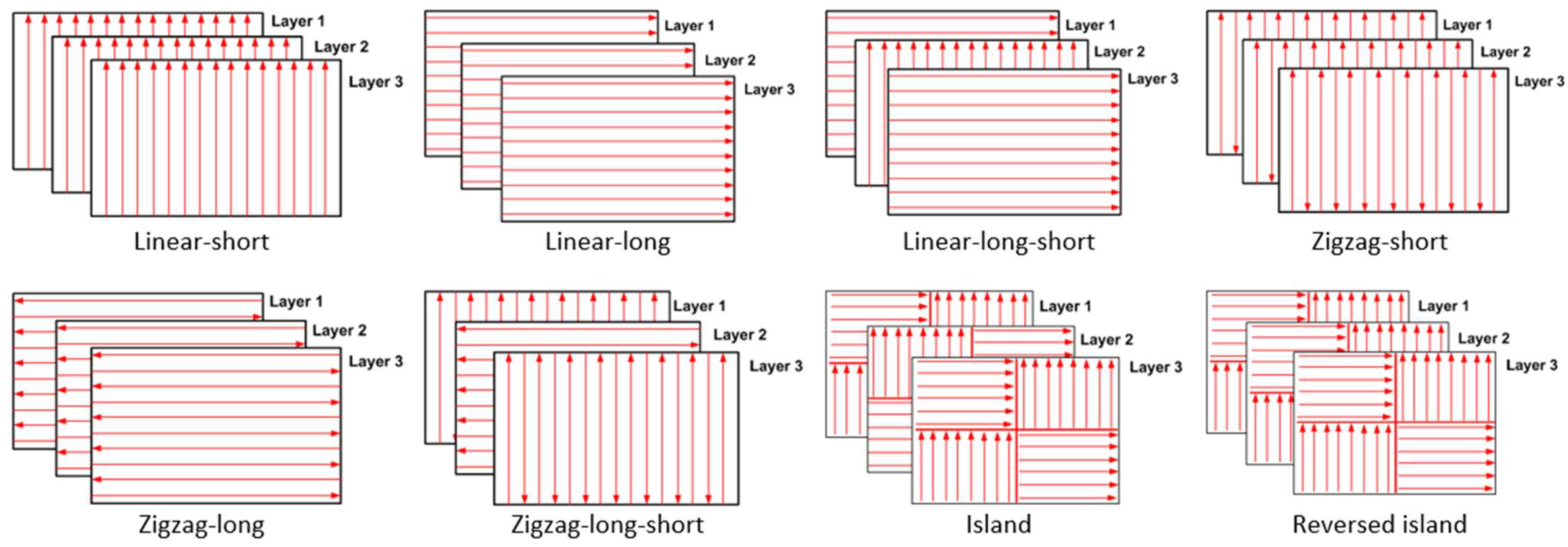
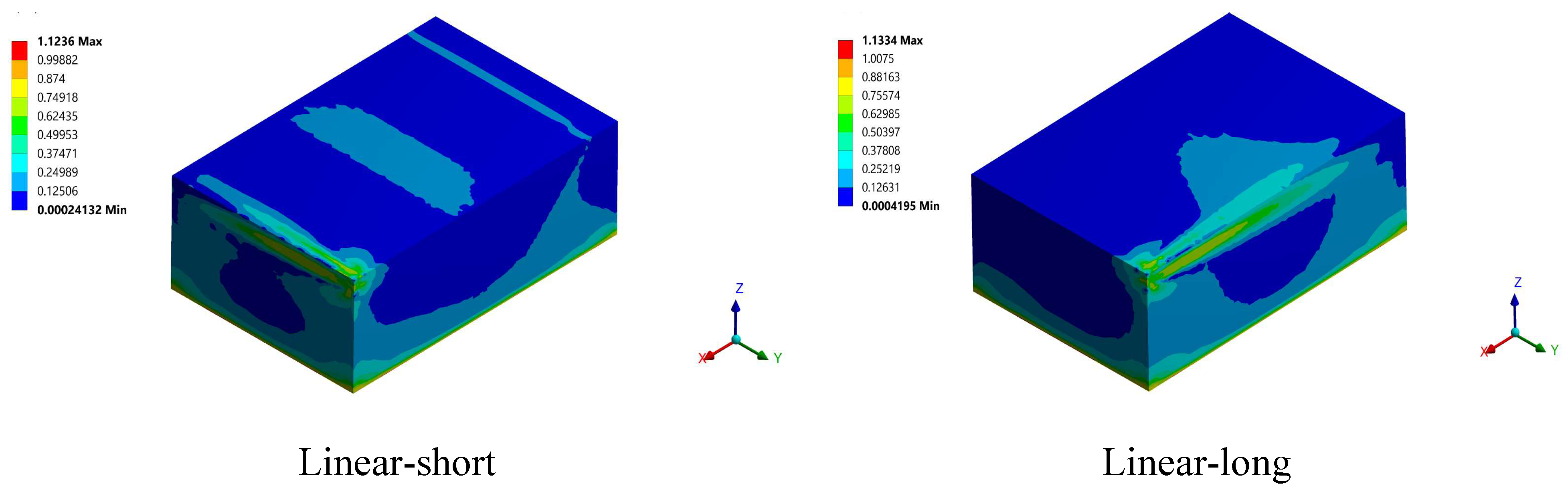
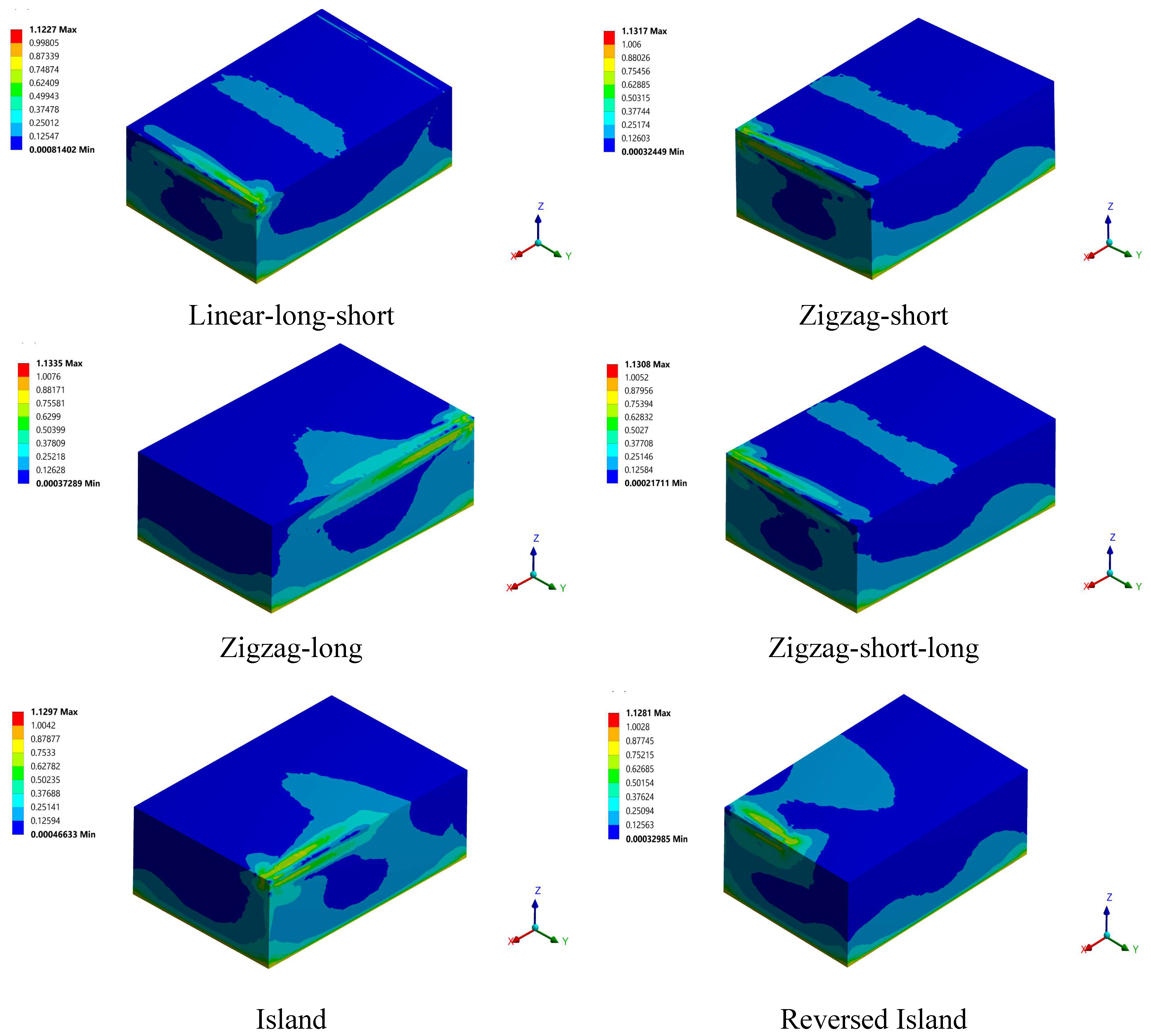
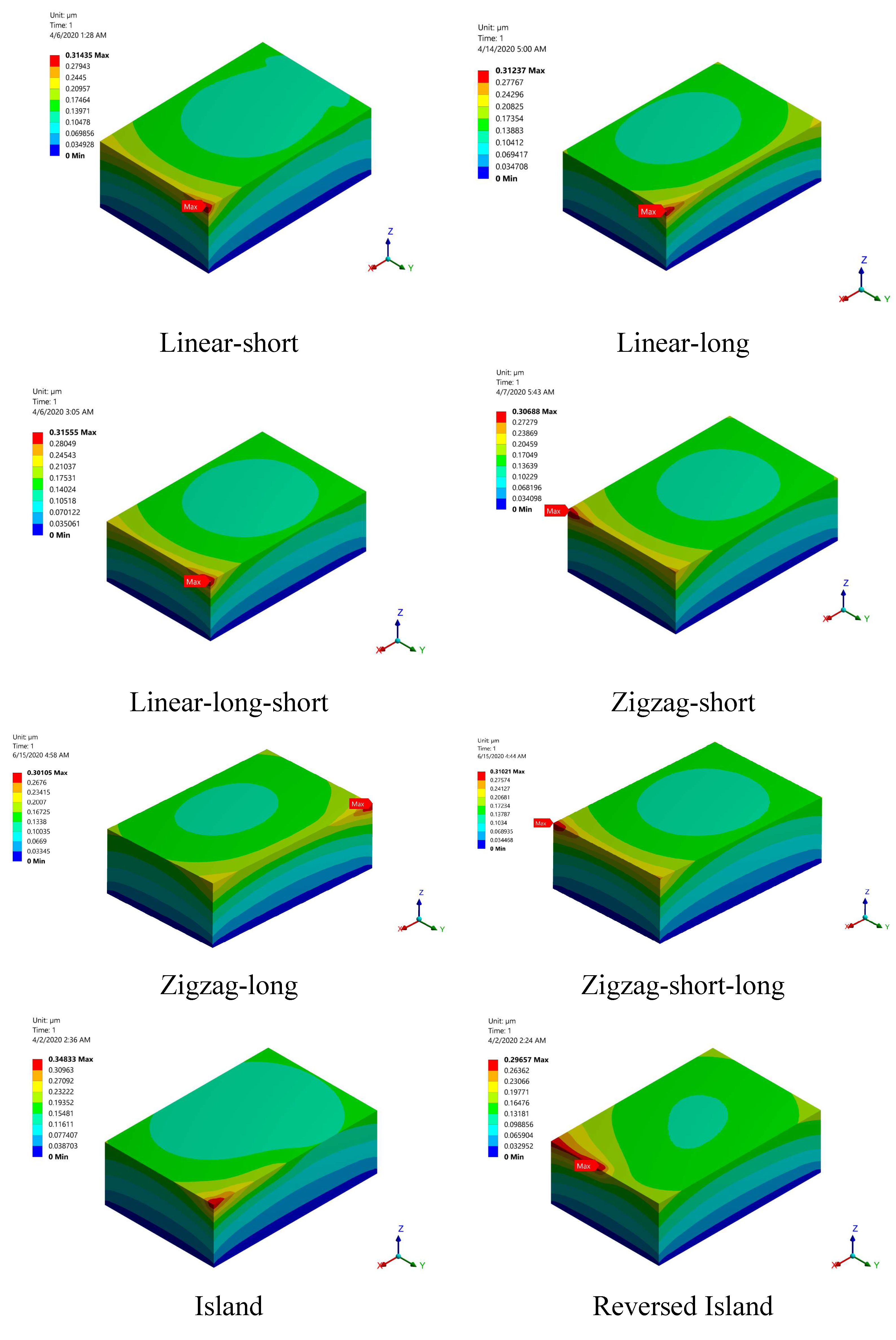
3.4. Residual Stress and Distortion
3.5. Effect of Preheating
4. Conclusions
- The model can be used to select the appropriate values of laser power, scanning speed, and hatching distance.
- The CO2 laser can be effectively used for the PBSLP of alumina with a low power value and high scanning speed leading to a high manufacturing rate and energy conservation.
- The model can obtain the printed part’s temperature history, temperature distribution, residual stress, and distortion.
- The developed residual stress for the printed part exceeds the yield limit for all the studied build orientations. When preheating by 800 K is applied, the developed residual stress is reduced by 23% and the distortion by 54%. The linear-short and linear-short-long build orientations both gave low distortion and residual stress compared to other build orientations.
- Commercially available printers cannot be used effectively for the PBSLP of ceramic materials, and a special printer equipped with a preheating system for the powder and temperature controller is needed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Auerkari, P. Mechanical and Physical Properties of Engineering Alumina Ceramics; Technical Research Centre: Espoo, Finland, 1996; p. 26. [Google Scholar]
- Bian, H.; Song, X.; Hu, S.; Lei, Y.; Jiao, Y.; Duan, S.; Feng, J.; Long, W. Microstructure Evolution and Mechanical Properties of Titanium/Alumina Brazed Joints for Medical Implants. Metals 2019, 9, 644. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-H.; Yoo, S.-J.; Kwak, D.-H.; Jung, H.-J.; Kim, T.-Y.; Park, K.-H.; Lee, J.-W. Characterization and Application of Electrospun Alumina Nanofibers. Nanoscale Res. Lett. 2014, 9, 44. [Google Scholar] [CrossRef] [Green Version]
- Hirashima, H.; Kojima, C.; Imai, H. Application of Alumina Aerogels as Catalysts. J. Sol-Gel Sci. Technol. 1997, 8, 843–846. [Google Scholar] [CrossRef]
- Fu, L.; Huang, A.; Gu, H.; Ni, H. Properties and Microstructures of Lightweight Alumina Containing Different Types of Nano-Alumina. Ceram. Int. 2018, 44, 17885–17894. [Google Scholar] [CrossRef]
- TarõÁ, G.; Ferreira, J.M.F.; Lyckfeldt, O. Infuence of the Stabilising Mechanism and Solid Loading on Slip Casting of Alumina. J. Eur. Ceram. Soc. 1998, 18, 479–486. [Google Scholar] [CrossRef]
- Thomas-Vielma, P.; Cervera, A.; Levenfeld, B.; Várez, A. Production of Alumina Parts by Powder Injection Molding with a Binder System Based on High Density Polyethylene. J. Eur. Ceram. Soc. 2008, 28, 763–771. [Google Scholar] [CrossRef]
- Ananthakumar, S.; Menon, A.R.R.; Prabhakaran, K.; Warrier, K.G.K. Rheology and Packing Characteristics of Alumina Extrusion Using Boehmite Gel as a Binder. Ceram. Int. 2001, 27, 231–237. [Google Scholar] [CrossRef]
- Alias, S.S.; Harun, Z.; Ismail, N.F. Microstructure and Physical Characterization of Alumina-Sintered Body via Hot Isostatic Pressing. J. Aust. Ceram. Soc. 2019, 55, 969–975. [Google Scholar] [CrossRef]
- Ozer, I.O.; Suvaci, E.; Karademir, B.; Missiaen, J.M.; Carry, C.P.; Bouvard, D. Anisotropic Sintering Shrinkage in Alumina Ceramics Containing Oriented Platelets. J. Am. Ceram. Soc. 2006, 89, 1972–1976. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Y.C. Experimental Investigations of Machining Characteristics and Removal Mechanisms of Advanced Ceramics in High Speed Deep Grinding. Int. J. Mach. Tools Manuf. 2003, 43, 811–823. [Google Scholar] [CrossRef]
- Druzgalski, C.L.; Ashby, A.; Guss, G.; King, W.E.; Roehling, T.T.; Matthews, M.J. Process Optimization of Complex Geometries Using Feed Forward Control for Laser Powder Bed Fusion Additive Manufacturing. Addit. Manuf. 2020, 34, 101169. [Google Scholar] [CrossRef]
- Panchagnula, J.S.; Simhambhatla, S. Manufacture of Complex Thin-Walled Metallic Objects Using Weld-Deposition Based Additive Manufacturing. Robot. Comput.-Integr. Manuf. 2018, 49, 194–203. [Google Scholar] [CrossRef]
- Baumers, M.; Tuck, C.; Wildman, R.; Ashcroft, I.; Hague, R. Shape Complexity and Process Energy Consumption in Electron Beam Melting: A Case of Something for Nothing in Additive Manufacturing?: Shape Complexity and Energy Usage in 3D Printing. J. Ind. Ecol. 2017, 21, S157–S167. [Google Scholar] [CrossRef] [Green Version]
- ISO/ASTM International 52900:2015; Additive Manufacturing—General Principles—Terminology. ISO/ASTM International 52900:2015. ASTM International: West Conshohocken, PA, USA, 2015.
- Lv, X.; Ye, F.; Cheng, L.; Fan, S.; Liu, Y. Binder Jetting of Ceramics: Powders, Binders, Printing Parameters, Equipment, and Post-Treatment. Ceram. Int. 2019, 45, 12609–12624. [Google Scholar] [CrossRef]
- Miyanaji, H.; Zhang, S.; Lassell, A.; Zandinejad, A.; Yang, L. Process Development of Porcelain Ceramic Material with Binder Jetting Process for Dental Applications. JOM 2016, 68, 831–841. [Google Scholar] [CrossRef]
- Snelling, D.A.; Williams, C.B.; Suchicital, C.T.A.; Druschitz, A.P. Binder Jetting Advanced Ceramics for Metal-Ceramic Composite Structures. Int. J. Adv. Manuf. Technol. 2017, 92, 531–545. [Google Scholar] [CrossRef]
- Huang, S.; Ye, C.; Zhao, H.; Fan, Z. Additive Manufacturing of Thin Alumina Ceramic Cores Using Binder-Jetting. Addit. Manuf. 2019, 29, 100802. [Google Scholar] [CrossRef]
- Du, W.; Ren, X.; Ma, C.; Pei, Z. Ceramic Binder Jetting Additive Manufacturing: Particle Coating for Increasing Powder Sinterability and Part Strength. Mater. Lett. 2019, 234, 327–330. [Google Scholar] [CrossRef]
- Kunchala, P.; Kappagantula, K. 3D Printing High Density Ceramics Using Binder Jetting with Nanoparticle Densifiers. Mater. Des. 2018, 155, 443–450. [Google Scholar] [CrossRef]
- Rabinskiy, L.; Ripetsky, A.; Sitnikov, S.; Solyaev, Y.; Kahramanov, R. Fabrication of Porous Silicon Nitride Ceramics Using Binder Jetting Technology. IOP Conf. Ser. Mater. Sci. Eng. 2016, 140, 012023. [Google Scholar] [CrossRef]
- Rane, K.; Petrò, S.; Strano, M. Evolution of Porosity and Geometrical Quality through the Ceramic Extrusion Additive Manufacturing Process Stages. Addit. Manuf. 2020, 32, 101038. [Google Scholar] [CrossRef]
- Faes, M.; Vleugels, J.; Vogeler, F.; Ferraris, E. Extrusion-Based Additive Manufacturing of ZrO2 Using Photoinitiated Polymerization. CIRP J. Manuf. Sci. Technol. 2016, 14, 28–34. [Google Scholar] [CrossRef]
- Slots, C.; Jensen, M.B.; Ditzel, N.; Hedegaard, M.A.B.; Borg, S.W.; Albrektsen, O.; Thygesen, T.; Kassem, M.; Andersen, M.Ø. Simple Additive Manufacturing of an Osteoconductive Ceramic Using Suspension Melt Extrusion. Dent. Mater. 2017, 33, 198–208. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Armani, A.; Martin, A.; Kroehler, B.; Henderson, A.; Huang, T.; Watts, J.; Hilmas, G.; Leu, M. Extrusion-Based Additive Manufacturing of Functionally Graded Ceramics. J. Eur. Ceram. Soc. 2021, 41, 2049–2057. [Google Scholar] [CrossRef]
- Montón, A.; Abdelmoula, M.; Küçüktürk, G.; Maury, F.; Grossin, D.; Ferrato, M. Experimental and Numerical Study for Direct Powder Bed Selective Laser Processing (Sintering/Melting) of Silicon Carbide Ceramic. Mater. Res. Express 2021, 8, 045603. [Google Scholar] [CrossRef]
- Abdelmoula, M.; Zarazaga, A.M.; Küçüktürk, G.; Maury, F.; Grossin, D.; Ferrato, M. Scanning Strategy Investigation for Direct Powder Bed Selective Laser Processing of Silicon Carbide Ceramic. Appl. Sci. 2022, 12, 788. [Google Scholar] [CrossRef]
- Abdelmoula, M.; Küçüktürk, G.; Juste, E.; Petit, F. Powder Bed Selective Laser Processing of Alumina: Scanning Strategies Investigation. Appl. Sci. 2022, 12, 764. [Google Scholar] [CrossRef]
- Sing, S.L.; Yeong, W.Y.; Wiria, F.E.; Tay, B.Y.; Zhao, Z.; Zhao, L.; Tian, Z.; Yang, S. Direct Selective Laser Sintering and Melting of Ceramics: A Review. Rapid Prototyp. J. 2017, 23, 611–623. [Google Scholar] [CrossRef]
- Yves-Christian, H.; Jan, W.; Wilhelm, M.; Konrad, W.; Reinhart, P. Net Shaped High Performance Oxide Ceramic Parts by Selective Laser Melting. Phys. Proc. 2010, 5, 587–594. [Google Scholar] [CrossRef]
- Wilkes, J.; Hagedorn, Y.C.; Meiners, W.; Wissenbach, K. Additive Manufacturing of ZrO2-Al2O3 Ceramic Components by Selective Laser Melting. Rapid Prototyp. J. 2013, 19, 51–57. [Google Scholar] [CrossRef]
- Liu, Q.; Danlos, Y.; Song, B.; Zhang, B.; Yin, S.; Liao, H. Effect of High-Temperature Preheating on the Selective Laser Melting of Yttria-Stabilized Zirconia Ceramic. J. Mater. Process. Technol. 2015, 222, 61–74. [Google Scholar] [CrossRef]
- Khmyrov, R.S.; Protasov, C.E.; Grigoriev, S.N.; Gusarov, A.V. Crack-Free Selective Laser Melting of Silica Glass: Single Beads and Monolayers on the Substrate of the Same Material. Int. J. Adv. Manuf. Technol. 2016, 85, 1461–1469. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, K.; Liu, T.T.; Liao, W.H.; Zhang, C.D.; Shao, H. Cracks of Alumina Ceramics by Selective Laser Melting. Ceram. Int. 2019, 45, 175–184. [Google Scholar] [CrossRef]
- Juste, E.; Petit, F.; Lardot, V.; Cambier, F. Shaping of Ceramic Parts by Selective Laser Melting of Powder Bed. J. Mater. Res. 2014, 29, 2086–2094. [Google Scholar] [CrossRef]
- Gan, M.X.; Wong, C.H. Properties of Selective Laser Melted Spodumene Glass-Ceramic. J. Eur. Ceram. Soc. 2017, 37, 4147–4154. [Google Scholar] [CrossRef]
- Song, B.; Dong, S.; Liao, H.; Coddet, C. Process Parameter Selection for Selective Laser Melting of Ti6Al4V Based on Temperature Distribution Simulation and Experimental Sintering. Int. J. Adv. Manuf. Technol. 2012, 61, 967–974. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Petkov, P.V. Laser Milling of Ceramic Components. Int. J. Mach. Tools Manuf. 2007, 47, 618–626. [Google Scholar] [CrossRef]
- Liu, Q.; Song, B.; Liao, H. Microstructure Study on Selective Laser Melting Yttria Stabilized Zirconia Ceramic with near IR Fiber Laser. Rapid Prototyp. J. 2014, 20, 346–354. [Google Scholar] [CrossRef]
- Navarrete-Segado, P.; Frances, C.; Tourbin, M.; Tenailleau, C.; Duployer, B.; Grossin, D. Powder Bed Selective Laser Process (Sintering/Melting) Applied to Tailored Calcium Phosphate-Based Powders. Addit. Manuf. 2022, 50, 102542. [Google Scholar] [CrossRef]
- Fan, Z.; Lu, M.; Huang, H. Selective Laser Melting of Alumina: A Single Track Study. Ceram. Int. 2018, 44, 9484–9493. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Guillemot, G.; Gandin, C.-A.; Bellet, M. Three-Dimensional Finite Element Thermomechanical Modeling of Additive Manufacturing by Selective Laser Melting for Ceramic Materials. Addit. Manuf. 2017, 16, 124–137. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Guillemot, G.; Gandin, C.-A.; Bellet, M. Numerical Modelling of the Impact of Energy Distribution and Marangoni Surface Tension on Track Shape in Selective Laser Melting of Ceramic Material. Addit. Manuf. 2018, 21, 713–723. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, T.; Liao, W.; Zhang, C.; Zheng, Y.; Shao, H. Simulation of the Thermal Behavior and Analysis of Solidification Process during Selective Laser Melting of Alumina. In 2018 International Solid Freeform Fabrication Symposium; University of Texas at Austin: Austin, TX, USA, 2018; pp. 1808–1820. [Google Scholar]
- Li, C.; Fu, C.H.; Guo, Y.B.; Fang, F.Z. A Multiscale Modeling Approach for Fast Prediction of Part Distortion in Selective Laser Melting. J. Mater. Process. Technol. 2016, 229, 703–712. [Google Scholar] [CrossRef]
- Casuso, M.; Veiga, F.; Suárez, A.; Bhujangrao, T.; Aldalur, E.; Artaza, T.; Amondarain, J.; Lamikiz, A. Model for the Prediction of Deformations in the Manufacture of Thin-Walled Parts by Wire Arc Additive Manufacturing Technology. Metals 2021, 11, 678. [Google Scholar] [CrossRef]
- Ding, J.; Colegrove, P.; Mehnen, J.; Ganguly, S.; Sequeira Almeida, P.M.; Wang, F.; Williams, S. Thermo-Mechanical Analysis of Wire and Arc Additive Layer Manufacturing Process on Large Multi-Layer Parts. Comput. Mater. Sci. 2011, 50, 3315–3322. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Colegrove, P.; Ding, J.; Zhou, X.; Diao, C.; Bridgeman, P.; Hönnige, J.R.; Zhang, H.; Williams, S. Numerical Analysis of Heat Transfer and Fluid Flow in Multilayer Deposition of PAW-Based Wire and Arc Additive Manufacturing. Int. J. Heat Mass Transf. 2018, 124, 504–516. [Google Scholar] [CrossRef] [Green Version]
- Moser, D.; Beaman, J.; Fish, S. Multi-Layer Computational Modeling of Selective Laser Sintering Processes. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition IMECE2014, Montreal, QC, Canada, 14–20 November 2014; American Society of Mechanical Engineers: New York, NY, USA, 2016; pp. 1–11. [Google Scholar]
- ANSYS Inc. ANSYS FLUENT Theory Guide; Release 18.2; ANSYS Inc.: Canonsburg, PA, USA, 2013; Volume 15317, pp. 373–464. [Google Scholar] [CrossRef]
- ANSYS Inc. U.S.A. Theory Reference for the Mechanical APDL and Mechanical Applications. Knowl. Creat. Diffus. Util. 2009, 3304, 724–746. [Google Scholar]
- Engineering, N. Modeling, Analysis and Experiments for Fusion Nuclear Technology: FNT Progress Report: Modeling and FINESSE; California University: Los Angeles, CA, USA, 2019; pp. 7–8. [Google Scholar]
- Touloukian, Y.S. Thermophysical Properties of High Temperature Solid Materials; Thermophysical and Electronic Properties Information Analysis Center: Boulder, CO, USA, 1966. [Google Scholar]
- Huang, Q.; Bando, Y.; Xu, X.; Nishimura, T.; Zhi, C.; Tang, C.; Xu, F.; Gao, L.; Golberg, D. Enhancing Superplasticity of Engineering Ceramics by Introducing BN Nanotubes. Nanotechnology 2007, 18, 485706. [Google Scholar] [CrossRef] [Green Version]
- ASM Engineered Materials Reference Book, 2nd ed.; Bauccio, M. (Ed.) ASM International: Materials Park, OH, USA, 1994; ISBN 0654701067. [Google Scholar]
- Edith Wiria, F.; Fai Leong, K.; Kai Chua, C. Modeling of Powder Particle Heat Transfer Process in Selective Laser Sintering for Fabricating Tissue Engineering Scaffolds. Rapid Prototyp. J. 2010, 16, 400–410. [Google Scholar] [CrossRef]







| Item | Symbol | Expression/Value | Unit | Ref. |
|---|---|---|---|---|
| Density | 3920 | kg/m3 | ||
| Specific heat 1 | 3 × 10−13 T5 − 3 × 10−9 T4 + 5 × 10−6 T3 − 0.0073 T2 + 5.0097 T − 190.71, (T ≤ 2450) 1360, (T > 2450) | J/kg-K | [42] | |
| Thermal conductivity 1 | −3 × 10−15 T5 − 3 × 10−11 T4 − 10−7 T3 + 0.0002 T2 − 0.203 T + 79.673, (T ≤ 2450) 5.5, (T > 2450) | W/kg-K | ||
| Melting point, | 2327 | K | ||
| Latent heat of melting, | 1,137,900 | J/kg | ||
| Emissivity | 0.7 | |||
| Stefan Boltzmann constant, | 5.6704 × 10−8 | W/m2 K4 | ||
| Thermal convection coefficient, | 200 | W/m2 K4 | ||
| Absorptivity/CO2 laser | 0.96 | [39] | ||
| Absorptivity/Fiber laser | 0.03 |
| Dimension | Base Plate (mm) | Printed Part (mm) |
|---|---|---|
| Length | 2 | 1.5 |
| Width | 1.5 | 1 |
| Thickness | 0.5 | 0.5 1 |
| Mesh | Mesh Edge Size (µm) | Elapsed Time to Solve One Time Step (s) | Temperature (K) |
|---|---|---|---|
| A | 10 | 3.6 | 3365.95 |
| B | 5 | 4.6 | 3388.48 |
| C | 2.5 | 5.7 | 3395.23 |
| D | 2 | 5.8 | 3396.35 |
| Item | Value |
|---|---|
| Laser power range, W | 15–50 |
| Scanning speed range, mm/s | 500–1200 |
| Layer thickness, µm | 50 |
| Power, W | Temperature Distribution | Top Melting Contour | Vertical Melting Contour |
|---|---|---|---|
| 95 |  | 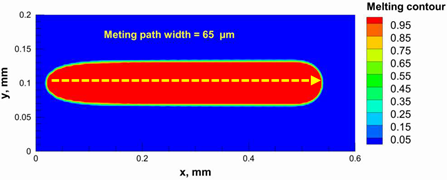 | 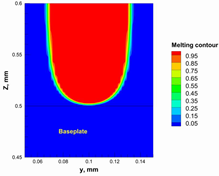 |
| 100 | 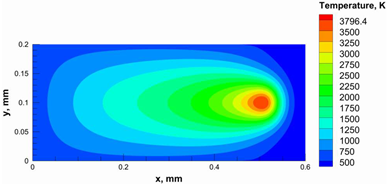 | 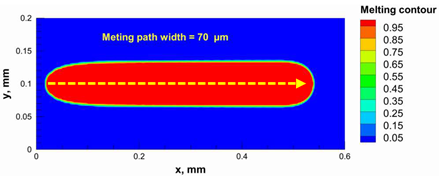 | 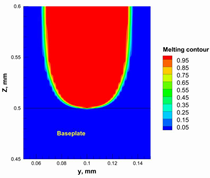 |
| 105 | 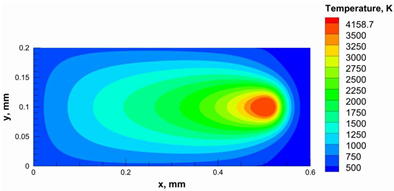 | 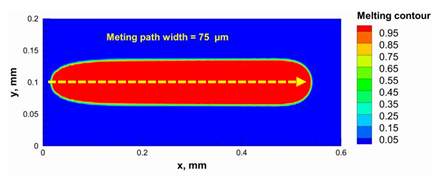 | 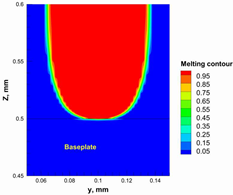 |
| Power, W | Scanning Speed, mm/s | Temperature Distribution | Top Melting Contour | Vertical Melting Contour |
|---|---|---|---|---|
| 30 | 600 | 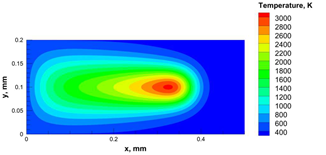 | 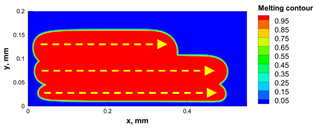 |  |
| 40 | 900 |  | 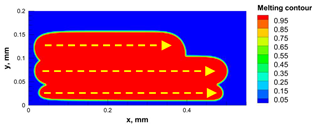 | 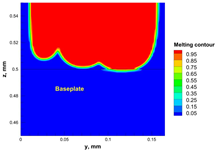 |
| 50 | 1200 | 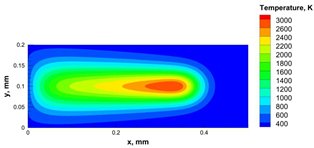 |  | 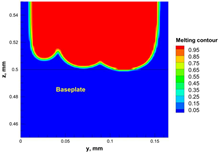 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmoula, M.; Küçüktürk, G. Multi-Layer Simulation of the Powder Bed Selective Laser Processing of Alumina for Residual Stress and Distortion Evaluation. Materials 2022, 15, 3498. https://doi.org/10.3390/ma15103498
Abdelmoula M, Küçüktürk G. Multi-Layer Simulation of the Powder Bed Selective Laser Processing of Alumina for Residual Stress and Distortion Evaluation. Materials. 2022; 15(10):3498. https://doi.org/10.3390/ma15103498
Chicago/Turabian StyleAbdelmoula, Mohamed, and Gökhan Küçüktürk. 2022. "Multi-Layer Simulation of the Powder Bed Selective Laser Processing of Alumina for Residual Stress and Distortion Evaluation" Materials 15, no. 10: 3498. https://doi.org/10.3390/ma15103498
APA StyleAbdelmoula, M., & Küçüktürk, G. (2022). Multi-Layer Simulation of the Powder Bed Selective Laser Processing of Alumina for Residual Stress and Distortion Evaluation. Materials, 15(10), 3498. https://doi.org/10.3390/ma15103498






