NSF-Based Analysis of the Structural Stressing State of Trussed Steel and a Concrete Box Girder
Abstract
:1. Introduction
2. Theory of Structural Stressing State Analysis
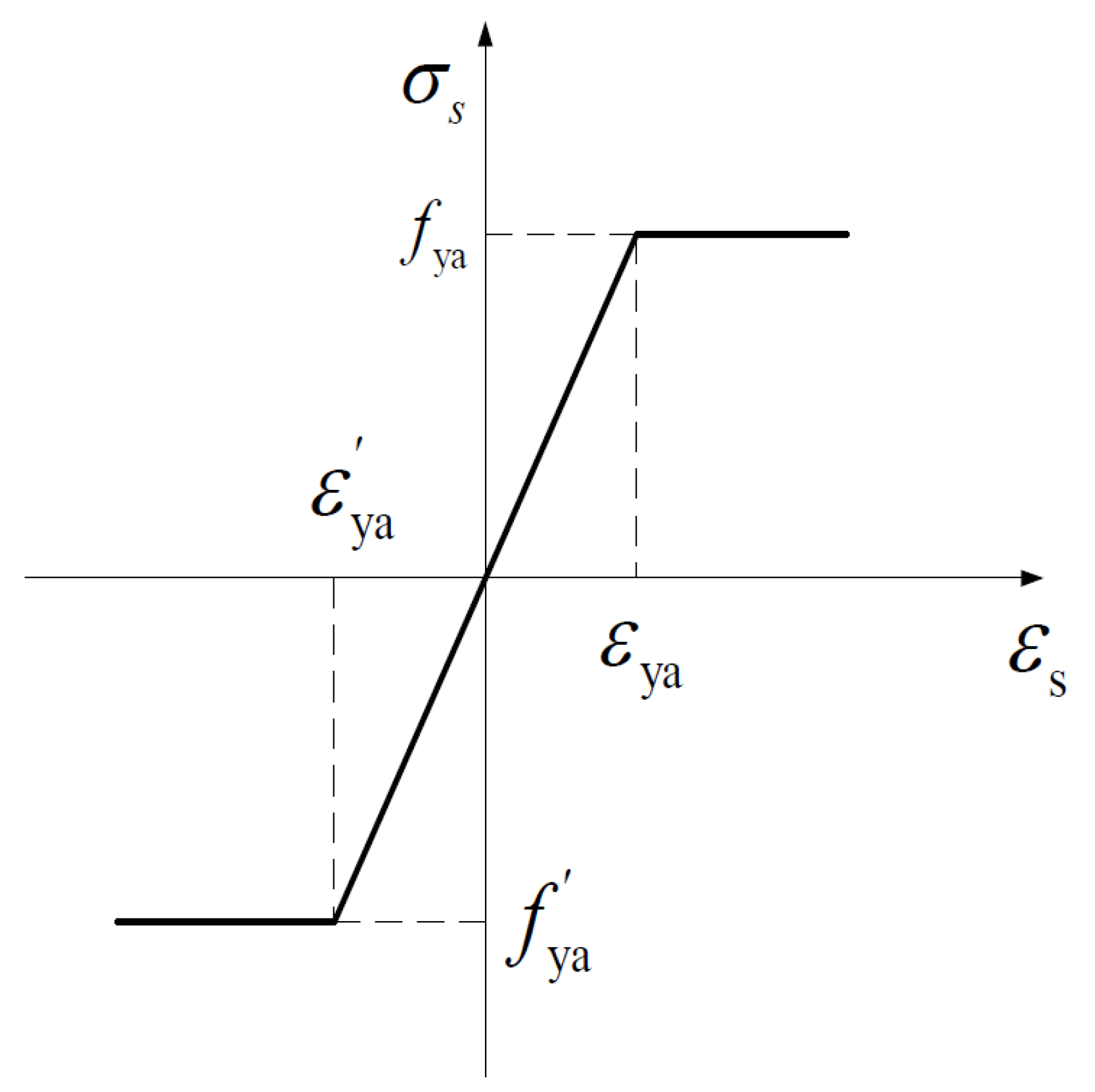
2.1. Method of Modeling a Structural Stressing State
2.2. The Application of the Mann-Kendall Criterion
3. Introduction of the Experiments
3.1. Specimen Design
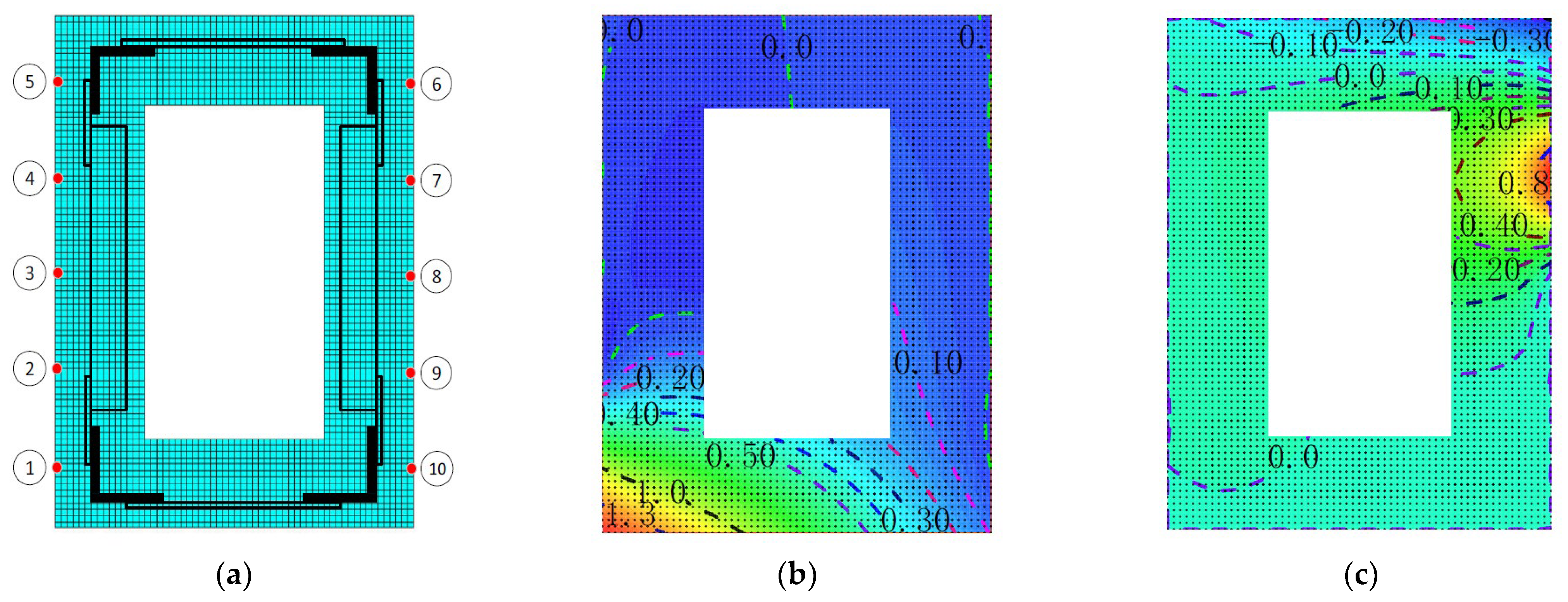
3.2. Measurement Point Arrangement and Loading Scheme
4. Analysis of the Structural Stressing State of the Beam-A3
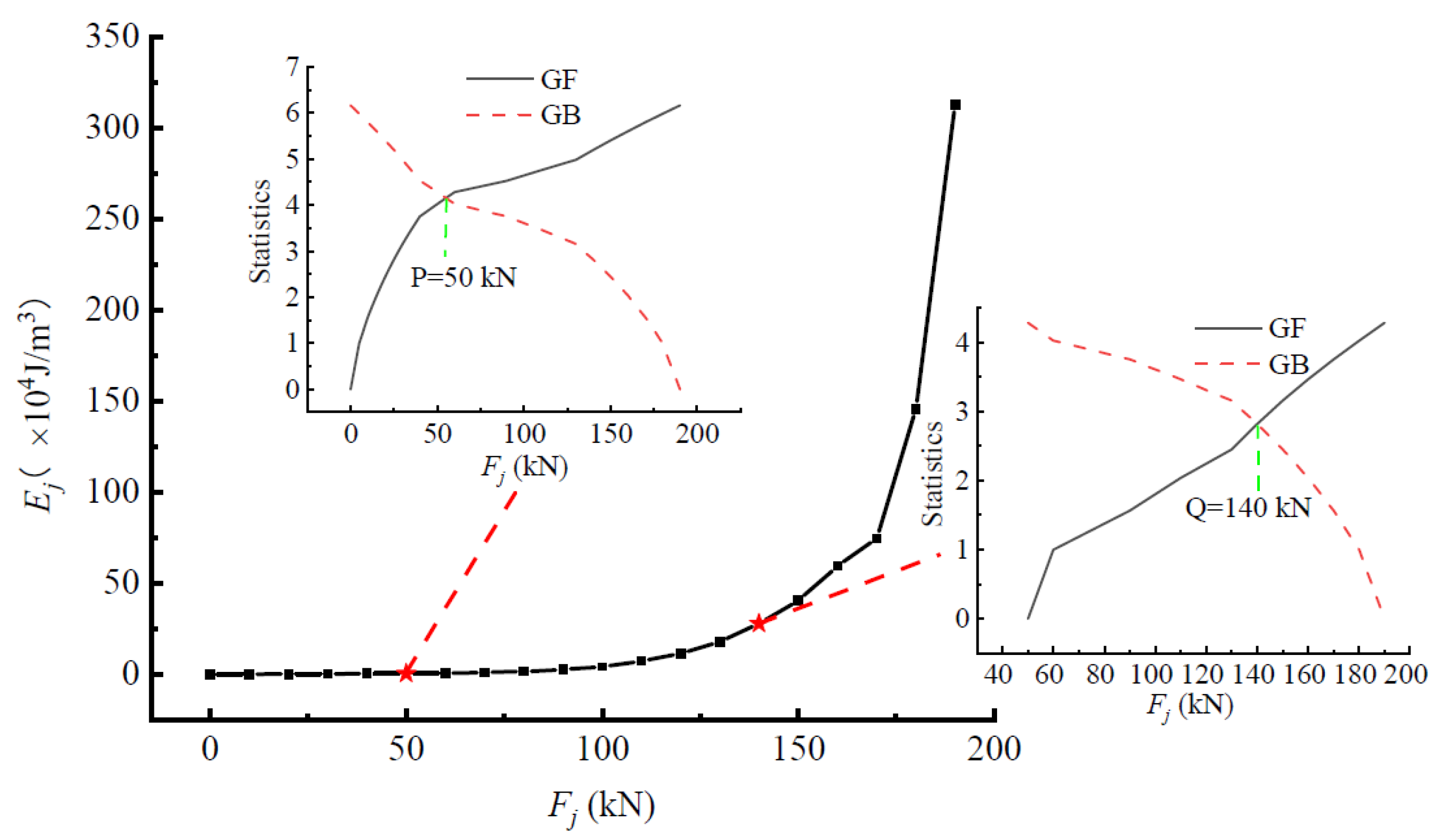
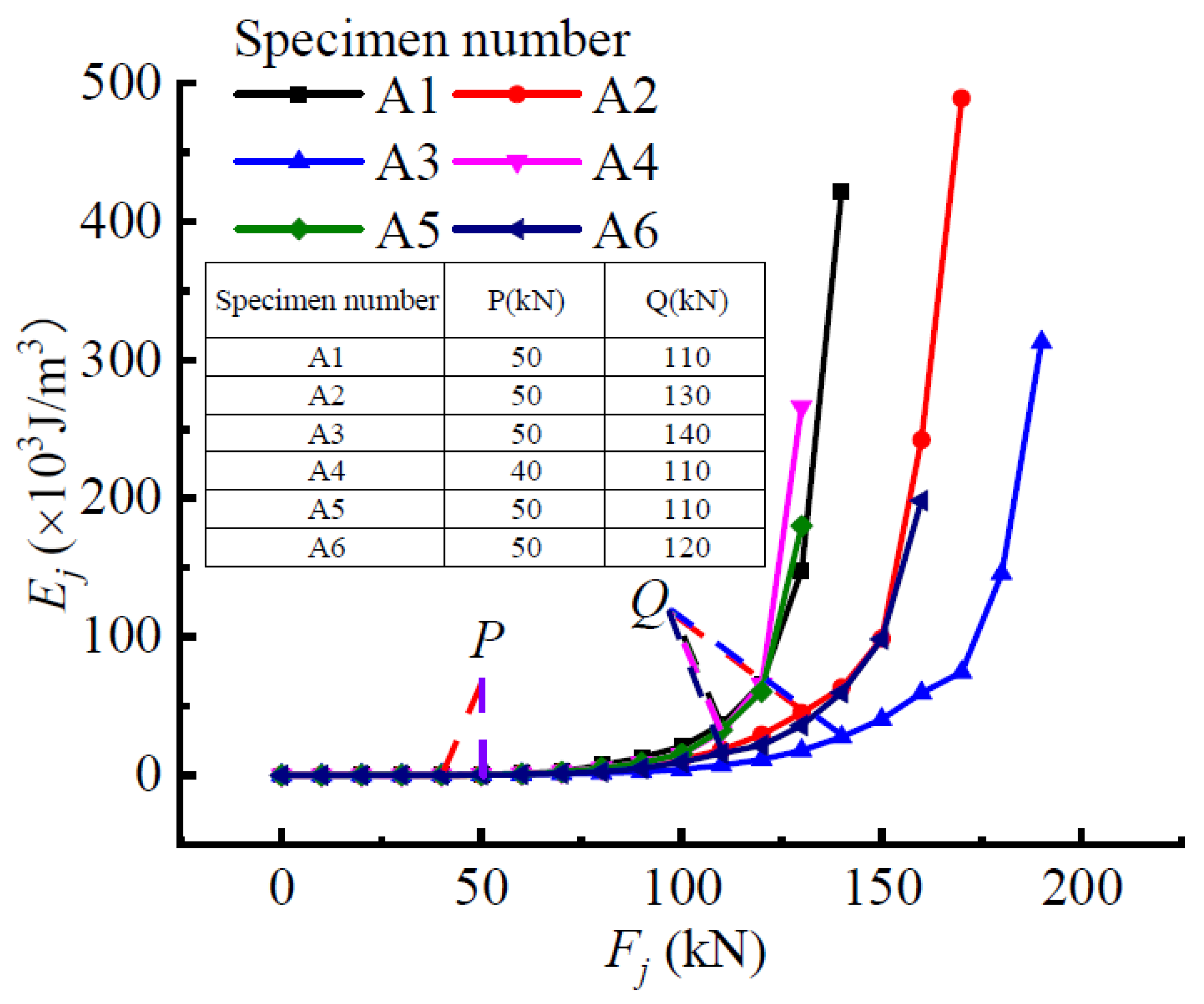
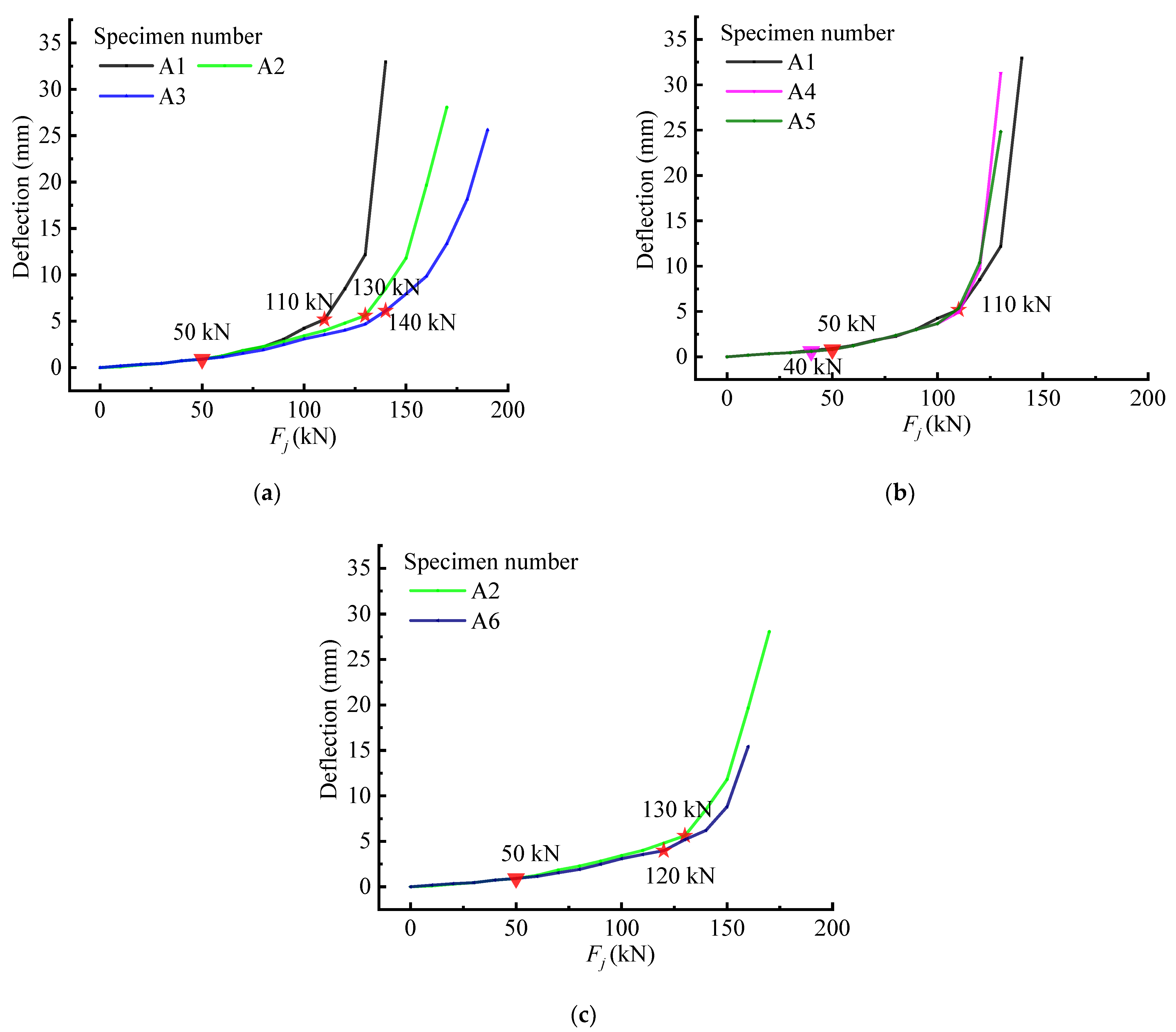
4.1. The Ej-Fj Curve of the Test Beam and Failure Load Analysis
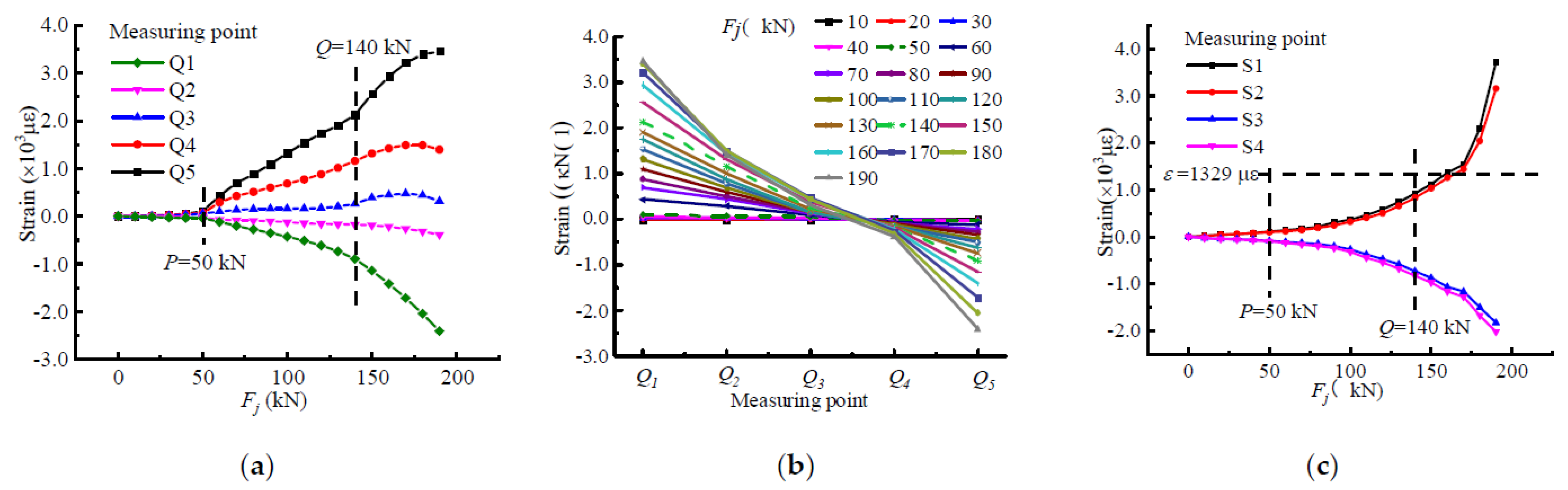
4.2. Strain-Based Characterization of the Stressing State for Beam-A3
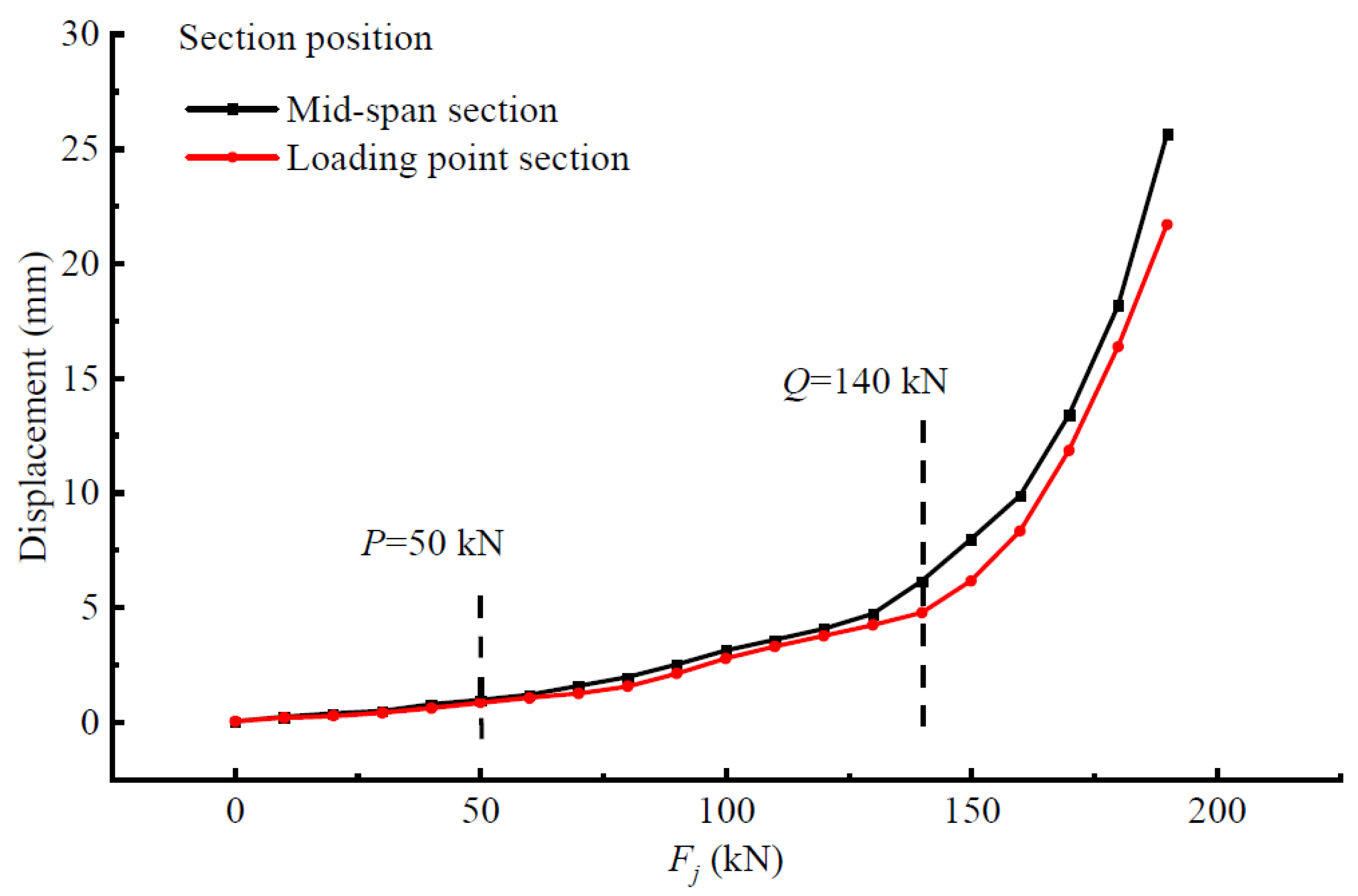
4.3. Displacement-Based Characterization of the Stressing State for Beam-A3
5. Stress State Analysis Based on Strain Interpolation
5.1. Numerical Shape Function Method
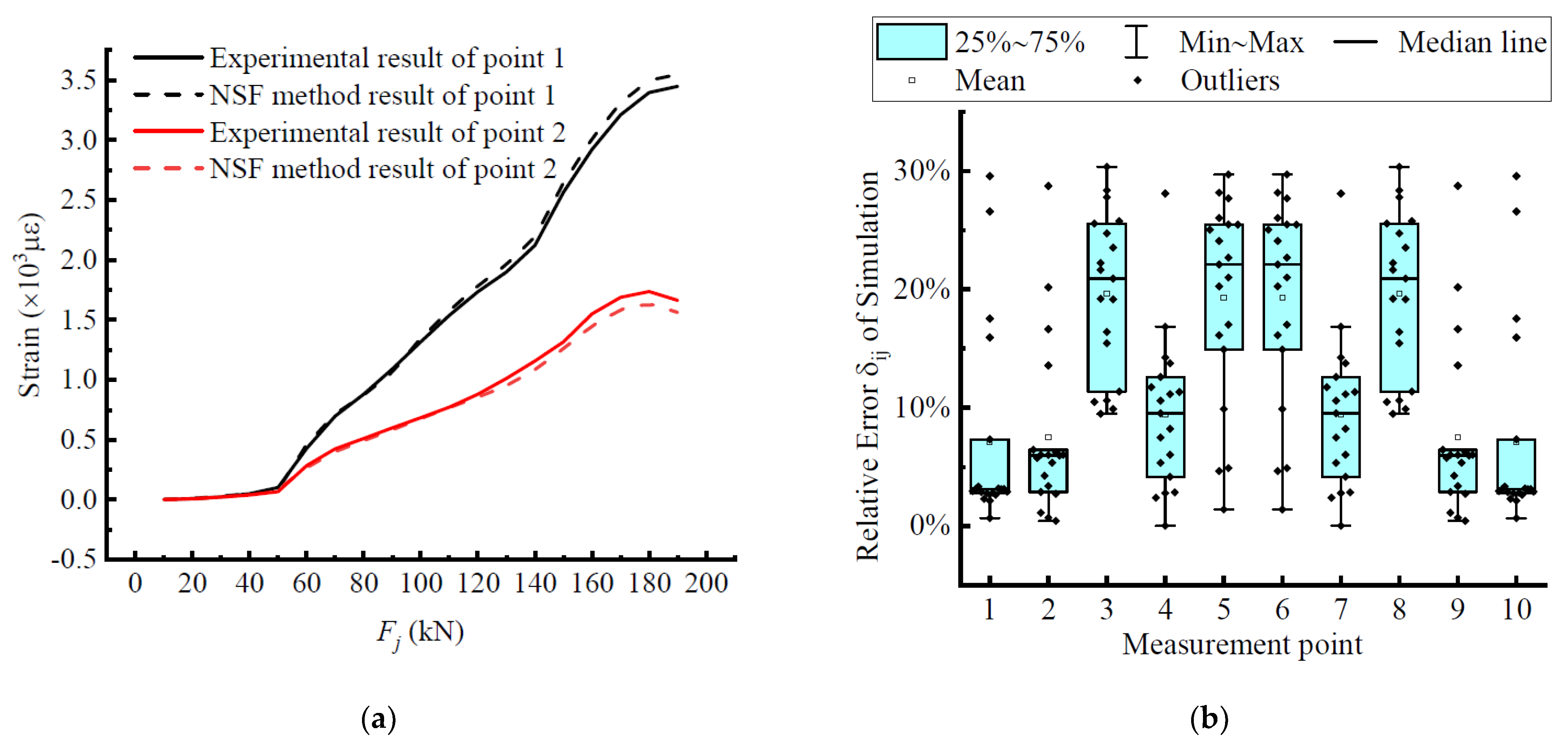
5.2. Extended Data Accuracy Analysis
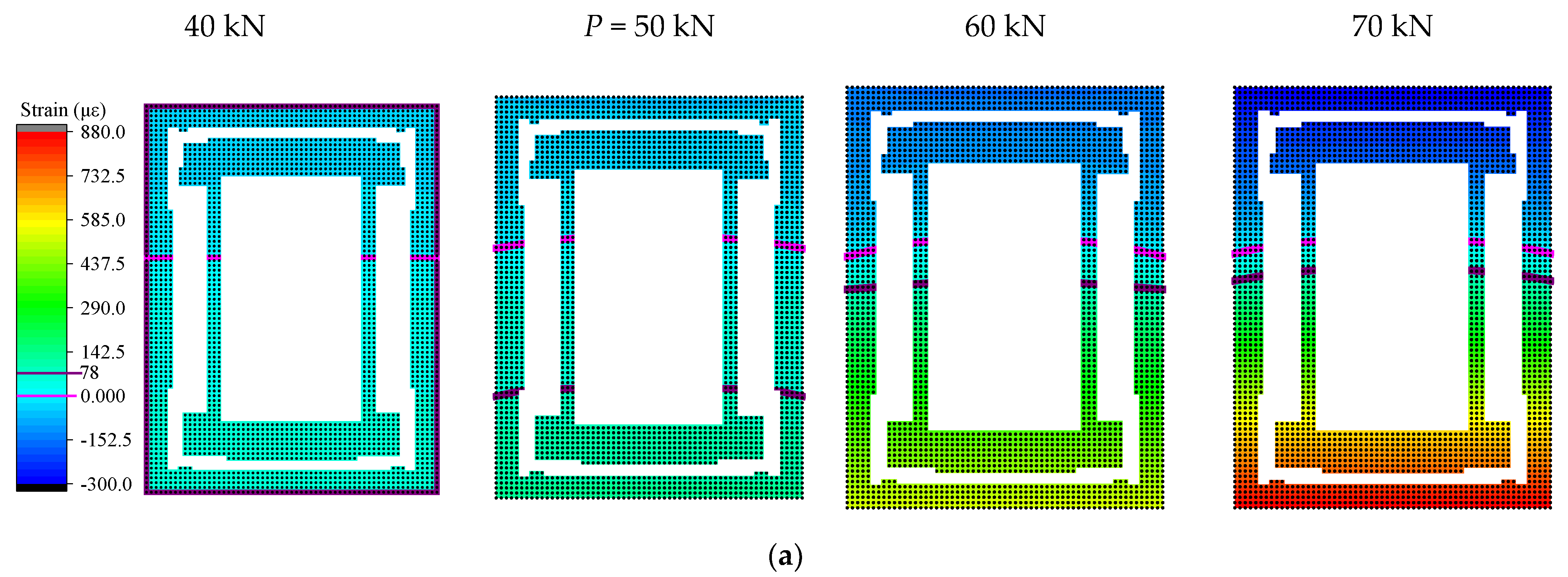
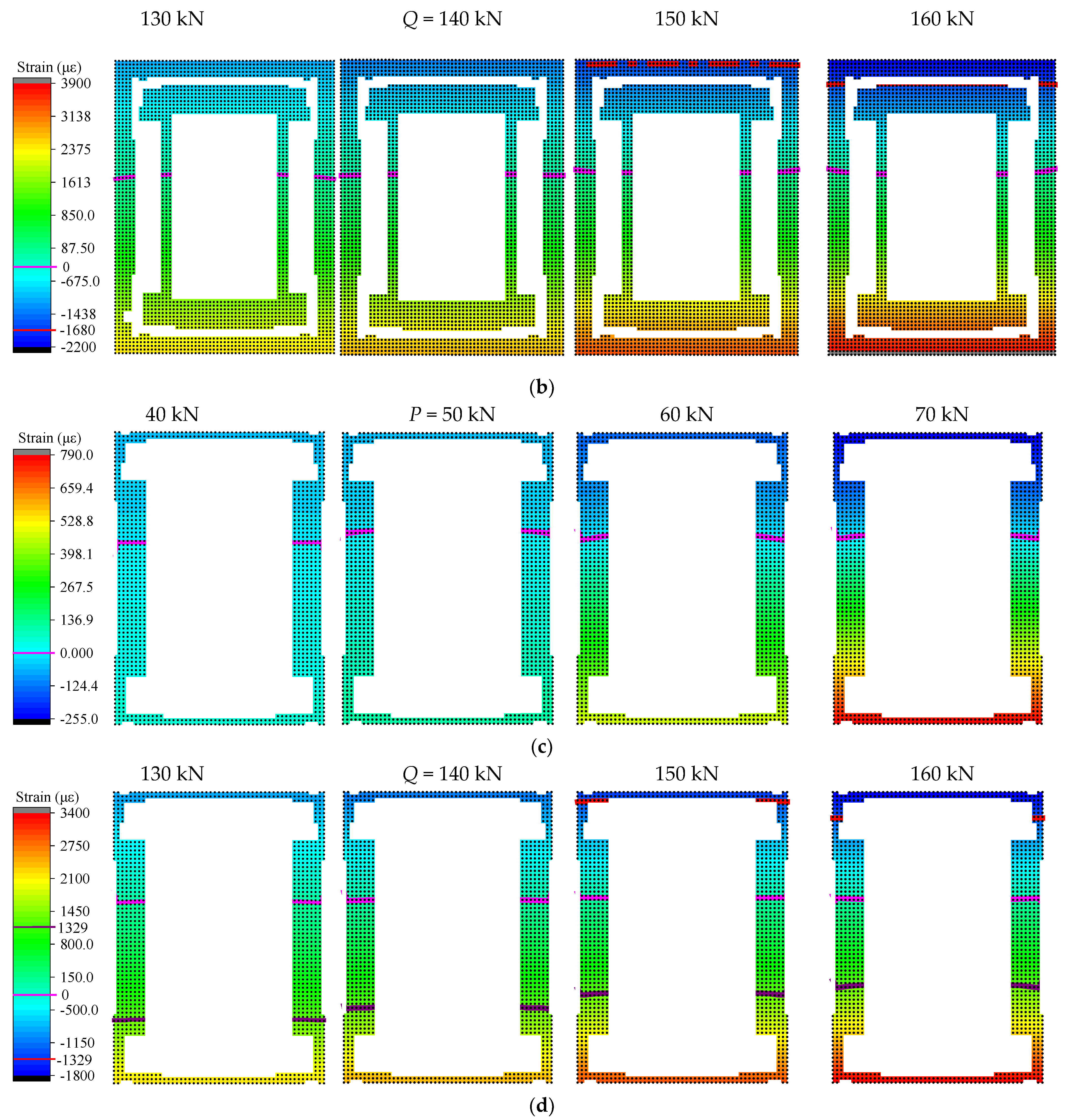
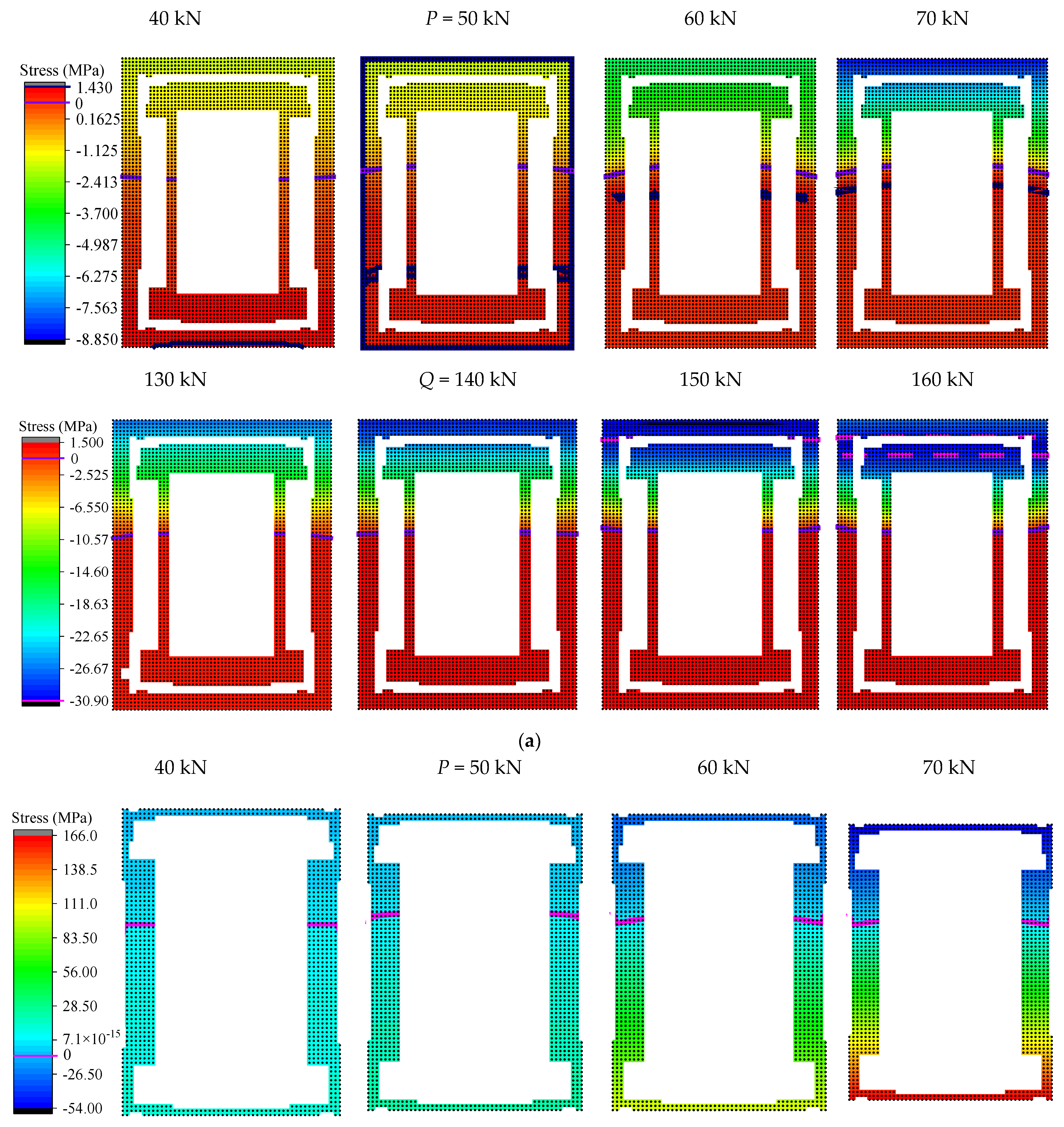
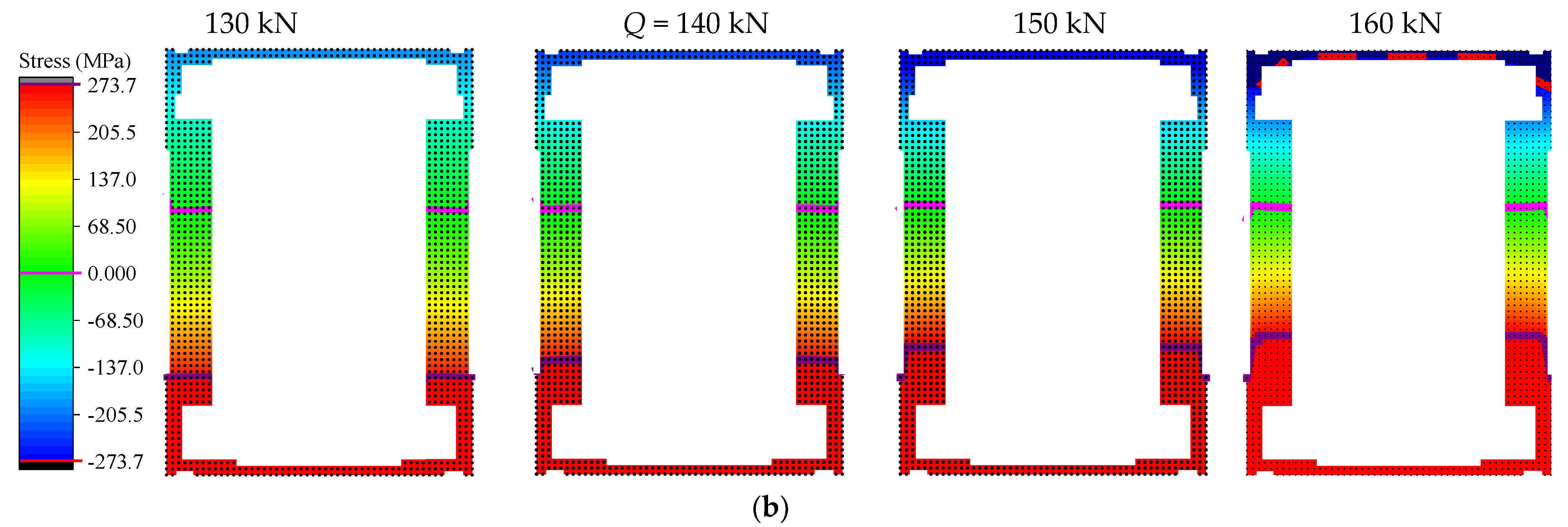
5.3. Strain/Stress Field Analysis
5.4. Internal Forces Analysis
6. Effects of Different Test Parameters on the Stress State Characteristics of a Steel Stud Concrete Box Girder
6.1. Analysis of Different Truss-Type Steel Stud Concrete Stress State Patterns Based on GSED
6.2. Analysis of Strains and Displacements of Different Steel Reinforced Concrete
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Montava, I.; Irles, R.; Pomares, J.C.; Gonzalez, A. Experimental study of steel reinforced concrete (SRC) joints. Appl. Sci. 2019, 9, 1528. [Google Scholar] [CrossRef] [Green Version]
- Tong, L.; Liu, B.; Xian, Q.; Zhao, X.-L. Experimental study on fatigue behavior of Steel reinforced concrete beams. Eng. Struct. 2016, 123, 247–262. [Google Scholar] [CrossRef]
- Yu, Y.; Wei, B.; Yang, Y.; Xue, Y.; Xue, H. Experimental study on flexural performance of steel-reinforced concrete slim floor beams. Adv. Struct. Eng. 2019, 22, 2406–2417. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Zeng, Q. Design methods of reinforce-concrete frame structure to resist progressive collapse in civil engineering. Syst. Eng. Procedia 2011, 1, 48–54. [Google Scholar] [CrossRef] [Green Version]
- Kalamkarov, A.; Saha, G.; Rokkam, S.; Newhook, J.; Georgiades, A. Strain and deformation monitoring in infrastructure using embedded smart FRP reinforcements. Compos. Part B Eng. 2005, 36, 455–467. [Google Scholar] [CrossRef]
- Chen, Z.P.; Zhong, M.; Chen, Y.L.; Zhang, X.G. Experimental Study on Torsion Behaviors of Angle Steel Reinforced Concrete Beams. Adv. Mater. Res. 2012, 368, 81–84. [Google Scholar] [CrossRef]
- Xu, J.; Sun, X. Nonlinear finite element parametric analysis of prestressed steel reinforced concrete beams. IOP Conf. Ser. Mater. Sci. Eng. 2018, 439, 042050. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Chen, Y. Comparision study on the mechanical properties between Steel Reinforce Concrete Beam and Prestressed Steel Reinforced Concrete Beam. IOP Conf. Ser. Mater. Sci. Eng. 2018, 439, 042045. [Google Scholar] [CrossRef]
- Kozlov, A.V.; Kozlov, V.A. Experimental study of SSS of a steel concrete beam taking into account the rigidity of the connecting seam. J. Phys. Conf. Ser. 2021, 1902, 012010. [Google Scholar] [CrossRef]
- Meng, X.H.; Zhang, S.Y. Application and development of stainless steel reinforced concrete structure. MATEC Web Conf. 2016, 63, 03009. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Cao, X.; Luo, Q. Numerical simulation of steel-concrete composite Virender beam. IOP Conf. Ser. Earth Environ. Sci. 2017, 81, 012136. [Google Scholar] [CrossRef] [Green Version]
- Yong, Y.; Yanni, C.; Yicong, X.; Yunlong, Y. Calculation method of stiffness of partially fabricated steel reinforced concrete beams. IOP Conf. Ser. Earth Environ. Sci. 2021, 676, 012067. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Hong, W.K. Part I: The analytical model predicting post-yield behavior of concrete-encased steel beams considering various confinement effects by transverse reinforcements and steels. Materials 2019, 12, 2302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Xue, Y.; Yu, Y.; Ma, N.; Shao, Y. Experimental study on flexural performance of partially precast steel reinforced concrete beams. J. Constr. Steel Res. 2017, 133, 192–201. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Yang, Y.; Yu, Y. Shear strength model for steel reinforced concrete composite members: Short columns and deep beams. Eng. Struct. 2020, 216, 110748. [Google Scholar] [CrossRef]
- Jeong, S.Y.; Hong, W.K.; Park, S.C.; Lim, G.T.; Kim, E. Investigation of the Neutral Axis in the Positive Moment Region of Composite Beams. Int. J. Civ. Environ. Eng. 2011, 5, 755–760. [Google Scholar]
- Hong, W.K.; Lee, Y.; Kim, S.; Kim, S.I.; Yun, Y.J. Analytical investigation of hybrid composite precast beams with modified strain compatibility for entire history of nominal flexural capacity. Struct. Des. Tall Spec. Build. 2015, 24, 835–852. [Google Scholar] [CrossRef]
- Shi, X.; Xie, N.; Fortune, K.; Gong, J. Durability of steel reinforced concrete in chloride environments: An overview. Constr. Build. Mater. 2012, 30, 125–138. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Zhang, M.; Zhou, G. Method for predicting the failure load of masonry wall panels based on generalized strain-energy density. J. Eng. Mech. 2014, 140, 04014061. [Google Scholar] [CrossRef]
- Qiang, L. Study on Flexural Capacity of Precast Truss Steel Reinforced Concrete Box Girder. Master’s Thesis, Yangzhou University, Yangzhou, China, 2019. (In Chinese). [Google Scholar]
- Shi, J.; Zheng, K.K.; Tan, Y.Q.; Yang, K.K.; Zhou, G.C. Response simulating interpolation methods for expanding experimental data based on numerical shape functions. Comput. Struct. 2019, 218, 1–8. [Google Scholar] [CrossRef]
- Madenci, E.; Guven, I. The Finite Element Method and Applications in Engineering Using ANSYS; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ministry of Construction of the People’s Republic of China. GB 50010-2010 Code for Design of Concrete Structures; China Construction Industry Press: Beijing, China, 2010.

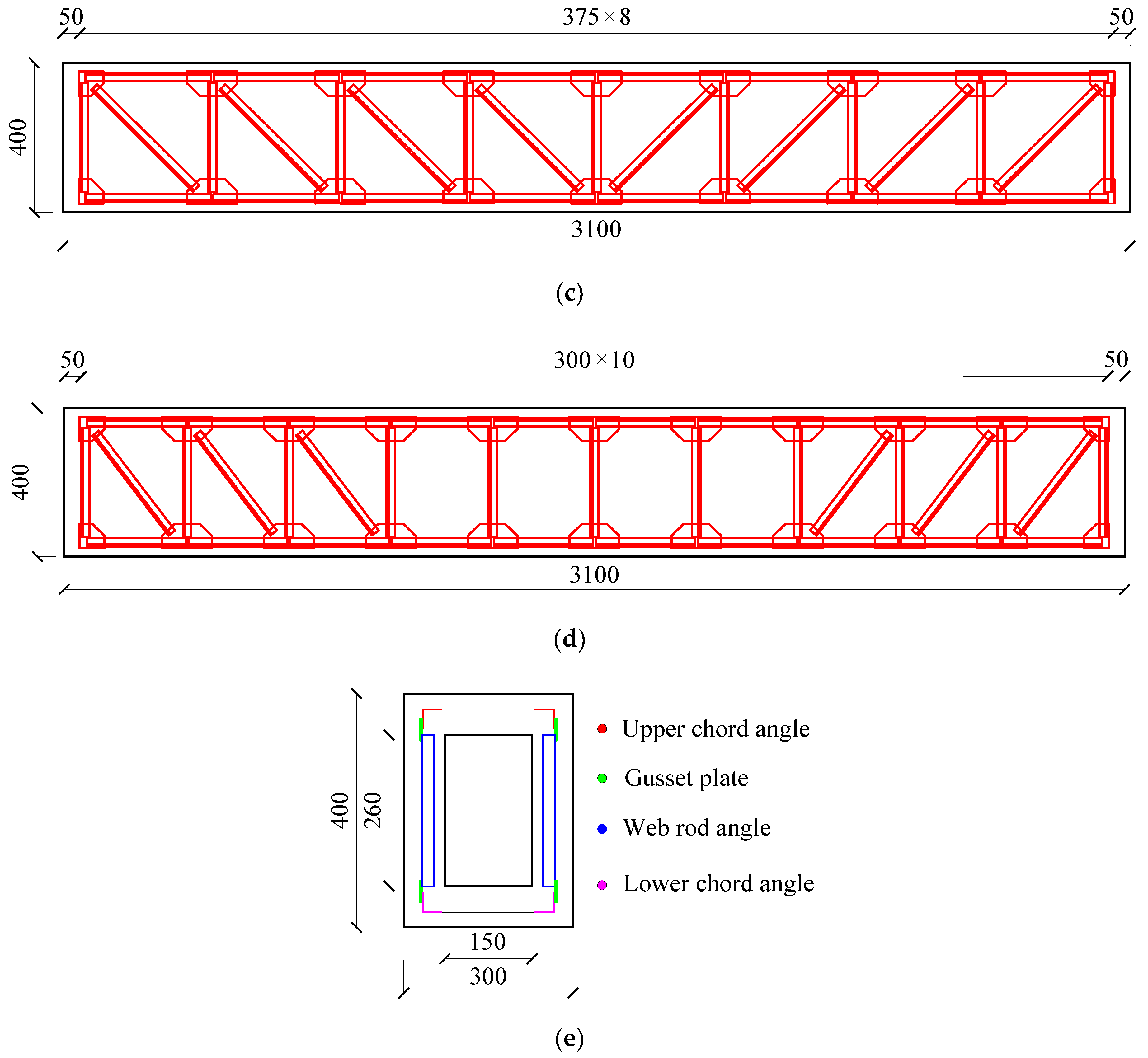
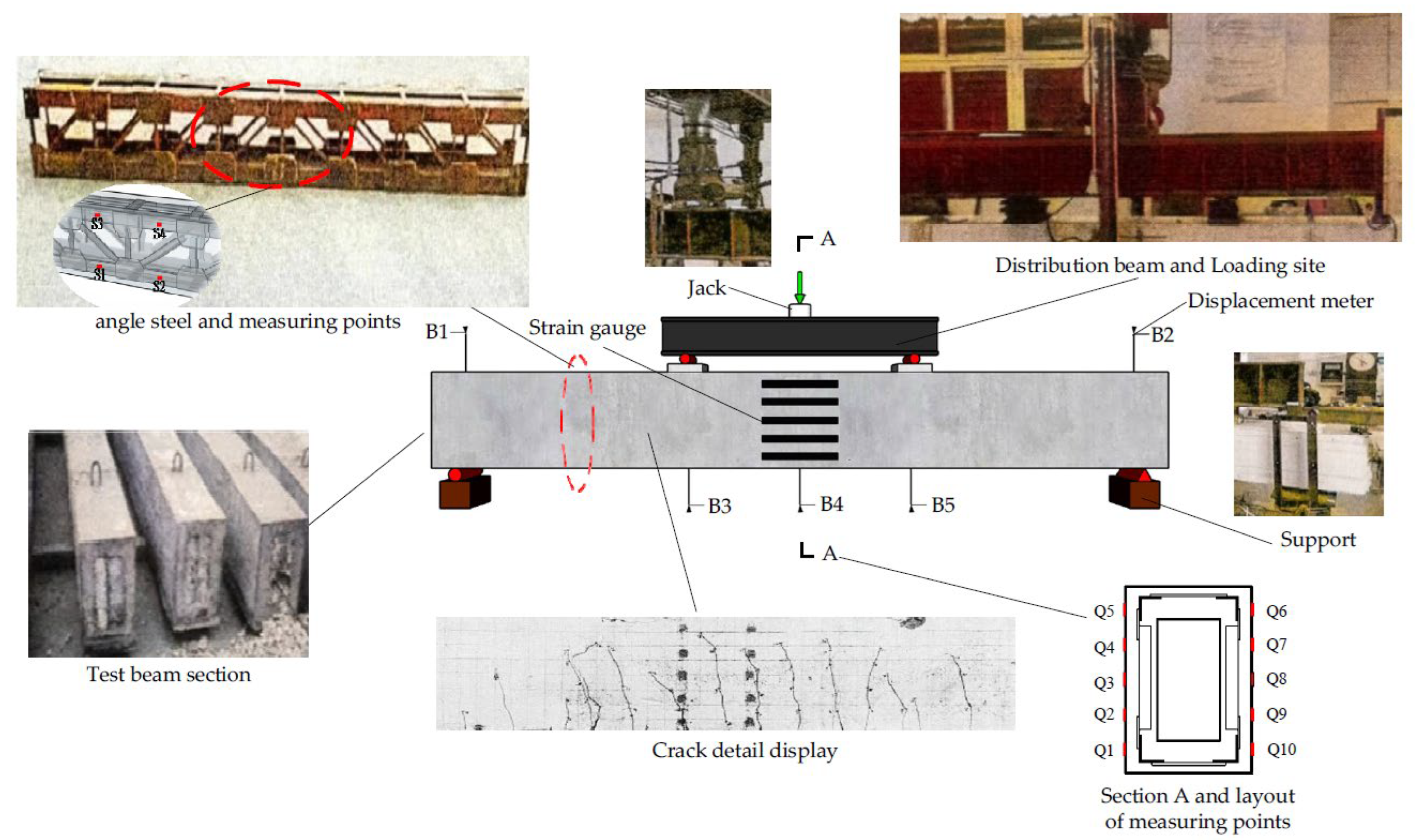

| Angle Steel Type | Specification | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| Equilateral angle steel | L30 × 3 | 273.7 | 379.5 | 206 |
| L40 × 4 | 306.4 | 438.7 | 192 | |
| L45 × 5 | 290.8 | 407.6 | 198 | |
| L50 × 5 | 279.2 | 393.8 | 200 |
| Specimen Number | Angle Steel | ||||
|---|---|---|---|---|---|
| Upper Chord Angle | Lower Chord Angle | Vertical Web Rod Angle | Oblique Web Angle Steel | Vertical Web Bar Spacing (mm) | |
| SRC-A1 | L30 × 3 | L40 × 4 | L30 × 3 | L30 × 3 | 300 |
| SRC-A2 | L30 × 3 | L45 × 5 | L30 × 3 | L30 × 3 | 300 |
| SRC-A3 | L30 × 3 | L50 × 5 | L30 × 3 | L30 × 3 | 300 |
| SRC-A4 | L30 × 3 | L40 × 4 | L30 × 3 | L30 × 3 | 450 |
| SRC-A5 | L30 × 3 | L40 × 4 | L30 × 3 | L30 × 3 | 375 |
| SRC-A6 | L30 × 3 | L45 × 5 | L30 × 3 | No(pure bending section) | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Lai, J.; Xu, F.; Wu, Z.; Yu, S.; Sun, G. NSF-Based Analysis of the Structural Stressing State of Trussed Steel and a Concrete Box Girder. Materials 2022, 15, 3785. https://doi.org/10.3390/ma15113785
Yuan J, Lai J, Xu F, Wu Z, Yu S, Sun G. NSF-Based Analysis of the Structural Stressing State of Trussed Steel and a Concrete Box Girder. Materials. 2022; 15(11):3785. https://doi.org/10.3390/ma15113785
Chicago/Turabian StyleYuan, Jian, Jie Lai, Feng Xu, Zhengfa Wu, Suhui Yu, and Guorui Sun. 2022. "NSF-Based Analysis of the Structural Stressing State of Trussed Steel and a Concrete Box Girder" Materials 15, no. 11: 3785. https://doi.org/10.3390/ma15113785





