Flow Behavior of AA5005 Alloy at High Temperature and Low Strain Rate Based on Arrhenius-Type Equation and Back Propagation Artificial Neural Network (BP-ANN) Model
Abstract
:1. Introduction
2. Materials and Methods
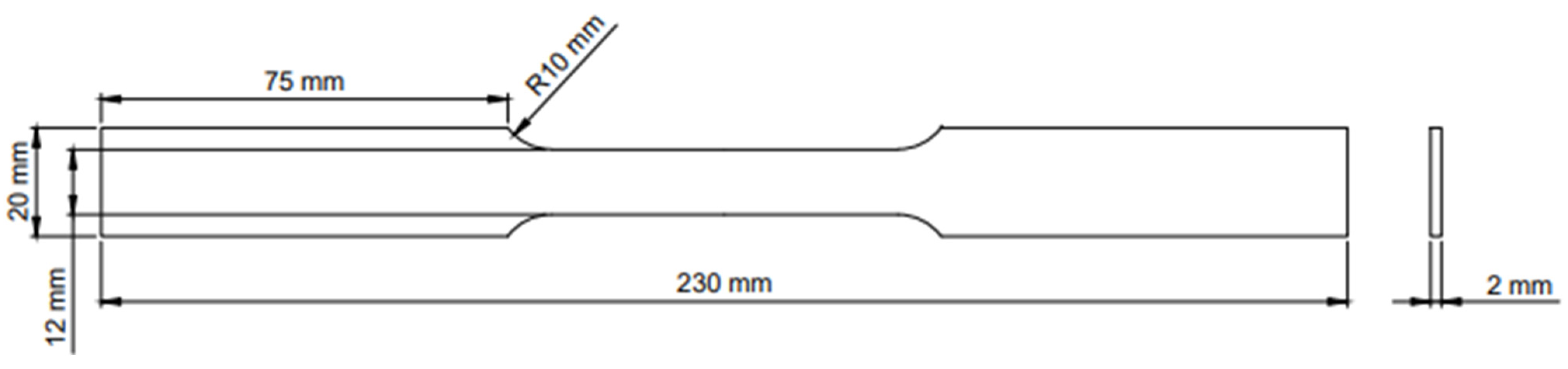
2.1. Experimental Procedures
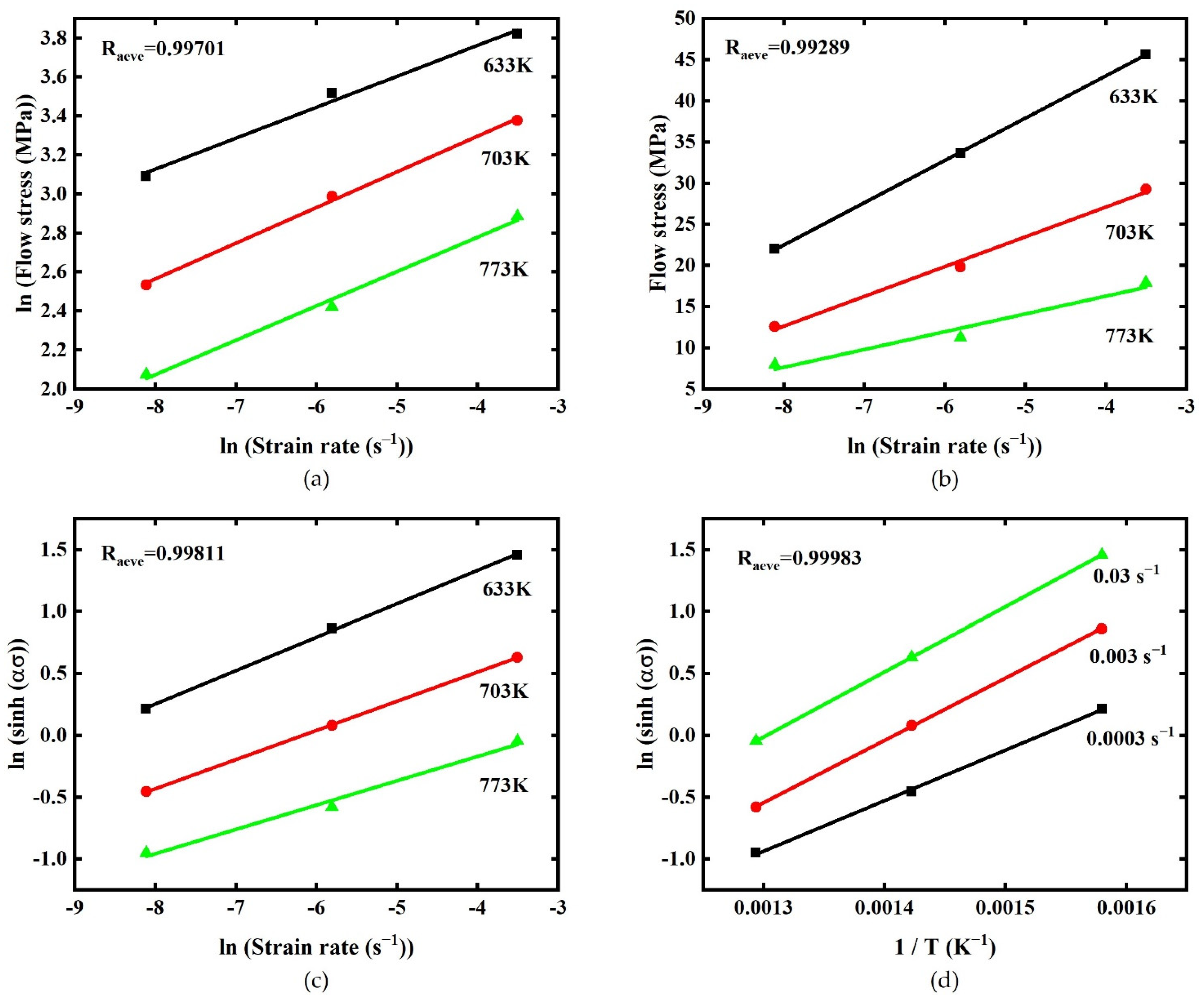
2.2. Establishment of Arrhenius-Type Constitutive Equation
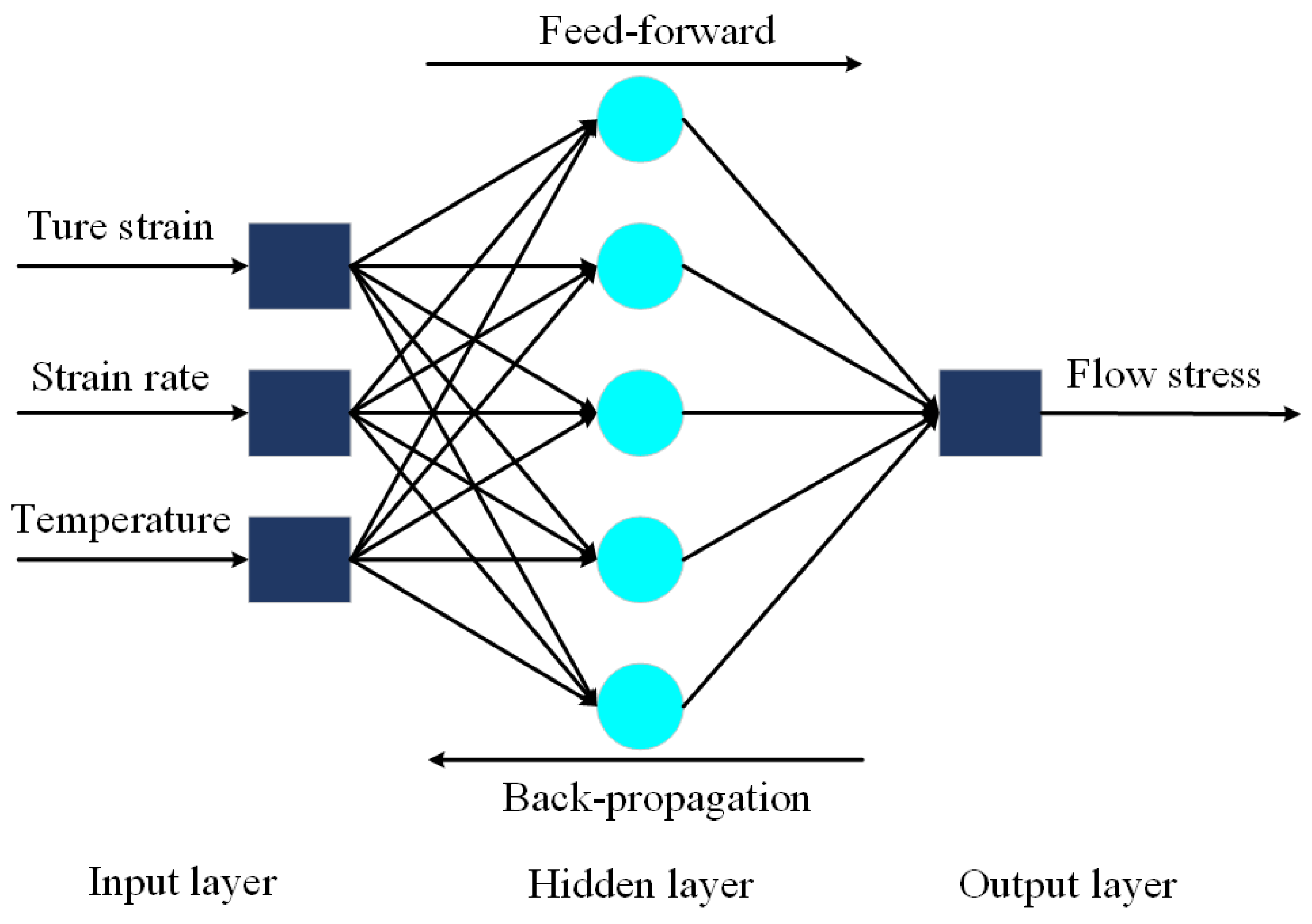
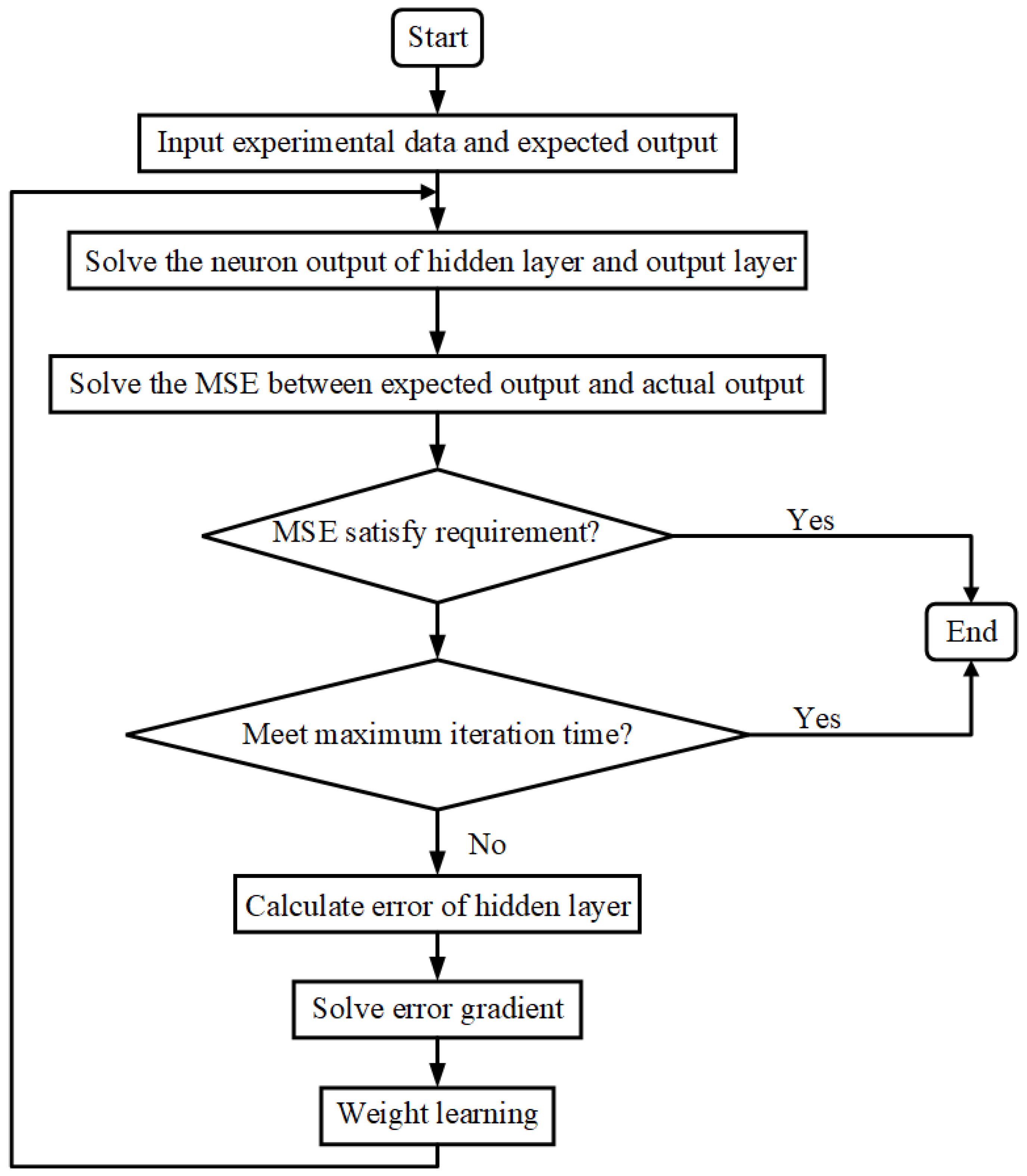
2.3. Modeling by BP-ANN Model
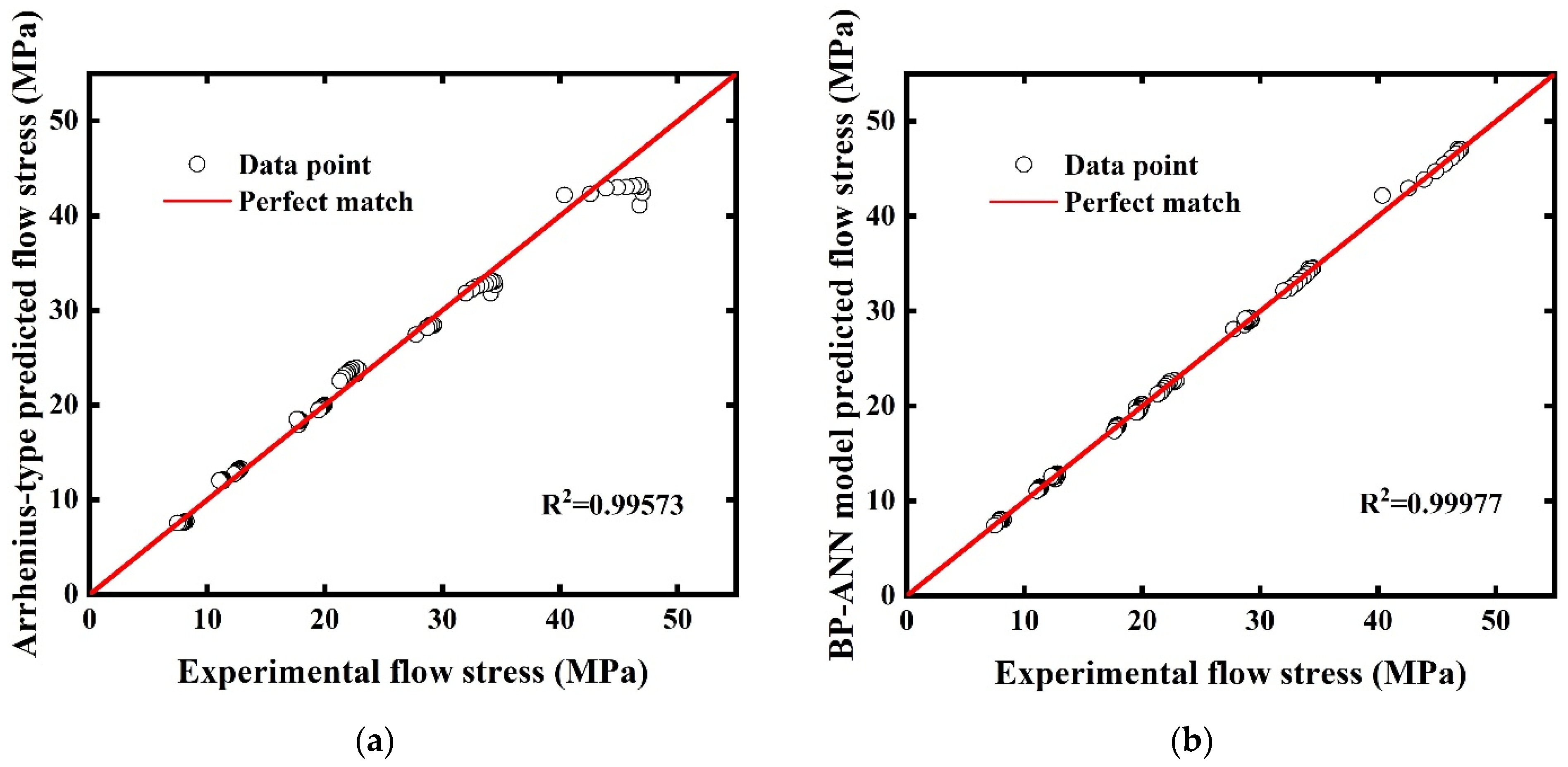
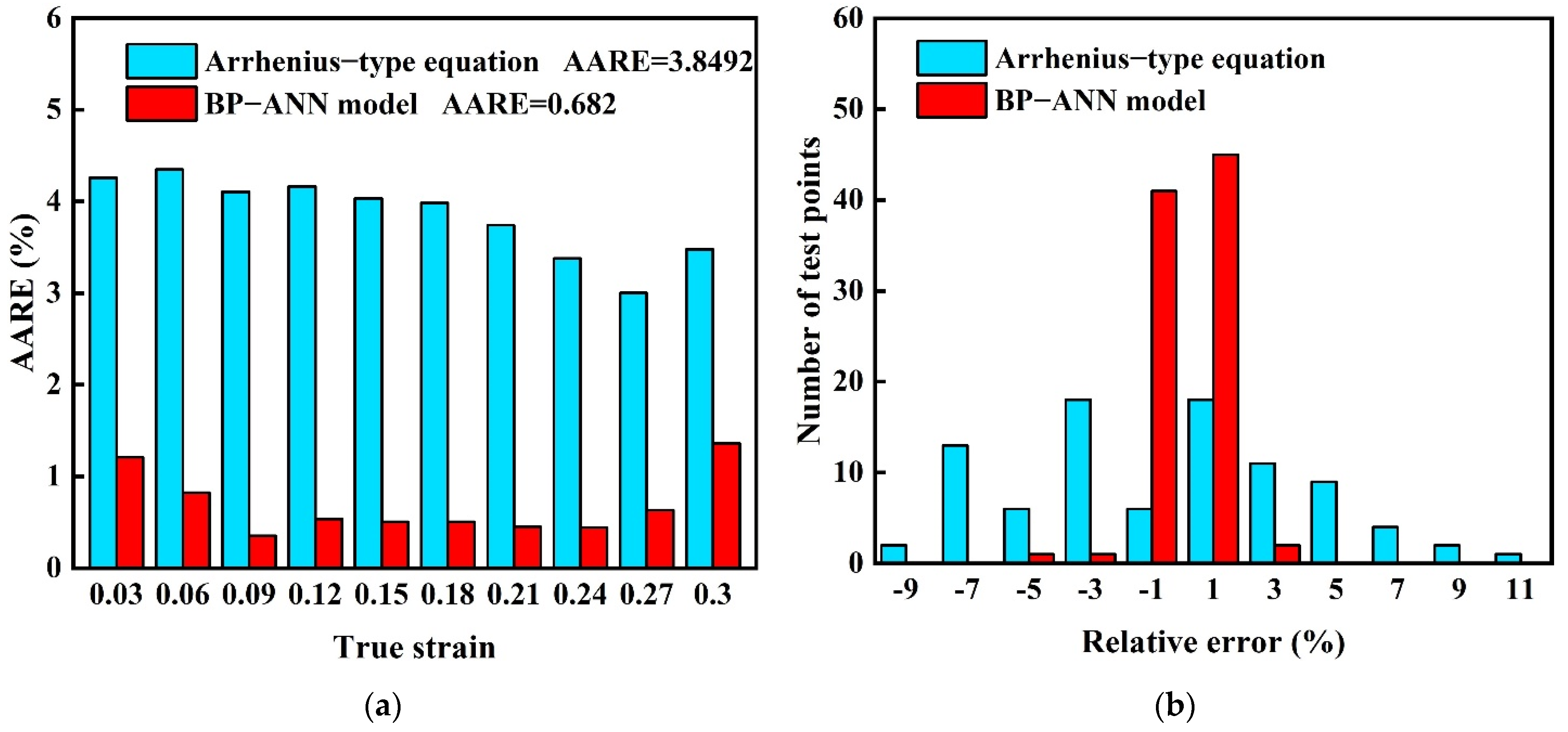
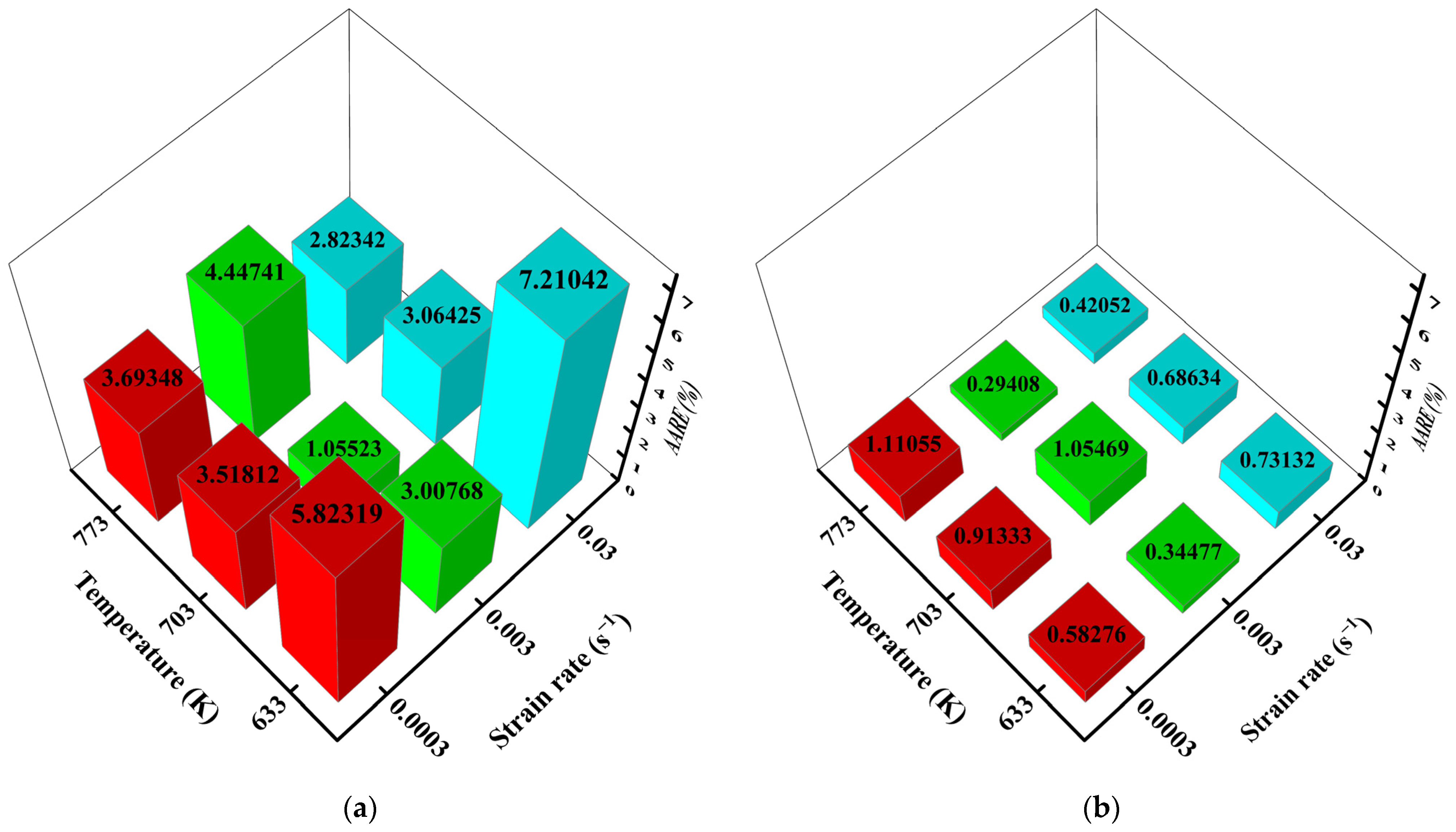
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Joost, W.J. Reducing Vehicle Weight and Improving U.S. Energy Efficiency Using Integrated Computational Materials Engineering. JOM 2012, 64, 1032–1038. [Google Scholar] [CrossRef] [Green Version]
- Engler, O.; Aegerter, J. Texture and anisotropy in the Al–Mg alloy AA 5005–Part II: Correlation of texture and anisotropic properties. Mater. Sci. Eng. A 2014, 618, 663–671. [Google Scholar] [CrossRef]
- Miller, W.S.; Zhuang, L.; Bottema, J.; Wittebrood, A.; De Smet, P.; Haszler, A.; Vieregge, A.J.M.S. Recent development in aluminium alloys for the automotive industry. Mater. Sci. Eng. A 2000, 280, 37–49. [Google Scholar] [CrossRef]
- Taleff, E.M.; Nevland, P.J.; Krajewski, P.E. Solute-drag creep and tensile ductility in aluminum alloys. In Creep Behavior of Advanced Materials for the 21st Century; Minerals, Metals & Materials Society: Warrendale, PA, USA, 1999; pp. 349–358. [Google Scholar]
- Lin, Y.C.; Chen, X.M.; Liu, G. A modified Johnson–Cook model for tensile behaviors of typical high-strength alloy steel. Mater. Sci. Eng. A 2010, 527, 6980–6986. [Google Scholar] [CrossRef]
- Cai, Z.; Ji, H.; Pei, W.; Pei, W.; Huang, X. Constitutive equation and model validation for 33Cr23Ni8Mn3N heat-resistant steel during hot compression. Results Phys. 2019, 15, 102633. [Google Scholar] [CrossRef]
- He, A.; Xie, G.; Zhang, H.; Wang, X. A modified Zerilli–Armstrong constitutive model to predict hot deformation behavior of 20CrMo alloy steel. Mater. Des. 2014, 56, 122–127. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Cai, J.; Wang, R. Comparative investigation on the modified Zerilli–Armstrong model and Arrhenius-type model to predict the elevated-temperature flow behaviour of 7050 aluminium alloy. Comput. Mater. Sci. 2013, 71, 56–65. [Google Scholar] [CrossRef]
- Shi, H.; McLaren, A.J.; Sellars, C.M.; Shahani, R.; Bolingbroke, R. Constitutive equations for high temperature flow stress of aluminium alloys. Mater. Sci. Technol. 1997, 13, 210–216. [Google Scholar] [CrossRef]
- Li, B.; Pan, Q.; Yin, Z. Microstructural evolution and constitutive relationship of Al–Zn–Mg alloy containing small amount of Sc and Zr during hot deformation based on Arrhenius-type and artificial neural network models. J. Alloy. Compd. 2014, 584, 406–416. [Google Scholar] [CrossRef]
- Pu, E.; Feng, H.; Liu, M.; Zheng, W. Constitutive modeling for flow behaviors of superaustenitic stainless steel S32654 during hot deformation. J. Iron Steel Res. Int. 2016, 23, 178–184. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, X.; Wang, X.; Liu, C. On the constitutive model of nitrogen-containing austenitic stainless steel 316LN at elevated temperature. PLoS ONE 2014, 9, e102687. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.; Zhang, S.; Liu, X.; Fei, F. A flow stress model of 300M steel for isothermal tension. Materials 2021, 14, 252. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Zhai, R.; Rui, M. New method to develop High temperature constitutive model of metal based on the Arrhenius-type model. Mater. Today Commun. 2020, 24, 101000. [Google Scholar] [CrossRef]
- Bodunrin, M.O. Flow stress prediction using hyperbolic-sine Arrhenius constants optimised by simple generalised reduced gradient refinement. J. Mater. Res. Technol. 2020, 9, 2376–2386. [Google Scholar] [CrossRef]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Bobbili, R.; Madhu, V.; Gogia, A.K. Neural network modeling to evaluate the dynamic flow stress of high strength armor steels under high strain rate compression. Def. Technol. 2014, 10, 334–342. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Pan, Q.-L.; Li, A.-D.; Song, W.-B. Flow behavior of Al–6.2 Zn–0.70 Mg–0.30 Mn–0.17 Zr alloy during hot compressive deformation based on Arrhenius and ANN models. Trans. Nonferrous Met. Soc. China 2017, 27, 638–647. [Google Scholar] [CrossRef]
- Han, Y.; Qiao, G.; Sun, J.P.; Zou, D. A comparative study on constitutive relationship of as-cast 904L austenitic stainless steel during hot deformation based on Arrhenius-type and artificial neural network models. Comput. Mater. Sci. 2013, 67, 93–103. [Google Scholar] [CrossRef]
- Ji, G.; Li, F.; Li, Q.; Li, H. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A 2011, 528, 4774–4782. [Google Scholar] [CrossRef]
- Di Pietro, P.; Yao, Y.L. An investigation into characterizing and optimizing laser cutting quality—A review. Int. J. Mach. Tools Manuf. 1994, 34, 225–243. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, B.; Wu, Y.; Yang, X. Constitutive modeling of flow behavior and microstructure evolution of AA7075 in hot tensile deformation. Mater. Sci. Eng. A 2018, 712, 704–713. [Google Scholar] [CrossRef]
- Kami, T.; Yamada, H.; Ogasawara, N. Strain rate dependence of serration behavior for 5000 series aluminum alloy in uniaxial and indentation tests. In Proceedings of the 16th International Aluminum Alloys Conference (ICAA16), Montreal, PQ, Canada, 17–21 June 2018. [Google Scholar]
- Jonas, J.J.; Sellars, C.M.; Tegart, W.J.M.G. Strength and structure under hot-working conditions. Metall. Rev. 1969, 14, 1–24. [Google Scholar] [CrossRef]
- Long, J.; Xia, Q.; Xiao, G.; Qin, Y. Flow characterization of magnesium alloy ZK61 during hot deformation with improved constitutive equations and using activation energy maps. Int. J. Mech. Sci. 2021, 191, 106069. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Lin, Y.C.; Wen, D.X.; Deng, J.; Liu, G. Constitutive models for high-temperature flow behaviors of a Ni-based superalloy. Mater. Des. 2014, 59, 115–123. [Google Scholar] [CrossRef]
- Kumar, S.; Karmakar, A.; Nath, S.K. Construction of hot deformation processing maps for 9Cr-1Mo steel through conventional and ANN approach. Mater. Today Commun. 2021, 26, 101903. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; McClelland, J.L. A general framework for parallel distributed processing. Parallel Distrib. Process. Explor. Microstruct. Cogn. 1986, 1, 26. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; NeurIPS: San Diego, CA, USA, 2012; Volume 25. [Google Scholar]
- Ding, S.; Su, C.; Yu, J. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Mandal, S.; Sivaprasad, P.V.; Venugopal, S.; Murthy, K.P.N. Artificial neural network modeling to evaluate and predict the deformation behavior of stainless steel type AISI 304L during hot torsion. Appl. Soft Comput. 2009, 9, 237–244. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation functions in neural networks. Towards Data Sci. 2017, 6, 310–316. [Google Scholar] [CrossRef]
- Ravi, R.; Prasad, Y.; Sarma, V.V.S. An artificial neural network (ANN) model for predicting instability regimes in copper–aluminum alloys. Mater. Manuf. Process. 2007, 22, 846–850. [Google Scholar] [CrossRef]
- Keong, K.G.; Sha, W.; Malinov, S. Artificial neural network modelling of crystallization temperatures of the Ni–P based amorphous alloys. Mater. Sci. Eng. A 2004, 365, 212–218. [Google Scholar] [CrossRef]
- Murugesan, M.; Jung, D.W. Johnson Cook material and failure model parameters estimation of AISI-1045 medium carbon steel for metal forming applications. Materials 2019, 12, 609. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.C.; Zhang, J.; Zhong, J. Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel. Comput. Mater. Sci. 2008, 43, 752–758. [Google Scholar] [CrossRef]
- Lin, Y.C.; Liu, G.; Chen, M.S.; Zhong, J. Prediction of static recrystallization in a multi-pass hot deformed low-alloy steel using artificial neural network. J. Mater. Process. Technol. 2009, 209, 4611–4616. [Google Scholar] [CrossRef]




| Test No. | Strain Rates (s−1) | Temperature (K) | Standard Deviation |
|---|---|---|---|
| 1 | 0.0003 | 633 | 0.0146 |
| 2 | 0.003 | 633 | 0.0159 |
| 3 | 0.03 | 633 | 0.0173 |
| 4 | 0.0003 | 703 | 0.0091 |
| 5 | 0.003 | 703 | 0.0121 |
| 6 | 0.03 | 703 | 0.0148 |
| 7 | 0.0003 | 773 | 0.0073 |
| 8 | 0.003 | 773 | 0.0117 |
| 9 | 0.03 | 773 | 0.0153 |
| Ture Strain | α | n | Q (J·mol−1) | lnA |
|---|---|---|---|---|
| 0.03 | 0.04772 | 4.87868 | 181,964.43806 | 24.9859 |
| 0.06 | 0.04619 | 4.81612 | 181,175.14546 | 24.92136 |
| 0.09 | 0.04524 | 4.75863 | 180,574.88746 | 24.94958 |
| 0.12 | 0.04504 | 4.72281 | 179,593.61103 | 24.79107 |
| 0.15 | 0.04484 | 4.70455 | 178,120.69435 | 24.61697 |
| 0.18 | 0.04448 | 4.70354 | 176,220.69435 | 24.32659 |
| 0.21 | 0.04434 | 4.68823 | 174,562.29940 | 24.11042 |
| 0.24 | 0.04404 | 4.68339 | 172,830.64202 | 23.82443 |
| 0.27 | 0.04395 | 4.67296 | 170,823.64202 | 23.56193 |
| 0.30 | 0.04393 | 4.67052 | 167,461.87983 | 23.01320 |
| Polynomial Order | α | n | Q (J·mol−1) | ln A |
|---|---|---|---|---|
| 0 | 0.04999 | 4.88046 | 184,672.26693 | 25.45296 |
| 1 | −0.08123 | 2.193 | −150,623.62814 | −29.35556 |
| 2 | 0.01167 | −103.62894 | 2.63224 × 106 | 605.05764 |
| 3 | 7.56052 | 1096.26352 | −2.30957 × 107 | −5582.67267 |
| 4 | −60.0279 | −5254.61372 | 8.83231 × 107 | 23,224.34498 |
| 5 | 182.34278 | 11,975.12441 | −1.39543 × 108 | −43,220.22732 |
| 6 | −197.18793 | −10,531.66483 | 5.25777 × 107 | 26,822.76943 |
| Training | Validation | Test | All | |
|---|---|---|---|---|
| R2 | 0.99967 | 0.99982 | 0.99979 | 0.9997 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Chen, W.; Bhandari, K.S.; Jung, D.W.; Chen, X. Flow Behavior of AA5005 Alloy at High Temperature and Low Strain Rate Based on Arrhenius-Type Equation and Back Propagation Artificial Neural Network (BP-ANN) Model. Materials 2022, 15, 3788. https://doi.org/10.3390/ma15113788
Li S, Chen W, Bhandari KS, Jung DW, Chen X. Flow Behavior of AA5005 Alloy at High Temperature and Low Strain Rate Based on Arrhenius-Type Equation and Back Propagation Artificial Neural Network (BP-ANN) Model. Materials. 2022; 15(11):3788. https://doi.org/10.3390/ma15113788
Chicago/Turabian StyleLi, Sijia, Wenning Chen, Krishna Singh Bhandari, Dong Won Jung, and Xuewen Chen. 2022. "Flow Behavior of AA5005 Alloy at High Temperature and Low Strain Rate Based on Arrhenius-Type Equation and Back Propagation Artificial Neural Network (BP-ANN) Model" Materials 15, no. 11: 3788. https://doi.org/10.3390/ma15113788
APA StyleLi, S., Chen, W., Bhandari, K. S., Jung, D. W., & Chen, X. (2022). Flow Behavior of AA5005 Alloy at High Temperature and Low Strain Rate Based on Arrhenius-Type Equation and Back Propagation Artificial Neural Network (BP-ANN) Model. Materials, 15(11), 3788. https://doi.org/10.3390/ma15113788










