Study on Meso-Material Parameters of Submarine Weathered Granite Based on Parallel Bond Model
Abstract
:1. Introduction
2. Laboratory Tests
2.1. Physical Properties of Rock Samples
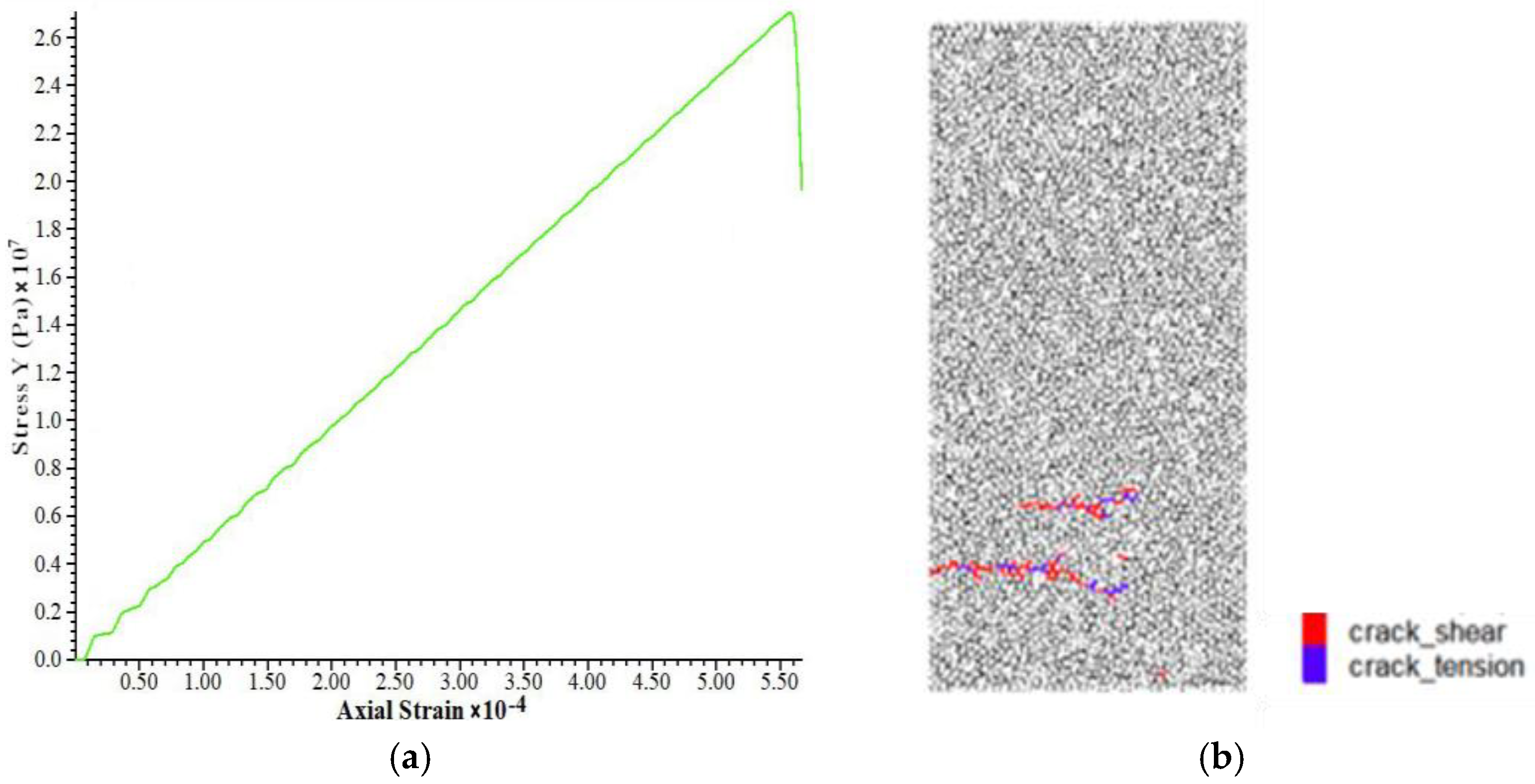
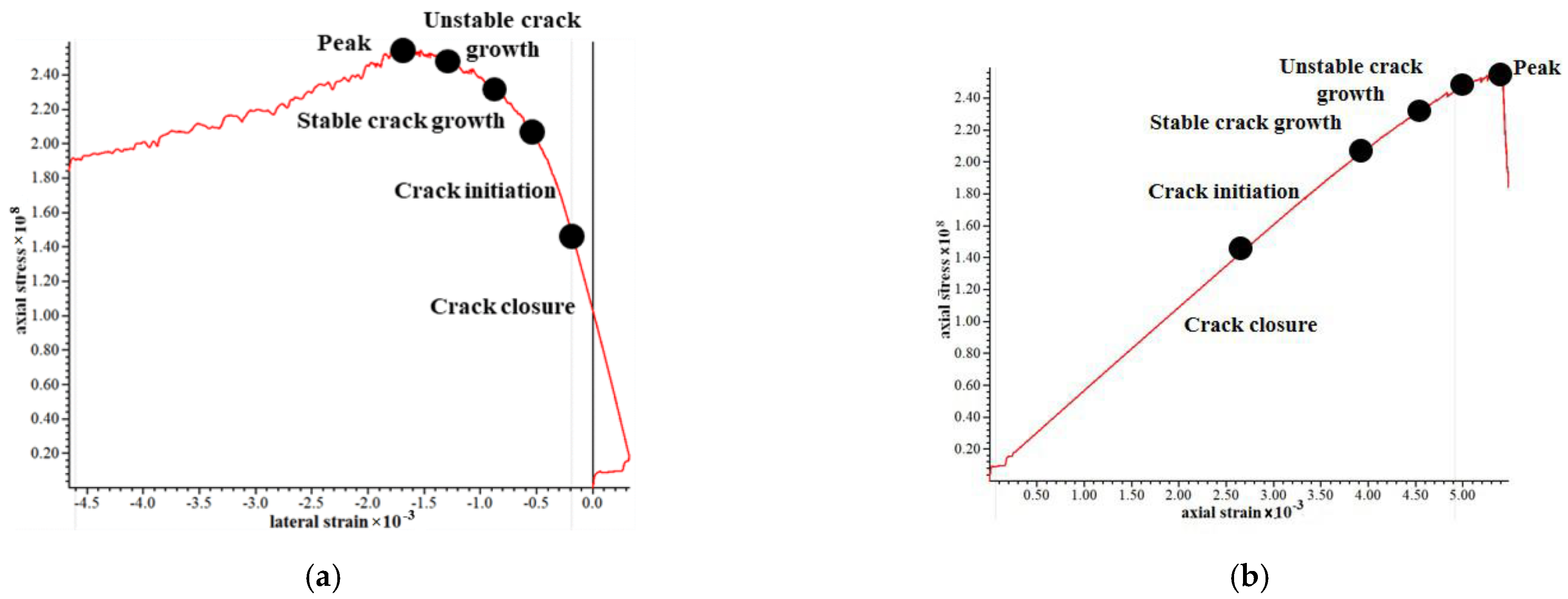
2.2. Uniaxial Compression Test of Weathered Granite
3. Numerical Model
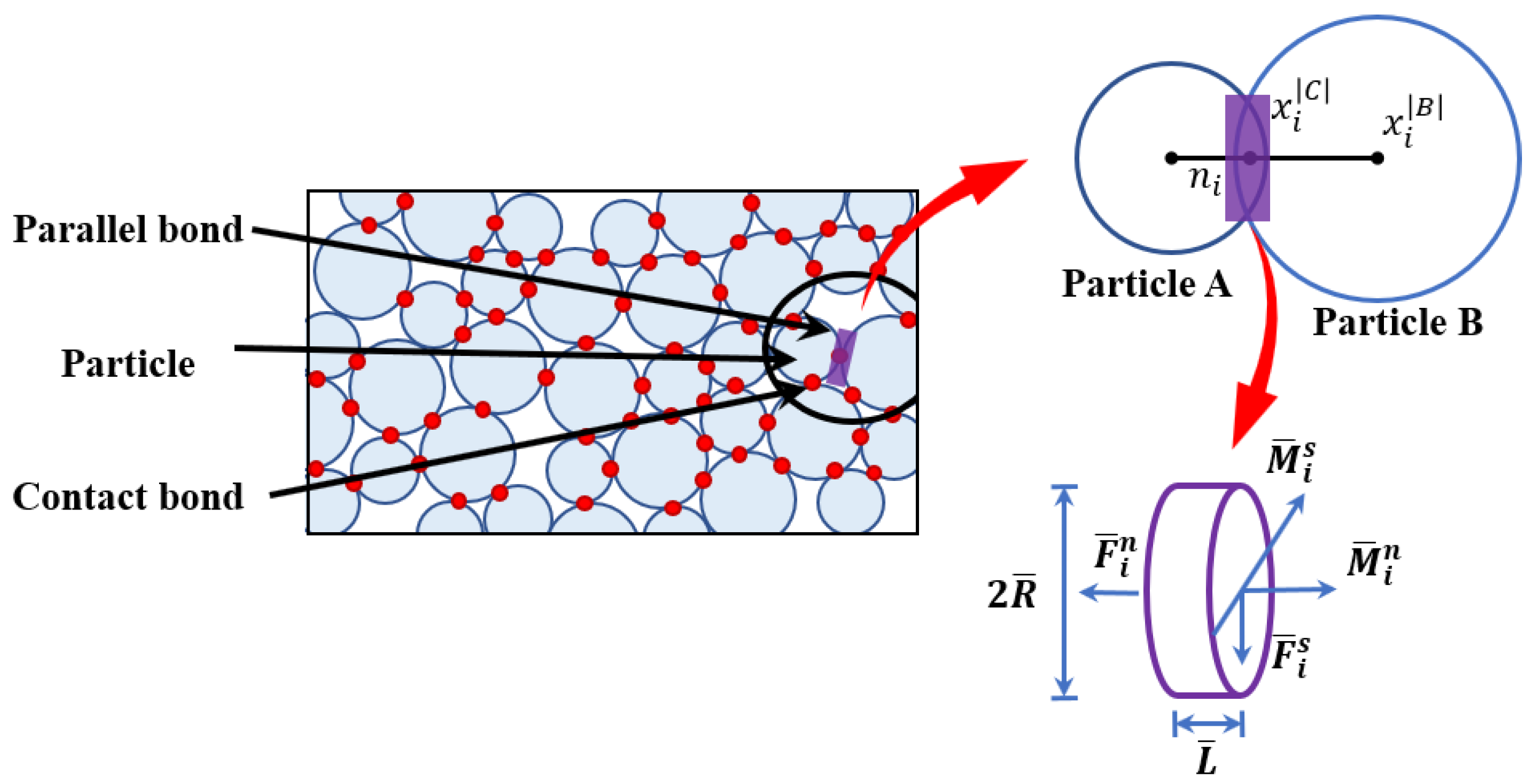
3.1. Fundamentals of the Standard BPM
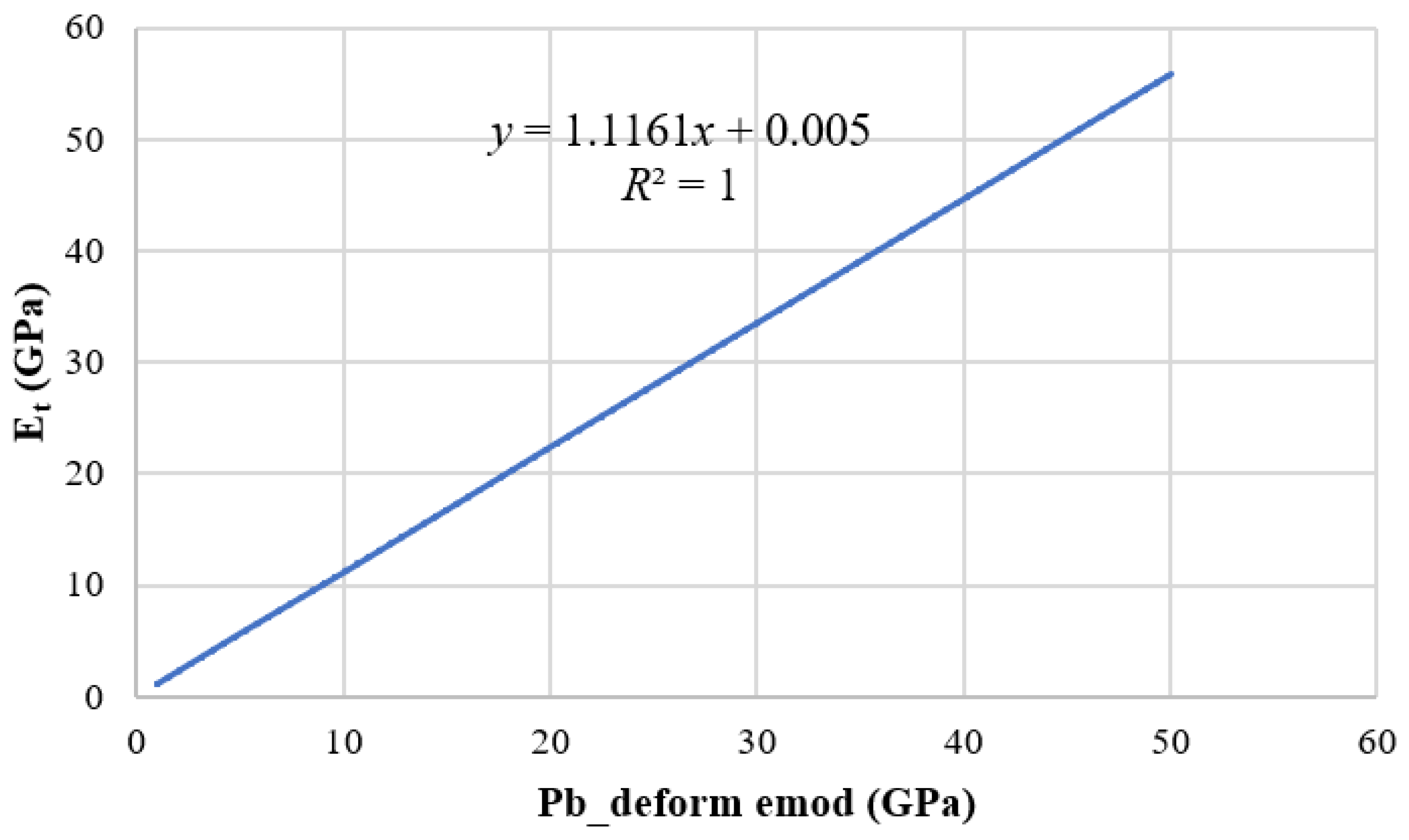
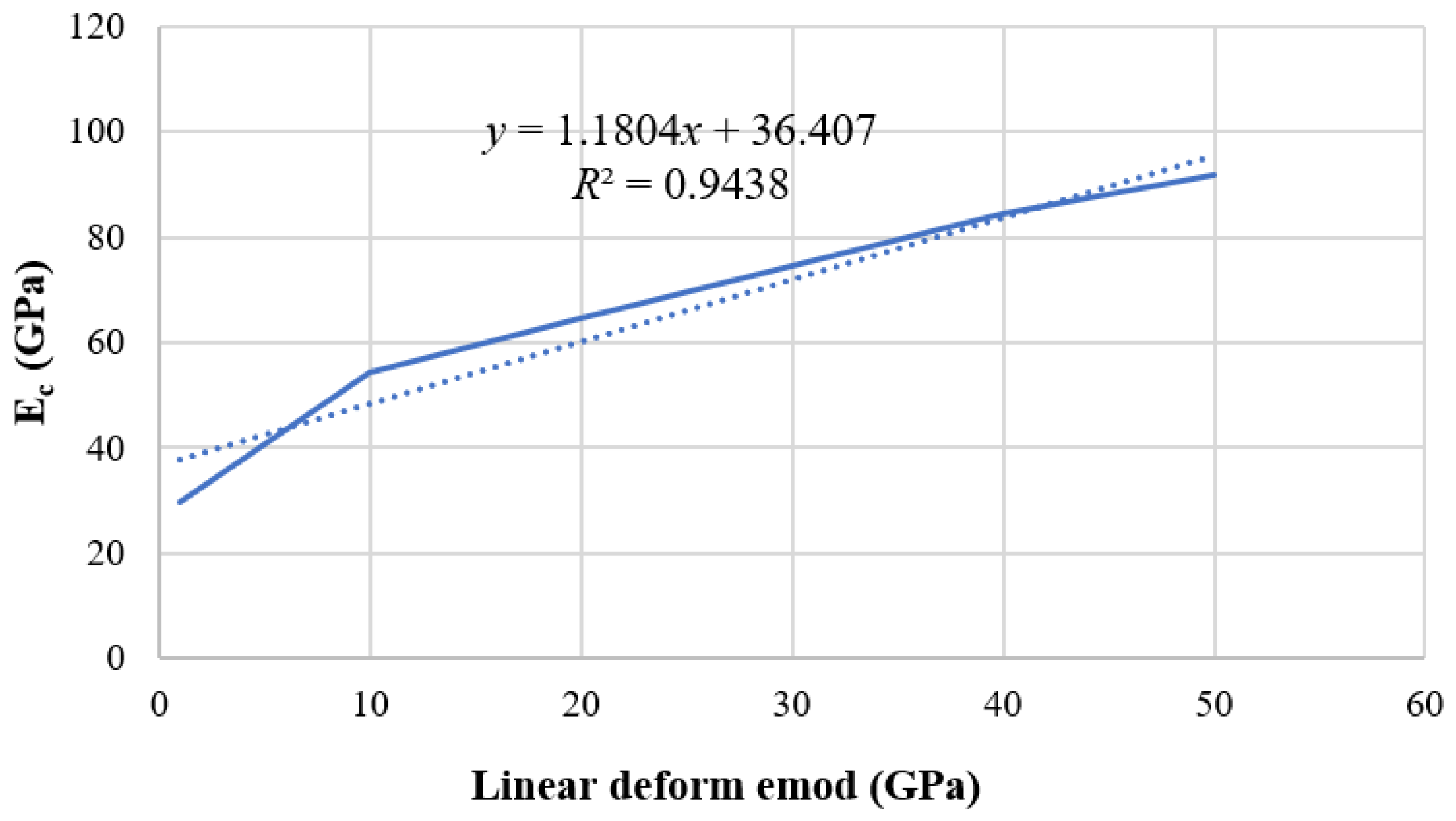
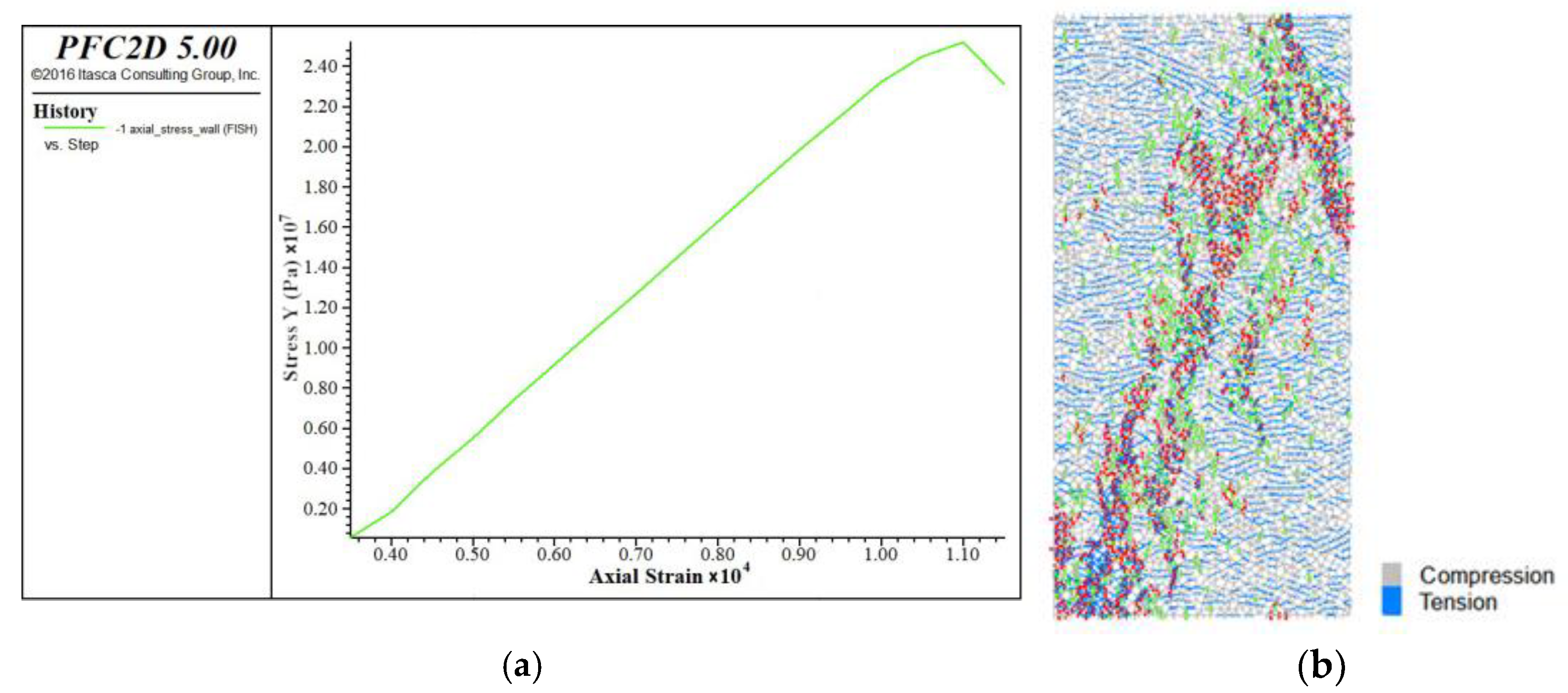
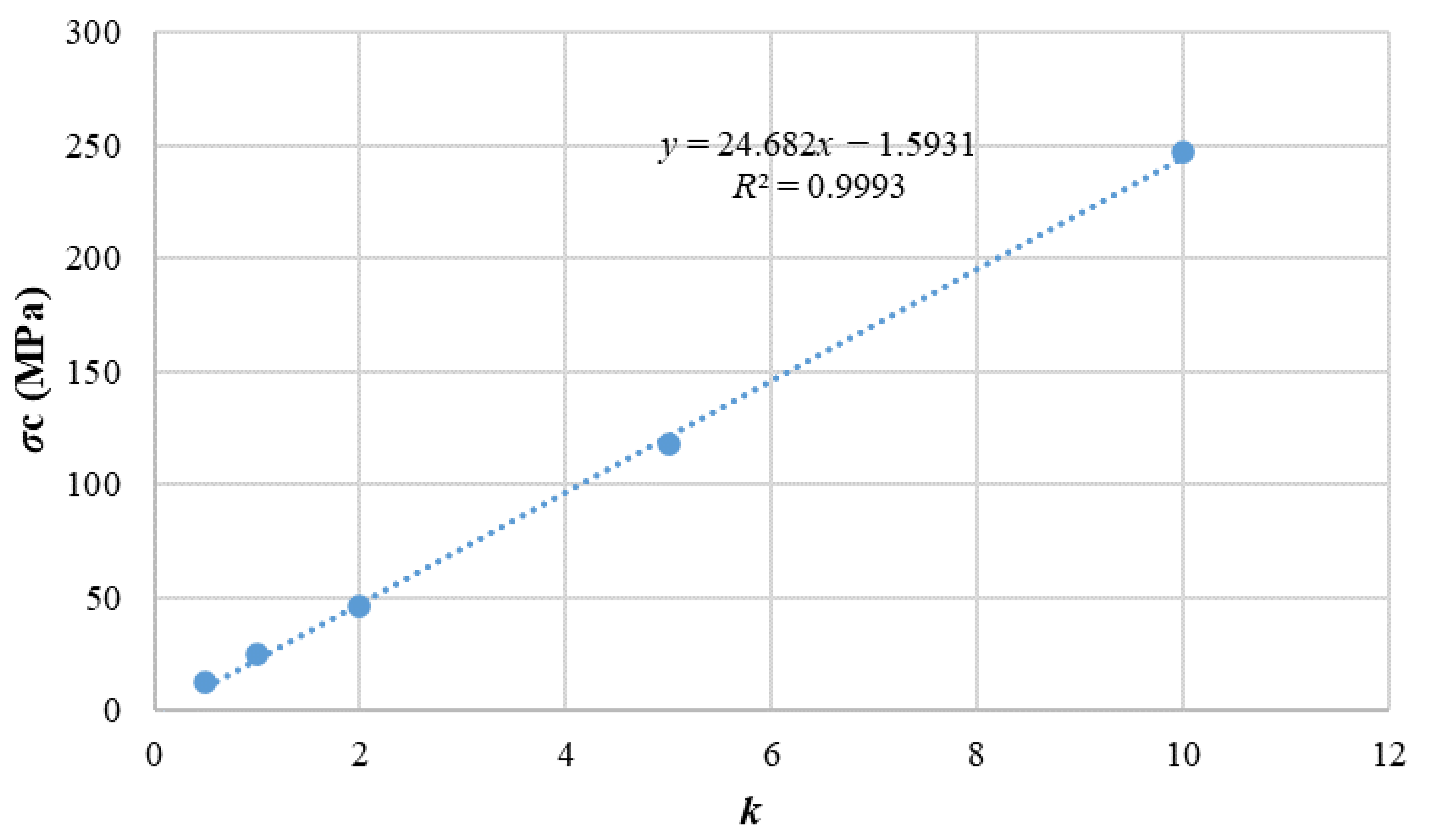
3.2. Calibration of Uniaxial Compression Test Parameters for Weathered Granite
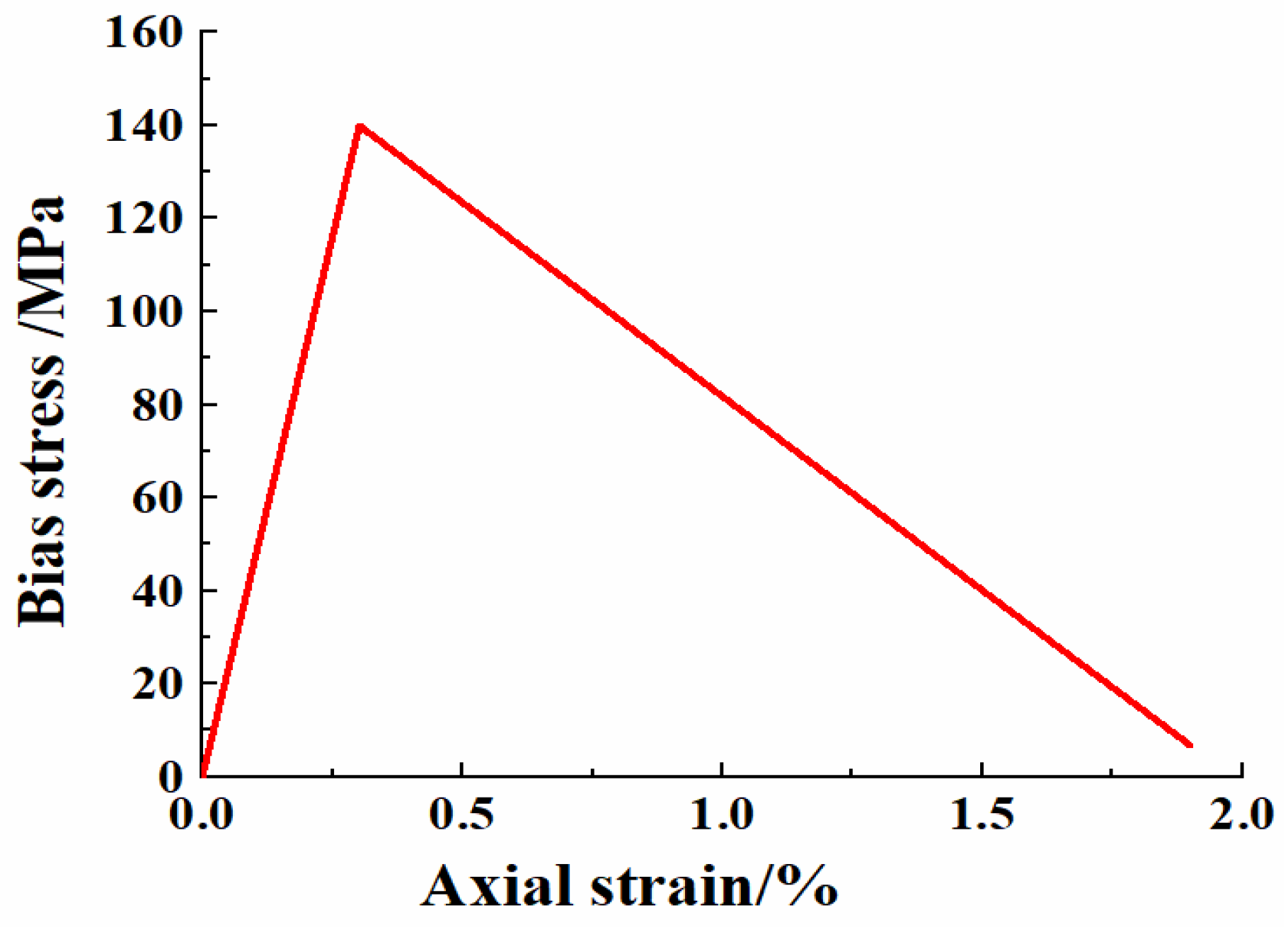
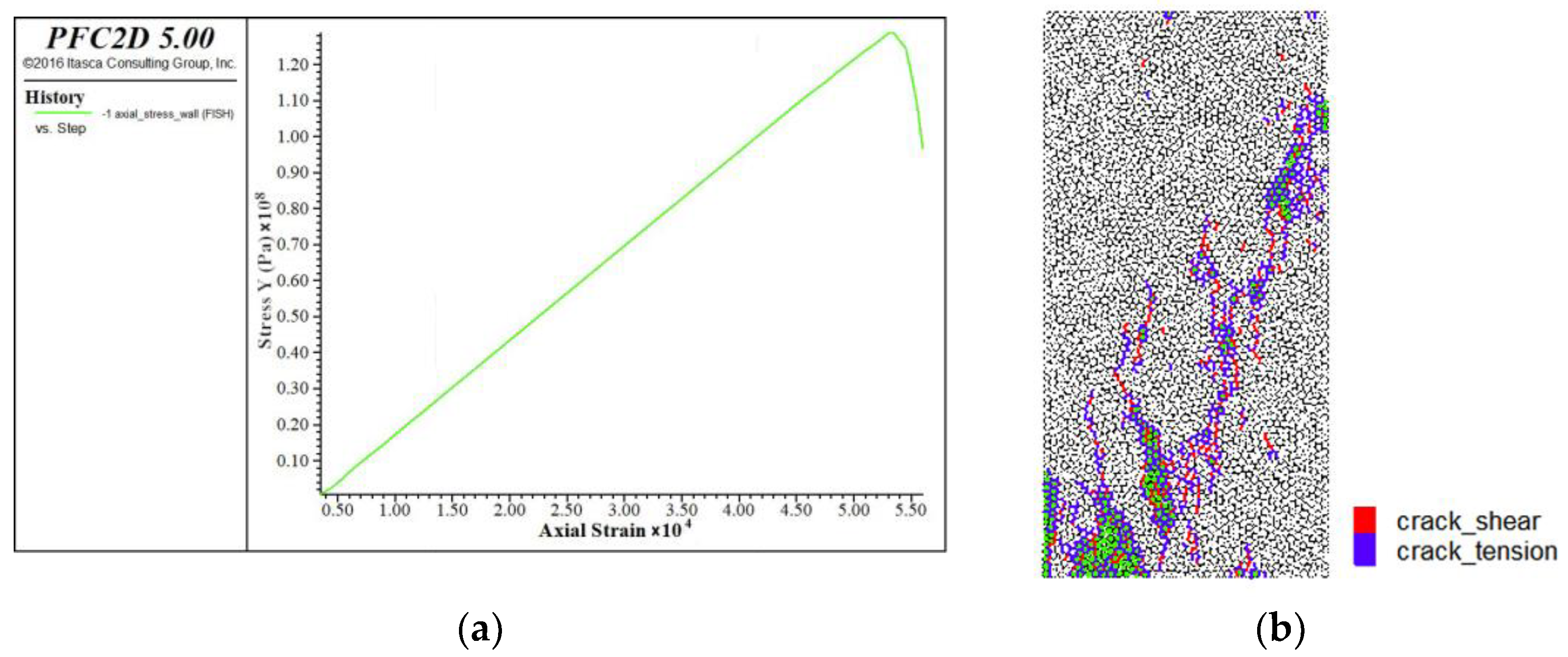
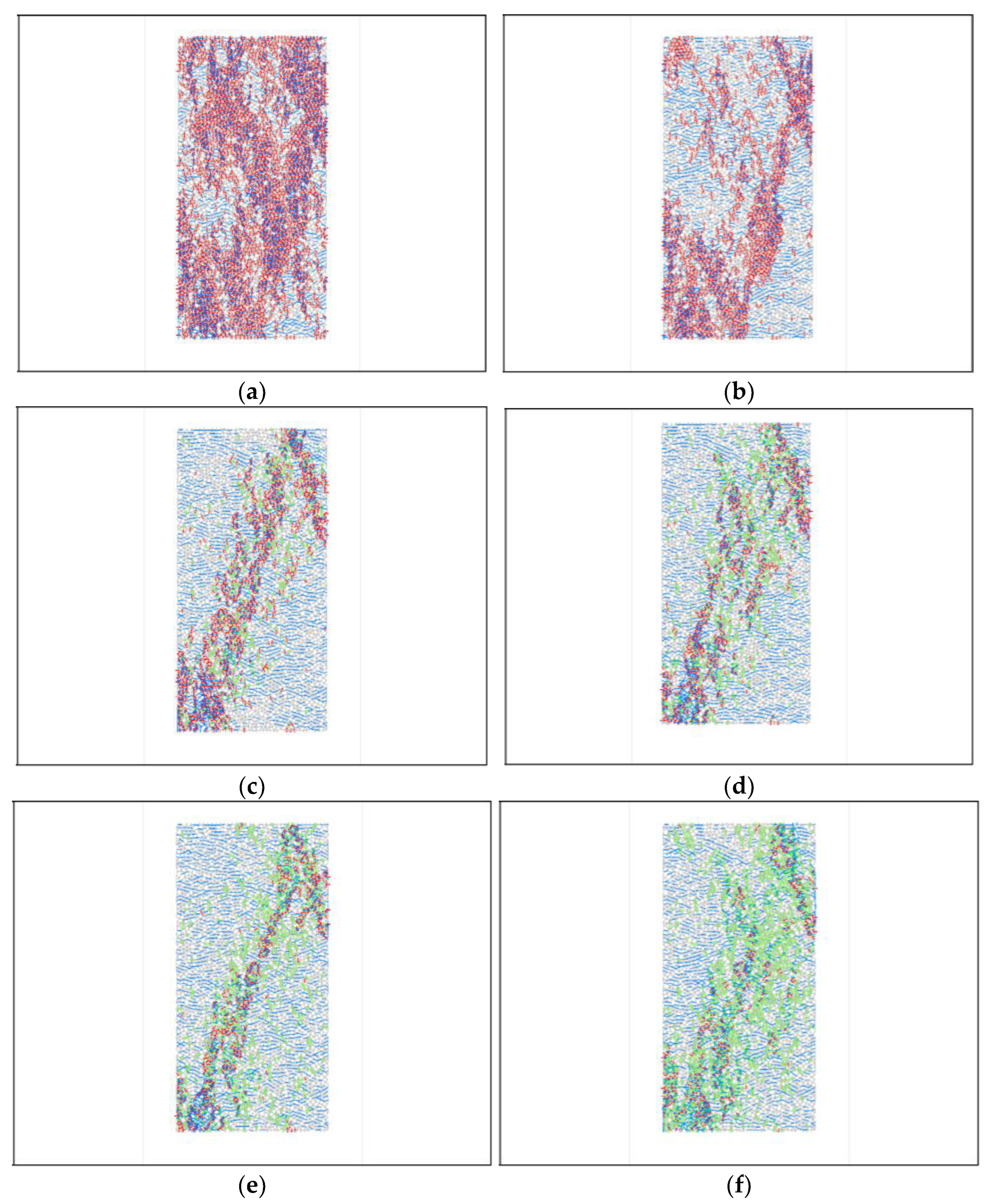
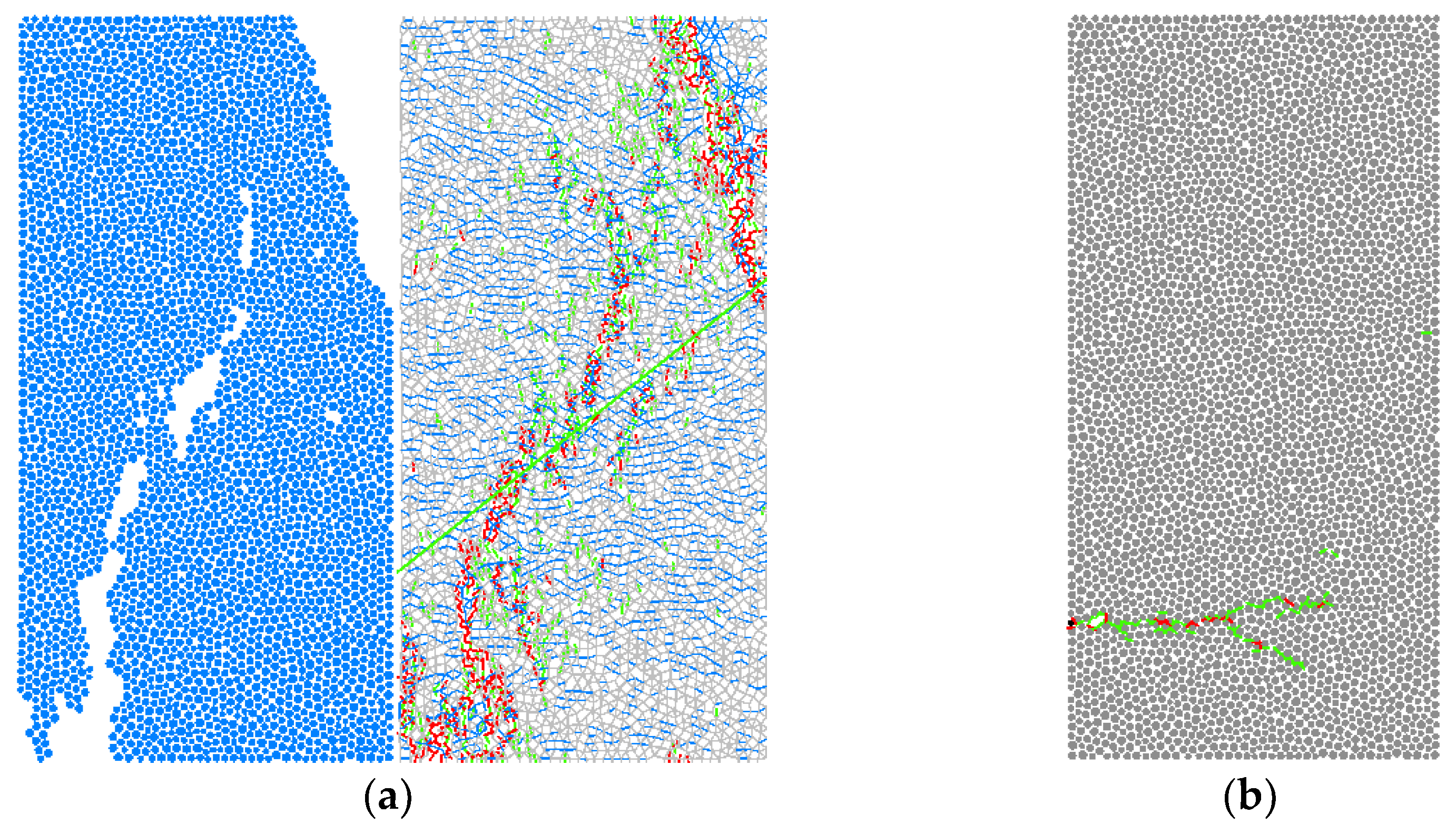
4. Simulation of Biaxial Compression Test
5. Conclusions
- The parallel bonding model was calibrated by uniaxial testing, which found the elastic modulus, Poisson’s ratio, and compressive strength were in good agreement with the experimental values. However, the tensile strength and tensile-compressive ratio differed significantly from the experimental values, and fine-tuning was still unable to achieve an error within 10%.
- To simplify the experimental process, The parameters obtained by uniaxial compression were used for biaxial tests. By changing the confining pressure, the calculated compressive strength is compared with the results of uniaxial compression. When the enclosing pressure was very small, the calculated compressive strength was closer to the strength of uniaxial compression. However, when the enclosing pressure increased, the simulation results are quite different from the experimental results and are smaller than the experimental values. By increasing the friction angle, the calculated compressive strength increased, but the error was still large.
- The reason for a certain gap between the calculation results and the experimental results is the large resistance of the parallel bonding model to particle rotation, and to consider the effect of normal stress on shear strength. The bonding model can be modified by adding coefficients based on laboratory test results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ρ | Density |
| Gs | Specific gravity |
| ω | Water content |
| e | Porosity ratio |
| ωL | Liquid limit |
| ωP | Plastic limit |
| Cu | Uneven coefficient |
| Cc | Curvature coefficient |
| Normal force | |
| Shear force | |
| Bending moment acting at the center of the parallel bond | |
| Twisting moment acting at the center of the parallel bond | |
| Et | Effective modulus |
| Ec | Compressive elastic modulus |
| μ | Macro Poisson’s ratio |
| σc | Uniaxial compressive strength |
References
- Dai, S.; Han, B.; Wang, B.; Luo, J.; He, B. Influence of soil scour on lateral behavior of large-diameter offshore wind-turbine monopile and corresponding scour monitoring method. Ocean Eng. 2021, 239, 109809. [Google Scholar] [CrossRef]
- Chen, J. Development of offshore wind power in China. Renew. Sustain. Energy Rev. 2011, 15, 5013–5020. [Google Scholar] [CrossRef]
- Xu, W.; Liu, B.; Zhou, Y.-Q.; Han, Y.-h. Construction of 8.0- m Diameter Rock-Socketed Piles in a Large-Scale Deep Excavation. Geotech. Geol. Eng. 2017, 35, 2455–2466. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, X.; He, J.; Chai, Q. Offshore wind energy development in China: Current status and future perspective. Renew. Sustain. Energy Rev. 2011, 15, 4673–4684. [Google Scholar] [CrossRef]
- He, R.; Ji, J.; Zhang, J.; Peng, W.; Sun, Z.; Guo, Z. Dynamic Impedances of Offshore Rock-Socketed Monopiles. J. Mar. Sci. Eng. 2019, 7, 134. [Google Scholar] [CrossRef] [Green Version]
- Kou, H.-L.; Guo, W.; Zhang, M.-Y.; Xu, Y.-Q. Axial resistance of long rock-socketed bored piles in stratified soils. Ocean Eng. 2016, 114, 58–65. [Google Scholar] [CrossRef]
- Zhang, B.-N.; Zhang, D.-F.; Han, B. Numerical and experimental investigation on hydraulic fracturing for offshore wind turbine rock-socketed pile foundation construction. Mar. Georesources Geotechnol. 2021. [Google Scholar] [CrossRef]
- Liao, W.; Zhang, J.; Wu, J.; Yan, K. Response of flexible monopile in marine clay under cyclic lateral load. Ocean Eng. 2018, 147, 89–106. [Google Scholar] [CrossRef]
- Achmus, M.; Kuo, Y.-S.; Abdel-Rahman, K. Behavior of monopile foundations under cyclic lateral load. Comput. Geotech. 2009, 36, 725–735. [Google Scholar] [CrossRef]
- Richards, I.; Byrne, B.; Houlsby, G. Physical modelling of monopile foundations under variable cyclic lateral loading. In Physical Modelling in Geotechnics; CRC Press: Boca Raton, FL, USA, 2018; pp. 737–741. [Google Scholar] [CrossRef]
- Hokmabadi, A.; Fakher, A.; Fatahi, B. Full scale lateral behaviour of monopiles in granular marine soils. Mar. Struct. 2012, 29, 198–210. [Google Scholar] [CrossRef]
- Xinbin, T.; Wang, S.; Yu, Z. Fragmentation of weatheres rock and its application in engineering geology. Chin. J. Rock Mech. Eng. 2005, 24, 587–595. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. Adiscrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Zhou, J.-X.; Zhou, Y.; Gao, Y.-T. Effect Mechanism of Fractures on the Mechanics Characteristics of Jointed Rock Mass under Compression. Arab. J. Sci. Eng. 2018, 43, 3659–3671. [Google Scholar] [CrossRef]
- Wu, T.; Gao, Y.; Zhou, Y.; Li, J. Experimental and numerical study on the interaction between holes and fissures in rock-like materials under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 106, 102488. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model fo rrock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Y.; Sun, W.; Sun, Z. Effect of the Interaction between Cavities and Flaws on Rock Mechanical Properties under Uniaxial Compression. Adv. Mater. Sci. Eng. 2019, 2019, 1242141. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Wu, S.C.; Gao, Y.T.; Misra, A. Macro and meso analysis of jointed rock mass triaxial compression test by using ERM technique. J. Cent. S. Univ. 2014, 21, 1125–1135. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, G.; Wu, S.C.; Zhang, L. The effect of flaw on rock mechanical properties under the Brazilian test. Kuwait J. Sci. 2018, 45, 94–103. [Google Scholar]
- Guo, W.H.; Chen, N.B.; Zhou, Y.; Gao, Y.; Sun, Z.; Wang, L. Meso research on the mechanical properties of rock specimens with double prefabricated circular holes based on digital image correlation. Kuwait J. Sci. 2020, 47, 2–14. [Google Scholar]
- Park, J.-W.; Song, J.-J. Numerical simulation of a direct shear test on a rock joint using a bonded-particle model. Int. J. Rock Mech. Min. Sci. 2009, 46, 1315–1328. [Google Scholar] [CrossRef]
- Zhang, S.H.; Wu, S.C.; Duan, K. Study on the deformation and strength characteristics of hard rock under true triaxial stres state using bonded-particle model. Comput. Geotech. 2019, 112, 1–16. [Google Scholar] [CrossRef]
- Zhang, X.P.; Zhang, Q.; Wu, S.C. Acoustic emission characteristics of the rock-likematerial containing a single flawunder different compressive loading rates. Comput. Geotech. 2017, 83, 83–97. [Google Scholar] [CrossRef]
- Wu, S.; Xu, X. A Study of Three Intrinsic Problems of the Classic Discrete Element Method Using Flat-Joint Model. Rock Mech. Rock Eng. 2016, 49, 1813–1830. [Google Scholar] [CrossRef]
- Einstein, H. Fractures: Tension and Shear. Rock Mech. Rock Eng. 2021, 54, 3389–3408. [Google Scholar] [CrossRef]



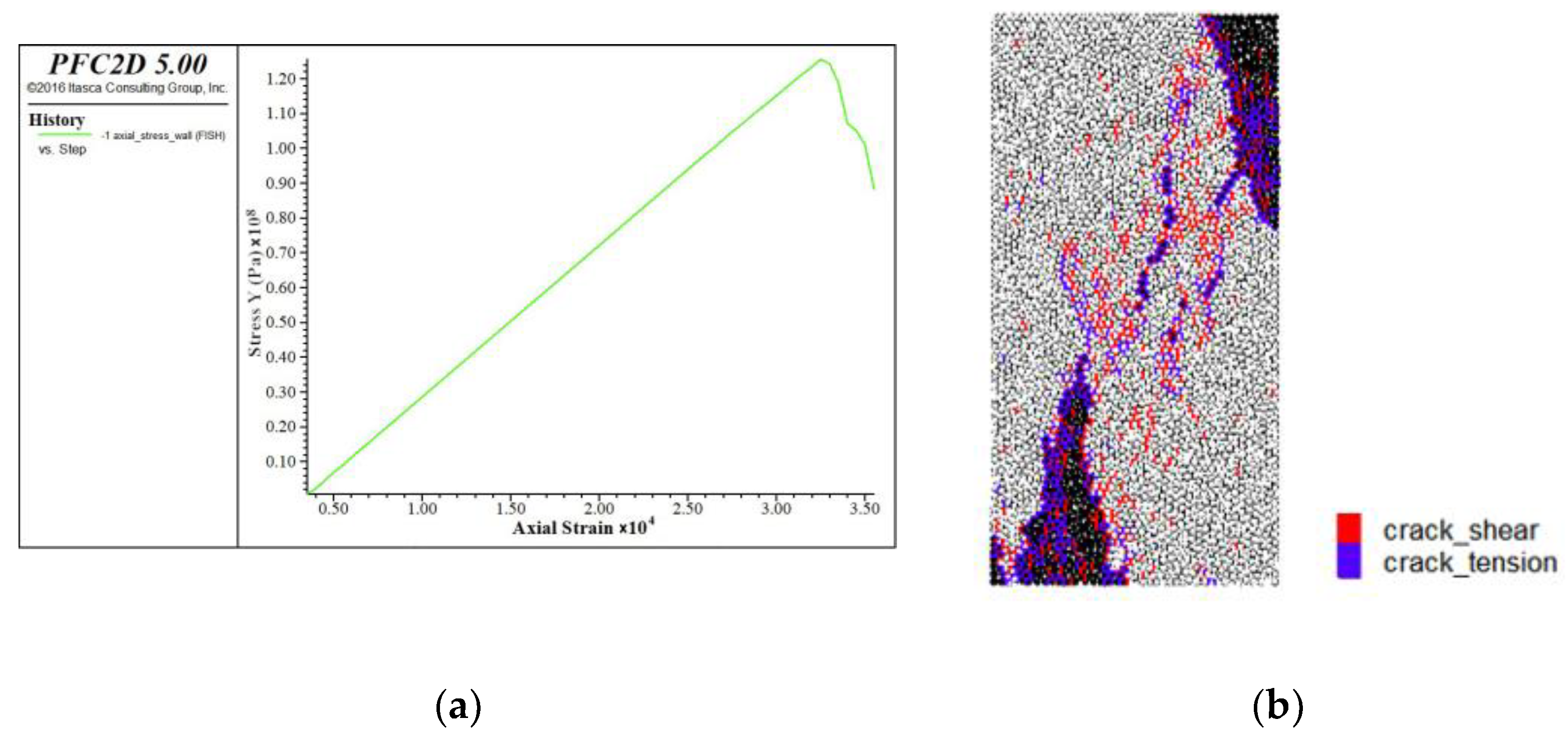



| Density ρ/(g/cm3) | Specific Gravity Gs | Water Content ω/% | Porosity Ratio e | Liquid Limit ωL/% | Plastic Limit ωP/% |
|---|---|---|---|---|---|
| 2.28 | 2.68 | 9.7 | 0.296 | 32.7 | 20.2 |
| Sample No. | Confining Pressure MPa | Compressive Strength MPa | Elastic Modulus GPa | Cohesion MPa | Friction Angle ° |
|---|---|---|---|---|---|
| 2-1 | 10 | 253.34 | 48.31 | 28.13 | 50.6 |
| 2-2 | 20 | 307.57 | 51.05 | ||
| 2-3 | 30 | 429.52 | 58.54 |
| Surrounding Pressure | σc Test Value/MPa | σc Simulated Value/MPa | Error |
|---|---|---|---|
| 1 × 106 | 132.37 | 143 | 4% |
| 10 × 106 | 253.34 | 207.7 | 18% |
| 20 × 106 | 307.57 | 258.9 | 15.8% |
| 30 × 106 | 429.52 | 302.7 | 29.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhang, B.; Han, B.; Zhang, Q.; Liu, D. Study on Meso-Material Parameters of Submarine Weathered Granite Based on Parallel Bond Model. Materials 2022, 15, 3878. https://doi.org/10.3390/ma15113878
Zhang S, Zhang B, Han B, Zhang Q, Liu D. Study on Meso-Material Parameters of Submarine Weathered Granite Based on Parallel Bond Model. Materials. 2022; 15(11):3878. https://doi.org/10.3390/ma15113878
Chicago/Turabian StyleZhang, Shilei, Bonan Zhang, Bo Han, Qiyue Zhang, and Di Liu. 2022. "Study on Meso-Material Parameters of Submarine Weathered Granite Based on Parallel Bond Model" Materials 15, no. 11: 3878. https://doi.org/10.3390/ma15113878
APA StyleZhang, S., Zhang, B., Han, B., Zhang, Q., & Liu, D. (2022). Study on Meso-Material Parameters of Submarine Weathered Granite Based on Parallel Bond Model. Materials, 15(11), 3878. https://doi.org/10.3390/ma15113878






