Assessment of Strains Produced by Thermal Expansion in Printed Circuit Boards
Abstract
:1. Introduction
2. Materials and Methods
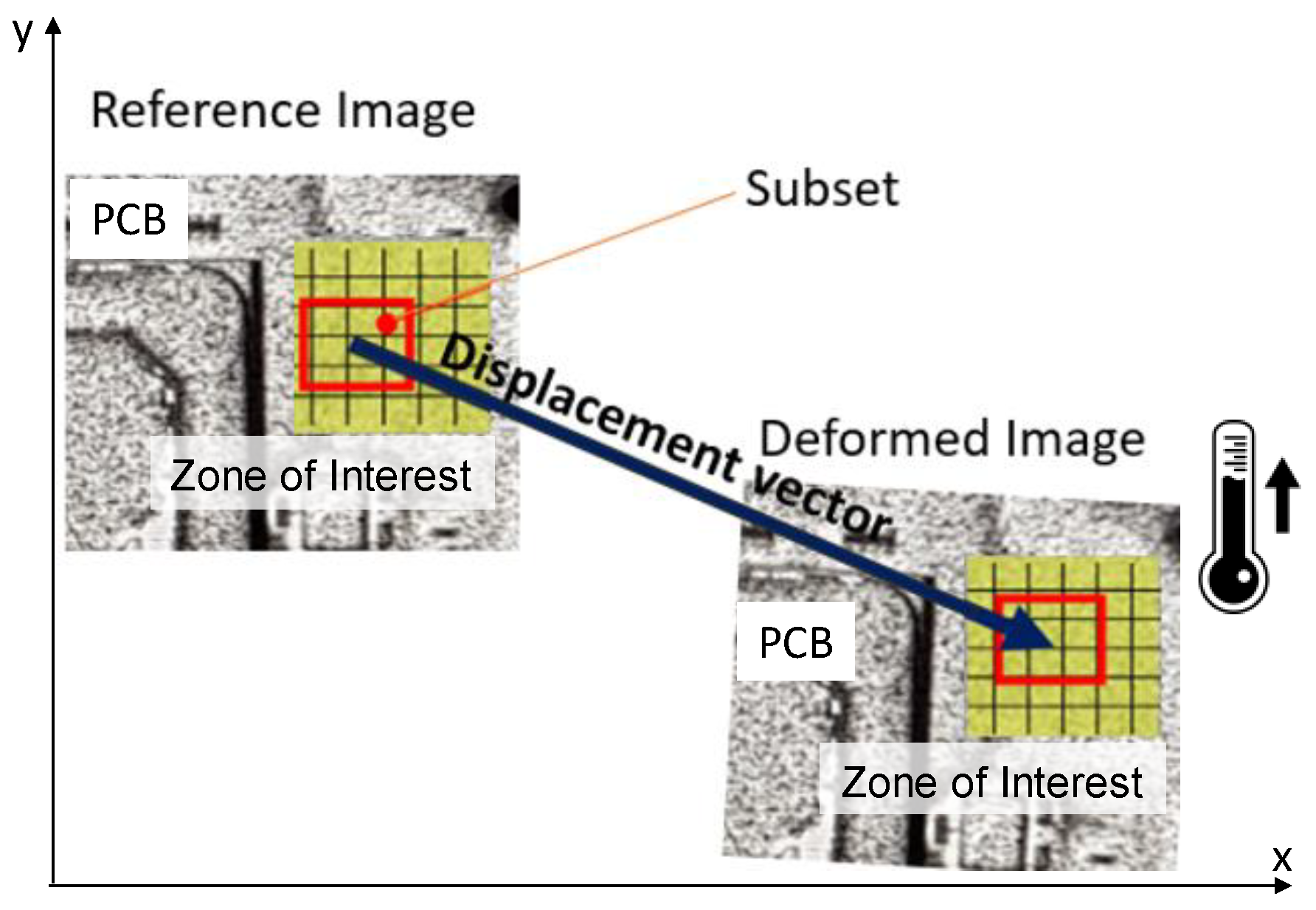
2.1. Digital Image Correlation (DIC)
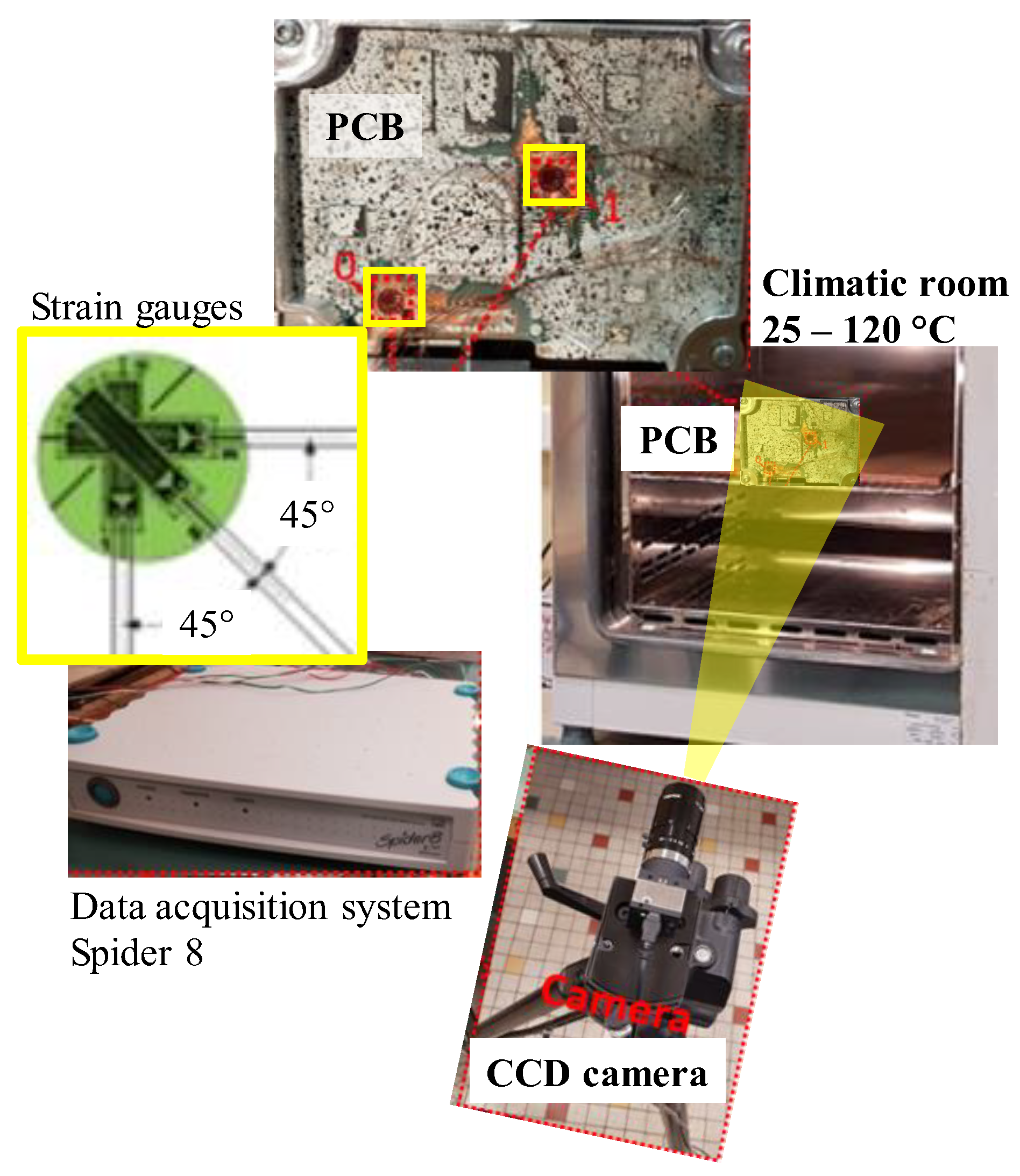
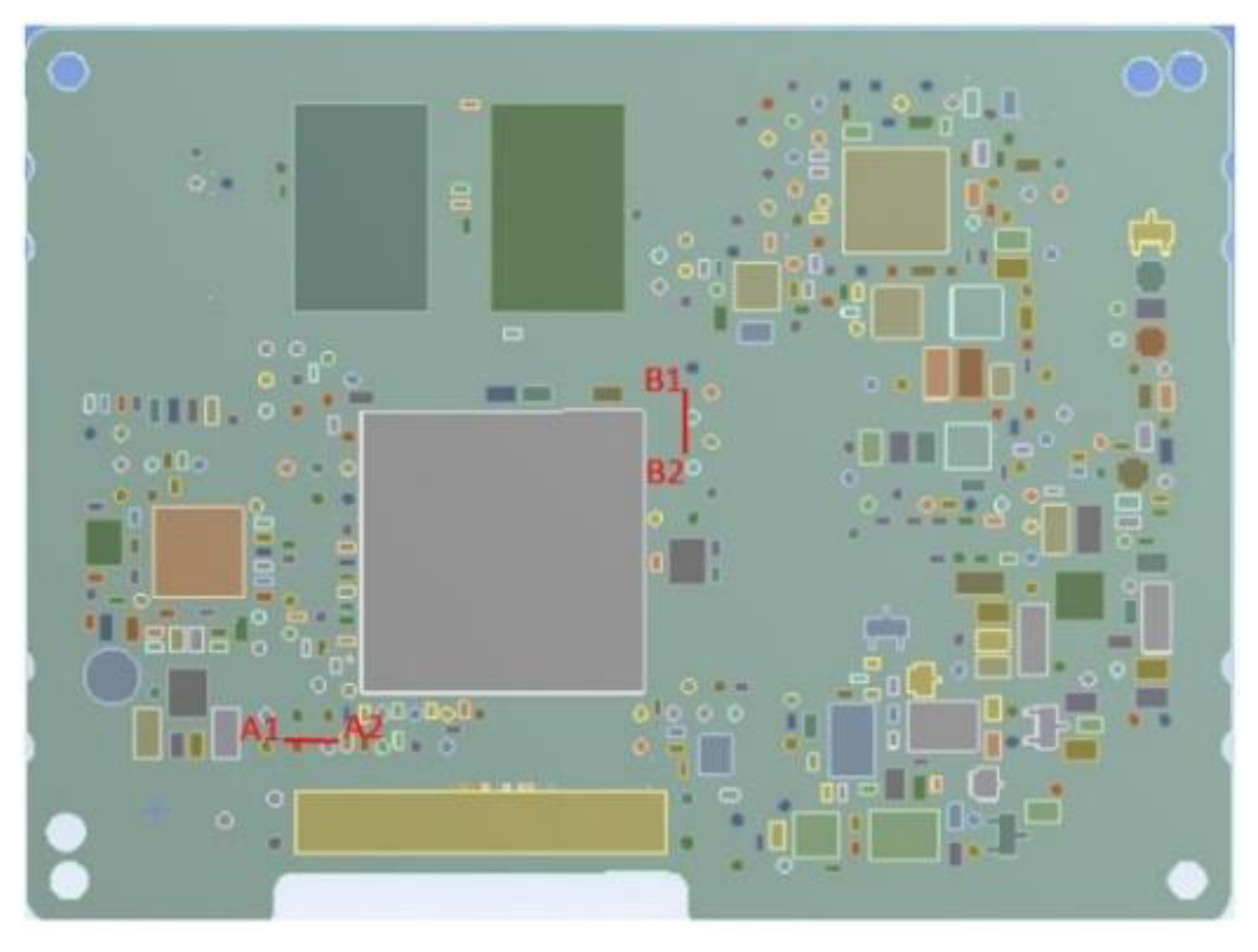
2.2. Experimental Setup
3. Results
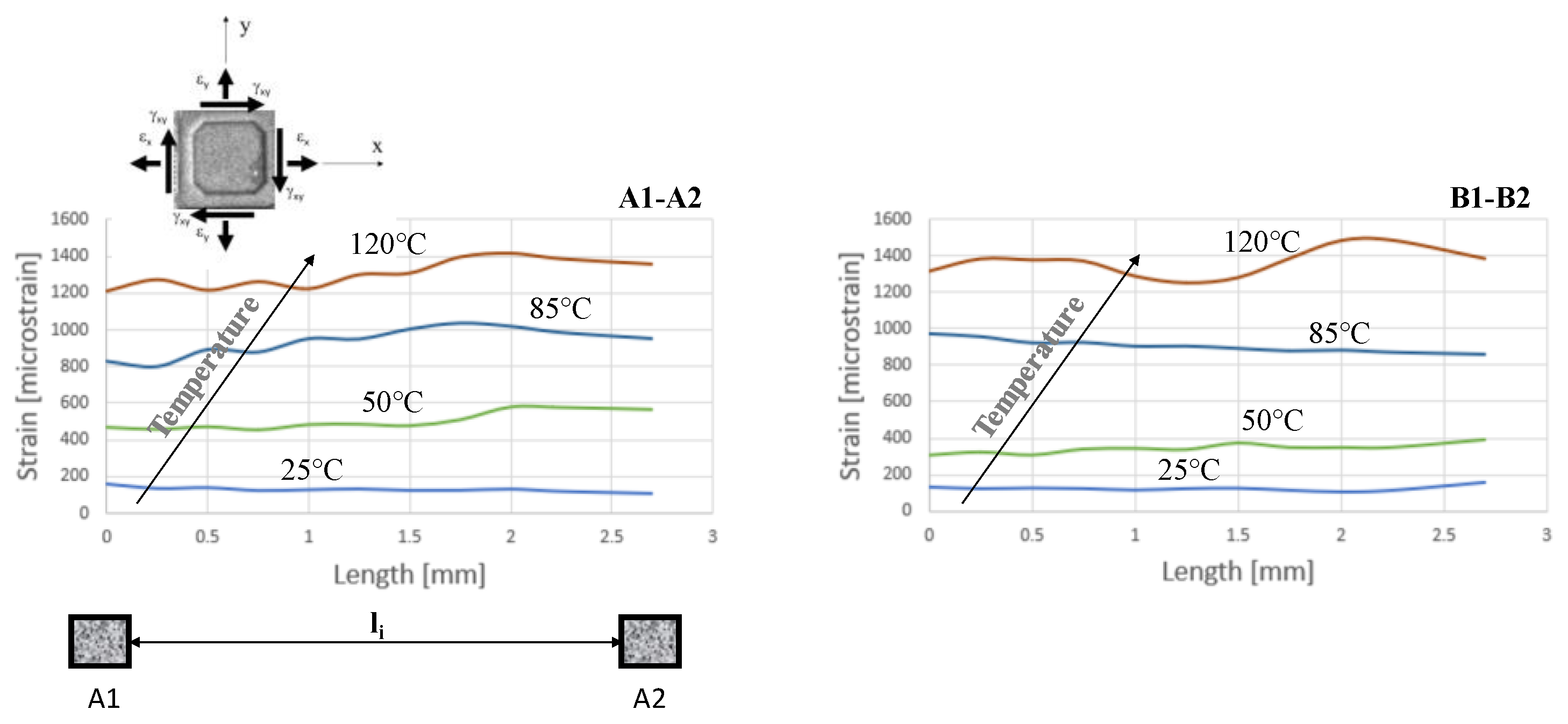
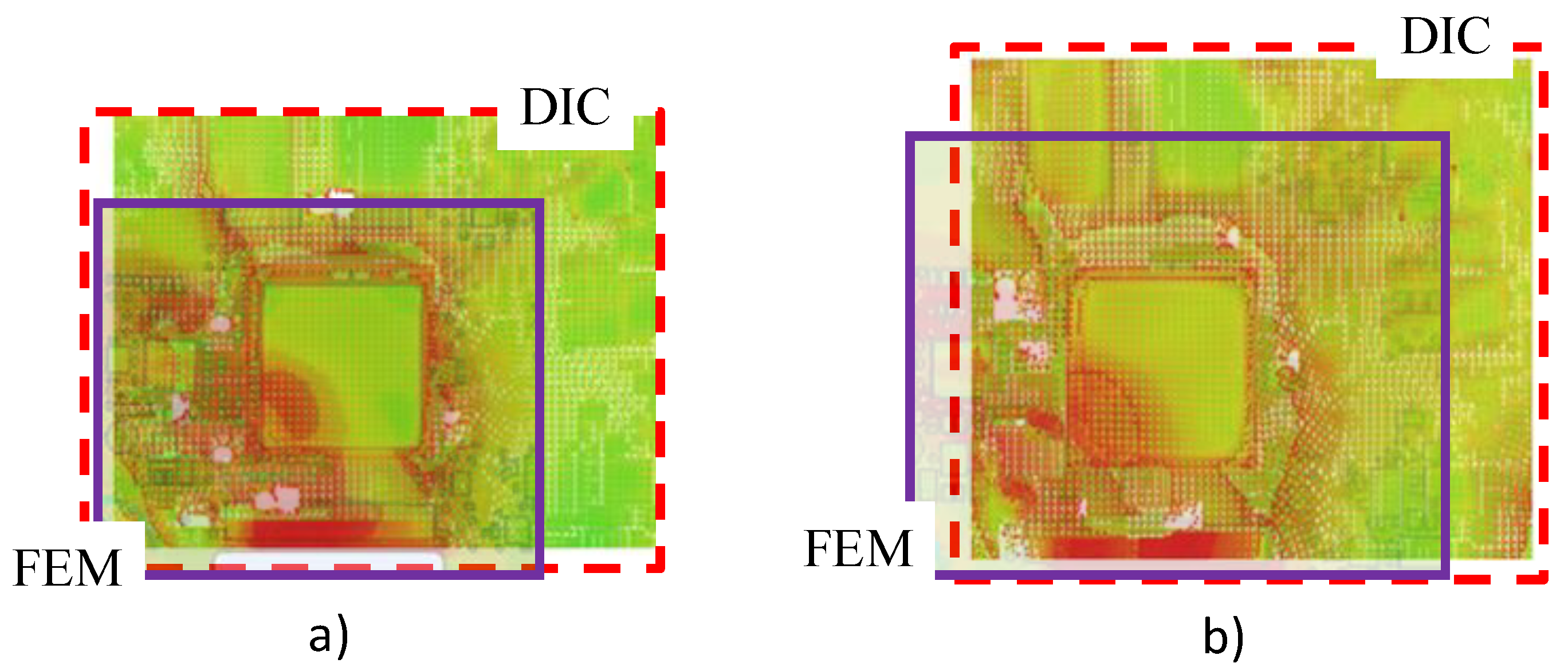
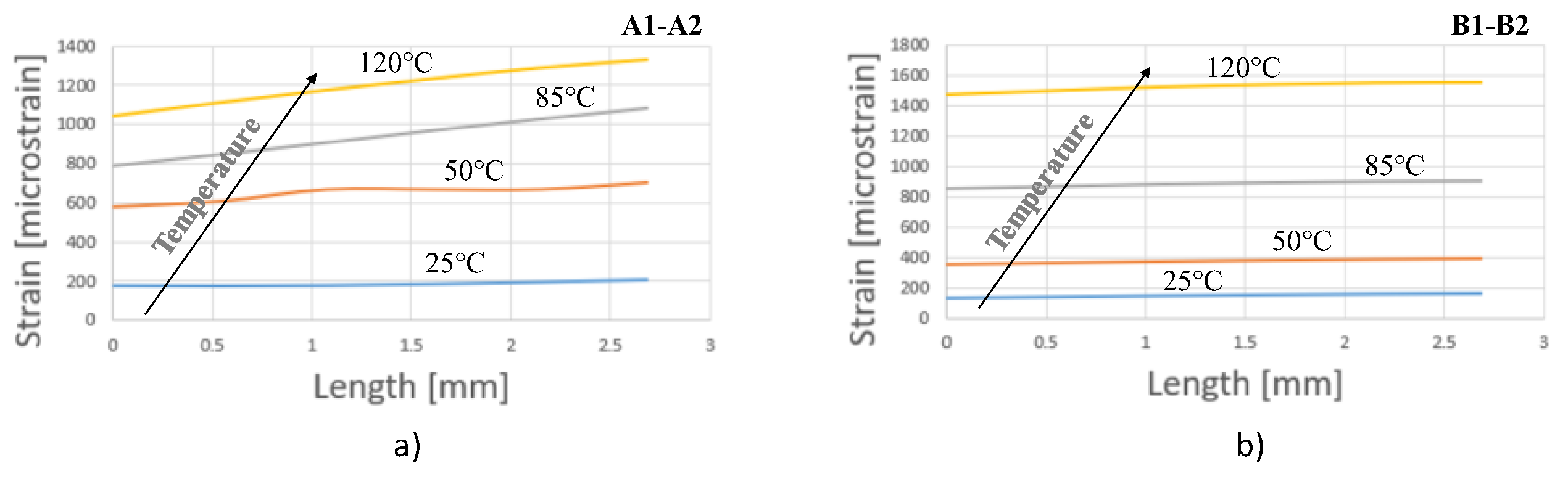
3.1. DIC Measurements
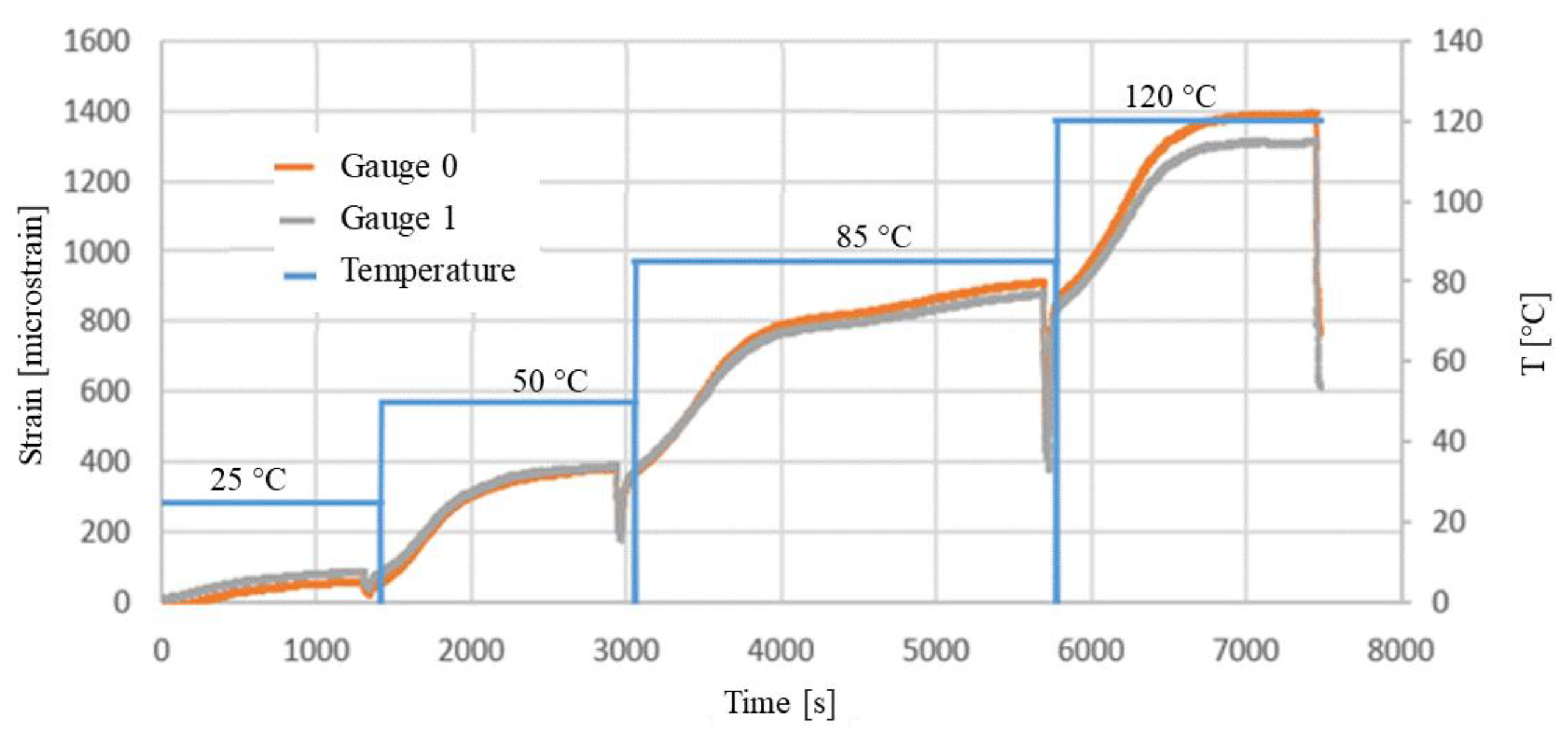
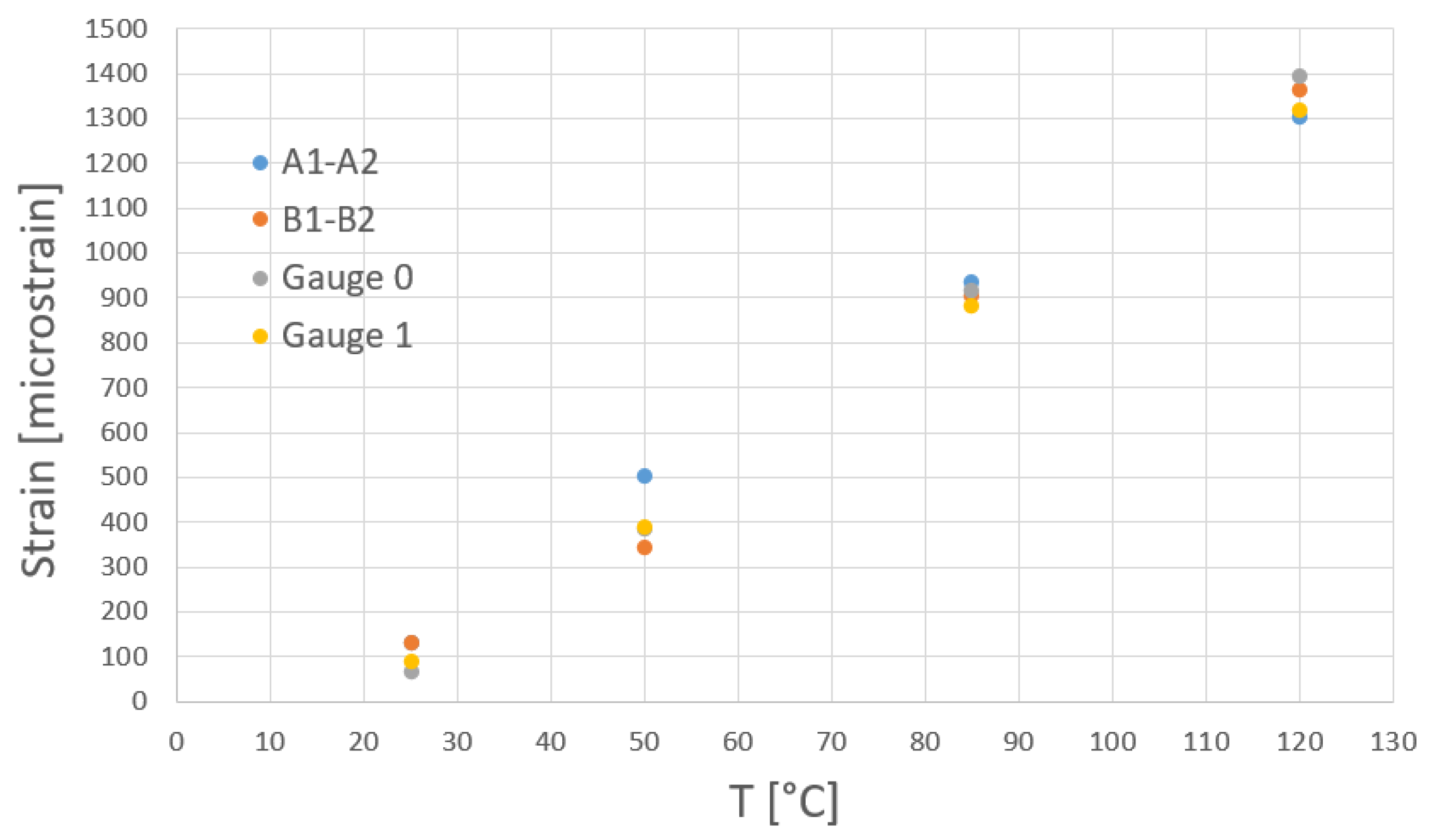
3.2. Strain Gauge Measurement
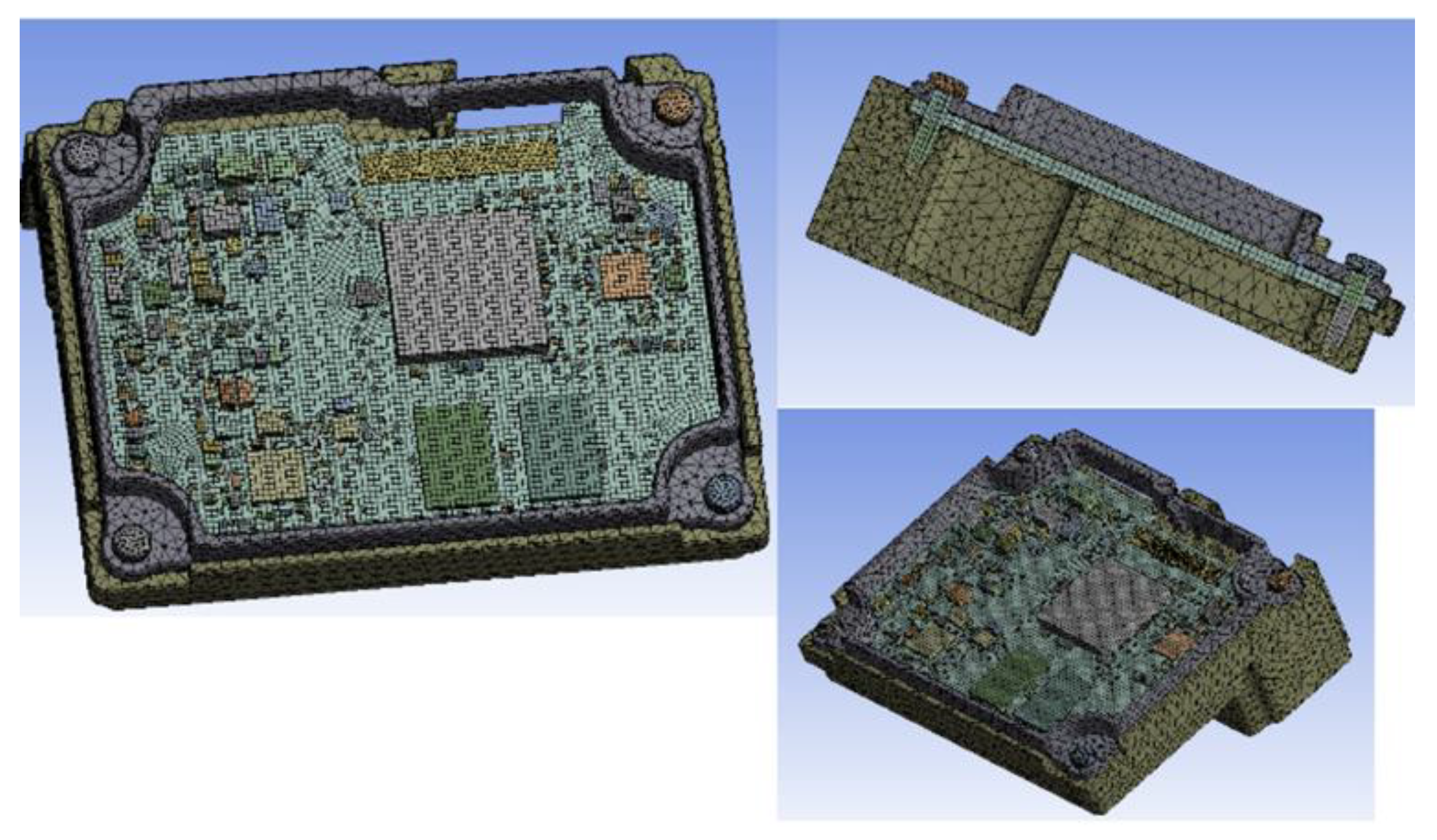
3.3. FEA Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benabou, L.; Sun, Z.; Dahoo, R. A thermo-mechanical cohesive zone model for solder joint lifetime prediction. Int. J. Fatigue 2013, 49, 18–30. [Google Scholar] [CrossRef]
- Han, J.; Guo, F.; Liu, J. Early stages of localized recrystallization in Pb-free BGA solder joints subjected to thermomechanical stress. J. Alloys Compd. 2017, 704, 574–584. [Google Scholar] [CrossRef]
- Amalu, E.H.; Ekere, N.N. High temperature reliability of lead-free solder joints in a flip chip assembly. J. Mater. Processing Technol. 2012, 212, 471–483. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, Z.; Chen, J. Introduction to Microsystem Packaging Technology; CRC Press: Boca Raton, FL, USA, 2007; pp. 182–184. [Google Scholar]
- IPC. Printed Circuit Assembly Strain Gage Test Guideline; IPC JEDEC 9704A; IPC: Bannockburn, IL, USA, 2005. [Google Scholar]
- IPC. Guidance for Strain Gage Limits for Printed Circuit Assemblies; IPC-WP-011; IPC: Bannockburn, IL, USA, 2011. [Google Scholar]
- Chvojan, J.; Václavík, J. PCB Tests during Assembly and Splitting. Proceedings 2018, 2, 472. [Google Scholar]
- Liao, M.G.; Huang, S.; Lin, Y.H.; Tsai, M.Y.; Huang, C.Y.; Huang, T.C. Measurements of Thermally-Induced Curvatures and Warpages of Printed Circuit Board during a Solder Reflow Process Using Strain Gauges. Appl. Sci. 2017, 7, 739. [Google Scholar] [CrossRef]
- Ratanawilai, T.B.; Hunter, B.; Subbarayan, G.; Rose, D. A study on the variation of effective CTE of printed circuit boards through a validated comparison between strain gauges and moiré interferometry. IEEE Trans. Compon. Packag. Technol. 2003, 26, 712–718. [Google Scholar] [CrossRef]
- Moulart, R.; Pierron, F.; Hallett, S.R.; Wisnom, M.R. Full-field strain measurement and identification of composites moduli at high strain rate with the virtual fields method. Exp. Mech. 2010, 51, 509–536. [Google Scholar] [CrossRef] [Green Version]
- Luo, F.; Chao, Y.J.; Sutton, M.A.; Peters, W.H. Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision. Exp. Mech. 1993, 33, 123–132. [Google Scholar] [CrossRef]
- Chean, V.; Robin, E.; Abdi, R.; Sangleboeuf, J.C.; Houizot, P. Use of the mark-tracking method for optical fiber characterization. Opt. Laser Technol. 2011, 43, 1172–1178. [Google Scholar] [CrossRef]
- Lyons, J.; Liu, J.; Sutton, M. High-temperature deformation measurements using digital image correlation. Exp. Mech. 1996, 36, 64–70. [Google Scholar] [CrossRef]
- Pan, B.; Wu, D.; Wang, Z.; Xia, Y. High-temperature digital image correlation method for full-field deformation measurement at 1200 C. Meas. Sci. Technol. 2011, 22, 015701. [Google Scholar] [CrossRef]
- Novak, M.D.; Zok, F.W. High-temperature materials testing with full-field strain measurement: Experimental design and practice. Rev. Sci. Instrum. 2011, 82, 115101. [Google Scholar] [CrossRef] [PubMed]
- De Stryckera, M.; Schueremansb, L.; Van Paepegemc, W.; Debruynead, D. Measuring the thermal expansion coefficient of tubular steel specimens with digital image correlation techniques. Opt. Lasers Eng. 2010, 48, 978–986. [Google Scholar] [CrossRef]
- Jin, T.L.; Ha, N.S.; Goo, N.S. A study of the thermal buckling behavior of a circular aluminum plate using the digital image correlation technique and finite element analysis. Thin-Walled Struct. 2014, 77, 187–197. [Google Scholar] [CrossRef]
- Lienhard, J.; Huberth, F. Strain rate dependent thermo-mechanical aspects of glass fiber reinforced thermoplastic based on experimental data. Int. J. Impact Eng. 2019, 131, 57–65. [Google Scholar] [CrossRef]
- Lin, S.; Lienert, U.; Haas, S.; Gutschimidt, S. Strain Measurement by Digital Image Correlation; Royal Institute of Technology: Stockholm, Sweden, 2015. [Google Scholar]
- Falk, A.; Marsavina, L.; Pop, O. Experimental determination of strain distribution on Printed Circuit Boards using Digital image correlation. Procedia Struct. Integr. 2019, 18, 214–222. [Google Scholar] [CrossRef]
- Falk, A.; Marsavina, L.; Pop, O. Analysis of Printed Circuit Boards strains using finite element analysis and digital image correlation. Frat. Ed Integrità Strutt. 2020, 51, 541–551. [Google Scholar]
- Szebényi, G.; Hliva, V. Detection of Delamination in Polymer Composites by Digital Image Correlation—Experimental Test. Polymers 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Elmahdy, A.; Verleysen, P. The Use of 2D and 3D High-Speed Digital Image Correlation in Full Field Strain Measurements of Composite Materials Subjected to High Strain Rates. Proceedings 2018, 2, 538. [Google Scholar]
- Zhu, M.; Gorbatikh, L.; Fonteyn, S.; Pyl, L.; Hemelrijck, D.V.; Payan, D.C.; Lomov, S.V. Digital Image Correlation Measurements of Mode I Fatigue Delamination in Laminated Composites. Proceedings 2018, 2, 430. [Google Scholar]
- Malesa, M.; Malowany, K.; Tomczak, U.; Siwek, B.; Małgorzata, K.; Lewandowska, A.S. Application of 3D digital image correlation in maintenance and process control in industry. Comput. Ind. 2013, 64, 1301–1315. [Google Scholar] [CrossRef]
- Li, J.; Xiea, X.; Yang, G.; Zhang, B.; Siebert, T.; Yang, L. Whole-field thickness strain measurement using multiple camera digital image correlation system. Opt. Lasers Eng. 2017, 90, 19–25. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Chiozzi, D.; Bernardoni, M.; Delmonte, N.; Cova, P. A simple 1-D finite elements approach to model the effect of PCB in electronic assembly. Microelectron. Reliab. 2016, 56, 126–132. [Google Scholar] [CrossRef]
- Fan, X.; Pei, M.; Bhatti, K. Effect of finite element modeling techniques on solder joint fatigue life prediction of flip-chip BGA packages. In Proceedings of the 56th Electronic Components and Technology Conference, San Diego, CA, USA, 30 May–2 June 2006. [Google Scholar]
- Li, L.; Kimb, S.M.; Song, S.H.; Ku, T.W.; Song, W.J.; Kim, J.; Chong, M.K.; Park, J.W.; Kang, B.S. Finite element modeling and simulation for bending analysis of multi-layer printed circuit boards using woven fiber composite. J. Mater. Process. Technol. 2008, 201, 746–750. [Google Scholar] [CrossRef]
- Zahn, B.A. Finite element-based solder joint fatigue life predictions for a same die size-stacked-chip scale-ball grid array package. In Proceedings of the Technology Symposium: International Electronics Manufacturing Technology (EMT) Symposium, San Jose, CA, USA, 17–18 July 2002. [Google Scholar]





| Property | Symbol | Unit | Value |
|---|---|---|---|
| Density | ρ | g/cm3 | 1.85 |
| Orthotropic Instantaneous Coefficient of Thermal Expansion | αx αy αz | °C−1 °C−1 °C−1 | 1.35 × 10−5 1.35 × 10−5 4.50 × 10−5 |
| Longitudinal Modulus of Elasticity | EX Ey Ez | MPa MPa MPa | 1.69 × 104 1.69 × 104 7.40 × 104 |
| Poisson’s Ratio | νxy | - | 0.11 |
| νyz | - | 0.39 | |
| νzx | - | 0.39 | |
| Shear Modulus | Gxy | MPa | 7.60 × 103 |
| Gyz | MPa | 3.30 × 103 | |
| Gzx | MPa | 3.30 × 103 |
| Property | Symbol | Unit | Value |
|---|---|---|---|
| Density | ρ | g/cm3 | 1.63 |
| Coefficient of Thermal Expansion | α | °C−1 | 6 × 10−5 |
| Young’s Modulus | E | MPa | 2.55 × 104 |
| Poisson’s Ratio | ν | 1.10 × 10−1 | |
| Bulk Modulus | B | MPa | 1.70 × 104 |
| Shear Modulus | G | MPa | 1.02 × 104 |
| Property | Symbol | Unit | Value |
|---|---|---|---|
| Coefficient of Thermal Expansion | α | °C−1 | 2.30 × 10−5 |
| Density | ρ | g/cm3 | 2.7 |
| Young’s Modulus | E | MPa | 2.55 × 104 |
| Poisson’s Ratio | ν | 1.10 × 10−1 | |
| Bulk Modulus | B | MPa | 1.70 × 104 |
| Shear Modulus | G | MPa | 1.02 × 104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falk, A.; Pop, O.; Dopeux, J.; Marsavina, L. Assessment of Strains Produced by Thermal Expansion in Printed Circuit Boards. Materials 2022, 15, 3916. https://doi.org/10.3390/ma15113916
Falk A, Pop O, Dopeux J, Marsavina L. Assessment of Strains Produced by Thermal Expansion in Printed Circuit Boards. Materials. 2022; 15(11):3916. https://doi.org/10.3390/ma15113916
Chicago/Turabian StyleFalk, Alexandru, Octavian Pop, Jérôme Dopeux, and Liviu Marsavina. 2022. "Assessment of Strains Produced by Thermal Expansion in Printed Circuit Boards" Materials 15, no. 11: 3916. https://doi.org/10.3390/ma15113916
APA StyleFalk, A., Pop, O., Dopeux, J., & Marsavina, L. (2022). Assessment of Strains Produced by Thermal Expansion in Printed Circuit Boards. Materials, 15(11), 3916. https://doi.org/10.3390/ma15113916






