RETRACTED: Numerical Case Study of Chemical Reaction Impact on MHD Micropolar Fluid Flow Past over a Vertical Riga Plate
Abstract
:1. Introduction
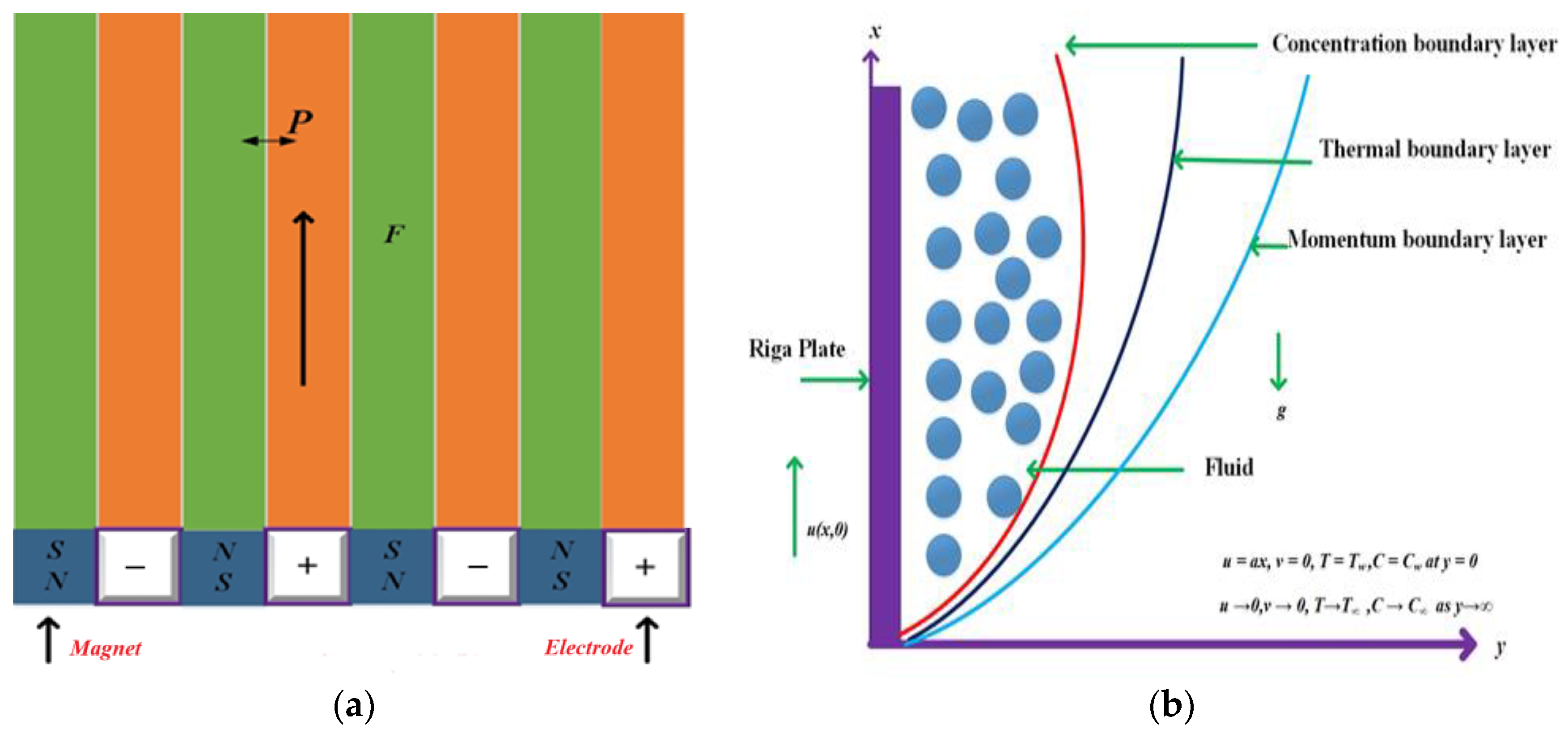
2. Description of Problem
3. Numerical Process
- if it gives:
- ▪
- Odes function for evaluating ODEs;
- ▪
- Function bcs (boundary conditions) for calculating the residual of the boundary condition;
- ▪
- Solinit structure that includes both a mesh estimate and the mesh solution. ODEs are processed similarly to IVP solvers in MATLAB.
4. Results and Discussion
5. Conclusions
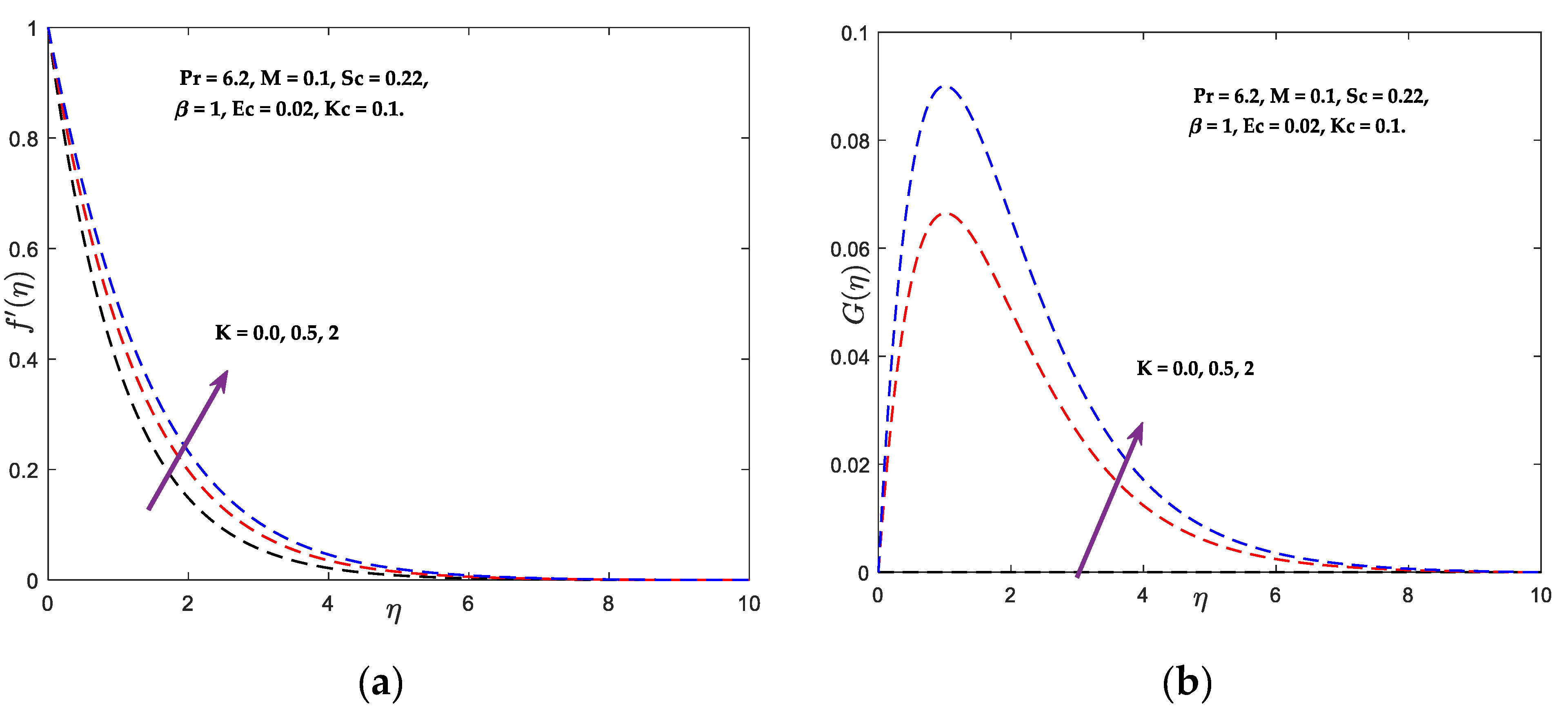
- With an increase in , velocity and angular velocity enhance. Additionally, Nusselt number and Sherwood number enhance while temperature and concentration drop.
- When the modified Hartman number is increased, the inner velocity exceeds the free stream velocity.
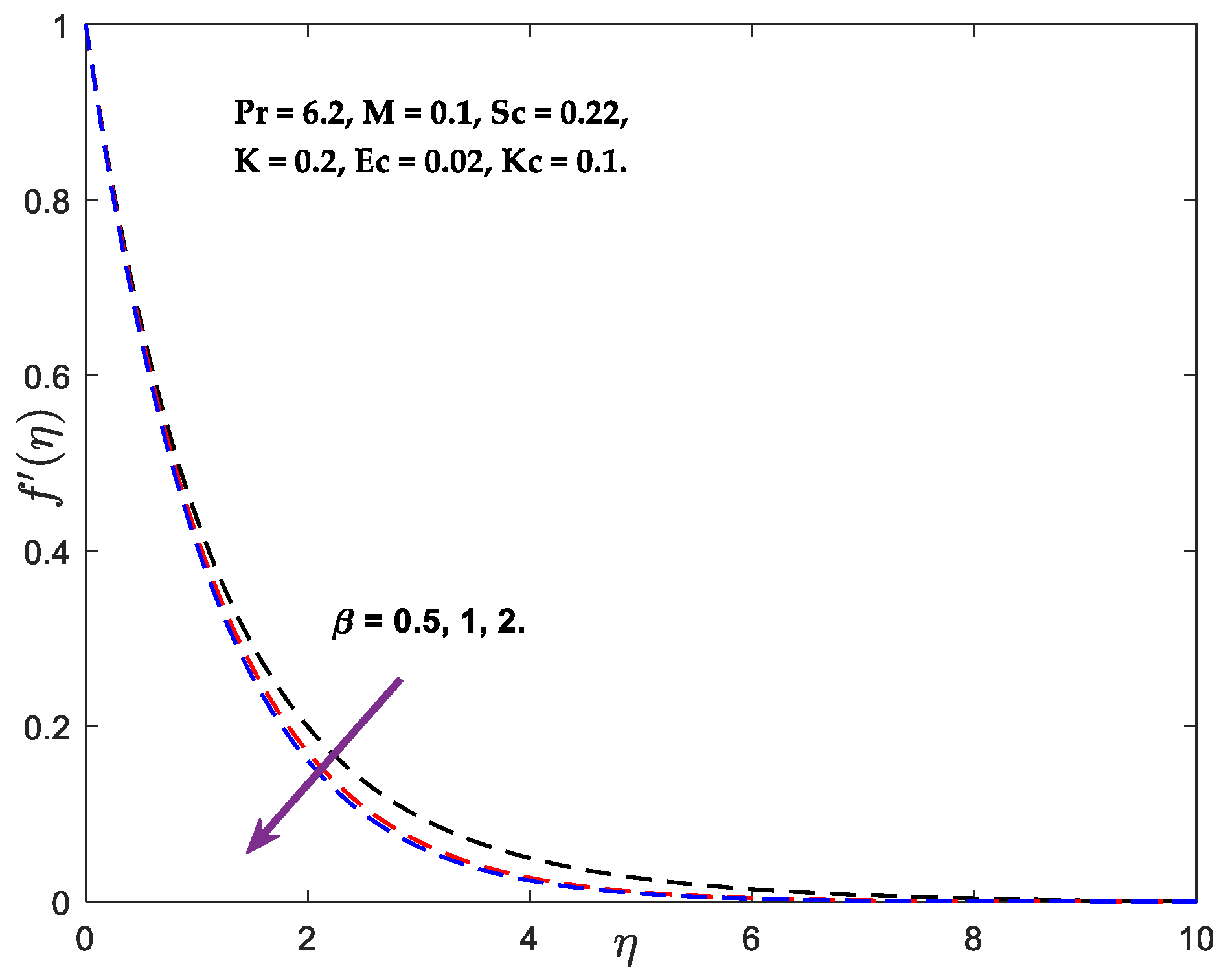
- With a rise in substantial parameter, rapidity, coupling stress, Sherwood, Nusselt quantities, enhances and energy, concentricity, and shearing stress decrease.
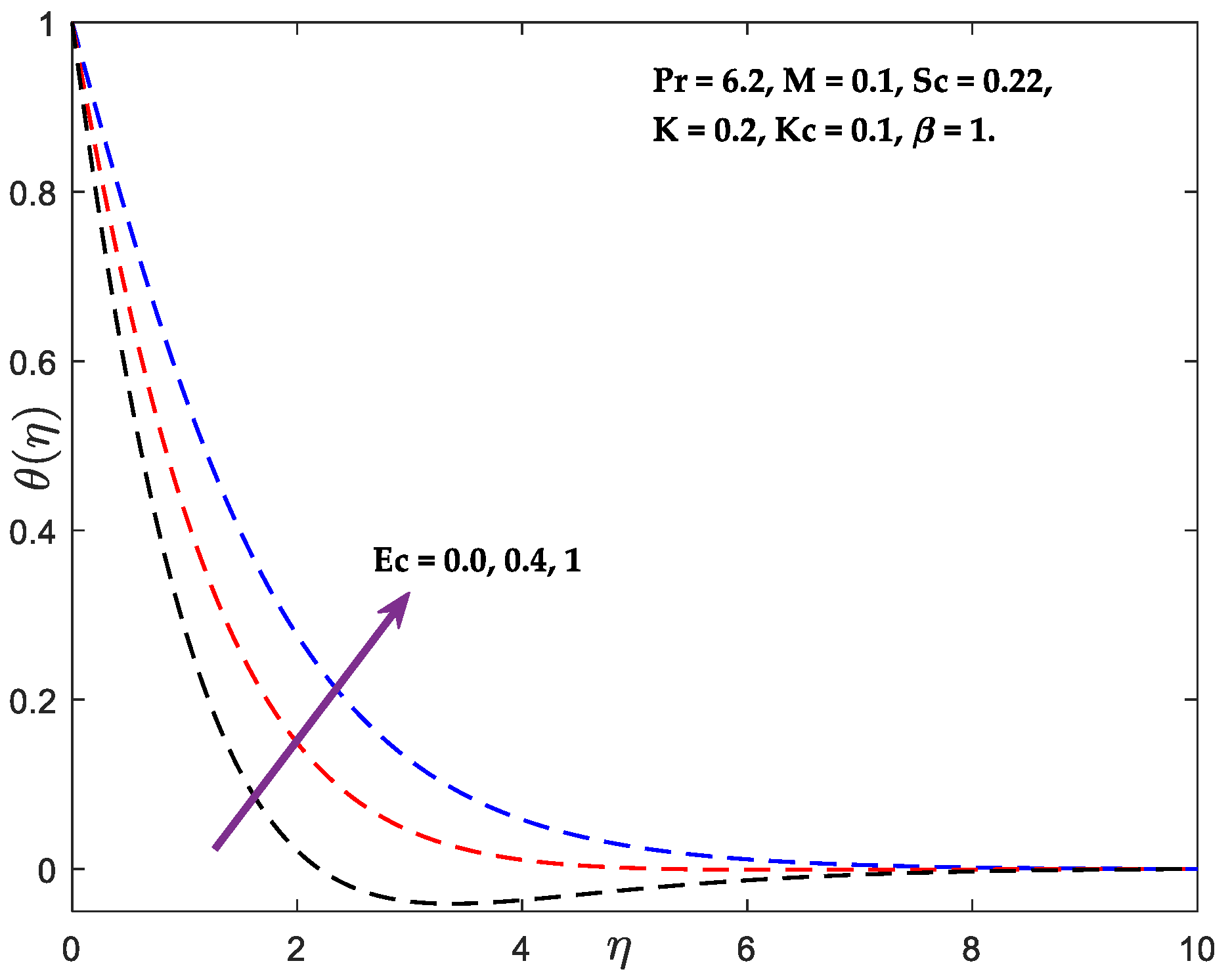
- Temperature decreases and increases as values grow.
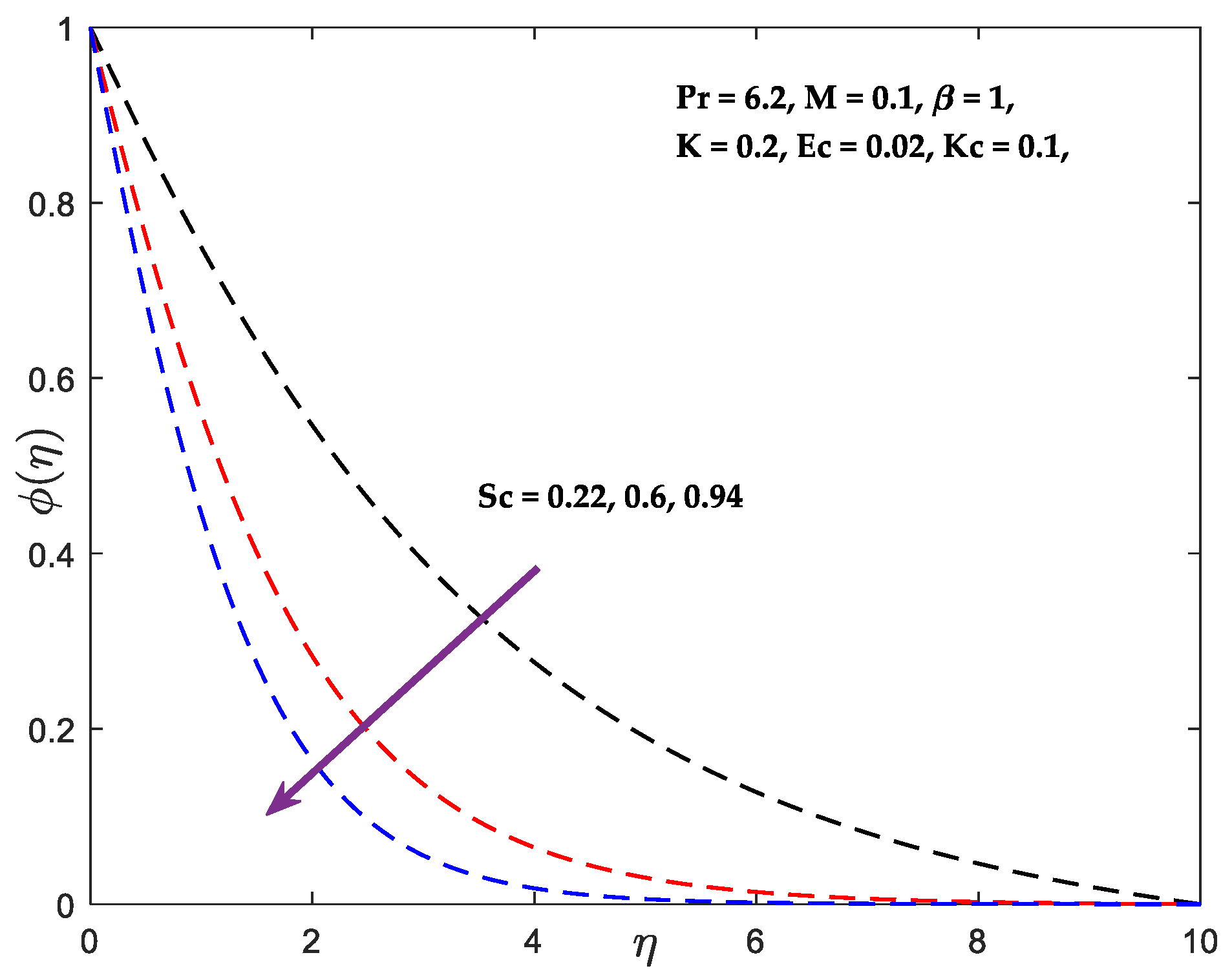
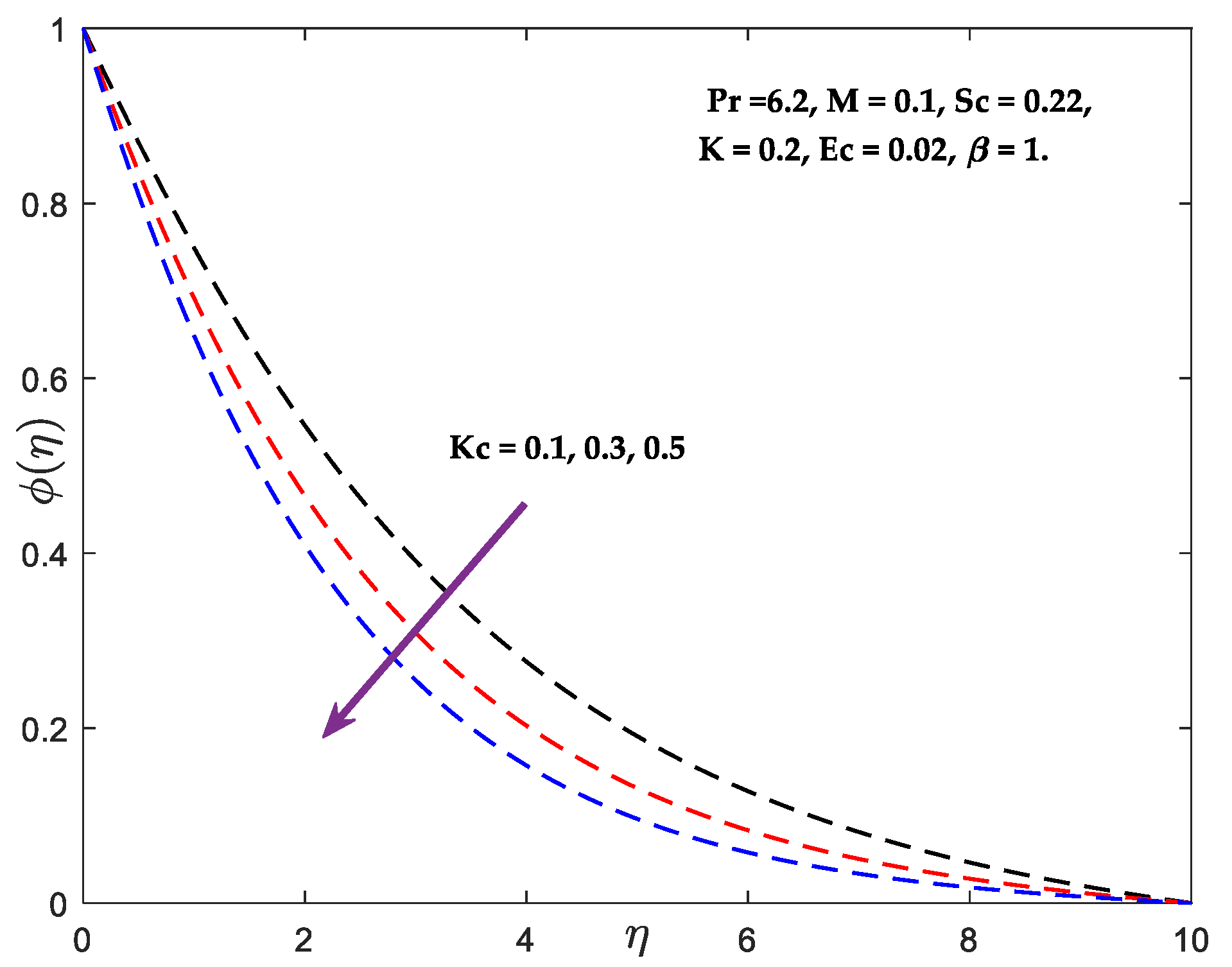
- The result of increasing and is a drop in concentration and a rise in .
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Vortex viscosity | Specific heat constant pressure | ||
| Viscosity of spin gradient | Mass diffusivity | ||
| Thermal conductivity | Material parameter | ||
| Surface velocity | wall temperature | ||
| Species concentration at the surface | Fluid concentration outlying the surface | ||
| Schmidt number | Eckert number | ||
| Microinertia per unit mass | Ambient temperature | ||
| Kinematic viscosity | Dynamic viscosity | ||
| Hartmann number | Prandtl number | ||
| Free stream density | Constant | ||
| Temperature | Concentricity | ||
| Dimensionless parameter |
References
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over an exponentially stretching continuous surface with suction. Arch. Mech. 2001, 53, 643–651. [Google Scholar]
- Fang, T. Boundary layer flow over a shrinking sheet with power-law velocity. Int. J. Heat Mass Transf. 2008, 51, 5838–5843. [Google Scholar] [CrossRef]
- Chamkha, A.J. Mhd flow of a uniformly stretched vertical permeable surface in the presence of heat generation/absorption and a chemical reaction. Int. Commun. Heat Mass Transf. 2003, 30, 413–422. [Google Scholar] [CrossRef]
- Makinde, O.D. On MHD heat and mass transfer over a moving vertical plate with a convective surface boundary condition. Can. J. Chem. Eng. 2010, 88, 983–990. [Google Scholar] [CrossRef]
- Sharma, K.; Gupta, S. Analytical study of MHD boundary layer flow and heat transfer towards a porous exponentially stretching sheet in presence of thermal radiation. Int. J. Adv. Appl. Math. Mech. 2016, 4, 1–10. [Google Scholar]
- Eringen, A.C. Theory of Micropolar Fluids. J. Math. Mech. 1972, 38, 469–480. [Google Scholar]
- Hassanien, I.A.; Gorla, R.S.R. Heat transfer to a micropolar fluid from a non-isothermal stretching sheet with suction and blowing. Acta Mech. 1990, 84, 191–199. [Google Scholar] [CrossRef]
- Takhar, H.S.; Agarwal, R.S.; Bhargava, R.; Jain, S. Mixed convection flow of a micropolar fluid over a stretching sheet. Heat Mass Transf. 1998, 34, 213–219. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Elshehawey, E.F.; Elbarbary, E.M.E.; Elgazery, N.S. Chebyshev finite difference method for MHD flow of a micropolar fluid past a stretching sheet with heat transfer. Appl. Math. Comput. 2005, 160, 437–450. [Google Scholar] [CrossRef]
- Fatunmbi, E.O.; Ogunseye, H.A.; Sibanda, P. Magnetohydrodynamic micropolar fluid flow in a porous medium with multiple slip conditions. Int. Commun. Heat Mass Transf. 2020, 15, 104577. [Google Scholar] [CrossRef]
- Gailitis, A.; Lielausis, O. On the possibility to reduce the hydrodynamic drag of a plate in an electrolyte. Appl. Magnetohydrodyn. Rep. Inst. Phys. Riga 1961, 13, 143–146. [Google Scholar]
- Pantokratoras, A.; Magyari, E. EMHD free-convection boundary-layer flow from a Riga-plate. J. Eng. Math. 2008, 64, 303–315. [Google Scholar] [CrossRef]
- Ahmad, R.; Mustafa, M.; Turkyilmazoglu, M. Buoyancy effects on nanofluid flow past a convectively heated vertical Riga-plate: A numerical study. Int. J. Heat Mass Transf. 2017, 111, 827–835. [Google Scholar] [CrossRef]
- Ayub, M.; Abbas, T.; Bhatti, M.M. Inspiration of slip effects on electromagnetohydrodynamics (EMHD) nanofluid flow through a horizontal Riga plate. Eur. Phys. J. Plus 2016, 131, 193. [Google Scholar] [CrossRef]
- Fatunmbi, E.O.; Adeosun, A.T.; Salawu, S.O. Irreversibility analysis for Eyring-Powell nanoliquid flow past magnetized Riga device with nonlinear thermal radiation. Fluids 2021, 6, 416. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Characteristics of chemical reaction and convective boundary conditions in Powell-Eyring nanofluid flow along a radiative Riga plate. Heliyon 2019, 5, e01479. [Google Scholar] [CrossRef]
- Goud, S.B. Heat generation/absorption influence on steady stretched permeable surface on MHD flow of a micropolar fluid through a porous medium in the presence of variable suction/injection. Int. J. Thermofluids 2020, 7, 100044. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Sidawi, I. Free convection on a vertical stretching surface with suction and blowing. Flow Turbul. Combust. 1994, 52, 247–257. [Google Scholar]
- Goyal, M.; Bhargava, R. Boundary layer flow and heat transfer of viscoelastic nanofluids past a stretching sheet with partial slip conditions. Appl. Nanosci. 2013, 4, 761–767. [Google Scholar] [CrossRef]
- Nazar, S.M.; Pop, I. Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Instit. Chem. Eng. 2010, 41, 651–655. [Google Scholar]

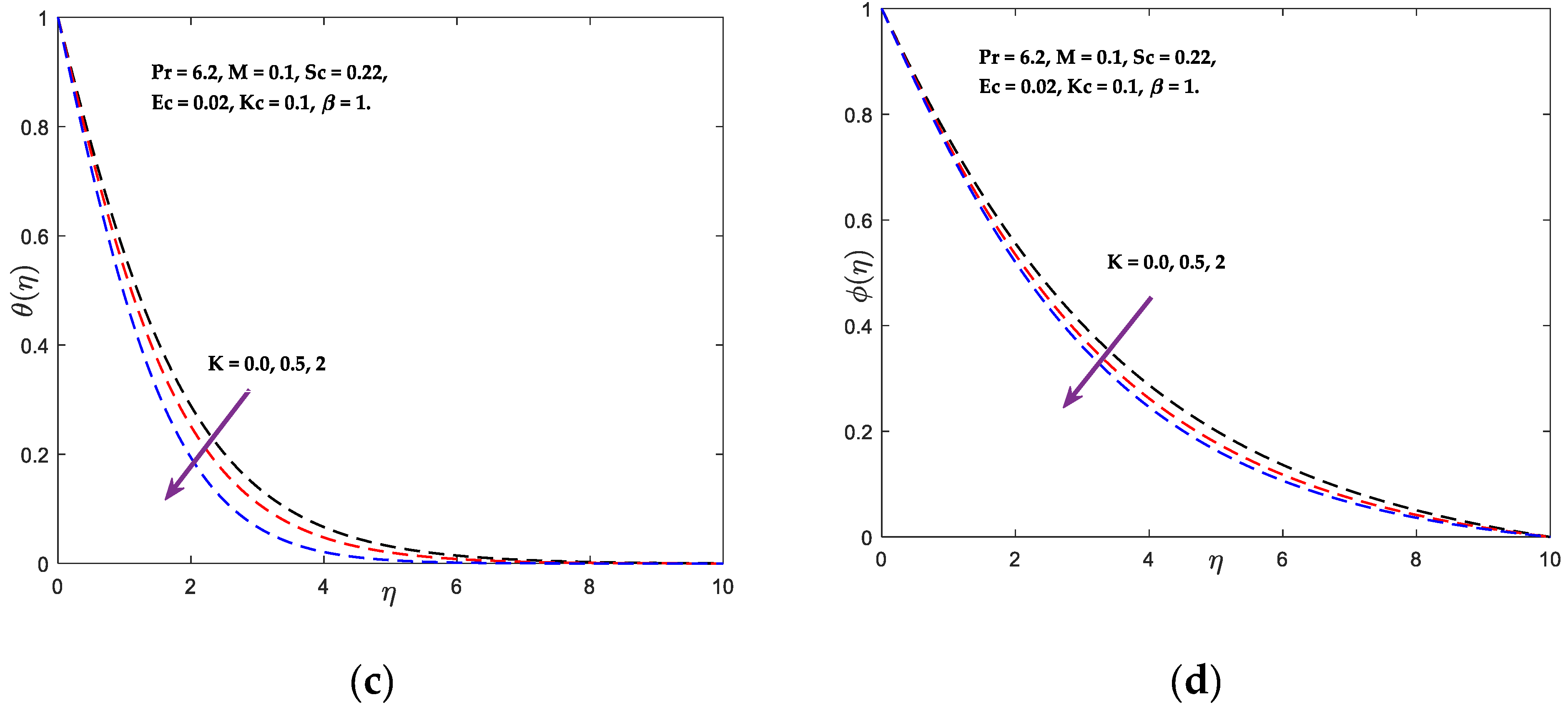

| Ref. [19] | Ref. [20] | Ref. [21] | Ref. [22] | Present Study | |
|---|---|---|---|---|---|
| 0.7 | - | 0.4539 | - | 0.4539 | 0.45445 |
| 2 | 0.91142 | 0.9113 | - | 0.9113 | 0.91135 |
| 3 | 1.1597 | - | 1.16522 | - | 1.16525 |
| 7 | 1.89046 | 1.8954 | 1.8954 | 1.8954 | 1.89541 |
| 0 | 0.2 | 1 | 0.90975 | 0.095 | 1.865537 | 0.26522 |
| 0.5 | 0.699167 | 0.084668 | 1.900295 | 0.280001 | ||
| 1 | 0.496288 | 0.07547 | 1.930793 | 0.292783 | ||
| 0 | 0.950328 | 0 | 1.845710 | 0.262482 | ||
| 0.5 | 0.769444 | 0.171601 | 1.906578 | 0.275290 | ||
| 2 | 0.520359 | 0.229950 | 2.017546 | 0.296674 | ||
| 0.2 | 0.2 | 0.815108 | 0.083641 | 1.883016 | 0.285358 | |
| 0.4 | 0.837795 | 0.088279 | 1.878961 | 0.276605 | ||
| 0.6 | 0.851606 | 0.090705 | 1.876191 | 0.272101 |
| 0.71 | 0.02 | 0.496574 |
| 1 | 0.625629 | |
| 3 | 1.235704 | |
| 6.2 | 1.872921 | |
| 0.04 | 1.946615 | |
| 0.06 | 2.020310 |
| 0.22 | 0.1 | 0.268390 |
| 0.6 | 0.502325 | |
| 0.96 | 0.672557 | |
| 0.22 | 0.3 | 0.346935 |
| 0.22 | 0.5 | 0.409794 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goud, B.S.; Reddy, Y.D.; Alshehri, N.A.; Jamshed, W.; Safdar, R.; Eid, M.R.; Bouazizi, M.L. RETRACTED: Numerical Case Study of Chemical Reaction Impact on MHD Micropolar Fluid Flow Past over a Vertical Riga Plate. Materials 2022, 15, 4060. https://doi.org/10.3390/ma15124060
Goud BS, Reddy YD, Alshehri NA, Jamshed W, Safdar R, Eid MR, Bouazizi ML. RETRACTED: Numerical Case Study of Chemical Reaction Impact on MHD Micropolar Fluid Flow Past over a Vertical Riga Plate. Materials. 2022; 15(12):4060. https://doi.org/10.3390/ma15124060
Chicago/Turabian StyleGoud, B. Shankar, Yanala Dharmendar Reddy, Nawal A. Alshehri, Wasim Jamshed, Rabia Safdar, Mohamed R. Eid, and Mohamed Lamjed Bouazizi. 2022. "RETRACTED: Numerical Case Study of Chemical Reaction Impact on MHD Micropolar Fluid Flow Past over a Vertical Riga Plate" Materials 15, no. 12: 4060. https://doi.org/10.3390/ma15124060
APA StyleGoud, B. S., Reddy, Y. D., Alshehri, N. A., Jamshed, W., Safdar, R., Eid, M. R., & Bouazizi, M. L. (2022). RETRACTED: Numerical Case Study of Chemical Reaction Impact on MHD Micropolar Fluid Flow Past over a Vertical Riga Plate. Materials, 15(12), 4060. https://doi.org/10.3390/ma15124060








