Experimental Study on Long-Term Mechanical Properties of Prestressed Glulam Continuous Beams
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Specimens
2.2. Long-Term Test
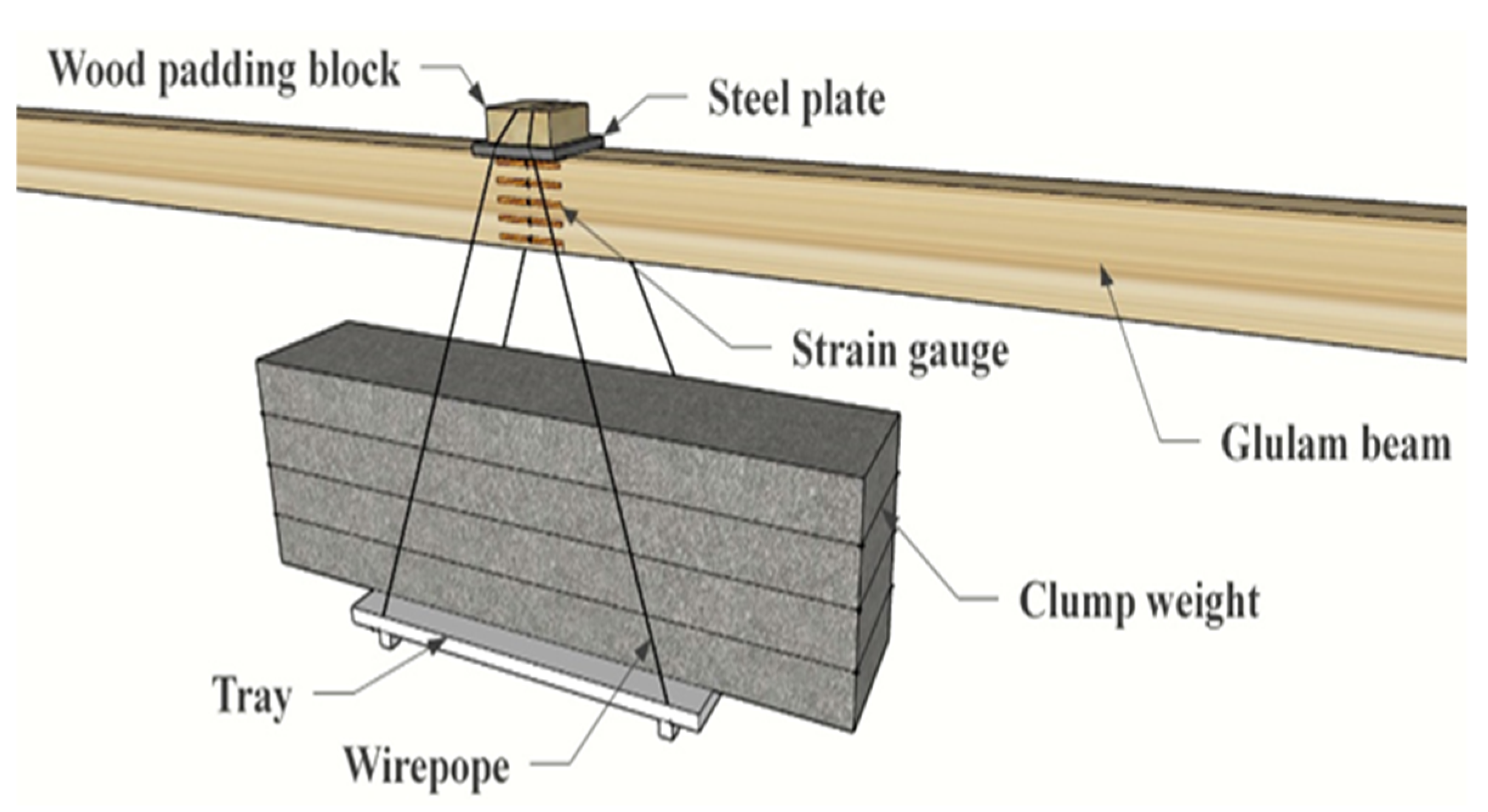
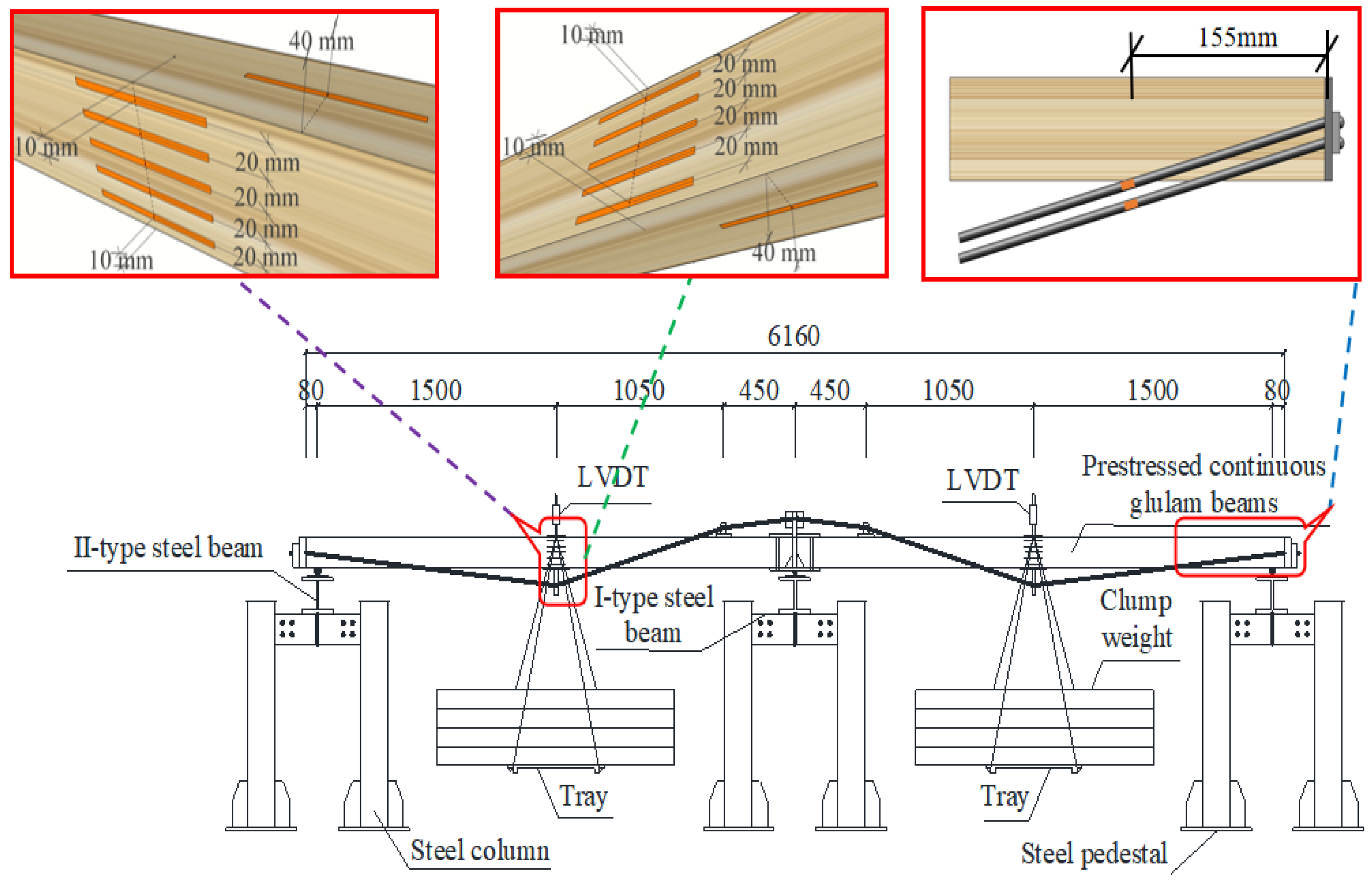
2.2.1. Loading Device and Method
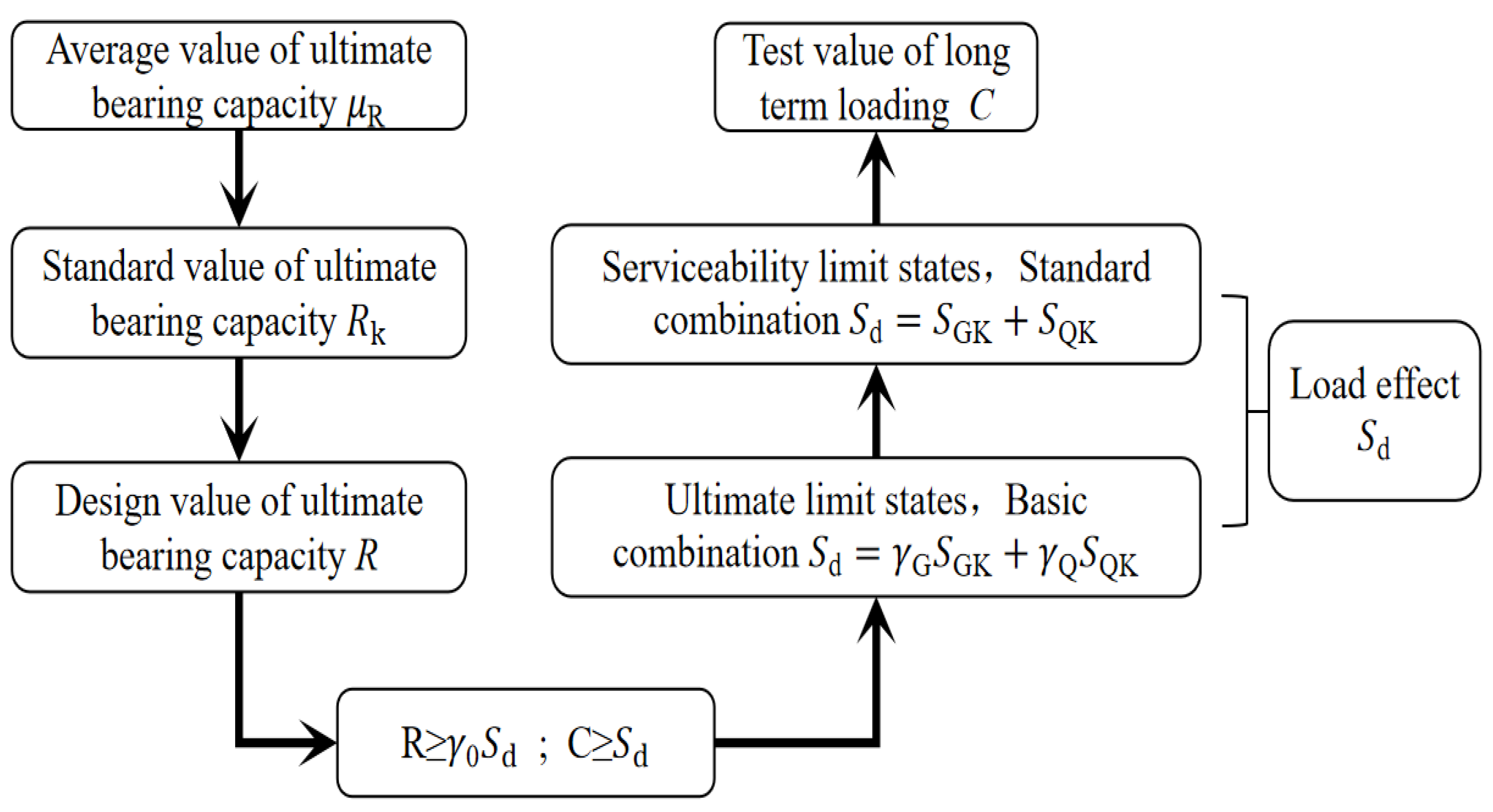
2.2.2. Determine Long-Term Loads and Times
2.2.3. Measurement Layout
3. Test Results and Analysis
3.1. Change in Temperature and Relative Humidity
3.2. Test Phenomenon
3.3. Stress Variation Law of Prestressed Steel Wire
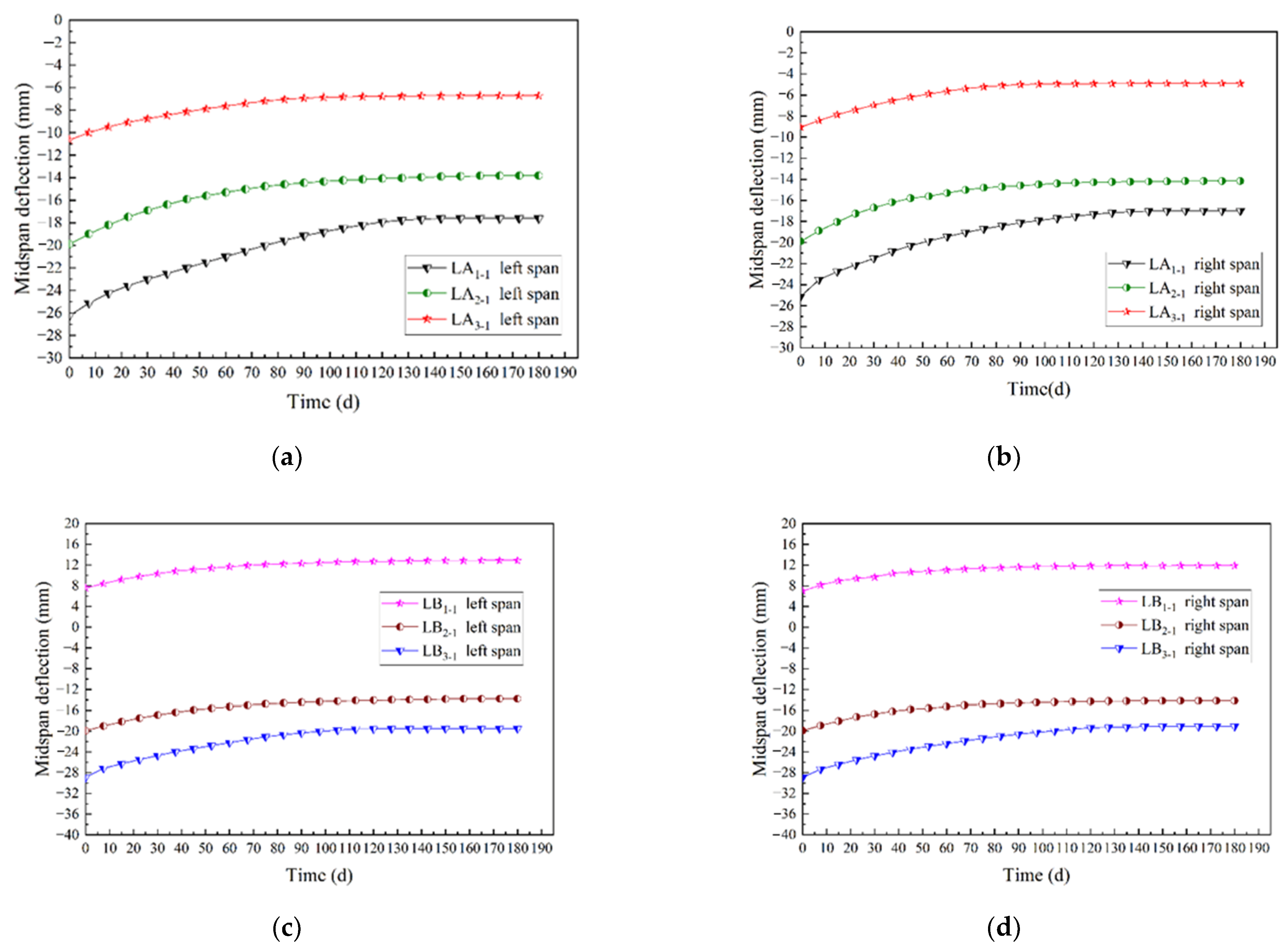
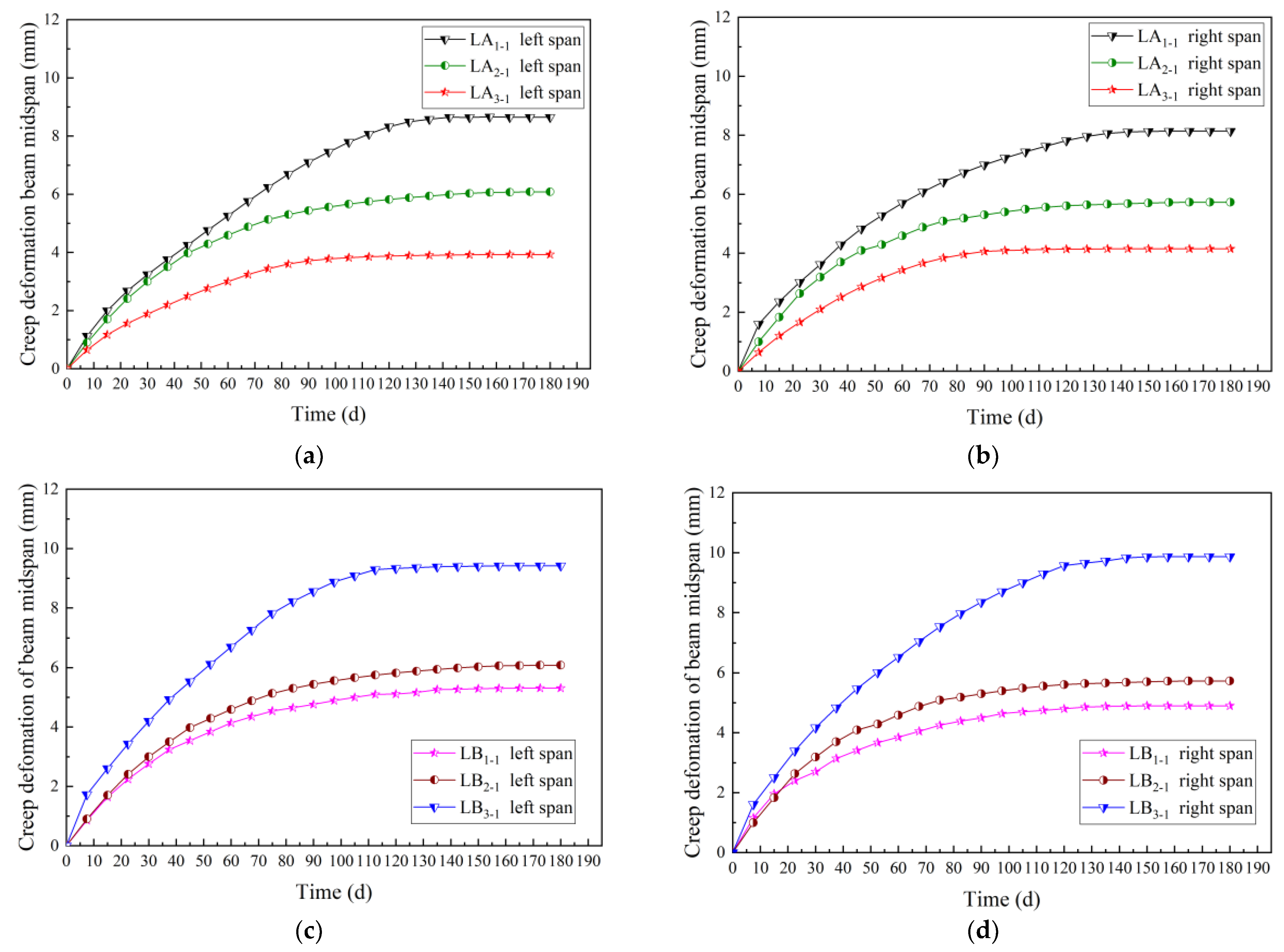
3.4. Variation Law of Beam Mid-Span Deflection
3.5. Theoretical Analysis
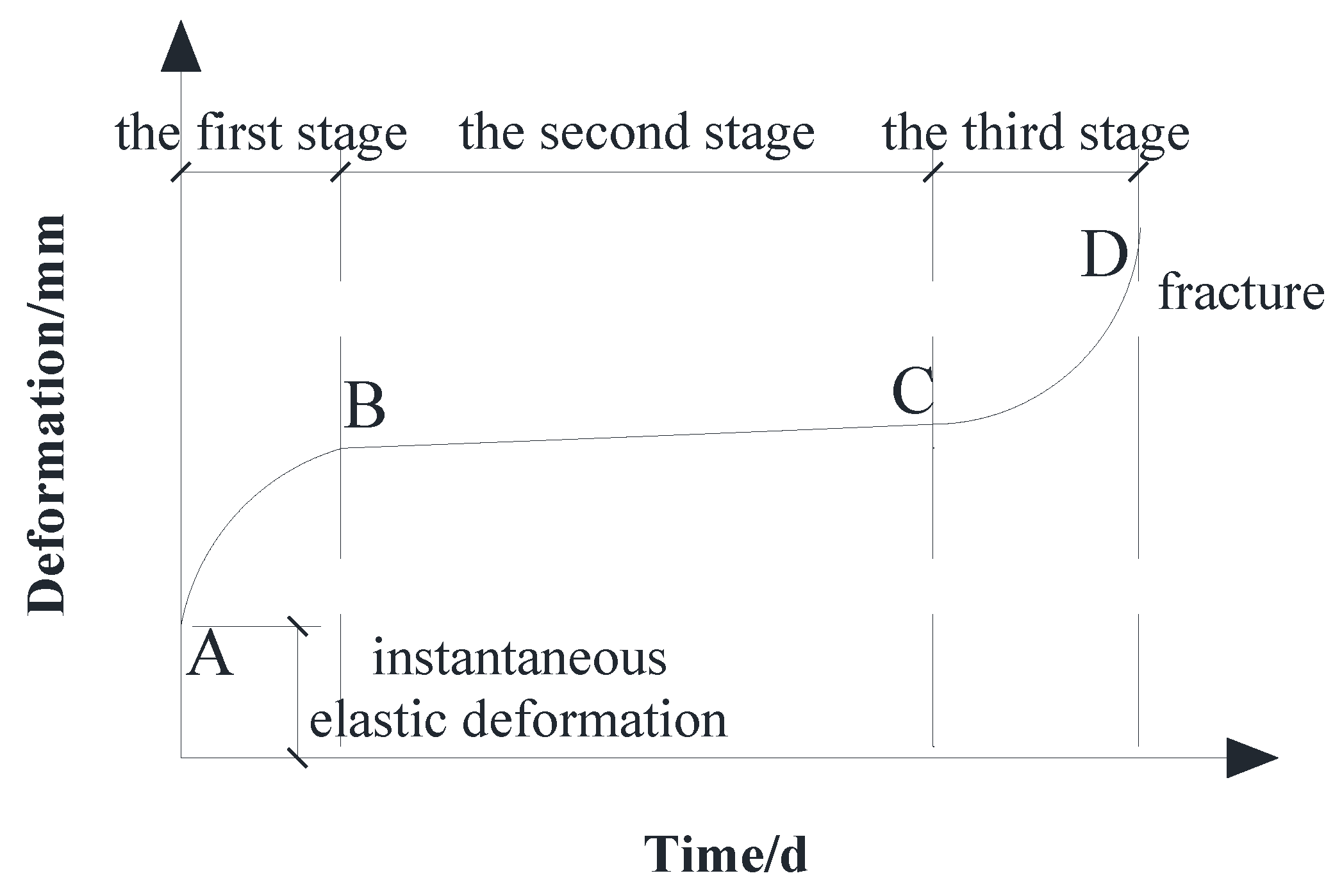
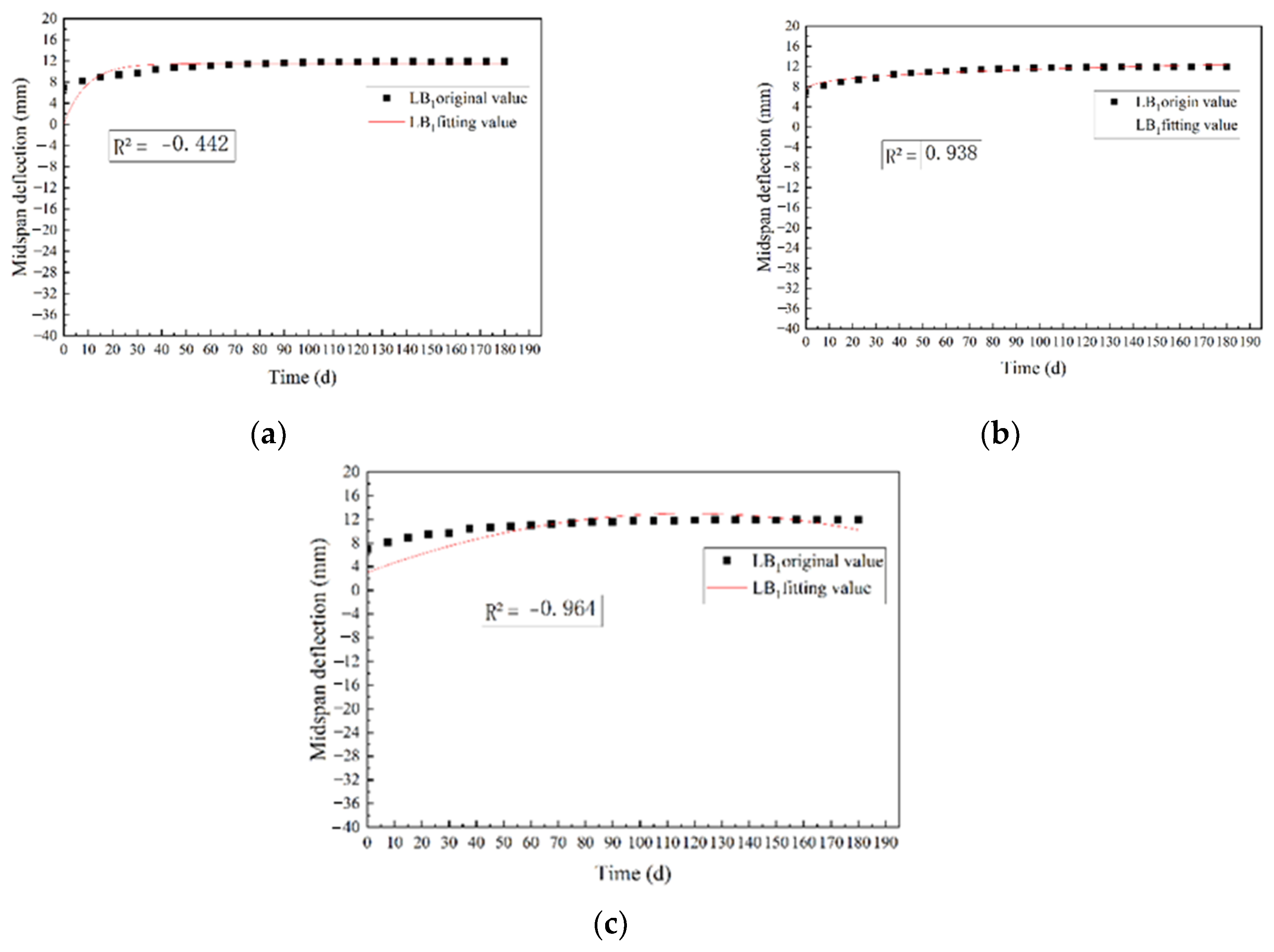
3.5.1. Establishment of Creep Model
3.5.2. Creep Deformation Coefficient θ and the Total Deflection
4. Conclusions
- When the number of the prestressed steel wires was 2, 4, and 6, the total stress of steel wires decreased by 60.39%, 66.49%, and 69.61%, respectively, from the beginning to the end of loading; when the prestress value was 0, 7, and 14 kN, the total stress of steel wires decreased by 61.60%, 66.53%, and 68.74%, respectively, from the beginning to the end of loading. This is because by increasing the number of prestressed steel wires and the prestress value, the external load on the continuous beam increased, then the section stress of the glulam also increased, and the wood creep was more obvious, and the total stress of the steel wires decreased more.
- Compared with the continuous beam with two steel wires, the long-term deflection average of the beams with four and six steel wires decreased by 32.0% and 48.0%, respectively; compared with the continuous beam without prestressing, the long-term deflection average of the beams with 7 kN and 14 kN prestress value increased by 18.75% and 88.40%, respectively, which shows that increasing the number of steel wires could effectively restrain the long-term deflection change rate of the continuous beams, and increasing the prestress value made the creep of glulam beams more obvious and promoted the long-term deflection change rate of the continuous beams, the deformation developed faster.
- Based on the comparison between three common creep models of exponential equation, power-law equation, and polynomial equation, it found that the power-law equation was the most suitable for simulating the creep process of the prestressed glulam continuous beams, and the fitting curve had higher accuracy. According to the experiment and numerical fitting results, at familiar steel wire quantities and prestress levels, the creep deformation coefficient of the test beams within the design service life of 50 years was determined to be 1.28–2.29.
- The calculation formula of long-term deflection and creep deformation coefficient of test beams were given by long-term experiment and model fitting. Later, the accuracy of fitting can be verified by longer longer-term experiments.
- The long-term performance of prestressed glulam continuous beams was mainly studied from the perspective of experiment in this paper. In the future, its long-term constitutive relation can be exploited by finite element analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, C.Y.; Yu, C.H. Green, Space, Construction—Interpretation of Modern Western Timber Structure. New Archit. 2005, 5, 19–23. [Google Scholar]
- He, M.J.; He, G.R.; Liang, F.; Li, Z. Development History of Chinese Wood Structures in the Past 20 Years. Build. Struct. 2019, 49, 83–90. [Google Scholar]
- Liu, W.Q.; Yang, H.F. Research Progress of Modern Wood Structure. J. Build. Struct. 2019, 40, 16–43. [Google Scholar]
- Shao, J.S.; Xue, W.C.; Liu, W.Q.; Wang, L. The Summarization of Research and Application of Wood Structure Strengthened with FRP. Compos. Sci. Eng. 2015, 04, 91–95. [Google Scholar]
- Liu, W.; Yang, H. Experimental Study on Flexural Behavior of Engineered Wood Beams. J. Build. Struct. 2008, 29, 90–95. [Google Scholar]
- Cao, L.; Zhang, Z.; Zeng, D.; He, G.; Cai, J. Experimental Research on Fatigue Behavior of Larch Glulam Beams. J. Build. Struct. 2016, 37, 27–35. [Google Scholar]
- Zhang, J.; Wang, W.C.; Qiu, R.G.; Shen, H.; Xu, Q.F.; Gao, S. Experimental Study on Short-Term Flexural Behavior of Internal Prestressed Glulam Beams. China Civ. Eng. J. 2019, 52, 23–34. [Google Scholar]
- Yang, H.F.; Ju, D.D.; Liu, W.Q.; Lu, W.D. Prestressed Glulam Beams Reinforced with CFRP Bars. Constr. Build. Mater. 2016, 109, 73–83. [Google Scholar] [CrossRef] [Green Version]
- Mei, L.D.; Guo, N.; Li, L.; Zuo, H.L.; Zhao, Y. Study on Flexural Performance of Prestressed Glulam Continuous Beams under Control Influence. J. Wood Sci. 2021, 67, 48. [Google Scholar] [CrossRef]
- Guo, N.; Wang, Y.J.; Zuo, H.L. Study of Short-Term Flexural Behavior for Glue-Bamboo and Lumber Beams under Different Pre-Stressed States. Civ. Eng. J. 2017, 26, 128–142. [Google Scholar] [CrossRef]
- Guo, N.; Wang, W.B.; Zuo, H.L. Flexural Property of String Beam of Pre-Stressed Glulam Based on Influence of Regulation and Control. Struct. Durab. Health Monit. 2019, 13, 143–179. [Google Scholar] [CrossRef]
- Guo, N.; Wu, M.T.; Li, L.; Li, G.D.; Zhao, Y. Bending Performance of Prestressed Continuous Glulam Beams. Adv. Civ. Eng. 2021, 2021, 5512350. [Google Scholar] [CrossRef]
- Fonseca, E.M.M.; Leite, P.A.S. Fire Design of Wood Connections Loaded in Shear. MATTER Int. J. Sci. Technol. 2019, 5, 68–84. [Google Scholar] [CrossRef] [Green Version]
- Peng, L.; Hadjisophocleous, G.; Mehaffey, J.; Mohammad, M. On the Fire Performance of Double-Shear Timber Connections. Fire Saf. Sci. 2011, 10, 1207–1218. [Google Scholar] [CrossRef]
- Frangi, A.; Erchinger, C.; Fontana, M. Experimental Fire Analysis of Steel-to-Timber Connections Using Dowels and Nails. Fire Mater. 2009, 34, 1–19. [Google Scholar] [CrossRef]
- Fonseca, E.M.M.; Leite, P.A.S.; Silva, L. Wood Connections Under Fire Conditions Protected with Gypsum Plasterboard Types A and F. In Advances in Fire Safety Engineering; Piloto, P.A.G., Rodrigues, J.P., Silva, V.P., Eds.; Lecture Notes in Civil Engineering; Springer International Publishing: Cham, Switzerland, 2020; Volume 1, pp. 93–106. ISBN 978-3-030-36239-3. [Google Scholar]
- BSEN 1995-1-1; Eurocode 5: Design of Timber Structures. Part 1-1: General Common Rules and Rules for Buildings. British Standards Institution: London, UK, 2004.
- Youngquist, J.A.; Product, P. Wood Handbook: Wood as an Engineering Material; General Technical Report FPL-GTR-190, Centennial Edition; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010. [Google Scholar]
- Fonseca, E.M.M.; Leite, P.A.S.; Silva, L.D.S.; Silva, V.S.B.; Lopes, H.M. Parametric Study of Three Types of Timber Connections with Metal Fasteners Using Eurocode 5. Appl. Sci. 2022, 12, 1701. [Google Scholar] [CrossRef]
- Hunt, D.G. The Prediction of Long-Time Viscoelastic Creep from Short-Time Data. Wood Sci. Technol. 2004, 38, 479–492. [Google Scholar] [CrossRef]
- Yazdani, N.; Johnson, E.; Duwadi, S. Creep Effect in Structural Composite Lumber for Bridge Applications. J. Bridge Eng. 2004, 9, 87–94. [Google Scholar] [CrossRef]
- Guo, N.; Ren, J.; Li, L.; Zhao, Y.; Wu, M.T. Long-Term Loading Test of Reinforced Glulam Beam. J. Renew. Mater. 2022, 10, 183–201. [Google Scholar] [CrossRef]
- Guo, N.; Yang, C.; Li, L.; Li, G.D.; Zhao, Y. Experimental Study on Flexural Performance of Regulated Reinforced Glulam Beam after Long-Term Loading. Sustainability 2021, 13, 5556. [Google Scholar] [CrossRef]
- GB/T 50329-2012; Standard for Test Methods of Timber Structures. China Architecture & Building Press: Beijing, China, 2012.
- GB/T 1938-2009; Method of Testing in Tensile Strength Parallel to Grain of Wood. Standardization Administration of the People’s Republic of China: Beijing, China, 2009.
- GB/T 228.1-2010; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2010.
- GB 50005-2017; Standard for Design of Timber Structures. China Architecture & Building Press: Beijing, China, 2017.
- O86-14; Engineering Design in Wood. CSA Group: Toronto, ON, Canada, 2017.
- GB 50009-2012; Load Code for the Design of Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Yue, K.; Zhang, W.; Xia, Y.; Lu, X.N. A review on creep of wood material. For. Grassl. Mach. 2008, 48–51. [Google Scholar]
- LY/T 1975-2011; Standard for Evaluation of Duration of Load and Creep Effects of Wood and Wood-Based Products. Standards Press of China: Beijing, China, 2011.
- Xu, Y.L.; Hua, Y.K. Creep Behavior and Bending Properties of Poplar LVL in Different Assembly Types. Chin. J. Wood Sci. Technol. 2002, 16, 10–12. [Google Scholar]
- Lu, W.D.; Song, E.W.; Yue, K.; Liu, W.Q. Experimental Study on Creep Behavior of FRP-Reinforced Glulam Beam. J. Build. Mater. 2013, 16, 294–297. [Google Scholar]
- Yang, T.Q.; Zhang, X.C.; Gang, Q.G. Temporal Characteristics of Loading for Creep Buckling of Plates. Acta Mech. Sin. 2000, 32, 319–325. [Google Scholar]
- Zhang, F.W.; Chen, X. Experimental Study on Mechanical Behavior of Timber Beam Strengthened with Steel Plate during 1200-Day Sustained Loading. J. Build. Struct. 2017, 38, 78–85. [Google Scholar]
- Dinwoodie, J.; Pierce, C.B.; Paxton, B.H. Creep in Chipboard. Part 4: The Influence of Temperature and Moisture Content on the Creep Behaviour of Range of Boards at Asingle Stress Levels. Wood Sci. Technol. 1984, 18, 205–224. [Google Scholar] [CrossRef]
- Hariharan, K.; Dubey, P.; Jain, J. Time Dependent Ductility Improvement of Stainless Steel SS 316 Using Stress Relaxation. Mater. Sci. Eng. A 2016, 673, 250–256. [Google Scholar] [CrossRef]
- Pommier, H.; Busso, E.P.; Morgeneyer, T.F.; Pineau, A. Intergranular Damage during Stress Relaxation in AISI 316L-Type Austenitic Stainless Steels: Effect of Carbon, Nitrogen and Phosphorus Contents. Acta Mater. 2016, 103, 893–908. [Google Scholar] [CrossRef]
- Seo, M.-K.; Na, K.W.; Han, S.H.; Park, S.-H.; Ha, S.-D. Inhibitory Effect of Ethanol and Thiamine Dilaurylsulfate against Loosely, Intermediately, and Tightly Attached Mesophilic Aerobic Bacteria, Coliforms, and Salmonella Typhimurium in Chicken Skin. Poult. Sci. 2020, 99, 1571–1580. [Google Scholar] [CrossRef]
- Cho, J.; Lee, C.-H. FE Analysis of Residual Stress Relaxation in a Girth-Welded Duplex Stainless Steel Pipe under Cyclic Loading. Int. J. Fatigue 2016, 82, 462–473. [Google Scholar] [CrossRef]
- Sá, E.R.; Rodrigues, S.F.; Aranas, C.; Siciliano, F.; Reis, G.S.; Cabrera-Marrero, J.-M.; Silva, E.S. Softening-Precipitation Interaction in a Nb-and N-Bearing Austenitic Stainless Steel under Stress Relaxation. J. Mater. Res. Technol. 2020, 9, 7807–7816. [Google Scholar] [CrossRef]
- Nguyen, N.-V.; Vu, Q.-A.; Kim, S.-E. An Experimental Study on Stress Relaxation Behaviour of High Strength Steel Wire: Microstructural Evolution and Degradation of Mechanical Properties. Constr. Build. Mater. 2020, 261, 119926. [Google Scholar] [CrossRef]
- Jozsef, B.; Benjamin, A.J. Mechanics of Wood and Wood Composites; Springer: Berlin/Heidelberg, Germany, 1982. [Google Scholar]
- Clouser, W.S. Creep of Small Wood Beams under Constant Bending Load; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 1959. [Google Scholar]
- Findley, W.N. Stress Relaxation and Combined Stress Creep of Plastics. SPE J. 1960, 16, 192–198. [Google Scholar]
- Holzer, S.M.; Loferski, J.R.; Dillard, D.A. A Review of Creep in Wood: Concepts Relevant to Develop Long-Term Behavior Predictions For Wood Structures. Wood Fiber Sci. 1989, 21, 376–392. [Google Scholar]
- Morlier, P. Creep in Timber Structures: Report of RILEM Technical Committee 112-TSC; E & FN Spon Ltd.: London, UK, 1994. [Google Scholar]
- NDS-1997; National Design Specification for Wood Construction. American Forest & Paper Association: Washington, DC, USA, 2005.







| Material | Characteristics | Average (N/mm2) | COV (%) |
|---|---|---|---|
| Spruce | Modulus of elasticity in compression | 8.301 × 103 | 4.630 |
| Compression strength parallel to grain | 38.67 | 6.151 | |
| Modulus of elasticity in tensile | 9.750 × 103 | 6.42 | |
| Tensile strength parallel to grain | 81.32 | 6.184 | |
| Steel wire | Modulus of elasticity | 1.92 × 105 | 1.710 |
| Tensile strength | 1.640 × 103 | 0.354 |
| Group | Number of the Component | Prestress Value (kN) | The Number of Steel Wire | Long-Term Loading Value (kN) | Loading Time (day) |
|---|---|---|---|---|---|
| A | LA1-1 | 7 | 2 | 8.24 | 180 |
| LA1-2 | 7 | 2 | 8.92 | ||
| LA2-1 * | 7 | 4 | 9.24 | ||
| LA2-2 * | 7 | 4 | 9.24 | ||
| LA3-1 | 7 | 6 | 10.06 | ||
| LA3-2 | 7 | 6 | 9.55 | ||
| B | LB1-1 | 0 | 4 | 8.24 | 180 |
| LB1-2 | 0 | 4 | 8.92 | ||
| LB2-1 * | 7 | 4 | 9.24 | ||
| LB2-2 * | 7 | 4 | 9.24 | ||
| LB3-1 | 14 | 4 | 10.06 | ||
| LB3-2 | 14 | 4 | 9.55 |
| Test Time | Collection Time Interval | Manual Data Collection Time Interval |
|---|---|---|
| Days 1~4 | 0.25 h/time | 0.25 h/time |
| Days 5~12 | 0.25 h/time | 0.5 h/time |
| Day 13~20 | 0.5 h/time | 1 h/time |
| Day 21~28 | 0.5 h/time | 2 h/time |
| Day 29~56 | 1 h/time | 4 h/time |
| Day 57~180 | 2 h/time | 12 h/time |
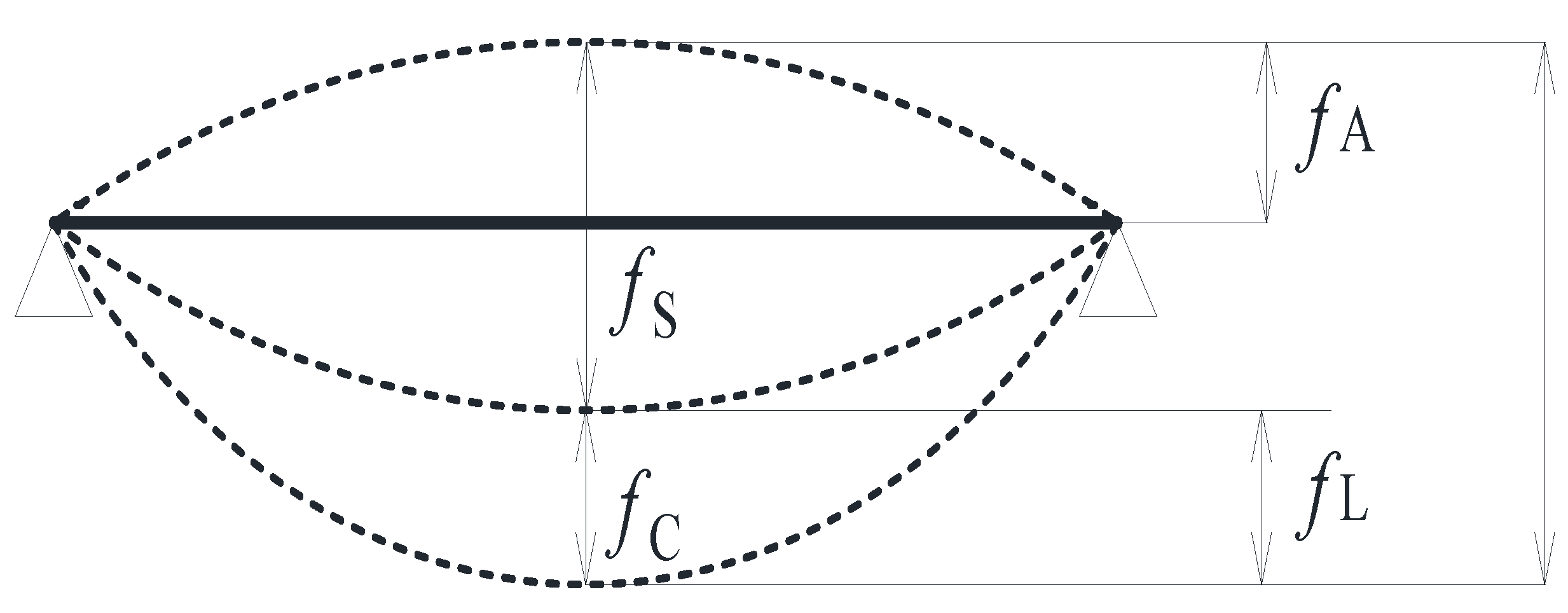
| Beam Number | Short-Term Deflection fS (mm) | Long-Term Deflection fL (mm) | Total Deflection fT (mm) | |
|---|---|---|---|---|
| LA1 | Left span | −26.61 | 8.70 | −17.91 |
| Right span | −25.35 | 8.42 | −16.93 | |
| LA2 | Left span | −20.03 | 6.00 | −14.03 |
| Right span | −20.09 | 5.64 | −14.45 | |
| LA3 | Left span | −10.18 | 4.33 | −5.85 |
| Right span | −10.28 | 4.56 | −5.72 | |
| LB1 | Left span | 7.51 | 4.93 | 12.44 |
| Right span | 7.60 | 4.87 | 12.47 | |
| LB2 | Left span | −20.03 | 6.00 | −14.03 |
| Right span | −20.09 | 5.64 | −14.45 | |
| LB3 | Left span | −29.21 | 8.97 | −20.24 |
| Right span | −28.87 | 9.49 | −19.38 | |
| Beam Number | a | b | c | R2 |
|---|---|---|---|---|
| LA1 | −29.24 | 3.04 | 0.28 | 0.96 |
| LA2/LB2 | −26.49 | 6.18 | 0.34 | 0.96 |
| LA3 | −14.75 | 2.82 | 0.22 | 0.94 |
| LB1 | 4.04 | 12.77 | 0.09 | 0.97 |
| LB3 | −30.71 | 3.11 | 0.42 | 0.98 |
| Project | Group A | Group B | ||||
| LA1 | LA2 | LA3 | LB1 | LB2 | LB3 | |
| Short-term deflection fs (mm) | 6.12 | 5.53 | 3.54 | 7.01 | 5.53 | 5.44 |
| 50-year total deflection fT (mm) | 20.15 | 15.38 | 8.08 | 22.20 | 15.38 | 14.63 |
| Creep deformation coefficient θ | 2.29 | 1.78 | 1.28 | 2.17 | 1.78 | 1.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, N.; Zhou, S.; Zhao, Y.; Mei, L.; Zhang, Y. Experimental Study on Long-Term Mechanical Properties of Prestressed Glulam Continuous Beams. Materials 2022, 15, 4182. https://doi.org/10.3390/ma15124182
Guo N, Zhou S, Zhao Y, Mei L, Zhang Y. Experimental Study on Long-Term Mechanical Properties of Prestressed Glulam Continuous Beams. Materials. 2022; 15(12):4182. https://doi.org/10.3390/ma15124182
Chicago/Turabian StyleGuo, Nan, Shouting Zhou, Yan Zhao, Lidan Mei, and Yunan Zhang. 2022. "Experimental Study on Long-Term Mechanical Properties of Prestressed Glulam Continuous Beams" Materials 15, no. 12: 4182. https://doi.org/10.3390/ma15124182
APA StyleGuo, N., Zhou, S., Zhao, Y., Mei, L., & Zhang, Y. (2022). Experimental Study on Long-Term Mechanical Properties of Prestressed Glulam Continuous Beams. Materials, 15(12), 4182. https://doi.org/10.3390/ma15124182





