Analytical Determination of Static Deflection Shape of an Asymmetric Extradosed Cable-Stayed Bridge Using Ritz Method
Abstract
:1. Introduction
2. Methodology
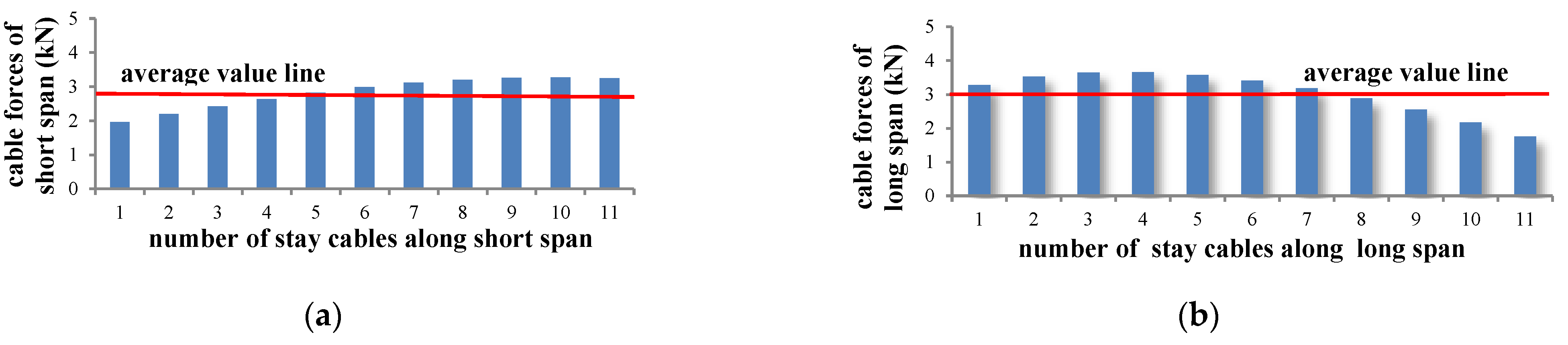
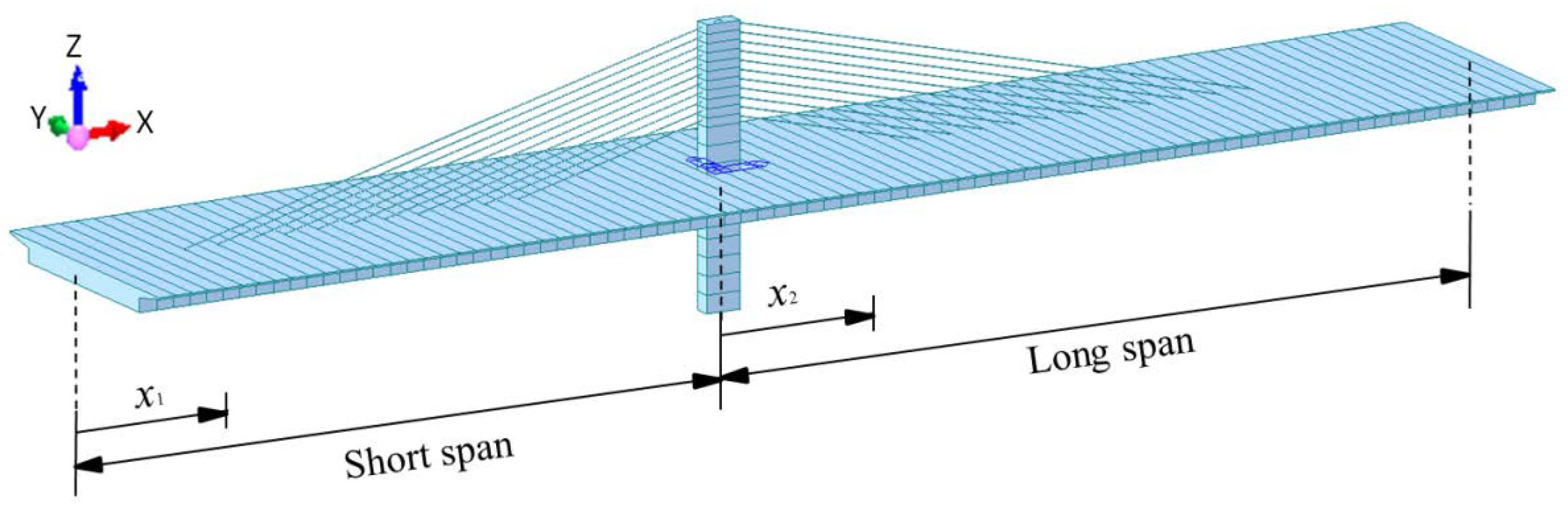
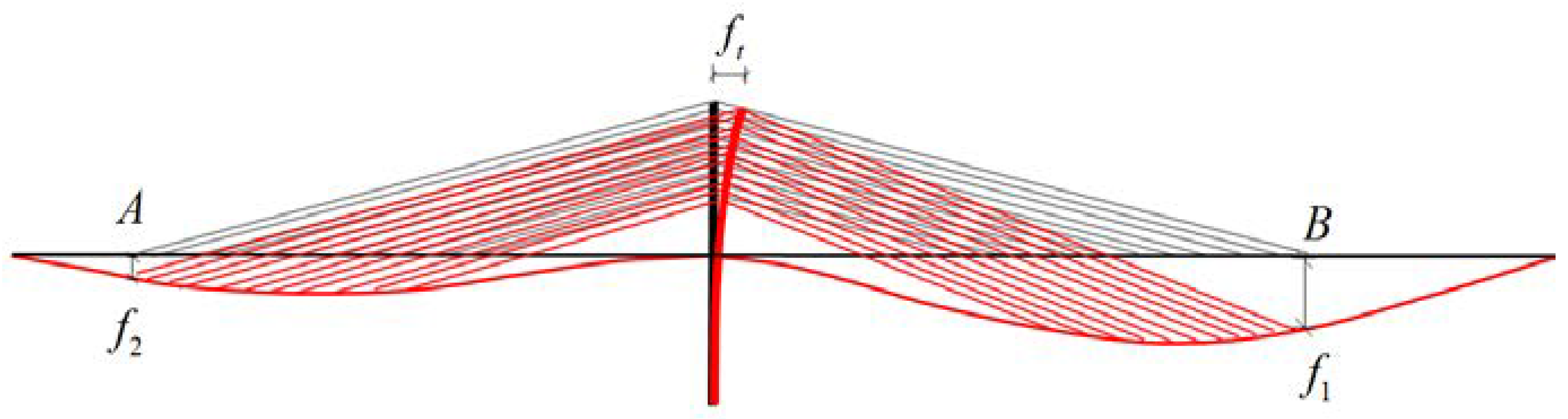
2.1. Engineering Background
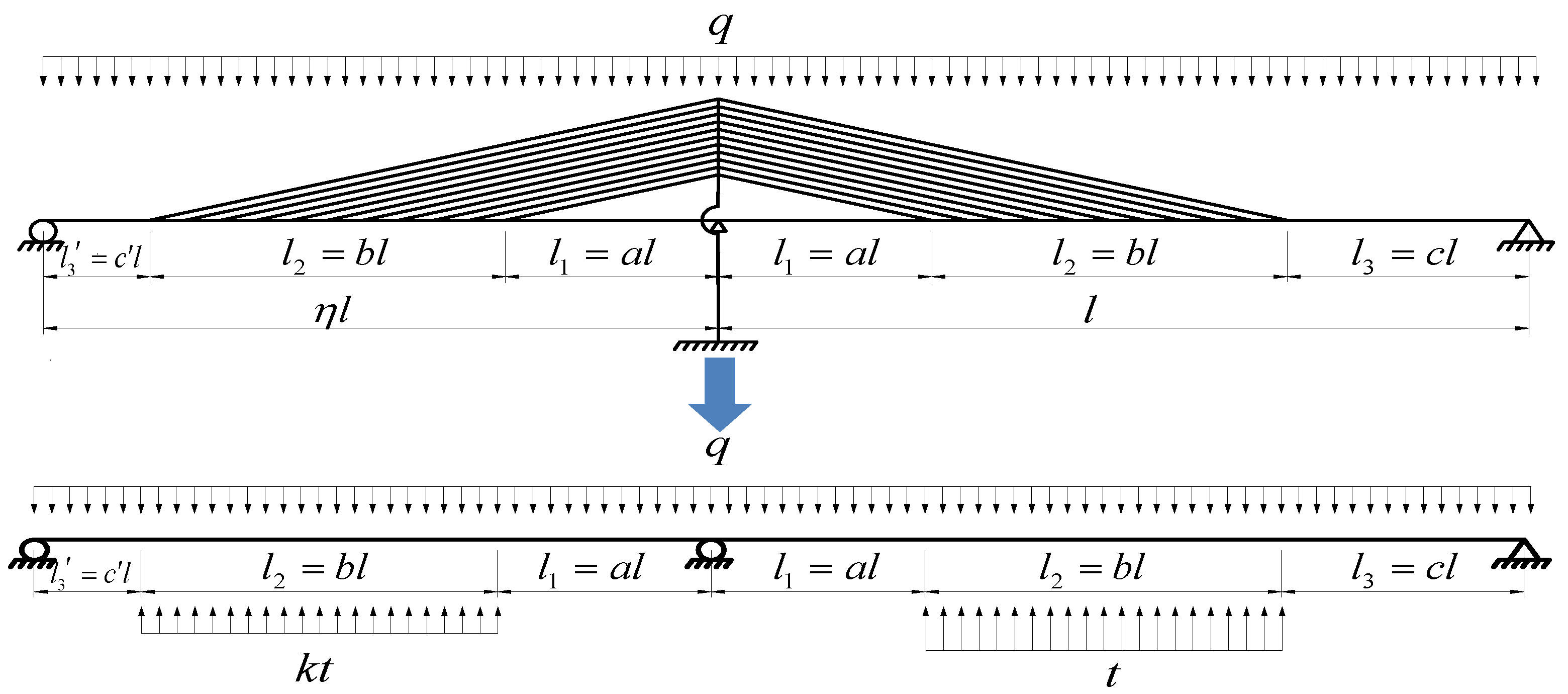
2.2. Assumptions
2.3. Formula Derivation
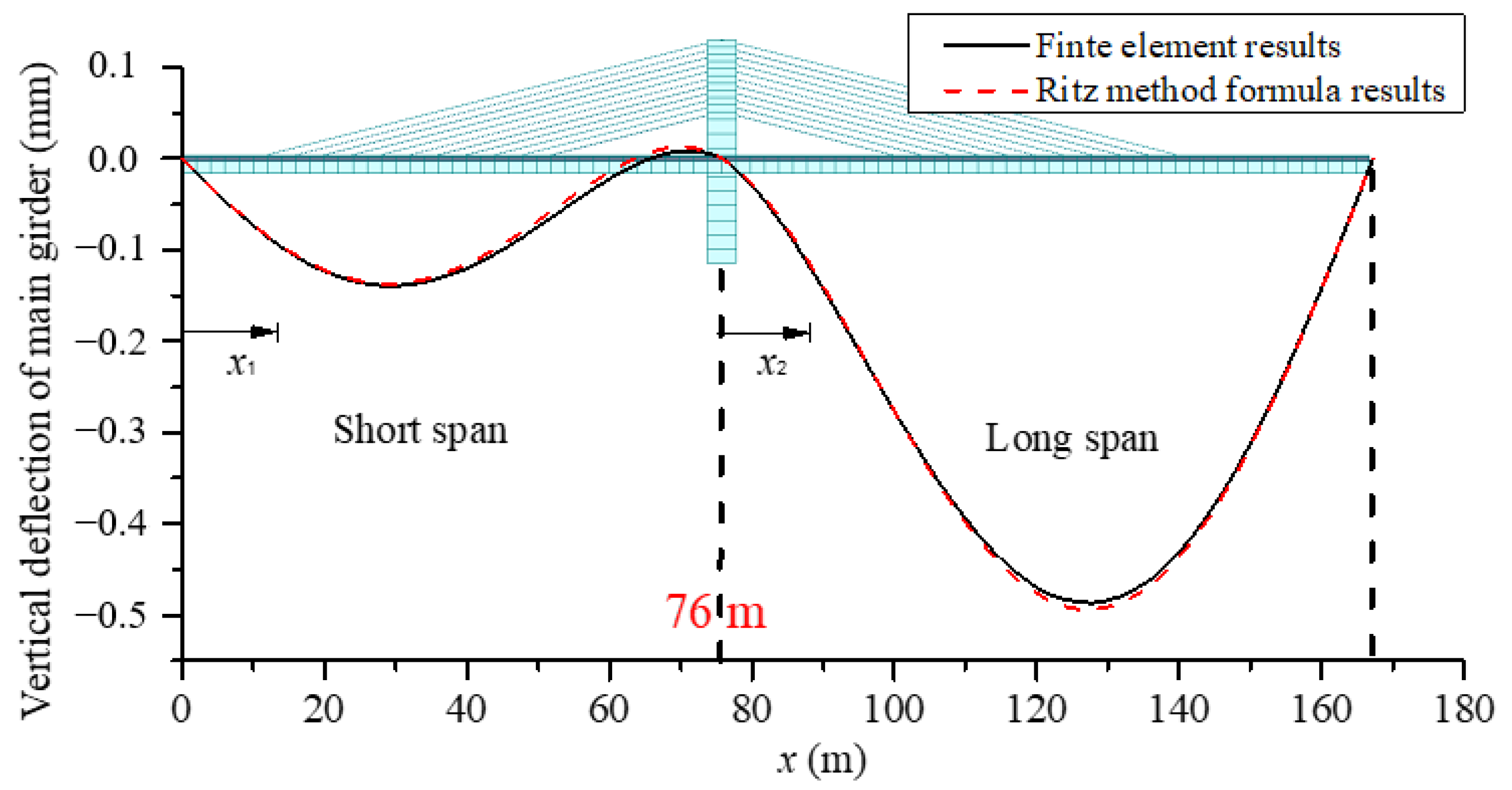
3. Formula Verification and Error Analysis
4. Parametric Studies
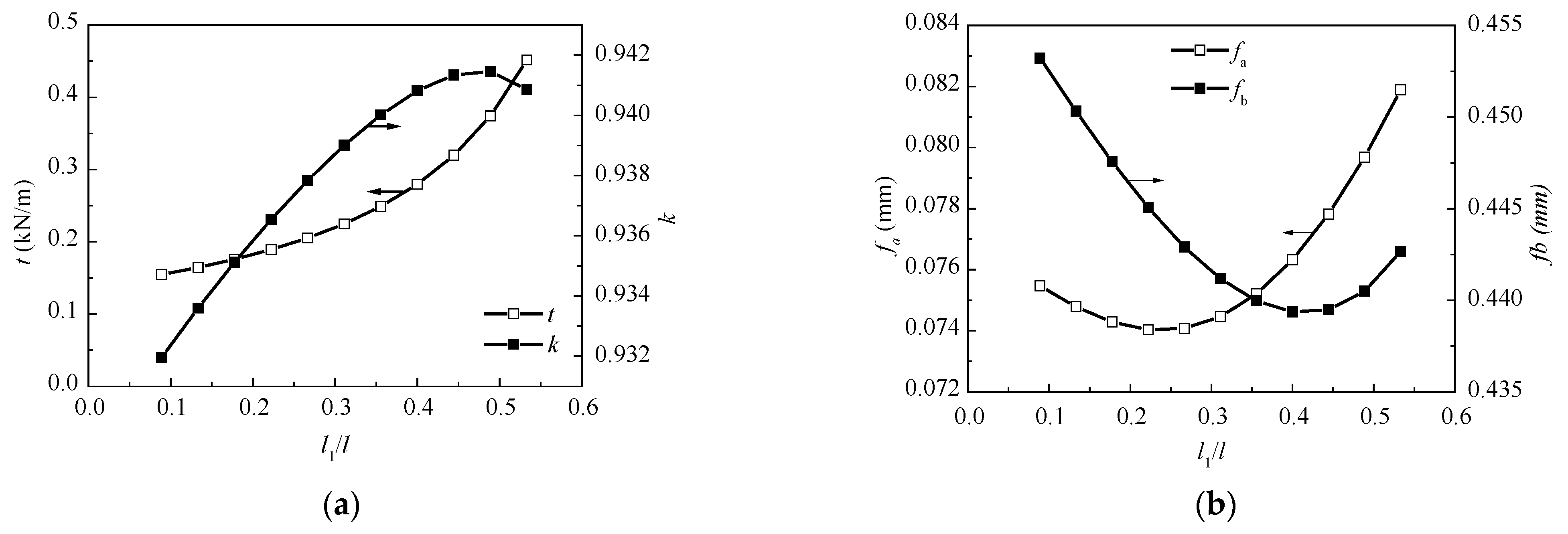
4.1. Length of the Unsupported Girder
4.2. Span Ratio
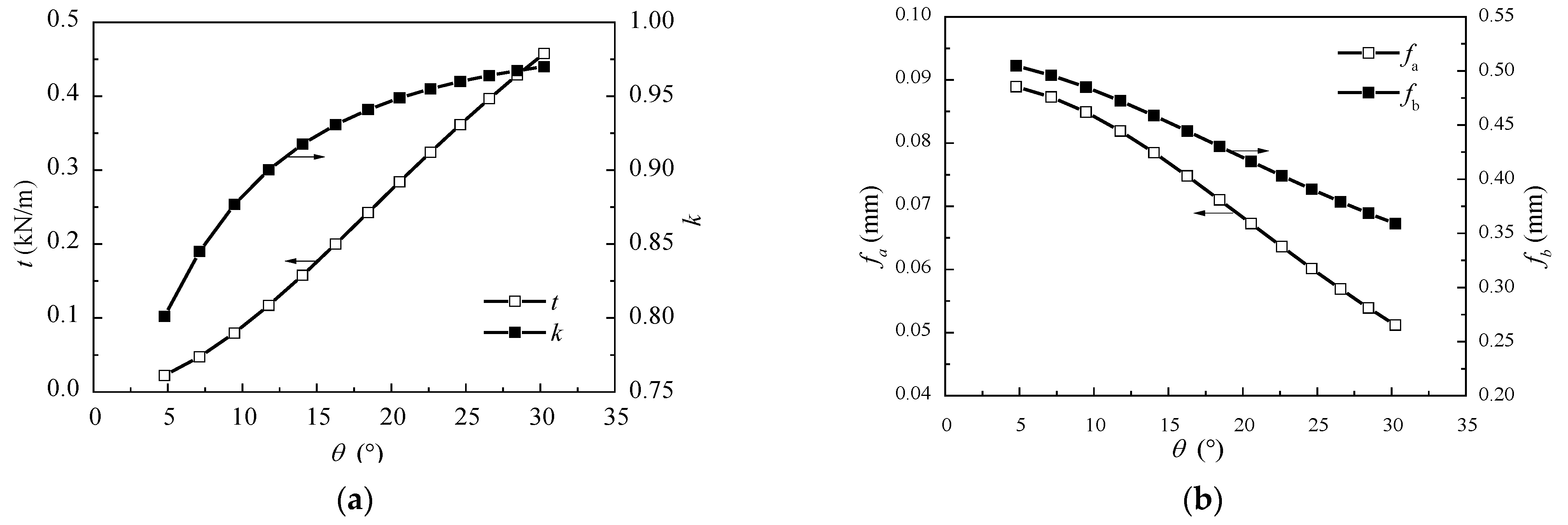
4.3. Inclination Angle of Cables
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- When i = 1, the are expressed as follows:;;;
- For i = 2, the are as follows:;;;
- When i = 3, the are as follows:;;;
- The are expressed as follows for i = 4:;;
- For coefficient ξij, when i = 1, the expressions for ξij are as follows:;;;
- For coefficient ξij, when i = 2, the expressions are as follows:;;;
- For i = 3, the expressions for ξij are as follows:;;;
- For i = 4, the expressions for ξij are as follows:;;;where the coefficients Ai and Bi are listed as follows:; ; ; ;; ;; .
References
- Chen, C.C.; Zhou, H.Z.; Xiao, R.C. Recent Research Advancement of Extradosed Cable-Stayed Bridge. World Bridges 2006, 1, 70–73. [Google Scholar]
- Lozano-Galant, J.A.; Paya-Zaforteza, I. Analysis of Eduardo Torroja’s Tempul Aqueduct an important precursor of modern cable-stayed bridges, extradosed bridges and prestressed concrete. Eng. Struct. 2017, 150, 955–968. [Google Scholar] [CrossRef]
- Oishi, T.; Inokuma, Y. Aesthetic Design of Odawara Port Bridge. Transp. Res. Rec. 1996, 1549, 108–113. [Google Scholar] [CrossRef]
- Ogawa AMatsuda, T.; Kasuga, A. The Tsukuhara Extradosed Bridge near Kobe. Struct. Eng. Int. 1998, 8, 172–173. [Google Scholar] [CrossRef]
- Kasuga, A. Extradosed bridges in Japan. Struct. Concr. 2006, 7, 91–103. [Google Scholar] [CrossRef]
- Nakayama, M.; Kayanoki, H.; Akiyama, H. Extradosed Prestressed Concrete Bridge with High-Strength Concrete, Japan—Yumekake Bridge. Struct. Eng. Int. 2011, 21, 366–371. [Google Scholar]
- Zhang, J.; Deng, W.; Hashino, T.; Liu, D. The world’s first extradosed bridge with corrugated steel webs: Japan’s Ohmi–Odori Bridge. In Bridge Engineering; Thomas Telford Ltd.: London, UK, 2018; Volume 171, pp. 237–245. [Google Scholar]
- Kim, W.J.; Joo, B.H.; Kim, B.G. Introduction of the First Extradosed Bridge in Korea. J. Korean Soc. Civ. Eng. 2005, 53, 156–162. [Google Scholar]
- Binns, J. Extradosed Bridge Distinguishes Tollway Project in India. Civ. Eng. 2005, 75, 20. [Google Scholar]
- Becze, J.; Barta, J. Korong Prestressed Extradosed Bridge. Struct. Eng. Int. 2006, 16, 28–30. [Google Scholar] [CrossRef]
- Vonganan, B. The Second Mekong International Bridge, Thailand. Struct. Eng. Int. 2009, 19, 67–68. [Google Scholar] [CrossRef]
- Markelj, V. The First Extradosed Bridge in Slovenia. Struct. Eng. Int. 2010, 20, 462–467. [Google Scholar] [CrossRef]
- Stroh, S.L.; Platosh, J.A. Design of the Pearl Harbor Memorial Bridge: The First Extradosed Prestressed Bridge in the U.S. In Proceedings of the 29th Annual International Bridge Conference, Pittsburgh, PA, USA, 10–13 June 2012; pp. 419–427. [Google Scholar]
- Meng, X.; Zhang, C. Extradosed and Intradosed Cable-Stayed Bridges with Continuous Cables: Conceptual Consideration. J. Bridge Eng. 2014, 19, 5–14. [Google Scholar] [CrossRef]
- Collings, D.; Gonzalez, A.S. Extradosed and cable-stayed bridges, exploring the boundaries. In Bridge Engineering; Thomas Telford Ltd.: London, UK, 2013; Volume 166, pp. 231–239. [Google Scholar]
- Liu, F.K.; Lin, P.Z.; Chen, Q. Investigation of Characteristic Parameters of Cable-stayed bridge with Low Towers. Eng. Mech. 2004, 21, 199–203. [Google Scholar]
- Lin, P.; Liu, F.K.; Zhou, S.J. Mechanical Characteristics and Defining of Extradosed Bridges. J. Railw. Eng. Soc. 2007, 29, 136–140. [Google Scholar]
- Chen, C.C. Study on Major Problems for Design Theory of Extradosed Cable-stayed Bridges. Ph.D. Thesis, Tongji University, Shanghai, China, 2005. [Google Scholar]
- Chen, C.C. Study on the Characteristics of Cable/Beam Live-load Ratio for Extradosed Cable-stayed Bridge. J. Highw. Transp. Res. Dev. 2009, 26, 99–103. [Google Scholar]
- Yi, Y.K.; Xiao, R.C. Practical Calculation of Beam-Arch Association Bridge Under Uniform Load. J. Tongji Univ. Nat. Sci. 2008, 36, 728–732. [Google Scholar]
- Cai, J.B.; Chen, H.L.; Hu, M. A Practical Computational Method for Three-span Continuous Beam-arch Through Bridge. J. Highw. Transp. Res. Dev. 2011, 28, 62–67. [Google Scholar]
- Chen, H.L.; Cai, J.B.; Xu, Y.; Guo, J.X.; He, T.G. Mechanical characteristics of two-tower single-span suspension bridge. J. Chang. Univ. 2013, 33, 69–74. [Google Scholar]
- Lonetti, P.; Pascuzzo, A. Optimum design analysis of hybrid cable-stayed suspension bridges. Adv. Eng. Softw. 2014, 73, 53–66. [Google Scholar] [CrossRef]
- Dou, S.T.; Chen, H.H.; Cui, S.G.; Zhu, J.B. Numerical Analysis of Control Indexes in Design of Low-Pylon Cable-Stayed Bridge. Appl. Mech. Mater. 2012, 178–181, 2468–2471. [Google Scholar] [CrossRef]
- Yi, L.; Mei, D.; Zhou, C. Design of a rail-cum-road asymmetrical low-pylon cable-stayed bridge with a main span of 588m. In Bridge Engineering; Thomas Telford Ltd.: London, UK, 2020; pp. 190–197. [Google Scholar]
- Kim, S.; Park, J.; Kim, H. Damping Identification and Serviceability Assessment of a Cable-Stayed Bridge Based on Operational Monitoring Data. J. Bridge Eng. 2017, 22, 4016123. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, R.; Li, J. Experimental Verification of a Cable-Stayed Bridge Model Using Passive Energy Dissipation Devices. J. Bridge Eng. 2016, 21, 4016092. [Google Scholar] [CrossRef]
- Lou, D.F.; Cai, J.B. Research on Mechanical Properties of Single-Pylon Two-Span Extradosed Cable-stayed Bridge Based on Energy Method. Ind. Constr. 2018, 48, 169–171. [Google Scholar]
- Su, Y.; Cai, J.B. The Cable Arrangement of the Extradosed Cable-stayed Bridge Based on Energy Method. East China Highw. 2019, 1, 84–86. [Google Scholar]
- Shi, F.; Cao, P.; Gan, Y.; Zhou, C.; Zhou, G. Calculating Precision Analysis of Static Characteristics of Multi-rib T-Beam Structure. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 44, 813–824. [Google Scholar] [CrossRef]
- Zhang, X.M. Research on the Rail Continuous Bending of Ballastless Track of High- speed Railway Based on Energy Method. J. Railw. Eng. Soc. 2019, 36, 7–12. [Google Scholar]
- Konstantakopoulos, T.G.; Michaltsos, G.T. A mathematical model for a combined cable system of bridges. Eng. Struct. 2010, 32, 2717–2728. [Google Scholar] [CrossRef]
- Michaltsos, G.T.; Ermopoulos, J.C.; Konstantakopoulos, T.G. Preliminary design of cable-stayed bridges for vertical static loads. J. Struct. Mech. 2003, 15, 1–15. [Google Scholar] [CrossRef]
- Hegab, H.I.A. Parametric Investigation of Cable-Stayed Bridges. J. Struct. Eng. 1988, 114, 1917–1928. [Google Scholar] [CrossRef]


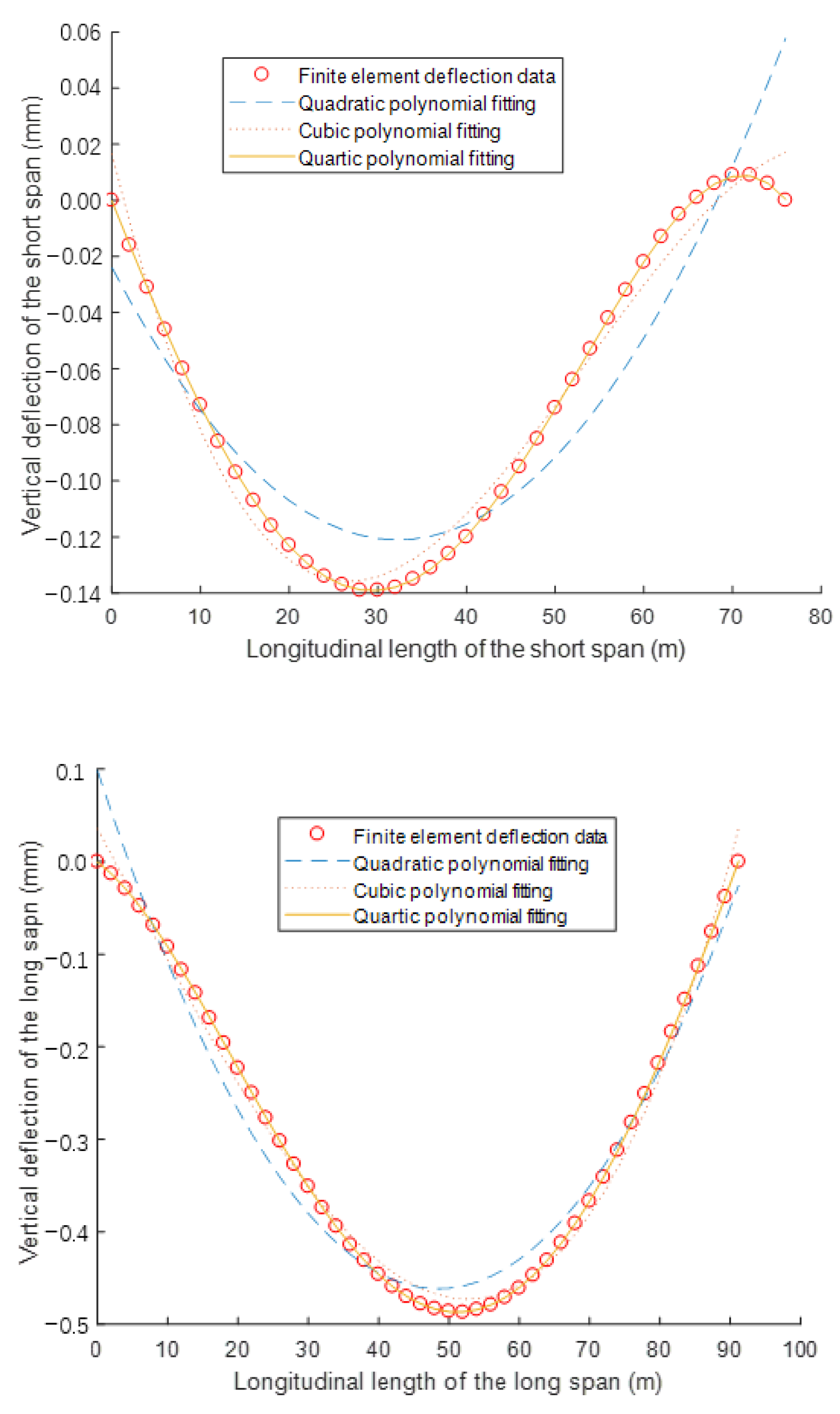

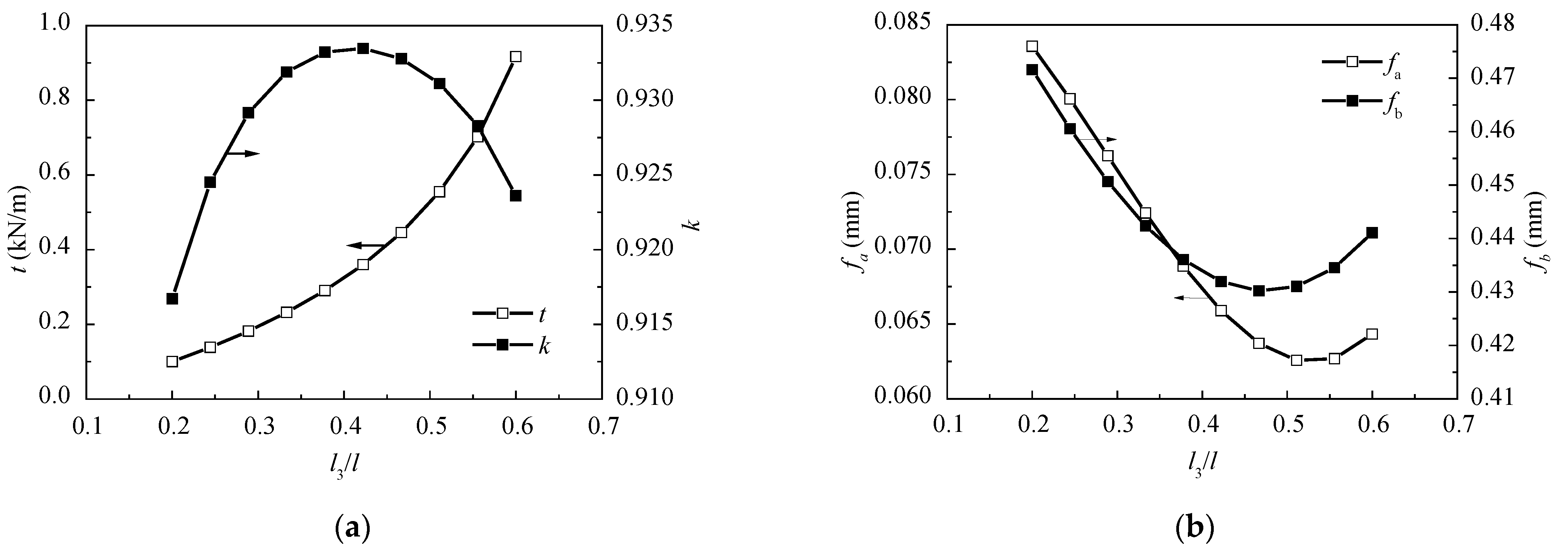
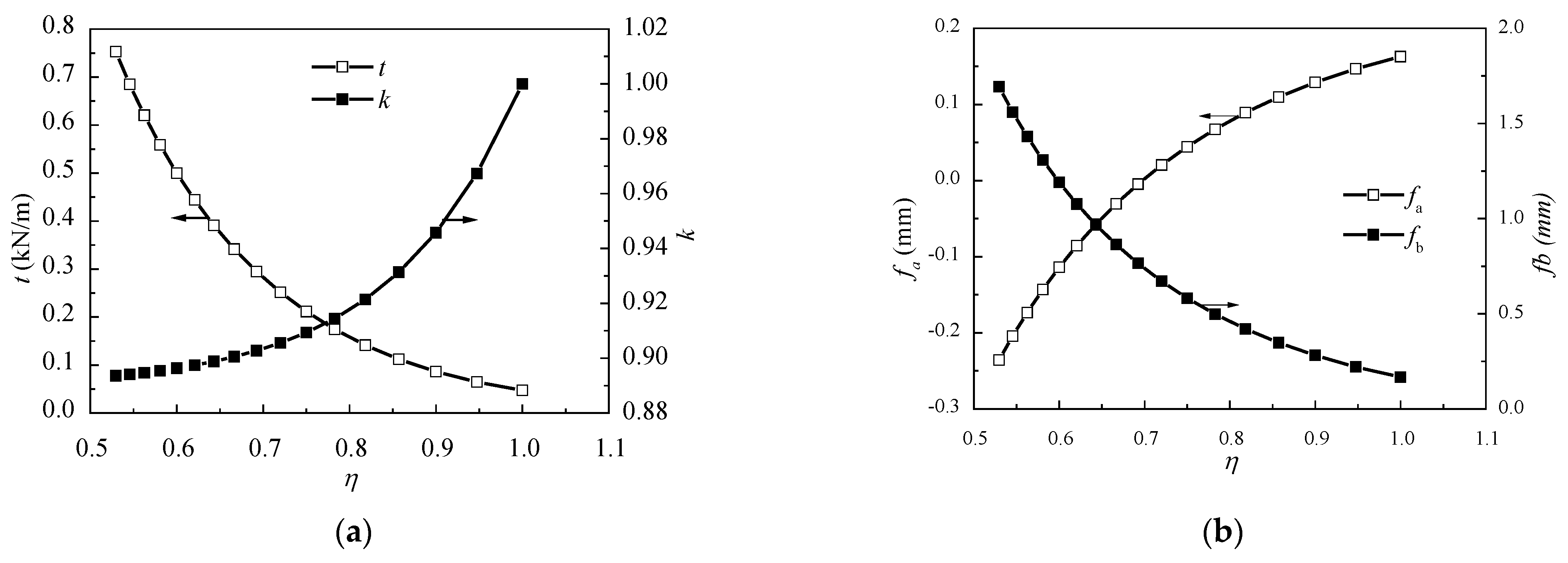
| Basic Model | FEM | RMF | Error |
|---|---|---|---|
| 0.925 | 0.900 | −2.66% | |
| 0.186 | 0.124 | −33.42% |
| Model Number | Parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FEM | RMF | Error (%) | FEM | RMF | Error (%) | FEM | RMF | Error (%) | FEM | RMF | Error (%) | ||
| 1 | Basic model | 0.925 | 0.930 | 0.56 | 0.185 | 0.176 | −5.10 | 0.086 | 0.080 | −6.56 | 0.431 | 0.421 | −2.28 |
| 2 | 0.650 | 0.632 | −2.64 | 0.028 | 0.026 | −8.43 | 0.100 | 0.092 | −7.91 | 0.483 | 0.466 | −3.51 | |
| 3 | 0.784 | 0.781 | −0.48 | 0.057 | 0.052 | −8.47 | 0.097 | 0.090 | −6.97 | 0.473 | 0.458 | −3.16 | |
| 4 | 0.973 | 0.980 | 0.71 | 0.490 | 0.511 | 4.26 | 0.057 | 0.053 | −7.23 | 0.334 | 0.322 | −3.72 | |
| 5 | 0.984 | 0.990 | 0.67 | 0.748 | 0.804 | 7.49 | 0.032 | 0.029 | −10.01 | 0.261 | 0.235 | −10.15 | |
| 6 | 0.987 | 0.912 | −7.63 | 0.124 | 0.121 | −2.24 | 0.089 | 0.085 | −5.04 | 0.453 | 0.437 | −3.43 | |
| 7 | 0.989 | 0.969 | −2.02 | 0.428 | 0.433 | 1.38 | 0.062 | 0.060 | −3.82 | 0.355 | 0.344 | −3.00 | |
| 8 | 0.692 | 0.664 | −4.00 | 0.210 | 0.201 | −4.38 | 0.092 | 0.086 | −6.26 | 0.419 | 0.408 | −2.56 | |
| 9 | 0.179 | 0.171 | −4.75 | 0.987 | 0.990 | 0.31 | 0.084 | 0.079 | −5.69 | 0.435 | 0.424 | −2.60 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, D.; Chen, Y.; Feng, Q.; Cai, J. Analytical Determination of Static Deflection Shape of an Asymmetric Extradosed Cable-Stayed Bridge Using Ritz Method. Materials 2022, 15, 4255. https://doi.org/10.3390/ma15124255
Lou D, Chen Y, Feng Q, Cai J. Analytical Determination of Static Deflection Shape of an Asymmetric Extradosed Cable-Stayed Bridge Using Ritz Method. Materials. 2022; 15(12):4255. https://doi.org/10.3390/ma15124255
Chicago/Turabian StyleLou, Danfeng, Yong Chen, Qian Feng, and Jinbiao Cai. 2022. "Analytical Determination of Static Deflection Shape of an Asymmetric Extradosed Cable-Stayed Bridge Using Ritz Method" Materials 15, no. 12: 4255. https://doi.org/10.3390/ma15124255






