Prediction of Strength and CBR Characteristics of Chemically Stabilized Coal Gangue: ANN and Random Forest Tree Approach
Abstract
:1. Introduction
2. Materials and Methodology
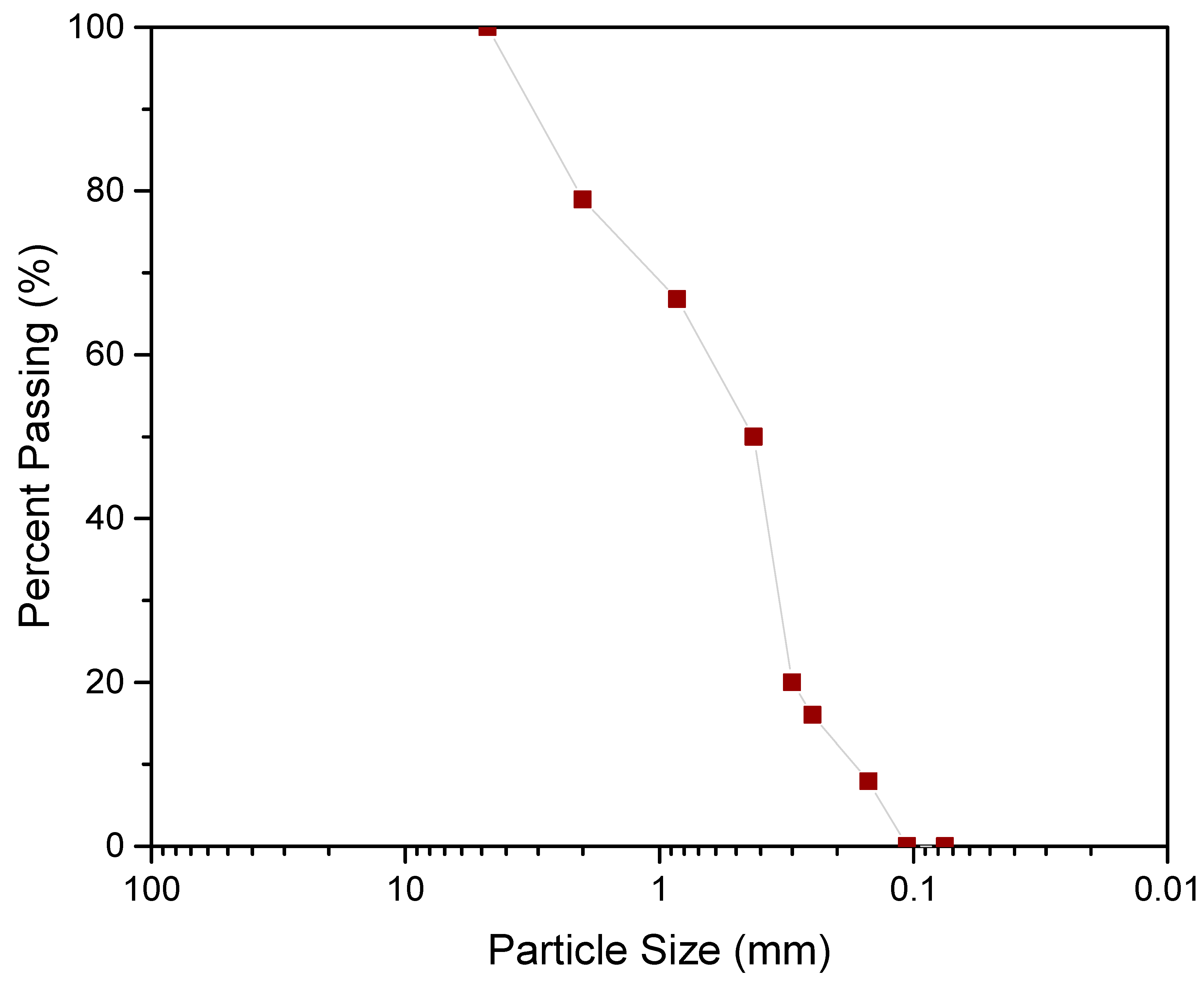
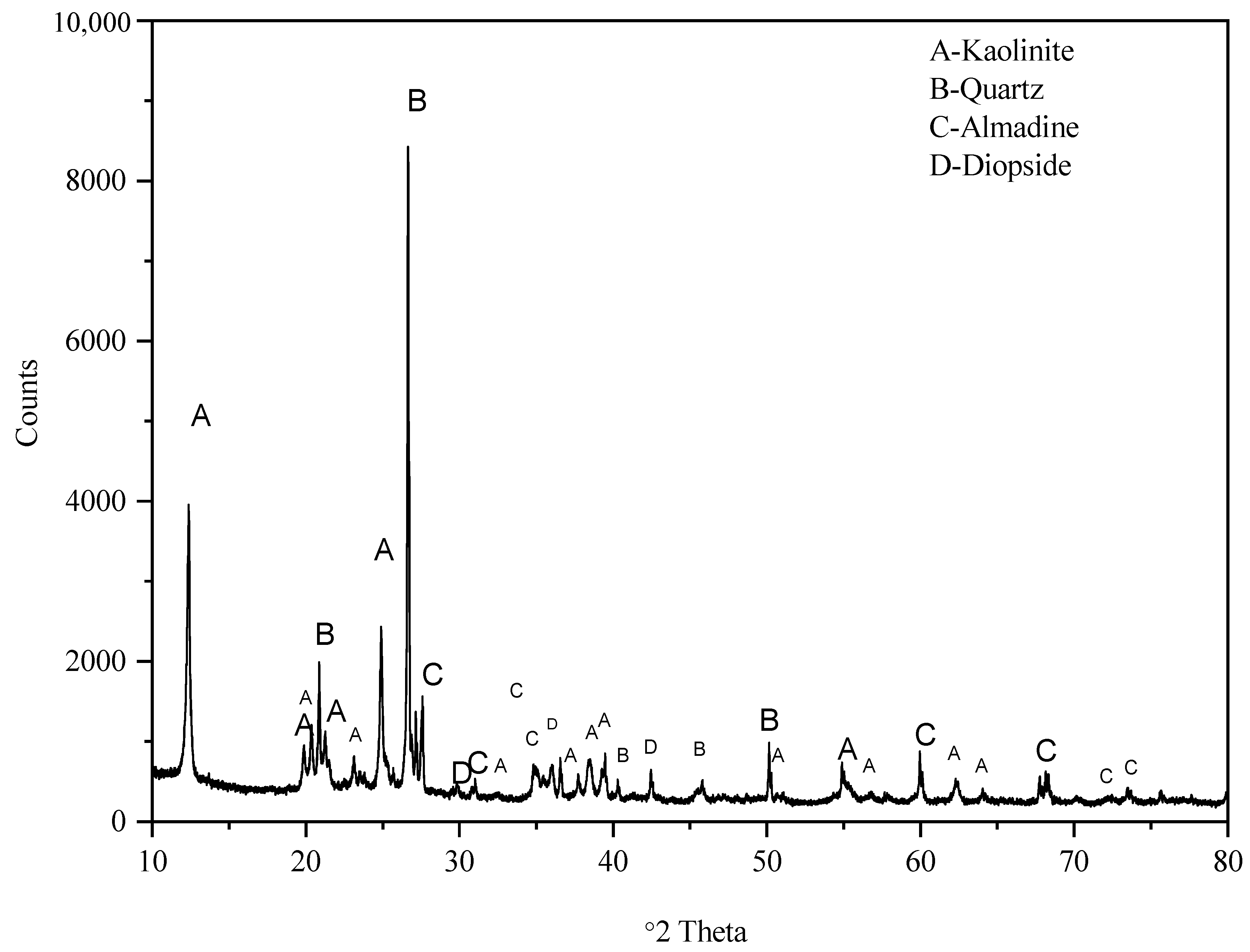
2.1. Laboratory Studies
2.2. Overview of the Developed Model
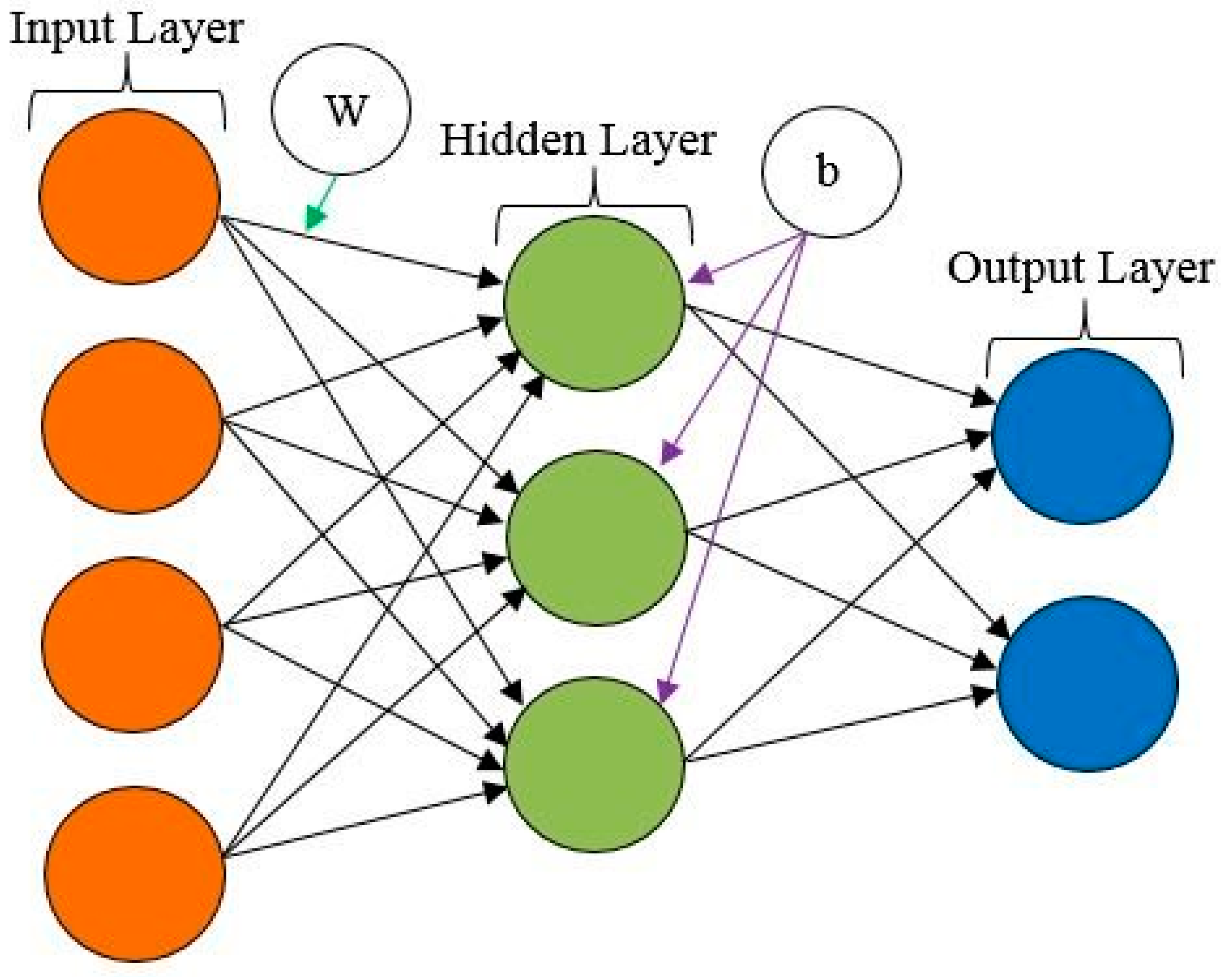
2.2.1. Artificial Neural Network Model
- (a)
- A signal xm in the input m of a synapse linked to neuron k is multiplied by synaptic weights wkm;
- (b)
- A linear combiner with an adder to total the inputs, which are weighted by the synapses of each neuron;
- (c)
- The activation function f(.) is used to limit the amplitude of a neuron’s output. The normalized output amplitude range can be either [0,1] or [1,1];
- (d)
- Bias, indicated by bk, is externally introduced; the purpose is to raise or reduce the overall impact of the activation function.
2.2.2. Random Forest Tree Model
2.3. Evaluation Criteria
3. Results and Discussions
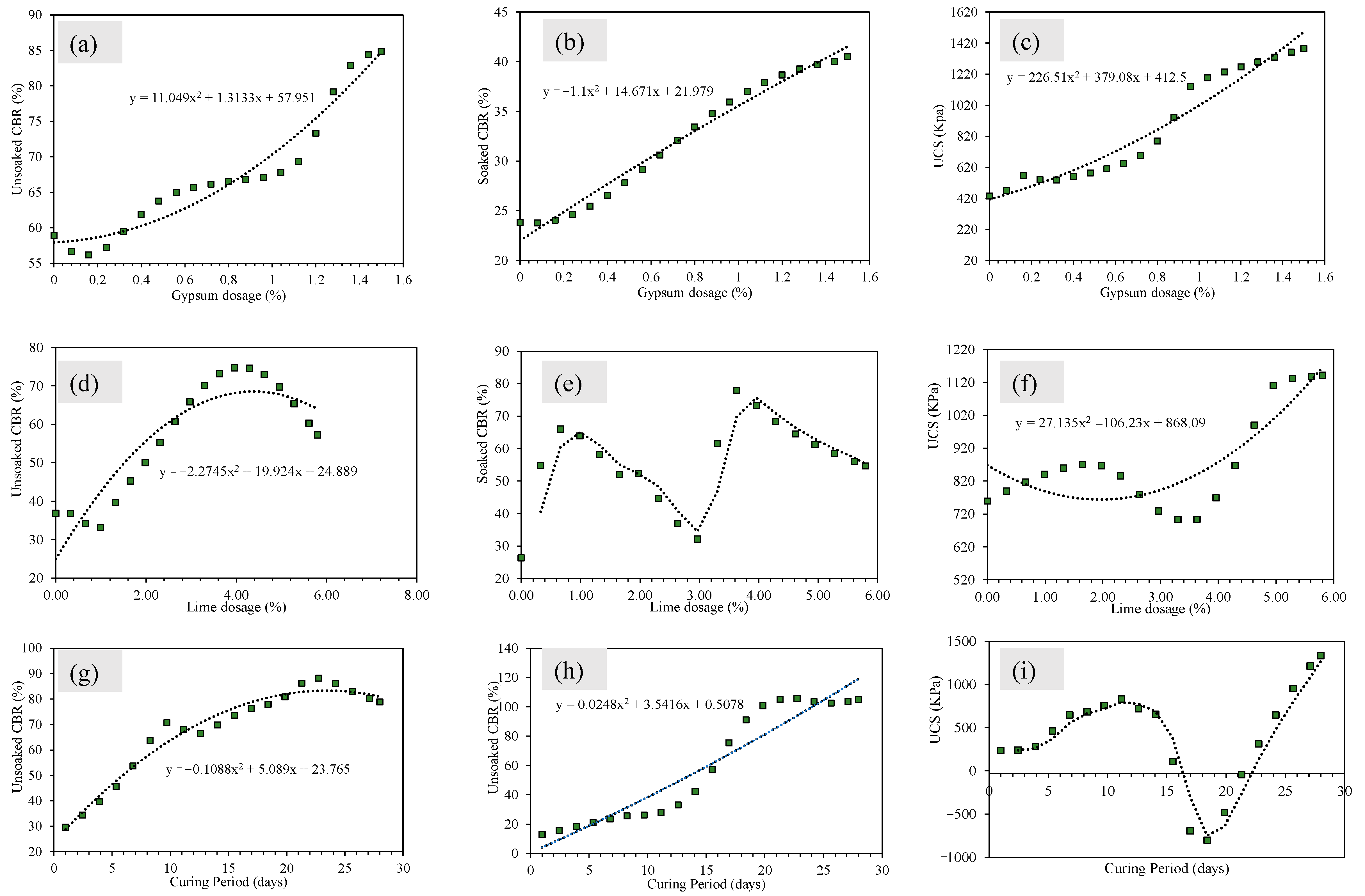
3.1. Unconfined Compressive Strength of CG
3.1.1. Role of Lime
3.1.2. Effect of Gypsum
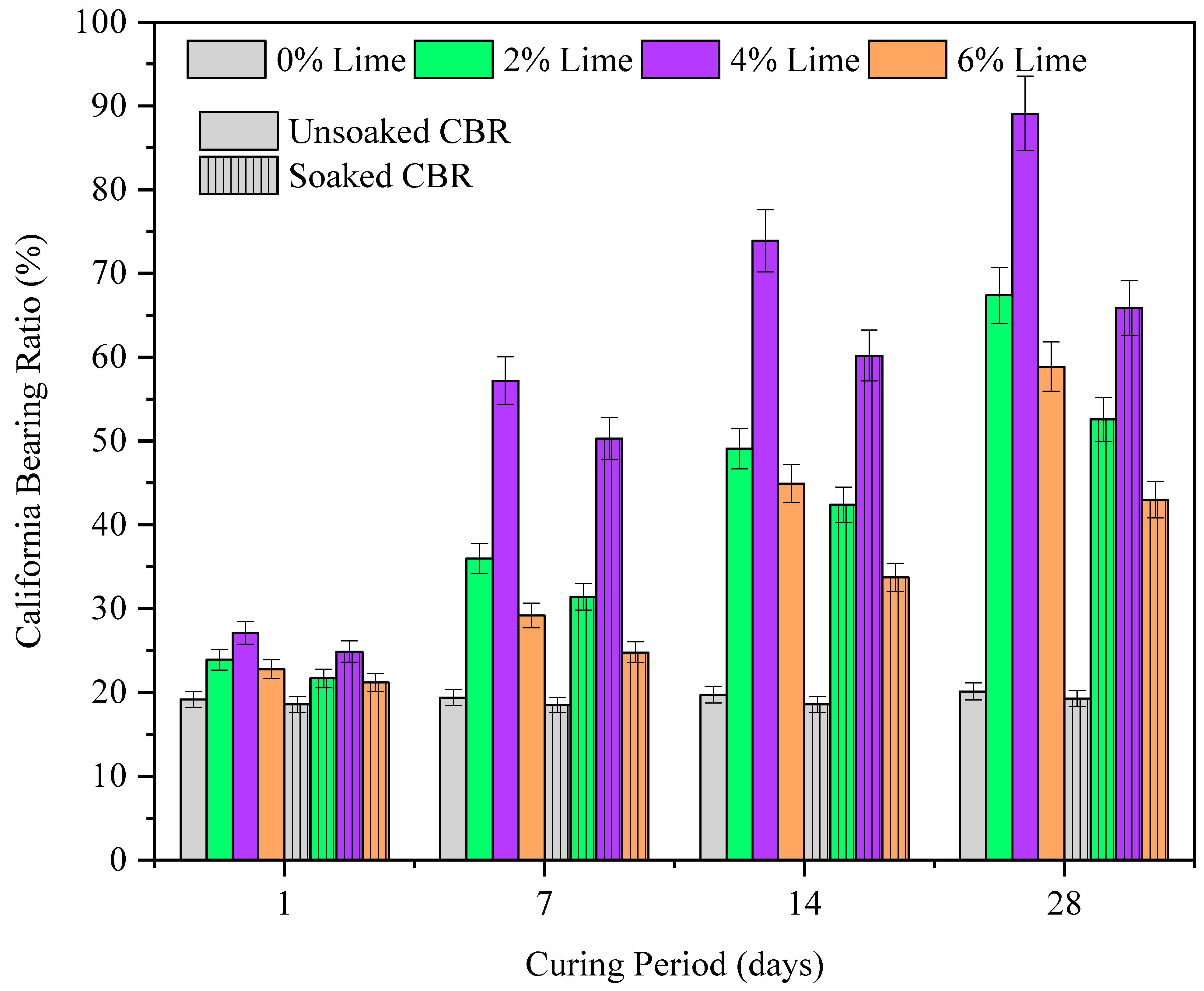
3.2. CBR of CG
3.2.1. Role of Lime
3.2.2. Effect of Lime and Gypsum
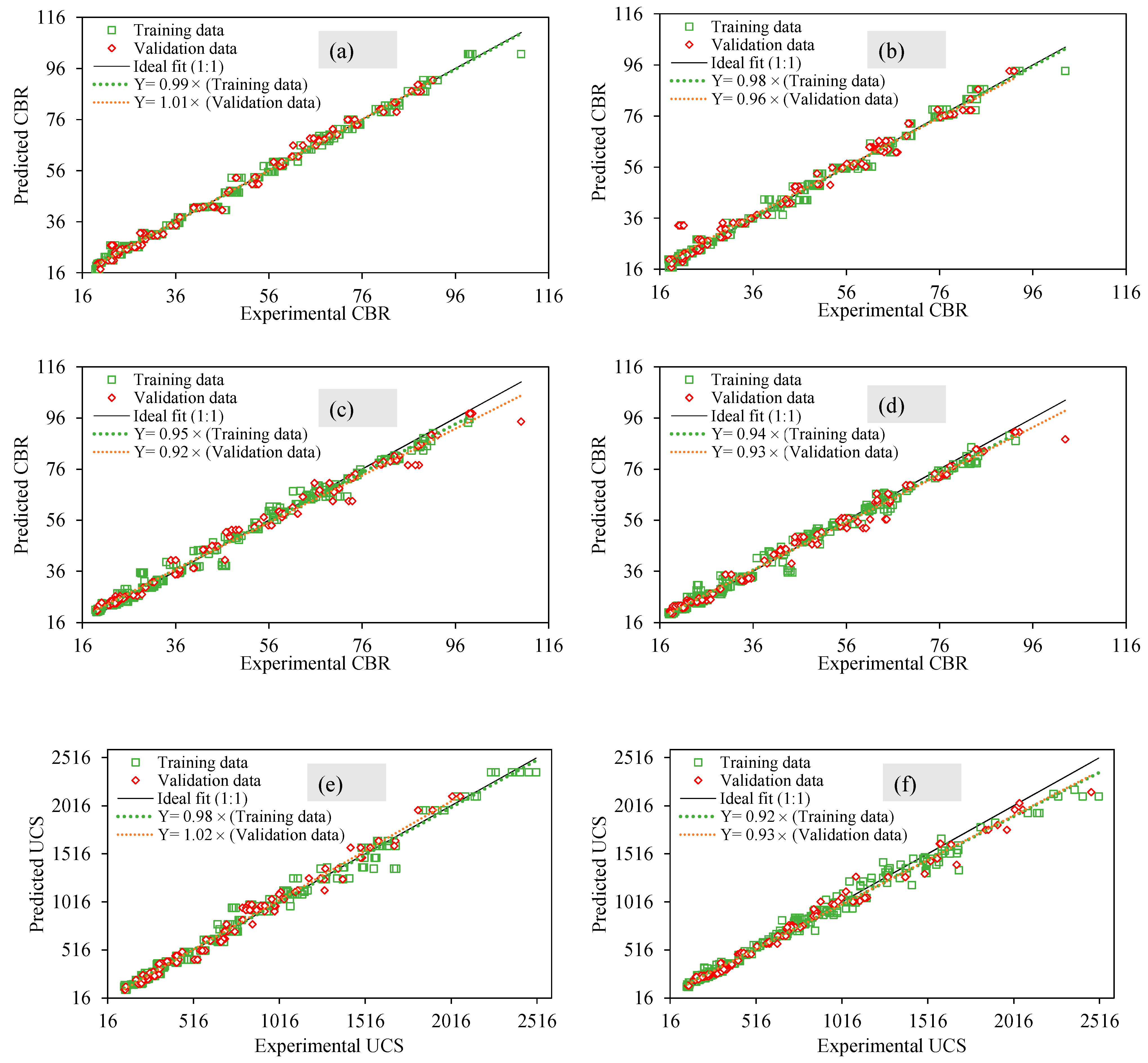
3.3. Prediction Performance of the Proposed Models
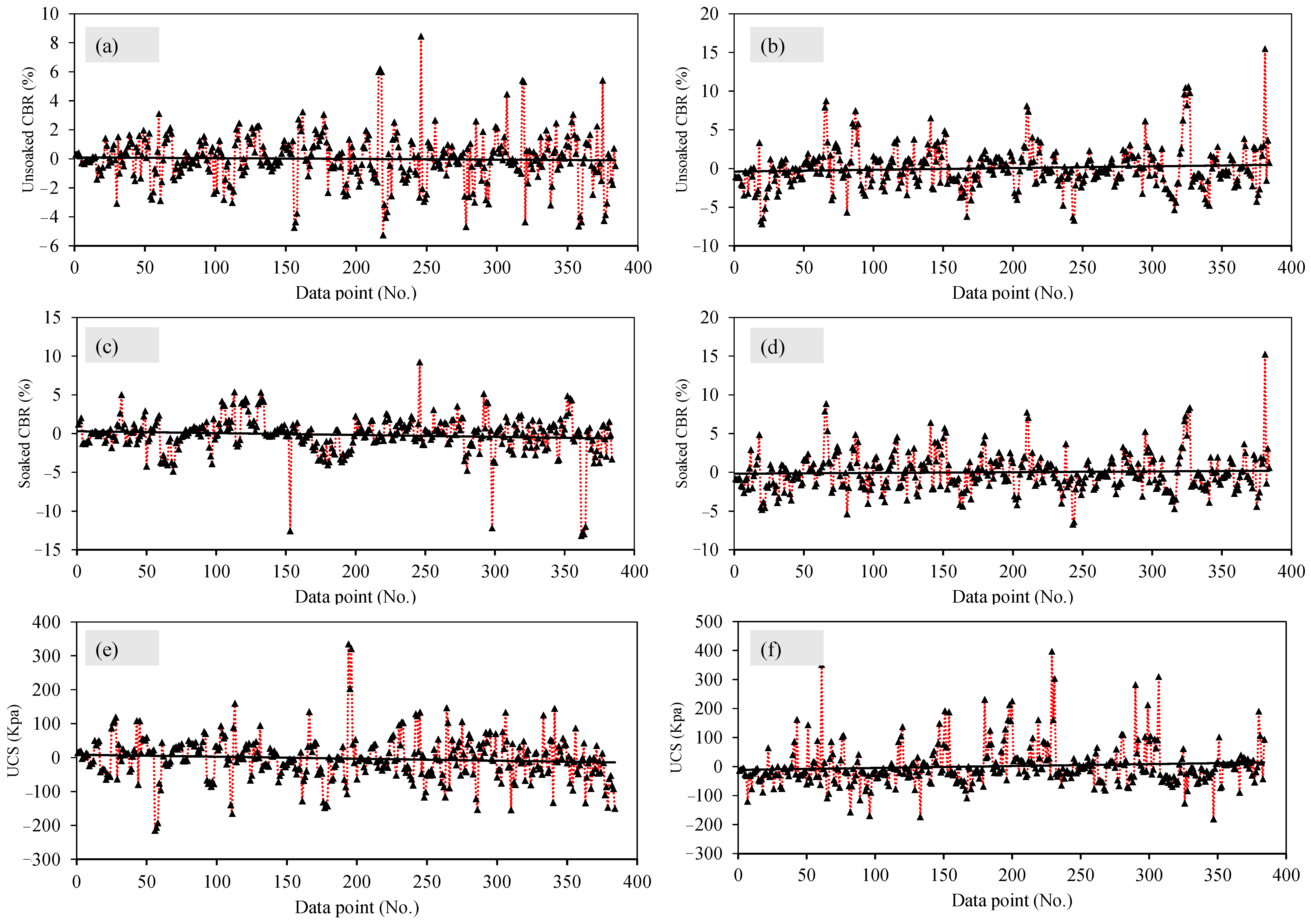
3.4. Model Validity
3.4.1. First Level Validation
3.4.2. Second Level Validation
4. Conclusions
- The stabilization of CG resulted in a linear increase in the UCS of CG, with the highest increment (10×) noted for the lime and gypsum dosages of 6% and 1.5%, respectively. In contrast to the strength behavior, the CBR value of CG attained optimum value at 4% lime dosage, and the subsequent addition of gypsum resulted in a further increase in CBR values;
- Levenberg Marquadt backpropagation with 10 neurons in the hidden layer yielded the optimal performance of the formulated ANN model. On the contrary, among several iterations in the form of optimization grid for developing RF regression model, the minimal gain criteria with 200 trees and a maximum depth of 20 manifested the best performance of the RF model;
- The performance of the developed models were evaluated using the slope of regression lines compared with the ideal slope, correlation values (R), and error indices, namely MAE, RMSE, and RSE. For the ANN model, the training set yielded the minimum correlation value (R = 0.993) whereas for soaked CBR and unsoaked CBR, R = 0.995 and 0.997, respectively. Furthermore, the values of MAE for the training sets were recorded as 45.98 kPa, 1.180%, and 1.409% for the UCS, unsoaked, and soaked CBR of chemically stabilized CG, respectively;
- The RF regression model reflected slightly lower accuracy in terms of R-values and error indices for the case of the training sets. The lowest value of R was observed comparable to the ANN model whereas the highest R was noted as 0.995. Similarly, the MAE values for the UCS, unsoaked, and soaked CBR equaled 46.95 kPa, 1.81%, and 1.77%, respectively;
- The developed ANN and RF models were tested using two-stage validation. In the first stage, an unused 30% of the dataset was utilized. The values of R and error indices reflected comparable performance to that of the training data. It was also seen that all these values were close to the training data, suggesting no overfitting issues in the developed models. In the 2nd stage of validation, the ANN model was employed to assess the impact of contributing parameters on the target variables (UCS, unsoaked CBR, and soaked CBR). In addition, a parametric analysis was conducted which showed 1.5% gypsum and 4% lime dosage levels as optimum for yielding maximum unsoaked and soaked CBR values; whereas the values of the optimum UCS were achieved at 1.5% gypsum and 6% lime. These results are in accordance with the experimental study conducted here and are also corroborated in past literature.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basu, D.; Puppala, A. Sustainability: An Emerging Discipline within Geotechnical Engineering. 2015. Available online: www.researchgate.net (accessed on 24 April 2022).
- Shillaber, C.M.; Mitchell, J.K.; Dove, J.E.; Ostrum, Z.A. Framework to account for uncertainty in energy and carbon assessment of ground improvement works. J. Geotech. Geoenviron. Eng. 2017, 143, 04016122. [Google Scholar] [CrossRef]
- Ashfaq, M.; Moghal, A.A.B. Cost and Carbon Footprint Analysis of Flyash Utilization in Earthworks. Int. J. Geosynth. Ground Eng. 2022, 8, 1–9. [Google Scholar] [CrossRef]
- Ashfaq, M.; Heeralal, M.; Reddy, P.H.P. A Study on Strength Behavior of Alkali-Contaminated Soils Treated with Fly Ash. In Recycled Waste Materials; Springer: Berlin/Heidelberg, Germany, 2019; pp. 137–143. [Google Scholar]
- Ashfaq, M.; Moghal, A.A.B.; Basha, B.M. The Sustainable Utilization of Coal Gangue in Geotechnical and Geoenvironmental Applications. J. Hazard. Toxic Radioact. Waste 2022, 26, 03122003. [Google Scholar] [CrossRef]
- Sivapullaiah, P.V.; Sankara, G.; Allam, M.M. Mineralogical changes and geotechnical properties of an expansive soil interacted with caustic solution. Environ. Earth Sci. 2010, 60, 1189–1199. [Google Scholar] [CrossRef]
- Indraratna, B. Geotechnical characterization of blended coal tailings for construction and rehabilitation work. Q. J. Eng. Geol. Hydrogeol. 1994, 27, 353–361. [Google Scholar] [CrossRef]
- Heitor, A.; Indraratna, B.; Kaliboullah, C.I.; Rujikiatkamjorn, C.; McIntosh, G.W. Drained and undrained shear behavior of compacted coal wash. J. Geotech. Geoenviron. Eng. 2016, 142, 04016006. [Google Scholar] [CrossRef] [Green Version]
- Indraratna, B.; Rujikiatkamjorn, C.; Chiaro, G. Characterization of compacted coal wash as structural fill material. In GeoCongress 2012: State of the Art and Practice in Geotechnical Engineering; Civil and Natural Resources Engineering, University of Canterbury: Christchurch, New Zealand, 2012; pp. 3826–3834. [Google Scholar]
- Indraratna, B.; Rujikiatkamjorn, C.; Chiaro, G. Compaction of Coal Wash as Reclamation Fill. 2013. Available online: https://www.researchgate.net/publication/265208941_Compaction_Of_Coal_Wash_As_Reclamation_Fill (accessed on 3 April 2022).
- Okagbue, C.; Ochulor, O. The potential of cement-stabilized coal-reject as a construction material. Bull. Eng. Geol. Environ. 2007, 66, 143–151. [Google Scholar] [CrossRef]
- Cao, D.; Ji, J.; Liu, Q.; He, Z.; Wang, H.; You, Z. Coal gangue applied to low-volume roads in China. Transp. Res. Rec. 2011, 2204, 258–266. [Google Scholar] [CrossRef]
- Rujikiatkamjorn, C.; Indraratna, B.; Chiaro, G. Compaction of coal wash to optimise its utilisation as water-front reclamation fill. Geomech. Geoengin. 2013, 8, 36–45. [Google Scholar] [CrossRef]
- Tasalloti, S.; Indraratna, B.; Rujikiatkamjorn, C.; Heitor, A.; Chiaro, G. A Laboratory Study on the Shear Behavior of Mixtures of Coal Wash and Steel Furnace Slag as Potential Structural Fill. Geotech. Test. J. 2015, 38, 361–372. [Google Scholar] [CrossRef] [Green Version]
- Ashfaq, M.; Moghal, A.A.B.; Basha, B.M. Reliability-Based Design Optimization of Chemically Stabilized Coal Gangue. J. Test. Eval. 2021, 51, 16. [Google Scholar] [CrossRef]
- Ali, S.; Kamran, M.A.; Khan, S. Effect of baffle size and orientation on lateral sloshing of partially filled containers: A numerical study. Eur. J. Comput. Mech. 2017, 26, 584–608. [Google Scholar] [CrossRef]
- Bhatti, U.N.; Khan, S.; Ali, S.; Horoub, M.M. A Numerical Modeling Study of the Effects of Various Joint Boundary Conditions on Stiffness Behavior of 6DOF Platform’s Top Plate. In Proceedings of the 2018 9th International Conference on Mechanical and Aerospace Engineering (ICMAE), Budapest, Hungary, 10–13 July 2018; pp. 243–248. [Google Scholar]
- Sinha, S.K.; Wang, M.C. Artificial neural network prediction models for soil compaction and permeability. Geotech. Geol. Eng. 2008, 26, 47–64. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Tariq, R.; Hameed, Z.; Ali, I.; Taqvi, S.A.; Naqvi, M.; Niazi, M.; Noor, T.; Farooq, W. Pyrolysis of high-ash sewage sludge: Thermo-kinetic study using TGA and artificial neural networks. Fuel 2018, 233, 529–538. [Google Scholar] [CrossRef]
- Bong, J.T.; Loy, A.C.M.; Chin, B.L.F.; Lam, M.K.; Tang, D.K.H.; Lim, H.Y.; Chai, Y.H.; Yusup, S. Artificial neural network approach for co-pyrolysis of Chlorella vulgaris and peanut shell binary mixtures using microalgae ash catalyst. Energy 2020, 207, 118289. [Google Scholar] [CrossRef]
- Jalal, F.E.; Mulk, S.; Memon, S.A.; Jamhiri, B.; Naseem, A. Strength, Hydraulic, and Microstructural Characteristics of Expansive Soils Incorporating Marble Dust and Rice Husk Ash. Adv. Civ. Eng. 2021, 2021, 9918757. [Google Scholar] [CrossRef]
- Bardhan, A.; Biswas, R.; Kardani, N.; Iqbal, M.; Samui, P.; Singh, M.; Asteris, P.G. A novel integrated approach of augmented grey wolf optimizer and ANN for estimating axial load carrying-capacity of concrete-filled steel tube columns. Constr. Build. Mater. 2022, 337, 127454. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Puppala, A.J.; Congress, S.S.; Talluri, N.; Wattanasanthicharoen, E. Sulfate-heaving studies on chemically treated sulfate-rich geomaterials. J. Mater. Civ. Eng. 2019, 31, 04019076. [Google Scholar] [CrossRef]
- Topcu, I.B.; Sarıdemir, M. Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 41, 305–311. [Google Scholar] [CrossRef]
- Gholami, V.; Booij, M.; Tehrani, E.N.; Hadian, M. Spatial soil erosion estimation using an artificial neural network (ANN) and field plot data. Catena 2018, 163, 210–218. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Li, X.; Jamhiri, B.; Iqbal, M. Fractal approach in expansive clay-based materials with special focus on compacted GMZ bentonite in nuclear waste disposal: A systematic review. Environ. Sci. Pollut. Res. 2021, 28, 43217–43314. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Xu, C.; Chen, X.; Zhang, W.; Xu, C.; Wang, Y. Kernel based progressive distillation for adder neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 12322–12333. [Google Scholar]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Artificial neural network applications in geotechnical engineering. Aust. Geomech. 2001, 36, 49–62. [Google Scholar]
- Zumrawi, M. Prediction of swelling pressure for compacted expansive soils. Univ. Khartoum Eng. J. 2013, 3, 35–39. [Google Scholar]
- Kaloop, M.R.; Samui, P.; Iqbal, M.; Hu, J.W. Soft computing approaches towards tensile strength estimation of GFRP rebars subjected to alkaline-concrete environment. Case Stud. Constr. Mater. 2022, 16, e00955. [Google Scholar] [CrossRef]
- Khan, S.; Horoub, M.M.; Shafiq, S.; Ali, S.; Bhatti, U.N. Optimization of Vehicle Suspension System Using Genetic Algorithm. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 203–207. [Google Scholar]
- Biswas, R.; Rai, B. Effect of cementing efficiency factor on the mechanical properties of concrete incorporating silica fume. J. Struct. Integr. Maint. 2020, 5, 190–203. [Google Scholar] [CrossRef]
- Biswas, R.; Bardhan, A.; Samui, P.; Rai, B.; Nayak, S.; Armaghani, D.J. Efficient soft computing techniques for the prediction of compressive strength of geopolymer concrete. Comput. Concr. 2021, 28, 221–232. [Google Scholar]
- Bell, F. Lime stabilization of clay minerals and soils. Eng. Geol. 1996, 42, 223–237. [Google Scholar] [CrossRef]
- Ashfaq, M.; Moghal, A.A.B. Influence of Lime and Coal Gangue on the CBR Behavior of Expansive Soil. In Proceedings of the Civil Infrastructures Confronting Severe Weathers and Climate Changes Conference, Nanchang, China, 19–21 July 2021; pp. 102–113. [Google Scholar]
- Moghal, A.A.B.; Obaid, A.A.K.; Al-Refeai, T.O.; Al-Shamrani, M.A. Compressibility and durability characteristics of lime treated expansive semiarid soils. J. Test. Eval. 2015, 43, 1–9. [Google Scholar] [CrossRef]
- Jalal, F.-E.; Xu, Y.; Jamhiri, B.; Memon, S.A. On the Recent Trends in Expansive Soil Stabilization Using Calcium-Based Stabilizer Materials (CSMs): A Comprehensive Review. Adv. Mater. Sci. Eng. 2020, 2020, 1510969. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A. Compaction characteristics and bearing ratio of pond ash stabilized with lime and phosphogypsum. J. Mater. Civ. Eng. 2010, 22, 343–351. [Google Scholar] [CrossRef]
- Ola, S.A. The potentials of lime stabilization of lateritic soils. Eng. Geol. 1977, 11, 305–317. [Google Scholar] [CrossRef]
- Sivapullaiah, P.; Moghal, A. CBR and strength behavior of class F fly ashes stabilized with lime and gypsum. Int. J. Geotech. Eng. 2011, 5, 121–130. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Xie, X. Prediction of Uniaxial Compression Strength of Limestone Based on the Point Load Strength and SVM Model. Minerals 2021, 11, 1387. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Ibrahim, H.H.; Abdulhamid, S.N.; Salim, S.G.; Ali, H.F.H.; Majeed, M.K. Artificial intelligence forecasting models of uniaxial compressive strength. Transp. Geotech. 2021, 27, 100499. [Google Scholar] [CrossRef]
- Iqbal, M.; Zhang, D.; Jalal, F.E.; Faisal Javed, M. Computational AI prediction models for residual tensile strength of GFRP bars aged in the alkaline concrete environment. Ocean. Eng. 2021, 232, 109134. Available online: https://www.sciencedirect.com/science/article/pii/S0029801821005680 (accessed on 3 March 2022). [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Jamhiri, B.; Javed, M.F. Predicting the compaction characteristics of expansive soils using two genetic programming-based algorithms. Transp. Geotech. 2021, 30, 100608. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Javed, M.F.; Jamhiri, B. Predictive modeling of swell-strength of expansive soils using artificial intelligence approaches: ANN, ANFIS and GEP. J. Environ. Manag. 2021, 289, 112420. [Google Scholar] [CrossRef]
- Bardhan, A.; Samui, P.; Ghosh, K.; Gandomi, A.H.; Bhattacharyya, S. ELM-based adaptive neuro swarm intelligence techniques for predicting the California bearing ratio of soils in soaked conditions. Appl. Soft Comput. 2021, 110, 107595. [Google Scholar] [CrossRef]


| Property | Value | ASTM Standard |
|---|---|---|
| Specific Gravity | 2.57 | ASTM D854 |
| Ph | 7.2 | ASTM D4972 |
| UCS Classification | SP | ASTM D2487 |
| Liquid Limit (%) | 28 | ASTM D4318 |
| Plasticity Index (%) | NP | ASTM D4318 |
| Optimum Moisture Content (%) | 17 | ASTM D698 |
| Maximum Dry Density (g/cc) | 1.90 | ASTM D698 |
| Unconfined Compressive Strength (kPa) | 116 | ASTM D2166 |
| California Bearing Ratio (soaked, %) | 18 | ASTM D1883 |
| Chemical Constituents | Value |
|---|---|
| Silica (SiO2) | 52.70 |
| Alumina (Al2O3) | 22.60 |
| Ferric oxide (Fe2O3) | 6.37 |
| Calcium oxide (CaO) | 3.45 |
| Magnesia (MgO) | 1.72 |
| Titanium (TiO2) | 0.98 |
| Potash (K2O) | 2.68 |
| Sodium oxide (Na2O) | 0.75 |
| Sulphur (SO3) | 0.53 |
| Loss on ignition | 8.22 |
| S. No | Input Variables Used in This Study | No. of Samples Tested for UCS and CBR (Target Variables) | ||
|---|---|---|---|---|
| Gypsum Dosage (%) | Lime Dosage (%) | Curing Period (Days) | ||
| 1 | 0 | 0 | 1 | 6 |
| 2 | 0 | 0 | 7 | 6 |
| 3 | 0 | 0 | 14 | 6 |
| 4 | 0 | 0 | 28 | 6 |
| 5 | 0 | 2 | 1 | 6 |
| 6 | 0 | 2 | 7 | 6 |
| 7 | 0 | 2 | 14 | 6 |
| 8 | 0 | 2 | 28 | 6 |
| 9 | 0 | 4 | 1 | 6 |
| 10 | 0 | 4 | 7 | 6 |
| 11 | 0 | 4 | 14 | 6 |
| 12 | 0 | 4 | 28 | 6 |
| 13 | 0 | 6 | 1 | 6 |
| 14 | 0 | 6 | 7 | 6 |
| 15 | 0 | 6 | 14 | 6 |
| 16 | 0 | 6 | 28 | 6 |
| 17 | 0.5 | 0 | 1 | 6 |
| 18 | 0.5 | 0 | 7 | 6 |
| 19 | 0.5 | 0 | 14 | 6 |
| 20 | 0.5 | 0 | 28 | 6 |
| 21 | 0.5 | 2 | 1 | 6 |
| 22 | 0.5 | 2 | 7 | 6 |
| 23 | 0.5 | 2 | 14 | 6 |
| 24 | 0.5 | 2 | 28 | 6 |
| 25 | 0.5 | 4 | 1 | 6 |
| 26 | 0.5 | 4 | 7 | 6 |
| 27 | 0.5 | 4 | 14 | 6 |
| 28 | 0.5 | 4 | 28 | 6 |
| 29 | 0.5 | 6 | 1 | 6 |
| 30 | 0.5 | 6 | 7 | 6 |
| 31 | 0.5 | 6 | 14 | 6 |
| 32 | 0.5 | 6 | 28 | 6 |
| 33 | 1 | 0 | 1 | 6 |
| 34 | 1 | 0 | 7 | 6 |
| 35 | 1 | 0 | 14 | 6 |
| 36 | 1 | 0 | 28 | 6 |
| 37 | 1 | 2 | 1 | 6 |
| 38 | 1 | 2 | 7 | 6 |
| 39 | 1 | 2 | 14 | 6 |
| 40 | 1 | 2 | 28 | 6 |
| 41 | 1 | 4 | 1 | 6 |
| 42 | 1 | 4 | 7 | 6 |
| 43 | 1 | 4 | 14 | 6 |
| 44 | 1 | 4 | 28 | 6 |
| 45 | 1 | 6 | 1 | 6 |
| 46 | 1 | 6 | 7 | 6 |
| 47 | 1 | 6 | 14 | 6 |
| 48 | 1 | 6 | 28 | 6 |
| 49 | 1.5 | 0 | 1 | 6 |
| 50 | 1.5 | 0 | 7 | 6 |
| 51 | 1.5 | 0 | 14 | 6 |
| 52 | 1.5 | 0 | 28 | 6 |
| 53 | 1.5 | 2 | 1 | 6 |
| 54 | 1.5 | 2 | 7 | 6 |
| 55 | 1.5 | 2 | 14 | 6 |
| 56 | 1.5 | 2 | 28 | 6 |
| 57 | 1.5 | 4 | 1 | 6 |
| 58 | 1.5 | 4 | 7 | 6 |
| 59 | 1.5 | 4 | 14 | 6 |
| 60 | 1.5 | 4 | 28 | 6 |
| 61 | 1.5 | 6 | 1 | 6 |
| 62 | 1.5 | 6 | 7 | 6 |
| 63 | 1.5 | 6 | 14 | 6 |
| 64 | 1.5 | 6 | 28 | 6 |
| Total number of samples | 384 | |||
| Model | Parameter | Training Data | Validation | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | RMSE | MAE | RSE | R | RMSE | MAE | RSE | ||
| ANN Model | Unsoaked CBR | 0.997 | 6.940 | 1.180 | 0.005 | 0.996 | 6.866 | 1.322 | 0.001 |
| Soaked CBR | 0.995 | 6.570 | 1.409 | 0.010 | 0.990 | 6.740 | 2.039 | 0.004 | |
| UCS | 0.993 | 65.96 | 45.980 | 0.014 | 0.993 | 60.54 | 46.792 | 0.005 | |
| RFT Model | Unsoaked CBR | 0.995 | 6.874 | 1.806 | 0.012 | 0.993 | 7.009 | 2.267 | 0.004 |
| Soaked CBR | 0.994 | 6.563 | 1.770 | 0.013 | 0.993 | 6.715 | 1.976 | 0.003 | |
| UCS | 0.993 | 71.67 | 46.955 | 0.018 | 0.994 | 68.659 | 45.522 | 0.006 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, M.N.; Iqbal, M.; Ashfaq, M.; Salami, B.A.; Khan, K.; Faraz, M.I.; Alabdullah, A.A.; Jalal, F.E. Prediction of Strength and CBR Characteristics of Chemically Stabilized Coal Gangue: ANN and Random Forest Tree Approach. Materials 2022, 15, 4330. https://doi.org/10.3390/ma15124330
Amin MN, Iqbal M, Ashfaq M, Salami BA, Khan K, Faraz MI, Alabdullah AA, Jalal FE. Prediction of Strength and CBR Characteristics of Chemically Stabilized Coal Gangue: ANN and Random Forest Tree Approach. Materials. 2022; 15(12):4330. https://doi.org/10.3390/ma15124330
Chicago/Turabian StyleAmin, Muhammad Nasir, Mudassir Iqbal, Mohammed Ashfaq, Babatunde Abiodun Salami, Kaffayatullah Khan, Muhammad Iftikhar Faraz, Anas Abdulalim Alabdullah, and Fazal E. Jalal. 2022. "Prediction of Strength and CBR Characteristics of Chemically Stabilized Coal Gangue: ANN and Random Forest Tree Approach" Materials 15, no. 12: 4330. https://doi.org/10.3390/ma15124330
APA StyleAmin, M. N., Iqbal, M., Ashfaq, M., Salami, B. A., Khan, K., Faraz, M. I., Alabdullah, A. A., & Jalal, F. E. (2022). Prediction of Strength and CBR Characteristics of Chemically Stabilized Coal Gangue: ANN and Random Forest Tree Approach. Materials, 15(12), 4330. https://doi.org/10.3390/ma15124330









