Effect of the Looseness of the Beam End Connection Used for the Pallet Racking Storage Systems, on the Mechanical Behavior of the Bearing Beams
Abstract
:1. Introduction
2. Materials and Methods
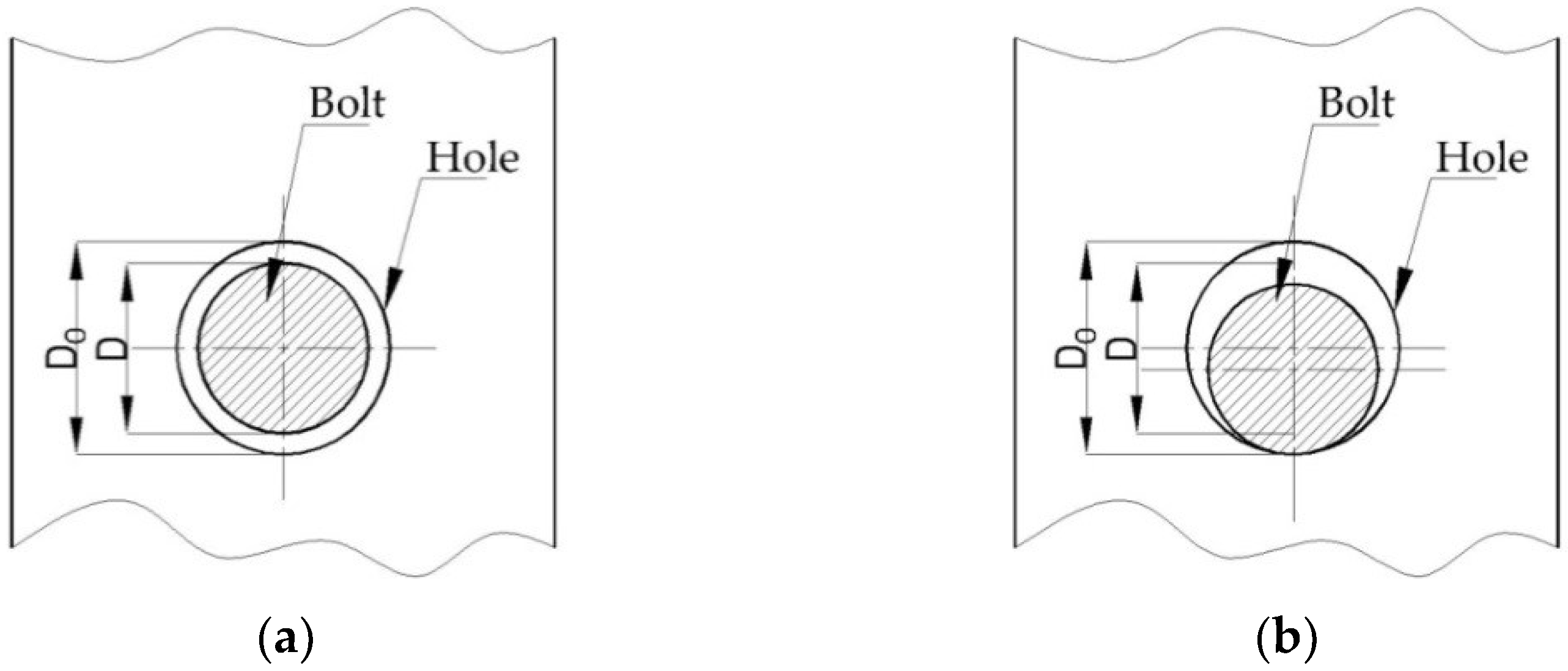
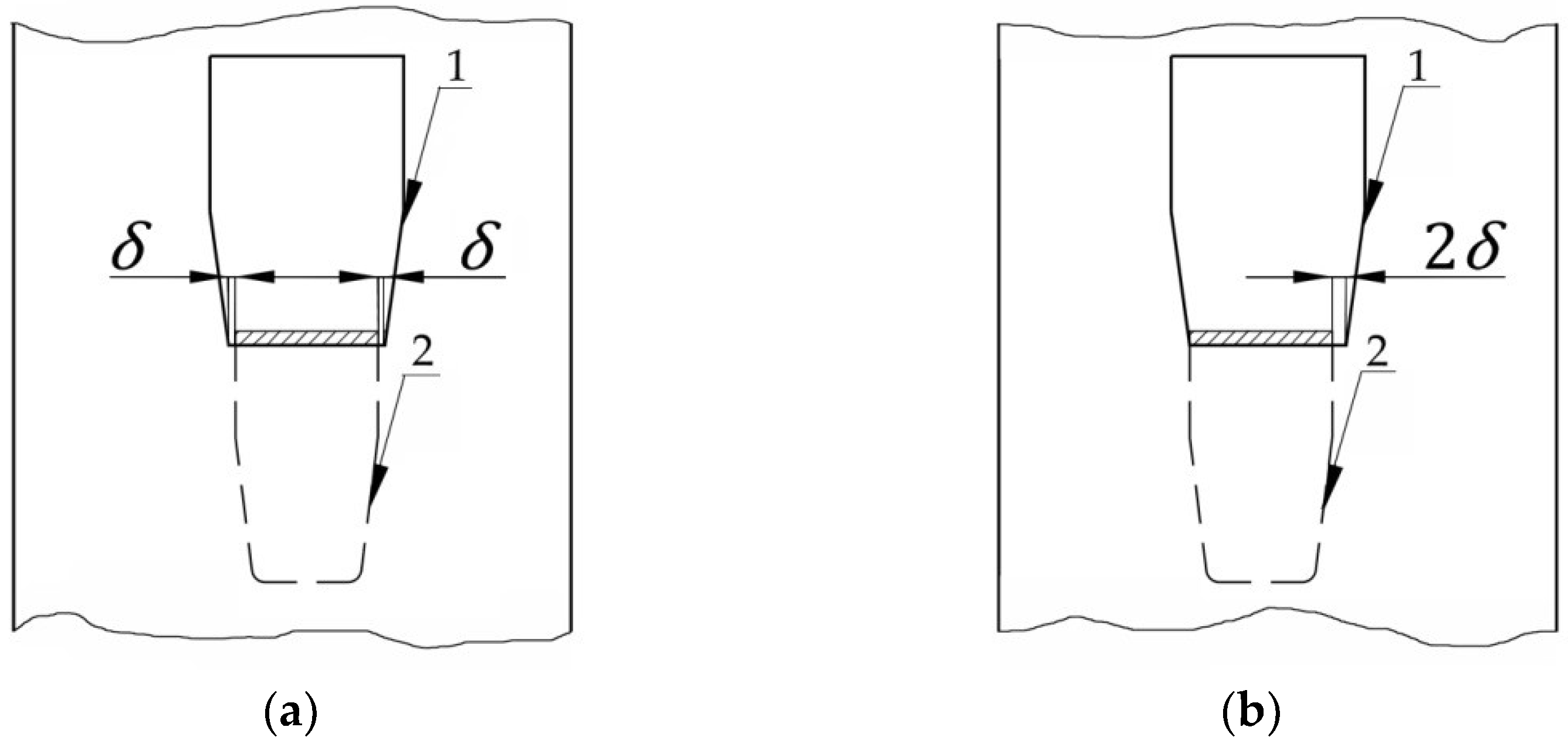
2.1. Assemblies Subjected to Looseness Tests
2.2. Work Method for Bending and Looseness Tests on Beam End Connectors
2.3. Theoretical Approach
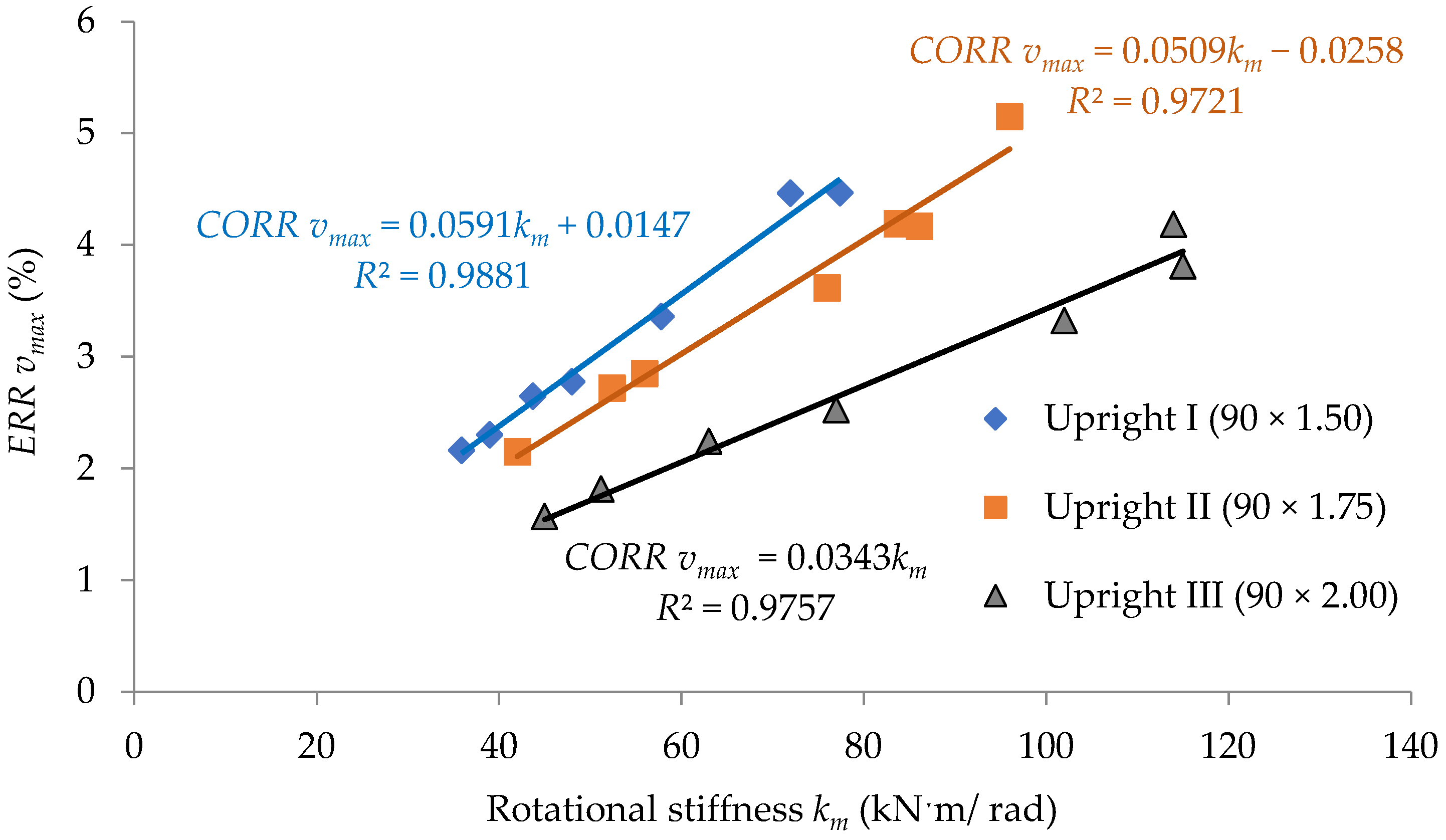
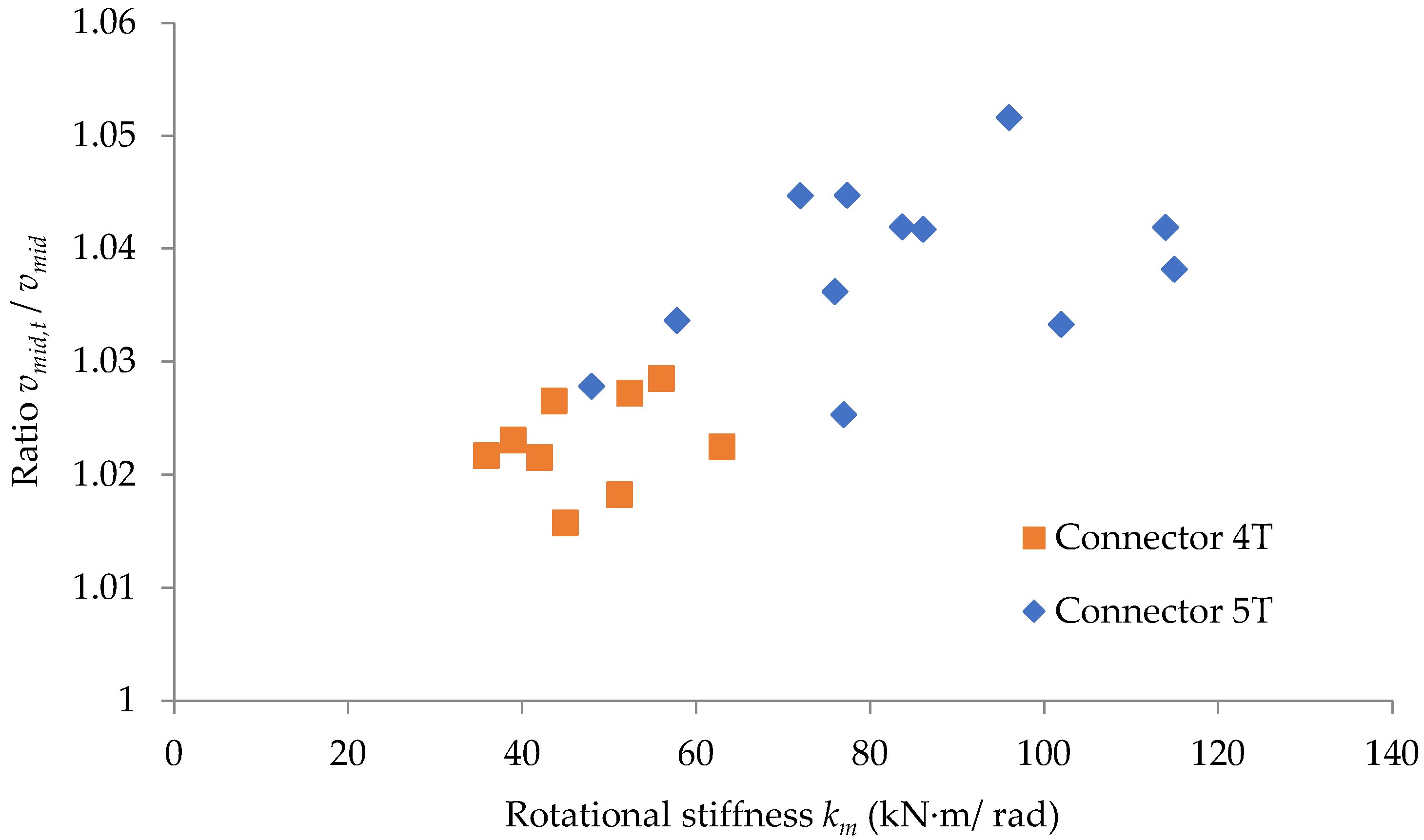
3. Results and Discussion
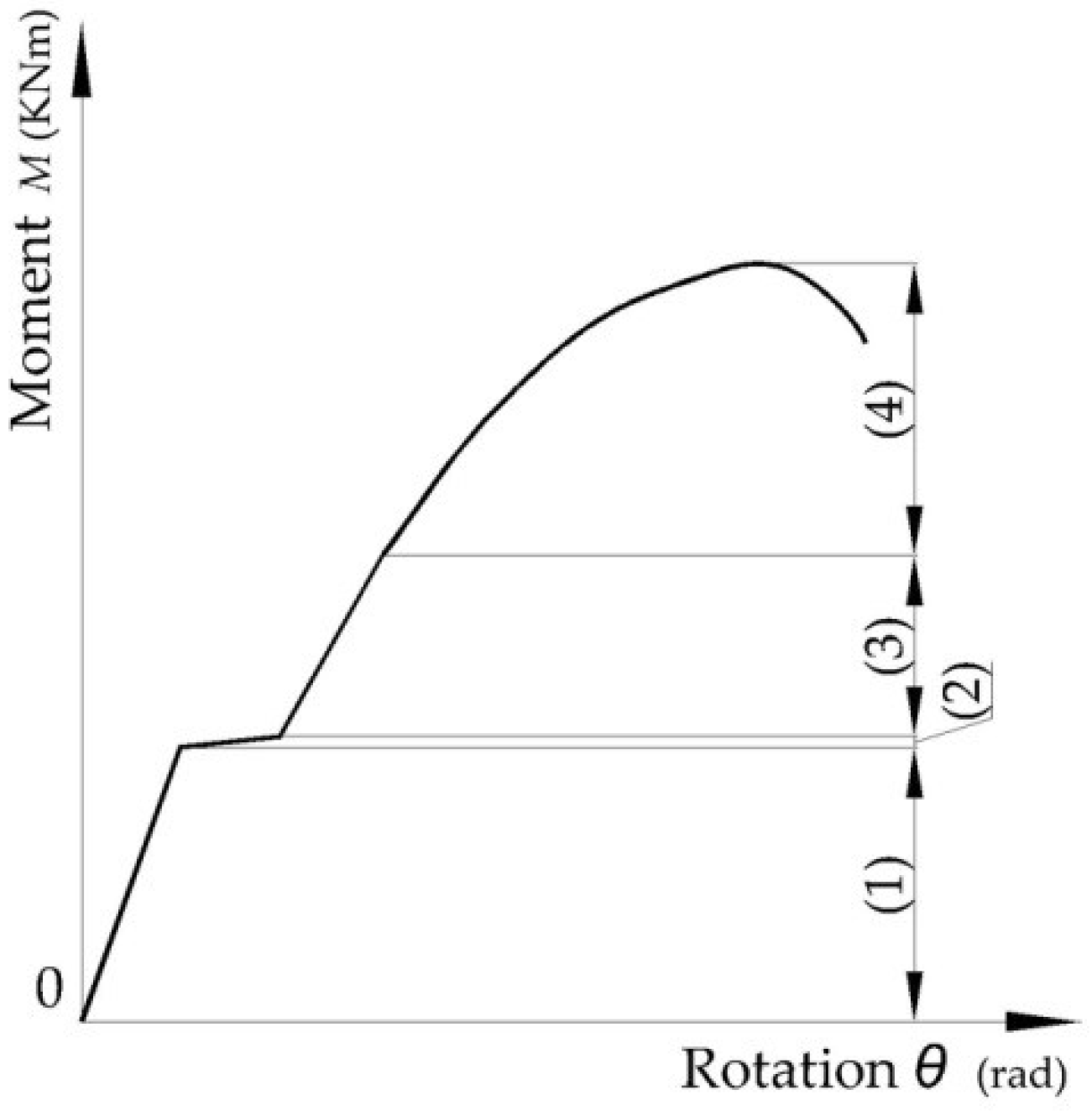
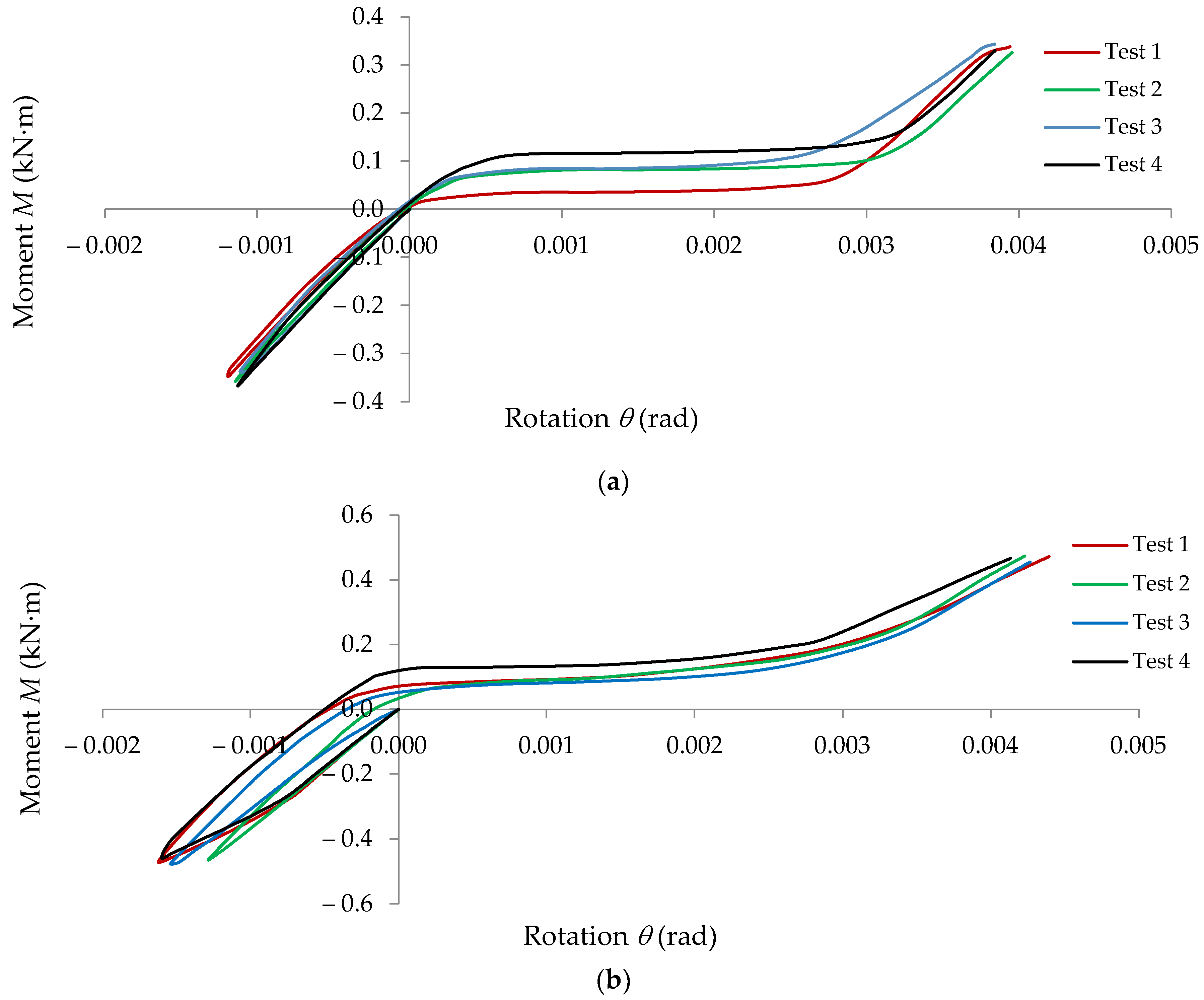
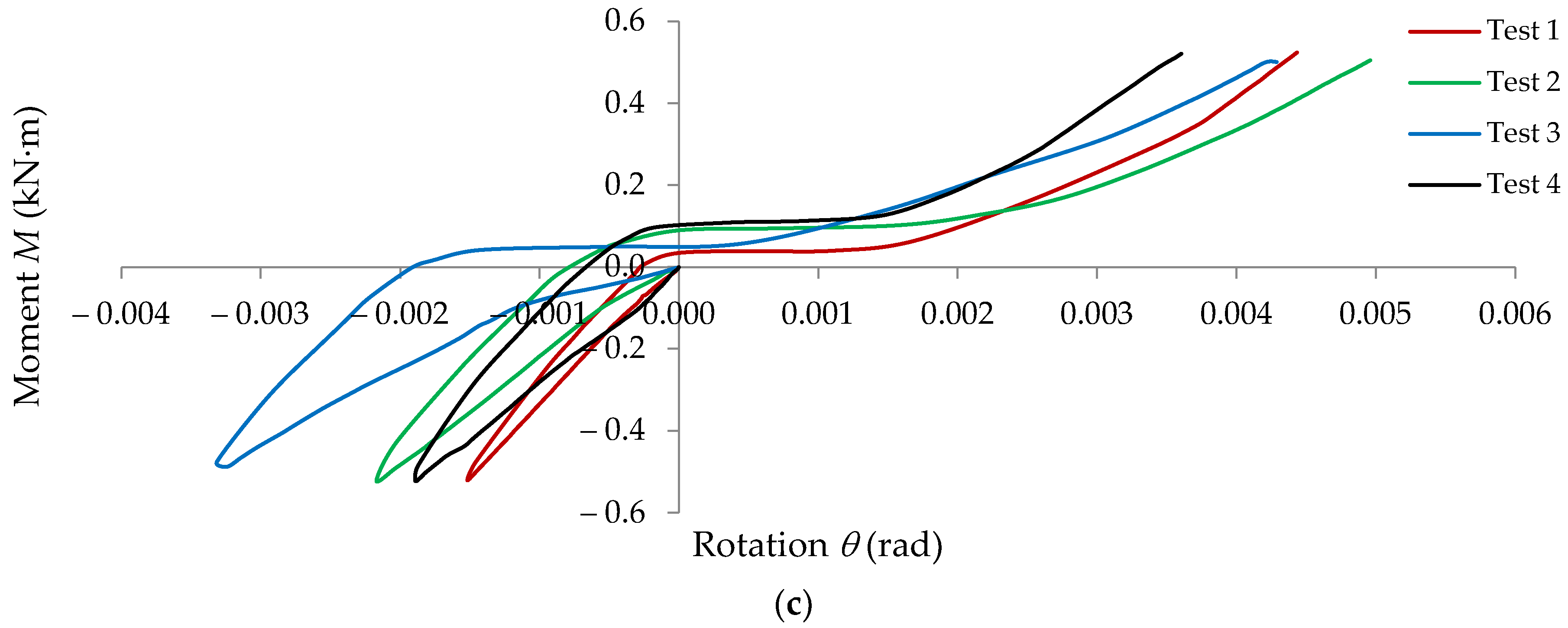
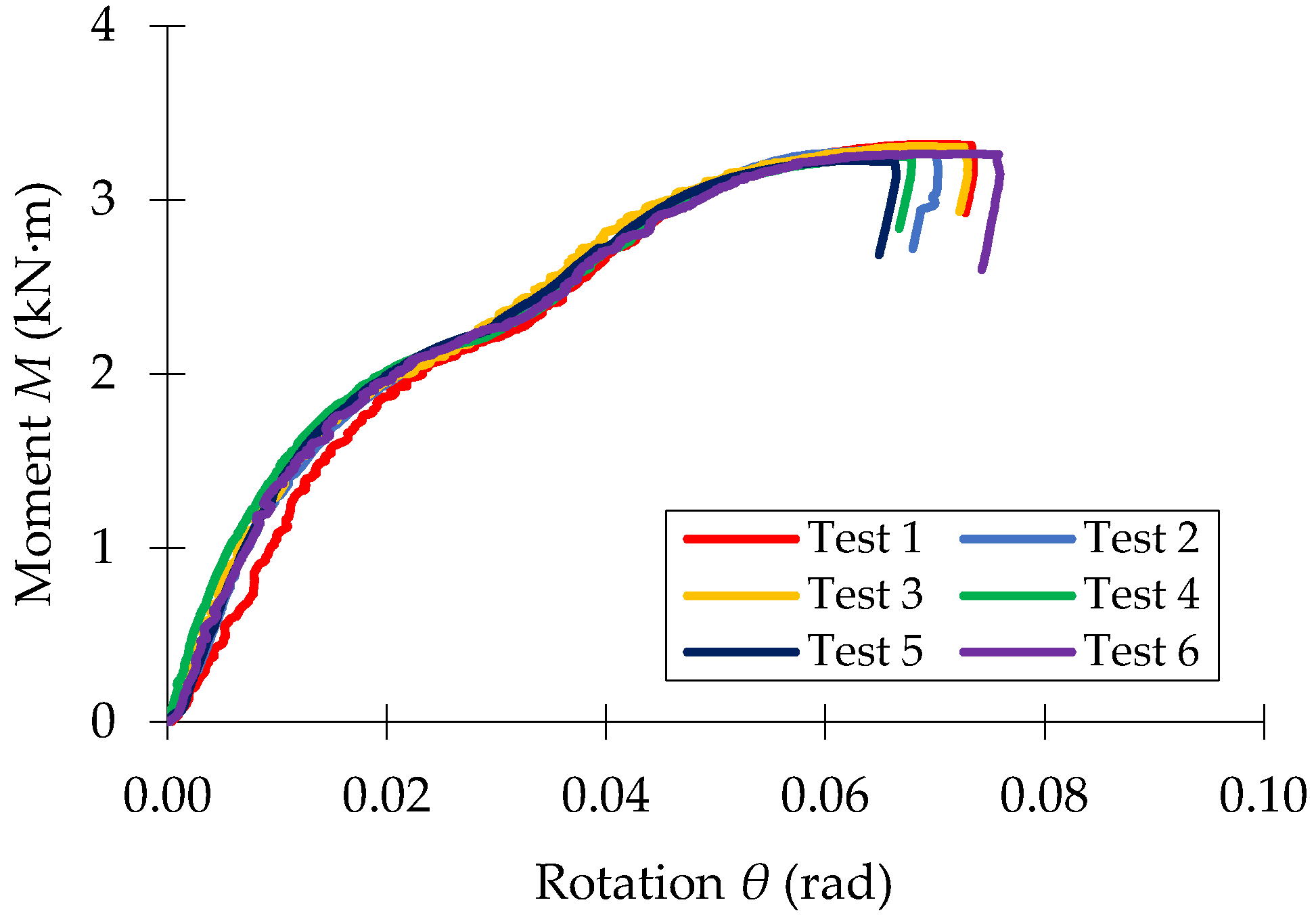
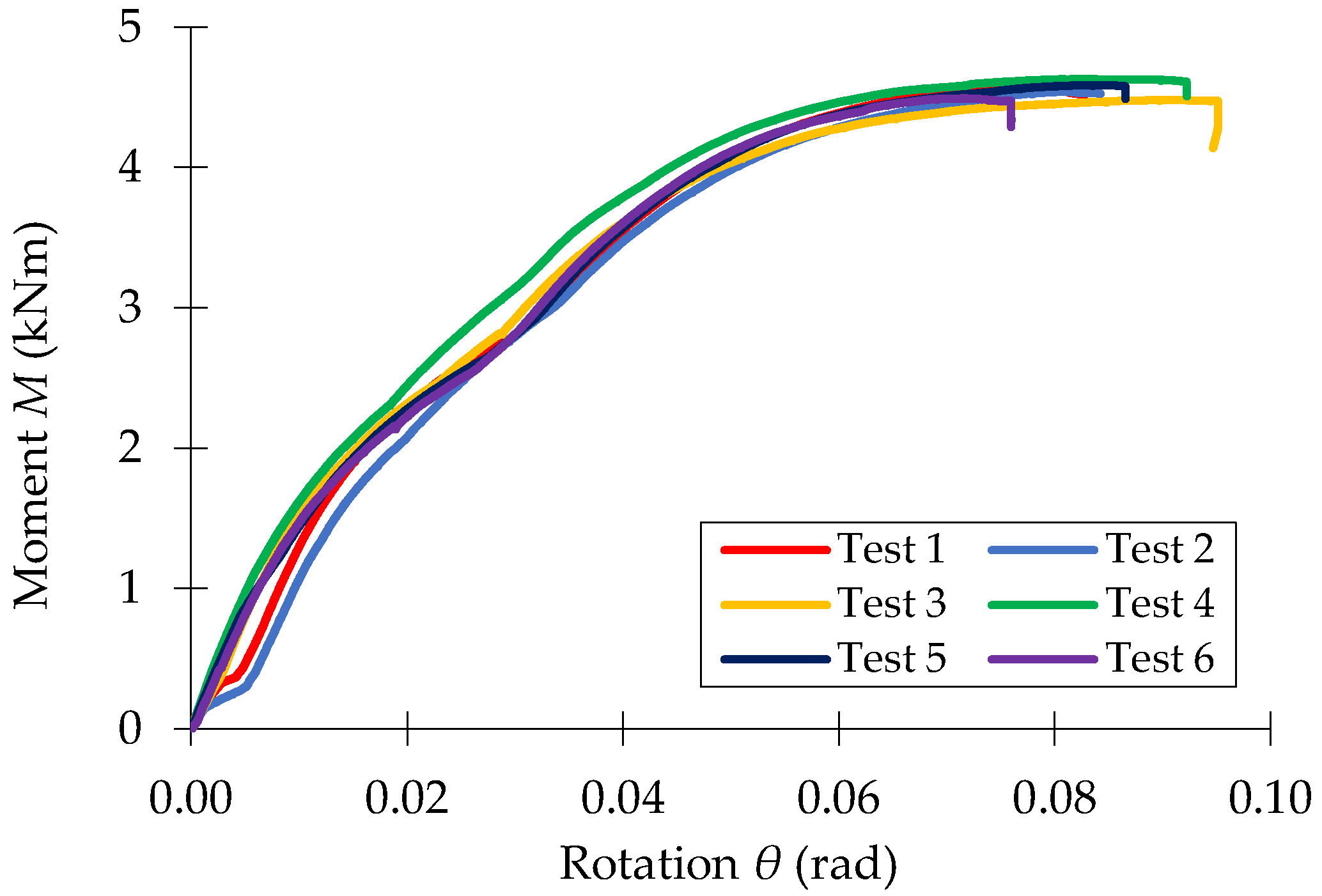
3.1. Experimental Results
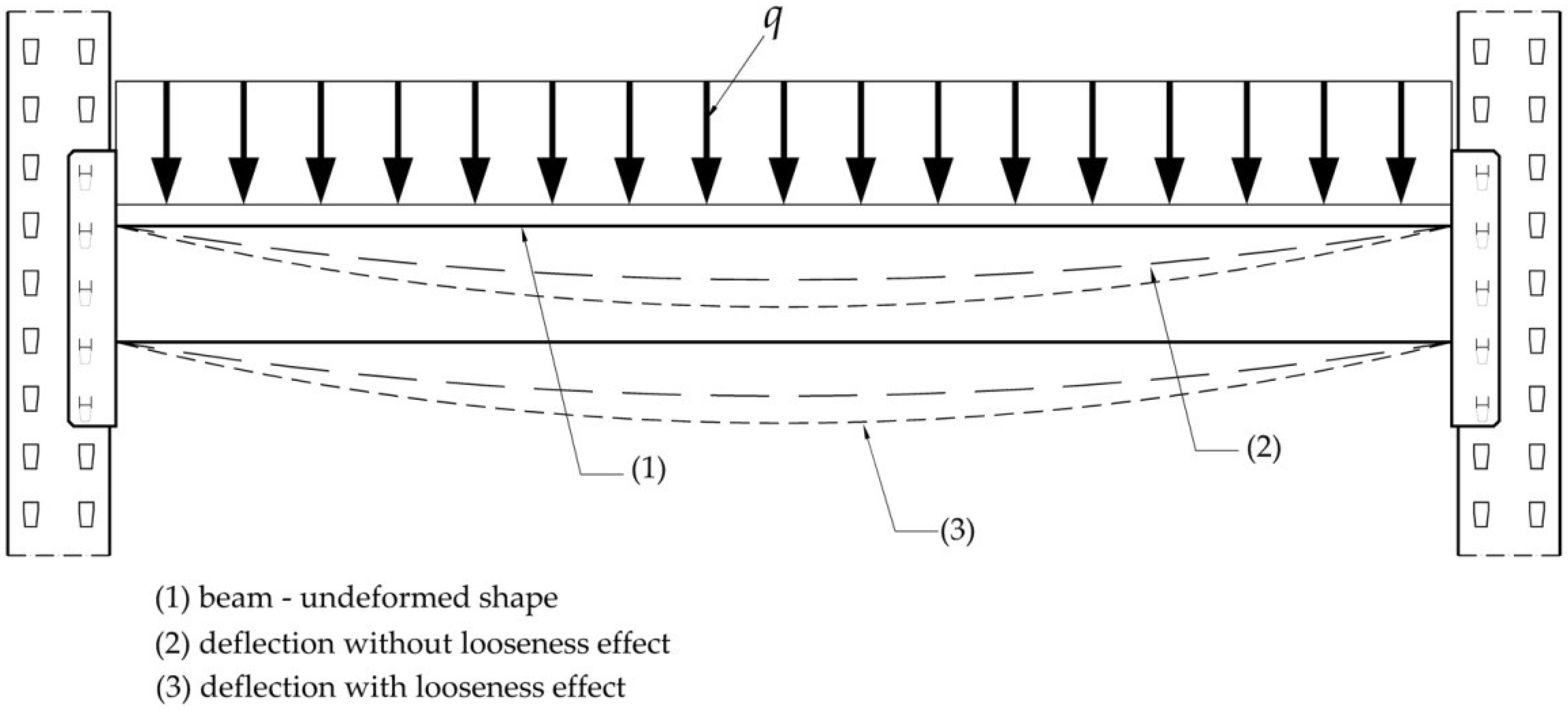
3.2. Effects of Looseness of the Semi-Rigid Connections on Mechanical Behavior of the Beam
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BS EN 15512; Steel Static Storage Systems—Adjustable Pallet Racking Systems—Principles for Structural Design. BSI: London, UK, 2009.
- EN 15512; Steel Static Storage Systems—Adjustable Pallet Racking Systems—Principles for Structural Design. BSI: London, UK, 2020.
- Gilbert, B.P.; Rasmussen, K.J.R. Bolted moment connections in drive-in and drive-through steel storage racks. J. Constr. Steel Res. 2010, 66, 755–766. [Google Scholar] [CrossRef] [Green Version]
- Coelho, A.M.G.; Bijlaard, F.S.K.; da Silva, L.S. Experimental assessment of the ductility of extended end plate connections. Eng. Struct. 2004, 26, 1185–1206. [Google Scholar] [CrossRef]
- Mohan, V.; Prabha, P.; Rajasankar, J.; Iyer, N.R.; Raviswaran, N.; Nagendiran, V.; Kamalakannan, S.S. Cold-formed steel pallet rack connection: An experimental study. Int. J. Adv. Struct. Eng. 2015, 7, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Dumbrava, F.; Cerbu, C. Experimental Study on the Stiffness of Steel Beam-to-Upright Connections for Storage Racking Systems. Materials 2020, 13, 27. [Google Scholar] [CrossRef] [PubMed]
- Dumbrava, F. Research Report: Experimental Research on Stress States and Deformations of Elements (Columns, Beams, etc.). In The Construction of Thin-Walled Metal Structures; Transilvania University of Brasov: Brașov, Romania, 2020. [Google Scholar]
- Gusella, F.; Arwade, S.R.; Orlando, M.; Peterman, K.D. Influence of mechanical and geometric uncertainty on rack connection structural response. J. Constr. Steel Res. 2019, 153, 343–355. [Google Scholar] [CrossRef]
- Escanio, L.A.; Elias, G.C.; Neiva, L.H.D.; Alves, V.N.; Sarmanho, A.M.C. Analysis of Beam-o-Upright End Connections Steel Storage Systems. Adv. Steel Constr. 2020, 16, 279–286. [Google Scholar] [CrossRef]
- Shah, S.N.R.; Sulong, N.H.R.; Shariati, M.; Khan, R.; Jumaat, M.Z. Behavior of steel pallet rack beam-to-column connections at elevated temperatures. Thin-Walled Struct. 2016, 106, 471–483. [Google Scholar] [CrossRef]
- Schabowicz, K. Testing of Materials and Elements in Civil Engineering. Materials 2021, 14, 20. [Google Scholar] [CrossRef] [PubMed]
- Zadanfarrokh, F.; Bryan, E.R. Testing and Design of Bolted Connections in Cold Formed Steel Sections. In Proceedings of the 11th International Specialty Conference on Cold-Formed Steel Structures, St. Louis, MO, USA, 20–21 October 1992; Missouri University of Science and Technology: St. Louis, MO, USA, 1992. [Google Scholar]
- Grondin, G.Y.; Jin, M.; Josi, G. Slip Critical Bolted Connections—A Reliability Analysis for Design at the Ultimate Limit State; University of Alberta: Edmonton, AB, Canada, 2007. [Google Scholar]
- Gharebaghi, R.; Hosseini, A. Local behavior of column-tree connections with considering bolt-hole clearance and bolt pretension effects. Int. J. Steel Struct. 2017, 17, 379–388. [Google Scholar] [CrossRef]
- Sanborn, M.; Stewart, L.K. Behavior of slip-critical bolted connections subjected to impulsive loads. Int. J. Impact Eng. 2020, 143, 12. [Google Scholar] [CrossRef]
- Kulak, G.L.; Fisher, J.W.; Struik, J.H.A. Guide to Design Criteria for Bolted and Riveted Joints, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Galeotti, C.; Gusella, F.; Orlando, M.; Spinelli, P. On the seismic response of steel storage pallet racks with selective addition of bolted joints. Structures 2021, 34, 3806–3817. [Google Scholar] [CrossRef]
- Godley, M.H.R.; Beale, R.G. Analysis of large proprietary access scaffold structures. Proc. Inst. Civ. Eng. -Struct. Build. 2001, 146, 31–39. [Google Scholar] [CrossRef]
- Prabhakaran, U.; Beale, R.G.; Godley, M.H.R. Analysis of scaffolds with connections containing looseness. Comput. Struct. 2011, 89, 1944–1955. [Google Scholar] [CrossRef] [Green Version]
- Asl, M.H.; Farivar, B.; Momenzadeh, S. Investigation of the rigidity of welded shear tab connections. Eng. Struct. 2019, 179, 353–366. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Dai, L.S.; Wang, T.; Sivakumaran, K.S.; Chen, Y.Y. A theoretical model for the rotational stiffness of storage rack beam-to-upright connections. J. Constr. Steel Res. 2017, 133, 269–281. [Google Scholar] [CrossRef]
- Mourya, U.; Jayachandran, S.A. Finite Element Model-Based Dynamic Characteristic Predictions for Cold-Formed Steel Storage Racks. In Proceedings of the Annual Stability Conference Structural Stability Research Council, Denver, CO, USA, 22–25 March 2022; pp. 1–9. [Google Scholar]
- Shariati, M.; Tahir, M.M.; Wee, T.C.; Shah, S.N.R.; Jalali, A.; Abdullahi, M.M.; Khorami, M. Experimental investigations on monotonic and cyclic behavior of steel pallet rack connections. Eng. Fail. Anal. 2018, 85, 149–166. [Google Scholar] [CrossRef]
- Yin, L.F.; Tang, G.; Zhang, M.; Wang, B.J.; Feng, B. Monotonic and cyclic response of speed-lock connections with bolts in storage racks. Eng. Struct. 2016, 116, 40–55. [Google Scholar] [CrossRef]
- Ślęczka, L.; Kozłowski, A. Design of beam-to-column joints in steel storage pallet racks by testing and by component method. Arch. Civ. Eng. 2008, 54, 263–291. [Google Scholar]
- Prabha, P.; Marimuthu, V.; Saravanan, M.; Jayachandran, S.A. Evaluation of connection flexibility in cold formed steel racks. J. Constr. Steel Res. 2010, 66, 863–872. [Google Scholar] [CrossRef]
- Cerbu, C. Strength of Materials. Theory and Applications; Transilvania University of Brasov: Brașov, Romania, 2014; p. 398. [Google Scholar]
- Jovanovic, D.; Zarkovic, D.; Vukobratovic, V.; Brujic, Z. Hysteresis model for beam-to-column connections of steel storage racks. Thin-Walled Struct. 2019, 142, 189–204. [Google Scholar] [CrossRef]







| Assembly Code | Upright W * × t * | Beam H ** × W1 ** × t1 ** | Connector Type | Number of Looseness Tests for Assembly | Number of Bending Tests for Assembly |
|---|---|---|---|---|---|
| 0-I-5T | 90 × 1.50 | BOX 150 × 50 × 1.75 | 5T | 4 | 6 |
| 0-II-5T | 90 × 1.75 | 4 | 6 | ||
| 0-III-5T | 90 × 2.00 | 4 | 6 |
| Assembly Identification Code | Upright W * × t * | Beam (H ** × W1 ** × t1 **) | Connector Type | Rotational Stiffness (kN·m/rad) | Design Moment (kN·m) |
|---|---|---|---|---|---|
| A-I-4T | 90 × 1.50 | A (BOX 90 × 40 × 1.25) | 4T | 39 | 1.54 |
| A-I-5T | 5T | 48 | 2.30 | ||
| A-II-4T | 90 × 1.75 | 4T | 42 | 2.43 | |
| A-II-5T | 5T | 76 | 2.21 | ||
| A-III-4T | 90 × 2.00 | 4T | 45 | 2.16 | |
| A-III-5T | 5T | 77 | 2.09 | ||
| B-I-4T | 90 × 1.50 | B (BOX 100 × 40 × 1.25) | 4T | 35.9 | 1.38 |
| B-I-5T | 5T | 57.8 | 2.24 | ||
| B-II-4T | 90 × 1.75 | 4T | 56 | 2.03 | |
| B-II-5T | 5T | 86.1 | 2.36 | ||
| B-III-4T | 90 × 2.00 | 4T | 51.2 | 2.43 | |
| B-III-5T | 5T | 102 | 2.18 | ||
| C-I-4T | 90 × 1.50 | C (BOX 110 × 40 × 1.25) | 4T | 43.7 | 1.70 |
| C-I-5T | 5T | 77.4 | 2.15 | ||
| C-II-4T | 90 × 1.75 | 4T | 52.4 | 2.74 | |
| C-II-5T | 5T | 83.7 | 2.95 | ||
| C-III-4T | 90 × 2.00 | 4T | 63 | 2.89 | |
| C-III-5T | 5T | 115 | 2.61 |
| Assembly Code | Looseness Angle | Design Moment | Rotational Stiffness | ||||
|---|---|---|---|---|---|---|---|
| (rad) | (rad) | Stdev (rad) | (kN·m) | Stdev (kN·m) | (kN·m/rad) | Stdev (kN·m/rad) | |
| 0-I-5T | 0.00139 | 0.00133 | 0.000124 | 2.91 | 0.035 | 72 | 10.029 |
| 0.00140 | |||||||
| 0.00114 | |||||||
| 0.00137 | |||||||
| 0-II-5T | 0.00115 | 0.00116 | 0.000171 | 4.02 | 0.058 | 96 | 4.118 |
| 0.00126 | |||||||
| 0.0013 | |||||||
| 0.00092 | |||||||
| 0-III-5T | 0.00075 | 0.00080 | 0.000104 | 4.32 | 0.086 | 114 | 4.425 |
| 0.00093 | |||||||
| 0.00083 | |||||||
| 0.00069 | |||||||
| Assembly Code | Looseness Angle (rad) | With Looseness Effects | Without Looseness Effects | (%) | (%) | ||
|---|---|---|---|---|---|---|---|
| Bending Moment at Mid. (kN·m) | Max. Deflection at Mid. (mm) | Bending Moment at Mid. (kN·m) | Max. Deflection at Mid. (mm) | ||||
| 0-I-5T | 0.00133 | 3.245 | 2.83 | 3.163 | 2.709 | 2.59 | 4.47 |
| 0-II-5T | 0.00116 | 3.168 | 2.753 | 3.076 | 2.618 | 2.99 | 5.16 |
| 0-III-5T | 0.00080 | 3.089 | 2.662 | 3.016 | 2.555 | 2.42 | 4.19 |
| A-I-4T | 0.00133 | 2.794 | 12.383 | 2.758 | 12.104 | 1.31 | 2.31 |
| A-I-5T | 2.692 | 11.831 | 2.651 | 11.511 | 1.55 | 2.78 | |
| A-II-4T | 0.00116 | 2.753 | 12.153 | 2.72 | 11.897 | 1.21 | 2.15 |
| A-II-5T | 2.441 | 10.45 | 2.394 | 10.085 | 1.96 | 3.62 | |
| A-III-4T | 0.00080 | 2.709 | 11.884 | 2.685 | 11.7 | 0.89 | 1.57 |
| A-III-5T | 2.419 | 10.297 | 2.387 | 10.043 | 1.34 | 2.53 | |
| B-I-4T | 0.00133 | 2.947 | 10.325 | 2.911 | 10.106 | 1.24 | 2.17 |
| B-I-5T | 2.735 | 9.429 | 2.684 | 9.122 | 1.90 | 3.37 | |
| B-II-4T | 0.00116 | 2.744 | 9.455 | 2.7 | 9.193 | 1.63 | 2.85 |
| B-II-5T | 2.522 | 8.515 | 2.465 | 8.174 | 2.31 | 4.17 | |
| B-III-4T | 0.00080 | 2.774 | 9.561 | 2.746 | 9.39 | 1.02 | 1.82 |
| B-III-5T | 2.41 | 8.01 | 2.368 | 7.752 | 1.77 | 3.33 | |
| C-I-4T | 0.00133 | 2.968 | 8.321 | 2.923 | 8.106 | 1.54 | 2.65 |
| C-I-5T | 2.715 | 7.478 | 2.649 | 7.158 | 2.49 | 4.47 | |
| C-II-4T | 0.00116 | 2.887 | 8.043 | 2.843 | 7.83 | 1.55 | 2.72 |
| C-II-5T | 2.668 | 7.306 | 2.607 | 7.012 | 2.34 | 4.19 | |
| C-III-4T | 0.00080 | 2.79 | 7.693 | 2.755 | 7.524 | 1.27 | 2.25 |
| C-III-5T | 2.479 | 6.64 | 2.426 | 6.396 | 2.18 | 3.81 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumbrava, F.; Cerbu, C. Effect of the Looseness of the Beam End Connection Used for the Pallet Racking Storage Systems, on the Mechanical Behavior of the Bearing Beams. Materials 2022, 15, 4728. https://doi.org/10.3390/ma15144728
Dumbrava F, Cerbu C. Effect of the Looseness of the Beam End Connection Used for the Pallet Racking Storage Systems, on the Mechanical Behavior of the Bearing Beams. Materials. 2022; 15(14):4728. https://doi.org/10.3390/ma15144728
Chicago/Turabian StyleDumbrava, Florin, and Camelia Cerbu. 2022. "Effect of the Looseness of the Beam End Connection Used for the Pallet Racking Storage Systems, on the Mechanical Behavior of the Bearing Beams" Materials 15, no. 14: 4728. https://doi.org/10.3390/ma15144728
APA StyleDumbrava, F., & Cerbu, C. (2022). Effect of the Looseness of the Beam End Connection Used for the Pallet Racking Storage Systems, on the Mechanical Behavior of the Bearing Beams. Materials, 15(14), 4728. https://doi.org/10.3390/ma15144728







