A DFT-Based Quantitative and Geometric Analysis of the Effect of Pressure on Boron Arsenate
Abstract
:1. Introduction
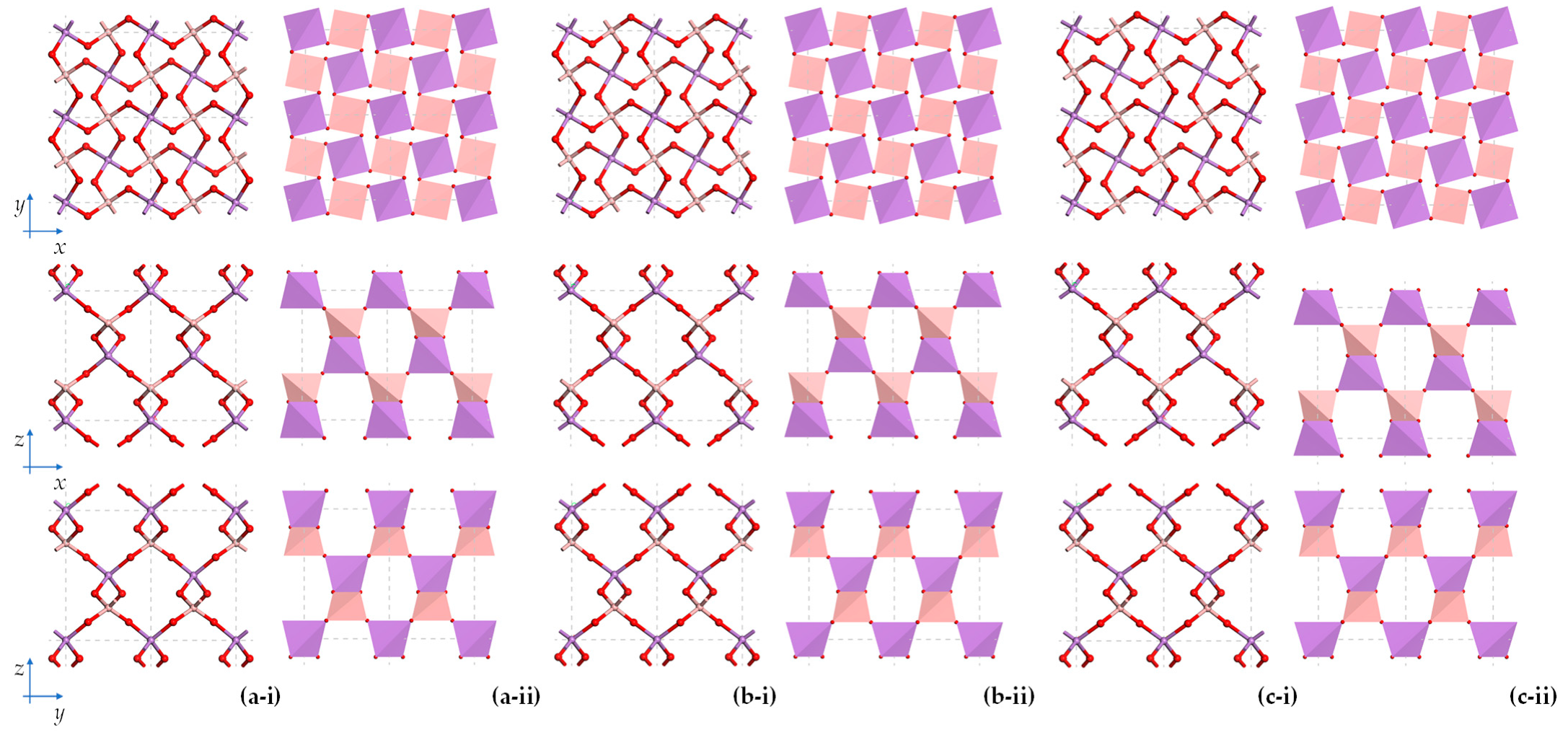
2. Boron Arsenate at Ambient Pressures
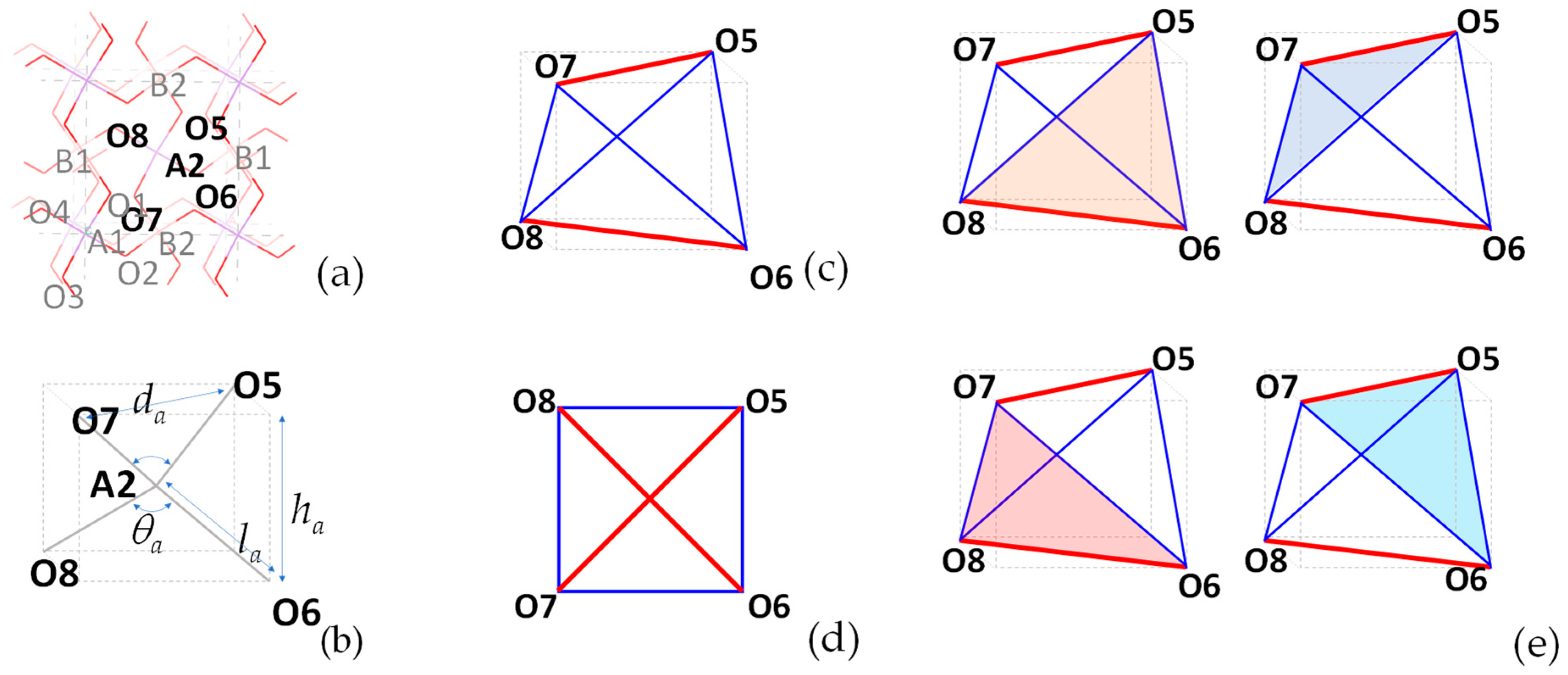
2.1. An Analysis of BAsO4 in Terms of Its Geometric Features
2.1.1. General Considerations
2.1.2. On the Shape of Tetrahedra under Ambient Pressures
2.1.3. On the Relative Orientation of Tetrahedra under Ambient Pressures
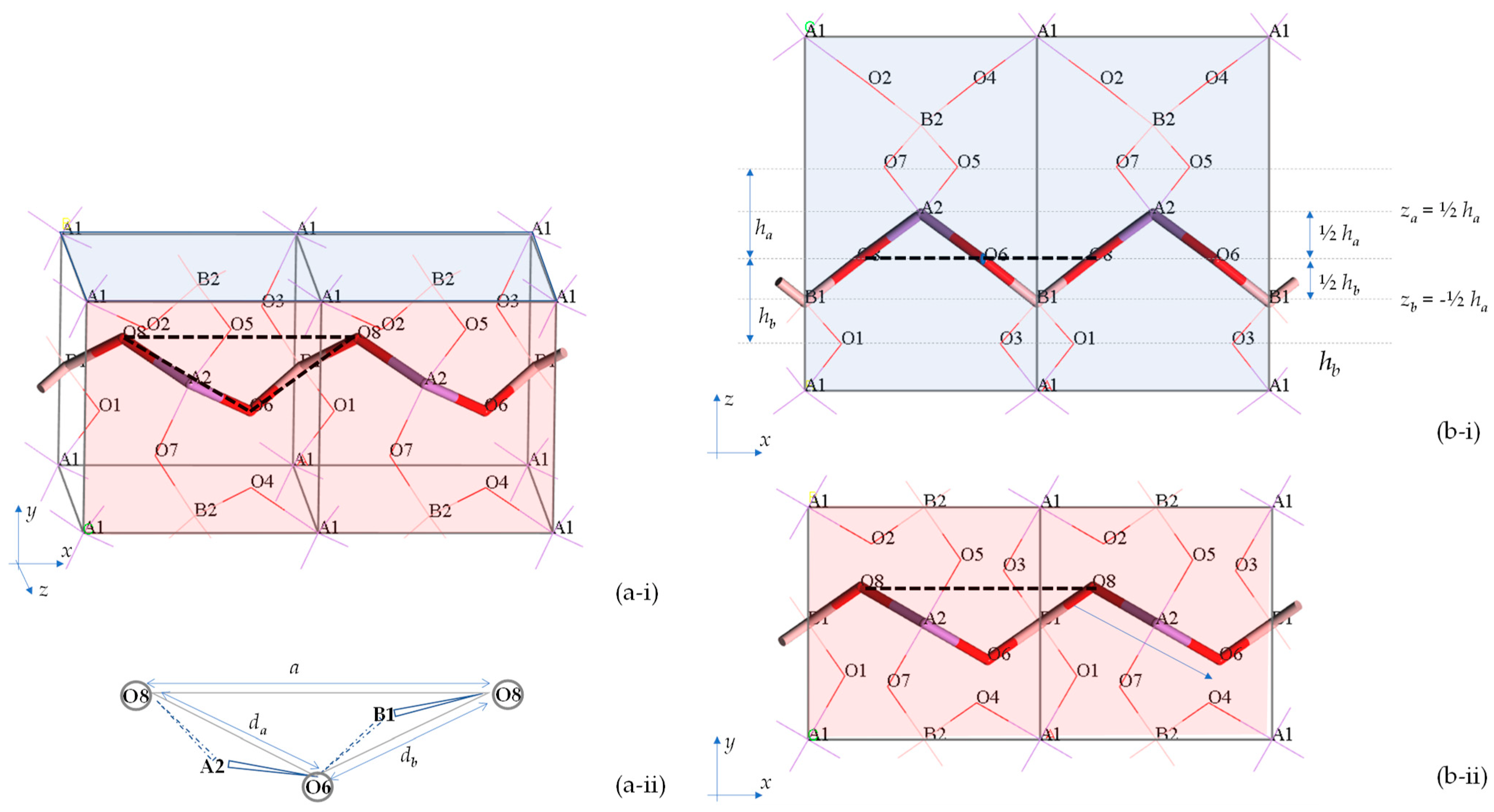
2.2. Mathematical Expressions for the Cell Parameters of BAsO4 at Ambient Pressures
2.2.1. Derivation
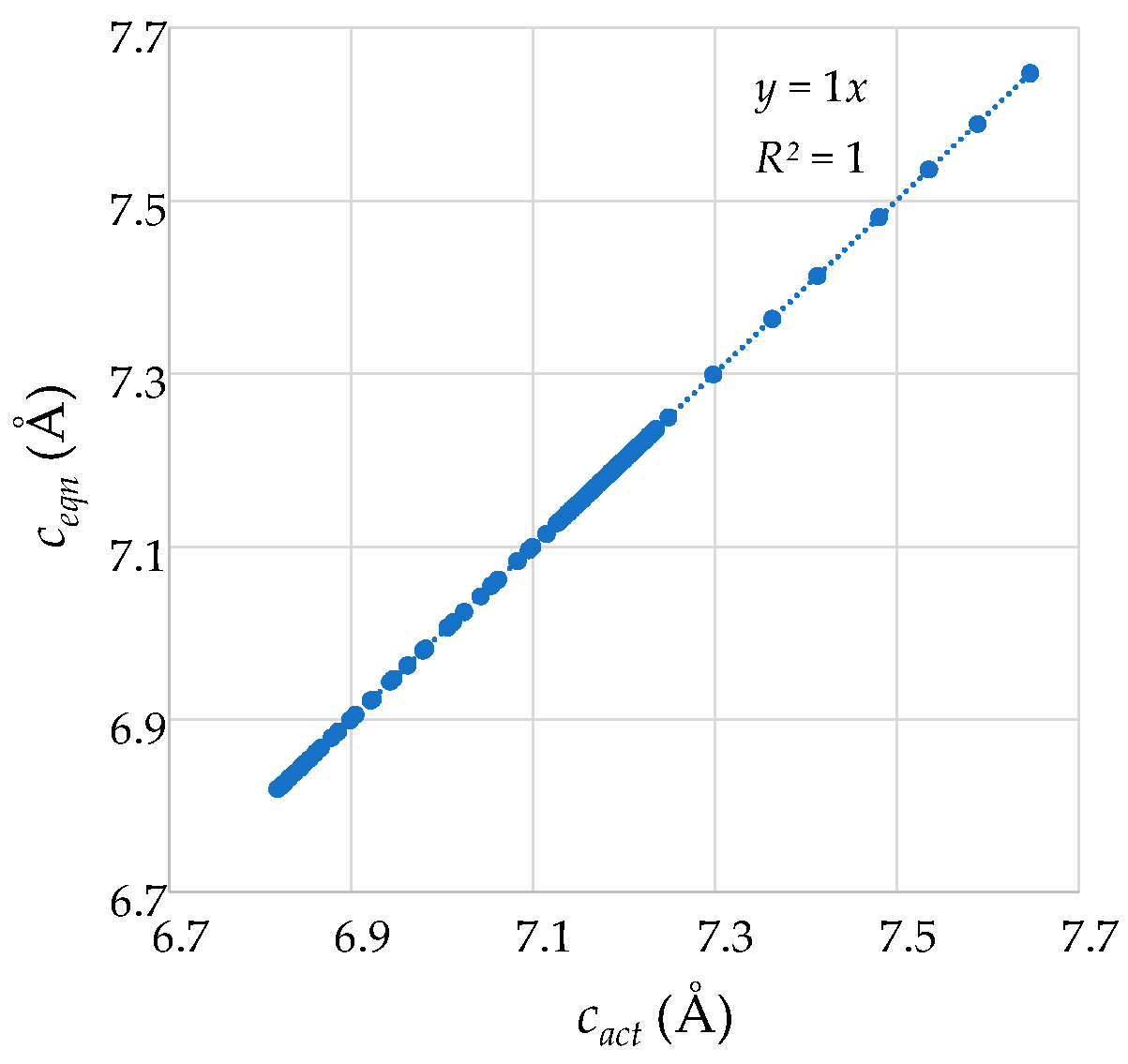
2.2.2. Quantitative Comparison and Verification of Derivation
| Schulze [2] | Haines [3] | Simulated | Schulze [2] | Haines [3] | Simulated | |||
|---|---|---|---|---|---|---|---|---|
| Set 1 | O1-A1-O3, O5-A2-O7 | 111.4 | 114.1 | 115.2 | O3-B1-O1, O7-B2-O5 | 113.2 | 111.0 | 113.9 |
| O2-A1-O4, O6-A2-O8 | 111.4 | 114.1 | 115.2 | O8-B1-O6, O4-B2-O2 | 113.2 | 111.0 | 113.9 | |
| Set 2 | O1-A1-O2, O5-A2-O6 | 108.5 | 107.2 | 106.7 | O3-B1-O8, O7-B2-O4 | 107.6 | 108.7 | 107.3 |
| O2-A1-O3, O6-A2-O7 | 108.5 | 107.2 | 106.7 | O8-B1-O1, O4-B2-O5 | 107.6 | 108.7 | 107.3 | |
| O3-A1-O4, O7-A2-O8 | 108.5 | 107.2 | 106.7 | O1-B1-O6, O5-B2-O2 | 107.6 | 108.7 | 107.3 | |
| O4-A1-O1, O8-A2-O5 | 108.5 | 107.2 | 106.7 | O6-B1-O3, O2-B2-O7 | 107.6 | 108.7 | 107.3 | |
| Sum (degrees): | 656.9 | 657.0 | 657.1 | Sum (degrees): | 657.0 | 656.8 | 657.0 |
| Schulze [2] | Haines [3] | Simulated | ||
|---|---|---|---|---|
| Bond lengths, as measured | la (Å) | 1.544 | 1.511 | 1.695 |
| lb (Å) | 1.436 | 1.481 | 1.479 | |
| Bond angles, as measured | θa (deg.) | 111.4 | 114.1 | 115.2 |
| θb (deg.) | 113.2 | 111.0 | 113.9 | |
| θ3d (deg.) | 132.6 | 132.0 | 128.6 | |
| Tetrahedral heights | ha (Å) | 1.740 | 1.644 | 1.816 |
| hb (Å) | 1.580 | 1.679 | 1.614 | |
| Tetrahedral Set 1 edges | da (Å) | 2.550 | 2.535 | 2.862 |
| /Square Diagonals | db (Å) | 2.399 | 2.441 | 2.479 |
| θ2d (deg.) | 122.1 | 121.4 | 118.0 | |
| Projected Squares | sa (Å) | 1.803 | 1.793 | 2.024 |
| sb (Å) | 1.696 | 1.726 | 1.753 | |
| θs (deg.) | 32.1 | 31.4 | 28.0 | |
| Unit Cell parameters * | a, b (Å) | 4.332 (4.332) | 4.340 (4.340) | 4.582 (4.582) |
| c (Å) | 6.640 (6.640) | 6.647 (6.647) | 6.859 (6.859) | |
| α,β,γ (deg.) | 90 | 90 | 90 |
3. Boron Arsenate at Non-Ambient Pressures
3.1. General Considerations
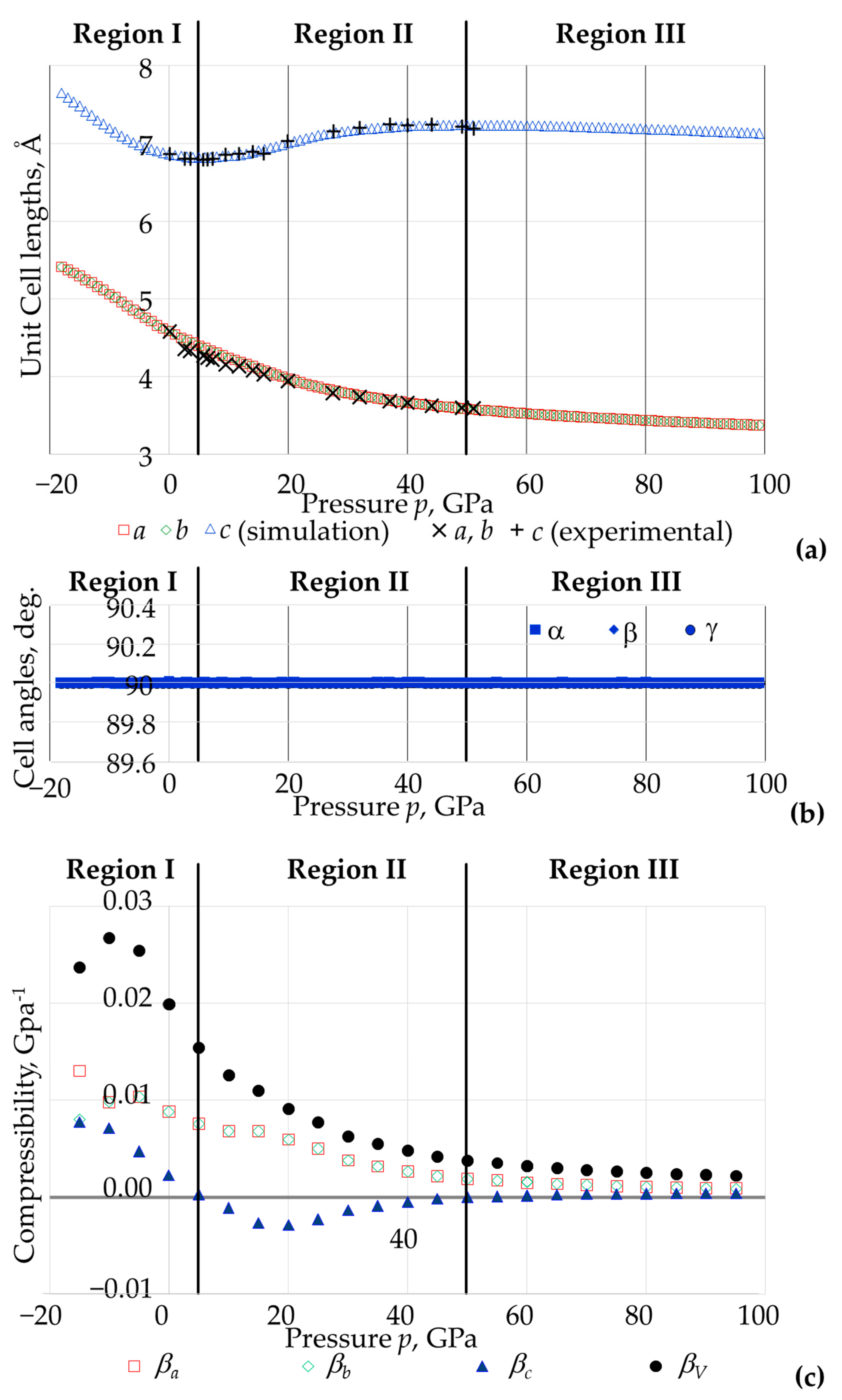
3.2. The Effect of Pressure on the Overall Size and Shape of the Unit Cell in Terms of Lattice Constants and Compressibility
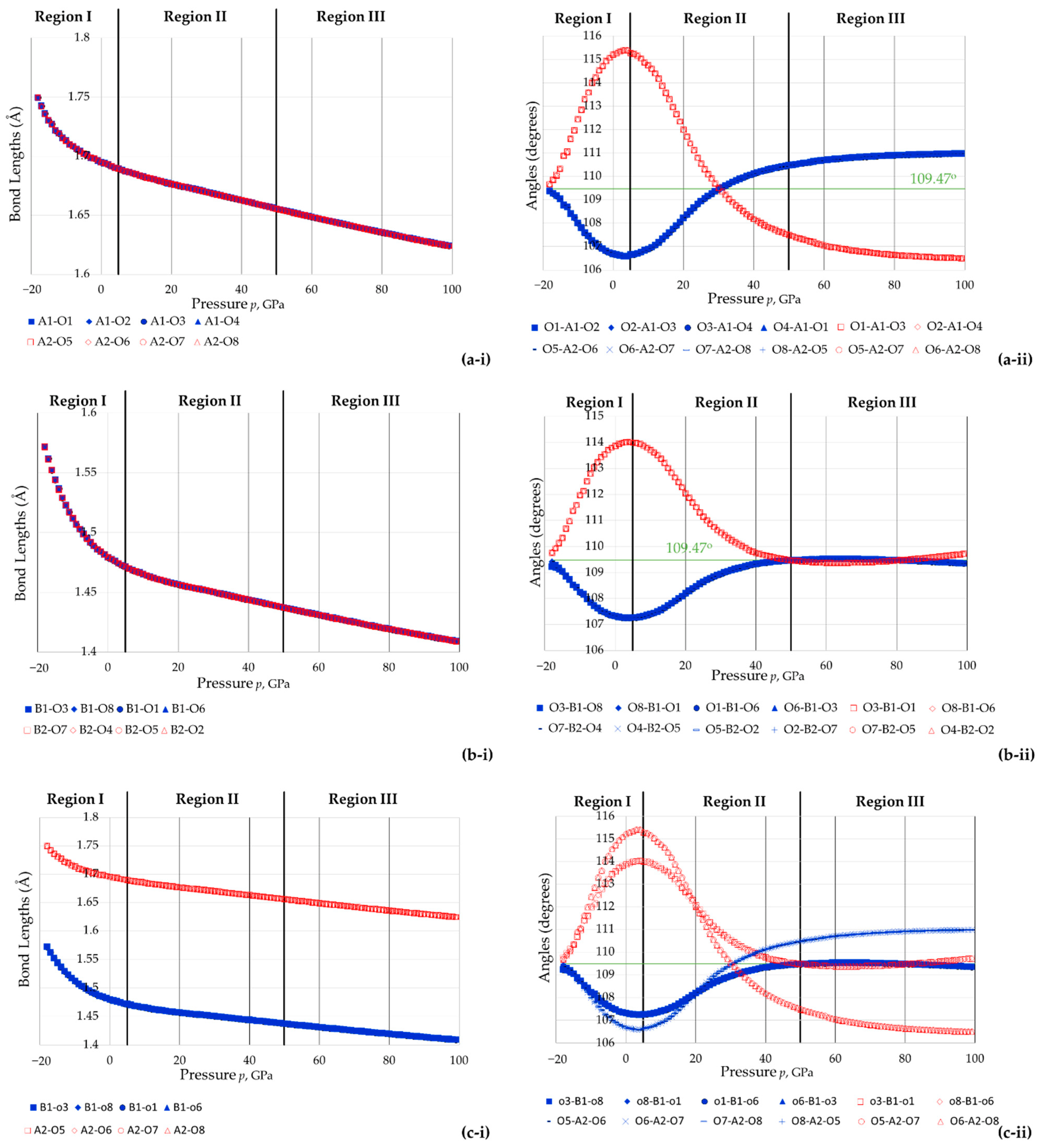
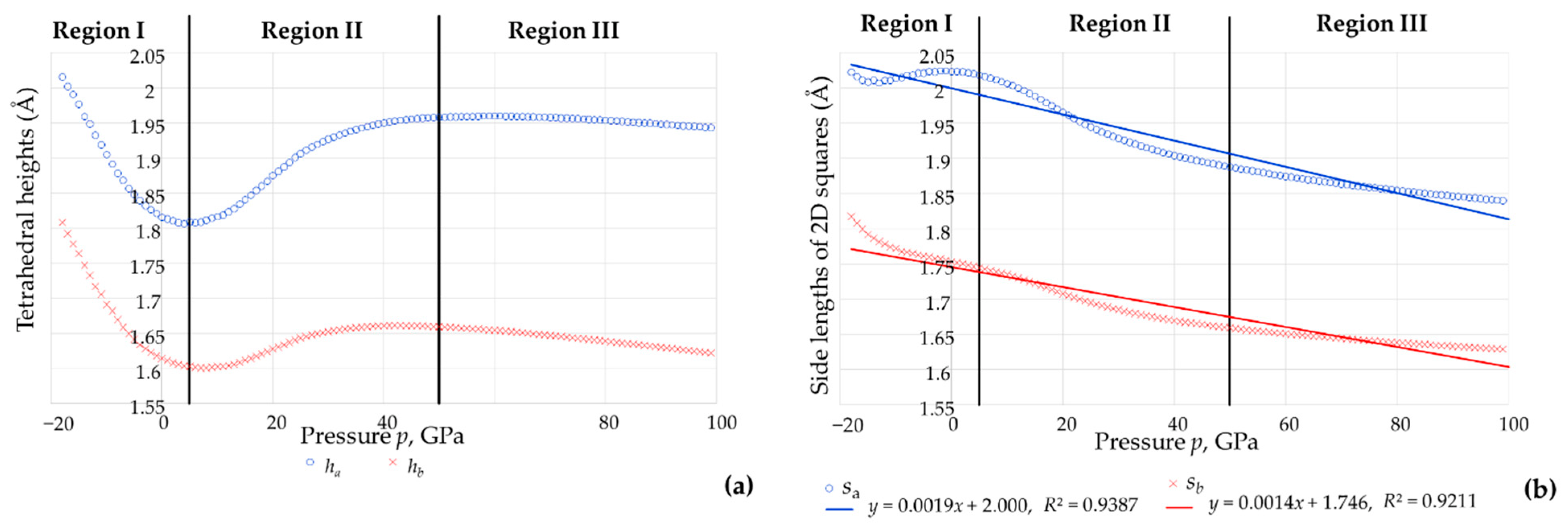
3.3. The Effect of Pressure on the Shape and Size of The BO4 and AsO4 Tetrahedra
- (i)
- The eight As-O bonds remain of equal length, as do the eight B-O bonds;
- (ii)
- The bond angles were found to retain their equality characteristics and could be divided into two types, Set 1 (shown in red in the graphs) and Set 2 (shown in blue in the graphs);
- (iii)
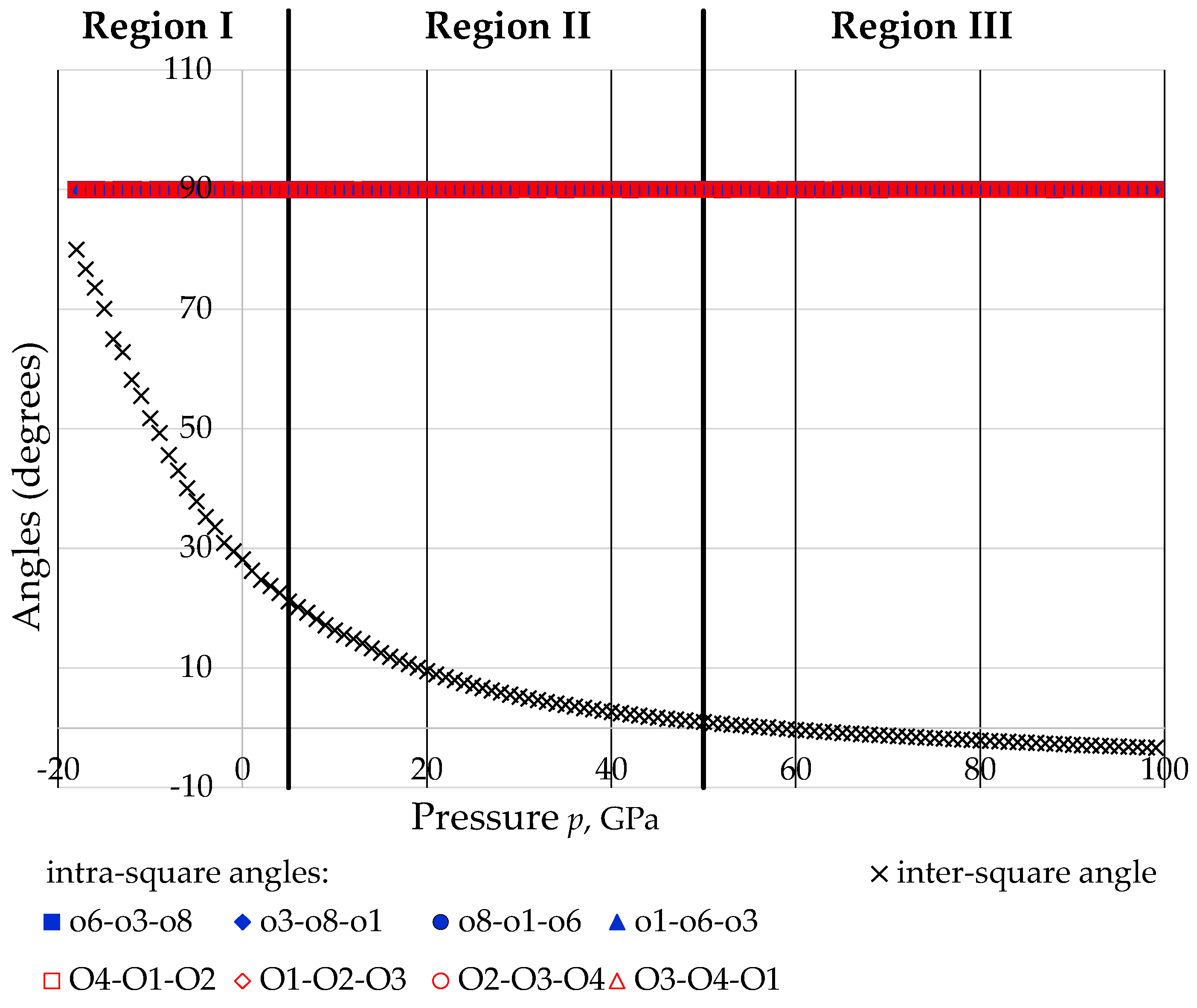
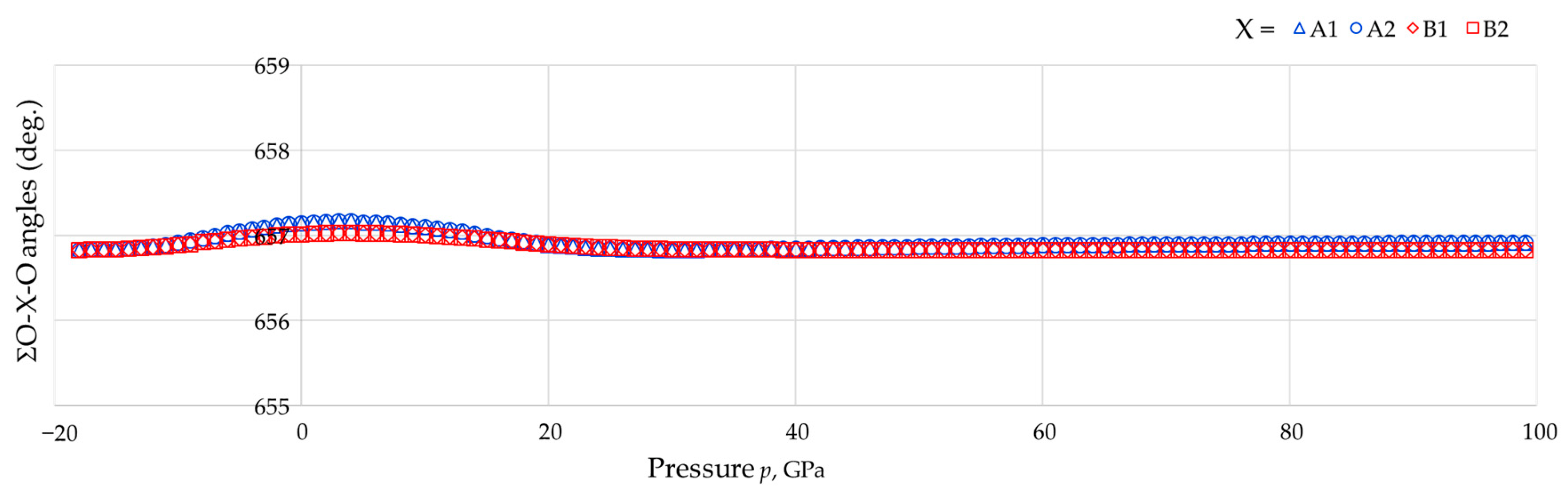
- For each tetrahedron, the sum of the six angles O-As-O or O-B-O remain at approximately 657° throughout the whole range of pressures studied (see Figure 8, average: 656.89°, standard deviation: 0.08°, difference between maximum and minimum value: 0.34°).
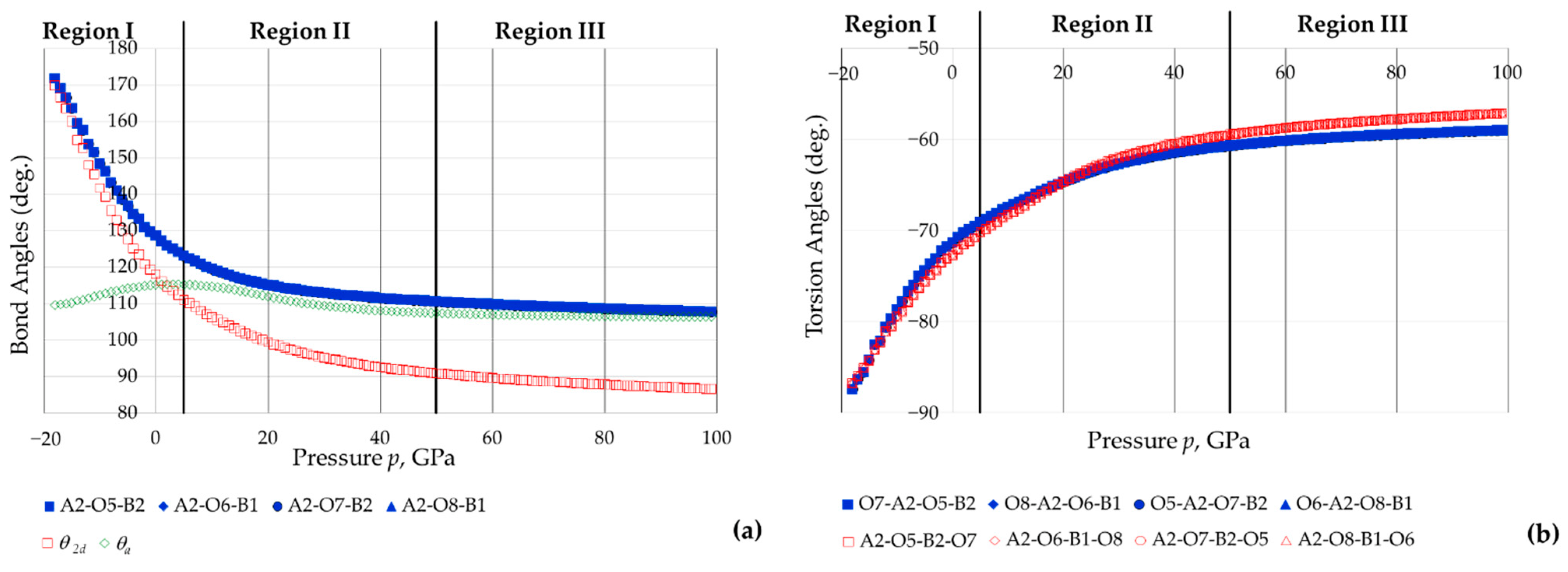
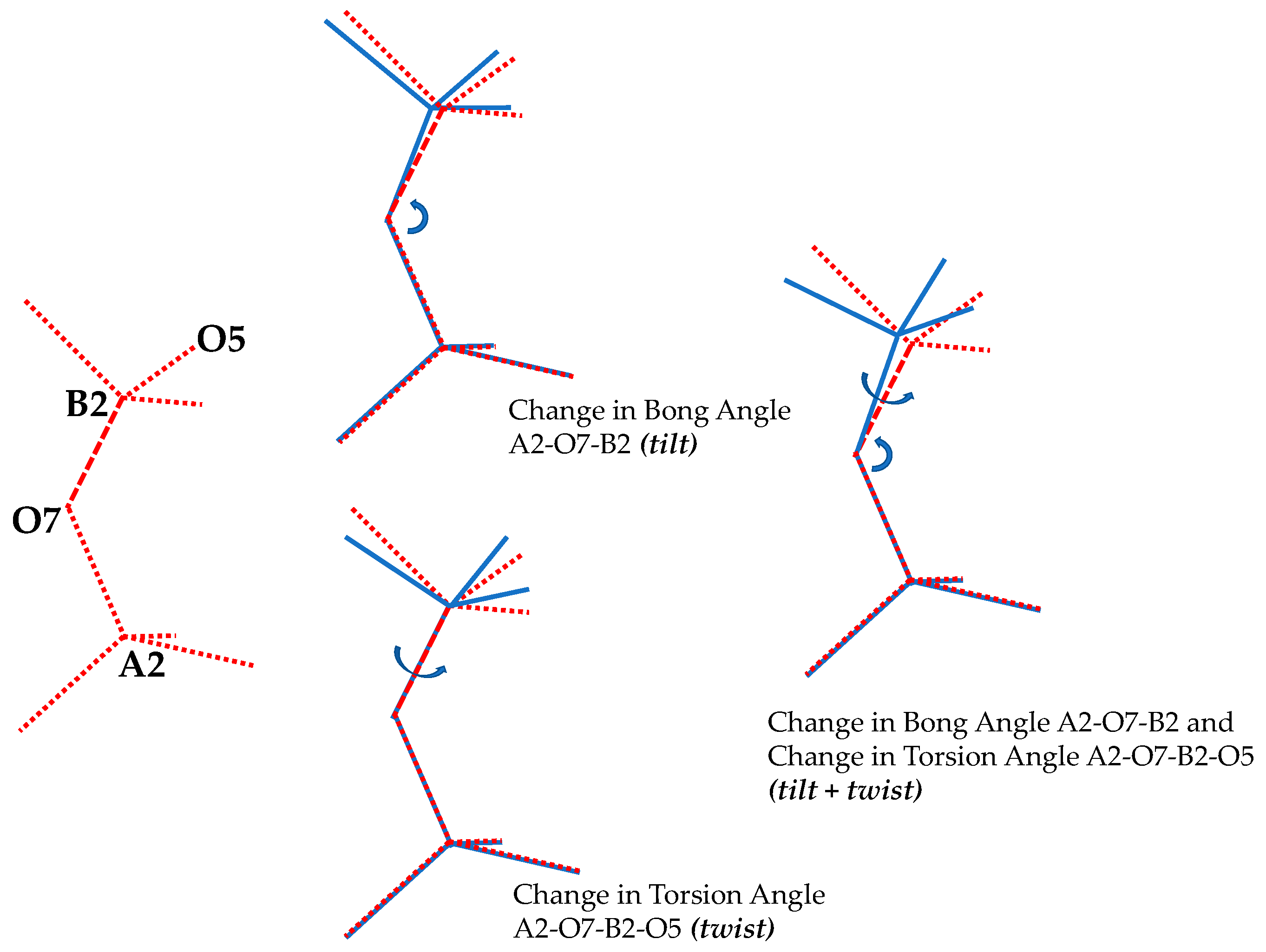
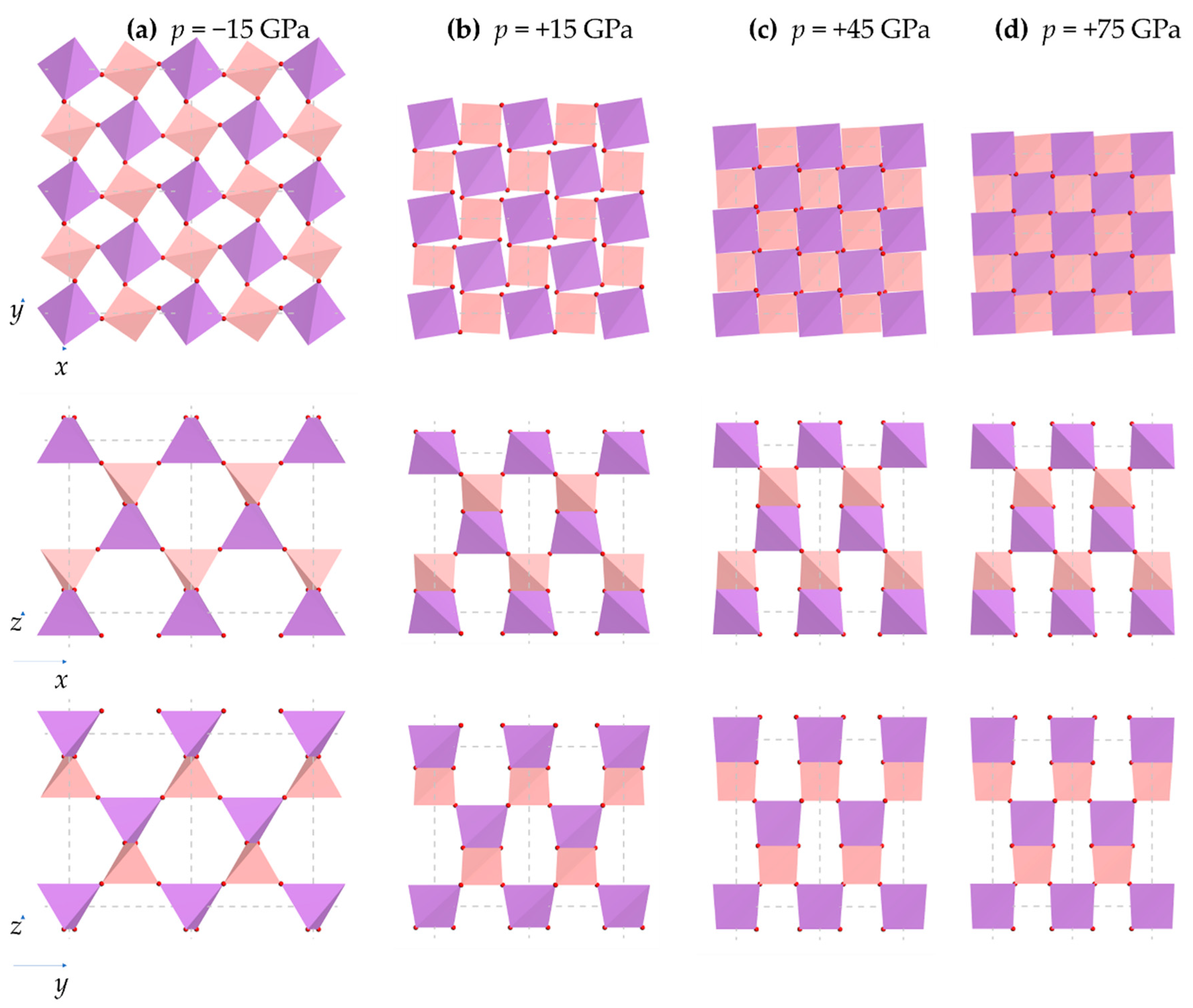
3.4. The Effect of Pressure on the Orientation of the BO4 and AsO4 Tetrahedra
- (i)
- All the As-O-B inter-tetrahedral bond angles remain equal to each other throughout the range of pressures considered, and that there is a monotonic decrease in these angles with an increase in pressure;
- (ii)
- (iii)
- (iv)
- There is extensive change in the angles between the 2D projected squares (the ‘inter-square’ angle) with practically no change in the 90° intra-square angles (see Figure 11).
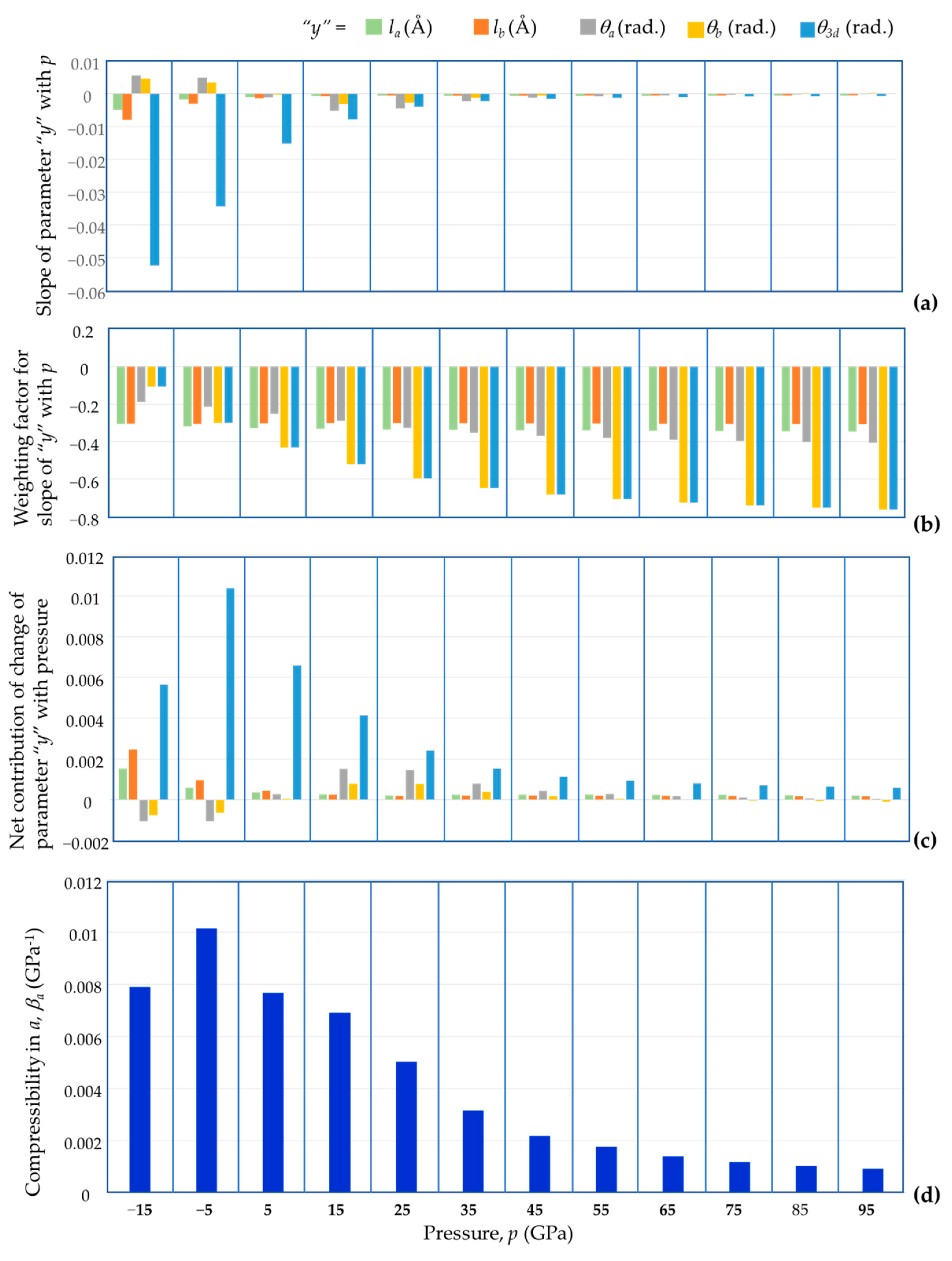
4. Discussion
- (1)
- The manner how these four parameters change with pressure, which is directly relatable to the slope of the parameter with pressure;
- (2)
- The ‘weighting’ that needs to be given to this change in parameter to the overall deformation.
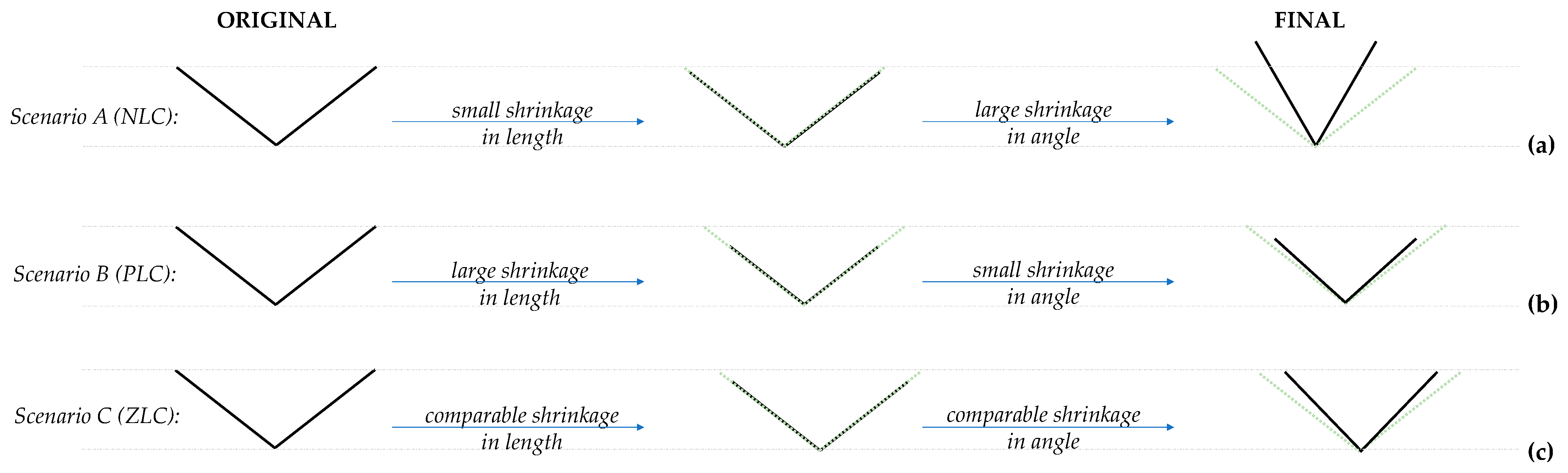
- (i)
- Positive slopes in the variation with the bond length with pressure, which is not the case, since these slopes are always negative for BAsO4 (and most other known materials), signifying that the bond lengths are shrinking with an increase in pressure, and/or
- (ii)
- Negative slopes in the variation of the specific angular values θa and θb with pressure, which is the case for BAsO4.
- (1)
- Reported the predicted compressibility of BAsO4 over a much wider range of pressures compared to what was reported before, including very extreme pressures;
- (2)
- Identified three rather distinct regions with different compressibility characteristics in c direction (one NLC region, two PLC regions);
- (3)
- Analysed the structure of BAsO4 from a purely geometric perspective, in the process revealing various interesting features such as the tetrahedra are tetragonal disphenoids, a shape which is retained over a very wide range of pressure;
- (4)
- Developed a new approach for examining compressibility by presenting a mathematical parametric model based on geometric and mechanistic considerations which permit the quantification of the relative contributions to the overall compressibility, both positive and negative, thus be able to unlock in a quantifiable manner what gives rise to NLC or otherwise;
- (5)
- Proved in a quantitative manner than the proposed ‘demi wine-rack’ mechanisms involving tetrahedra deformations is indeed the mechanisms which leads to NLC, rather than the more conspicuous tetrahedra rotations;
- (6)
- Verified that the rule proposed around two decades ago by McNelis and Blandino [60] concerning tetrahedral bond angles is not just applicable at ambient pressures but also at the extreme pressures such as the ones applied here.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calculation Method: DFT Simulation of BAsO4 at Ambient and On-Ambient Pressures
Appendix B
References
- Schulze, G.E.R. Die Kristallstruktur von BPO4 und BAsO4. Naturwissenschaften 1933, 21, 562. [Google Scholar] [CrossRef]
- Schulze, G. Die Kristallstruktur von BPO4 und BAsO4. Z. Phys. Chem. 1934, B24, 215–240. [Google Scholar] [CrossRef]
- Haines, J.; Chateau, C.; Bogicevic, C.; Hull, S.; Klug, D.D.; Léger, J.M.; Tse, J.S. Collapsing Cristobalitelike Structures in Silica Analogues at High Pressure. Phys. Rev. Lett. 2003, 91, 015503. [Google Scholar] [CrossRef] [PubMed]
- Grima-Cornish, J.N.; Vella-Żarb, L.; Grima, J.N. Negative Linear Compressibility and Auxeticity in Boron Arsenate. Ann. Phys. 2020, 532, 1900550. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Vella-Żarb, L.; Grima, J.N. On the behaviour of β-cristobalite-like BAsO4 when subjected to uniaxial loading in its [001] direction and the implications on its ‘negative’ characteristics. Phys. Stat. Sol. B 2021, 258, 2000326. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Vella-ZŻarb, L.; Wojciechowski, K.W.; Grima, J.N. Shearing Deformations of β-Cristobalite-Like Boron Arsenate. Symmetry 2021, 13, 977. [Google Scholar] [CrossRef]
- Baughman, R.H.; Stafström, S.; Cui, C.; Dantas, S.O. Materials with negative compressibilities in one or more dimensions. Science 1998, 279, 1522–1524. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Attard, D.; Grima, J.N.; Evans, K.E. Auxetic Behavior and Other Negative Thermomechanical Properties from Rotating Rigid Units. Phys. Stat. Sol. RRL 2021, 16, 2100322. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Deformation mechanisms leading to auxetic behaviour in the α-cristobalite and α-quartz structures of both silica and germania. J. Phys. Condens. Matter 2008, 21, 025401. [Google Scholar] [CrossRef] [Green Version]
- Alderson, A.; Evans, K.E. Molecular Origin of Auxetic Behavior in Tetrahedral Framework Silicates. Phys. Rev. Lett. 2002, 89, 225503. [Google Scholar] [CrossRef]
- Nazaré, F.; Alderson, A. Models for the prediction of Poisson’s ratio in the ‘α-cristobalite’ tetrahedral framework. Phys. Stat. Sol. B 2015, 252, 1465–1478. [Google Scholar] [CrossRef]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Sci. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Lim, T.-C. Auxetic Materials and Structures, 1st ed.; Springer: Singapore, 2015; ISBN 978-981-287-274-6. [Google Scholar]
- Cairns, A.B.; Goodwin, A.L. Negative linear compressibility. Phys. Chem. Chem. Phys. 2015, 17, 20449–20465. [Google Scholar] [CrossRef] [Green Version]
- Kolken, H.M.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef] [Green Version]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Strek, T.; Maruszewski, B.T.; Narojczyk, J.W.; Wojciechowski, K.W. Finite element analysis of auxetic plate deformation. J. Non-Cryst. Solids 2008, 354, 4475–4480. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Poisson’s ratio of simple planar ‘isotropic’ solids in two dimensions. Phys. Stat. Sol. B 2007, 244, 1038–1046. [Google Scholar] [CrossRef]
- Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Tretiakov, K.V.; Kowalik, M. Elastic properties of dense solid phases of hard cyclic pentamers and heptamers in two dimensions. Phys. Rev. E 2003, 67, 036121. [Google Scholar] [CrossRef] [Green Version]
- Caddock, B.D.; Evans, K.E. Microporous materials with negative Poisson’s ratios. I. Microstructure and mechanical properties. J. Phys. D Appl. Phys. 1989, 22, 1877–1882. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Monte Carlo simulation of two-dimensional hard body systems with extreme values of the Poisson’s ratio. Phys. Stat. Sol. B 2005, 242, 730–741. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Grima, J.N.; Attard, D. Negative Mechanical Materials and Metamaterials: Giant Out-of-Plane Auxeticity from Multi- Dimensional Wine-Rack-like Motifs. MRS Adv. 2020, 5, 717–725. [Google Scholar] [CrossRef]
- Brańka, A.C.; Heyes, D.M.; Wojciechowski, K.W. Auxeticity of cubic materials under pressure. Phys. Stat. Sol. B 2011, 248, 96–104. [Google Scholar] [CrossRef]
- Grima-Cornish, J.N.; Grima, J.N.; Attard, D. A Novel Mechanical Metamaterial Exhibiting Auxetic Behavior and Negative Compressibility. Materials 2019, 13, 79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bezazi, A.; Scarpa, F.; Remillat, C. A novel centresymmetric honeycomb composite structure. Compos. Struct. 2005, 71, 356–364. [Google Scholar] [CrossRef]
- Grima, J.N.; Mizzi, L.; Azzopardi, K.M.; Gatt, R. Auxetic Perforated Mechanical Metamaterials with Randomly Oriented Cuts. Adv. Mater. 2015, 28, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Hewage, T.; Alderson, K.L.; Alderson, A.; Scarpa, F. Double-Negative Mechanical Metamaterials Displaying Simultaneous Negative Stiffness and Negative Poisson’s Ratio Properties. Adv. Mater. 2016, 28, 10323–10332. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R. Perforated Sheets Exhibiting Negative Poisson’s Ratios. Adv. Eng. Mater. 2010, 12, 460–464. [Google Scholar] [CrossRef]
- Milton, G.W. Complete characterization of the macroscopic deformations of periodic unimode metamaterials of rigid bars and pivots. J. Mech. Phys. Solids 2013, 61, 1543–1560. [Google Scholar] [CrossRef] [Green Version]
- Farrugia, P.S.; Gatt, R.; Grima, J.N. The push drill mechanism as a novel method to create 3D mechanical metamaterial structures. Phys. Stat. Sol. RRL 2020, 14, 2000125. [Google Scholar] [CrossRef]
- Attard, D.; Farrugia, P.S.; Gatt, R.; Grima, J.N. Starchirals—A novel class of auxetic hierarchal structures. Int. J. Mech. Sci. 2020, 179, 105631. [Google Scholar] [CrossRef]
- Sigmund, O. Tailoring materials with prescribed elastic properties. Mech. Mater. 1995, 20, 351–368. [Google Scholar] [CrossRef]
- Gatt, R.; Mizzi, L.; Azzopardi, J.I.; Azzopardi, K.M.; Attard, D.; Casha, A.; Briffa, J.; Grima, J.N. Hierarchical Auxetic Mechanical Metamaterials. Sci. Rep. 2015, 5, 8395. [Google Scholar] [CrossRef] [Green Version]
- Mizzi, L.; Mahdi, E.M.; Titov, K.; Gatt, R.; Attard, D.; Evans, K.E.; Grima, J.N.; Tan, J.-C. Mechanical metamaterials with star-shaped pores exhibiting negative and zero Poisson’s ratio. Mater. Des. 2018, 146, 28–37. [Google Scholar] [CrossRef]
- Airoldi, A.; Fournier, S.; Borlandelli, E.; Bettini, P.; Sala, G. Design and manufacturing of skins based on composite corrugated laminates for morphing aerodynamic surfaces. Smart Mater. Struct. 2017, 26, 045024. [Google Scholar] [CrossRef]
- Shan, S.; Kang, S.H.; Zhao, Z.; Fang, L.; Bertoldi, K. Design of planar isotropic negative Poisson’s ratio structures. Extrem. Mech. Lett. 2015, 4, 96–102. [Google Scholar] [CrossRef]
- Taylor, M.; Francesconi, L.; Gerendás, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low Porosity Metallic Periodic Structures with Negative Poisson’s Ratio. Adv. Mater. 2013, 26, 2365–2370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, P.; Shofner, M.L.; Griffin, A.C. Deconstructing the auxetic behavior of paper. Phys. Stat. Sol. B 2013, 251, 289–296. [Google Scholar] [CrossRef]
- Dmitriev, S.V. Auxetic Behavior of Crystals from Rotational Degrees of Freedom. Ferroelectrics 2007, 349, 33–44. [Google Scholar] [CrossRef]
- Ishibashi, Y.; Iwata, M. A Microscopic Model of a Negative Poisson’s Ratio in Some Crystals. J. Phys. Soc. Jpn. 2000, 69, 2702–2703. [Google Scholar] [CrossRef]
- Baughman, R.H.; Galvão, D.S.; Galv, D.S. Crystalline networks with unusual predicted mechanical and thermal properties. Nature 1993, 365, 735–737. [Google Scholar] [CrossRef]
- Lim, T.-C. 2D Structures Exhibiting Negative Area Compressibility. Phys. Stat. Sol. B 2017, 254, 1600682. [Google Scholar] [CrossRef]
- Cairns, A.B.; Thompson, A.L.; Tucker, M.G.; Haines, J.; Goodwin, A.L. Rational Design of Materials with Extreme Negative Compressibility: Selective Soft-Mode Frustration in KMn[Ag(CN)2]3. J. Am. Chem. Soc. 2011, 134, 4454–4456. [Google Scholar] [CrossRef]
- Gatt, R.; Grima, J.N. Negative compressibility. Phys. Stat. Sol. RRL 2008, 2, 236–238. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Gatt, R. Truss-type systems exhibiting negative compressibility. Phys. Stat. Sol. B 2008, 245, 2405–2414. [Google Scholar] [CrossRef]
- Degabriele, E.P.; Attard, D.; Grima-Cornish, J.N.; Caruana-Gauci, R.; Gatt, R.; Evans, K.E.; Grima, J.N. On the Compressibility Properties of the Wine-Rack-Like Carbon Allotropes and Related Poly(phenylacetylene) Systems. Phys. Stat. Sol. B 2018, 256, 1800572. [Google Scholar] [CrossRef] [Green Version]
- Qu, J.; Kadic, M.; Wegener, M. Poroelastic metamaterials with negative effective static compressibility. Appl. Phys. Lett. 2017, 110, 171901. [Google Scholar] [CrossRef]
- Lakes, R.; Wojciechowski, K.W. Negative compressibility, negative Poisson’s ratio, and stability. Phys. Stat. Sol. B 2008, 245, 545–551. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Auxetic materials and their potential applications in textiles. Text. Res. J. 2014, 84, 1600–1611. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater. Struct. 2016, 25, 065012. [Google Scholar] [CrossRef]
- Ali, M.N.; Busfield, J.J.C.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. J. Mater. Sci. Mater. Med. 2013, 25, 527–553. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Für Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Coxeter, H.S.M. Regular Polytopes; Methuen & Co. Ltd.: London, UK, 1947. [Google Scholar]
- McNelis, E.; Blandino, M. 657, a method for estimating tetrahedral bond angles. N. J. Chem. 2001, 25, 772–774. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grima-Cornish, J.N.; Vella-Żarb, L.; Grima, J.N.; Evans, K.E. A DFT-Based Quantitative and Geometric Analysis of the Effect of Pressure on Boron Arsenate. Materials 2022, 15, 4858. https://doi.org/10.3390/ma15144858
Grima-Cornish JN, Vella-Żarb L, Grima JN, Evans KE. A DFT-Based Quantitative and Geometric Analysis of the Effect of Pressure on Boron Arsenate. Materials. 2022; 15(14):4858. https://doi.org/10.3390/ma15144858
Chicago/Turabian StyleGrima-Cornish, James N., Liana Vella-Żarb, Joseph N. Grima, and Kenneth E. Evans. 2022. "A DFT-Based Quantitative and Geometric Analysis of the Effect of Pressure on Boron Arsenate" Materials 15, no. 14: 4858. https://doi.org/10.3390/ma15144858








