Analytical Model for Early Design Stage of Cable-Stayed Suspension Bridges Based on Hellinger–Reissner Variational Method
Abstract
1. Introduction
2. Mechanical Model for Early Design Stage
- (1)
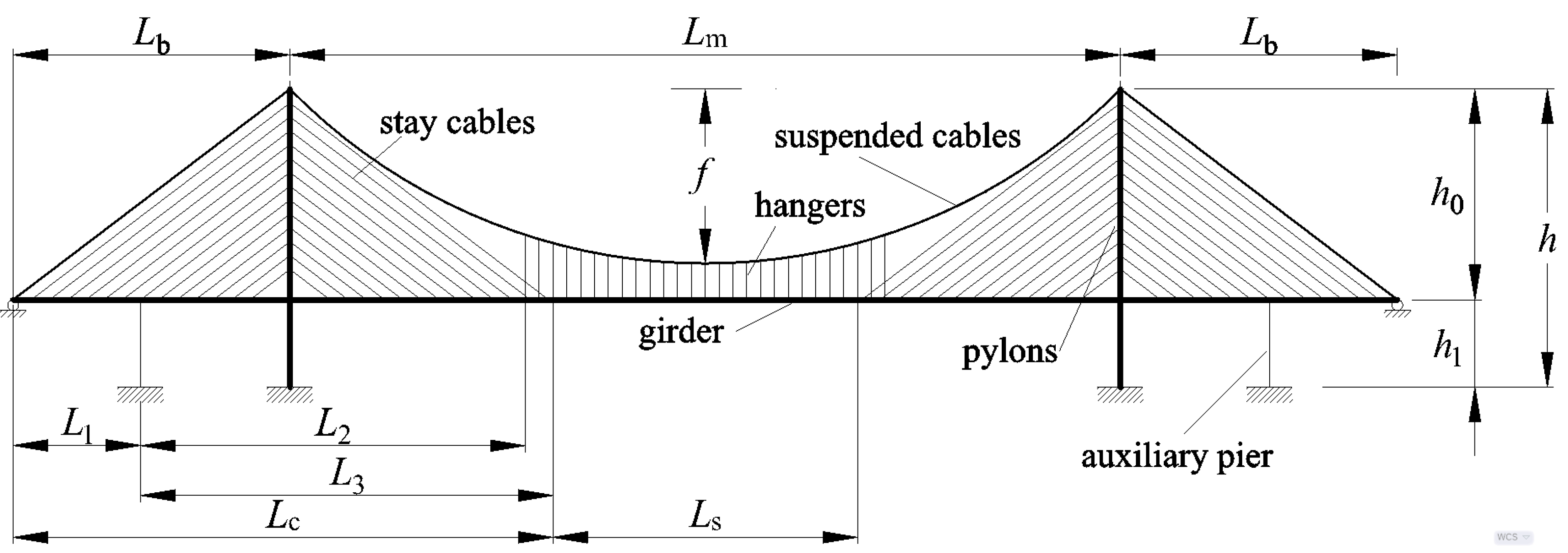
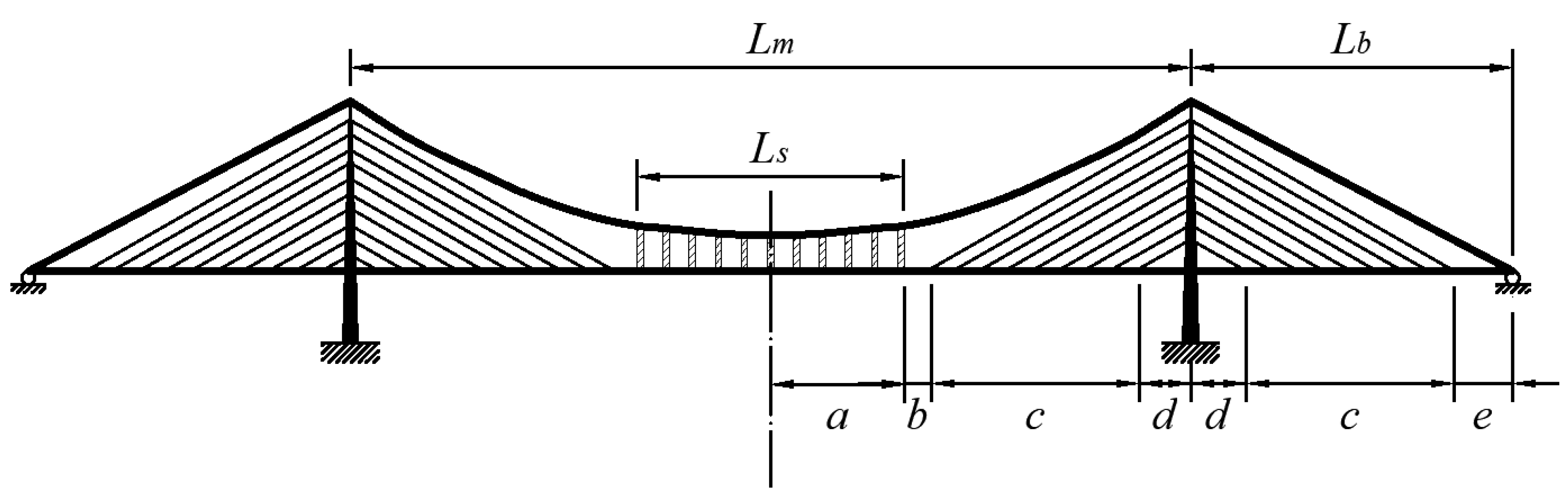
- A symmetrical three-span cable-stayed suspension bridge with two pylons is taken as an example to analyze this type of bridge, as shown in Figure 1. The girder of the suspension and girder of the cable-stayed part are linked continuously. The fully floating deck system is considered in the analysis because of the presence of the auxiliary pier on the side span. This means that the pylon and girder in this case are not connected with any linkage vertically and longitudinally, but are still coupled in the lateral direction. Otherwise, without any auxiliary pier, the semi-floating deck system is applied here to simulate the additional linkage connecting the girder and pylon in the vertical direction.
- (2)
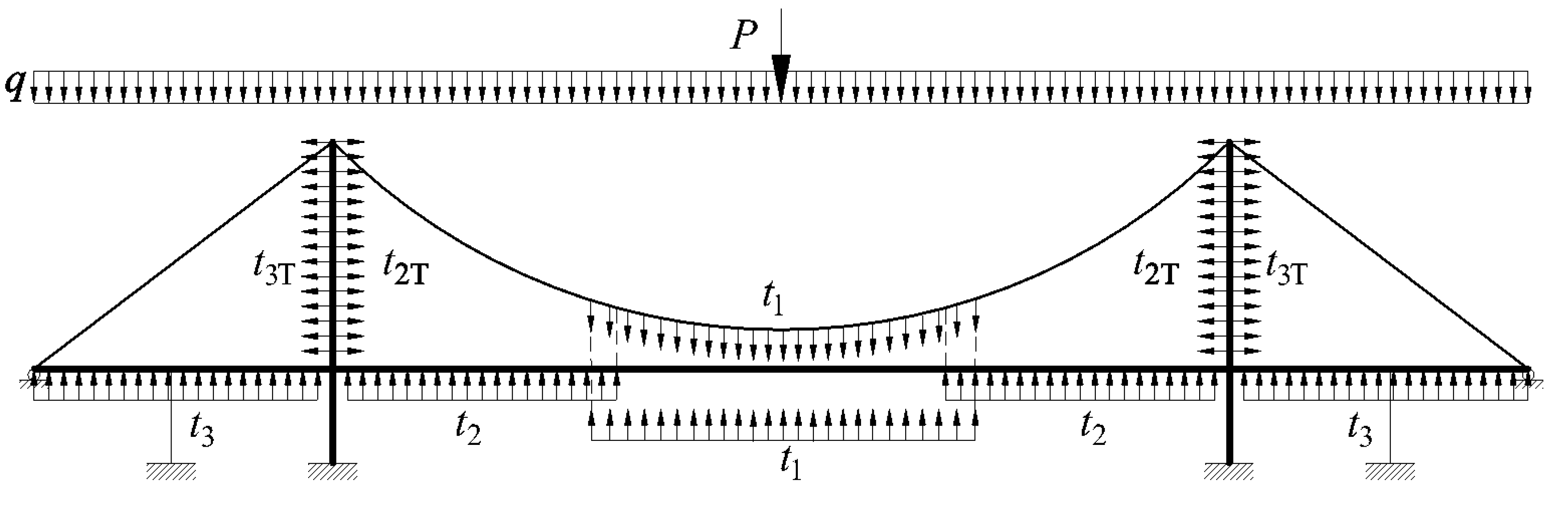
- The hangers and stay cables are distributed uniformly along the girder of the suspension and girder of the cable-stayed part, respectively. According to the membrane analogy, the force effects of the hangers and cables could be equivalent to those of a membrane between the catenary and girder. The rationality of this step is also supported by the results of a previous study [16]. As shown in Figure 2, the forces in the hangers can be replaced by a uniformly distributed load t1. Meanwhile, for the stay cables connecting the pylon and girder in the main span, the forces in the stay cables are equivalent to the uniformly distributed load t2 acting on the girder and t2T acting on the pylon. Similarly, in the side span, the forces in the stay cables are changed into a uniformly distributed load t3 acting on the girder and t3T acting on the pylon.
- (3)
- The live load caused by traffic and walking people could be replaced by a distributed load and concentrated load for static analysis. Meanwhile, the dead load of the bridge could also be equivalent to a uniformly distributed load. According to the superimposition principle, the load on the bridge can be assumed to be a combination of the distributed load q and concentrated load P, as shown in Figure 2. The different combinations of the distributed load q and concentrated load P are considered in the following calculation.
- (4)
- The axial force and deformation of either the main beam or pylon are neglected. Hence, the corresponding terms of the strain energy are also neglected. The effect of the shear force of the main beam and pylon is also not considered here. The strain energy of the auxiliary pier is neglected.
3. Analysis
- (1)
- Trial functions of force and deformation should be proposed first with the coefficients to be solved. In this stage, the engineer is required to have the basic knowledge about how the structural members would deform with the load.
- (2)
- The trial functions are then applied to the Hellinger–Reissner principle to obtain the expression of the functional.
- (3)
- Partial differential equations for individual coefficients are obtained.
- (4)
- The deformation compatibility conditions are introduced to obtain the following equations.
- (5)
- By combining the equations from Step 3 and Step 4, the expressions of the coefficients are obtained by solving the equation sets.
- (6)
- By employing the expressions of the coefficients in the trial functions of force and deformation, the force and deformation expressions are obtained.
3.1. Girder
3.1.1. Hypotheses of Trial Functions
- (1)
- Force functions:
- (2)
- Deformation function:
3.1.2. Derivation of Equations
- (1)
- For the cable-stayed part from 0 to L1, as shown in Figure 1, which is also from 0 to L1 in the local coordinate system, the deformation and force assumptions are described as follows:
- (2)
- For the cable-stayed part from L1 to Lc in the global coordinate system, as shown in Figure 1, the location in the local coordinate system ranges from 0 to L3. The deformation and force expressions are as follows:
- (3)
- For the suspension part from Lc to (Lc+Ls) in the global coordinate system, as shown in Figure 1, while the location is from 0 to Ls in the local coordinate system, the deformation and force expressions are as follows:
3.2. Pylon
3.3. Main Cable of the Suspension Part
3.4. External Load Effects on the Bridge
- (1)
- Effects of live load on girder:
- (2)
- Effect of membrane tension t1 on girder:
- (3)
- Effect of membrane tension t1 on main cable:
- (4)
- Effects of membrane tensions t2 and t3 on girder:
- (5)
- Effects of membrane tensions t2T and t3T on the pylon:
3.5. Total Potential Energy
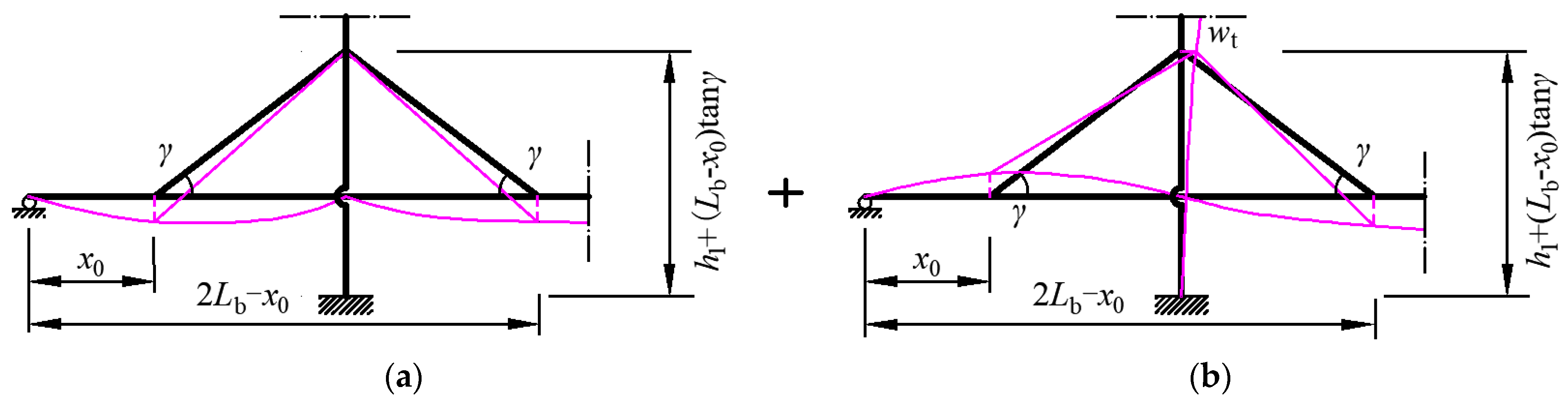
3.6. Deformation Compatibility Conditions
- (1)
- Side span:
- (2)
- Main span:
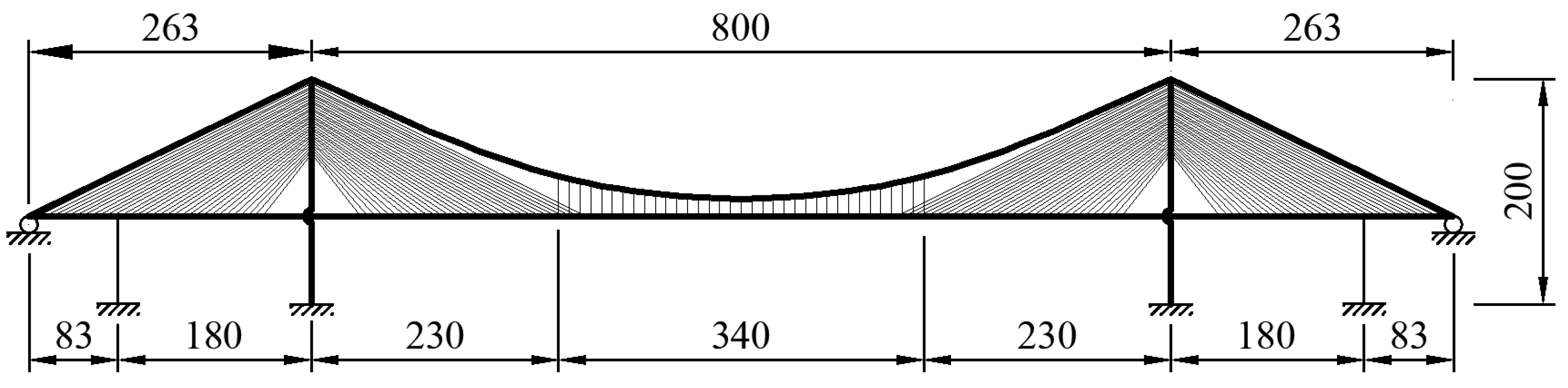
4. Verification
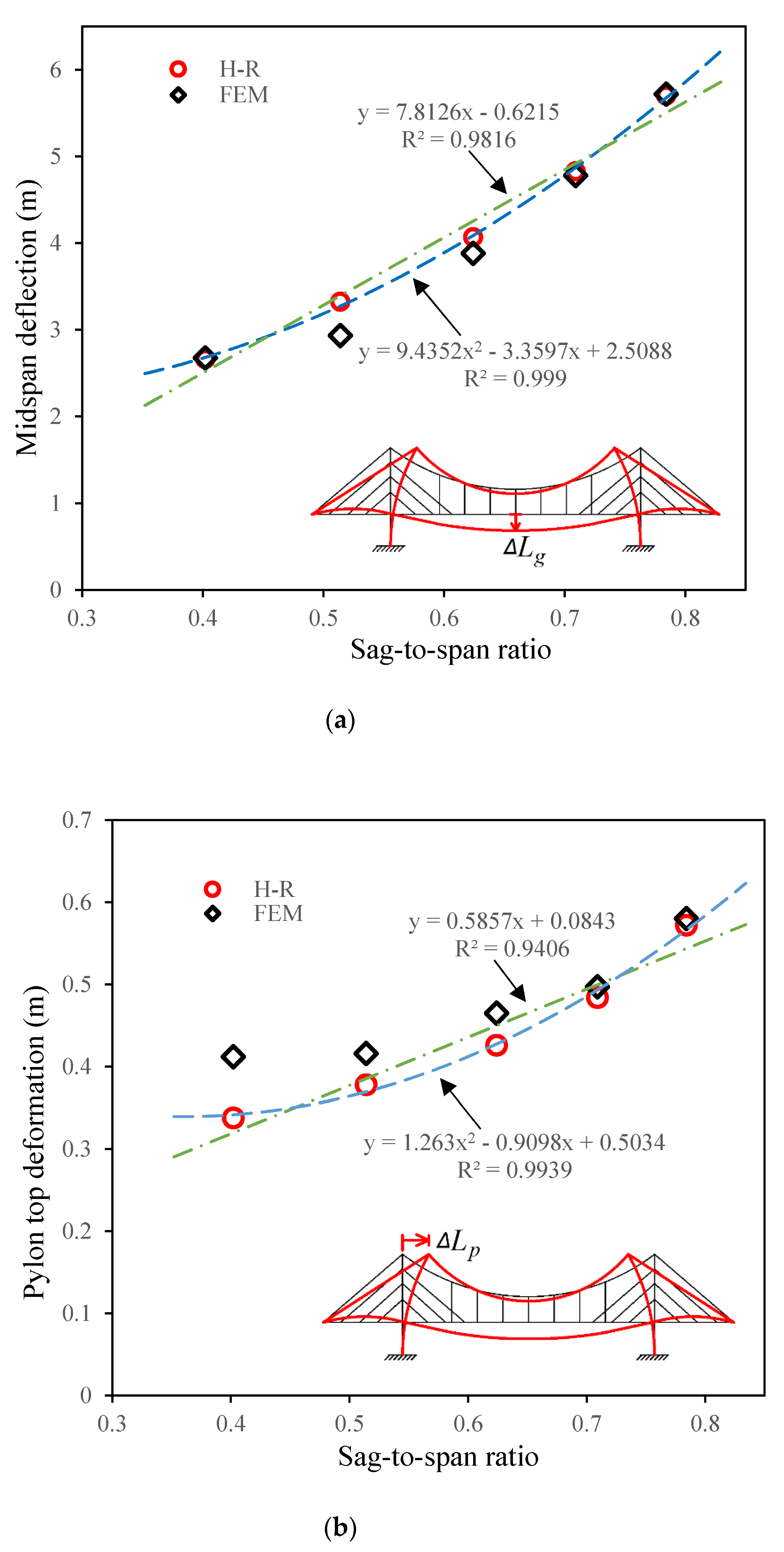
5. Sensitivity Analyses
6. Conclusions
7. Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | cross-section area |
| d | distance between stay cables |
| E | Young’s modulus |
| f | rise of the main cable |
| h | height of the pylon |
| I | inertia moment |
| M | function for bending moment |
| Lb | length of the side span |
| Lm | length of the main span |
| Ls | length of the suspension part |
| P | concentrated load on the bridge |
| q | uniformly distributed load on the bridge |
| t1 | membrane tension of hangers |
| t2 | membrane tension of stay cable on main span |
| t3 | membrane tension of stay cable on side span |
| w | function for deflection |
| Δf | elongation of the hanger |
| π | function for potential energy |
| θ | inclination angle of the stay cable |
Appendix A
References
- Gimsing, N.J. Cable Supported Bridges—Concept & Design; John Wiley & Sons: Chichester, UK, 1997. [Google Scholar]
- Sun, B.; Cai, C.S.; Xiao, R.C. Analysis strategy and parametric study of cable-stayed-suspension bridges. Adv. Struct. Eng. 2013, 16, 1081–1102. [Google Scholar] [CrossRef]
- Ito, M. Cable-Supported steel bridges: Design problems and solutions. J. Constr. Steel Res. 1996, 39, 69–84. [Google Scholar] [CrossRef]
- Ermopoulos, J.; Vlahinos, A.; Wang, Y.C. Stability analysis of cable-stayed bridges. Comput. Struct. 1992, 44, 1083–1089. [Google Scholar] [CrossRef]
- Khalil, M.S. Nonlinear analysis of cable-stayed bridges at ultimate load level. Can. J. Civ. Eng. 1996, 23, 1111–1117. [Google Scholar] [CrossRef]
- Oliveira, P.; Jose, J.; Reis, A.J. Simplified assessment of cable-stayed bridges buckling stability. Eng. Struct. 2016, 114, 93–103. [Google Scholar] [CrossRef]
- Hashemi, S.K.; Bradford, M.A.; Valipour, H.R. Dynamic response of cable-stayed bridge under blast load. Eng. Struct. 2016, 127, 719–736. [Google Scholar] [CrossRef]
- Peter, G.; Buckland, P.E. Increasing the load capacity of suspension bridges. J. Bridge Eng. 2003, 8, 288–296. [Google Scholar]
- Gwon, S.G.; Choi, D.H. Static and dynamic analyses of a suspension bridge with three-dimensionally curved main cables using a continuum model. Eng. Struct. 2018, 161, 250–264. [Google Scholar] [CrossRef]
- Xiao, X.; Xue, H.; Chen, B. Nonlinear model for the dynamic analysis of a time-dependent vehicle-cableway bridge system. Appl. Math. Model. 2021, 90, 1049–1068. [Google Scholar] [CrossRef]
- Adanur, S.; Gunaydin, M.; Altunişik, A.C.; Sevim, B. Construction stage analysis of Humber Suspension Bridge. Appl. Math. Model. 2012, 36, 5492–5505. [Google Scholar] [CrossRef]
- Irvine, H.M. Cable Structures; The MIT Press: Cambridge, UK, 1981. [Google Scholar]
- Chen, C.C.; Wu, W.H.; Chen, S.Y.; Lai, G. A novel tension estimation approach for elastic cables by elimination of complex boundary condition effects employing mode shape functions. Eng. Struct. 2018, 166, 152–166. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.C.; Chen, C.C.; Lin, T.K.; Tullini, N. Bending tests for the structural safety assessment of space truss members. Int. J. Space Struct. 2018, 33, 138–149. [Google Scholar] [CrossRef]
- Wu, W.H.; Chen, C.C.; Chen, Y.C.; Lai, G.; Huang, C.M. Tension determination for suspenders of arch bridge based on multiple vibration measurements concentrated at one end. Measurement 2018, 123, 254–269. [Google Scholar] [CrossRef]
- Konstantakopoulos, T.G.; Michaltsos, G.T. A mathematical model for a combined cable system of bridges. Eng. Struct. 2010, 32, 2717–2728. [Google Scholar] [CrossRef]
- Wang, F.; Lv, Z.D.; Gu, M.J.; Chen, Q.K.; Zhao, Z.; Luo, J. Experimental study on stability of orthotropic steel box girder of self-anchored suspension cable-stayed bridge. Thin-Walled Struct. 2021, 163, 107727. [Google Scholar] [CrossRef]
- Du, G.M. Analysis on the Structural Behavior of Large-Span Self-Anchored Cable-Stayed Suspension Bridge. Master’s Thesis, Dalian University of Technology, Dalian, China, 2006. [Google Scholar]
- Wang, H.L. Structure Properties Analysis and Experiment Study of Self-Anchored Cable-Stayed Suspension Bridge. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2006. [Google Scholar]
- Granata, M.F.; Longo, G.; Recupero, A.; Arici, M. Construction sequence analysis of long-span cable-stayed bridges. Eng. Struct. 2018, 174, 267–281. [Google Scholar] [CrossRef]
- Ding, Z. Natural Frequencies of Rectangular Plates Using a Set of Static Beam Functions in Rayleigh-Ritz Method. J. Sound Vib. 1996, 189, 81–87. [Google Scholar] [CrossRef]
- Wang, S. A Unified Timoshenko Beam B-Spline Rayleigh–Ritz Method for Vibration and Buckling Analysis of Thick And Thin Beams And Plates. Int. J. Numer. Methods Eng. 1997, 40, 473–491. [Google Scholar] [CrossRef]
- Xue, W.C.; Liu, S. Linear elastic and limit state solutions of beam string structures by the Ritz-method. Struct. Eng. Mech. 2010, 35, 67–82. [Google Scholar] [CrossRef]
- Kiani, Y. Analysis of FG-CNT reinforced composite conical panel subjected to moving load using Ritz method. Thin-Walled Struct. 2017, 119, 47–57. [Google Scholar] [CrossRef]
- Albas, S.D.; Ersoy, H.; Akgoz, B.; Civalek, O. Dynamic Analysis of a Fiber-Reinforced Composite Beam under a Moving Load by the Ritz Method. Mathematics 2021, 9, 1048. [Google Scholar]
- Belardi, V.G.; Fanelli, P.; Vivio, F. Elastic analysis of rectilinear orthotropic composite circular plates subject to transversal and in-plane load conditions using Ritz method. Compos. Struct. 2018, 199, 63–75. [Google Scholar] [CrossRef]
- Reissner, E. On a variational theorem in elasticity. J. Mathemactics Phys. 1950, 29, 90–95. [Google Scholar] [CrossRef]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons, Inc.: Chichester, UK, 1984. [Google Scholar]
- Beltempo, A.; Balduzzi, G.; Alfano, G.; Auricchio, F. Analytical derivation of a general 2D non-prismatic beam model based on the Hellinger-Reissner principle. Eng. Struct. 2015, 101, 88–98. [Google Scholar] [CrossRef]
- Trinh, L.C.; Ojo, S.O.; Groh, R.M.J.; Weaver, P.M. A mixed inverse differential quadrature method for static analysis of constant- and variable-stiffness laminated beams based on Hellinger-Reissner mixed variational formulation. Int. J. Solids Struct. 2021, 210, 66–87. [Google Scholar] [CrossRef]
- Lee, Y.; Yoon, K.; Lee, P.S. Improving the MITC3 shell finite element by using the Hellinger–Reissner principle. Comput. Struct. 2012, 110, 93–106. [Google Scholar] [CrossRef]
- Auricchio, F.; Balduzzi, G.; Khoshgoftar, M.J.; Rahimi, G.; Sacco, E. Enhanced modeling approach for multilayer anisotropic plates based on dimension reduction method and Hellinger–Reissner principle. Compos. Struct. 2014, 118, 622–633. [Google Scholar] [CrossRef]
- Kikuchi, F.; Ando, Y. Rectangular Finite Element for Plate Bending Analysis Based on Hellinger-Reissner’s Variational Principle. J. Nucl. Sci. Technol. 1972, 9, 28–35. [Google Scholar] [CrossRef][Green Version]
- Auricchio, F.; Balduzzi, G.; Lovadina, C. The dimensional reduction modelling approach for 3D beams: Differential equations and finite-element solutions based on Hellinger–Reissner principle. Int. J. Solids Struct. 2013, 50, 4184–4196. [Google Scholar] [CrossRef]
- Qian, R.L. A modified Hellinger-Reissner variational functional including only two independent variables for large displacement of thin shallow shell. Appl. Math. Mech. 1997, 18, 663–670. [Google Scholar]
- Morley, L.S.D. Hellinger-Reissner principles for plate and shell finite elements. Int. J. Numer. Methods Eng. 1984, 20, 773–777. [Google Scholar] [CrossRef]
- Chai, S.B.; Xiao, R.C.; Sun, B. Deformation characteristics of main cable in suspension bridge caused by live load. J. Tongji Univ. (Nat. Sci.) 2012, 40, 1452–1457. [Google Scholar]
- Li, G.P. State revision method in nonlinear analysis of stay cable. J. Tongji Univ. (Nat. Sci.) 2000, 28, 1–4. [Google Scholar]
- Jin, G.S.; Yang, Z.J.; Liu, Y.H. Analysis of main design parameters of cable-stayed and suspension combined system bridge. Highway 2007, 3, 80–84. [Google Scholar]


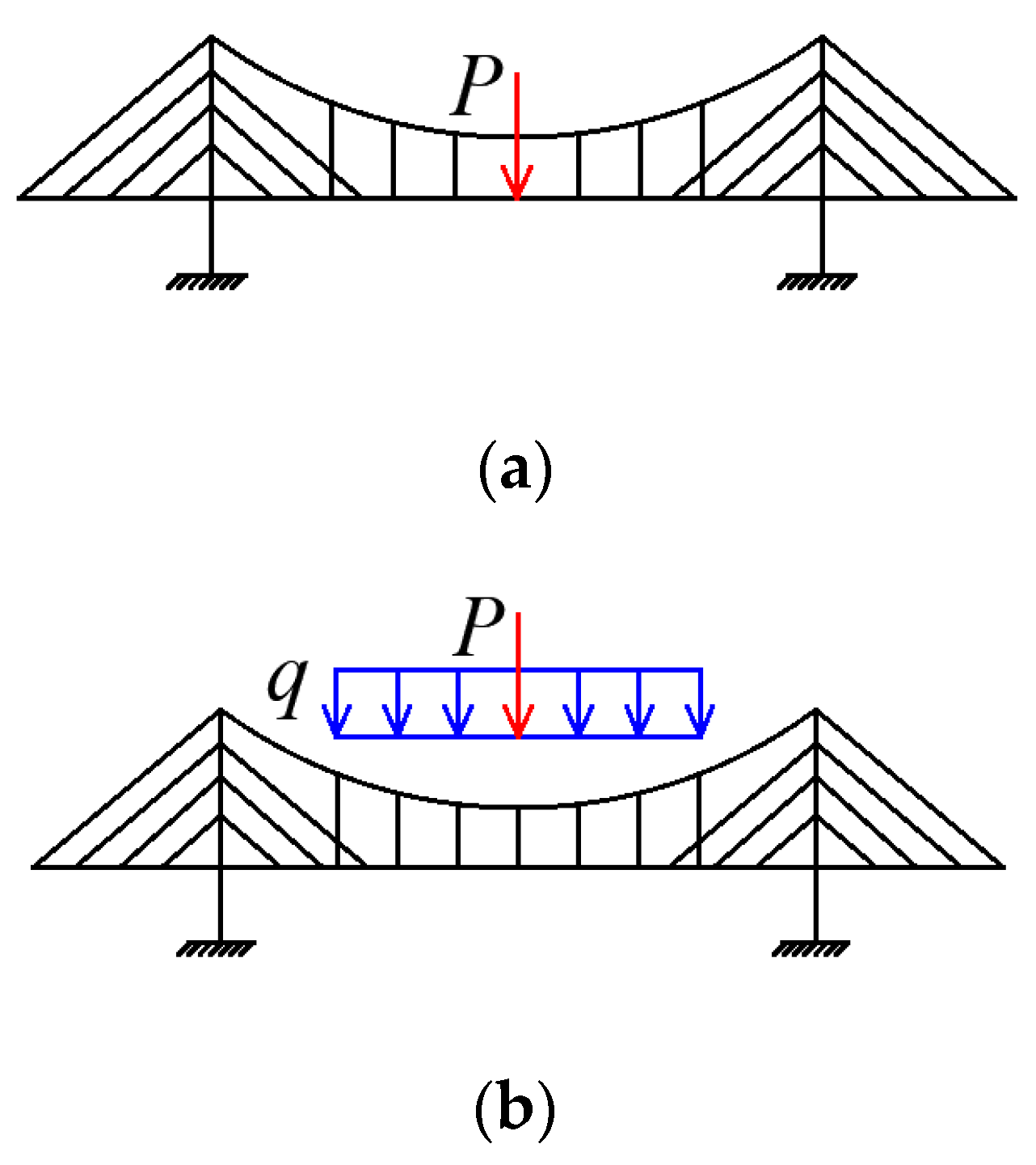
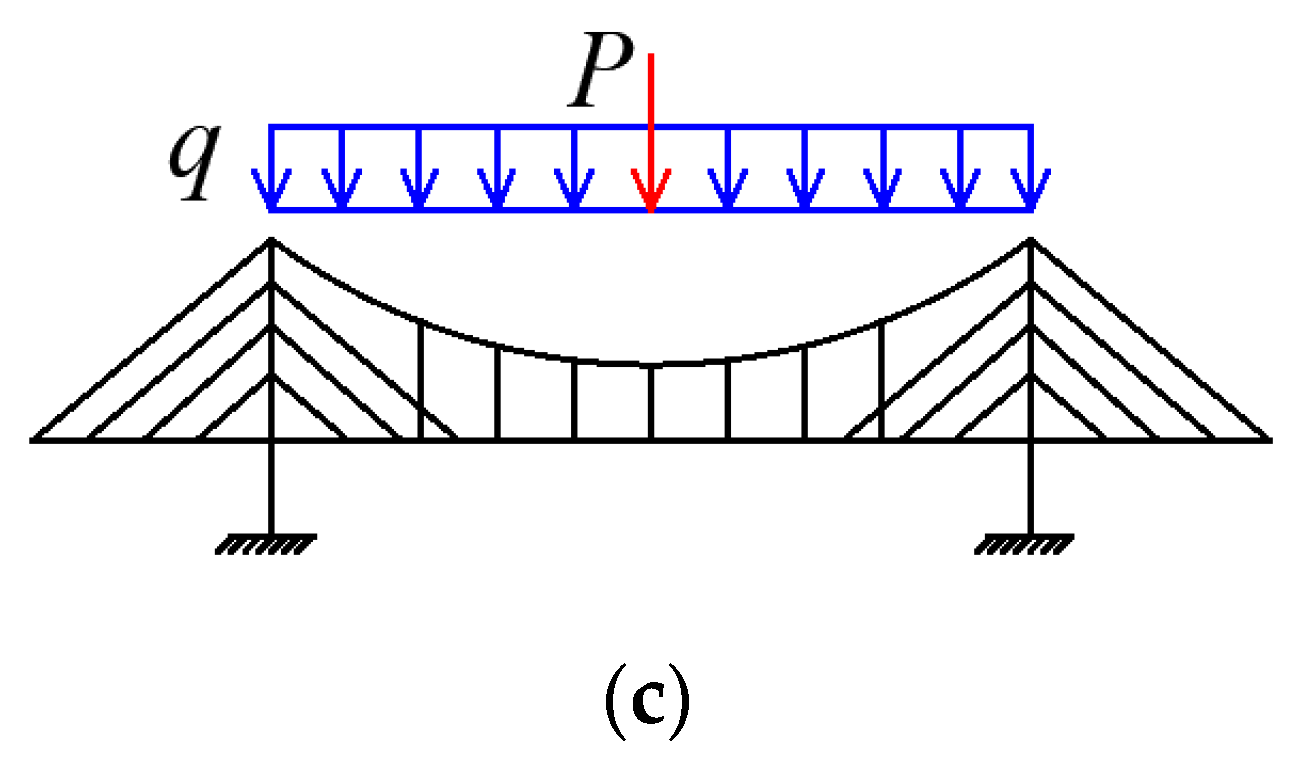
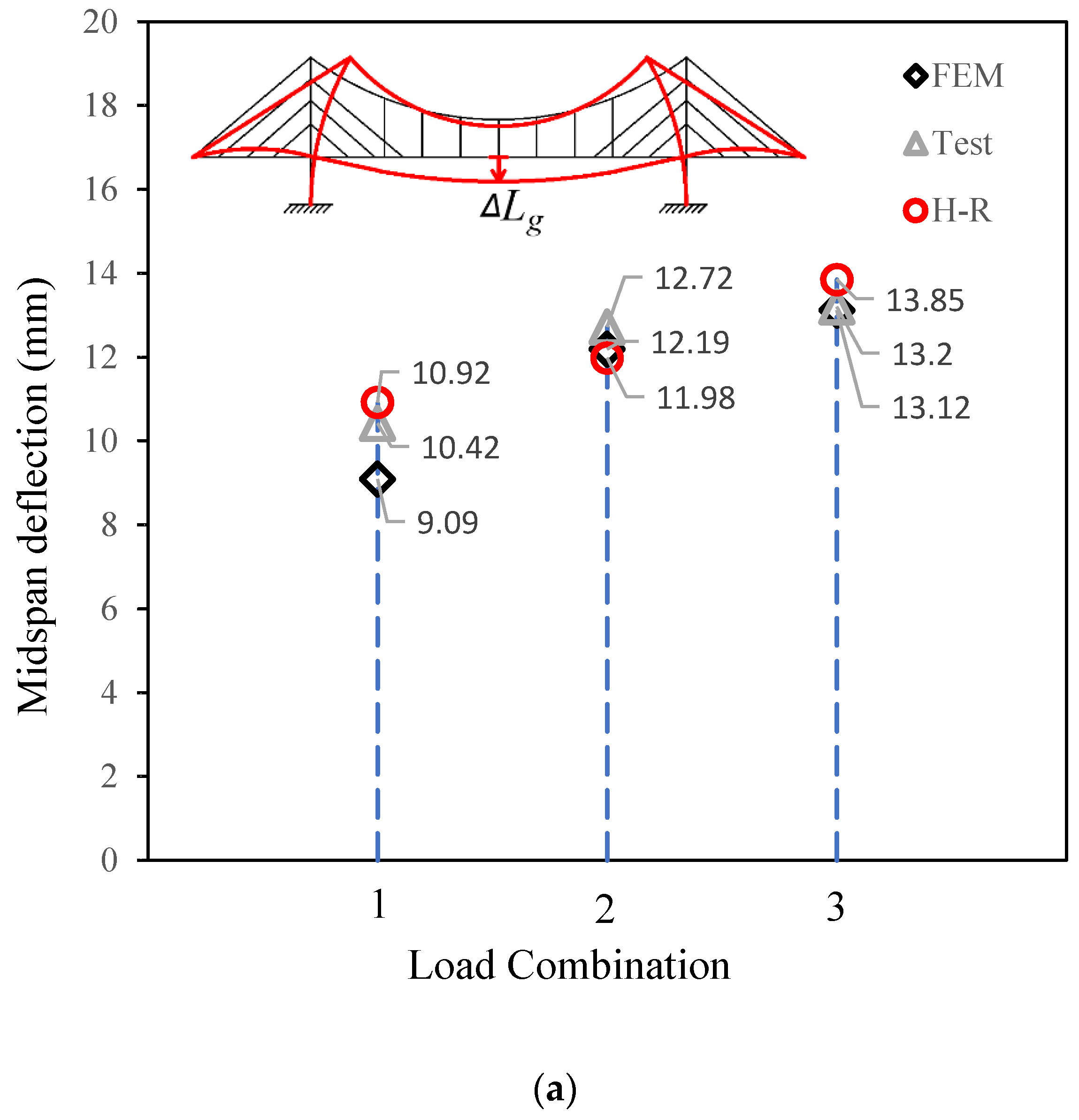
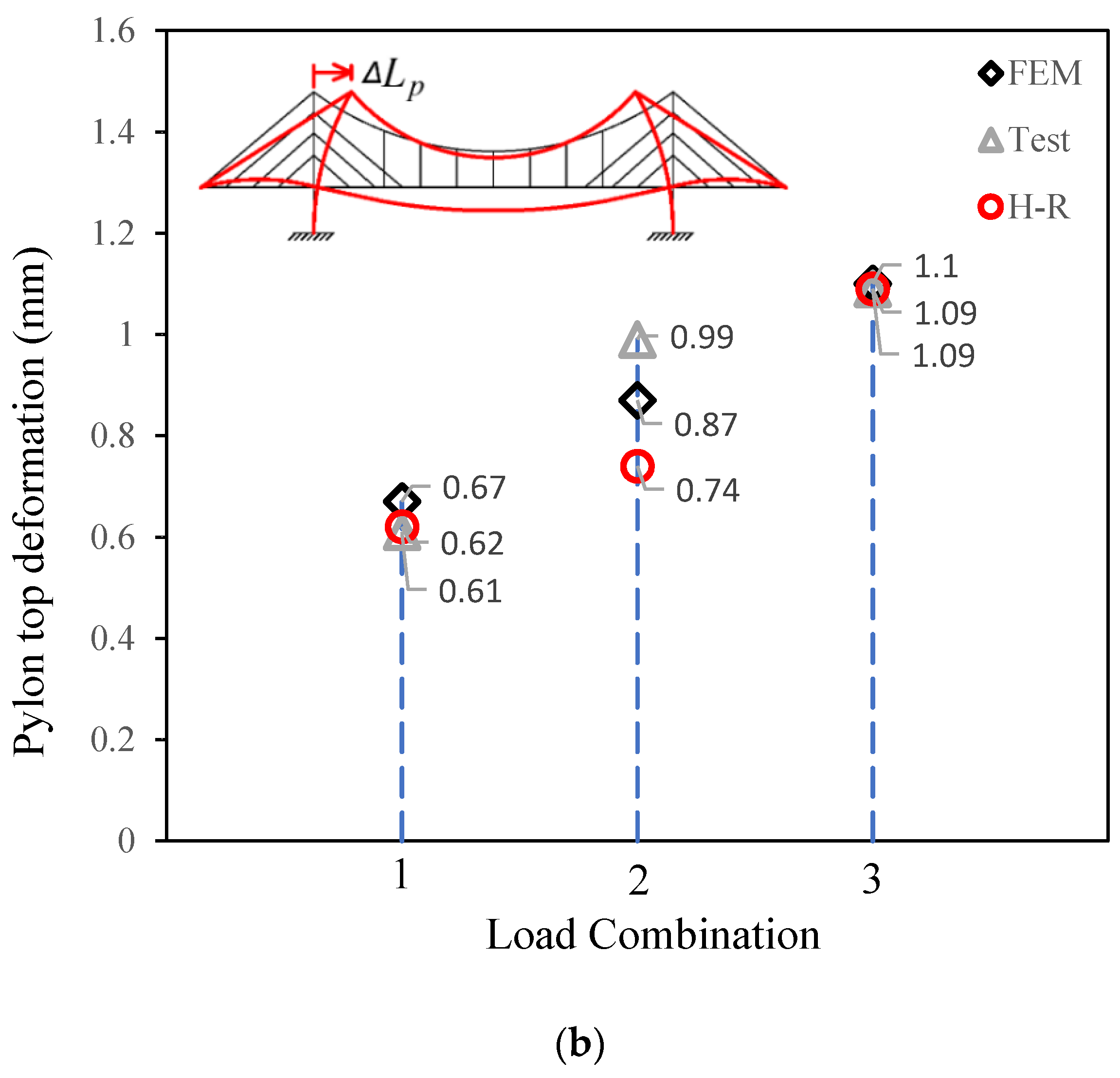
| Structural Member | E (MPa) | Dimension |
|---|---|---|
| Girder (concrete part) | 3.45 × 104 | I (m4) = 1.883 × 10−6 |
| Girder (aluminum alloy part) | 7.0 × 104 | I (m4) = 4.819 × 10−7 |
| Pylon | 3.45 × 104 | I (m4) = 5.0 × 10−6 |
| Main cable | 2.05 × 105 | A (m2) = 7.854 × 10−7 |
| Stay cable | 2.05 × 105 | A (m2) = 1.964 × 10−7 |
| Model | Main Span (m) 2 × (a + b + c + d) | Side Span (m) d + c + e | Side Span/Main Span Lb/Lm | Sag-to-Span Ratio f/Lm |
|---|---|---|---|---|
| A | 2 × (28 × 9 + 13 + 39 × 9 + 34) = 1300 | 34 + 39 × 9 + 10 = 395 | 0.304 | 0.402 |
| B | 2 × (39 × 9 + 18 + 33 × 9 + 34) = 1400 | 34 + 33 × 9 + 14 = 345 | 0.246 | 0.514 |
| C | 2 × (51 × 9 + 14 + 27 × 9 + 34) = 1500 | 34 + 27 × 9 + 18 = 295 | 0.197 | 0.624 |
| D | 2 × (62 × 9 + 10 + 22 × 9 + 34) = 1600 | 34 + 22 × 9 + 13 = 245 | 0.153 | 0.709 |
| E | 2 × (73 × 9 + 15 + 16 × 9 + 34) = 1700 | 34 + 16 × 9 + 17 = 195 | 0.115 | 0.784 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Q.; Wei, P.; Lou, J.; Wang, D.; Cai, J.; Xu, R. Analytical Model for Early Design Stage of Cable-Stayed Suspension Bridges Based on Hellinger–Reissner Variational Method. Materials 2022, 15, 4863. https://doi.org/10.3390/ma15144863
Feng Q, Wei P, Lou J, Wang D, Cai J, Xu R. Analytical Model for Early Design Stage of Cable-Stayed Suspension Bridges Based on Hellinger–Reissner Variational Method. Materials. 2022; 15(14):4863. https://doi.org/10.3390/ma15144863
Chicago/Turabian StyleFeng, Qian, Peng Wei, Junbin Lou, Daiwei Wang, Jinbiao Cai, and Rongqiao Xu. 2022. "Analytical Model for Early Design Stage of Cable-Stayed Suspension Bridges Based on Hellinger–Reissner Variational Method" Materials 15, no. 14: 4863. https://doi.org/10.3390/ma15144863
APA StyleFeng, Q., Wei, P., Lou, J., Wang, D., Cai, J., & Xu, R. (2022). Analytical Model for Early Design Stage of Cable-Stayed Suspension Bridges Based on Hellinger–Reissner Variational Method. Materials, 15(14), 4863. https://doi.org/10.3390/ma15144863






