Vibration-Based Fatigue Analysis of Octet-Truss Lattice Infill Blades for Utilization in Turbine Rotors
Abstract
:1. Introduction
2. Theoretical Background
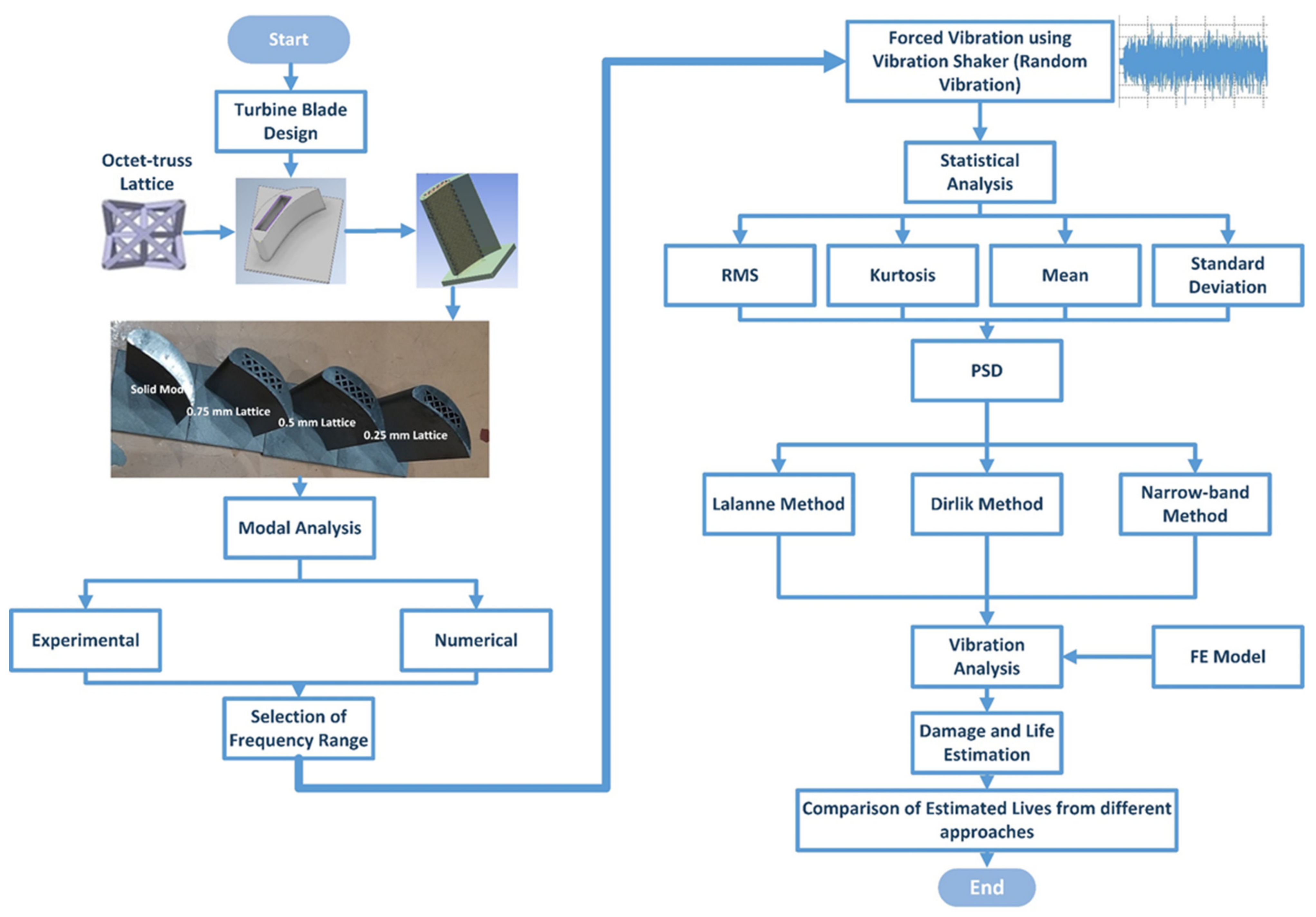
3. Materials and Methods
3.1. Blade Design and Manufacturing
3.2. Modal Analysis
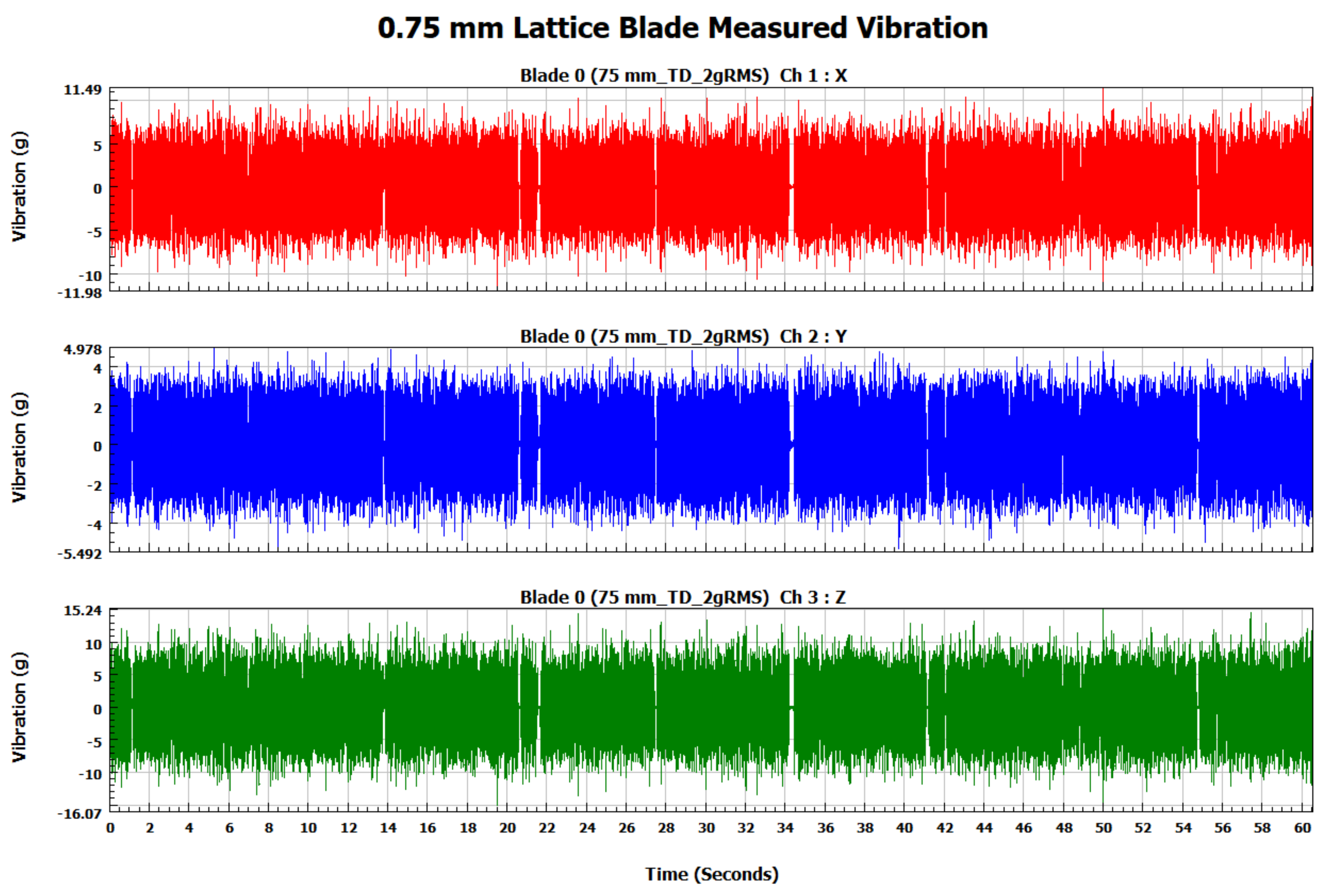
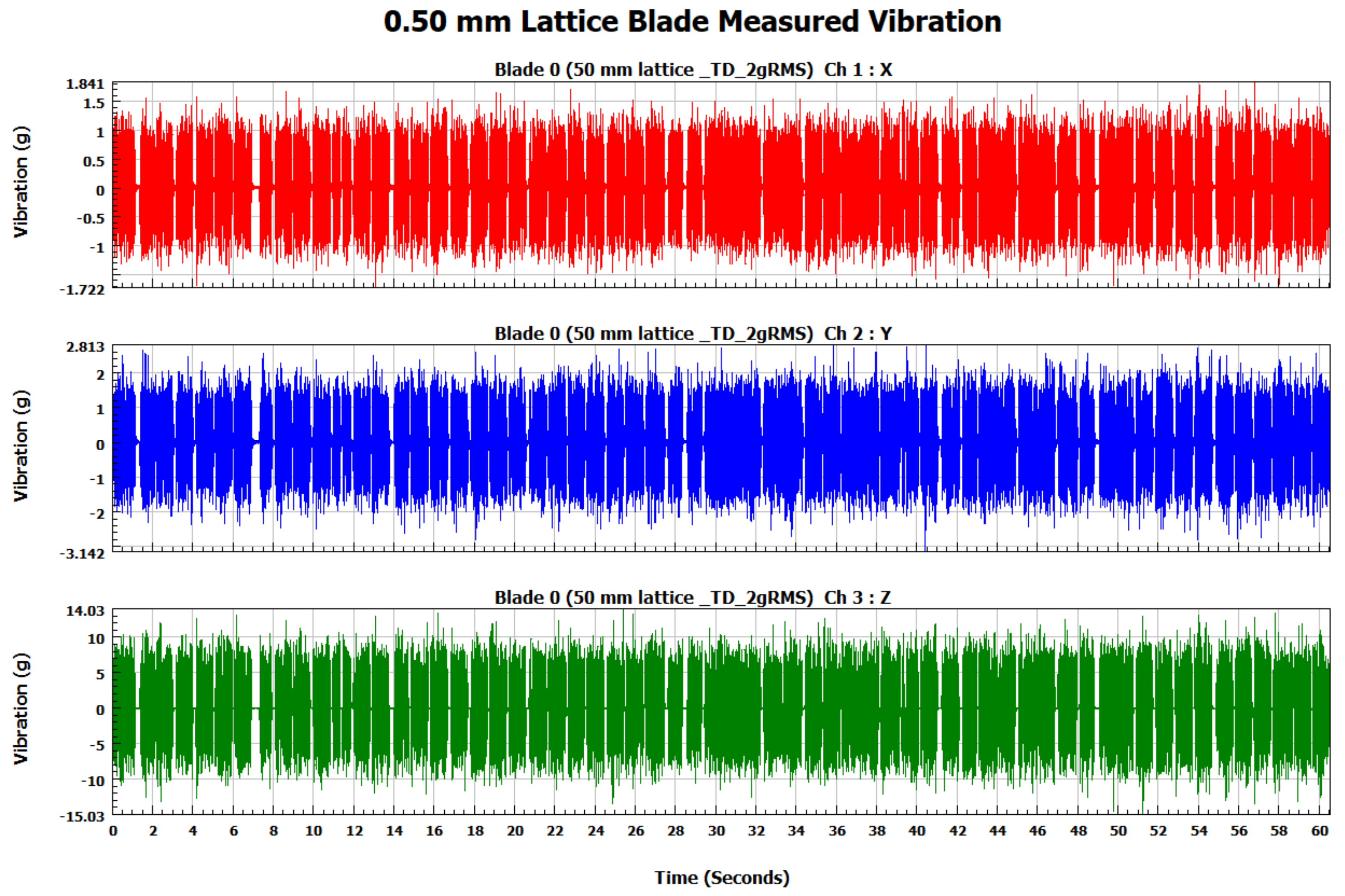
3.3. Forced Vibration Response
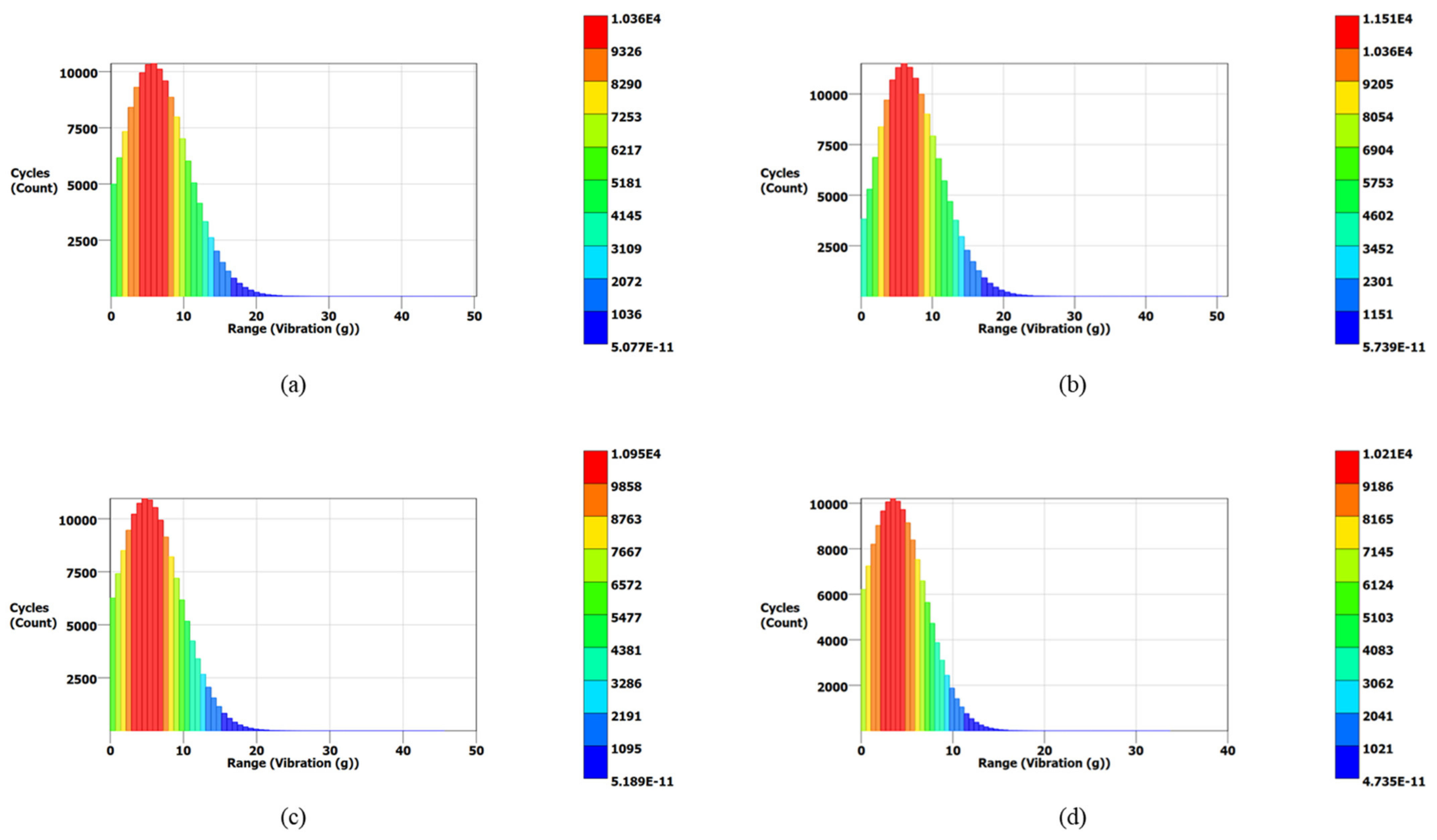
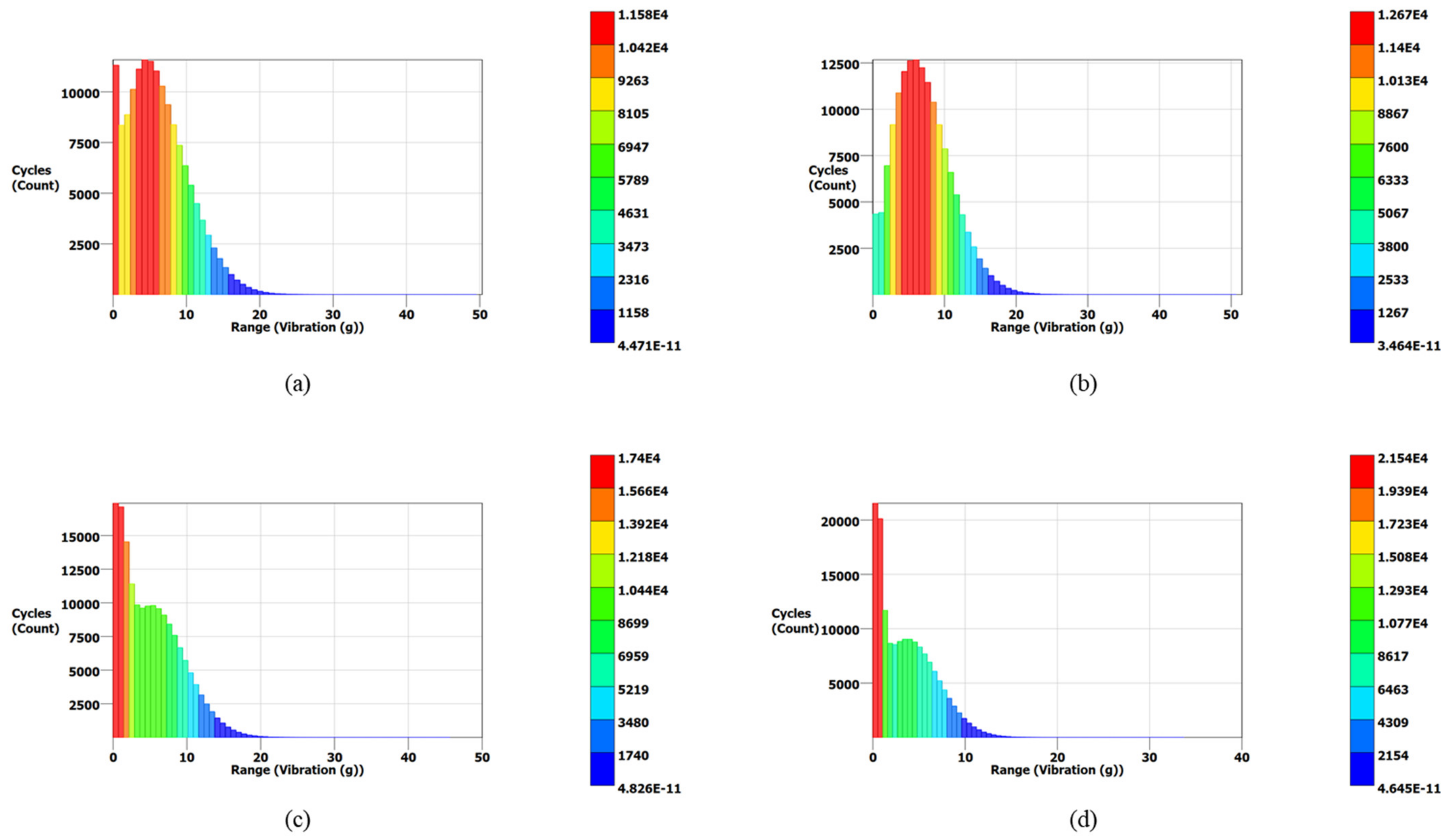
3.4. Vibration Fatigue Analysis
4. Results and Discussion
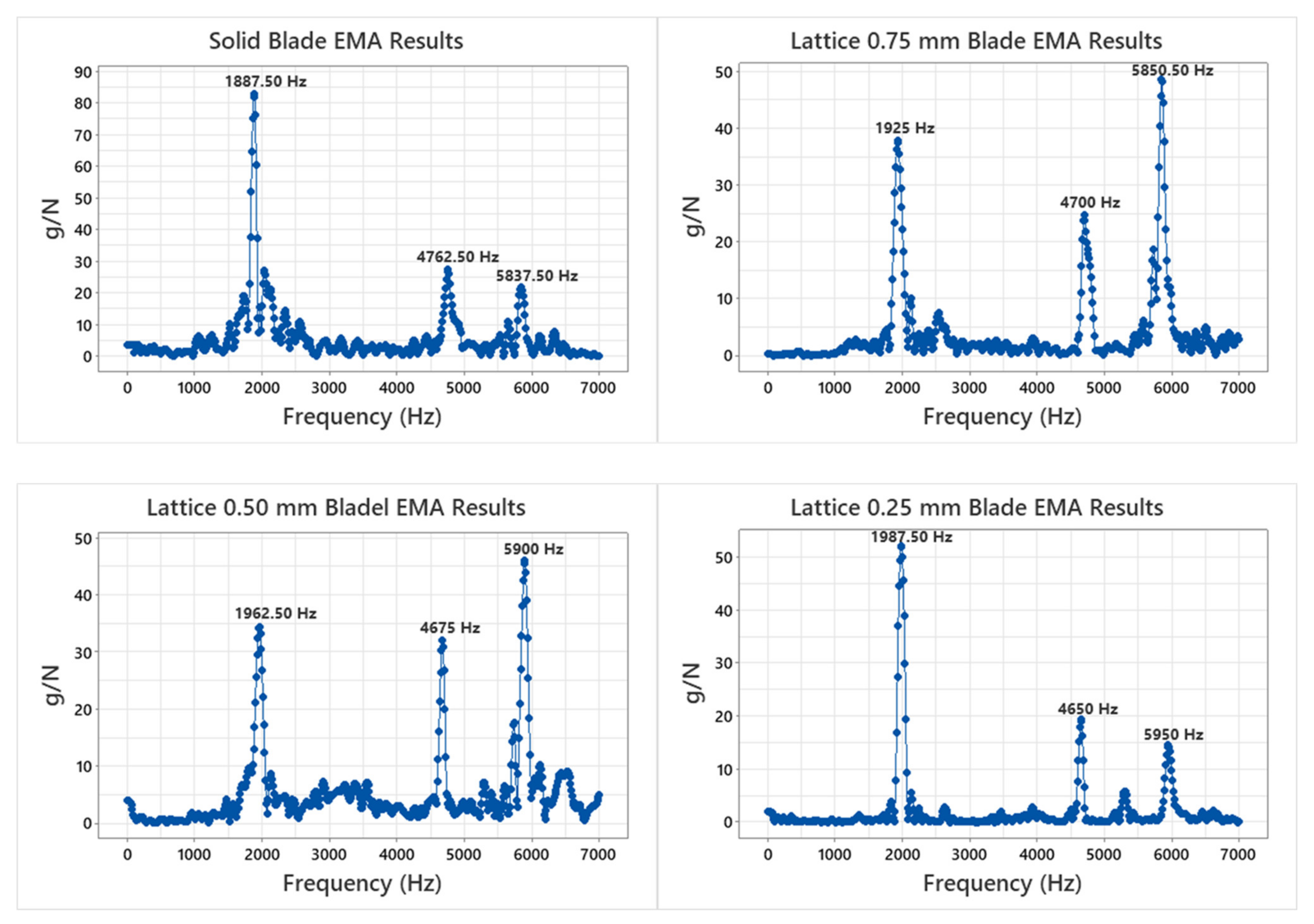
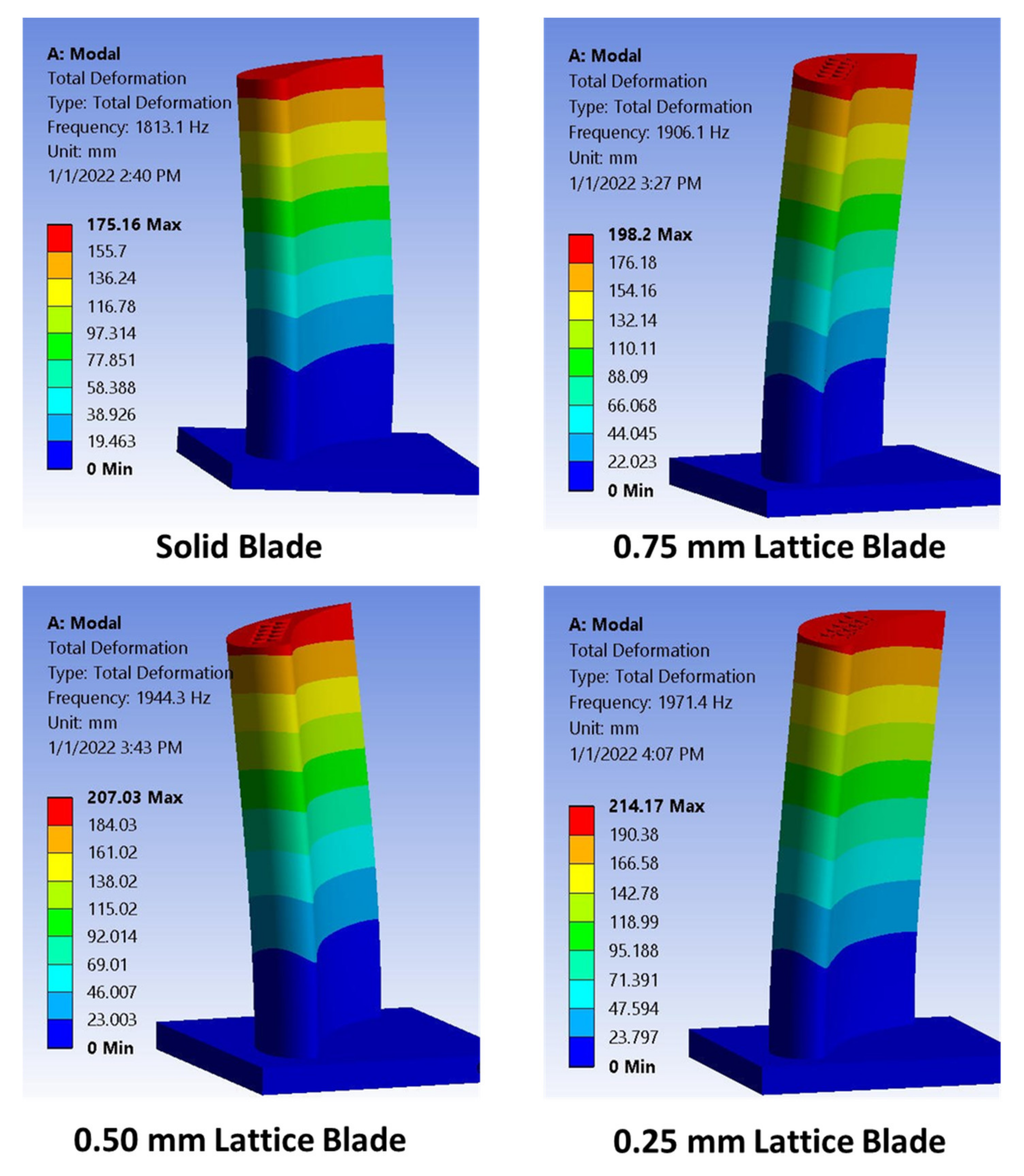
4.1. Modal Analysis Results
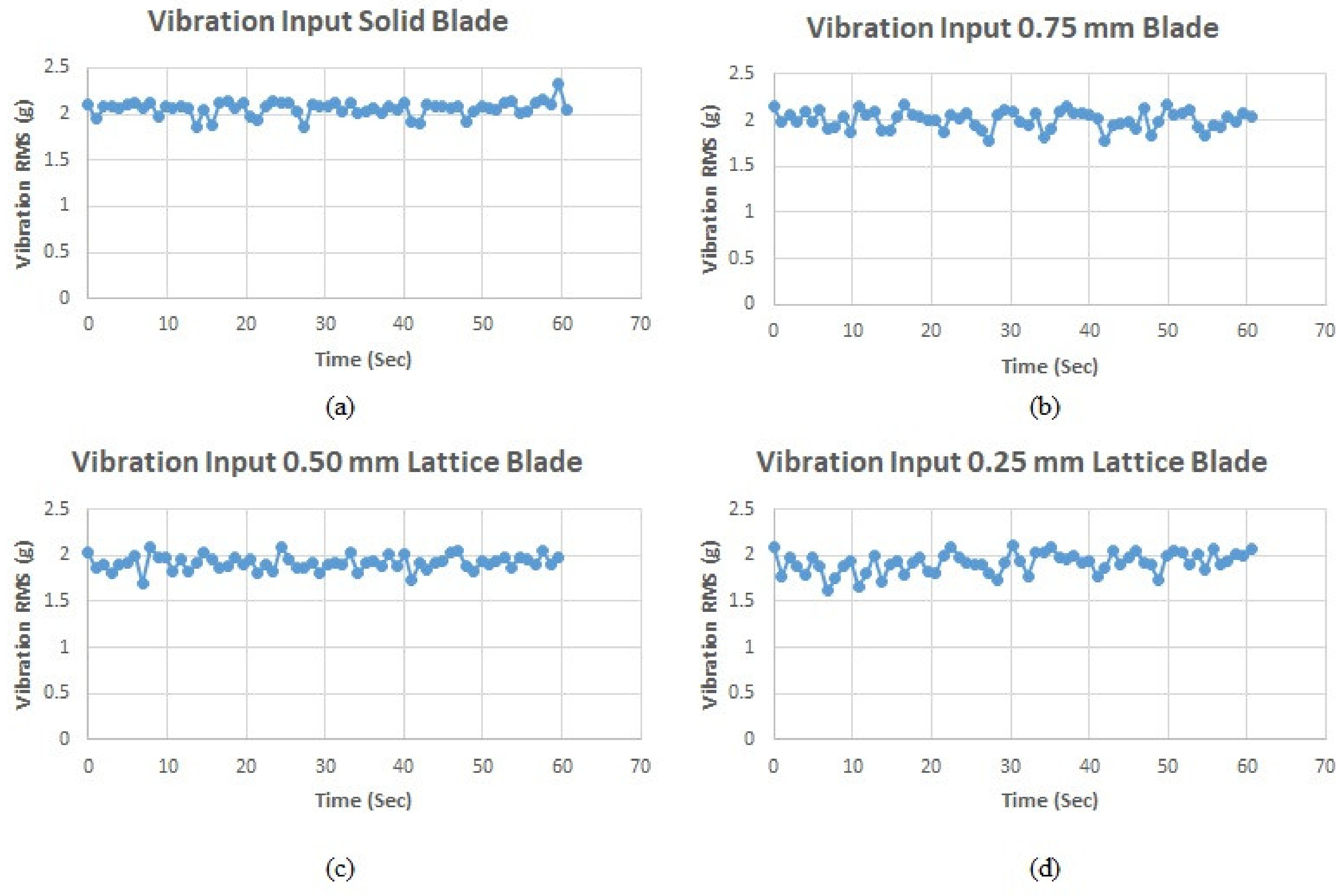
4.2. Forced Vibration Analysis Results
5. Conclusions
- Using octet-truss lattice structures with variable strut thickness, a weight reduction of 15.58% to 24.91% compared to the solid blade was achieved.
- The natural frequencies of lattice infilled blades were found to be higher than those of solid blades at the first and third modes.
- For vibration fatigue analysis, three frequency domain fatigue approaches were utilized. The results indicate that the Dirlik approach exhibited the highest fatigue lives, while the narrow-band approach resulted in the lowest fatigue lives for the respective blades.
- Lattice-based blades have better fatigue lives compared to the solid blade; the 0.25 mm lattice blade, which is the lightest of all blades, exhibited a the least damage of all four blades followed by the 0.50 and 0.75 mm lattice blades, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| The ith spectral moment | |
| Spectral width | |
| Expected occurrence of peak | |
| Expected rate of zero crossing | |
| Irregularity factor | |
| Probability density function | |
| x | Variable load |
| Mean | |
| Nf | Data sample size |
| Number of stress cycles expected per second | |
| Probability density function of stress range | |
| erf | Predicted rain flow count per second |
| ith function of spectral moments | |
| R | Function of spectral moments |
References
- Hosseinimaab, S.M.; Tousi, A.M. A New Approach to Off-Design Performance Analysis of Gas Turbine Engines and Its Application. Energy Convers. Manag. 2021, 243, 114411. [Google Scholar] [CrossRef]
- George, T.J.; Seidt, J.; Shen, M.-H.H.; Nicholas, T.; Cross, C.J. Development of a Novel Vibration-Based Fatigue Testing Methodology. Int. J. Fatigue 2004, 26, 477–486. [Google Scholar] [CrossRef]
- Zhu, S.P.; Yue, P.; Yu, Z.Y.; Wang, Q. A Combined High and Low Cycle Fatigue Model for Life Prediction of Turbine Blades. Materials 2017, 10, 698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, D.; Wang, R. Combined Fatigue Experiments on Full Scale Turbine Components. Aircr. Eng. Aerosp. Technol. 2013, 85, 4–9. [Google Scholar] [CrossRef]
- Hu, D.; Meng, F.; Liu, H.; Song, J.; Wang, R. Experimental Investigation of Fatigue Crack Growth Behavior of GH2036 under Combined High and Low Cycle Fatigue. Int. J. Fatigue 2016, 85, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.Y.; Zhu, S.P.; Liu, Q.; Liu, Y. A New Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Life Prediction of Turbine Blades. Materials 2017, 10, 513. [Google Scholar] [CrossRef] [Green Version]
- Correia, J.; Apetre, N.; Arcari, A.; de Jesus, A.; Muñiz-Calvente, M.; Calçada, R.; Berto, F.; Fernández-Canteli, A. Generalized Probabilistic Model Allowing for Various Fatigue Damage Variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Blason, S.; Correia, J.A.F.O.; de Jesus, A.M.P.; Calcada, R.A.B.; Fernandez-Canteli, A. A Probabilistic Analysis of Miner’s Law for Different Loading Conditions. Struct. Eng. Mech. 2016, 60, 71–90. [Google Scholar] [CrossRef]
- Beretta, S.; Foletti, S.; Rusconi, E.; Riva, A.; Socie, D. A Log-Normal Format for Failure Probability under LCF: Concept, Validation and Definition of Design Curve. Int. J. Fatigue 2016, 82, 2–11. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Lei, Q.; Wang, Q. Probabilistic Fatigue Life Prediction and Reliability Assessment of a High Pressure Turbine Disc Considering Load Variations. Int. J. Damage Mech. 2018, 27, 1569–1588. [Google Scholar] [CrossRef]
- Rehman, S.; Alam, M.M.; Alhems, L.M.; Rafique, M.M. Horizontal AxisWind Turbine Blade Design Methodologies for Efficiency Enhancement A Review. Energies 2018, 11, 506. [Google Scholar] [CrossRef] [Green Version]
- Vdovin, R.A. Improving the Quality of the Manufacturing Process of Turbine Blades of the Gas Turbine Engine. J. Phys. Conf. Ser. 2019, 1399, 044035. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, Q.; Zhu, G.; Li, P. Transient Analysis and Design Improvement of a Gas Turbine Rotor Based on Thermal-Mechanical Method. Shock Vib. 2018, 2018, 1029520. [Google Scholar] [CrossRef]
- Nourin, F.N.; Amano, R.S. Review of Gas Turbine Internal Cooling Improvement Technology. J. Energy Resour. 2021, 143, 080801. [Google Scholar] [CrossRef]
- Wang, L.; Wang, T.; Wu, J.; Chen, G. Multi-Objective Differential Evolution Optimization Based on Uniform Decomposition for Wind Turbine Blade Design. Energy 2017, 120, 346–361. [Google Scholar] [CrossRef]
- Vasiliev, V.; Barynin, V.A.; Razin, A.F. Anisogrid Composite Lattice Structures—Development and Aerospace Applications. Compos. Struct. 2012, 94, 1117–1127. [Google Scholar] [CrossRef]
- Kulangara, A.J.; Rao, C.S.P.P.; Subhash Chandra Bose, P. Generation and Optimization of Lattice Structure on a Spur Gear. Mater. Today 2018, 5, 5068–5073. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Design and Optimization of Lattice Structures: A Review. Appl. Sci. 2020, 10, 6374. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM Lattice Structures: Properties, Performance, Applications and Challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Helou, M.; Kara, S. Design, Analysis and Manufacturing of Lattice Structures: An Overview. Int. J. Comput. Integr. Manuf. 2018, 31, 243–261. [Google Scholar] [CrossRef]
- Alkebsi, E.A.A.; Ameddah, H.; Outtas, T.; Almutawakel, A. Design of Graded Lattice Structures in Turbine Blades Using Topology Optimization. Int. J. Comput. Integr. Manuf. 2021, 34, 370–384. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-Scale Design and Optimization for Solid-Lattice Hybrid Structures and Their Application to Aerospace Vehicle Components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Akzhigitov, D.; Srymbetov, T.; Aldabergen, A.; Spitas, C. Structural and Aerodynamical Parametric Study of Truss-Core Gas Turbine Rotor Blade. J. Appl. Comput. Mech. 2021, 7, 831–838. [Google Scholar] [CrossRef]
- Hussain, S.; Ghopa, W.A.W.; Singh, S.S.K.; Azman, A.H.; Abdullah, S. Experimental and Numerical Vibration Analysis of Octet-Truss-Lattice-Based Gas Turbine Blades. Metals 2022, 12, 340. [Google Scholar] [CrossRef]
- Šmíd, M.; Horník, V.; Kunz, L.; Hrbáček, K.; Hutař, P. High Cycle Fatigue Data Transferability of MAR-M 247 Superalloy from Separately Cast Specimens to Real Gas Turbine Blade. Metals 2020, 10, 1460. [Google Scholar] [CrossRef]
- Kauss, O.; Tsybenko, H.; Naumenko, K.; Hütter, S.; Krüger, M. Structural Analysis of Gas Turbine Blades Made of Mo-Si-B under Transient Thermo-Mechanical Loads. Comput. Mater. Sci. 2019, 165, 129–136. [Google Scholar] [CrossRef]
- Borello, D.; Anielli, D.; Rispoli, F.; Salvagni, A.; Venturini, P. Unsteady Cfd Analysis of Erosion Mechanism in the Coolant Channels of a Rotating Gas Turbine Blade. In Proceedings of the ASME Turbo Expo, Montreal, QC, Canada, 15–19 June 2015; Volume 5A. [Google Scholar]
- Bacci, T.; Gamannossi, A.; Mazzei, L.; Picchi, A.; Winchler, L.; Carcasci, C.; Andreini, A.; Abba, L.; Vagnoli, S. Experimental and CFD Analyses of a Highly-Loaded Gas Turbine Blade. Energy Procedia 2017, 126, 770–777. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Huang, K. Fast Prediction and Sensitivity Analysis of Gas Turbine Cooling Performance Using Supervised Learning Approaches. Energy 2022, 246, 123373. [Google Scholar] [CrossRef]
- Wu, W.; Yao, R.; Wang, J.; Su, H.; Wu, X. Leading Edge Impingement Cooling Analysis with Separators of a Real Gas Turbine Blade. Appl. Therm. Eng. 2022, 208, 118275. [Google Scholar] [CrossRef]
- Ziaei-Asl, A.; Ramezanlou, M.T. Thermo-Mechanical Behavior of Gas Turbine Blade Equipped with Cooling Ducts and Protective Coating with Different Thicknesses. Int. J. Mech. Sci. 2019, 150, 656–664. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Optimization of Spring Fatigue Life Prediction Model for Vehicle Ride Using Hybrid Multi-Layer Perceptron Artificial Neural Networks. Mech. Syst. Signal Process. 2019, 122, 597–621. [Google Scholar] [CrossRef]
- Nuawi, M.Z. Mesokurtosis Zonal Nonparametric Signal Analysis for Dynamic Characterisation of Metallic Material. J. Kejuruter. 2012, 24, 21–27. [Google Scholar]
- Habtour, E.; Connon, W.; Pohland, M.F.; Stanton, S.C.; Paulus, M.; Dasgupta, A. Review of Response and Damage of Linear and Nonlinear Systems under Multiaxial Vibration. Shock Vib. 2014, 2014, 294271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dirlik, T.; Benasciutti, D. Dirlik and Tovo-Benasciutti Spectral Methods in Vibration Fatigue: A Review with a Historical Perspective. Metals 2021, 11, 1333. [Google Scholar] [CrossRef]
- Kamei, K.; Khan, M.A. Current Challenges in Modelling Vibrational Fatigue and Fracture of Structures: A Review. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 77. [Google Scholar] [CrossRef]
- Wang, Y.; Serra, R. Vibration Fatigue Damage Estimation by New Stress Correction Based on Kurtosis Control of Random Excitation Loadings. Sensors 2021, 21, 4518. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Development of Multiple Linear Regression-Based Models for Fatigue Life Evaluation of Automotive Coil Springs. Mech. Syst. Signal Process. 2019, 118, 675–695. [Google Scholar] [CrossRef]
- Prasad, S.R.; Sekhar, A.S. Life Estimation of Shafts Using Vibration Based Fatigue Analysis. J. Mech. Sci. Technol. 2018, 32, 4071–4078. [Google Scholar] [CrossRef]
- Wu, T.; Yao, W.; Xu, C.; Li, P. A Natural Frequency Degradation Model for Very High Cycle Fatigue of Woven Fiber Reinforced Composite. Int. J. Fatigue 2020, 134, 105398. [Google Scholar] [CrossRef]
- Khoshmanesh, S.; Watson, S.J.; Zarouchas, D. The Effect of the Fatigue Damage Accumulation Process on the Damping and Stiffness Properties of Adhesively Bonded Composite Structures. Compos. Struct. 2022, 287, 115328. [Google Scholar] [CrossRef]
- Chen, X. Experimental Observation of Fatigue Degradation in a Composite Wind Turbine Blade. Compos. Struct. 2019, 212, 547–551. [Google Scholar] [CrossRef]
- Mršnik, M.; Slavič, J.; Boltežar, M. Vibration Fatigue Using Modal Decomposition. Mech. Syst. Signal Process. 2018, 98, 548–556. [Google Scholar] [CrossRef]
- Kihm, F.; Langelier, A.; Munson, K. Influence of the Modal Damping on the Estimated Fatigue Life. Procedia Eng. 2018, 213, 270–281. [Google Scholar] [CrossRef]
- Li, F.; Wu, H.; Wu, P. Vibration Fatigue Dynamic Stress Simulation under Non-Stationary State. Mech. Syst. Signal Process. 2021, 146, 107006. [Google Scholar] [CrossRef]
- Rodríguez, J.A.; Castro, L.; Tejeda, A.L.; García, J.C.; Rodríguez, J.M.; Galindo, E.; Hamzaoui, Y. Fatigue of Steam Turbine Blades at Resonance Conditions. Eng. Fail. Anal. 2019, 104, 39–46. [Google Scholar] [CrossRef]
- Mohammed, O.D.; Rantatalo, M. Gear Fault Models and Dynamics-Based Modelling for Gear Fault Detection—A Review. Eng. Fail. Anal. 2020, 117, 104798. [Google Scholar] [CrossRef]
- Putra, T.; Husaini; Machmud, M. Predicting the Fatigue Life of an Automotive Coil Spring Considering Road Surface Roughness. Eng. Fail. Anal. 2020, 116, 104722. [Google Scholar] [CrossRef]
- Fan, C.; Fan, Q.; Li, H. Base-Scale Entropy and Energy Analysis of Flow Characteristics of the Two-Phase Flow. Syst. Sci. Control Eng. 2018, 6, 262–269. [Google Scholar] [CrossRef]
- Datta, S.; Bishop, N.; Sweitzer, K.; Atkins, A. Simultaneous Durability Assessment and Relative Random Analysis under Base Shake Loading Conditions. In Proceedings of the WCX™ 17: SAE World Congress Experience, Cobo Center, Detroit, MI, USA, 4–6 April 2017. SAE Technical Papers. [Google Scholar]
- Qiang, R.; Hongyan, W. Frequency Domain Fatigue Assessment of Vehicle Component under Random Load Spectrum. J. Phys. Conf. Ser. 2011, 305, 012060. [Google Scholar] [CrossRef]
- Kong, Y.S.; Abdullah, S.; Schramm, D.; Omar, M.Z.; Haris, S.M. Vibration Fatigue Analysis of Carbon Steel Coil Spring under Various Road Excitations. Metals 2018, 8, 617. [Google Scholar] [CrossRef] [Green Version]
- Benasciutti, D.; Tovo, R. Spectral Methods for Lifetime Prediction under Wide-Band Stationary Random Processes. Int. J. Fatigue 2005, 27, 867–877. [Google Scholar] [CrossRef]
- Salwan, G.K.; Subbarao, R.; Mondal, S. Comparison and Selection of Suitable Materials Applicable for Gas Turbine Blades. Mater. Today 2021, 46, 8864–8887. [Google Scholar] [CrossRef]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical Response of Ti-6Al-4V Octet-Truss Lattice Structures. Int. J. Solids Struct. 2015, 60, 107–124. [Google Scholar] [CrossRef]
- Qiu, X.; Cheng, X.; Dong, P.; Peng, H.; Xing, Y.; Zhou, X. Sensitivity Analysis of Johnson-Cook Material Constants and Friction Coeffcient Influence on Finite Element Simulation of Turning Inconel 718. Materials 2019, 12, 3121. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.P.; Lei, Q.; Huang, H.Z.; Yang, Y.J.; Peng, W. Mean Stress Effect Correction in Strain Energy-Based Fatigue Life Prediction of Metals. Int. J. Damage Mech. 2017, 26, 1219–1241. [Google Scholar] [CrossRef]
- Jang, J.; Cho, J.M.; Lee, K.H.; Lee, W.W.; Choi, W.C. Comparison of PSD Analysis Methods in Frequency Domain Fatigue Analysis. J. Korean Soc. Precis. Eng. 2019, 36, 737–743. [Google Scholar] [CrossRef]
- Lee, J.W.; Yoon, G.H.; Jeong, S.H. Topology Optimization Considering Fatigue Life in the Frequency Domain. Comput. Math. Appl. 2015, 70, 1852–1877. [Google Scholar] [CrossRef]
- Manouchehrynia, R.; Abdullah, S.; Singh, S.S.K. Fatigue-Based Reliability in Assessing the Failure of an Automobile Coil Spring under Random Vibration Loadings. Eng. Fail. Anal. 2022, 131, 105808. [Google Scholar] [CrossRef]









| Parameter | Description |
|---|---|
| Laser power | 200 W |
| Laser speed | 875 mm/s |
| Layer thickness | 60 μm |
| Hatching distance | 90 μm |
| Energy density | 42.32 J/mm3 |
| Blade Description | Weight (kg) | Weight Reduction from Complete Solid (%) |
|---|---|---|
| Complete Solid | 0.185 | 0 |
| 0.75 mm Lattice | 0.156 | 15.58 |
| 0.50 mm Lattice | 0.147 | 20.78 |
| 0.25 mm lattice | 0.139 | 24.91 |
| Property | Description |
|---|---|
| Density | 8190 Kg/m3 |
| Young’s Modulus Poisson’s ratio | 200 GPa 0.3 |
| Ultimate Tensile Strength Yield Tensile Strength | 1375 MPa 1100 MPa |
| Bulk Modulus | 137 GPa |
| Shear Modulus | 63.46 MPa |
| Property | Description |
|---|---|
| Cyclic strength coefficient | 776.21 MPa |
| Fatigue strength coefficient | 725.52 MPa |
| Fatigue strength exponent Fatigue ductility coefficient | −0.066 0.990 |
| Fatigue ductility exponent | −0.701 |
| Cyclic strain hardening exponent | 0.0942 |
| Parameter (g) | Solid Blade | 0.75 mm Lattice Blade | 0.50 mm Lattice Blade | 0.25 mm Lattice Blade | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | X | Y | Z | |
| RM | 0.739 | 1.15 | 2.06 | 2.06 | 1.09 | 2.13 | 0.33 | 0.54 | 2.12 | 2.01 | 0.61 | 1.77 |
| Kurtosis | 3.46 | 3.37 | 3.66 | 3.41 | 3.21 | 3.33 | 3.91 | 3.76 | 3.91 | 3.43 | 3.58 | 3.46 |
| Mean | 0.016 | 0.006 | 0.024 | 0.016 | 0.008 | 0.024 | 0.015 | 0.007 | 0.023 | 0.015 | 0.008 | 0.022 |
| Standard Deviation | 0.739 | 1.15 | 2.06 | 2.06 | 1.09 | 2.13 | 0.33 | 0.54 | 2.12 | 2.01 | 0.61 | 1.76 |
| Cycle Counter | Solid Blade | 0.75 mm Lattice Blade | 0.50 mm Lattice Blade | 0.25 mm Lattice Blade | ||||
|---|---|---|---|---|---|---|---|---|
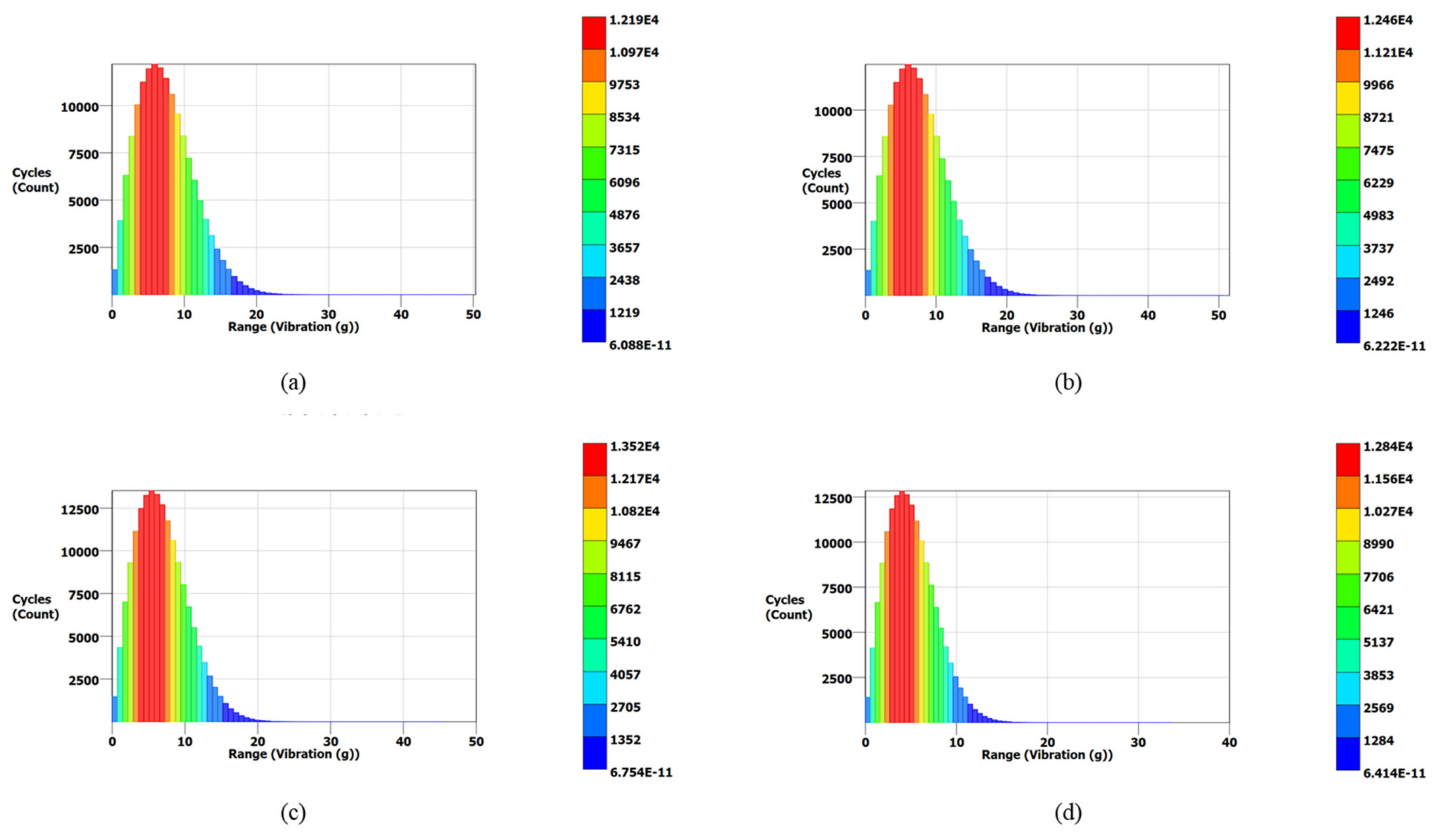
| Range (g) | Cycle Count | Range (g) | Cycle Count | Range (g) | Cycle Count | Range (g) | Cycle Count | |
| Lalanne | 50.34 | 5.07 × 10−11 | 51.50 | 5.73 × 10−11 | 46.36 | 5.18 × 10−11 | 34.28 | 4.73 × 10−11 |
| Dirlik | 50.34 | 4.47 × 10−11 | 51.50 | 3.46 × 10−11 | 46.36 | 4.82 × 10−11 | 34.28 | 4.64 × 10−11 |
| Narrow Band | 50.34 | 6.08 × 10−11 | 51.50 | 6.22 × 10−11 | 46.36 | 6.75 × 10−11 | 34.28 | 6.41 × 10−11 |
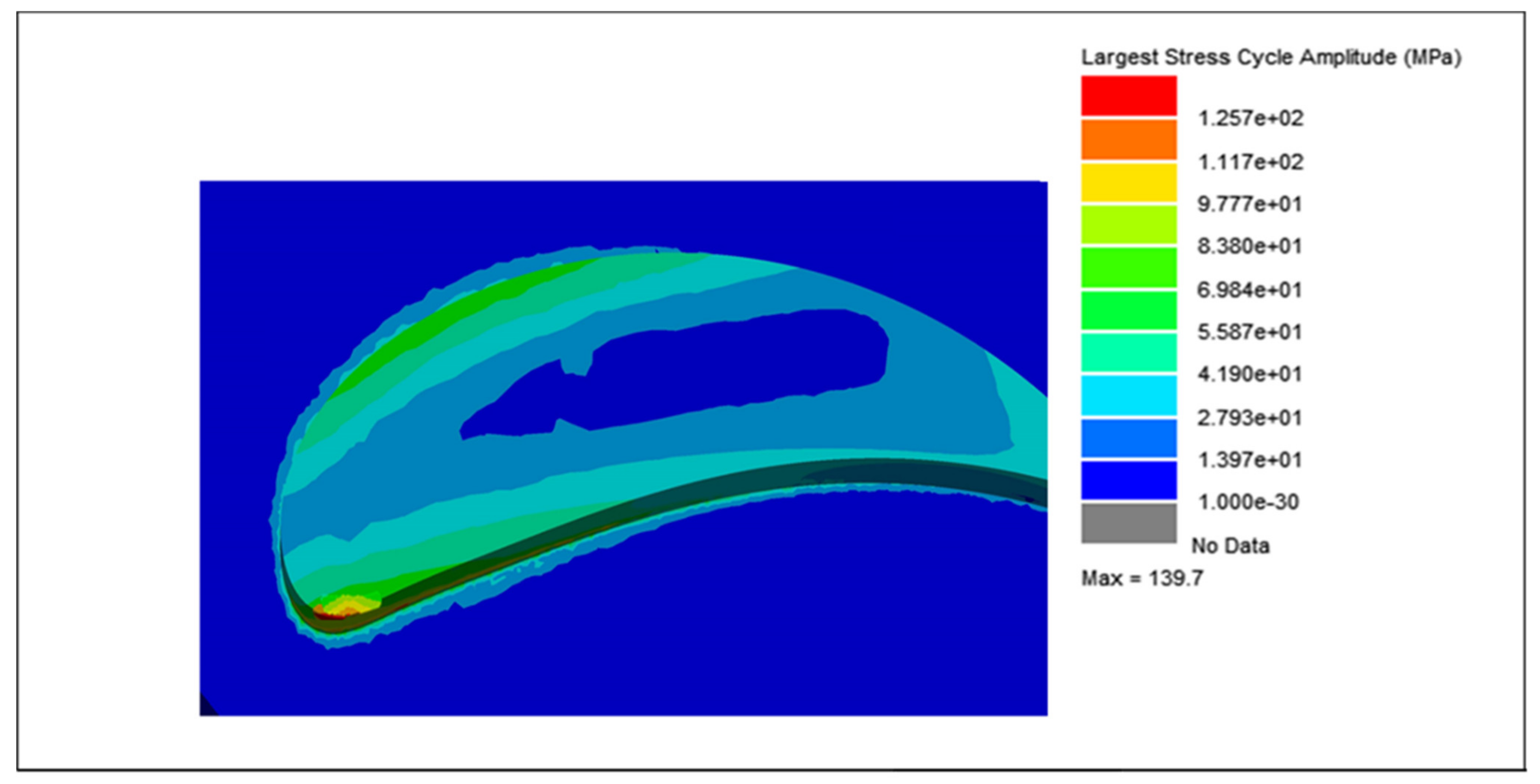
| Cycle Counter | Largest Stress Cycle Amplitude (MPa) | Fatigue Damage | Fatigue Life (Blocks to Failure) |
|---|---|---|---|
| Lalanne | 139.7 | 3.79 × 10−10 | 2.64 × 109 |
| Dirlik | 139.7 | 2.60 × 10−10 | 3.85 × 109 |
| Narrow Band | 139.7 | 5.15 × 10−10 | 1.94 × 109 |
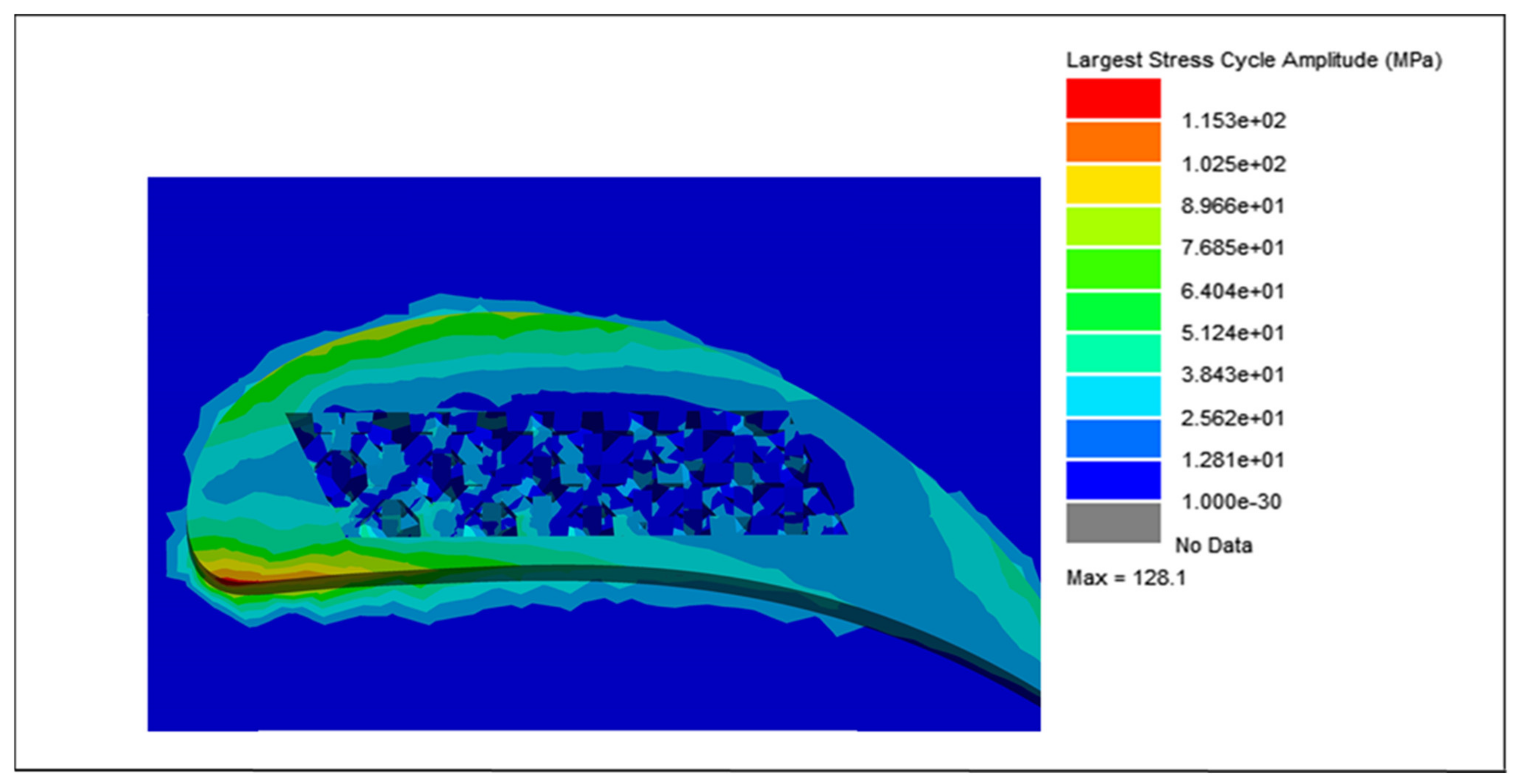
| Cycle Counter | Largest Stress Cycle Amplitude (MPa) | Fatigue Damage | Fatigue Life (Blocks to Failure) |
|---|---|---|---|
| Lalanne | 128.1 | 1.06 × 10−11 | 9.39 × 1010 |
| Dirlik | 128.1 | 7.41 × 10−12 | 1.35 × 1011 |
| Narrow Band | 128.1 | 1.45 × 10−11 | 6.90 × 1010 |
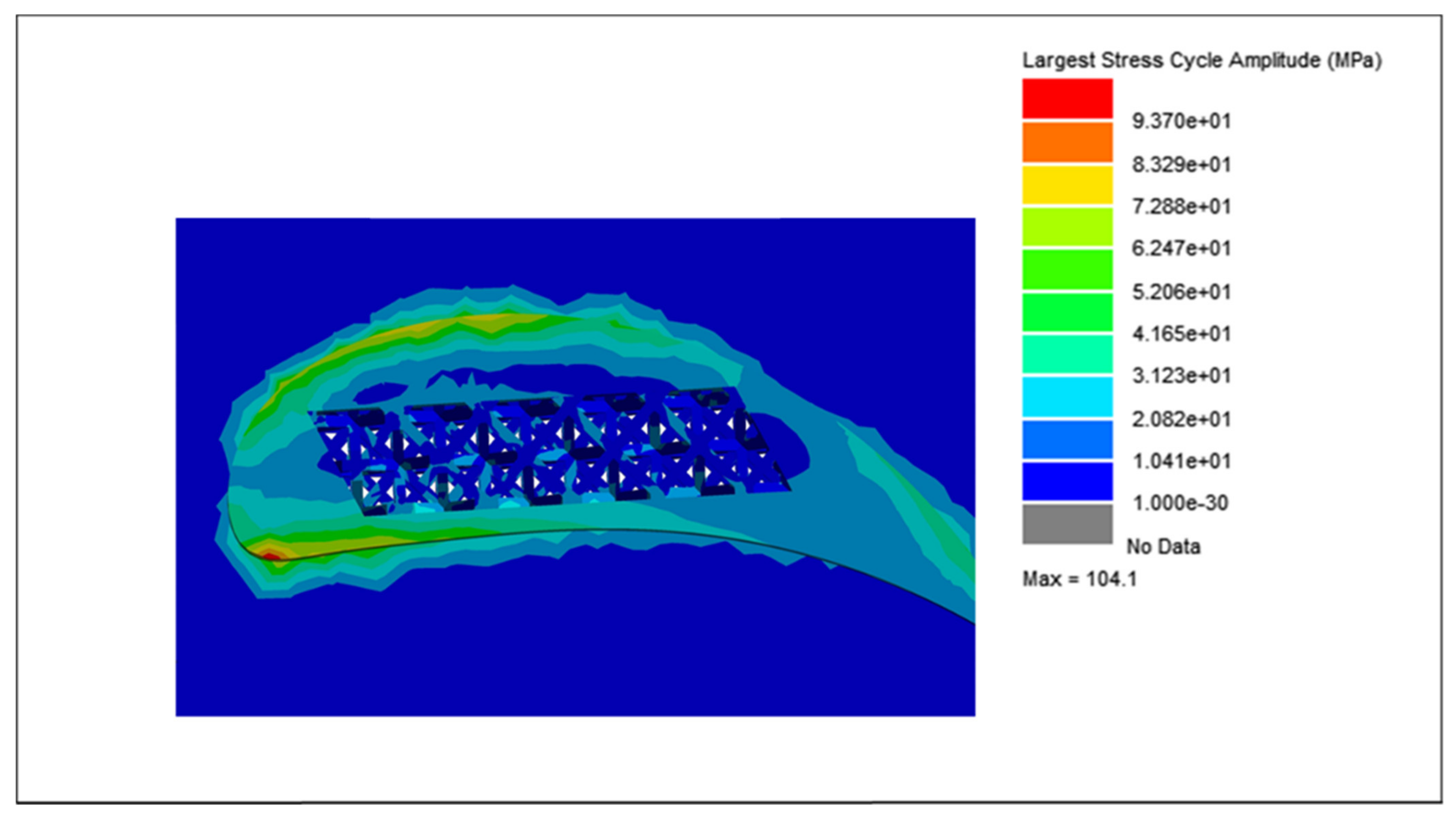
| Cycle Counter | Largest Stress Cycle Amplitude (MPa) | Fatigue Damage | Fatigue Life (Blocks to Failure) |
|---|---|---|---|
| Lalanne | 104.1 | 1.54 × 10−12 | 6.49 × 1011 |
| Dirlik | 104.1 | 1.01 × 10−12 | 9.94 × 1011 |
| Narrow Band | 104.1 | 1.98 × 10−12 | 5.04 × 1011 |
| Cycle Counter | Largest Stress Cycle Amplitude (MPa) | Fatigue Damage | Fatigue Life (Blocks to Failure) |
|---|---|---|---|
| Lalanne | 85.3 | 2.08 × 10−13 | 4.81 × 1012 |
| Dirlik | 85.3 | 1.44 × 10−13 | 6.94 × 1012 |
| Narrow Band | 85.3 | 2.83 × 10−13 | 3.53 × 1012 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, S.; Ghopa, W.A.W.; Singh, S.S.K.; Azman, A.H.; Abdullah, S.; Harun, Z.; Hishamuddin, H. Vibration-Based Fatigue Analysis of Octet-Truss Lattice Infill Blades for Utilization in Turbine Rotors. Materials 2022, 15, 4888. https://doi.org/10.3390/ma15144888
Hussain S, Ghopa WAW, Singh SSK, Azman AH, Abdullah S, Harun Z, Hishamuddin H. Vibration-Based Fatigue Analysis of Octet-Truss Lattice Infill Blades for Utilization in Turbine Rotors. Materials. 2022; 15(14):4888. https://doi.org/10.3390/ma15144888
Chicago/Turabian StyleHussain, Sajjad, Wan Aizon W. Ghopa, S. S. K. Singh, Abdul Hadi Azman, Shahrum Abdullah, Zambri Harun, and Hawa Hishamuddin. 2022. "Vibration-Based Fatigue Analysis of Octet-Truss Lattice Infill Blades for Utilization in Turbine Rotors" Materials 15, no. 14: 4888. https://doi.org/10.3390/ma15144888
APA StyleHussain, S., Ghopa, W. A. W., Singh, S. S. K., Azman, A. H., Abdullah, S., Harun, Z., & Hishamuddin, H. (2022). Vibration-Based Fatigue Analysis of Octet-Truss Lattice Infill Blades for Utilization in Turbine Rotors. Materials, 15(14), 4888. https://doi.org/10.3390/ma15144888










