Investigation of Bamboo Fibrous Tensile Strength Using Modified Weibull Distribution
Abstract
:1. Introduction
2. Experimental Details
2.1. Description of the Study Area
2.2. Harvesting of the Bamboo Culm
2.3. Microscopy Structures of Ethiopian Bamboo Species
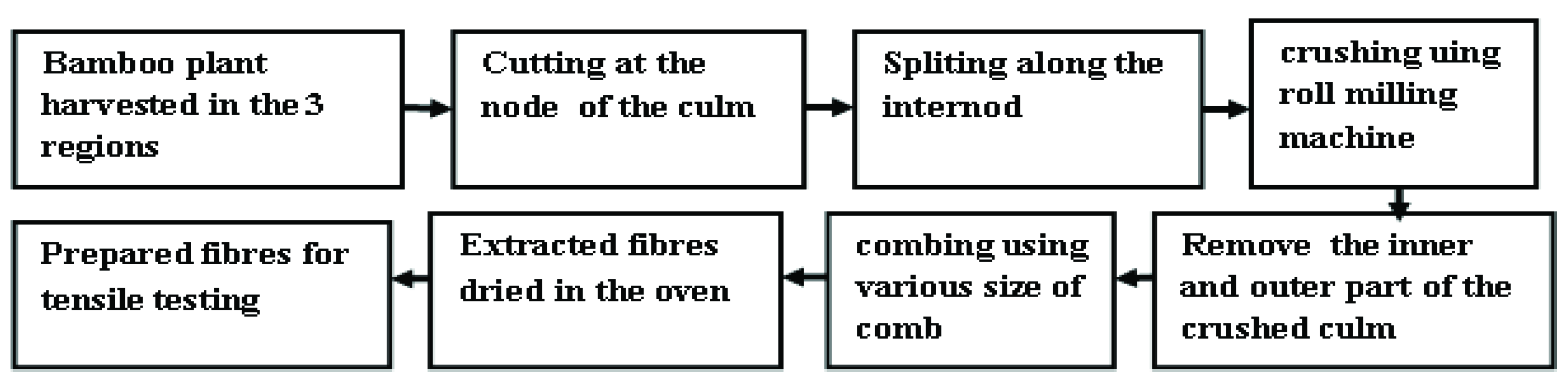
2.4. Extraction of Continuous Bamboo Fiber
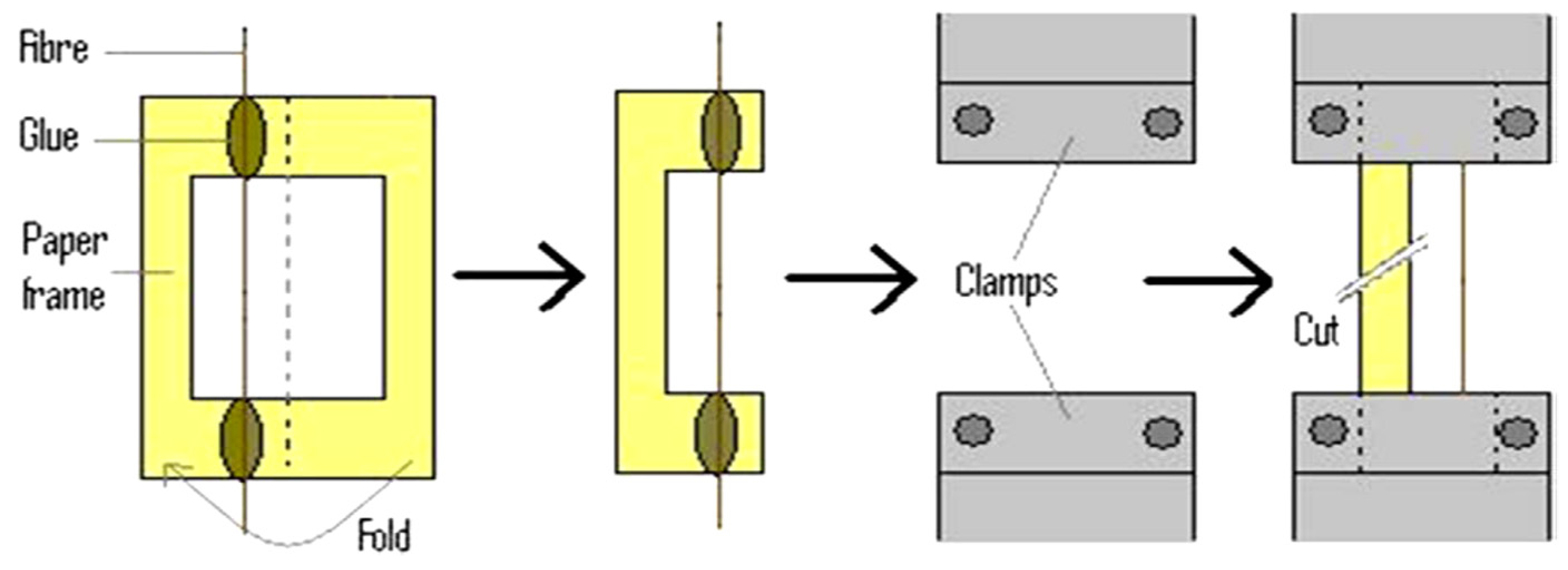
2.5. Tensile Test
2.6. Bamboo Fibers Cross-Section Area Measuring
3. Results and Discussions
3.1. Microstructure of Specimens
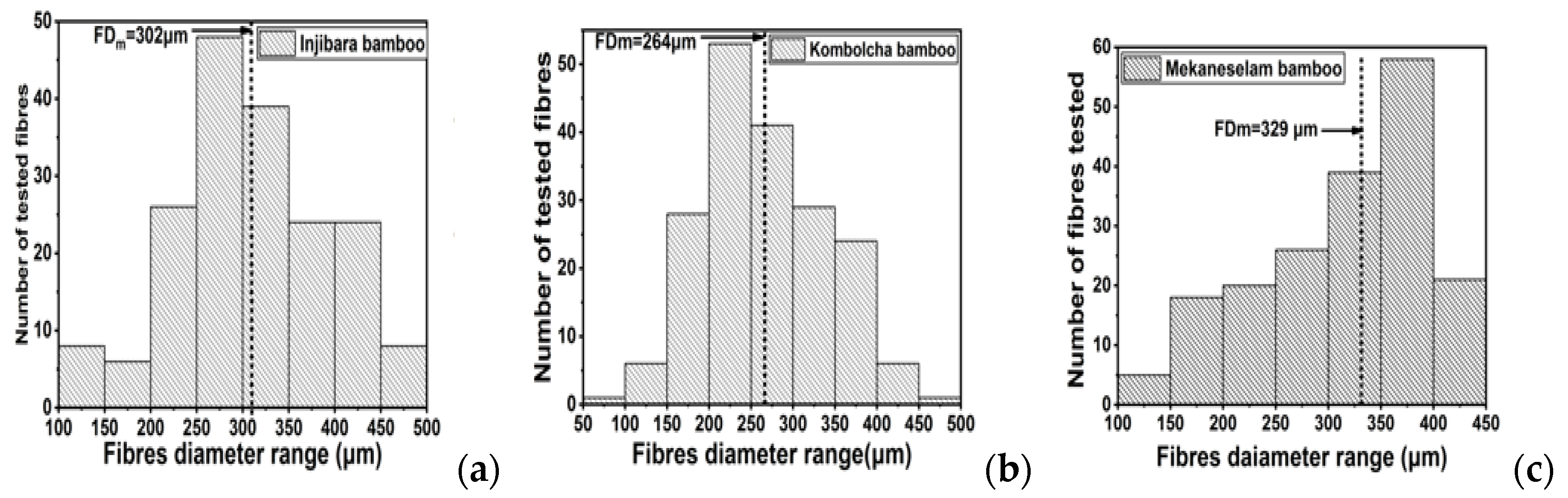
3.2. Description of the Fiber Diameters
3.3. Determination of Fiber Density
3.4. Correlation with Within-Fiber Diameter Variations
3.5. The Significance of Diameter for Fiber Strength
3.6. Measuring Tensile Strength
3.7. Effect of Tested Length on the Predictive Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emamverdian, A.; Ding, Y.; Ranaei, F.; Ahmad, Z. Application of Bamboo Plants in Nine Aspects. Sci. World J. 2020, 2020, 7284203. [Google Scholar] [CrossRef]
- Abdul Khalil, H.P.S.; Bhat, I.U.H.; Jawaid, M.; Zaidon, A.; Hermawan, D.; Hadi, Y.S. Bamboo fibre reinforced biocomposites: A review. Mater. Des. 2012, 42, 353–368. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, F.; Liang, W.; Wang, Z.; Duan, Z.; Yang, B. Thermal and mechanical properties of bamboo fiber reinforced epoxy composites. Polymers 2018, 8, 608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuentes, C.A.; Tran, L.Q.N.; Dupont-Gillain, C.; Vanderlinden, W.; De Feyter, S.; Van Vuure, A.W.; Verpoest, I. Wetting behaviour and surface properties of technical bamboo fibres. Colloids Surf. A Physicochem. Eng. Asp. 2011, 380, 89–99. [Google Scholar] [CrossRef]
- Supian, A.B.M.; Jawaid, M.; Rashid, B.; Fouad, H.; Saba, N.; Dhakal, H.N.; Khiari, R. Mechanical and physical performance of date palm/bamboo fibre reinforced epoxy hybrid composites. J. Mater. Res. Technol. 2021, 15, 1330–1341. [Google Scholar] [CrossRef]
- Javadian, A.; Smith, I.F.C.; Saeidi, N.; Hebel, D.E. Mechanical properties of bamboo through measurement of culm physical properties for composite fabrication of structural concrete reinforcement. Front. Mater. 2019, 6, 15. [Google Scholar] [CrossRef]
- Osorio, L.; Trujillo, E.; Lens, F.; Ivens, J.; Verpoest, I.; Van Vuure, A.W. In-depth study of the microstructure of bamboo fibres and their relation to the mechanical properties. J. Reinf. Plast. Compos. 2018, 37, 1099–1113. [Google Scholar] [CrossRef]
- Engelbrecht-Wiggans, A.; Phoenix, S.L. A Stochastic Model Based on Fiber Breakage and Matrix Creep for the Stress-Rupture Failure of Unidirectional Continuous Fiber Composites 2. Non-linear Matrix Creep Effects. Front. Phys. 2021, 9, 644815. [Google Scholar] [CrossRef]
- Xia, Z.P.; Yu, J.Y.; Cheng, L.D.; Liu, L.F.; Wang, W.M. Study on the breaking strength of jute fibres using modified Weibull distribution. Compos. Part A Appl. Sci. Manuf. 2009, 40, 54–59. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, H.; Wang, G.; Yu, Z.; Shi, S.Q. Tensile properties of bamboo in different sizes. J. Wood Sci. 2015, 61, 552–561. [Google Scholar] [CrossRef]
- Huang, Y.H.; Fei, B.H.; Yu, Y.; Zhao, R.J. Plant age effect on mechanical properties of moso bamboo (Phyllostachys heterocycla var. pubescens). Wood Fiber Sci. 2012, 44, 196–201. [Google Scholar]
- Yu, Y.; Tian, G.; Wang, H.; Fei, B.; Wang, G. Mechanical characterization of single bamboo fibers with nanoindentation and microtensile technique. Holzforschung 2011, 65, 113–119. [Google Scholar] [CrossRef]
- Wang, F.; Shao, Z. Study on the variation law of bamboo fibers’ tensile properties and the organization structure on the radial direction of bamboo stem. Ind. Crops Prod. 2020, 152, 112521. [Google Scholar] [CrossRef]
- Huang, X.; Netravali, A. Biodegradable green composites made using bamboo micro/nano-fibrils and chemically modified soy protein resin. Compos. Sci. Technol. 2009, 69, 1009–1015. [Google Scholar] [CrossRef]
- Barkoula, N.M.; Alcock, B.; Cabrera, N.O.; Peijs, T. Flame-Retardancy Properties of Intumescent Ammonium Poly(Phosphate) and Mineral Filler Magnesium Hydroxide in Combination with Graphene. Polym. Polym. Compos. 2008, 16, 101–113. [Google Scholar] [CrossRef]
- Trujillo, E.; Moesen, M.; Osorio, L.; Van Vuure, A.W.; Ivens, J.; Verpoest, I. Bamboo fibres for reinforcement in composite materials: Strength Weibull analysis. Compos. Part A Appl. Sci. Manuf. 2014, 61, 115–125. [Google Scholar] [CrossRef]
- Zok, F.W. On weakest link theory and Weibull statistics. J. Am. Ceram. Soc. 2017, 100, 1265–1268. [Google Scholar] [CrossRef]
- Shao, J.; Wang, F.; Li, L.; Zhang, J. Scaling analysis of the tensile strength of bamboo fibers using weibull statistics. Adv. Mater. Sci. Eng. 2013, 2013, 167823. [Google Scholar] [CrossRef] [Green Version]
- Defoirdt, N.; Biswas, S.; De Vriese, L.; Tran, L.Q.N.; Van Acker, J.; Ahsan, Q.; Gorbatikh, L.; Van Vuure, A.; Verpoest, I. Assessment of the tensile properties of coir, bamboo and jute fibre. Compos. Part A Appl. Sci. Manuf. 2010, 41, 588–595. [Google Scholar] [CrossRef] [Green Version]
- Watson, A.S.; Smith, R.L. An examination of statistical theories for fibrous materials in the light of experimental data. J. Mater. Sci. 1985, 20, 3260–3270. [Google Scholar] [CrossRef]
- Zaremba, L.S.; Smoleński, W.H. Optimal portfolio choice under a liability constraint. Ann. Oper. Res. 2000, 97, 131–141. [Google Scholar] [CrossRef]
- Sabiston, T.; Li, B.; Muhammad, W.; Kang, J.; Engler-Pinto, C. The Role of Fibre Length on the Fatigue Failure of Injection-Moulded Composites at Elevated Temperatures under a Range of Axial Loading Conditions. J. Compos. Sci. 2022, 6, 38. [Google Scholar] [CrossRef]
- Virk, A.S.; Hall, W.; Summerscales, J. Multiple Data Set (MDS) weak-link scaling analysis of jute fibres. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1764–1771. [Google Scholar] [CrossRef]
- Wang, F.; Shao, J. Modified Weibull distribution for analyzing the tensile strength of bamboo fibers. Polymers 2014, 6, 3005–3018. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, X.; Pan, N.; Postle, R. Weibull analysis of the tensile behavior of fibers with geometrical irregularities. J. Mater. Sci. 2002, 37, 1401–1406. [Google Scholar] [CrossRef] [Green Version]
- Shinde, A.B.; Veer, S.; Shinde, T.; Sagale, P.; Kamble, D.P. A Review on Extraction of Bamboo Fibres and Its Properties. Chemistry 2017, 6. [Google Scholar]
- Osorio, L.; Trujillo, E.; Van Vuure, A.W.; Verpoest, I. Morphological aspects and mechanical properties of single bamboo fibers and flexural characterization of bamboo/epoxy composites. J. Reinf. Plast. Compos. 2011, 30, 396–408. [Google Scholar] [CrossRef]
- Depuydt, D.E.C.; Soete, J.; Asfaw, Y.D.; Wevers, M.; Ivens, J.; van Vuure, A.W. Sorption behaviour of bamboo fibre reinforced composites, why do they retain their properties? Compos. Part A Appl. Sci. Manuf. 2019, 119, 48–60. [Google Scholar] [CrossRef]
- ASTM-C1557; ASTM Internasional ASTM C 1557: Standard Test Method for Tensile Strength and Young ’ s Modulus of Fibers. ASTM Internasional: West Conshohocken, PA, USA, 2003; pp. 1–10.
- Tomczak, F.; Sydenstricker, T.H.D.; Satyanarayana, K.G. Studies on lignocellulosic fibers of Brazil. Part II: Morphology and properties of Brazilian coconut fibers. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1710–1721. [Google Scholar] [CrossRef]
- Depuydt, D.; Hendrickx, K.; Biesmans, W.; Ivens, J.; Van Vuure, A.W. Digital image correlation as a strain measurement technique for fibre tensile tests. Compos. Part A Appl. Sci. Manuf. 2017, 99, 76–83. [Google Scholar] [CrossRef]
- Hamburg, U. On the Anatomy of Asian Bamboos, with Special Reference to their Vascular Bundles. Wood Sci. Technol. 1971, 5, 290–312. [Google Scholar]
- Li, H.; Shen, S. The mechanical properties of bamboo and vascular bundles. J. Mater. Res. 2011, 26, 2749–2756. [Google Scholar] [CrossRef]
- Depuydt, D.E.C.; Sweygers, N.; Appels, L.; Ivens, J.; Van Vuure, A.W. Bamboo fibres sourced from three global locations: A microstructural, mechanical and chemical composition study. J. Reinf. Plast. Compos. 2019, 38, 397–412. [Google Scholar] [CrossRef]
- Ivanov, Y.; Valerii Cheshkov, M.N. Polymer Composite Materials; Kluwer Academic Publishers: Alphen, The Netherland, 2001; ISBN 9789460188831. [Google Scholar]
- Edy Pramono, A.; Rebet, I.; Zulfia, A. Tensile and Shear Punch Properties of Bamboo Fibers Reinforced Polymer Composites. Int. J. Compos. Mater. 2015, 5, 9–17. [Google Scholar] [CrossRef]
- Wang, X.; Pan, N. Deakin Research Online Deakin University’ s Institutional Research Repository; Deakin University: Melbourne, Austrlia, 2002. [Google Scholar]




| Name of Testing Sites | Administrative Location of the Testing Site | Climate, Average Value | |||||
|---|---|---|---|---|---|---|---|
| Zone | Region | Lat-Long | Alt. (m) | An.RF (mm) | Max. Temp. (°C) | Min. Temp. (°C) | |
| Injibara | Awi | Amahara | 10°59′ N 36°55′ E | 2540–2865 | 1813 | 24 | 14 |
| Kombolcha | S/wollo | Amahara | 11°5′ N 39°44′ E | 1842–1915 | 1027 | 26 | 20 |
| Mekaneselam | S/wollo | Amahara | 10°45′ N 38°45′ E | 2605–3000 | 1048 | 21 | 10 |
| Bamboo Species | Gauge Length (mm) | Sensitivity Parameter (γ) | Shape Parameter (β) | Characteristic Strength (MPa) | Ref. |
|---|---|---|---|---|---|
| Injibara | 15 | 0.63 | 6.24 | 642 | |
| 25 | 0.63 | 7.66 | 617 | ||
| 30 | 0.63 | 6.40 | 595 | study | |
| 40 | 0.63 | 6.02 | 582 | ||
| 50 | 0.63 | 7.83 | 459 | ||
| Kombolcha | 15 | 0.33 | 10.21 | 638 | |
| 25 | 0.33 | 6.58 | 470 | ||
| 30 | 0.33 | 5.87 | 438 | study | |
| 40 | 0.33 | 7.32 | 425 | ||
| 50 | 0.33 | 7.33 | 408 | ||
| Mekaneselam | 15 | 0.33 | 9.63 | 597 | |
| 25 | 0.33 | 6.05 | 568 | ||
| 30 | 0.33 | 6.18 | 552 | study | |
| 40 | 0.33 | 5.87 | 488 | ||
| 50 | 0.33 | 8.36 | 474 | ||
| Literature | 10–100 | - | 6.3–7.9 | 197–201 | [25] |
| 5–20 | - | 1.19–2.18 | 377–436 | [9] | |
| 20–50 | - | 3.22–4.77 | 402–566 | [24] | |
| 20 | - | 4.02 | 612 | [36] | |
| 5–35 | - | 3.5–9.3 | 683–855 | [35] | |
| 1–40 | 0.48 | 7.6 | 982 | [16] |
| Bamboo Species | Gauge Length (mm) | Average Fiber Diameter (μm) | Average Strength All Fibers (MPa) | Average Strength “Thin” Fibers (MPa) | Average Strength “Thick” Fibers (MPa) | p-Value “Thin” and ”Thick” Fiber (α = 0.05) | R-Square (Linear Regression) |
|---|---|---|---|---|---|---|---|
| Injibara | 15 | 296 ± 33 | 600 ± 105 | 602 ± 79 | 597 ± 128 | 0.876 | 0.0007 |
| 25 | 339 ± 51 | 580 ± 81 | 512 ± 58 | 648 ± 23 | 0.000 | 0.7101 | |
| 30 | 327 ± 62 | 553 ± 90 | 560 ± 62 | 545 ± 75 | 0.000 | 0.6174 | |
| 40 | 275 ± 58 | 542 ± 100 | 563 ± 107 | 522 ± 91 | 0.207 | 0.0416 | |
| 50 | 340 ± 78 | 432 ± 59 | 431 ± 52 | 433 ± 68 | 0.916 | 0.0006 | |
| Kombolcha | 15 | 253 ± 33 | 608 ± 66 | 614 ± 68 | 602 ± 65 | 0.57 | 0.0086 |
| 25 | 248 ± 37 | 423 ± 83 | 414 ± 80 | 432 ± 74 | 0.479 | 0.0133 | |
| 30 | 256 ± 41 | 385 ± 73 | 512 ± 70 | 374 ± 76 | 0.372 | 0.021 | |
| 40 | 276 ± 47 | 378 ± 69 | 376 ± 59 | 380 ± 80 | 0.868 | 0.0007 | |
| 50 | 322 ± 64 | 360 ± 60 | 390 ± 75 | 386 ± 52 | 0.908 | 0.0005 | |
| Mekaneselam | 15 | 299 ± 45 | 566 ± 65 | 590 ± 68 | 543 ± 55 | 0.022 | 0.1314 |
| 25 | 309 ± 49 | 528 ± 94 | 531 ± 98 | 524 ± 94 | 0.817 | 0.0014 | |
| 30 | 317 ± 57 | 515 ± 93 | 527 ± 102 | 504 ± 86 | 0.442 | 0.0157 | |
| 40 | 339 ± 68 | 452 ± 84 | 454 ± 84 | 451 ± 86 | 0.925 | 0.0002 | |
| 50 | 320 ± 70 | 448 ± 57 | 438 ± 72 | 433 ± 54 | 0.903 | 0.0006 |
| Bamboo Species | Gauge Length (mm) | Diameter (μm) | CVFD (%) | Fiber Strength (MPa) | Young’s Modulus (GPa) | Breaking Strain (%) | Ref. |
|---|---|---|---|---|---|---|---|
| Injibara | 15 | 296 ± 33 | 11 | 600 ± 105 | 50 ± 8 | 1.24 ± 0.24 | |
| 25 | 339 ± 51 | 15 | 580 ± 81 | 33 ± 5 | 1.45 ± 0.17 | study | |
| 30 | 327 ± 62 | 19 | 553 ± 90 | 32 ± 6 | 1.54 ± 0.30 | ||
| 40 | 275 ± 58 | 21 | 542 ± 100 | 30 ± 4 | 1.62 ± 0.25 | ||
| 50 | 340 ± 78 | 23 | 432 ± 59 | 28 ± 5 | 1.56 ± 0.27 | ||
| Kombolcha | 15 | 253 ± 33 | 13 | 508 ± 66 | 48 ± 10 | 1.04 ± 0.18 | |
| 25 | 248 ± 37 | 15 | 470 ± 83 | 38 ± 5 | 1.19 ± 0.24 | ||
| 30 | 256 ± 41 | 16 | 385 ± 73 | 30 ± 4 | 1.21 ± 0.16 | study | |
| 40 | 276 ± 47 | 17 | 378 ± 69 | 27 ± 5 | 1.45 ± 0.25 | ||
| 50 | 322 ± 64 | 20 | 400 ± 60 | 21 ± 3 | 1.57 ± 0.32 | ||
| Mekaneselam | 15 | 299 ± 45 | 15 | 566 ± 65 | 55 ± 7 | 1.08 ± 0.25 | |
| 25 | 309 ± 49 | 16 | 528 ± 94 | 43 ± 8 | 1.43 ± 0.31 | ||
| 30 | 317 ± 57 | 18 | 515 ± 93 | 42 ± 5 | 1.46 ± 0.27 | study | |
| 40 | 339 ± 68 | 20 | 452 ± 84 | 28 ± 5 | 1.59 ± 0.23 | ||
| 50 | 320 ± 70 | 22 | 448 ± 57 | 26 ± 5 | 1.78 ± 0.38 | ||
| Literature | 10–100 | 24–26 | 9–13 | 201–213 | - | - | [25] |
| 20–60 | - | 6–7 | 352–518 | - | - | [24] | |
| 1–40 | 132–146 | - | 790–943 | - | - | [16] | |
| 20–60 | - | - | 442–555 | - | - | [36] | |
| 5–35 | 366 | - | 639–813 | 33 | 2.0–2.9 | [35] | |
| 50 | - | - | 658 | 52 | 1.33 | [31] |
| Bamboo Species | Gauge Length (mm) | Measured Strength (Mpa) | Weibull Strength (Mpa) | Modified Weibull Strength (Mpa) |
|---|---|---|---|---|
| Injibara | 15 | 600 ± 105 | 600 | 600 |
| 25 | 580 ± 81 | 552 | 570 | |
| 30 | 553 ± 90 | 537 | 559 | |
| 40 | 542 ± 100 | 512 | 543 | |
| 50 | 432 ± 59 | 494 | 531 | |
| Kombolcha | 15 | 508 ± 66 | 508 | 508 |
| 25 | 470 ± 83 | 578 | 500 | |
| 30 | 385 ± 73 | 568 | 497 | |
| 40 | 378 ± 69 | 552 | 492 | |
| 50 | 370 ± 60 | 540 | 489 | |
| Mekaneselam | 15 | 566 ± 65 | 566 | 566 |
| 25 | 528 ± 94 | 537 | 556 | |
| 30 | 515 ± 93 | 527 | 553 | |
| 40 | 452 ± 84 | 511 | 547 | |
| 50 | 448 ± 57 | 499 | 543 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dessalegn, Y.; Singh, B.; Vuure, A.W.v.; Badruddin, I.A.; Beri, H.; Hussien, M.; Ahmed, G.M.S.; Hossain, N. Investigation of Bamboo Fibrous Tensile Strength Using Modified Weibull Distribution. Materials 2022, 15, 5016. https://doi.org/10.3390/ma15145016
Dessalegn Y, Singh B, Vuure AWv, Badruddin IA, Beri H, Hussien M, Ahmed GMS, Hossain N. Investigation of Bamboo Fibrous Tensile Strength Using Modified Weibull Distribution. Materials. 2022; 15(14):5016. https://doi.org/10.3390/ma15145016
Chicago/Turabian StyleDessalegn, Yalew, Balkeshwar Singh, Aart W. van Vuure, Irfan Anjum Badruddin, Habtamu Beri, Mohamed Hussien, Gulam Mohammed Sayeed Ahmed, and Nazia Hossain. 2022. "Investigation of Bamboo Fibrous Tensile Strength Using Modified Weibull Distribution" Materials 15, no. 14: 5016. https://doi.org/10.3390/ma15145016
APA StyleDessalegn, Y., Singh, B., Vuure, A. W. v., Badruddin, I. A., Beri, H., Hussien, M., Ahmed, G. M. S., & Hossain, N. (2022). Investigation of Bamboo Fibrous Tensile Strength Using Modified Weibull Distribution. Materials, 15(14), 5016. https://doi.org/10.3390/ma15145016







