Microstructure Evolution Mechanism of Ultra-Thin Dual Phase Magnesium–Lithium Alloy during Asymmetric Warm Rolling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment
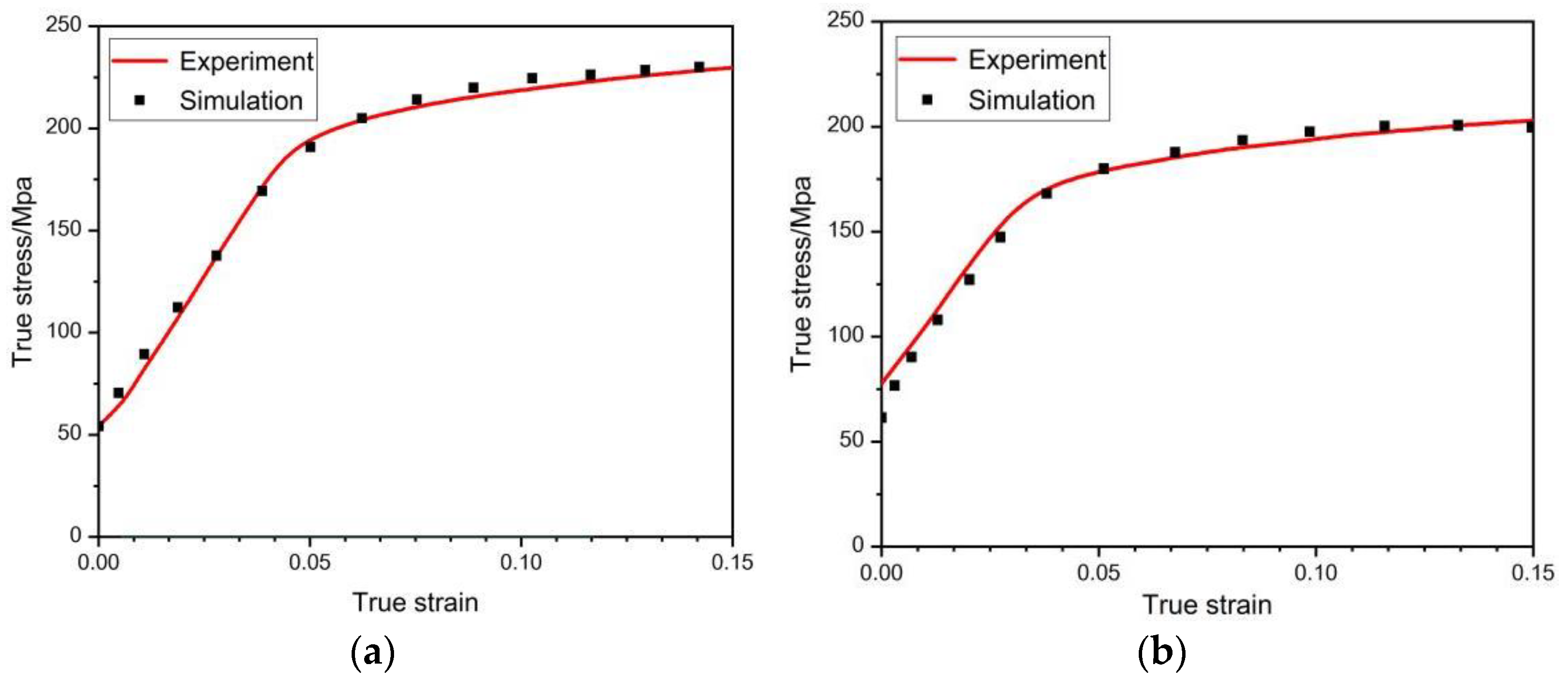
2.2. Simulation
3. Results and Discussions
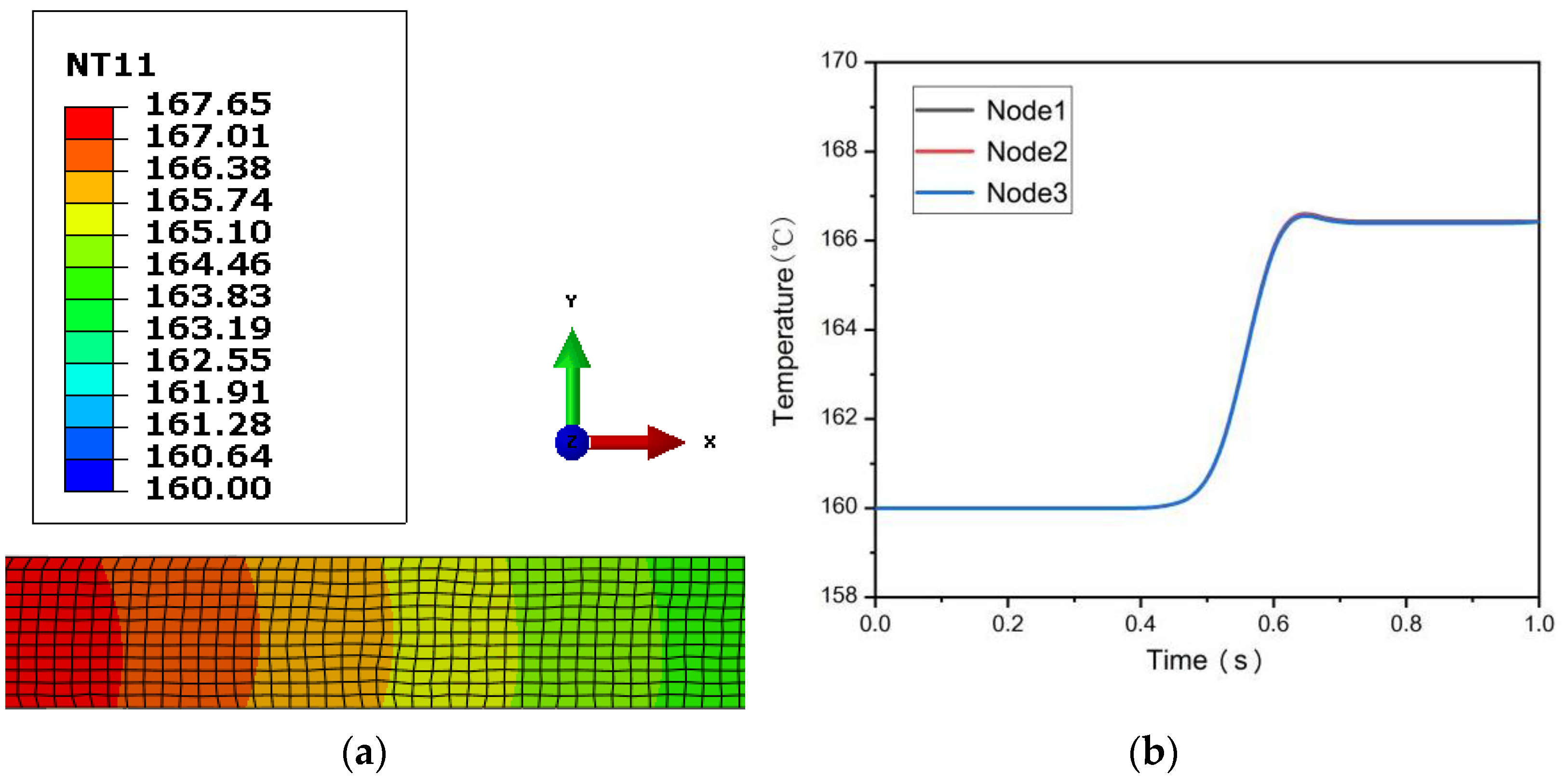
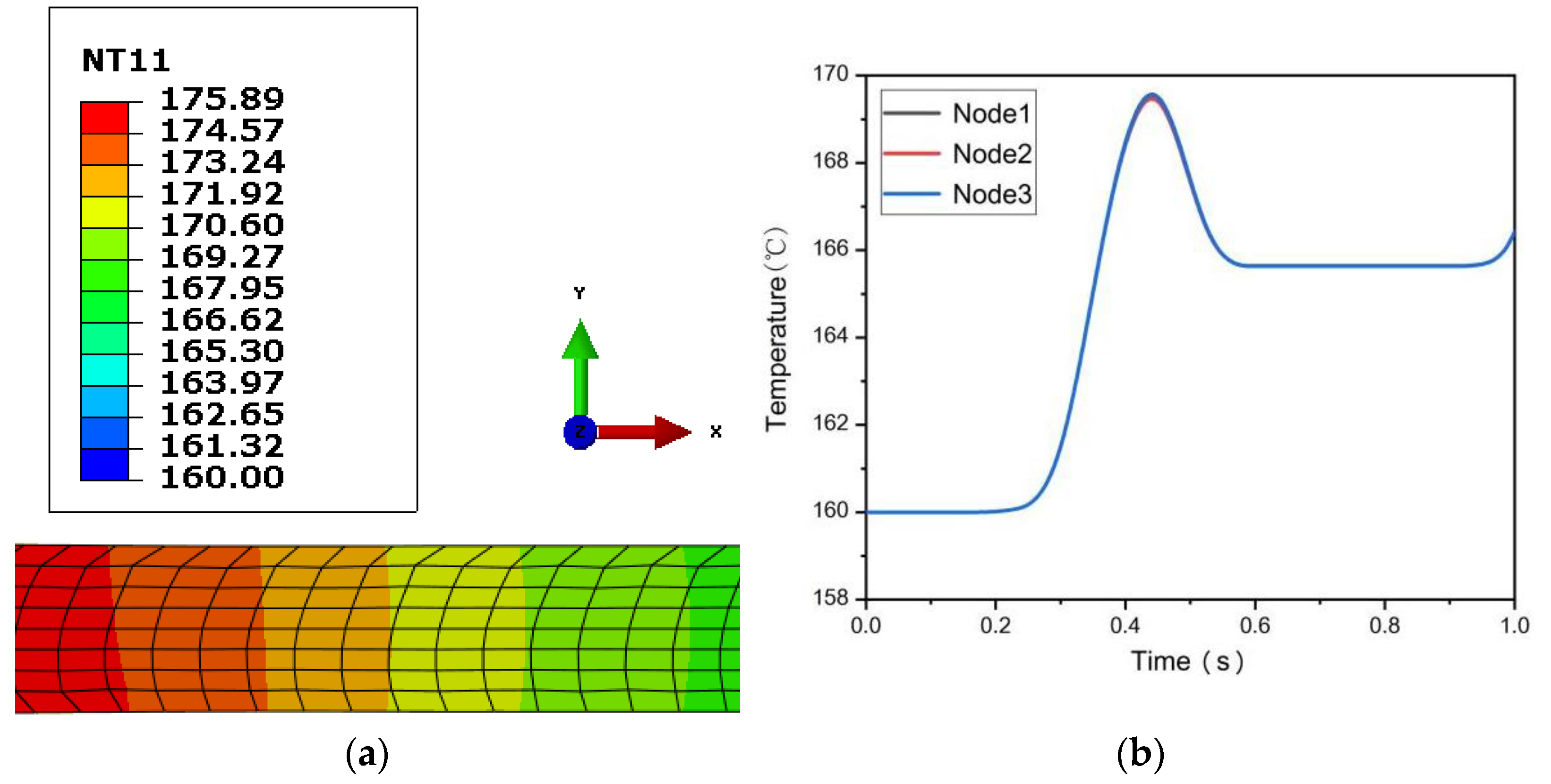
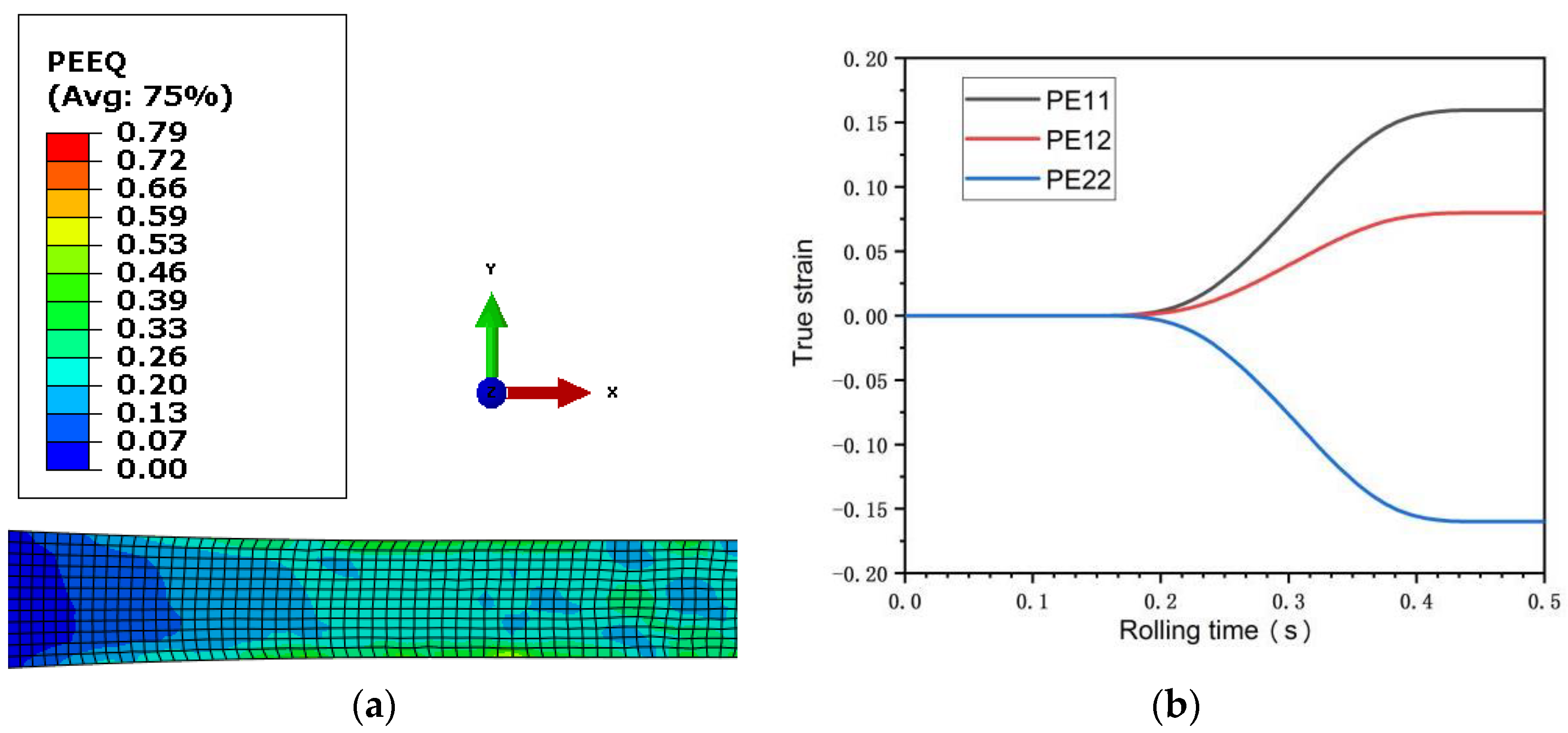
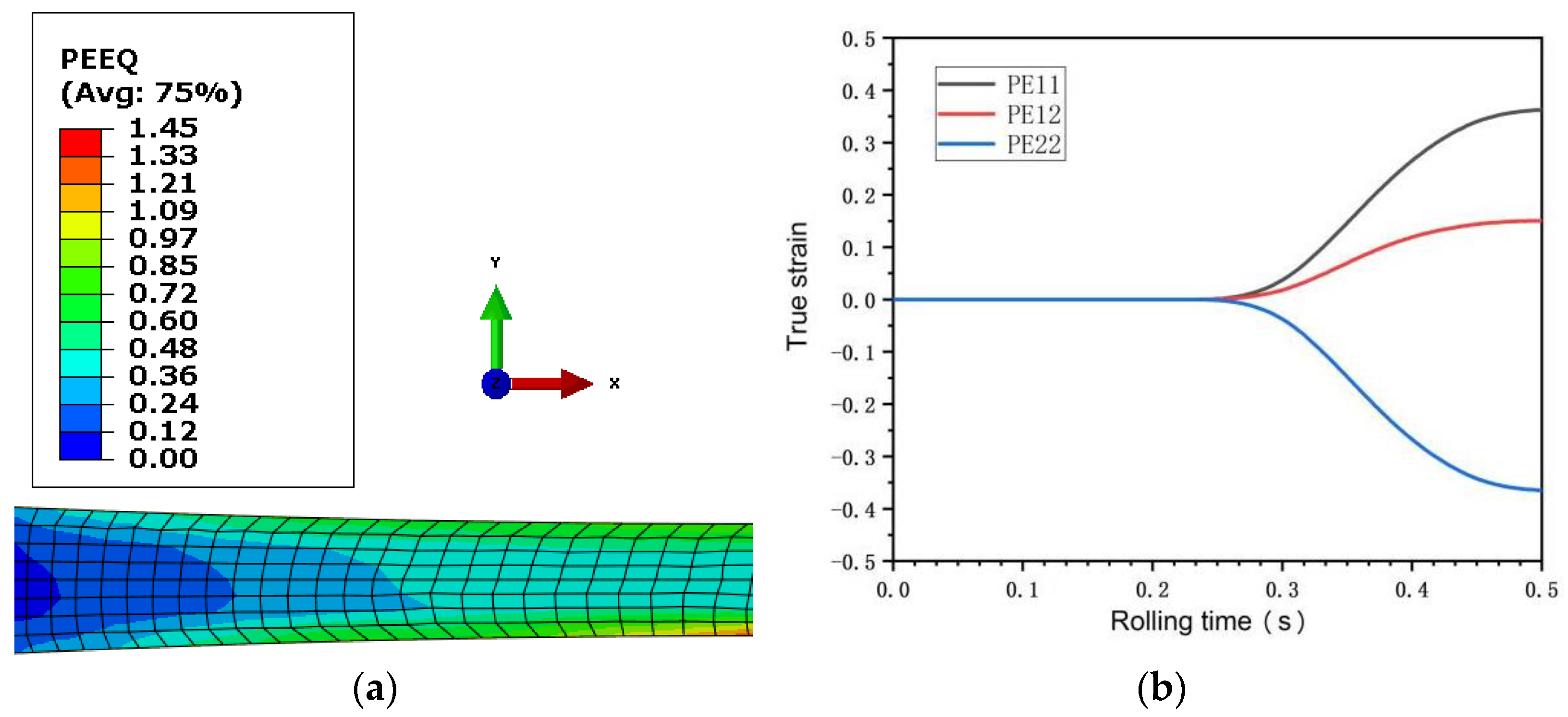
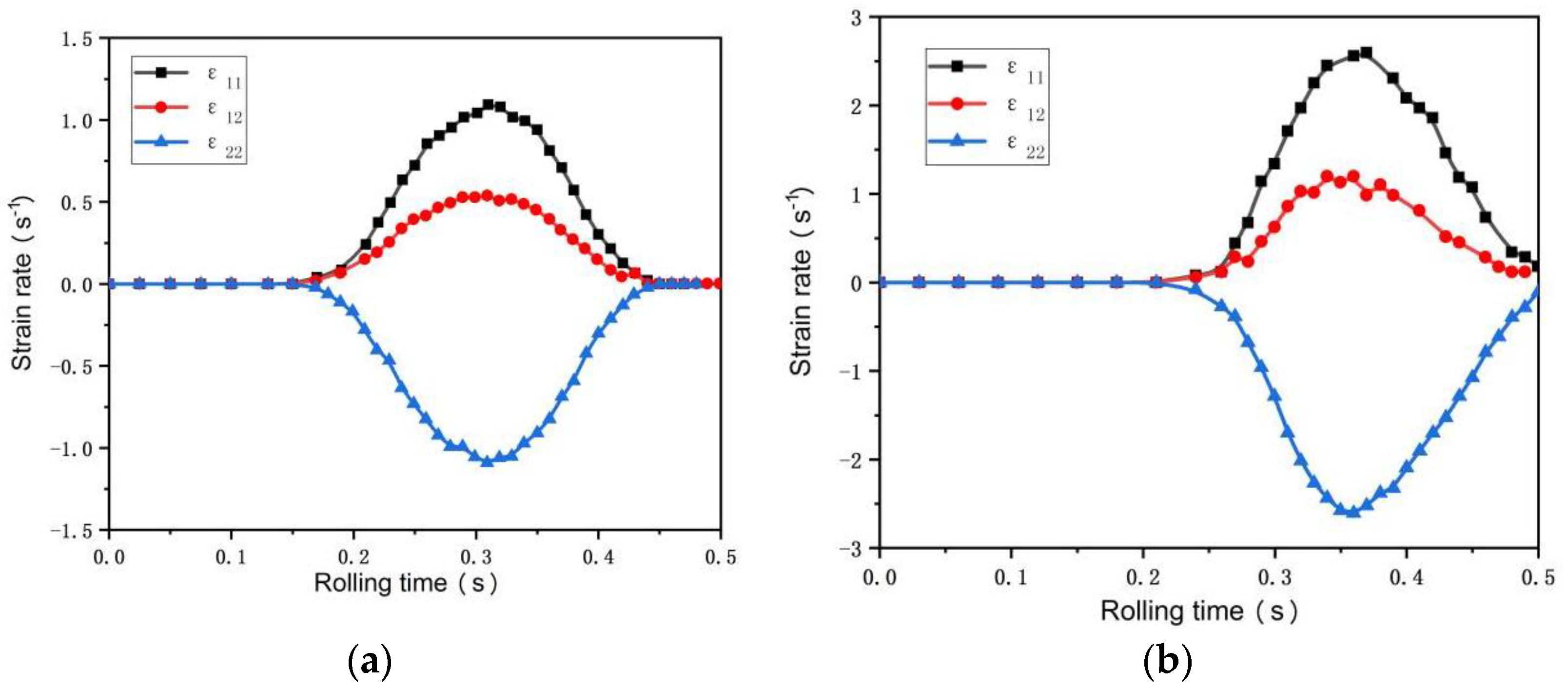
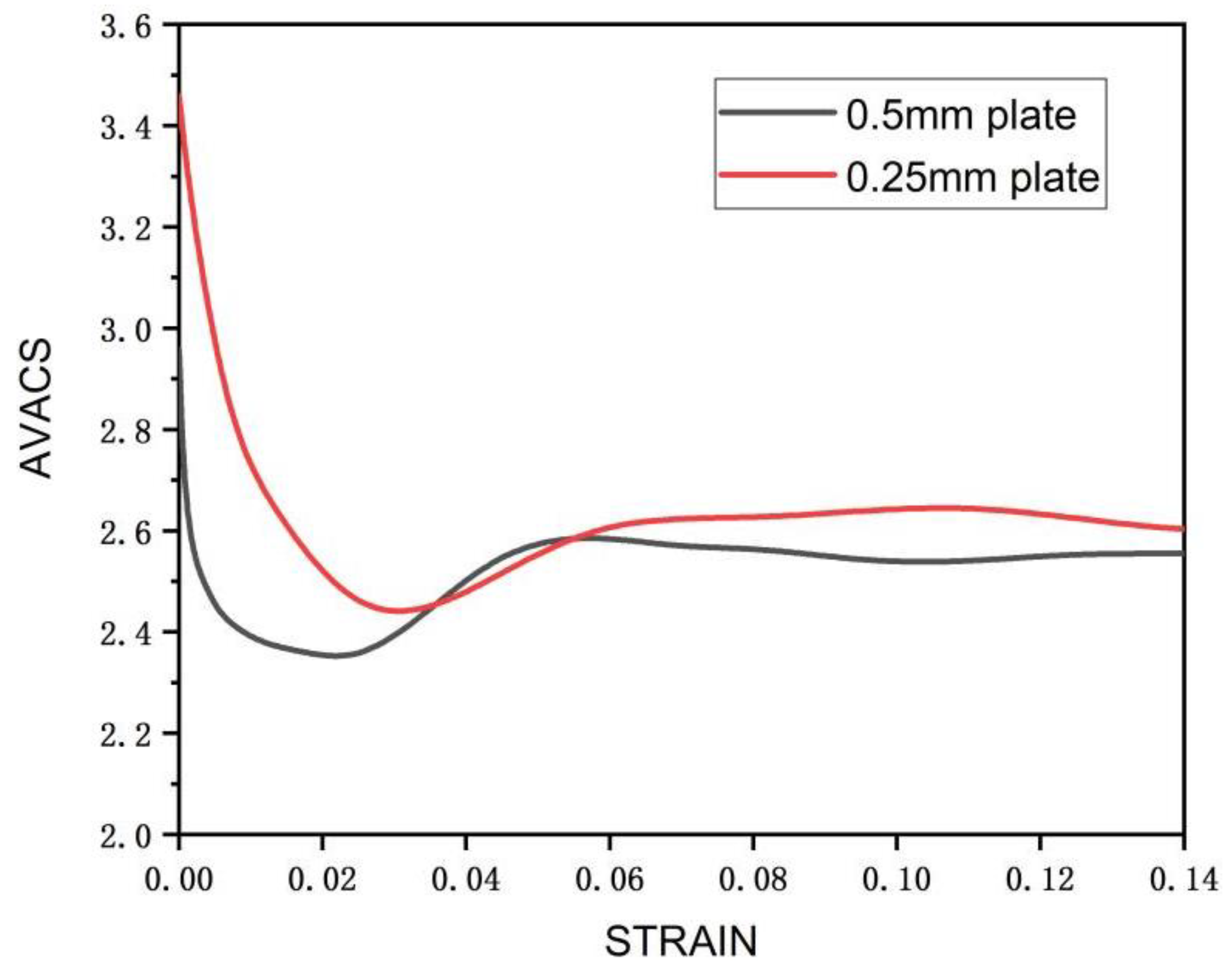
3.1. FEM Results Analysis
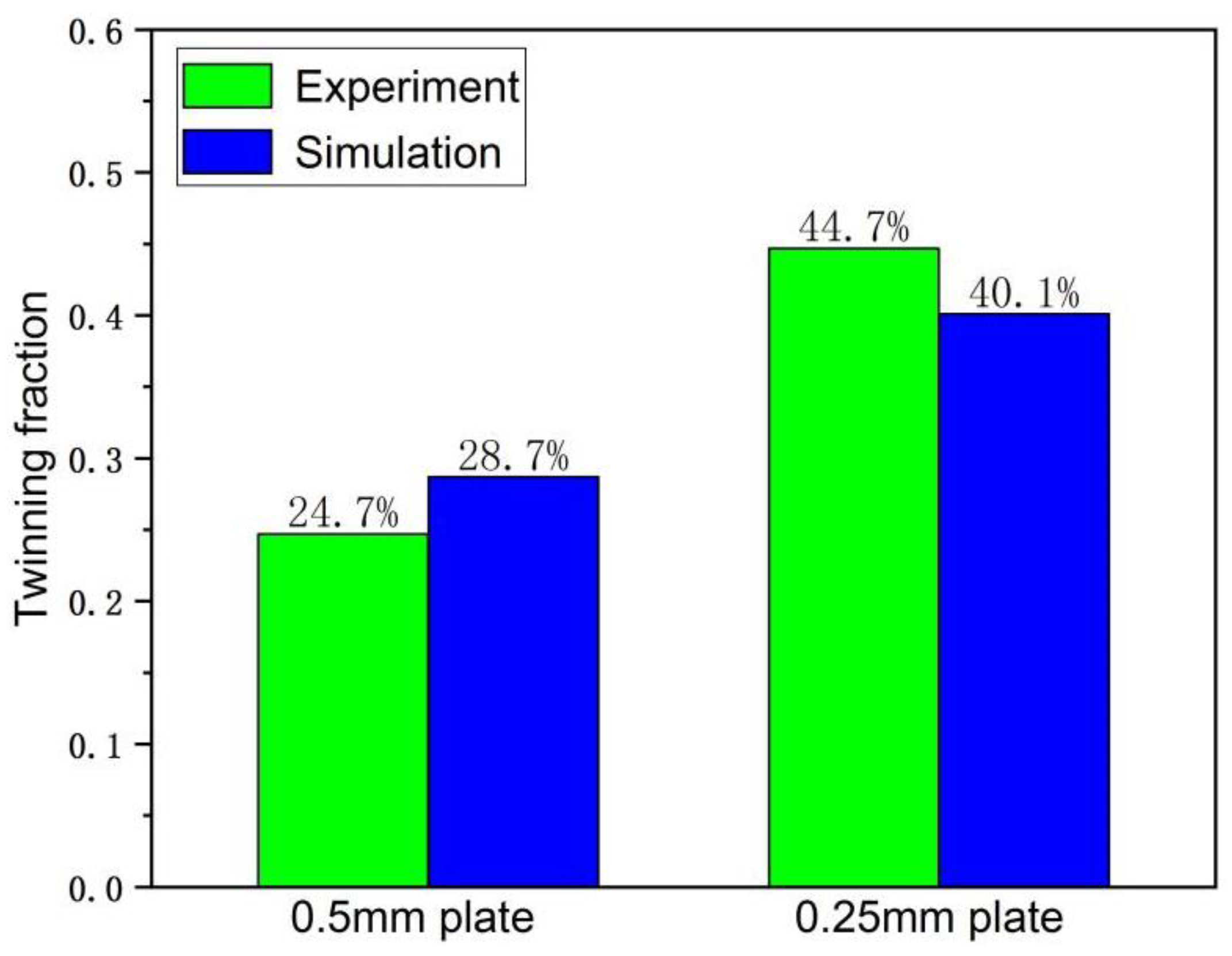
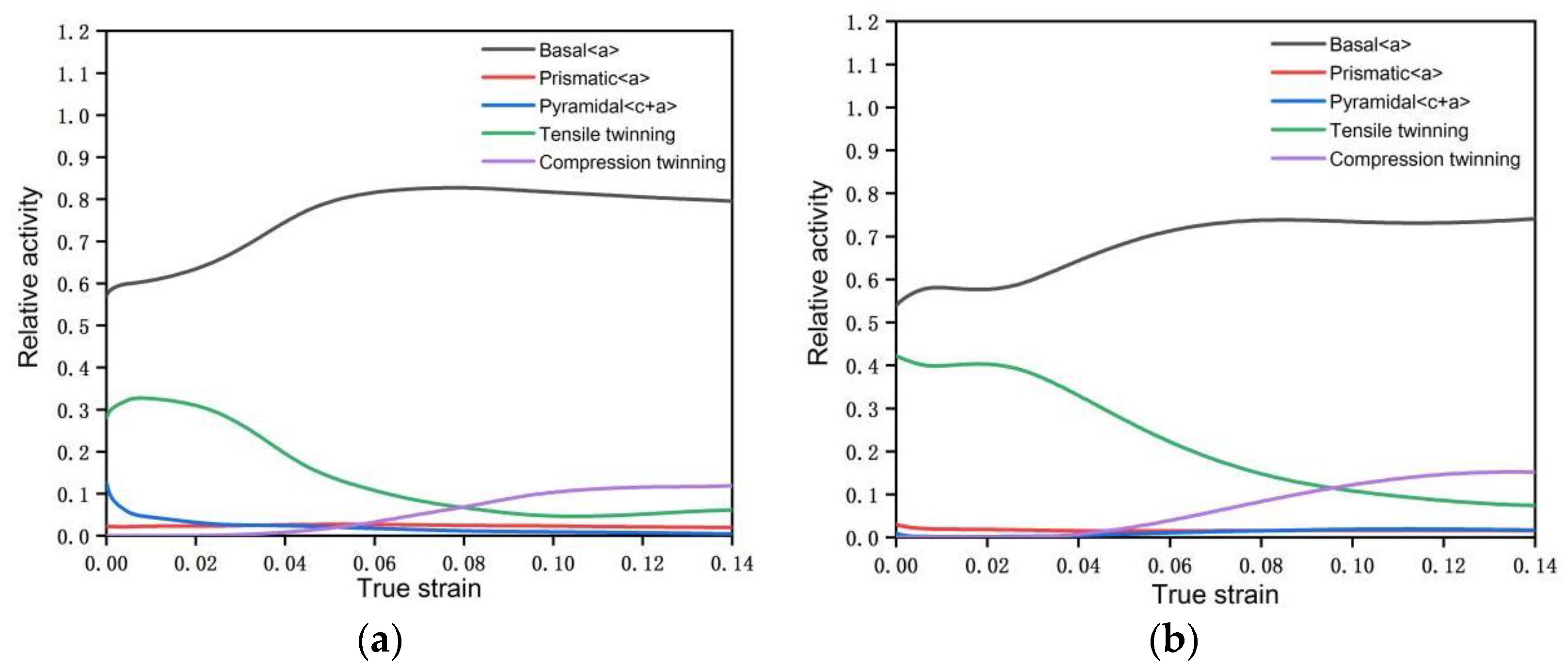
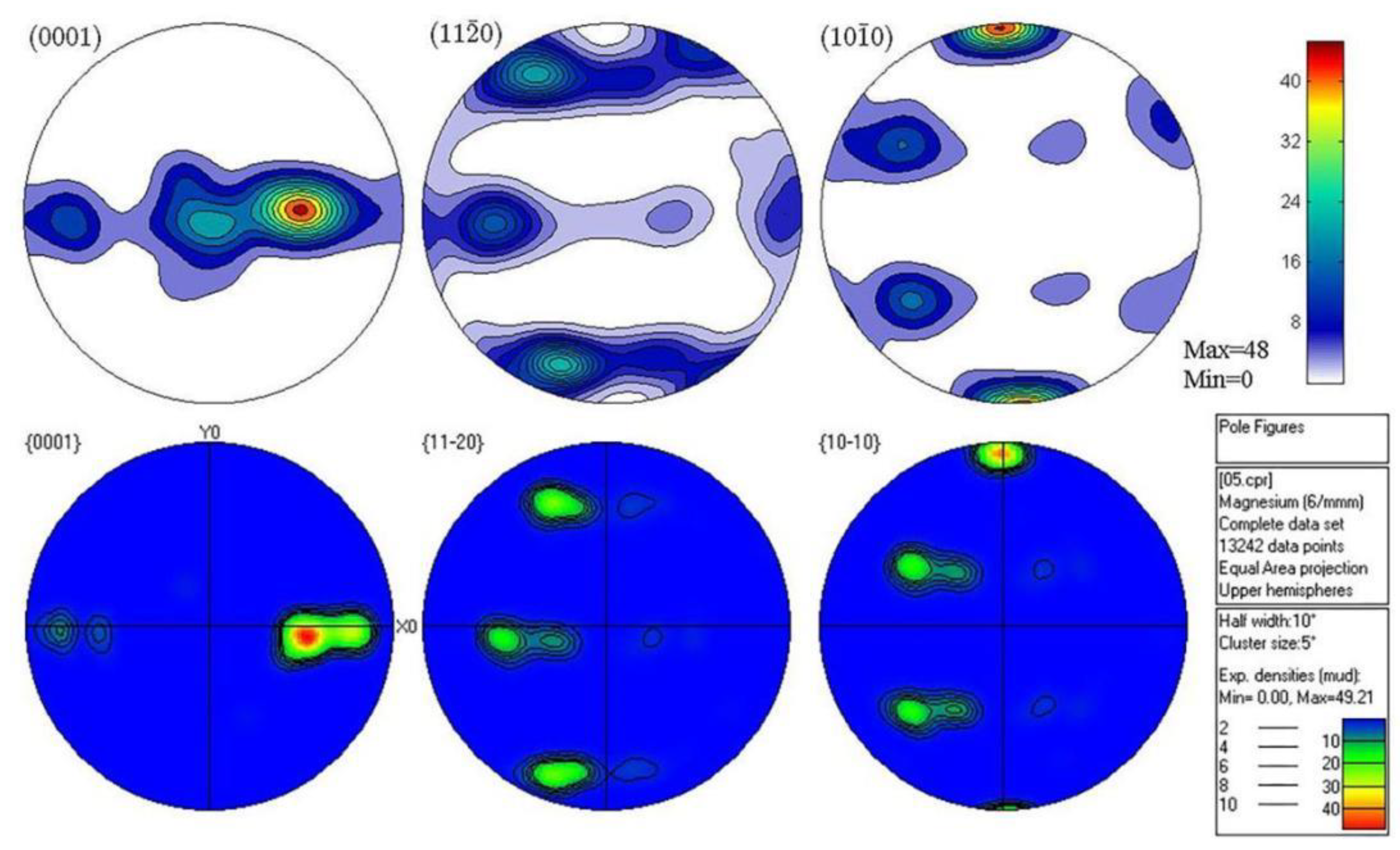
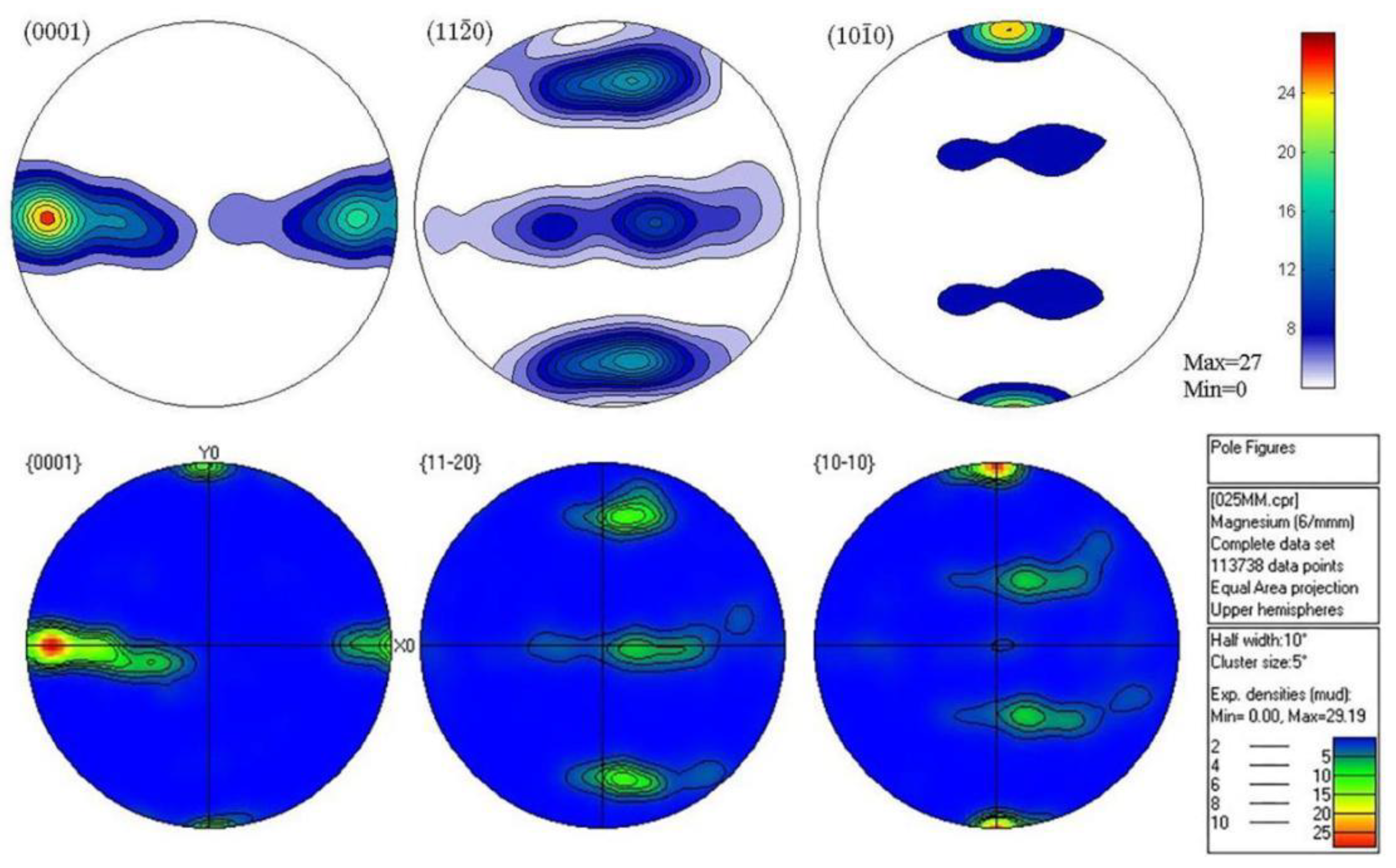
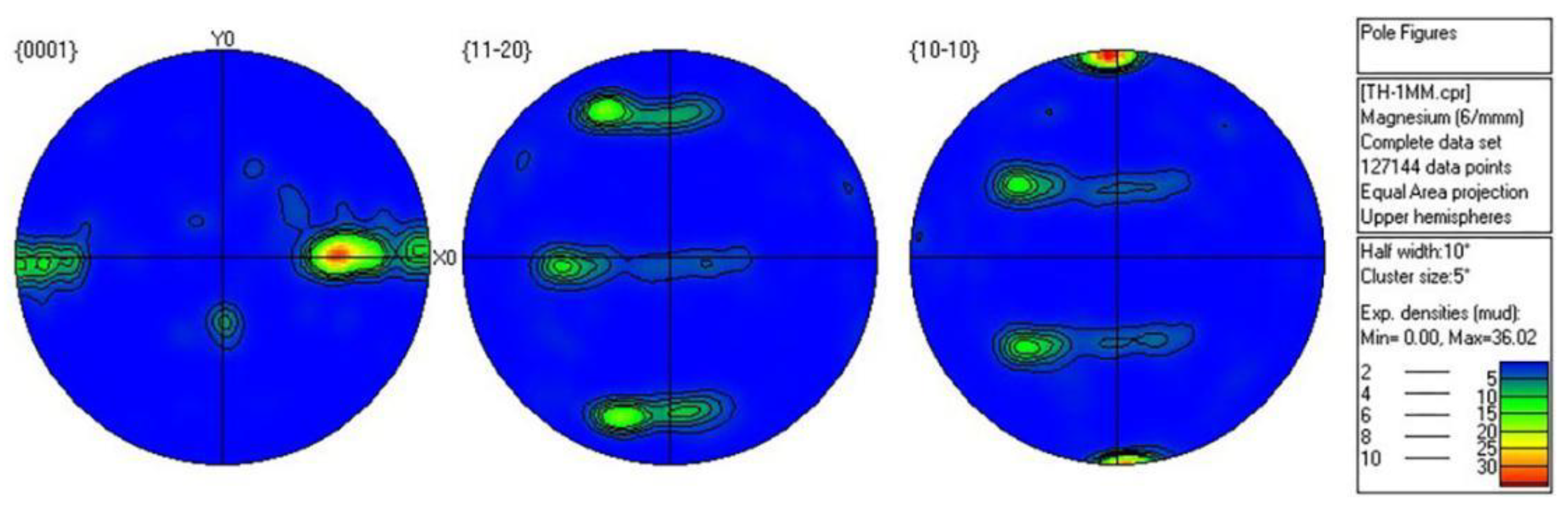
3.2. VPSC Calculation and EBSD Experimental Results Analysis
3.3. Tensile Results Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.B.; Ma, Y.W.; Lou, M.; Lei, H.Y.; Lin, Z.Q. Advances in welding and joining processes of multi-material lightweight car body. Mech. Eng. J. 2016, 52, 1–23. [Google Scholar] [CrossRef]
- Rahulan, N.; Gopalan, S.; Kumaran, S. Mechanical behavior of Mg-Li-Al alloys. Mater. Today 2016, 5, 17935–17943. [Google Scholar] [CrossRef]
- Islam, R.; Haghshenas, M. Statistical optimization of stress level in Mg-Li-Al alloys upon hot compression testing. J. Magnes. Alloy 2019, 7, 203–217. [Google Scholar] [CrossRef]
- Shin, I.; Carter, E.A. First-principles simulations of plasticity in body-centered-cubic magnesium-lithium alloys. Acta Mater. 2014, 64, 198–207. [Google Scholar] [CrossRef]
- Xu, T.C.; Peng, X.D.; Qin, J.; Chen, Y.F.; Yang, Y.; Wei, G.B. Dynamic recrystallization behavior of Mg-Li-Al-Nd duplex alloy during hot compression. J. Alloys Compd. 2015, 639, 79–88. [Google Scholar] [CrossRef]
- Li, J.; Jin, L.; Wang, F.; Dong, S.; Dong, J. Effect of phase morphology on microscopic deformation behavior of Mg–Li–Gd dual-phase alloys. Mater. Sci. Eng. 2021, 809, 140871. [Google Scholar] [CrossRef]
- Gasior, W.; Moser, Z.; Zakulski, W.; Schwitzgebel, G. Thermodynamic studies and the phase diagram of the Li-Mg system. Metall. Mater. Trans. A 1996, 27, 2419–2428. [Google Scholar] [CrossRef]
- Catorceno, L.L.C.; Abreu, H.F.G.; Padilha, A.F. Effects of cold and warm cross-rolling on microstructure and texture evolution of AZ31B magnesium alloy sheet. J. Magnes. Alloy 2019, 6, 121–133. [Google Scholar] [CrossRef]
- Xu, D.K.; Li, C.Q.; Wang, B.J.; Han, E.H. Effect of icosahedral phase on the crystallographic texture and mechanical anisotropy of duplex structured Mg-Li alloys. Mater. Des. 2015, 88, 88–97. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, L.; Mansoor, A.; Liu, K.; Li, S.; Du, W. Microstructures and mechanical properties of as-extruded Mg-8Gd-2Y-1Zn-6Li alloy. J. Alloys Compd. 2021, 864, 158826. [Google Scholar] [CrossRef]
- Liu, J.W.; Zhao, Z.G.; Lu, S.Q. Microstructure evolution and constitutive equation for the hot deformation of LZ91 Mg alloy. Catal. Today 2017, 318, 119–125. [Google Scholar]
- Liu, M.D.; Zheng, H.P.; Zhang, T.L.; Wu, R.Z. The deformation behavior and microstructure evolution of duplex Mg-9Li-1Al alloy during superplasticity tensile testing. Mater. Sci. Eng. 2017, 274, 012113. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Yang, Y.; Zhou, G.; Ren, F.J.; Deng, H.J.; Wei, G.B. Effect of rolling reduction and annealing process on microstructure and corrosion behavior of LZ91 alloy sheet. Trans. Nonferrous Met. Soc. China 2020, 30, 1816–1825. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.W.; Dai, M.H.; Zhang, Y.; Yao, J. Constitutive model and microstructure evolution of LZ91 magnesium lithium alloy during hot deformation. Trans. Mater. Heat Treat. 2021, 42, 167–174. [Google Scholar]
- Vinod, K.; Rajiv, S.; Kantesh, B. Microstructure and Texture Evolution during Hot Rolling of Mg-9Li-7Al-1Sn Alloy for Aerospace Application. Mater. Sci. Forum 2011, 702–703, 85–88. [Google Scholar]
- Li, X.Y.; Li, X.L.; Guo, F.; Jiang, L.Y.; Hu, H.J.; Yang, M.B. Research progress on recrystallization texture and its modification of magnesium alloys. Trans. Mater. Heat Treat. 2020, 41, 17–29. [Google Scholar]
- Chaudry, U.M.; Hamad, K.; Kim, J.G. Ca-induced Plasticity in Magnesium Alloy: EBSD Measurements and VPSC Calculations. Crystals 2020, 10, 67. [Google Scholar] [CrossRef] [Green Version]
- Chapuis, A.; Liu, Q. Modeling strain rate sensitivity and high temperature deformation of Mg-3Al-1Zn alloy. J. Magnes. Alloy 2010, 7, 433–443. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Zecevic, M.; Knezevic, M.; McCabe, R.J. Average intragranular misorientation trends in polycrystalline materials predicted by a viscoplastic self-consistent approach. Acta Mater. 2016, 104, 228–236. [Google Scholar] [CrossRef] [Green Version]
- Kang, G.P.; Lee, K.; Kim, Y.H.; Park, S.J.; Shin, K.S. Implementation of VPSC polycrystal model into rigid plastic finite element method and its application to Erichsen test of Mg alloy. Met. Mater. Int. 2016, 23, 930–939. [Google Scholar] [CrossRef]
- Zhou, S.L.; Liu, W.; Fu, S.C. Constitutive modelling of LZ91 magnesium-lithium alloy sheet by uniaxial tension loading tests. Mater. Today 2020, 33, 1787–1791. [Google Scholar] [CrossRef]
- Zhong, F.; Wu, H.; Jiao, Y.; Wu, R.; Zhang, J.; Hou, L. Effect of Y and Ce on the microstructure, mechanical properties and anisotropy of as-rolled Mg-8Li-1Al alloy. J. Mater. Sci. Technol. 2020, 39, 124–134. [Google Scholar] [CrossRef]
- Tang, Y.; Le, Q.C.; Jia, W.T.; Liu, X.; Cui, J.Z. Influences of warm rolling and annealing processes on microstructure and mechanical properties of three parent structures containing Mg-Li alloys. Mater. Sci. Eng. A 2018, 711, 1–11. [Google Scholar] [CrossRef]
- Shah, S.S.A.; Sang, H.; Sun, B.L.; Bian, M.Z.; Jing, H.M.; Song, G.S. Microhardness and Texture Evolution of Ultralight Mg–Li Alloy Processed by Cold Rolling. Russ. J. Non-Ferr. Met. 2020, 61, 280–290. [Google Scholar] [CrossRef]
- Shen, G.J.; Duggan, B.J. Texture Development in a Cold-Rolled and Annealed Body-Centered-Cubic Mg-Li Alloy. Metall. Mater. Trans. A 2007, 38, 2593–2601. [Google Scholar] [CrossRef]
- Catoor, D.; Gao, Y.F.; Geng, J.; Prasad, M.J.N.V.; Herbert, E.G.; Kumar, K.S. Incipient plasticity and deformation mechanisms in single-crystal Mg during spherical nanoindentation. Acta Mater. 2013, 61, 2953–2965. [Google Scholar] [CrossRef]
- Perugu, C.S.; Kumar, S.; Suwas, S. Evolution of Microstructure, Texture, and Tensile Properties in Two-Phase Mg-Li Alloys: Effect of Zn Addition. JOM 2020, 72, 1627–1637. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, L.H.; Wang, H.T.; Tong, X.; Zhang, M.L.; Zhang, Z.W. Texture evolution and their effects on the mechanical properties of duplex Mg-Li alloy. J. Alloys Compd. 2016, 669, 72–78. [Google Scholar] [CrossRef]
- Liu, W.H.; Liu, X.; Tang, C.P.; Yao, W.; Xiao, Y.; Liu, X.H. Microstructure and texture evolution in LZ91 magnesium alloy during cold rolling. J. Magnes. Alloy 2018, 6, 77–82. [Google Scholar] [CrossRef]
- Barnett, M.R. A Taylor Model Based Description of the Proof Stress of Magnesium AZ31 during Hot Working. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2003, 34, 1799–1806. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B. Study on the Plastic Deformation Mechanism of Magnesium Alloy Materials with Viscoplastic Self-Consistent Model. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2019. [Google Scholar]
- Kumar, V.; Govind; Shekhar, R.; Balani, K. Effect of Hot Rolling on Microstructure and Texture Evolution of Mg-Li Based Alloy. Mater. Sci. Forum 2011, 131, 347–350. [Google Scholar] [CrossRef]
- Pugazhendhi, B.S.; Kar, A.; Sinnaeruvadi, K.; Suwas, S. Effect of aluminium on microstructure, mechanical property and texture evolution of dual phase Mg-8Li alloy in different processing conditions. Arch. Civ. Mech. Eng. 2018, 18, 1332–1344. [Google Scholar] [CrossRef]
- Kumar, V.; Govind; Shekhar, R.; Balasubramaniam, R.; Balani, K. Microstructure evolution and texture development in thermomechanically processed Mg-Li-Al based alloys. Mater. Sci. Eng. A 2012, 547, 38–50. [Google Scholar] [CrossRef]
- He, J.J. Investigation of Texture Modification on Formability of Magnesium Alloy Sheet. Ph.D. Thesis, Chongqing University, Chongqing, China, 2018. [Google Scholar]
- Lin, Y.N.; Wu, H.Y.; Zhou, G.Z.; Chiu, C.H.; Lee, S. Mechanical and anisotropic behaviors of Mg-Li-Zn alloy thin sheets. Mater. Des. 2008, 29, 2061–2065. [Google Scholar] [CrossRef]
- Guo, F.; Liu, L.; Ma, Y.L.; Jiang, L.Y.; Zhang, Y.H.; Zhang, D.F. Slip behavior and its effect on rolling texture development in a dual-phase Mg–Li alloy. J. Alloys Compd. 2020, 813, 152117. [Google Scholar] [CrossRef]
- Miyano, H.; Takemoto, K.; Tsushida, M.; Kitahara, H.; Ando, S. Evaluation of Non-Basal Slip Activity in Rolled Mg-Li Alloys: Mechanics of Materials. Mater. Trans. 2021, 62, 1097–1101. [Google Scholar] [CrossRef]
- Haruka, M.; Keisuke, T.; Hiromoto, K.; Shinji, A. Activities of Non-Basal Slips in Rolled Mg-Li and Mg-Ce Alloys Sheets. Mater. Sci. Forum. 2021, 5994, 917–921. [Google Scholar]


| Alloying Element | Li | Zn | Mn | Si | Fe | Cu | Ni | Mg |
|---|---|---|---|---|---|---|---|---|
| Content (wt.%) | 9.0200 | 0.9630 | 0.0160 | 0.0051 | 0.0035 | 0.0018 | 0.0002 | balance |
| Rolling | Deformation Mode | ||||
|---|---|---|---|---|---|
| 0.5 mm | Basal<a> | 12 | 40 | 600 | 1 |
| Prismal<a> | 14 | 80 | 1000 | 2 | |
| Pyramidal<c+a> | 18 | 220 | 2500 | 1 | |
| Tensile twinning | 13 | 50 | 600 | 6 | |
| Compression twinning | 30 | 80 | 2900 | 10 | |
| 0.25 mm | Basal<a> | 18 | 21 | 450 | 8 |
| Prismal<a> | 35 | 33 | 680 | 8 | |
| Pyramidal<c+a> | 46 | 55 | 1500 | 9 | |
| Tensile twinning | 30 | 20 | 480 | 12 | |
| Compression twinning | 70 | 30 | 2250 | 20 |
| Tensile Samples | Yield Strength | Tensile Strength | Elongation | Yield Ratio | |
|---|---|---|---|---|---|
| 0.5 mm | RD | 165.5 | 237.4 | 28.00 | 0.70 |
| 45° | 128.2 | 214.4 | 51.51 | 0.60 | |
| TD | 138.4 | 200.5 | 18.13 | 0.69 | |
| 0.25 mm | RD | 138.4 | 206.8 | 24.68 | 0.67 |
| 45° | 106.9 | 208.7 | 34.36 | 0.51 | |
| TD | 137.1 | 179.8 | 13.97 | 0.76 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, S.; Shang, D.; Chen, M.; Ma, C.; Lu, Y.; Hu, X. Microstructure Evolution Mechanism of Ultra-Thin Dual Phase Magnesium–Lithium Alloy during Asymmetric Warm Rolling. Materials 2022, 15, 5026. https://doi.org/10.3390/ma15145026
An S, Shang D, Chen M, Ma C, Lu Y, Hu X. Microstructure Evolution Mechanism of Ultra-Thin Dual Phase Magnesium–Lithium Alloy during Asymmetric Warm Rolling. Materials. 2022; 15(14):5026. https://doi.org/10.3390/ma15145026
Chicago/Turabian StyleAn, Shuang, Deli Shang, Ming Chen, Cong Ma, Yanqing Lu, and Xiaodong Hu. 2022. "Microstructure Evolution Mechanism of Ultra-Thin Dual Phase Magnesium–Lithium Alloy during Asymmetric Warm Rolling" Materials 15, no. 14: 5026. https://doi.org/10.3390/ma15145026
APA StyleAn, S., Shang, D., Chen, M., Ma, C., Lu, Y., & Hu, X. (2022). Microstructure Evolution Mechanism of Ultra-Thin Dual Phase Magnesium–Lithium Alloy during Asymmetric Warm Rolling. Materials, 15(14), 5026. https://doi.org/10.3390/ma15145026





