Finite Element Simulation of Punch Structure and Its Effect on Microstructure Evolution of Mg-Gd-Y-Zn-Zr Alloy via Rotary Extrusion Method
Abstract
:1. Introduction
2. Materials and Methods
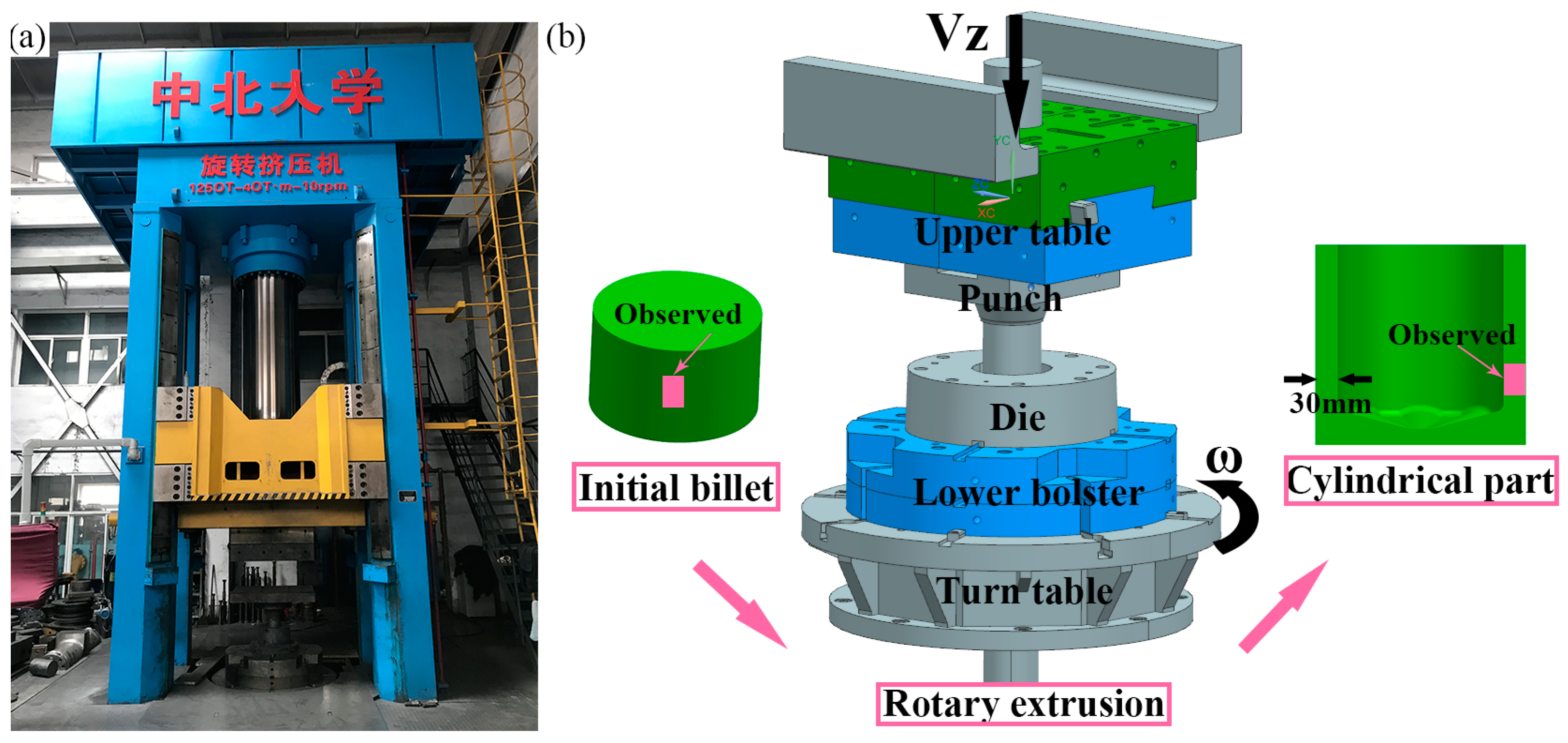
2.1. Finite Element Simulation (FEM) of Punch Structure
2.2. Microstructure Characterization
3. Results
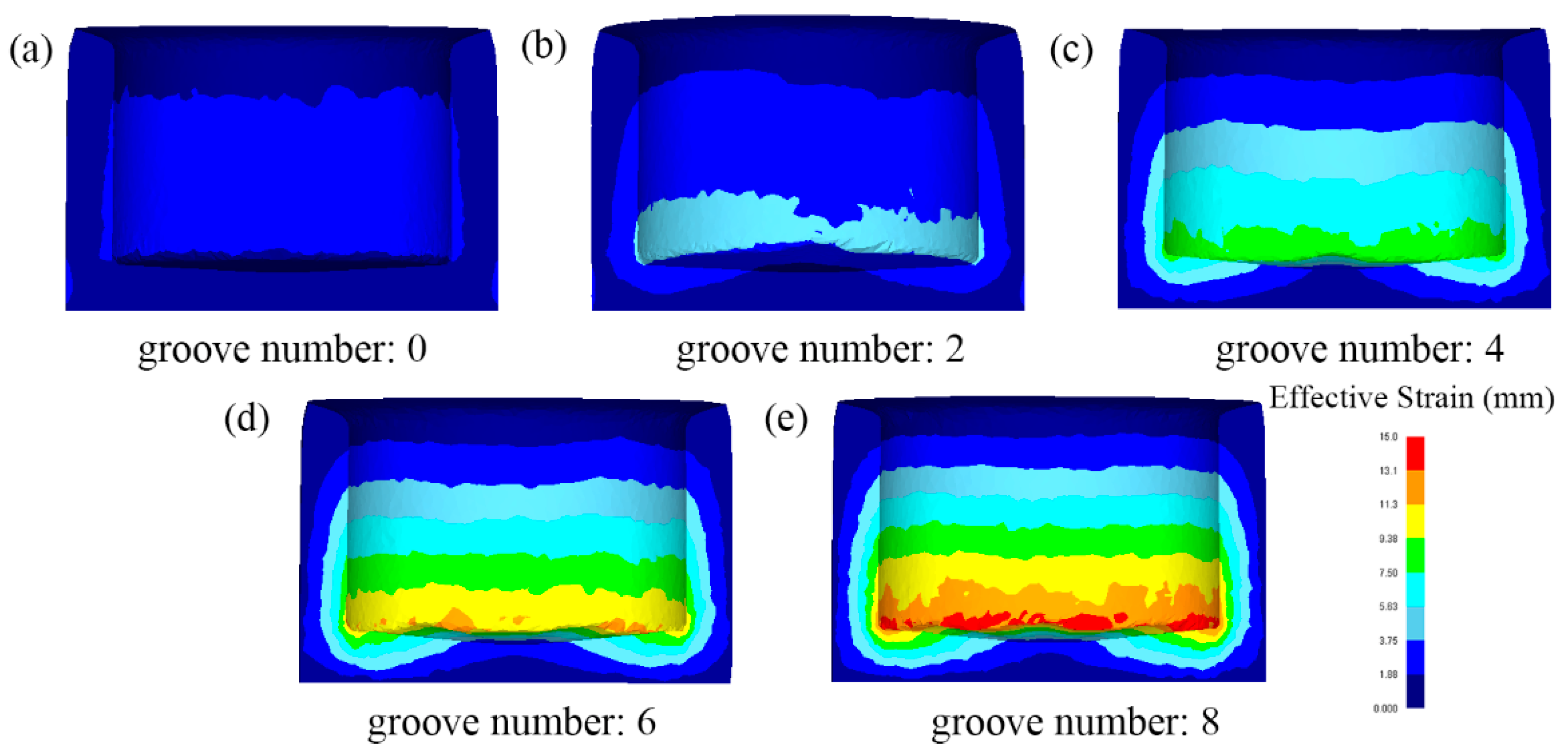
3.1. FEM Results and Analysis
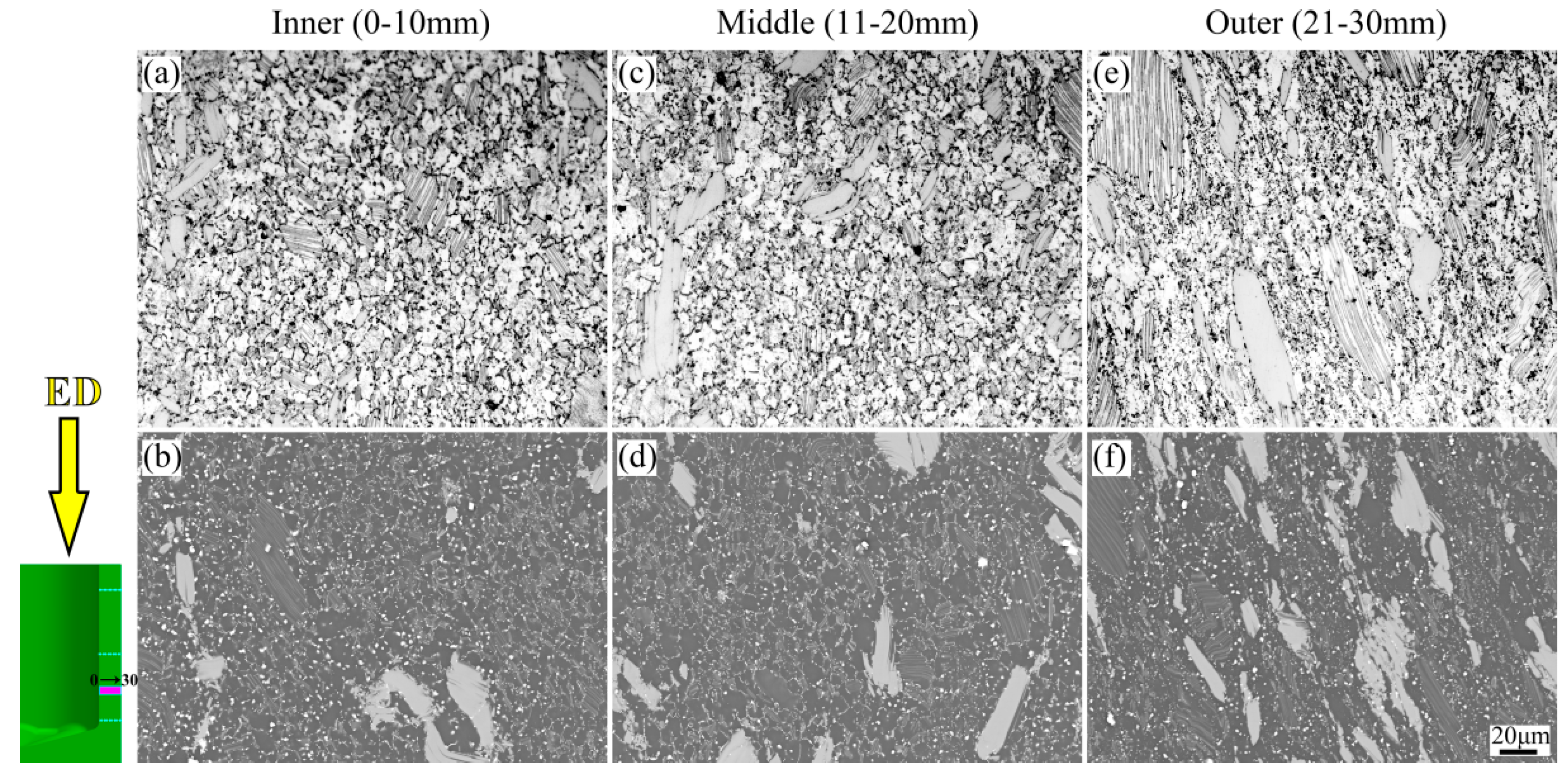
3.2. Microstructure of Mg-Gd-Y-Zn-Zr Alloy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, B.; Zhang, Z.; Che, X.; Yu, J.; Meng, M. Microstructure, Texture Evolution, and Mechanical Properties of MDFed GWZ Alloy Containing LPSO Phases on the Condition of High and Low Temperature Cycle Deformation. Metals 2020, 10, 136. [Google Scholar] [CrossRef] [Green Version]
- Dong, B.B.; Zhang, Z.M.; Yu, J.M.; Che, X.; Meng, M.; Zhang, J.L. Microstructure, texture evolution and mechanical properties of multi-directional forged Mg-13Gd-4Y-2Zn-0.5Zr alloy under decreasing temperature. J. Alloys Compd. 2020, 823, 153776. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, Y.; Zhang, A.; Jiang, H.; Pan, H.; Feng, X.; Yang, C.; Luo, T.; Li, Y.; Yang, Y. Age hardening responses of as-extruded Mg-2.5Sn-1.5Ca alloys with a wide range of Al concentration. J. Mater. Sci. Technol. 2020, 38, 39–46. [Google Scholar] [CrossRef]
- Chen, X.R.; Ning, S.C.; Le, Q.C.; Wang, H.N.; Zou, Q.; Guo, R.Z.; Hou, J.; Jia, Y.H.; Atrens, A.; Yu, F.X. Effects of external filed treatment on the electrochemical behaviors and discharge performance of AZ80 anodes for Mg-air batteries. J. Mater. Sci. Technol. 2020, 38, 47–55. [Google Scholar] [CrossRef]
- Yu, Z.; Xu, C.; Meng, J.; Kamado, S. Microsructure evolution and mechanical properties of a high strength Mg-11.7Gd-4.9Y-0.3Zr (wt%) alloy prepared by pre-deformation annealing, hot extrusion and ageing. Mater. Sci. Eng. A 2017, 703, 348–358. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Wu, R.; Hou, L.; Zhang, M. Microstructure and mechanical properties of Mg-8Li-(0, 1, 2)Ca-(0, 2)Gd alloys. J. Magnes. Alloy. 2017, 703, 348–358. [Google Scholar]
- Jia, L.Y.; Du, W.B.; Fu, J.L.; Wang, Z.H.; Liu, K.; Li, S.B.; Du, X. Obtaining ultra-high strength and ductility in a Mg-Gd-Er-Zn-Zr alloy via extrusion, pre-deformation and two-stage aging. Acta Metall. Sin. Engl. Lett. 2021, 34, 39–44. [Google Scholar] [CrossRef]
- Zhang, G.S.; Zhang, Z.M.; Li, X.B.; Yan, Z.M.; Che, X.; Yu, J.M.; Meng, Y.Z. Effects of repetitive upsetting-extrusion parameters on microstructure and texture evolution of Mg-Gd-Y-Zn-Zr alloy. J. Alloys Compd. 2019, 790, 48–57. [Google Scholar] [CrossRef]
- Lee, S.-W.; Chen, Y.-L.; Wang, H.-Y.; Yang, C.-F.; Yeh, J.-W. On mechanical properties and superplasticity of Mg–15Al–1Zn alloys processed by reciprocating extrusion. Mater. Sci. Eng. A 2007, 464, 76–84. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, L.-X.; Sun, Y.; Jia, J.-B.; Jiang, J.-F.; Ma, Q.-G. Microstructure and mechanical properties of AZ61 magnesium alloy prepared by repetitive upsetting-extrusion. Trans. Nonferrous Met. Soc. China 2015, 25, 381–388. [Google Scholar] [CrossRef]
- Huang, C.; Liu, C.M.; Jiang, S.N.; Wan, Y.C.; Gao, Y.H. Inhomogenerous microstructure and mechanical anisotropy of multi-directional forged Mg-Gd-Y-Zn-Ag-Zr alloy. Mater. Sci. Eng. A 2021, 807, 140853. [Google Scholar] [CrossRef]
- Furukawa, M.; Horita, Z.; Nemoto, M.; Langdon, T.G. Review: Processing of metals by equal-channel angular pressing. J. Mater. Sci. 2001, 36, 2835–2843. [Google Scholar] [CrossRef]
- Li, B.; Teng, B.; Chen, G. Microstructure evolution and mechanical properties of Mg-Gd-Y-Zn-Zr alloy during equal channel angular pressing. Mater. Sci. Eng. A 2018, 744, 396–405. [Google Scholar] [CrossRef]
- Jahadi, R.; Sedighi, M.; Jahed, H. ECAP effect on the micro-structure and mechanical properties of AM30 magnesium alloy. Mater. Sci. Eng. A 2013, 593, 178–184. [Google Scholar] [CrossRef]
- Al-Zubaydi, A.S.J.; Zhilyaev, A.P.; Wang, S.C.; Kucita, P.; Reed, P.A.S. Evolution of microstructure in AZ91 alloy processed by high-pressure torsion. J. Mater. Sci. 2015, 51, 3380–3389. [Google Scholar] [CrossRef] [Green Version]
- Qiao, X.G.; Zhao, Y.W.; Gan, W.M.; Chen, Y.; Zheng, M.Y.; Wu, K.; Gao, N.; Starink, M.J. Hardening mechanism of commercially pure Mg processed by high pressure torsion at room temperature. Mater. Sci. Eng. A 2014, 619, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Harai, Y.; Kai, M.; Kaneko, K.; Horita, Z.; Langdon, T.G. Microstructural and mechanical characteristics of an AZ61 magnesium alloy processed by high pressure torsion. Mater. Trans. 2008, 49, 76–83. [Google Scholar] [CrossRef] [Green Version]
- Honma, T.; Ohkubo, T.; Hono, K.; Kamado, S. Chemistry of nanoscale precipitates in Mg–2.1Gd–0.6Y–0.2Zr (at.%) alloy investigated by the atom probe technique. Mater. Sci. Eng. A 2005, 395, 301–306. [Google Scholar] [CrossRef]
- Rokhlin, L.L.; Nikitina, N.I. Electron-microscopic investigated of the structure of a precipitated supersaturated Mg-22wt%Gd solid solution. Fiz. Met. I Metalloved. 1986, 62, 781–787. [Google Scholar]
- Drits, M.E.; Sviderskaya, Z.A.; Rokhlin, L.L.; Nikitina, N.I. Effect of alloying on properties of Mg-Gd alloys. Met. Sci. Heat Treat. 1979, 21, 62–64. [Google Scholar] [CrossRef]
- Peng, Q.; Wu, Y.; Fang, D.; Meng, J.; Wang, L. Microstructures and properties of Mg–7Gd alloy containing Y. J. Alloys Compd. 2007, 430, 252–256. [Google Scholar] [CrossRef]
- Hong, M.; Shah, S.S.A.; Wu, D.; Chen, R.S.; Du, X.H.; Hu, N.T.; Zhang, Y.F. Ultra-high strength Mg-9Gd-4Y-0.5Zr alloy with bimodal structure processed by traditional extrusion. Met. Mater. Int. 2016, 22, 1091–1097. [Google Scholar] [CrossRef]
- Xu, C.; Zheng, M.Y.; Xu, S.W.; Wu, K.; Wang, E.; Fan, G.H.; Kamado, S. Improving strength and ductility of Mg-Gd-Y-Zn-Zr alloy simultaneously via extrusion, hot rolling and ageing. Mater. Sci. Eng. A 2015, 643, 137–141. [Google Scholar] [CrossRef]
- Dong, B.; Che, X.; Wang, Q.; Meng, M.; Gao, Z.; Ma, J.; Yang, F.; Zhang, Z. Refining the microstructure and modifying the texture of the AZ80 alloy cylindrical tube by the rotating backward extrusion with different rotating revolutions. J. Alloys Compd. 2020, 836, 155442. [Google Scholar] [CrossRef]
- Mizunuma, S. Large Straining Behavior and Microstructure Refinement of Several Metals by Torsion Extrusion Process. Mater. Sci. Forum 2006, 503–504, 185–192. [Google Scholar] [CrossRef]
- Ma, X.; Barnett, M.; Kim, Y. Experimental and theoretical investigation of compression of a cylinder using a rotating platen. Int. J. Mech. Sci. 2003, 45, 1717–1737. [Google Scholar] [CrossRef]
- Ma, X.; Barnett, M.; Kim, Y. Forward extrusion through steadily rotating conical dies. Part I: Experiments. Int. J. Mech. Sci. 2004, 46, 449–464. [Google Scholar] [CrossRef]
- Ma, X.; Barnett, M.; Kim, Y. Forward extrusion through steadily rotating conical dies. Part II: Theoretical analysis. Int. J. Mech. Sci. 2004, 46, 465–489. [Google Scholar] [CrossRef]
- Shahbaz, M.; Pardis, N.; Kim, J.G.; Ebrahimi, R.; Kim, H.S. Experimental and finite analyses of olastic deformation behavior in vortex extrusion. Mater. Sci. Eng. A 2016, 674, 472–479. [Google Scholar] [CrossRef]
- Lu, L.; Liu, C.; Zhao, J.; Zeng, W.; Wang, Z. Modification of grain refinement and texture in AZ31 Mg alloy by a new plastic deformation method. J. Alloys Compd. 2014, 628, 130–134. [Google Scholar] [CrossRef]
- Ammarullah, M.I.; Afif, I.Y.; Maula, M.I.; Winarni, T.I.; Tauviqirrahman, M.; Akbar, I.; Basri, H.; van der Heide, E.; Jamari, J. Tresca Stress Simulation of Metal-on-Metal Total Hip Arthroplasty during Normal Walking Activity. Materials 2021, 14, 7554. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.; Yu, J.; Liu, K.; Yu, H.; Zhang, F.; Wu, Y.; Zhang, Z.; Luo, N.; Wang, H. The evolution of long-period stacking ordered phase and its effect on dynamic recrystallization in Mg-Gd-Y-Zn-Zr alloy processed by repetitive upsetting-extrusion. J. Alloys Compd. 2020, 828, 154454. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, Z.; Xue, Y.; Xu, J.; Dong, B.; Li, X. Effect of rotating shear extrusion on the microstructure, texture evolution and mechanical properties of Mg-Gd-Y-Zn-Zr alloy. J. Alloys Compd. 2022, 906, 164406. [Google Scholar] [CrossRef]
- Arash, V.; Anoush, K.; Rabieer, S.M.; Rahmatei, M.; Tavanafar, S. The effects of silver coating on friction coeffificient and shear bond strength of steel orthodontic brackets. Scanning 2015, 37, 294–299. [Google Scholar] [CrossRef]
- Nazanin, H.; Ali, R.E.; Mohammad, R.A. Finite element simulation of deformation and heat transfer during friction stir processing of as-cast AZ91 magnesium alloy. J. Mater. Res. Technol. 2021, 14, 2998–3017. [Google Scholar]

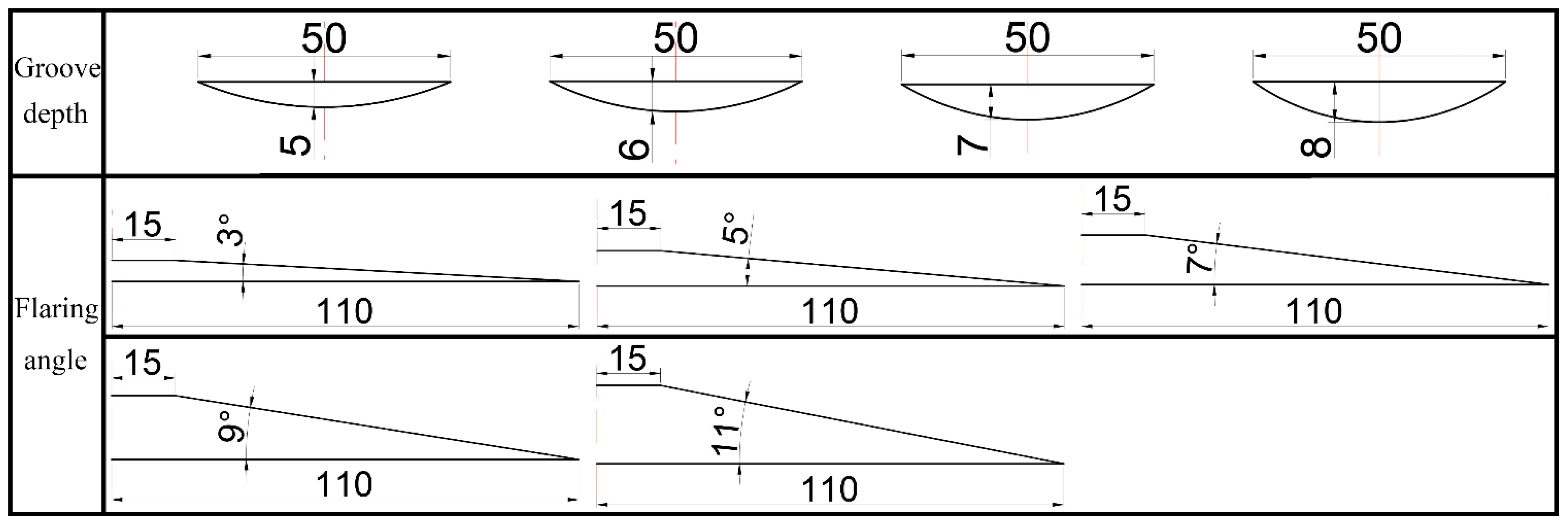
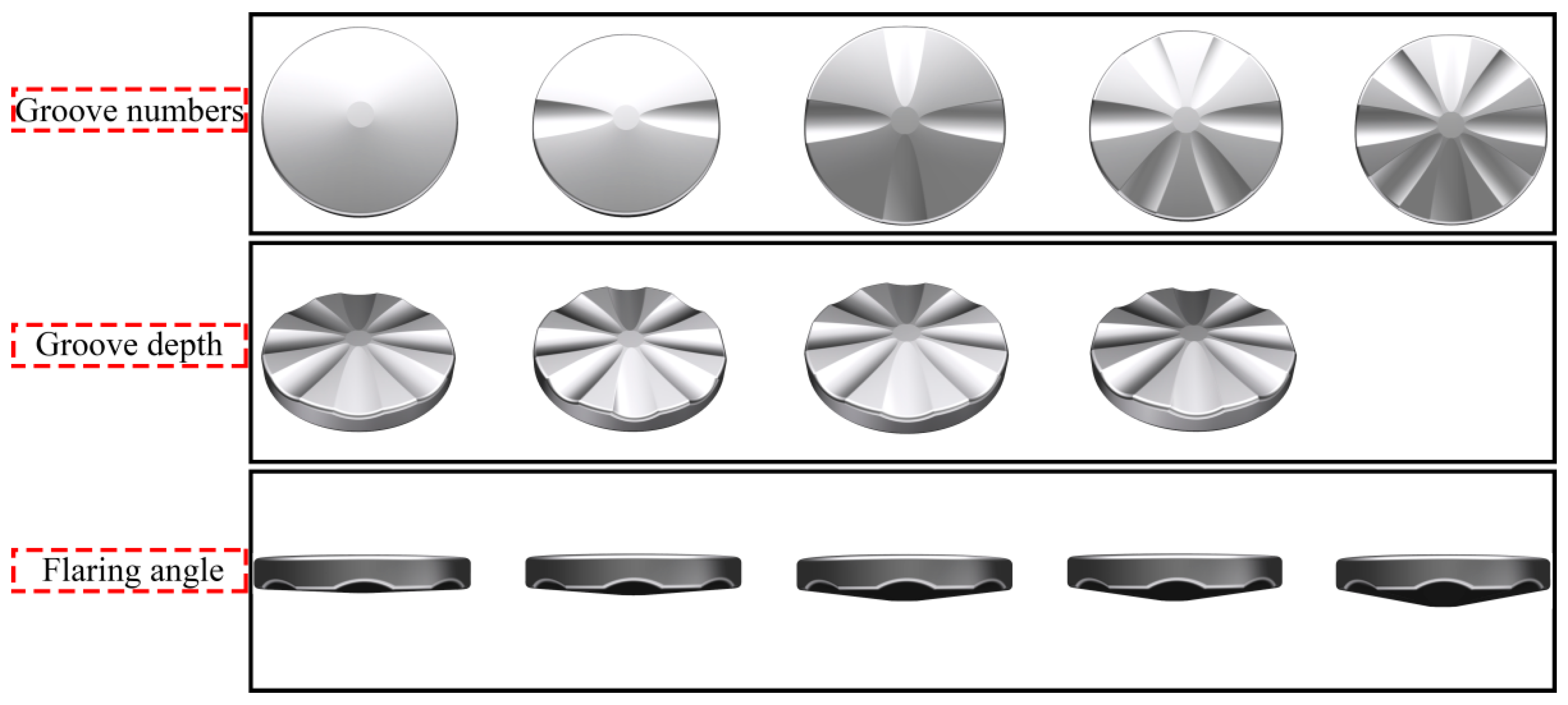

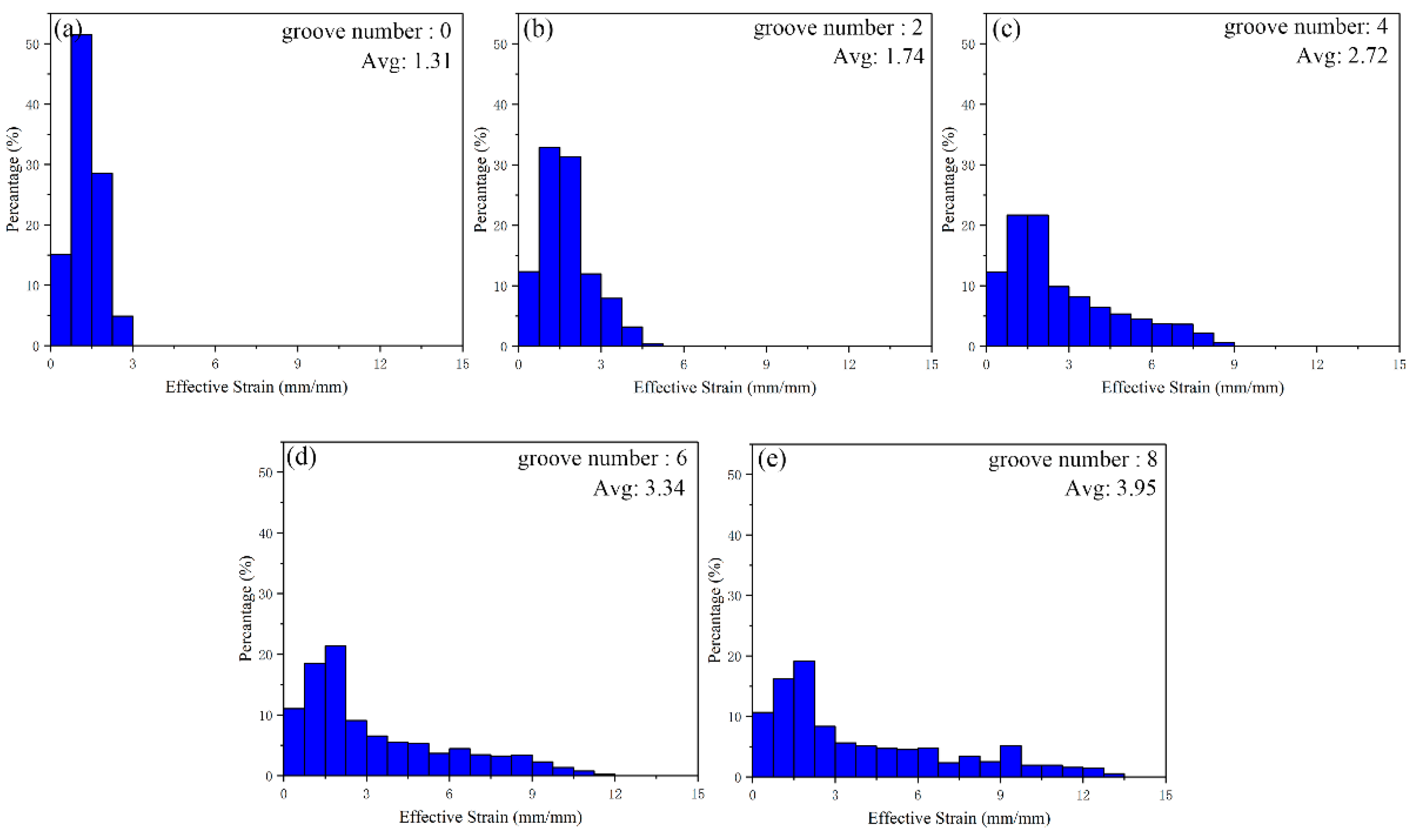
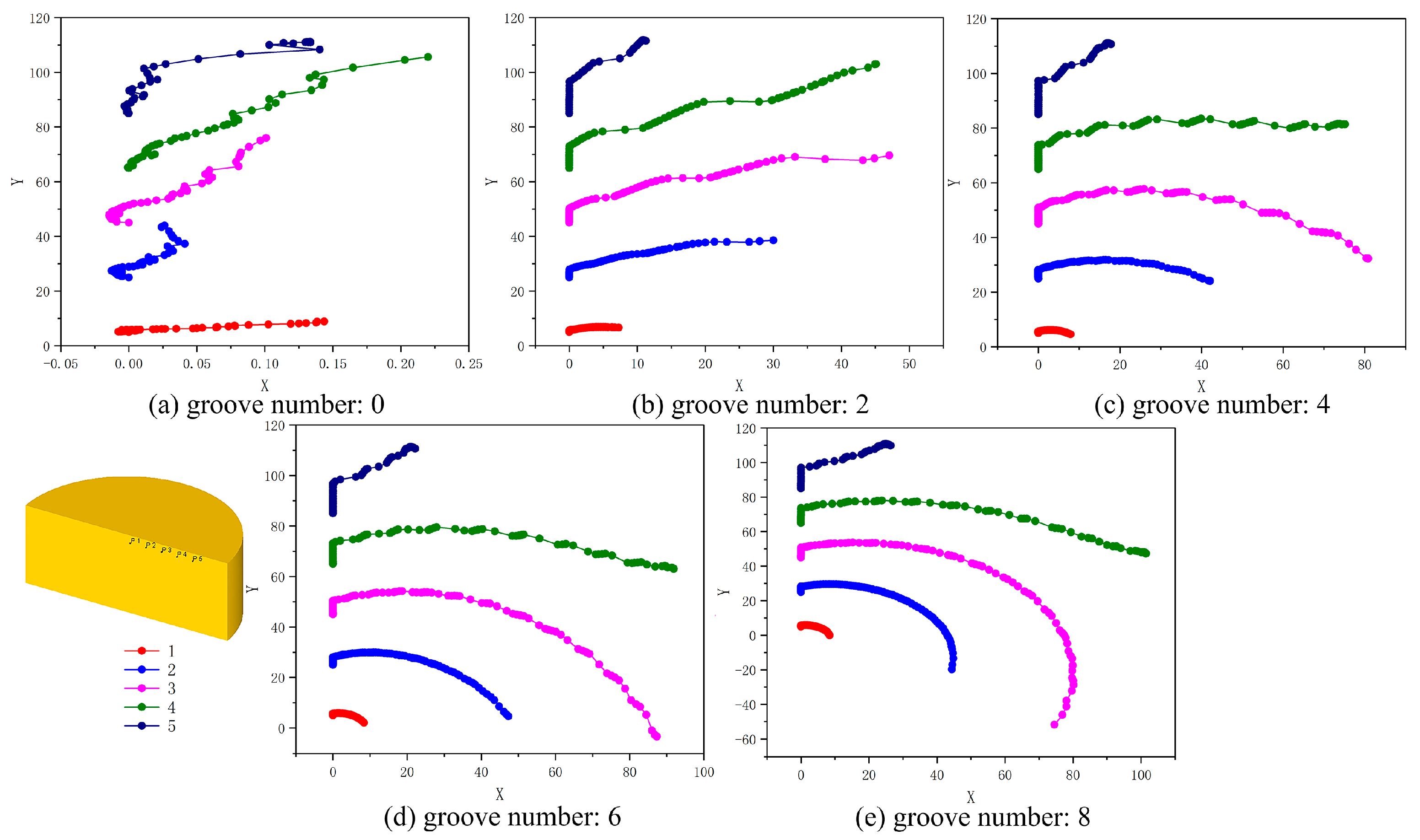
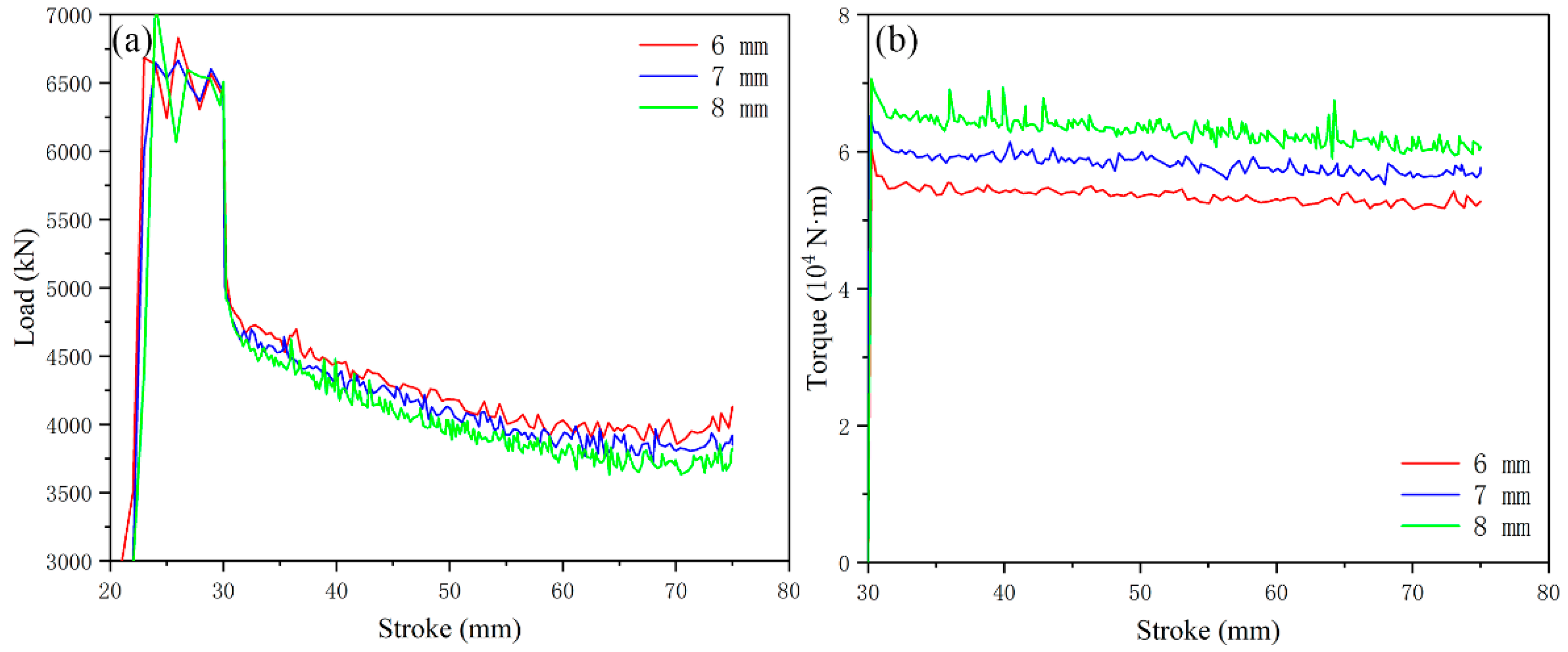

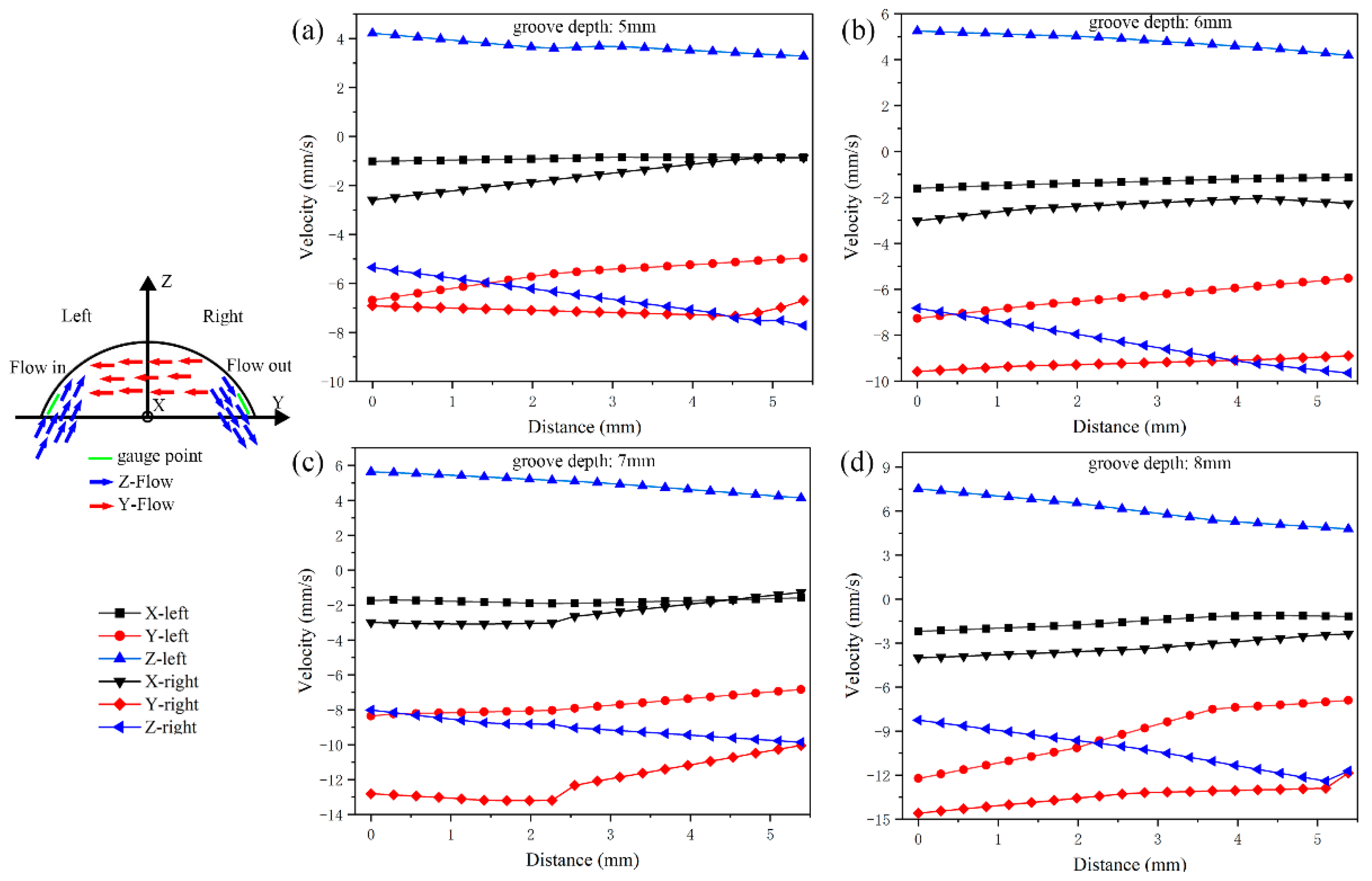
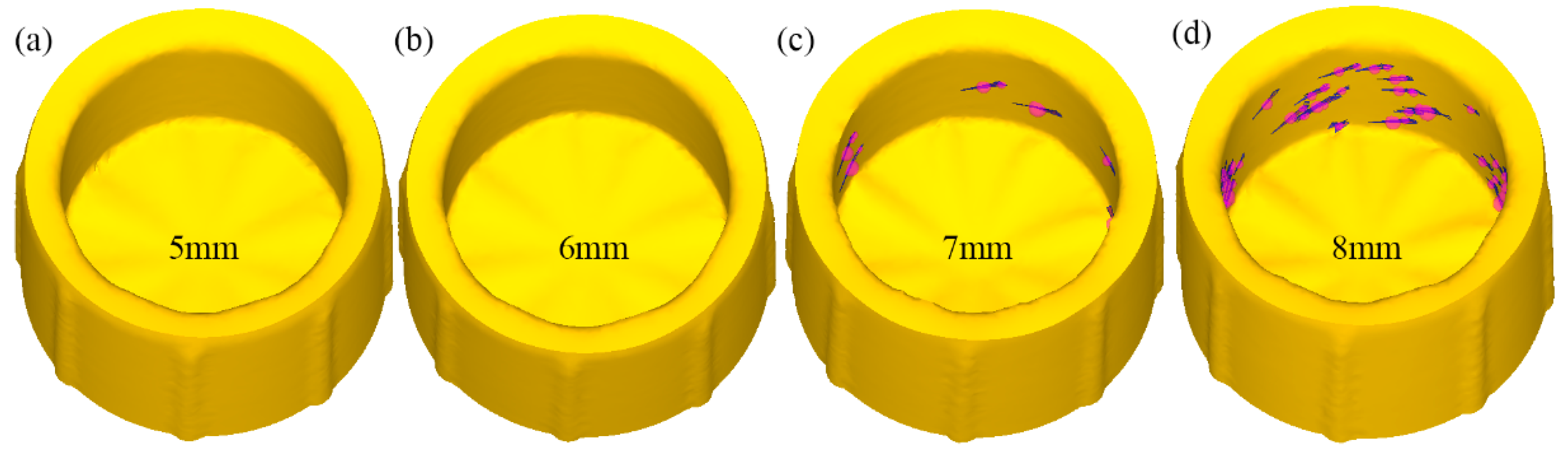
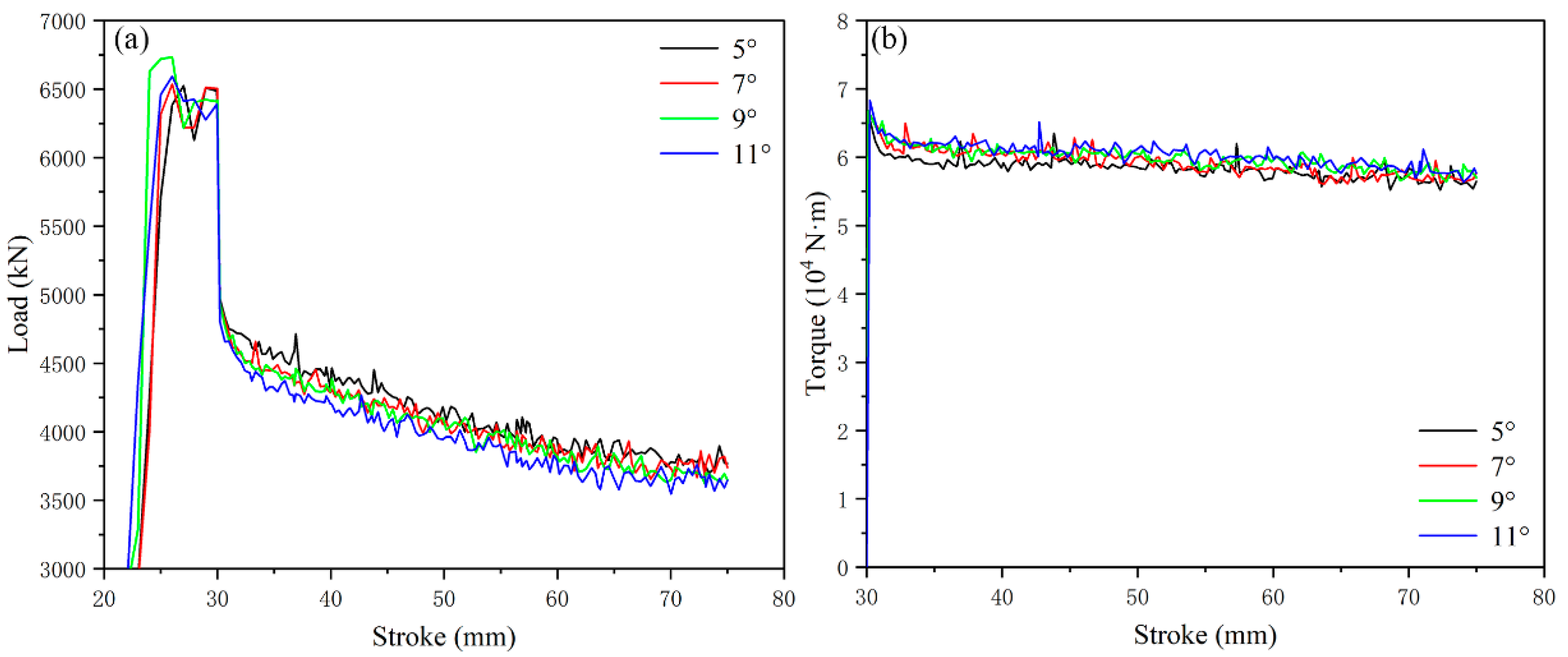
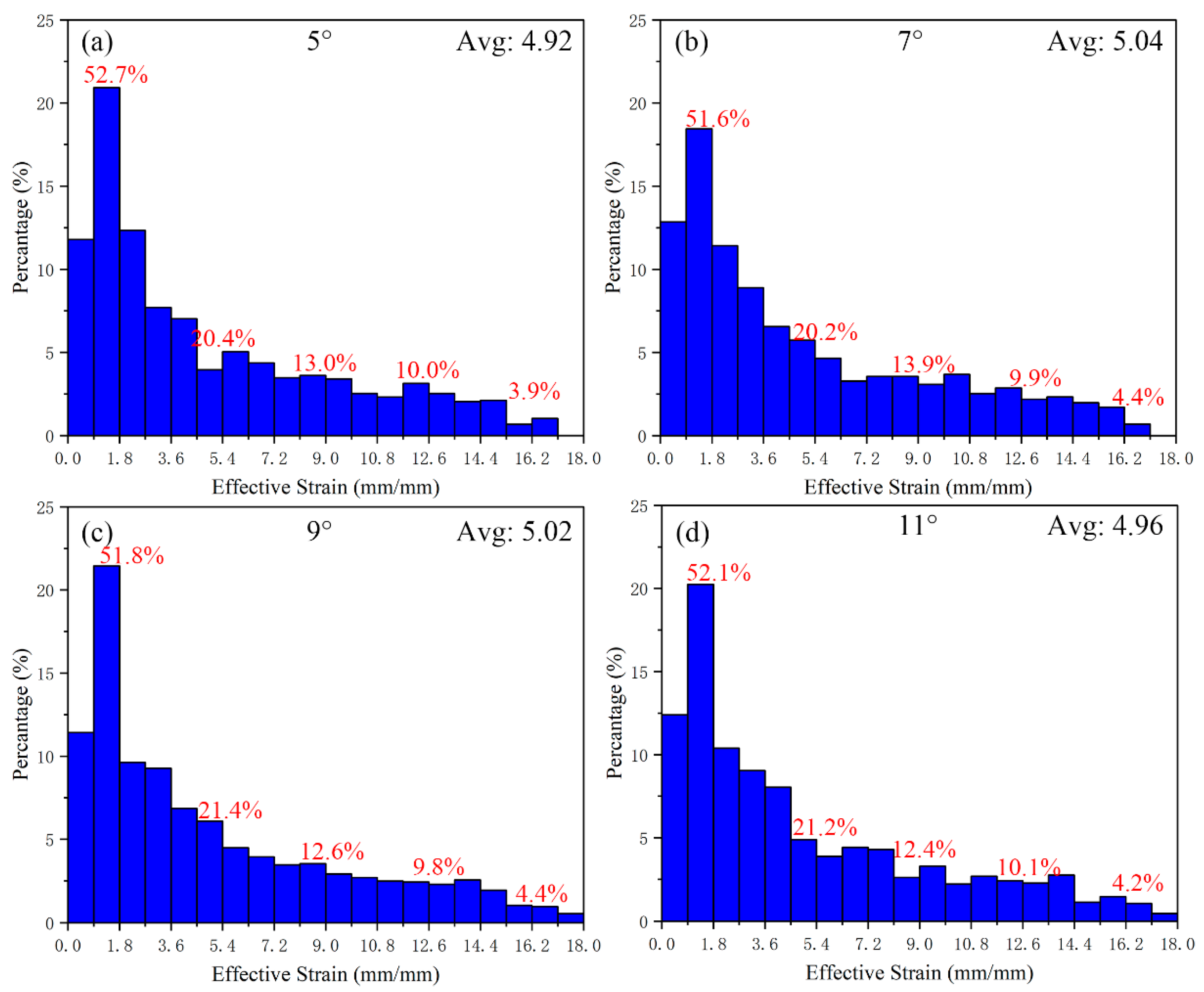


| Grooves | Gradient Values | |||||
|---|---|---|---|---|---|---|
| Number | 0 | 2 | 4 | 6 | 8 | Depth: 5 mm flaring angle: 3° |
| Area ratio | 0% | 16.12% | 33.30% | 48.39% | 64.49% | |
| Depth | 5 mm | 6 mm | 7 mm | 8 mm | Number: 8 flaring angle: 3° | |
| Flaring angle | 3° | 5° | 7° | 9° | 11° | Umber: 8 Depth: 7 mm |
| Depth | Region | (mm/s) | Absolute Difference (mm/s) | (mm/s) | Absolute Difference (mm/s) | (mm/s) | Absolute Difference (mm/s) |
|---|---|---|---|---|---|---|---|
| 5 mm | left | −0.91 | 0.72 | −5.64 | 1.45 | 3.68 | 2.85 |
| right | −1.63 | −7.09 | −6.53 | ||||
| 6 mm | left | −1.33 | 1.05 | −6.35 | 2.87 | 4.82 | 3.51 |
| right | −2.38 | −9.22 | −8.33 | ||||
| 7 mm | left | −1.77 | 0.68 | −7.93 | 4.07 | 4.98 | 4.05 |
| right | −2.45 | −12.0 | −9.03 | ||||
| 8 mm | left | −1.56 | 1.73 | −9.19 | 4.21 | 6.08 | 4.22 |
| right | −3.29 | −13.4 | −10.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Dong, B.; Zhang, Z.; Xue, Y.; Cheng, M. Finite Element Simulation of Punch Structure and Its Effect on Microstructure Evolution of Mg-Gd-Y-Zn-Zr Alloy via Rotary Extrusion Method. Materials 2022, 15, 5248. https://doi.org/10.3390/ma15155248
Yan L, Dong B, Zhang Z, Xue Y, Cheng M. Finite Element Simulation of Punch Structure and Its Effect on Microstructure Evolution of Mg-Gd-Y-Zn-Zr Alloy via Rotary Extrusion Method. Materials. 2022; 15(15):5248. https://doi.org/10.3390/ma15155248
Chicago/Turabian StyleYan, Lin, Beibei Dong, Zhimin Zhang, Yong Xue, and Mei Cheng. 2022. "Finite Element Simulation of Punch Structure and Its Effect on Microstructure Evolution of Mg-Gd-Y-Zn-Zr Alloy via Rotary Extrusion Method" Materials 15, no. 15: 5248. https://doi.org/10.3390/ma15155248
APA StyleYan, L., Dong, B., Zhang, Z., Xue, Y., & Cheng, M. (2022). Finite Element Simulation of Punch Structure and Its Effect on Microstructure Evolution of Mg-Gd-Y-Zn-Zr Alloy via Rotary Extrusion Method. Materials, 15(15), 5248. https://doi.org/10.3390/ma15155248





