Structural, Electronic, Mechanical, and Thermodynamic Properties of Na Deintercalation from Olivine NaMnPO4: First-Principles Study
Abstract
:1. Introduction
2. Computational Method
3. Results and Discussion
3.1. Structural Properties
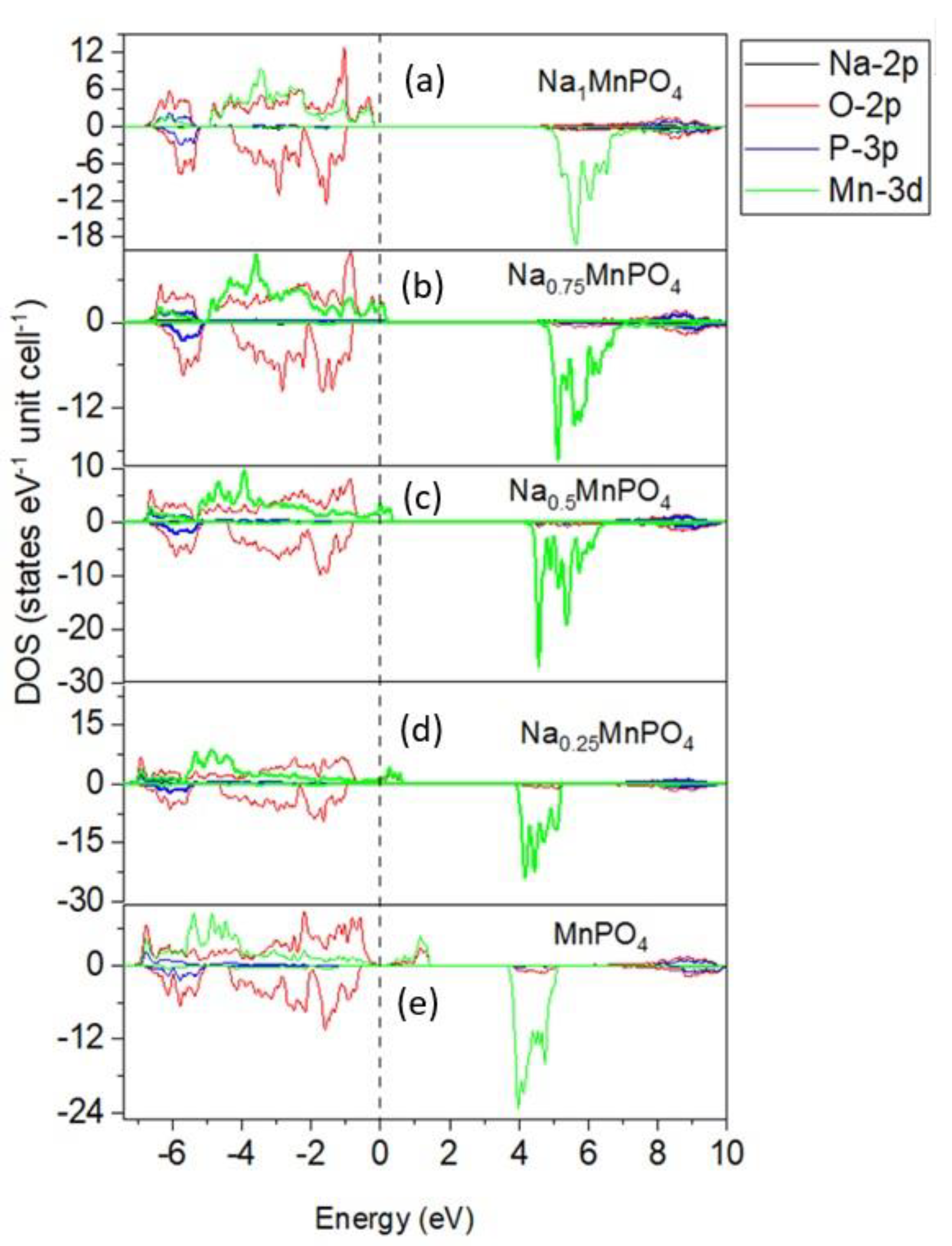
3.2. Electronic Properties
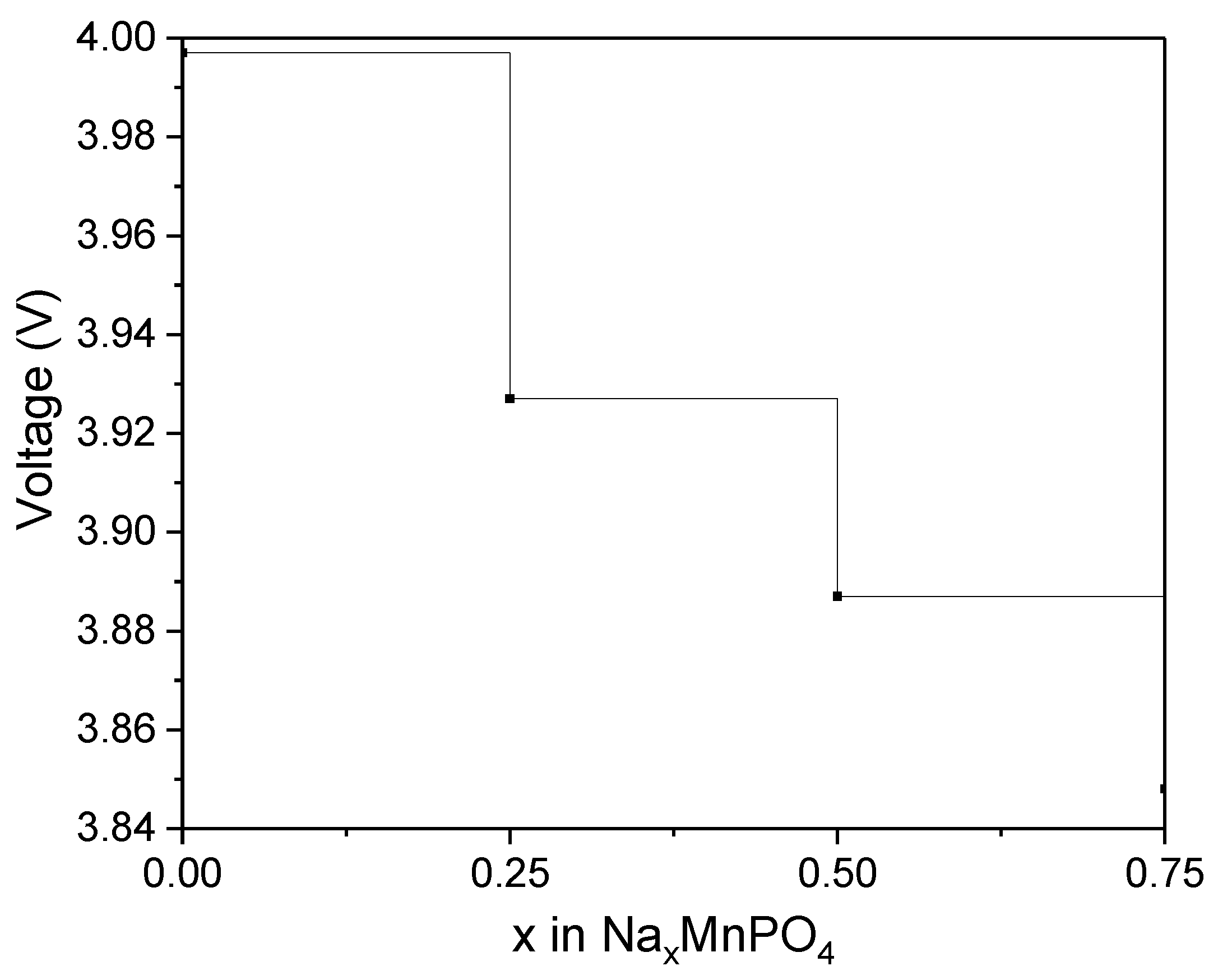
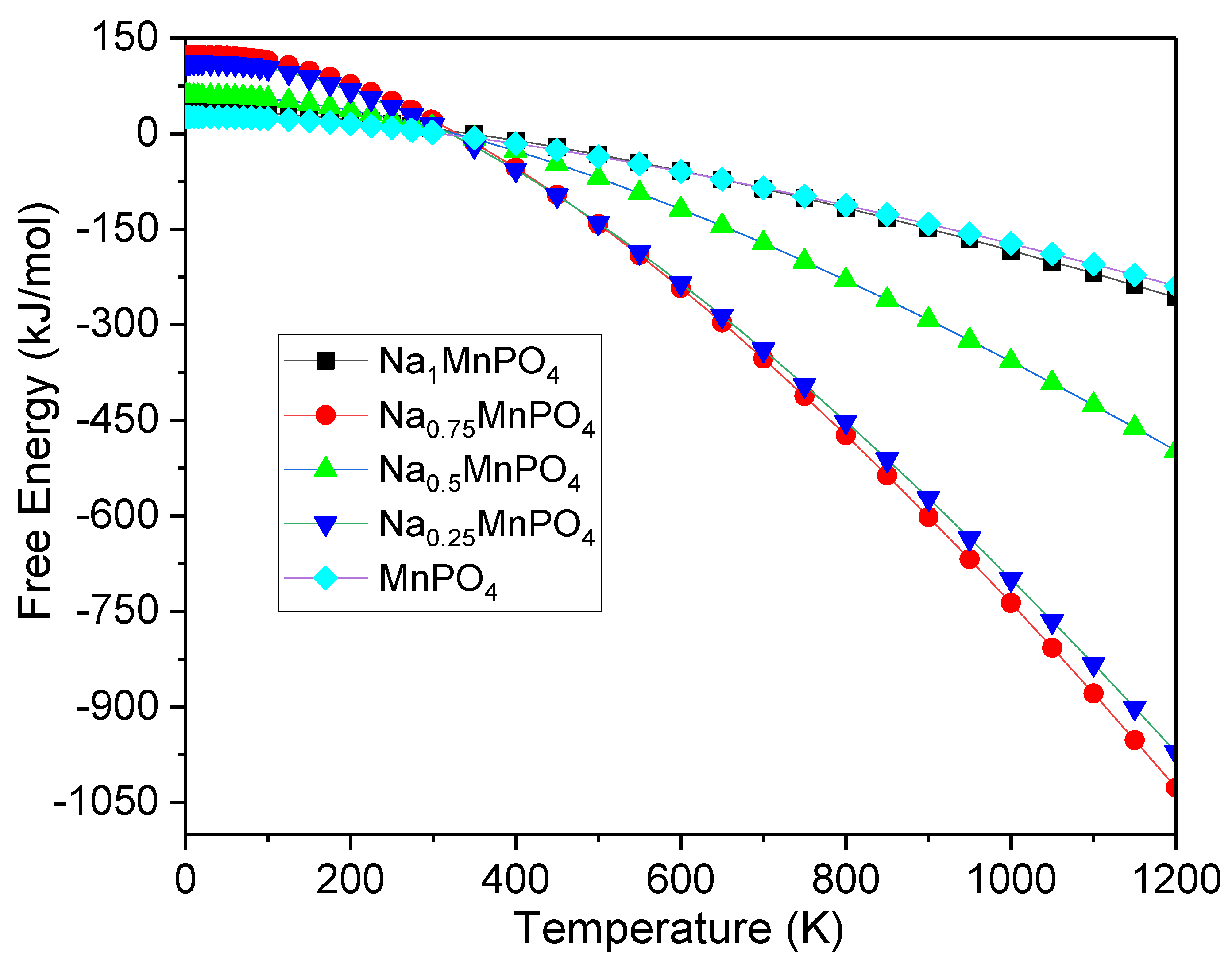
3.3. Voltages/Redox Potential and Formation Energy
3.4. Mechanical Properties
3.4.1. Elasticity
3.4.2. Anisotropy in Elastic Constants
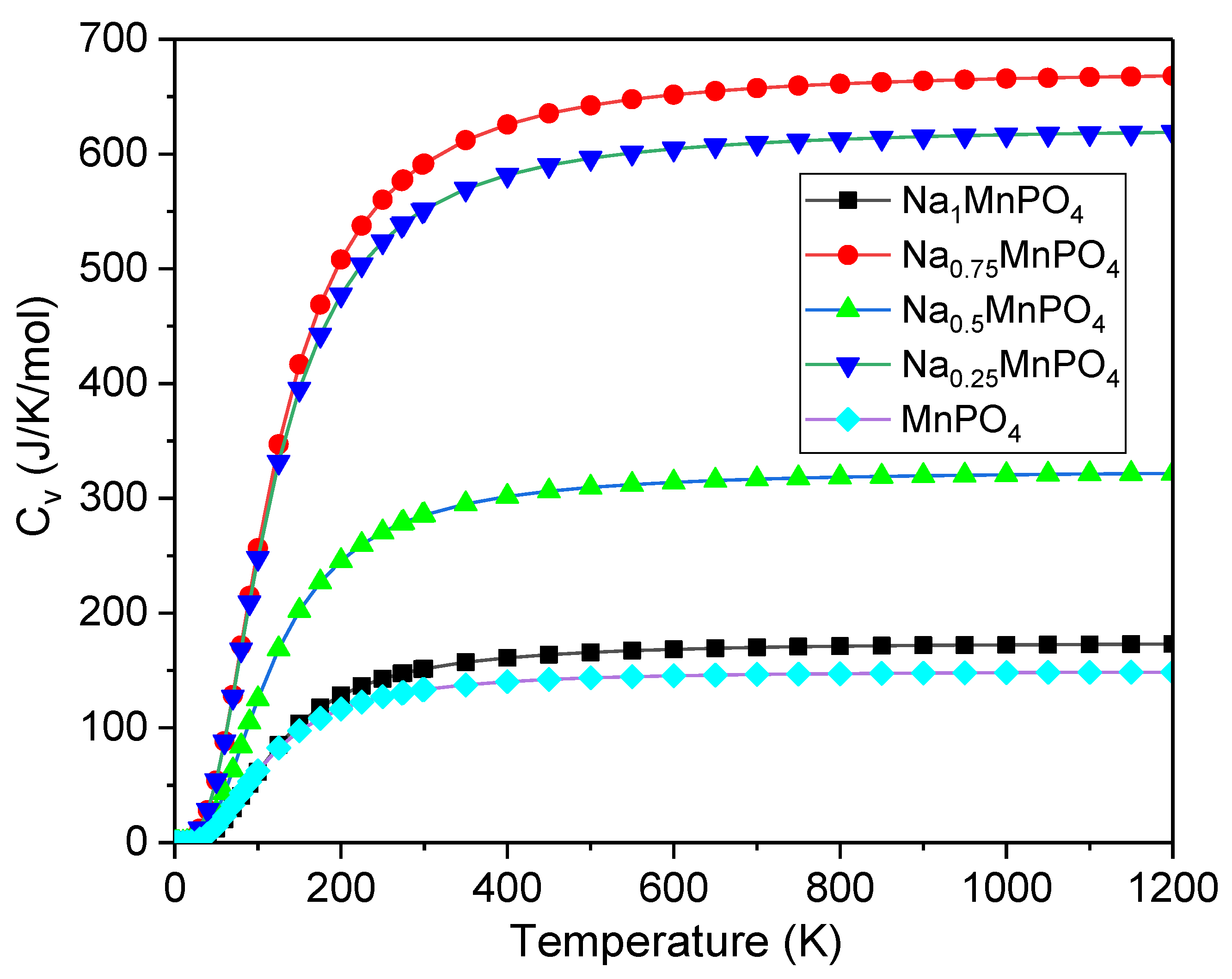
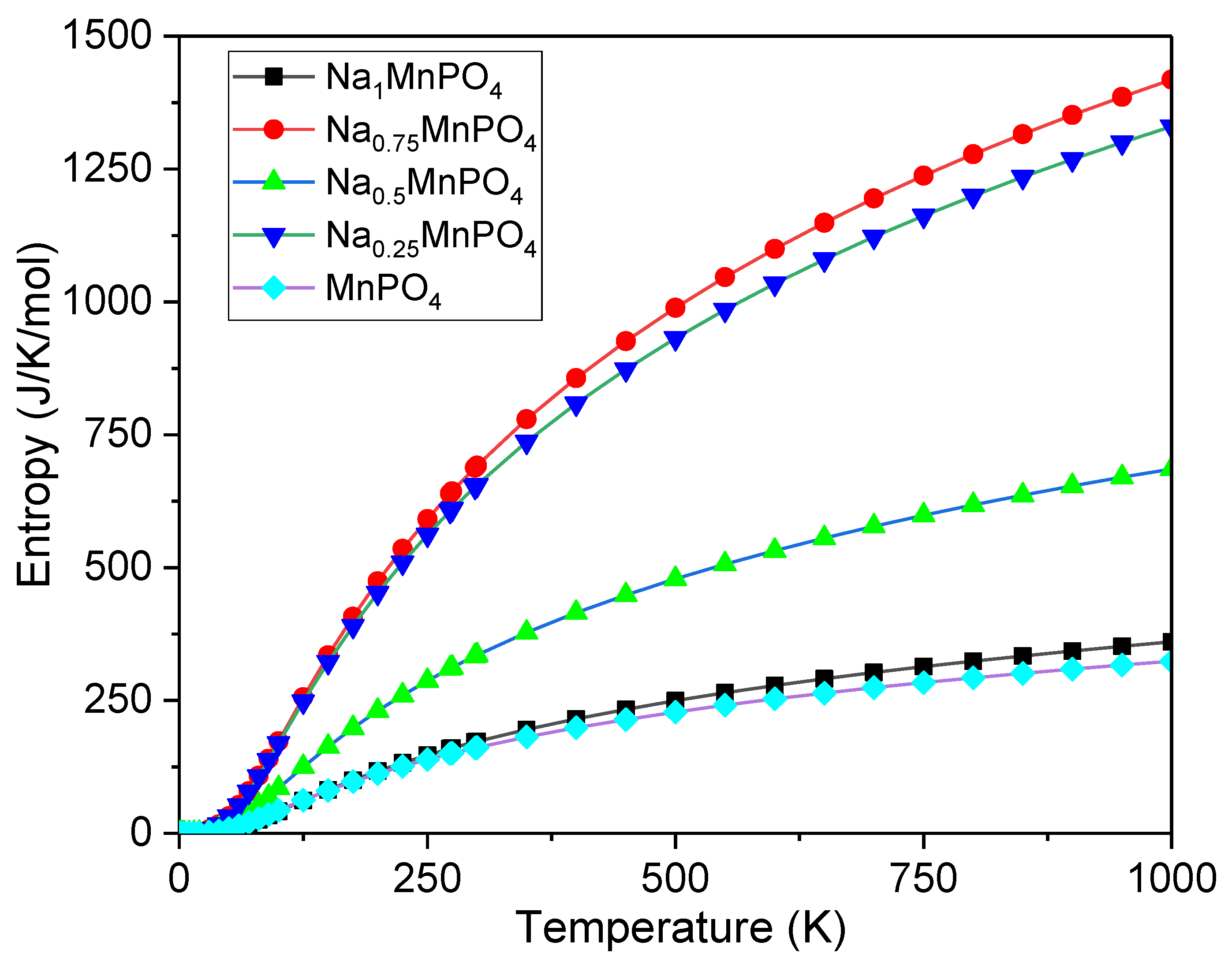
3.4.3. Debye Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palomares, V.; Serras, P.; Villaluenga, I.; Hueso, K.B.; Carretero-Gonzlez, J.; Rojo, T. Na-ion batteries, recent advances, and present challenges to become low-cost energy storage systems. Energy Environ. Sci. 2012, 5, 5884–5901. [Google Scholar]
- Ong, S.P.; Chevrier, V.L.; Hautier, G.; Jain, A.; Moore, C.; Kim, S.; Ma, X.; Ceder, G. Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials. Energy Environ. Sci. 2011, 4, 3680. [Google Scholar]
- Adelhelm, P.; Hartmann, P.; Bender, C.L.; Busche, M.; Eufinger, C.; Janek, J. From lithium to sodium: Cell chemistry of room temperature sodium–air and sodium–sulfur batteries. Beilstein J. Nanotechnol. 2015, 6, 1016–1055. [Google Scholar] [PubMed]
- Berthelot, R.; Carlier, D.; Delmas, C. Electrochemical investigation of the P2–NaxCoO2 phase diagram. Nat. Mater. 2011, 10, 74–80. [Google Scholar] [PubMed]
- Wang, Y.; Yu, X.; Xu, S.; Bai, J.; Xiao, R.; Hu, Y.; Li, H.; Yang, X.; Chen, L.; Huang, X. A zero-strain layered metal oxide as the negative electrode for long-life sodium-ion batteries. Nat. Commun. 2013, 4, 2365. [Google Scholar]
- Komaba, S.; Takei, C.; Nakayama, T.; Ogata, A.; Yabuuchi, N. Electrochemical intercalation activity of layered NaCrO2 vs. LiCrO2. Electrochem. Commun. 2010, 12, 355–358. [Google Scholar] [CrossRef]
- Oh, S.; Myung, S.; Hassoun, J.; Scrosati, B.; Sun, Y. Reversible NaFePO4 electrode for sodium secondary batteries. Electrochem. Commun. 2012, 22, 149–152. [Google Scholar]
- Kim, H.; Shakoor, R.A.; Park, C.; Lim, S.Y.; Kim, J.; Jo, Y.N.; Cho, W.; Miyasaka, K.; Kahraman, R.; Jung, Y.; et al. Na2FeP2O7 as a promising iron-based pyrophosphate cathode for sodium rechargeable batteries: A combined experimental and theoretical study. Adv. Funct. Mater. 2013, 23, 1147–1155. [Google Scholar]
- Lee, M.; Lho, E.; Bai, P.; Chae, S.; Li, J.; Cho, J. Low-temperature carbon coating of nanosized Li1.015Al0.06Mn1.925O4 and high-density electrode for high-power Li-ion batteries. Nano Lett. 2017, 17, 3744. [Google Scholar]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research development on sodium-ion batteries. Chem. Rev. 2014, 114, 11636. [Google Scholar]
- Huang, H.; Yin, S.; Nazar, L.F. Approaching theoretical capacity of LiFePO4 at room temperature at high rates. Electrochem. Solid-State Lett. 2001, 4, 170–172. [Google Scholar] [CrossRef]
- Yamada, A.; Chung, S.C.; Hinokuma, K. Optimized LiFePO4 for lithium battery cathodes. J. Electrochem. Soc. 2001, 148, 224. [Google Scholar] [CrossRef]
- Andersson, A.S. Thermal stability of LiFePO4-based cathodes. Electrochem. Solid-State Lett. 1999, 3, 66. [Google Scholar] [CrossRef]
- Fang, Y.; Liu, Q.; Xiao, L.; Ai, X.; Yang, H.; Cao, Y. High-performance olivine NaFePO4 microsphere cathode synthesized by aqueous electrochemical displacement method for sodium ion batteries. ACS Appl. Mater. Interfaces 1900, 7, 17977–17984. [Google Scholar] [CrossRef]
- Han, M.H.; Gonzalo, E.; Casas-Cabanas, M.; Rojo, T. Structural evolution and electrochemistry of monoclinic NaNiO2 upon the first cycling process. J. Power Sources 2014, 258, 266–271. [Google Scholar] [CrossRef]
- Jian, Z.; Zhao, L.; Pan, H.; Hu, Y.S.; Li, H.; Chen, W.; Chen, L. Carbon coated Na3V2(PO4)3 as novel electrode material for sodium ion batteries. Electrochem. Commun. 2012, 14, 86–89. [Google Scholar] [CrossRef]
- Losey, A.; Rakovan, J.; Hughes, J.M.; Francis, C.A.; Dyar, M.D. Structural variation in the lithiophilite-triphylite series and other olivine-group structures. Can. Miner. 2004, 42, 1105–1115. [Google Scholar] [CrossRef] [Green Version]
- Moring, J.; Kostiner, E. The Crystal Structure of NaMnPO4. J. Solid-State Chem. 1986, 61, 379. [Google Scholar] [CrossRef]
- Dima, R.S.; Maleka, P.M.; Maluta, E.N.; Maphanga, R.R. First principles study on sodium de-intercalation from NaMnPO4. Mater. Today Proceedings 2022, 62, S7–S11. [Google Scholar] [CrossRef]
- Lee, K.T.; Ramesh, T.N.; Nan, F.; Botton, G.; Nazar, L.F. Topochemical synthesis of sodium metal phosphate olivines for sodium-ion batteries. Chem. Mater. 2011, 23, 3593–3600. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B86. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, W. Comment on “Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Koyama, Y.; Tanaka, I.; Nagao, M.; Kanno, R. First-principles study on lithium removal from Li2MnO3. J. Power Sources 2009, 189, 798–801. [Google Scholar] [CrossRef]
- Koleva, V.; Boyadzhieva, T.; Zhecheva, E.; Nihtianova, D.; Simova, S.; Tyuliev, G.; Stoyanova, R. Precursor-based methods for low-temperature synthesis of defectless NaMnPO4 with an olivine- and maricite-type structure. Cryst. Eng. Commun. 2013, 15, 98–989. [Google Scholar] [CrossRef]
- Lethole, N.L.; Ngoepe, P.E.; Chauke, H.R. First-principles study: Effect of lithium and sodium intercalation in transition metal phosphates, MPO4 (M: Mn, Fe, Co). Comput. Condens. Matter. 2020, 22, 00437. [Google Scholar] [CrossRef]
- Beckstein, O.; Klepeis, J.E.; Hart, G.L.W.; Pankratov, O. First-principles elastic constants and electronic structure of α−Pt2Si and PtSi. Phys. Rev. B Condens. Matter 2001, 63, 134112. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Joós, B. Stability criteria for homogeneously stressed materials and the calculation of elastic constants. Phys. Rev. B 1996, 54, 3841–3850. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical theory of crystal Lattices. Am. J. Phys. 1955, 23, 474. [Google Scholar] [CrossRef]
- Fast, L.; Wills, J.; Johansson, B.; Eriksson, O. Elastic constants of hexagonal transition metals: Theory. Phys. Rev. B 1995, 51, 17431–17438. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Khare, S.V.; Tuttle, B.R.; Bording, J.K.; Kodambaka, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev. B 2006, 73, 104118. [Google Scholar] [CrossRef] [Green Version]
- Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef] [Green Version]
- Ravindran, P.; Fast, L.; Korzhavyl, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Wang, D.; Wu, X.; Wang, Z.; Chen, L. Cracking causing cyclic instability of LiFePO4 cathode material. J. Power Sources 2005, 140, 125–128. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The elastic anisotropy of crystals. J. Appl. Phys. 1967, 38, 2010–2012. [Google Scholar] [CrossRef]
- Debye, P. On the Theory of Specific Heats. Ann. Phys. 1912, 39, 789–839. [Google Scholar] [CrossRef] [Green Version]
- Petit, A.T.; Dulong, P.L. Recherches sur quelques points importants de la Théorie de la Chaleur. Ann. Chim. Phys. 1819, 10, 395–413. [Google Scholar]


| Lattice Parameter | PBE + U = 5 | Exp [25] | % Deviations |
|---|---|---|---|
| a (Å) | 10.693 | 10.528 | 1.555 |
| b (Å) | 6.421 | 6.321 | 1.570 |
| c (Å) | 5.053 | 4.985 | 1.355 |
| Volume (Å3) | 346.995 | 331.74 | 4.951 |
| a (Å) | b (Å) | c (Å) | V (Å3) | V Deviation (%) | a Deviation (%) | b Deviation (%) | c Deviation (%) | |
|---|---|---|---|---|---|---|---|---|
| Na1MnPO4 | 10.693 | 6.421 | 5.053 | 346.995 | –– | –– | –– | –– |
| Na0.75MnPO4 | 10.537 | 6.325 | 5.066 | 337.644 | 2.7 | 1.5 | 1.5 | 0.3 |
| Na0.5MnPO4 | 10.350 | 6.231 | 5.062 | 326.453 | 3.3 | 1.8 | 1.5 | 0.1 |
| Na0.25MnPO4 | 10.082 | 6.166 | 5.028 | 312.509 | 4.3 | 2.6 | 1.0 | 0.7 |
| MnPO4 | 9.874 | 5.057 | 4.918 | 294.152 | 5.9 | 2.1 | 1.8 | 2.2 |
| Cij | Na1MnPO4 | Na0.75MnPO4 | Na0.5MnPO4 | Na0.25MnPO4 | MnPO4 |
|---|---|---|---|---|---|
| C11 | 124.46 | 116.46 | 119.25 | 116.19 | 201.63 |
| C12 | 61.43 | 50.10 | 35.94 | 17.73 | 55.84 |
| C13 | 58.55 | 48.93 | 43.67 | 36.24 | 72.41 |
| C22 | 125.29 | 127.87 | 140.41 | 171.12 | 153.41 |
| C23 | 51.49 | 33.59 | 21.92 | 9.29 | 38.30 |
| C33 | 148.46 | 131.67 | 114.56 | 94.66 | 139.66 |
| C44 | 42.28 | 32.12 | 25.48 | 24.25 | −39.20 |
| C55 | 49.01 | 47.22 | 46.74 | 45.05 | 56.59 |
| C66 | 46.71 | 38.99 | 36.35 | 33.95 | 11.88 |
| C11 + C22 − 2C12 | 126.89 | 144.13 | 187.78 | 251.85 | 243.36 |
| C11 + C33 − 2C13 | 155.82 | 150.27 | 146.47 | 138.37 | 196.47 |
| C22 + C33 − 2C23 | 170.79 | 192.36 | 211.13 | 247.20 | 216.47 |
| BH | GH | EH | B/G | ν | |
|---|---|---|---|---|---|
| Na1MnPO4 | 81.48 | 42.36 | 108.3 | 1.924 | 0.2785 |
| Na0.75MnPO4 | 69.97 | 38.78 | 98.19 | 1.805 | 0.2661 |
| Na0.5MnPO4 | 63.08 | 38.34 | 95.63 | 1.655 | 0.2473 |
| Na0.25MnPO4 | 53.76 | 37.25 | 90.74 | 1.443 | 0.2185 |
| MnPO4 | 89.81 | 35.73 | 94.05 | 2.514 | 0.1384 |
| Na1MnPO4 | 1.085 | 1.145 | 1.409 | 1.4 | 1.2 |
| Na0.75MnPO4 | 0.855 | 0.989 | 1.065 | 1.9 | 1.3 |
| Na0.5MnPO4 | 0.696 | 0.886 | 0.844 | 4.1 | 3.7 |
| Na0.25MnPO4 | 0.701 | 0.937 | 0.632 | 10.9 | 9.8 |
| MnPO4 | −0.798 | 1.046 | 0.226 | 8.9 | 7.6 |
| Na1MnPO4 | 3309 | 3576 | 6454 | 3984 | 512.7 |
| Na0.75MnPO4 | 3288 | 3435 | 6084 | 3821 | 490.0 |
| Na0.5MnPO4 | 3284 | 3417 | 5897 | 3792 | 485.0 |
| Na0.25MnPO4 | 3308 | 3357 | 5593 | 3713 | 476.2 |
| MnPO4 | 3385 | 3379 | 5216 | 3707 | 497.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dima, R.S.; Maleka, P.M.; Maluta, N.E.; Maphanga, R.R. Structural, Electronic, Mechanical, and Thermodynamic Properties of Na Deintercalation from Olivine NaMnPO4: First-Principles Study. Materials 2022, 15, 5280. https://doi.org/10.3390/ma15155280
Dima RS, Maleka PM, Maluta NE, Maphanga RR. Structural, Electronic, Mechanical, and Thermodynamic Properties of Na Deintercalation from Olivine NaMnPO4: First-Principles Study. Materials. 2022; 15(15):5280. https://doi.org/10.3390/ma15155280
Chicago/Turabian StyleDima, Ratshilumela S., Prettier M. Maleka, Nnditshedzeni E. Maluta, and Rapela R. Maphanga. 2022. "Structural, Electronic, Mechanical, and Thermodynamic Properties of Na Deintercalation from Olivine NaMnPO4: First-Principles Study" Materials 15, no. 15: 5280. https://doi.org/10.3390/ma15155280
APA StyleDima, R. S., Maleka, P. M., Maluta, N. E., & Maphanga, R. R. (2022). Structural, Electronic, Mechanical, and Thermodynamic Properties of Na Deintercalation from Olivine NaMnPO4: First-Principles Study. Materials, 15(15), 5280. https://doi.org/10.3390/ma15155280






