Alkali Niobate Powder Synthesis Using an Emerging Microwave-Assisted Hydrothermal Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Regent Suspension Preparation and Hydrothermal Microwave-Assisted (HTMW) Maturation
2.2. Characterization Methods
3. Results and Discussion
3.1. X-ray Fluorescence Spectra
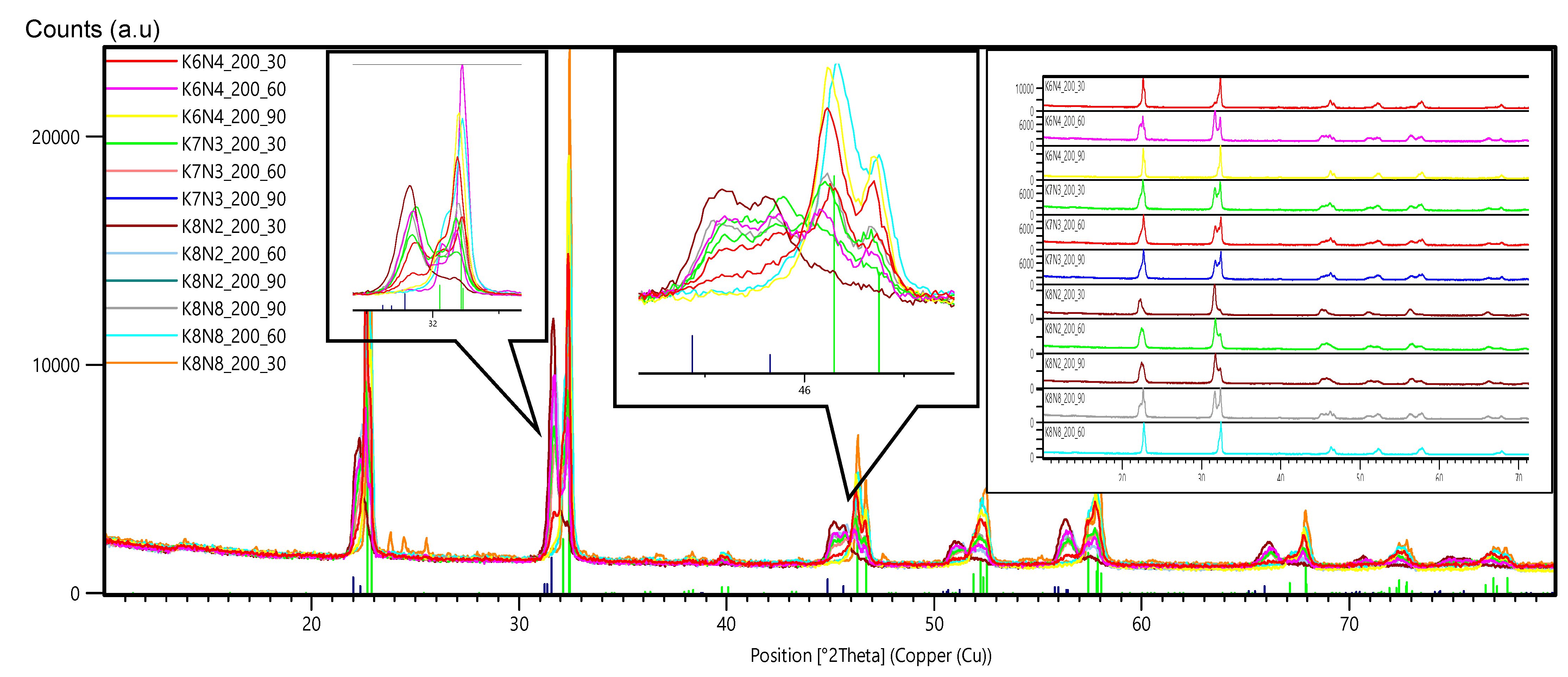
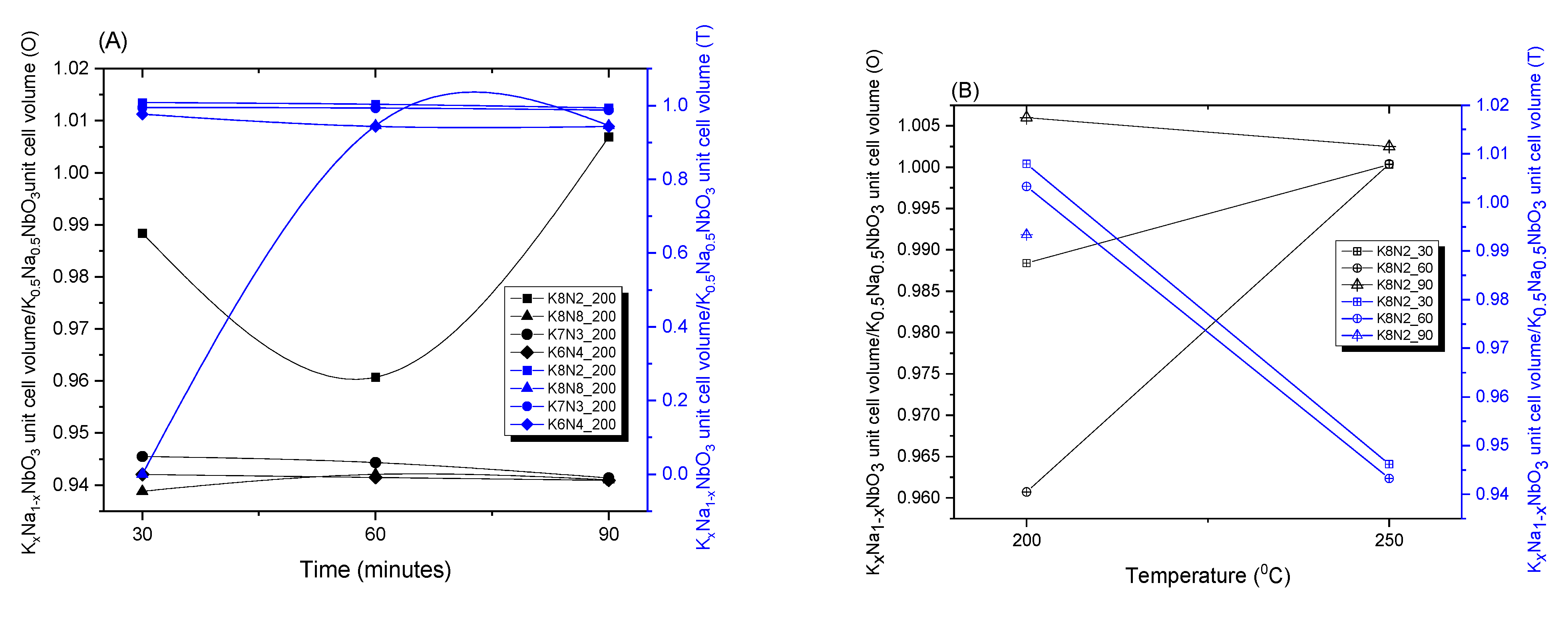
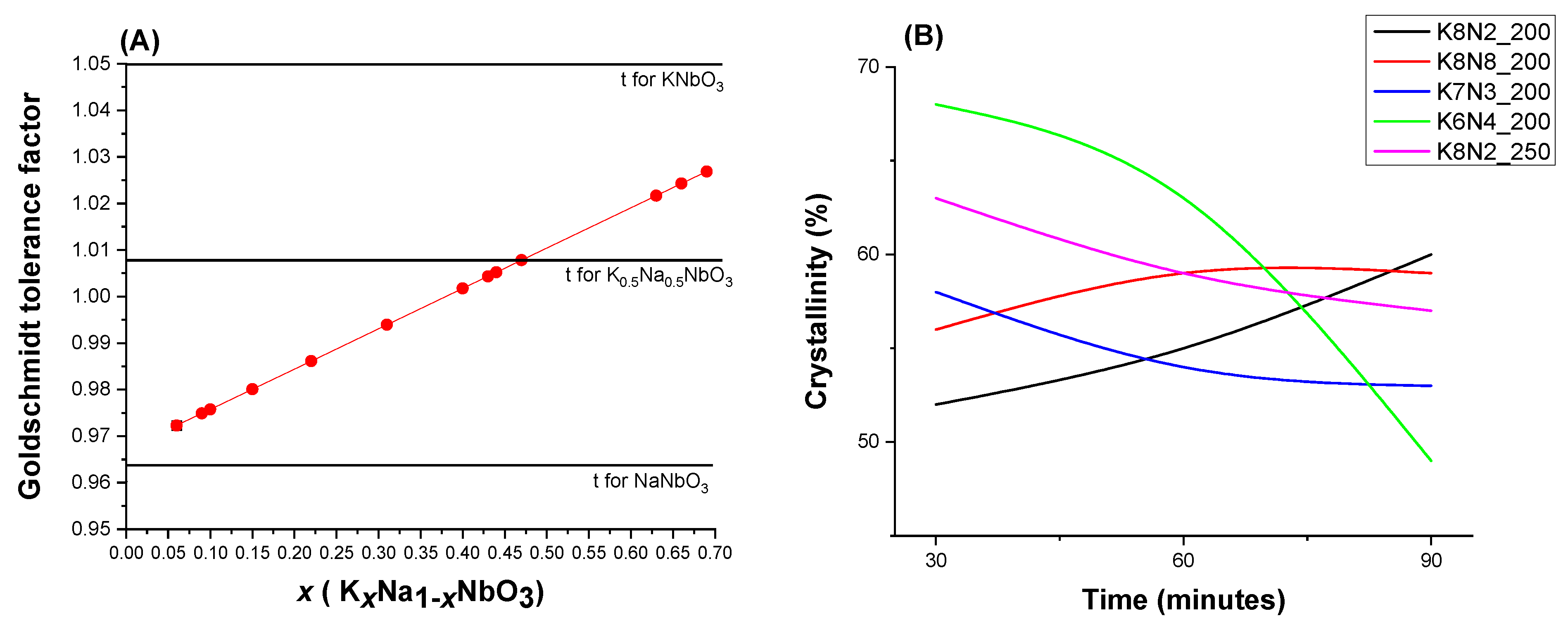
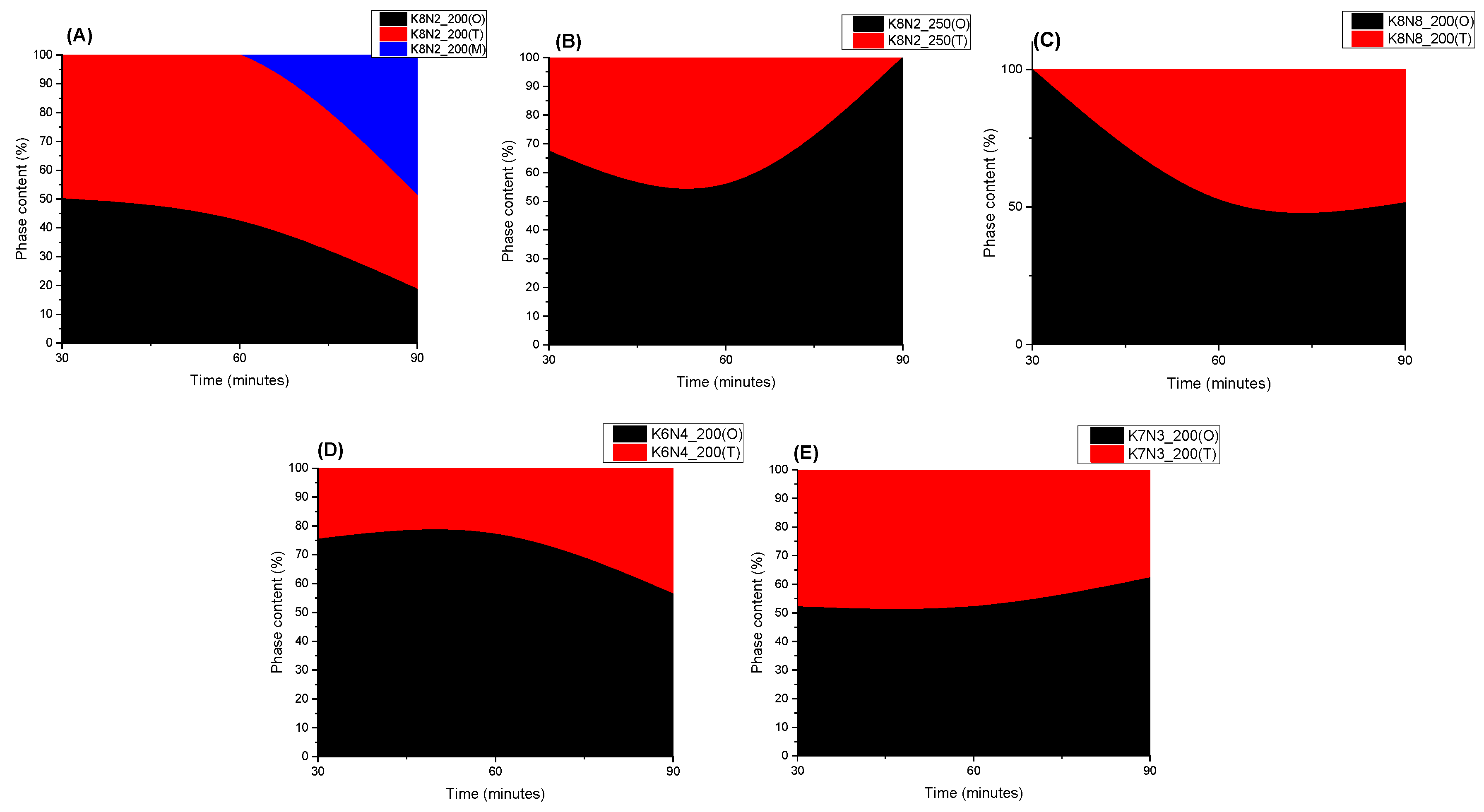
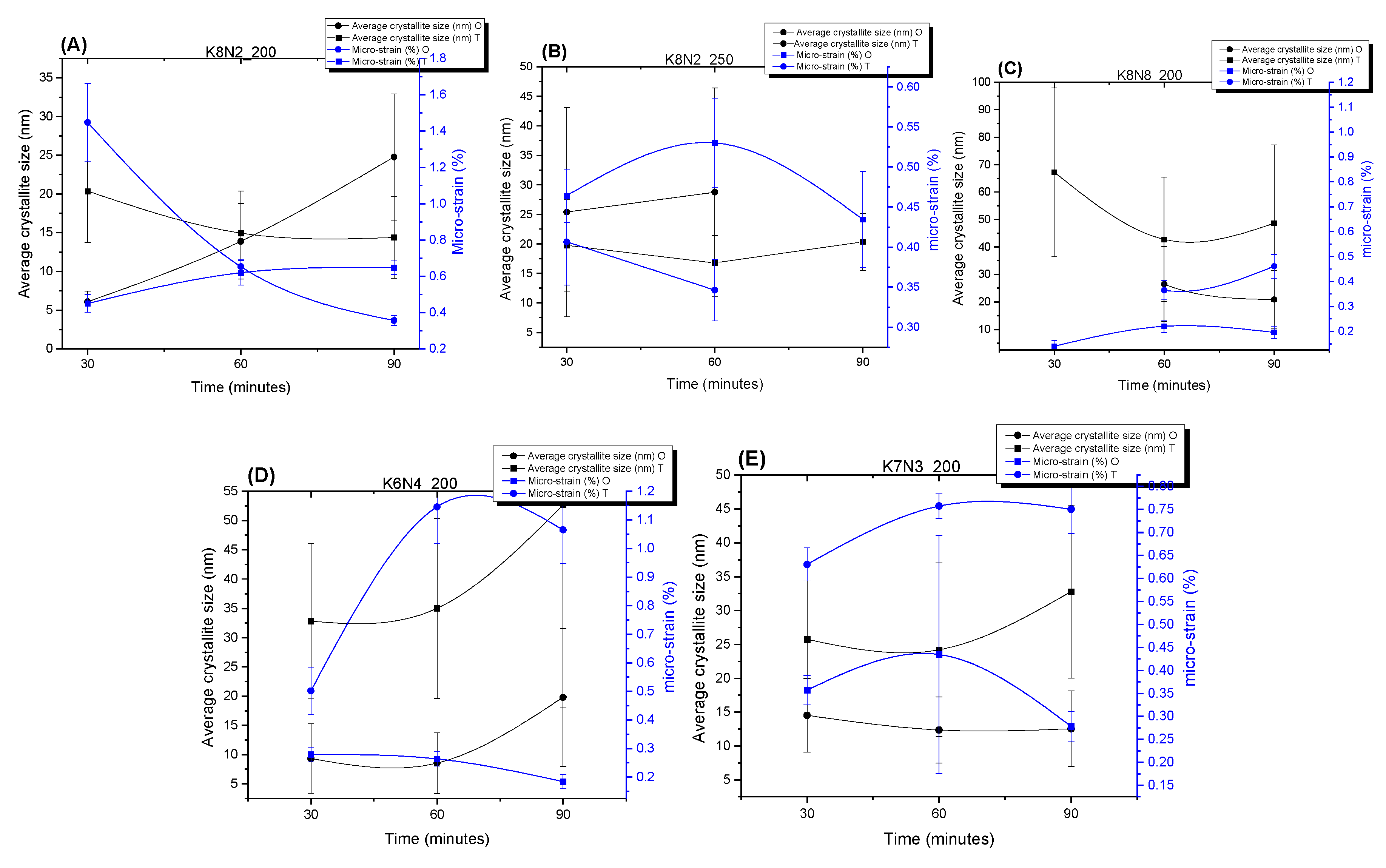
3.2. X-ray Powder Diffraction (XRPD) and Rietveld Structure Refinement
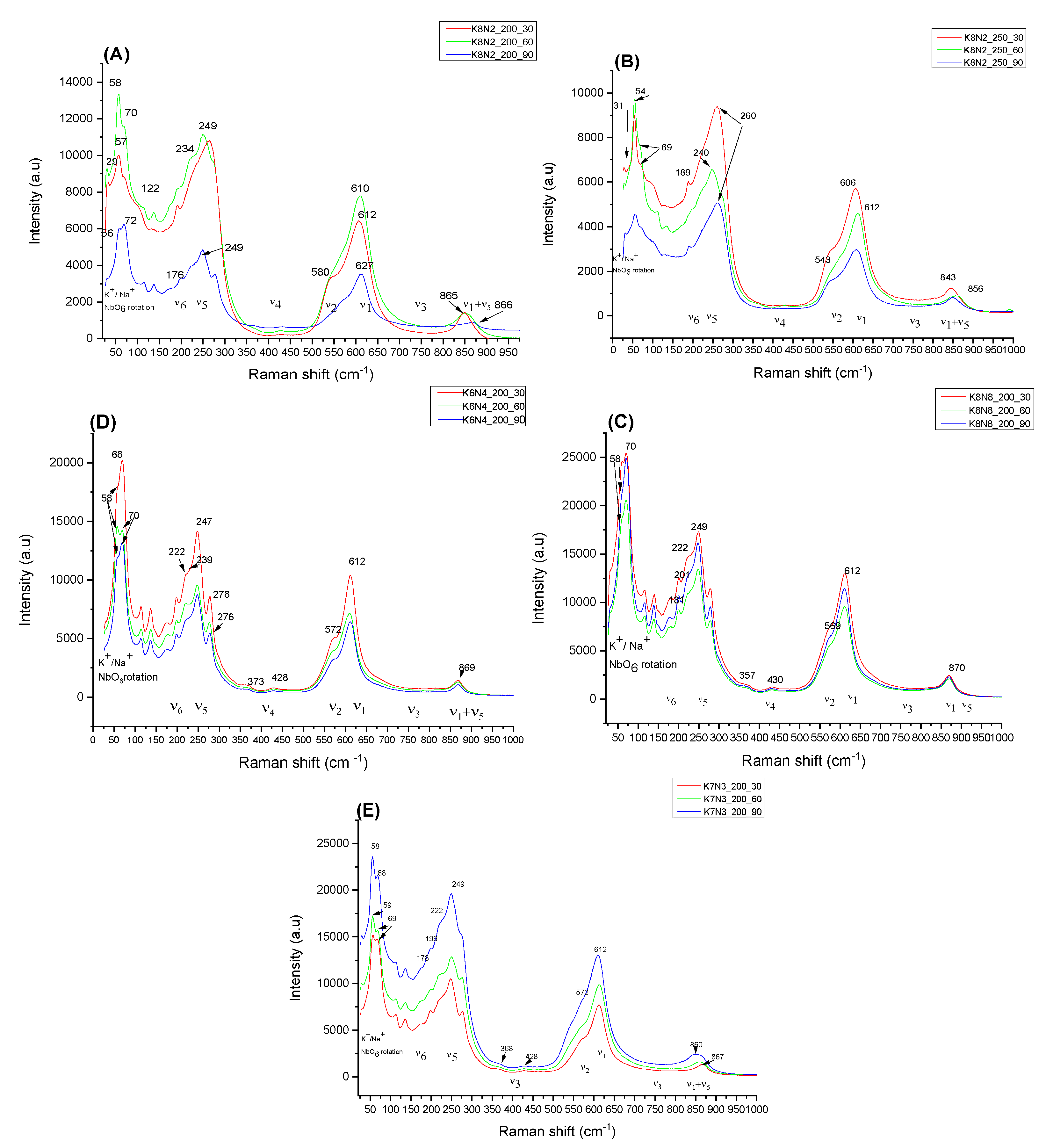
3.3. Raman Spectra
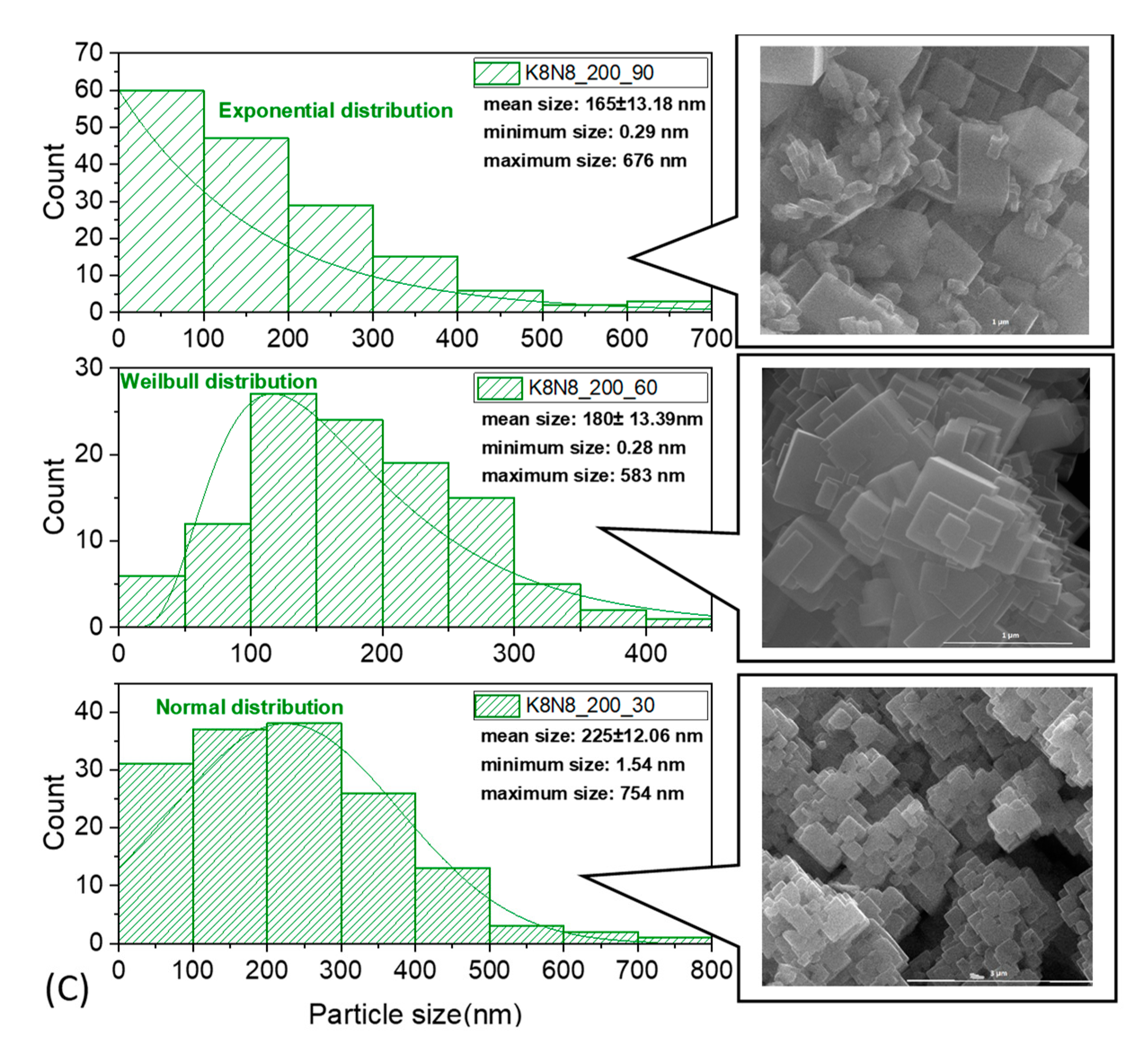
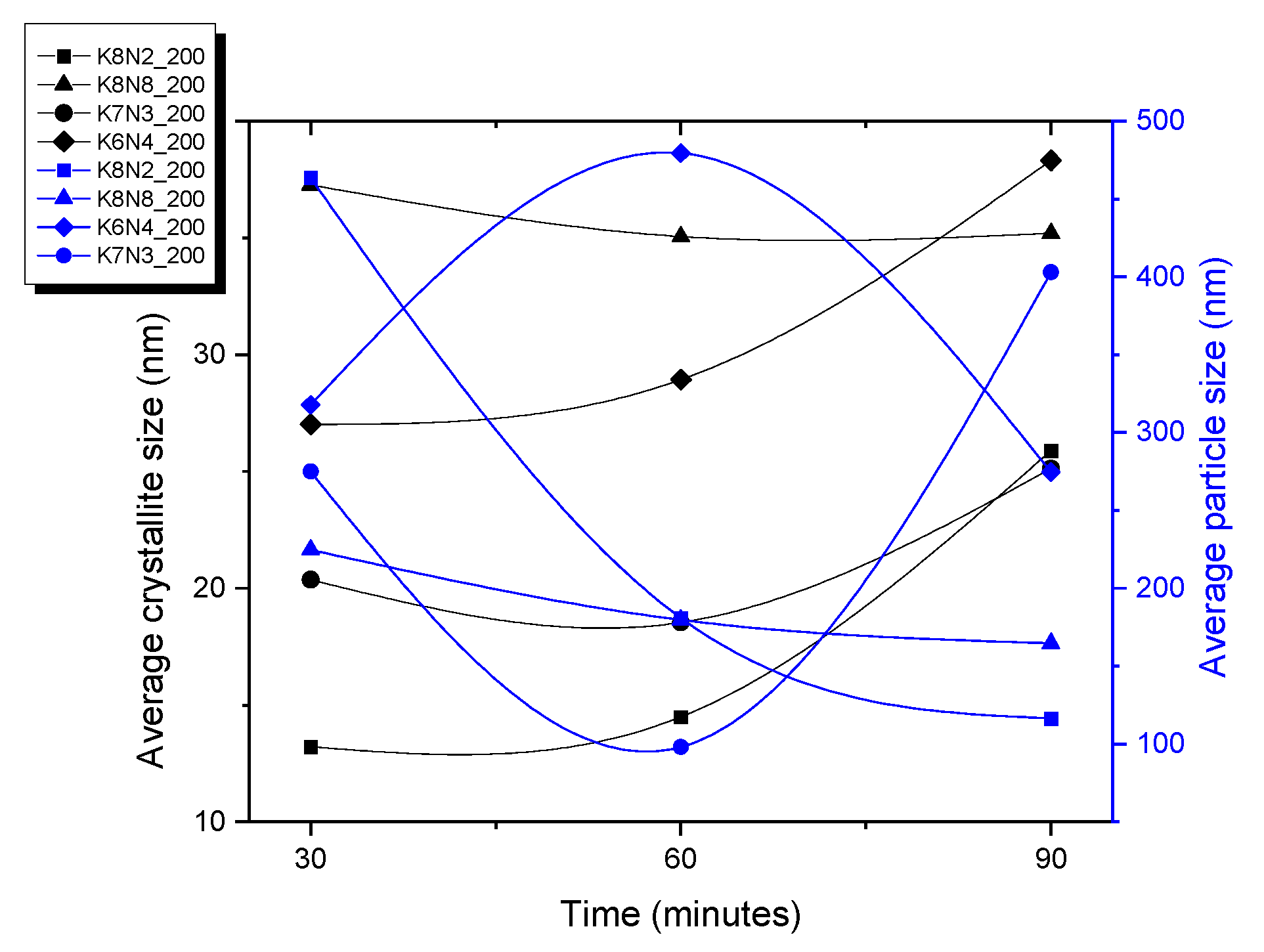
3.4. Scanning Electron Microscopy
3.5. Transmission Electron Microscopy (TEM)
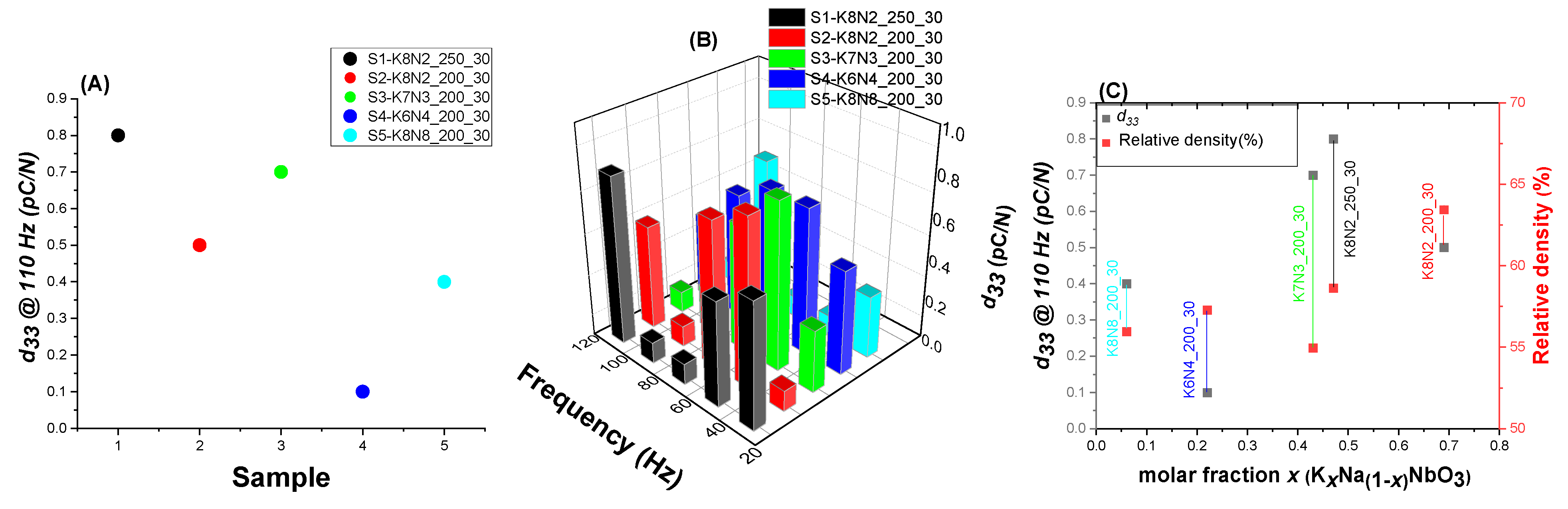
3.6. Piezoelectric Constant Measurement
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]
- Ma, J.; Jia, Y.; Chen, L.; Zheng, Y.; Wu, Z.; Luo, W.; Jiang, M.; Cui, X.; Li, Y. Dye wastewater treatment driven by cyclically heating/ cooling the poled (K0.5Na0.5)NbO3 pyroelectric crystal catalyst. J. Clean. Prod. 2020, 276, 124218. [Google Scholar] [CrossRef]
- Huang, J.S.; Liew, J.X.; Ademiloye, A.S.; Liew, K.M. Artificial Intelligence in Materials Modeling and Design. Arch. Comput. Methods Eng. 2020, 28, 3399–3413. [Google Scholar] [CrossRef]
- Zhang, D.-Q.; Wang, D.-W.; Zhu, H.-B.; Yang, X.-Y.; Lu, R.; Wen, B.; Cao, W.-Q.; Yuan, J.; Cao, M.-S. Synthesis and characterization of single-crystalline (K,Na)NbO3 nanorods. Ceram. Int. 2013, 39, 5931–5935. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Singh, S. Coexistence of Large Negative and Positive Electrocaloric Effects and Energy Storage Performance in LiNbO3 Doped K0.5Na0.5NbO3 Nanocrystalline Ceramics. ACS Appl. Electron. Mater. 2019, 1, 454–460. [Google Scholar] [CrossRef]
- Lv, X.; Zhu, J.; Xiao, D.; Zhang, X.X.; Wu, J. Emerging new phase boundary in potassium sodium-niobate based ceramics. Chem. Soc. Rev. 2020, 49, 671–707. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, J. Feasible acid-etching method for investigating temperature-dependent domain configurations of ferroelectric ceramics. J. Eur. Ceram. Soc. 2020, 40, 4469–4474. [Google Scholar] [CrossRef]
- Cui, A.; Cao, X.; Ye, Y.; Jiang, K.; Zhu, L.; Jiang, M.; Rao, G.; Li, Y.; Hu, Z.; Chu, J. Phase transitions and phonon thermodynamics in giant piezoelectric Mn-doped K0.5Na0.5NbO3-LiBiO3 crystals studied by Raman spectroscopy. Phys. Rev. B 2020, 102, 214102. [Google Scholar] [CrossRef]
- Guo, X.; Xiao, P.; Liu, J.; Shen, Z. Fabrication of Nanostructured Hydroxyapatite via Hydrothermal Synthesis and Spark Plasma Sintering. J. Am. Ceram. Soc. 2005, 88, 1026–1029. [Google Scholar] [CrossRef]
- Kohlenbach, N.D.; Kijatkin, C.; Konig, M.; Haase, M.; Imlau, M.; Kompe, K. The role of cations in hydrothermal synthesis of nonlinear optical sodium niobate nanocrystals. Nanoscale 2020, 12, 19223–19229. [Google Scholar] [CrossRef]
- Lv, X.; Wu, J.; Zhang, X.-X. Reduced degree of phase coexistence in KNN-Based ceramics by competing additives. J. Eur. Ceram. Soc. 2020, 40, 2945–2953. [Google Scholar] [CrossRef]
- Xing, J.; Jiang, L.; Zhao, C.; Tan, Z.; Xu, Q.; Wu, J.; Chen, Q.; Xiao, D.; Zhu, J. Potassium sodium niobate based lead-free ceramic for high-frequency ultrasound transducer applications. J. Mater. 2020, 6, 513–522. [Google Scholar] [CrossRef]
- Ito, Y.; Tateyama, A.; Nakamura, Y.; Shimizu, T.; Kurosawa, M.; Uchida, H.; Shiraishi, T.; Kiguchi, T.; Konno, T.J.; Ishikawa, M.; et al. High yield preparation of (100)c-oriented (K,Na)NbO3 thick films by hydrothermal method using amorphous niobium source. J. Ceram. Soc. Jpn. 2020, 128, 512–517. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.-F. Review of chemical modification on potassium sodium niobate lead-free piezoelectrics. J. Mater. Chem. C 2019, 7, 4284–4303. [Google Scholar] [CrossRef]
- Sharma, J.P.; Kumar, D.; Sharma, A.K. Structural and dielectric properties of pure potassium sodium niobate (KNN) lead free ceramics. Solid State Commun. 2021, 334–335, 114345. [Google Scholar] [CrossRef]
- Xu, Q.; Gao, X.; Zhao, S.; Liu, Y.N.; Zhang, D.; Zhou, K.; Khanbareh, H.; Chen, W.; Zhang, Y.; Bowen, C. Construction of Bio-Piezoelectric Platforms: From Structures and Synthesis to Applications. Adv. Mater. 2021, 33, e2008452. [Google Scholar] [CrossRef]
- Montoya, C.; Du, Y.; Gianforcaro, A.L.; Orrego, S.; Yang, M.; Lelkes, P.I. On the road to smart biomaterials for bone research: Definitions, concepts, advances, and outlook. Bone Res. 2021, 9, 12. [Google Scholar] [CrossRef]
- Li, J.; Long, Y.; Yang, F.; Wang, X. Degradable Piezoelectric Biomaterials for Wearable and Implantable Bioelectronics. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100806. [Google Scholar] [CrossRef]
- Zheng, T.; Huang, Y.; Zhang, X.; Cai, Q.; Deng, X.; Yang, X. Mimicking the electrophysiological microenvironment of bone tissue using electroactive materials to promote its regeneration. J. Mater. Chem. B 2020, 8, 10221–10256. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Mandal, D. Envisioned strategy for an early intervention in virus-suspected patients through non-invasive piezo- and pyro-electric-based wearable sensors. J. Mater. Chem. A 2021, 9, 1887–1909. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, L.; Duan, Z.; Zhao, K.; Wu, Z. Enhanced compressive strengths and induced cell growth of 1-3-type BaTiO3/PMMA bio-piezoelectric composites. Mater. Sci. Eng. C 2021, 120, 111699. [Google Scholar] [CrossRef] [PubMed]
- Khare, D.; Basu, B.; Dubey, A.K. Electrical stimulation and piezoelectric biomaterials for bone tissue engineering applications. Biomaterials 2020, 258, 120280. [Google Scholar] [PubMed]
- Hiley, C.I.; Walton, R.I. Controlling the Crystallisation of Oxide Materials by Solvothermal Chemistry: Tuning Composition, Substitution and Morphology of Functional Solids. CrystEngComm 2016, 18, 7656–7670. [Google Scholar] [CrossRef]
- Politova, E.D.; Golubko, N.V.; Kaleva, G.M.; Mosunov, A.V.; Sadovskaya, N.V.; Stefanovich, S.Y.; Kiselev, D.A.; Kislyuk, A.M.; Chichkov, M.V.; Panda, P.K. Structure, ferroelectric and piezoelectric properties of KNN-based perovskite ceramics. Ferroelectrics 2019, 538, 45–51. [Google Scholar] [CrossRef]
- Hussain, F.; Khesro, A.; Lu, Z.; Alotaibi, N.; Mohamad, A.A.; Wang, G.; Wang, D.; Zhou, D. Acceptor and Donor Dopants in Potassium Sodium Niobate Based Ceramics. Front. Mater. 2020, 7, 160. [Google Scholar] [CrossRef]
- Park, S.; Peddigari, M.; Kim, J.H.; Kim, E.; Hwang, G.T.; Kim, J.W.; Ahn, C.W.; Choi, J.J.; Hahn, B.D.; Choi, J.H.; et al. Selective Phase Control of Dopant-Free Potassium Sodium Niobate Perovskites in Solution. Inorg. Chem. 2020, 59, 3042–3052. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Y.; Wu, J.; Wang, J.; Pennycook, S.J. Microstructural Origins of High Piezoelectric Performance: A Pathway to Practical Lead-Free Materials. Adv. Funct. Mater. 2019, 29, 1902911. [Google Scholar] [CrossRef]
- Garcia, J.E.; Rubio-Marcos, F. Polymorphic phase boundary in piezoelectric oxides. J. Appl. Phys. 2020, 127, 131102. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Zhang, Y.; Gao, J.; Zhou, Z.; Yang, D.; Lee, K.-Y.; Studer, A.; Hinterstein, M.; Wang, K.; Zhang, X.; et al. Practical High-Performance Lead-Free Piezoelectrics: Structural Flexibility Beyond Utilizing Multiphase Coexistence. Natl. Sci. Rev. 2020, 7, 355–365. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Ma, J.; Gou, Q.; Wu, W.; Chen, M. Enhanced temperature stability in the O–T phase boundary of (K, Na)NbO3-based ceramics. J. Am. Ceram. Soc. 2019, 103, 1698–1708. [Google Scholar] [CrossRef]
- Sun, X.-X.; Zhang, J.; Lv, X.; Zhang, X.-X.; Liu, Y.; Li, F.; Wu, J. Understanding the piezoelectricity of high-performance potassium sodium niobate ceramics from diffused multi-phase coexistence and domain feature. J. Mater. Chem. A 2019, 7, 16803–16811. [Google Scholar] [CrossRef]
- Malic, B.; Koruza, J.; Hrescak, J.; Bernard, J.; Wang, K.; Fisher, J.G.; Bencan, A. Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics. Materials 2015, 8, 8117–8146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rubio-Marcos, F.; Romero, J.J.; Martín-Gonzalez, M.S.; Fernández, J.F. Effect of stoichiometry and milling processes in the synthesis and the piezoelectric properties of modified KNN nanoparticles by solid state reaction. J. Eur. Ceram. Soc. 2010, 30, 2763–2771. [Google Scholar] [CrossRef] [Green Version]
- Rubio-Marcos, F.; Romero, J.J.; Fernandez, J.F. Effect of the temperature on the synthesis of (K,Na)NbO3-modified nanoparticles by a solid state reaction route. J. Nanopart. Res. 2009, 12, 2495–2502. [Google Scholar] [CrossRef]
- Cheng, L.-Q.; Zhou, J.-J.; Wang, K.; Li, J.-F.; Wang, Q.-M. Influence of ball milling on sintering behavior and electrical properties of (Li, Na, K)NbO3 lead-free piezoceramics. J. Mater. Sci. 2012, 47, 6908–6914. [Google Scholar] [CrossRef]
- Shiratori, Y.; Magrez, A.; Pithan, C. Phase transformation of KNaNb2O6 induced by size effect. Chem. Phys. Lett. 2004, 391, 288–292. [Google Scholar] [CrossRef]
- Zhen, Y.; Li, J.-F. Normal Sintering of (K, Na)NbO3-Based Ceramics: Influence of Sintering Temperature on Densification, Microstructure, and Electrical Properties. J. Am. Ceram. Soc. 2006, 89, 3669–3675. [Google Scholar] [CrossRef]
- Hungría, T.; Galy, J.; Castro, A. Spark Plasma Sintering as a Useful Technique to the Nanostructuration of Piezo-Ferroelectric Materials. Adv. Eng. Mater. 2009, 11, 615–631. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, Y.; Zhao, L.; Gao, J.; Zhou, Z.; Wang, K.; Zhang, X.; Li, L.; Li, J.-F. Simultaneous enhancement of piezoelectricity and temperature stability in (K, Na)NbO3-based lead-free piezoceramics by incorporating perovskite zirconates. J. Mater. Chem. C 2018, 6, 10618–10627. [Google Scholar] [CrossRef]
- Zheng, T.; Wu, J. Electric field compensation effect driven strain temperature stability enhancement in potassium sodium niobate ceramics. Acta Mater. 2020, 182, 1–9. [Google Scholar] [CrossRef]
- Lv, X.; Wu, J.; Zhang, X.-X. A new concept to enhance piezoelectricity and temperature stability in KNN ceramics. Chem. Eng. J. 2020, 402, 126215. [Google Scholar] [CrossRef]
- Walton, R.I. Perovskite Oxides Prepared by Hydrothermal and Solvothermal Synthesis: A Review of Crystallisation, Chemistry, and Compositions. Chemistry 2020, 26, 9041–9069. [Google Scholar] [CrossRef] [PubMed]
- Oghbaei, M.; Mirzaee, O. Microwave versus conventional sintering: A review of fundamentals, advantages and applications. J. Alloys Compd. 2010, 494, 175–189. [Google Scholar] [CrossRef]
- Feizpour, M.; Barzegar Bafrooei, H.; Hayati, R.; Ebadzadeh, T. Microwave-assisted synthesis and sintering of potassium sodium niobate lead-free piezoelectric ceramics. Ceram. Int. 2014, 40, 871–877. [Google Scholar] [CrossRef]
- Yang, G.; Park, S.J. Conventional and Microwave Hydrothermal Synthesis and Application of Functional Materials: A Review. Materials 2019, 12, 1177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Yan, Y.; Wang, G.; Li, Q.; Gu, Y.; Huang, J. Hydrothermal solvothermal synthesis potassium sodium niobate lead-free piezoelectric ceramics assisted with microwave. J. Mater. Sci. 2017, 29, 746–752. [Google Scholar] [CrossRef]
- Ji, S.; Liu, H.; Sang, Y.; Liu, W.; Yu, G.; Leng, Y. Synthesis, Structure, and Piezoelectric Property of Ferroelectric and Antiferroelectric NaNbO3 Nanostructures. CrystEngComm 2014, 16, 7598–7604. [Google Scholar] [CrossRef]
- Sun, C.; Xing, X.; Chen, J.; Deng, J.; Li, L.; Yu, R.; Qiao, L.; Liu, G. Hydrothermal Synthesis of Single Crystalline (K,Na)NbO3 Powders. Eur. J. Inorg. Chem. 2007, 2007, 1884–1888. [Google Scholar] [CrossRef]
- Hassan, M.N.; Mahmoud, M.M.; El-Fattah, A.A.; Kandil, S. Microwave-assisted preparation of Nano-hydroxyapatite for bone substitutes. Ceram. Int. 2016, 42, 3725–3744. [Google Scholar] [CrossRef]
- Kanie, K.; Mizutani, H.; Terabe, A.; Numamoto, Y.; Tsukamoto, S.; Takahashi, H.; Nakaya, M.; Tani, J.; Muramatsu, A. Precursor Effect on Hydrothermal Synthesis of Sodium Potassium Niobate Fine Particles and Their Piezoelectric Properties. Jpn. J. Appl. Phys. 2011, 50, 09ND09. [Google Scholar] [CrossRef]
- Fang, C.Y.; Randal, C.A.; Lanagan, M.T.; Agrawal, D.K. Microwave processing of electroceramic materials and devices. J. Electroceramics 2008, 22, 125–130. [Google Scholar] [CrossRef]
- Wojnarowicz, J.; Chudoba, T.; Majcher, A.; Łojkowski, W. 12. Microwaves applied to hydrothermal synthesis of nanoparticles. In Microwave Chemistry; Walter de Gruyter: Berlin, Germany, 2017; pp. 205–224. [Google Scholar]
- González-Prieto, R.; Herrero, S.; Jiménez-Aparicio, R.; Morán, E.; Prado-Gonjal, J.; Priego, J.L.; Schmidt, R. Microwave-assisted solvothermal synthesis of inorganic compounds (molecular and non molecular). Methods 2017, 10, 225–247. [Google Scholar]
- Horikoshi, S.; Serpone, N. 14. Microwave-assisted synthesis of nanoparticles. In Microwave Chemistry; Walter de Gruyter: Berlin, Germany, 2017; pp. 248–269. [Google Scholar]
- Kuscer, D.; Kocjan, A.; Majcen, M.; Meden, A.; Radan, K.; Kovač, J.; Malič, B. Evolution of phase composition and microstructure of sodium potassium niobate –based ceramic during pressure-less spark plasma sintering and post-annealing. Ceram. Int. 2019, 45, 10429–10437. [Google Scholar] [CrossRef]
- Zlouzeova, K. Partially Sintered Lead-Free Ceramics from Piezoelectric Powders Prepared Via Conventional Firing and Spark Plasma Sintering (Sps)-Characterization of Microstructure and Dielectric Properties. Ceramics—Silikaty 2021, 65, 30–37. [Google Scholar] [CrossRef]
- Ahtee, M.; Glazer, A.M. Lattice Parameters and Tilted Octahedra in Sodium-Potassium Niobate Solid Solutions. Acta Cryst. 1976, A32, 434–446. [Google Scholar] [CrossRef]
- Rao, C.N.R. Perovskites. In Encyclopedia of Physical Science and Technology; Academic Press: New York, NY, USA, 2003; pp. 707–714. [Google Scholar]
- Sebastian, M.T. ABO3 TYPE PEROVSKITES. In Dielectric Materials for Wireless Communications; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- López-Juárez, R.; Castañeda-Guzmán, R.; Villafuerte-Castrejón, M.E. Fast synthesis of NaNbO3 and K0.5Na0.5NbO3 by microwave hydrothermal method. Ceram. Int. 2014, 40, 14757–14764. [Google Scholar] [CrossRef]
- Brahlek, M.; Choquette, A.K.; Smith, C.R.; Engel-Herbert, R.; May, S.J. Structural refinement ofPbnm-type perovskite films from analysis of half-order diffraction peaks. J. Appl. Phys. 2017, 121, 045303. [Google Scholar] [CrossRef]
- Chowdhury, A.; Bould, J.; Zhang, Y.; James, C.; Milne, S.J. Nano-powders of Na0.5K0.5NbO3 made by a sol–gel method. J. Nanopart. Res. 2009, 12, 209–215. [Google Scholar] [CrossRef]
- Rubio-Marcos, F.; Lopez-Juarez, R.; Rojas-Hernandez, R.E.; del Campo, A.; Razo-Perez, N.; Fernandez, J.F. Lead-Free Piezoceramics: Revealing the Role of the Rhombohedral-Tetragonal Phase Coexistence in Enhancement of the Piezoelectric Properties. ACS Appl. Mater. Interfaces 2015, 7, 23080–23088. [Google Scholar] [CrossRef]
- Petkov, V.; Kim, J.W.; Shastri, S.; Gupta, S.; Priya, S. Geometrical frustration and piezoelectric response in oxide ferroics. Phys. Rev. Mater. 2020, 4, 014405. [Google Scholar] [CrossRef]
- Bartel, C.J.; Sutton, C.; Goldsmith, B.R.; Ouyang, R.; Musgrave, C.B.; Ghiringhelli, L.M.; Scheffler, M. New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv. 2019, 5, eaav0693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, Z.X.; Wang, X.B.; Kuok, M.H.; Tang, S.H. Raman Scattering Investigations of the Antiferroelectric–Ferroelectric Phase Transition of NaNbO3. J. Raman Spectrosc. 1998, 29, 379–384. [Google Scholar] [CrossRef]
- Golovina, I.S.; Bryksa, V.P.; Strelchuk, V.V.; Geifman, I.N.; Andriiko, A.A. Size effects in the temperatures of phase transitions in KNbO3nanopowder. J. Appl. Phys. 2013, 113, 144103. [Google Scholar] [CrossRef]
- Mahdi, R.; Al-Bahnam, N.J.; Ajeel, M.A.; Al-Keisy, A.; Hussein, T.A.; Majid, W.H.A. High-performance (K,Na)NbO3-based binary lead-free piezoelectric ceramics modified with acceptor metal oxide. Ceram. Int. 2020, 46, 21762–21770. [Google Scholar] [CrossRef]
- Hu, C.; Meng, X.; Zhang, M.-H.; Tian, H.; Daniels, J.E.; Tan, P.; Huang, F.; Li, L.; Wang, K.; Li, J.-F.; et al. Ultra-large electric field induced strain in potassium sodium niobate crystals. Sci. Adv. 2020, 6, eaay5979. [Google Scholar] [CrossRef] [Green Version]
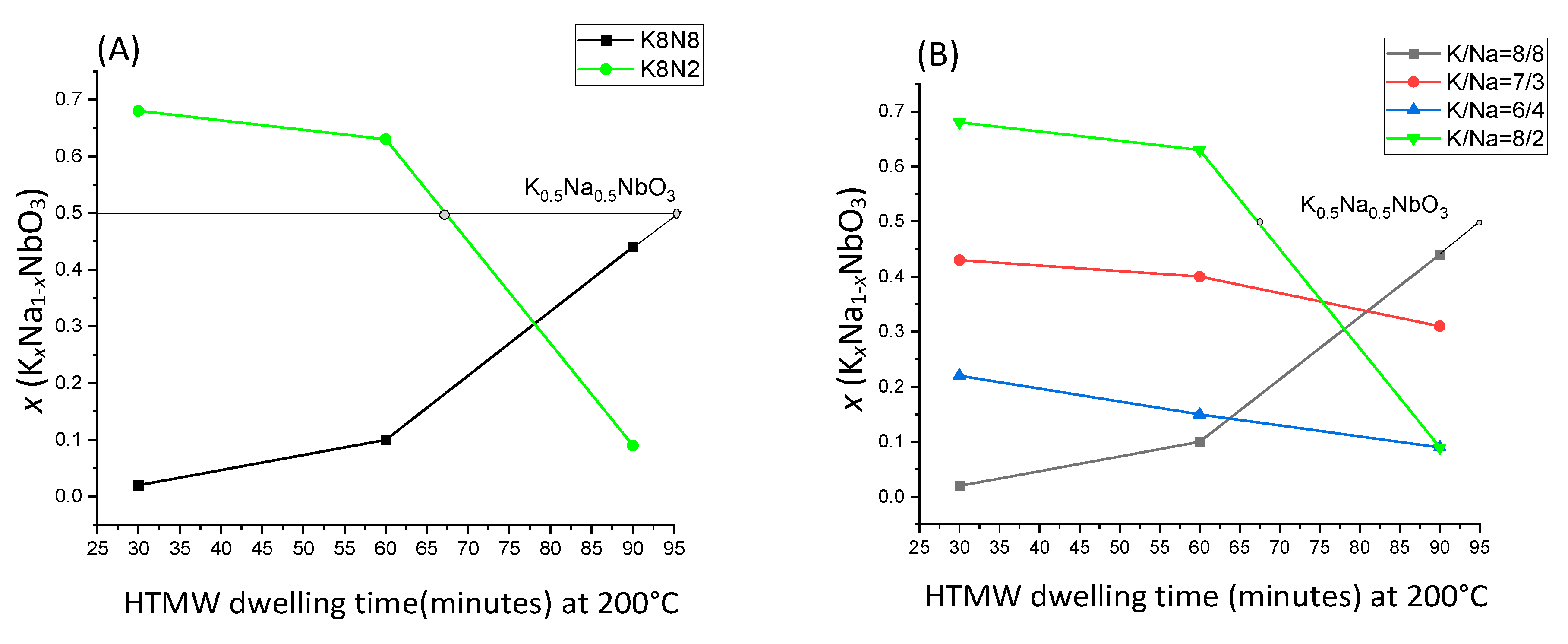
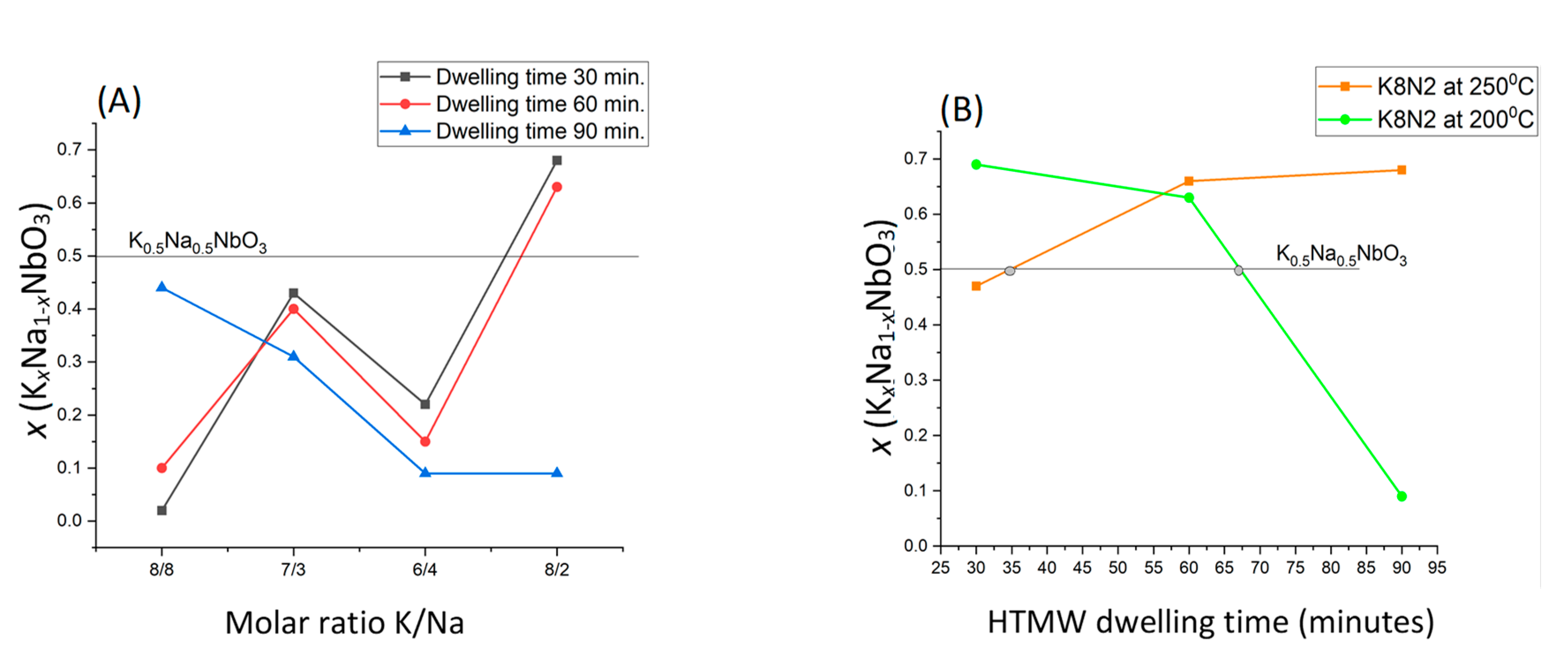




| Sample Precursors K/Na Rate | x Value (KxNa1−xNbO3) Evaluated from XRF Analysis Temperature(°C)_ Time (Minutes) | x Value (KxNa1−xNbO3) Evaluated from EDS-SEM Analysis Temperature(°C)_ Time (Minutes) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 200_30 | 200_60 | 200_90 | 250_30 | 250_60 | 250_90 | 200_30 | 200_60 | 200_90 | 250_30 | 250_60 | 250_90 | |
| K8N8 1:1 = 1 | 0.06 | 0.10 | 0.44 | - | - | - | 0.03–0.07 | 0.02–0.05 | 0.24–0.28 | - | - | - |
| K7N3 7:3 = 2.33 | 0.43 | 0.40 | 0.31 | - | - | - | 0.31–0.36 | 0.30–0.32 | 0.10–0.28 | - | - | - |
| K6N4 3:2 = 1.5 | 0.22 | 0.15 | 0.09 | - | - | - | 0.13–0.18 | 0.17–0.18 | 0.01–0.09 | - | - | - |
| K8N2 4:1 = 4 | 0.69 | 0.63 | 0.09 | 0.47 | 0.66 | 0.68 | 0.60–0.61 | 0.35–0.48 | 0.10–0.12 | 0.40–0.42 | 0.40–0.5 | 0.55–0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dumitrescu, C.-R.; Surdu, V.-A.; Stroescu, H.; Nicoara, A.-I.; Neacsu, I.A.; Trusca, R.; Andronescu, E.; Ciocan, L.T. Alkali Niobate Powder Synthesis Using an Emerging Microwave-Assisted Hydrothermal Method. Materials 2022, 15, 5410. https://doi.org/10.3390/ma15155410
Dumitrescu C-R, Surdu V-A, Stroescu H, Nicoara A-I, Neacsu IA, Trusca R, Andronescu E, Ciocan LT. Alkali Niobate Powder Synthesis Using an Emerging Microwave-Assisted Hydrothermal Method. Materials. 2022; 15(15):5410. https://doi.org/10.3390/ma15155410
Chicago/Turabian StyleDumitrescu, Cristina-Rodica, Vasile-Adrian Surdu, Hermine Stroescu, Adrian-Ionut Nicoara, Ionela Andreea Neacsu, Roxana Trusca, Ecaterina Andronescu, and Lucian Toma Ciocan. 2022. "Alkali Niobate Powder Synthesis Using an Emerging Microwave-Assisted Hydrothermal Method" Materials 15, no. 15: 5410. https://doi.org/10.3390/ma15155410








